Investigation into local white matter abnormality in emotional processing and sensorimotor areas using an automatically annotated fiber clustering in major depressive disorder

Abstract

This work presents an automatically annotated fiber cluster (AAFC) method to enable identification of anatomically meaningful white matter structures from the whole brain tractography. The proposed method consists of 1) a study-specific whole brain white matter parcellation using a well-established data-driven groupwise fiber clustering pipeline to segment tractography into multiple fiber clusters, and 2) a novel cluster annotation method to automatically assign an anatomical tract annotation to each fiber cluster by employing cortical parcellation information across multiple subjects. The novelty of the AAFC method is that it leverages group-wise information about the fiber clusters, including their fiber geometry and cortical terminations, to compute a tract anatomical label for each cluster in an automated fashion. We demonstrate the proposed AAFC method in an application of investigating white matter abnormality in emotional processing and sensorimotor areas in major depressive disorder (MDD). Seven tracts of interest related to emotional processing and sensorimotor functions are automatically identified using the proposed AAFC method as well as a comparable method that uses a cortical parcellation alone. Experimental results indicate that our proposed method is more consistent in identifying the tracts across subjects and across hemispheres in terms of the number of fibers. In addition, we perform a between-group statistical analysis in 31 MDD patients and 62 healthy subjects on the identified tracts using our AAFC method. We find statistical differences in diffusion measures in local regions within a fiber tract (e.g. 4 fiber clusters within the identified left hemisphere cingulum bundle (consisting of 14 clusters) are significantly different between the two groups), suggesting the ability of our method in identifying potential abnormality specific to subdivisions of a white matter structure.

1. Introduction

Diffusion magnetic resonance imaging (dMRI) enables detection of microstructural white matter (WM) changes in vivo (Makris et al., 1997; Pajevic and Basser, 2003; Shimony et al., 1999). dMRI tractography is a noninvasive neuroimaging technique that is able to identify WM fiber tracts in the human brain (Basser et al., 2000; Ciccarelli et al., 2008). A fiber tract is a collection of central nervous system axons having a common site of origin and a common destination (Makris et al., 1997; Noback et al., 2005). For instance, the corticospinal tract (CST) originates in the cerebral cortex and ends in the spinal cord. Important goals of tractography research are to identify brain connective structures in vivo and to measure biological properties of these structures that are sensitive to clinical abnormalities. To investigate local WM abnormalities in specific structures, tractography has been employed in quantitative analysis of scalar measures derived from the diffusion tensor, such as anisotropy or diffusivity measures (Johansen-Berg and Behrens, 2006; O’Donnell and Westin, 2011). Whole-brain tractography, however, produces an unstructured set of thousands of fiber trajectories by estimating the course of all connections in the entire WM, whereas clinical applications often demand targeted tracking of specific fiber tracts.

To understand such massive amounts of data, whole-brain tractography is often segmented to identify fiber tract(s) of interest. One commonly used method identifies key fiber tracts by requiring manual tracing of regions of interest (ROIs) followed by assessment of the fibers that pass through the ROIs (Mori et al., 2006). This manual identification of ROIs used to define fiber tracts is operator dependent and time-consuming (Huang et al., 2004). Moreover, manual selection methods can suffer from operator bias (Bürgel et al., 2009; Radmanesh et al., 2015; Voineskos et al., 2009). Therefore, a number of automatic tract identification strategies have been proposed, which can be generally categorized into cortical-parcellation-based (CPB) (Cloutman and Ralph, 2012; O’Donnell et al., 2013; Wassermann et al., 2016) and fiber clustering (FC) methods (Guevara et al., 2016; Moberts et al., 2005; O’Donnell et al., 2013). CPB takes into account morphological information from the cortical folding pattern, while FC considers the shape and the trajectory of the fibers once these leave the cortex.

CPB methods (O’Donnell et al., 2013; Sporns et al., 2005; Wassermann et al., 2016), e.g. the white matter query language (WMQL) (Wasser-mann et al., 2016), segment tractography according to a cortical parcellation, focusing on the structural connectivity between pairs of parcellated cortical/subcortical regions (Gong et al., 2008; Honey et al., 2009; Zhang et al., 2017). While this allows for highly specific identification, fibers that do not intersect the gray matter (GM) are excluded from the identification and this may hence result in a low sensitivity of tract identification (Vercruysse et al., 2014). In addition, the CPB method is dependent on the cortical parcellation of individual subjects, which could be affected by individual anatomical variations (Ashburner and Friston, 2000; Bonilha et al., 2015; Fischl et al., 2004).

Compared to CPB, FC relies on a different WM connectivity modeling assumption, aiming to group neighboring fibers with similar trajectories into clusters, which reconstruct fiber tracts according to the WM anatomy (Guevara et al., 2012; Maddah et al., 2008; O’Donnell and Westin, 2007). A variety of methods have been developed for unsupervised clustering of whole brain tractography in individual subjects based on various types of features such as geometry, anatomy, connection, or function (Garyfallidis et al., 2012; Ge et al., 2012, 2013; Guevara et al., 2011; Wassermann et al., 2010). Our work in groupwise fiber clustering (O’Donnell et al., 2012; O’Donnell and Westin, 2007) has demonstrated that white matter regions can be automatically clustered, correspond across subjects, and be augmented with anatomical annotations. Recently, we have applied the groupwise fiber clustering strategy to perform data-driven white matter parcellation, enabling whole-brain white matter analyses in groups of subjects, for example in autism (Zhang et al., 2018a), attention deficit hyperactivity disorder (Zhang et al., 2018b) and patients with brain tumors (O’Donnell et al., 2017). While both CPB and FC eliminate operator-specific intra- and inter-subject inconsistencies in tract delineation, our previous work (Zhang et al., 2017) demonstrated that FC may have a higher white matter parcellation consistency across subjects than the CPB method.

While the data-driven fiber clustering method has high consistency across subjects, it does have one drawback in interpretation of the fiber clusters. Fiber clusters obtained by unsupervised clustering need anatomical labels to identify anatomically meaningful white matter structures. Unlike the connections defined by a CPB method that are easily interpreted because their cortical terminations are known, in the FC approach this interpretation requires additional expert analyses to identify anatomically meaningful tracts by manually assigning an anatomical annotation to each fiber cluster (Guevara et al., 2012; O’Donnell and Westin, 2007). The combination of the two methods, representing a hybrid strategy, has been suggested to have advantages over their individual usages (Xia et al., 2005; Li et al., 2010; Ros et al., 2013; Wassermann et al., 2016; Ge et al., 2012; Siless et al., 2018; Tunç et al., 2013; Wang et al., 2013a; Guevara et al., 2017; Román et al., 2017).

In this study, we propose a hybrid white matter atlasing approach by combining CPB and FC strategies for automatic anatomical annotation of fiber clusters, which we refer to as the automatically annotated fiber clustering (AAFC) method. The goal of the proposed method is to provide an automated pipeline to perform white matter parcellation to identify anatomical fiber tracts. While FC provides a data-driven groupwise fiber clustering for fine parcellation according to white matter anatomy, CPB allows us to define anatomical annotations (such as the corticospinal tract (CST)) of fiber clusters. The combination of the two strategies allows the anatomical annotation of fiber tracts by including both brain GM and WM anatomy into the analysis. The benefits of the AAFC method are that: 1) it provides an automatic anatomical tract annotation pipeline to create study-specific white matter parcellations without using any expert annotation of fiber tracts, 2) it derives a high consistency of the identified fiber tracts across multiple subjects and across hemispheres, and 3) it allows investigation of local regions of certain fiber tracts (e.g. we obtained 7 subdivisions of the CST tract).

We demonstrate the proposed method in an application to analyze between-group white matter tract differences in a dataset including major depressive disorder (MDD) and healthy control (HC) groups. MDD is a common psychiatric disorder that is characterized by cognitive deficits and affective symptoms. Research studies have recognized MDD as a disconnection problem that involves many neural connections between brain functional regions (Cheng et al., 2016; Fu et al., 2015; Gong and He, 2015; Korgaonkar et al., 2014; Kostic et al., 2016; Liao et al., 2013). An increasing number of neuroimaging studies have focused on emotion regulation and have consistently shown that emotion dysregulation is one of the central features and underlying mechanisms of MDD. In particular, dMRI studies have suggested that there could be white matter abnormalities in emotional processing and sensorimotor areas in MDD (Delvecchio et al., 2012; Lu et al., 2016; Rizk et al., 2017; Smith and Bulman-Fleming, 2005; Tucker et al., 1999; Tymofiyeva et al., 2017; Zhang et al., 2011). Therefore, in this study, we apply our AAFC method to automatically identify the fiber tracts that are related to these brain functional areas and investigate potential white matter group differences specific to local regions of these tracts. We hypothesize that our method can reveal white matter changes within subdivisions of the fiber tracts, as defined by fiber clustering. A between-group (MDD vs HC) difference analysis is performed by comparing fractional anisotropy (FA) and mean diffusivity (MD) measured from each identified fiber tract and each fiber cluster of the fiber tract. To our knowledge this work represents the first automatic anatomical tract annotation method applied to investigate local white matter abnormality in MDD.

2. Materials and methods

2.1. Overview

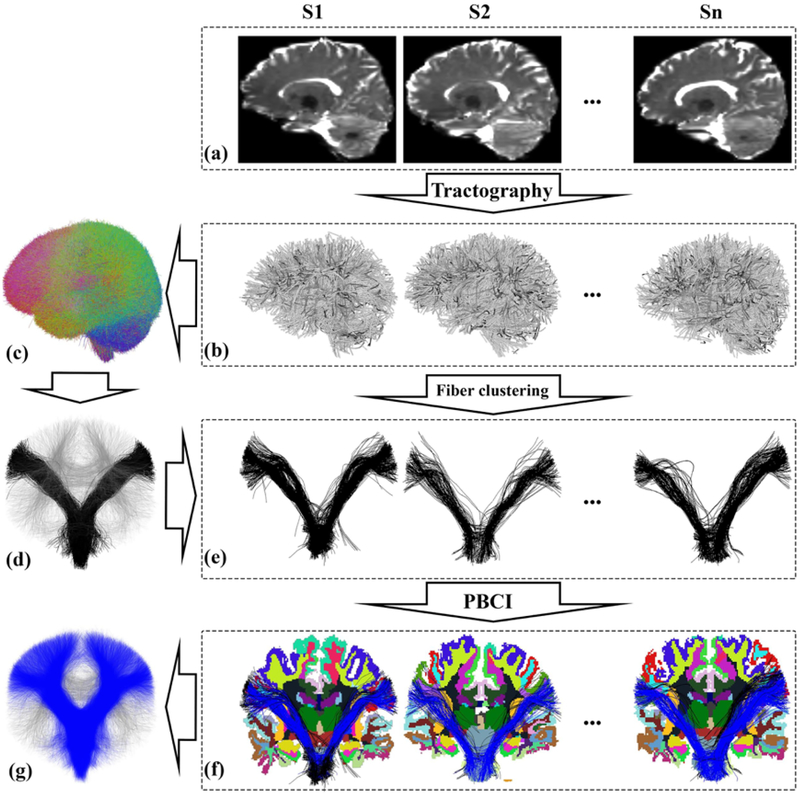
The proposed AAFC method has four main steps (Figure 1): whole brain tractography, study-specific data-driven groupwise fiber clustering, parcellation-based cluster identification, and automatic tract annotation across subjects. The purpose of these steps is to identify common white matter structures (fiber clusters) in the population and then to assign the fiber clusters to anatomically known white matter tracts according to the anatomical definitions that are predefined in the white matter query language (WMQL) (Wassermann et al., 2016).

Figure 1:

Overview of the automatically annotated fiber cluster (AAFC) method. Given the diffusion MRI dataset (a) of each subject, whole-brain tractography (b) is performed. Next, data-driven groupwise whole brain fiber clustering is performed to produce a fiber cluster atlas (c) across multiple subjects, which is applied to obtain fiber clusters (e) (black fibers show one example cluster from the cluster atlas (d)) in each individual subject. Then, a parcellation-based cluster identification (PBCI) is performed using each subject’s cortical parcellation to identify fibers belonging to known tracts (e.g. the blue fibers in (f) belong to the corticospinal tract (CST)). Finally, an annotating strategy for each fiber cluster across subjects is performed to label all fiber clusters belonging to CST (g).

2.2. Data acquisition and processing

2.2.1. Participants and MRI acquisition

The study requested access to data collected at the Department of Psychiatry at the Affiliated Brain Hospital of Guangzhou Medical University for the purpose of scientific investigation. Demographic information and results of between-group comparisons are shown in Table 1. A total of 93 subjects were studied, including 31 medication-free MDD patients and 62 healthy controls. All subjects were right-handed and of Han Chinese ancestry (age, 28.7±6.5; male/female, 39/54). The diagnosis of MDD was established with the Structured Clinical Interview of the DSM-IV (SCID) criteria. All patients had a score of at least 20 on the 24-item Hamilton Depression Rating Scale (HDRS). Patients were not taking any antidepressants in the current episode. HCs were screened using the SCID Non-Patient Edition to confirm the lifetime absence of Axis I illness and no history of psychiatric illness in the healthy comparison subjects or in any of their first-degree relatives. All subjects had no lifetime history of seizures, head trauma, serious medical or surgical illness, substance abuse or dependence, or contraindications for MRI. Written informed consent was obtained from all subjects and approved by the local ethics committees of the Affiliated Brain Hospital of Guangzhou Medical University. No significant differences in age, gender or education were observed between participants with MDD in comparison to HC participants (Two-sample t-tests were performed for age and education and chi-square distribution test for gender).

Table 1:

Demographics and Clinical Characteristics of the Subjects

	HC	MDD	p-value
Number of subjects	62	31	-
Age (years)	19–44 (28.69 ± 6.20)	19–45 (28.84 ± 7.11)	0.92
Gender (male/female)	26/36	13/18	0.93
Education	6–20 (13.66 ± 2.57)	6–22 (13.61 ± 3.79)	0.92
HAMD	NA	21–53 (32.5 ± 7.40)	-
HAMA	NA	7–39 (20.0 ± 8.60)	-
Onset age (years)	NA	16–43 (27.0 ± 7.40)	-
Episodes (n, patients) (First)	NA	24	-
Episodes (n, patients) (Recurrence)	NA	7	-

HAMD, Hamilton Depression Rating Scale; HAMA, Hamilton Anxiety Scale; MDD, major depressive disorder; HC, healthy control; Course of Disease, General course.

MRI data was acquired on a 3.0-Tesla MR imaging system (Achieva X-series, Philips Medical Systems, Best, the Netherlands) with an eight-channel SENSE head coil, in the Department of Radiology, the Affiliated Brain Hospital of Guangzhou Medical University, Guangzhou, China. Tight but comfortable foam padding was used to reduce head motion and earplugs to muffle scanner noise. Participants were instructed to rest with their eyes closed during scanning. No participant reported falling asleep during the scan when routinely asked immediately after scanning. High resolution anatomical T1-weighted images were acquired for each subject. T1-weighted three-dimensional (3-D) turbo field-echo (TFE) parameters included 188 sagittal 1mm slices; 1mm isotropic; 256 × 256 matrix; repetition time/echo time (TR/TE)=8.2/3.7ms; flip angle=7°; and inversion time=1100ms. Single-shot spin echo-echo planar imaging (SE-EPI) diffusion-weighted imaging was acquired aligned with the AC-PC plane using the following parameters: repetition time/echo time (TR/TE) 10067/92ms; flip angle 90, field of view (FOV) 256 × 256mm²; acquisition matrix 128 × 128; slice thickness 2mm, no gap; voxel size 2 × 2 × 2mm³; and 75 continuous axial slices. The diffusion sensitizing gradients were applied along 32 non-collinear directions (b = 1000s/mm²), together with an acquisition without diffusion weighting (b = 0).

2.2.2. Data processing

For both images (T1-weighted and diffusion weighted images (DWIs)), the DICOM images were converted to NRRD format using DWIConvert software. For each participant, a brain mask of the T1-weighted image was calculated by applying the 3D skull strip tool from Analysis of Functional NeuroImages (AFNI) (Cox, 1996). Automated reconstruction and labeling of cortical and subcortical regions was performed using Freesurfer (Fischl, 2012) on the masked T1-weighted images.

Pre-processing was performed on DWI images including eddy current-induced distortion correction and motion correction using the Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library tool (Jenkinson et al., 2012). Prior to tractography, each DWI data was aligned to its image center¹ so that the DWI data from all subjects was roughly aligned. To further correct for distortions caused by magnetic field inhomogeneity (which leads to intensity loss and voxel shifts), an EPI distortion correction was performed with reference to the T2-weighted image using the Advanced Normalization Tools (ANTS) (Avants et al., 2009). We corrected for EPI distortion using the T2-weighted image because our DWI data was acquired with only one phase encode direction. Because T2-weighted images were not acquired in this project, we generated a synthetic T2-weighted image from a T1 weighted image using the T1 to T2 conversion toolbox². For each participant a nonlinear registration (restricted to the phase-encode direction) was computed from the b0 image to the synthetic T2-weighted image to make a EPI corrective warp. Then, the warp was applied to each DWI image. Finally, each individual’s Freesurfer segmentation was transformed from T1 space into DWI corrected (b0) space via nonlinear registration using ANTS.

2.2.3. Whole-brain Tractography

Whole brain tractography was performed using a multi-fiber model to improve sensitivity in anatomical regions of crossing fibers. The unscented Kalman filter (UKF) tractography method (Baumgartner et al., 2012; Malcolm et al., 2010b,a) with a combined two-tensor and free-water model (Pasternak et al., 2009) was conducted to trace whole brain tractography. The free water model is a second tensor that is isotropic, with eigenvalues equal to the diffusivity of free water (Bergamino et al., 2016). UKF tractography fits the diffusion model to the data during fiber tracking, taking advantage of prior information from the previous step along the fiber. The UKF tractography method is widely used for neuroscientific studies (Chen et al., 2015, 2016; Cho et al., 2015; Joo et al., 2017; Liao et al., 2017). In this study, UKF tractography was employed to obtain the whole-brain tractography for each subject, with default seeding and stopping parameters that have been well tuned for datasets with a b-value of 1000. In details, tractography was seeded within the binary brain mask in all voxels where FA was greater than 0.15. 5 seeds were initiated per voxel. A two-tensor diffusion model was fitted at each point while tracking, and FA (as well as mean diffusivity (MD)) was measured from the first tensor of each point. Tractography stopped when FA (of the tensor being tracked) fell below 0.15 or the normalized average signal (the sum of the normalized signal across all gradient directions) fell below 0.1. The normalized average signal measure was employed to robustly distinguish between white/gray matter and cerebrospinal fluid (CSF) regions. As a result, the whole brain tractography obtained for each subject contained approximately 338,000 fibers. Tractography results for all subjects underwent a quality check using the quality control tool in the whitematteranalysis package³.

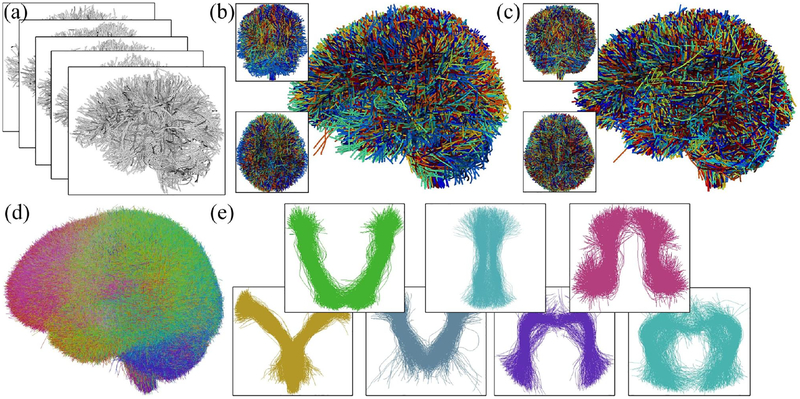
2.3. Data-driven Groupwise Whole Brain Fiber Clustering

A study-specific groupwise fiber clustering was conducted using a well-established pipeline to parcellate the whole-brain tractography into multiple fiber clusters (O’Donnell et al., 2012; O’Donnell and Westin, 2007), aiming to segment common white matter structures in the study population. This process (Figure 2) included the three steps of groupwise tractography registration, groupwise fiber clustering atlas generation, and subject-specific fiber clustering according to the atlas. This pipeline has been successfully applied in multiple recent studies (O’Donnell et al., 2017; Zhang et al., 2018b,a). Note that the whole pipeline works in an automated data-driven groupwise way based on the input tractography, without using any additional prior information of brain anatomy.

Figure 2:

Overview of the data-driven groupwise whole brain fiber clustering. Input tractography across all subjects (a) for data-driven learning of a white matter parcellation. Sub figures (b) and (c) show the overlaid tractography from 10 randomly selected example subjects (different colors indicate different subjects) before and after the groupwise tractography registration. Then, group-wise clustering produces the fiber atlas (d), where the colors represent different atlas fiber clusters. Some example clusters are displayed in (e).

2.3.1. Multi-subject group registration for whole brain tractography

Tractography from all subjects is registered into a common space (Figure 2c) via an unbiased multi-subject affine then B-spline-based tractography registration (O’Donnell et al., 2012). The method performs an entropy-based registration in a multiscale manner based on the pairwise fiber trajectory distances to simultaneously align fibers from the multiple subjects. The B-spline model is used to enable non-rigid groupwise registration to improve the spatial correspondence quality. 20,000 fibers were randomly sampled from each subject’s full tractography to perform the tractography registration.

2.3.2. High-dimensional data-driven fiber cluster atlas

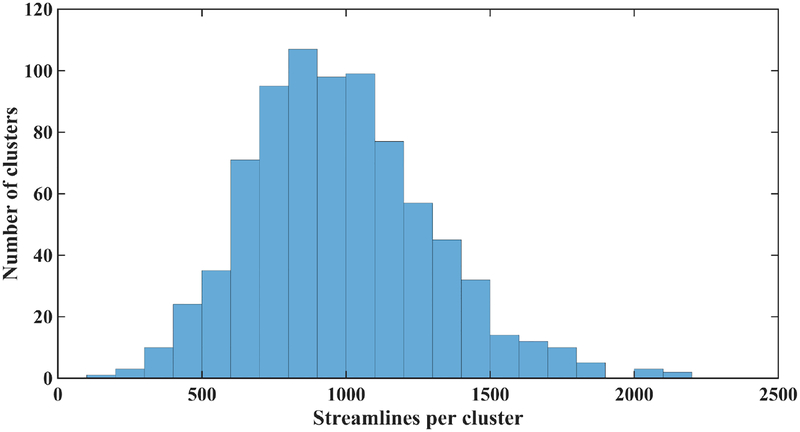
After group registration, each fiber is converted to a point in a spectral embedding space, where the fiber clustering is performed. In this step, a high-dimensional data-driven fiber atlas (O’Donnell and Westin, 2007) is automatically generated using the group spectral clustering of tractography from all subjects. In this study, 10,000 fibers were randomly sampled from each subject (n = 93) for a total of 930,000 fibers for the fiber clustering atlas generation. Similar fibers from all or most subjects are thus grouped into the same population white matter cluster, leading to the cluster atlas (Figure 2d). To improve clustering robustness, bilateral clustering is applied to simultaneously cluster fibers in both hemispheres (O’Donnell and Westin, 2007). We generated an atlas of 800 fiber clusters to provide a fine scale parcellation with the goal of separating all WM structures considered to be different anatomically (O’Donnell et al., 2017). Figure 3 shows the histogram of the number of fibers of each cluster in the atlas. In general, 89.5% had between 500 and 1500 fibers.

Figure 3:

Histogram of the number of fibers of each cluster in the atlas.

2.3.3. Cluster tractography for each subject

In this step, fiber clustering is performed for subject-specific WM segmentation according to the data-driven atlas to divide all fibers in the whole-brain tractography into clusters (O’Donnell et al., 2017). We note that unlike the atlas generation that used a sample of fibers per subject (10,000 fibers from about a total of 338,000 fibers), in this step each subject’s full tractography data was clustered according to the atlas. Each fiber from the whole-brain tractography of each subject is assigned to the closest atlas cluster in the spectral embedding space (O’Donnell et al., 2017; O’Donnell and Westin, 2007). After that, outlier fibers of each fiber cluster of each subject were removed if their fiber probability/affinity given the atlas cluster was over 2 standard deviations from the cluster’s mean fiber probability (O’Donnell et al., 2017). Considering the bilateral clustering of the atlas (O’Donnell and Westin, 2007), the subject clusters represented fiber tracts in both hemispheres or commissural. We separated fiber clusters per subject into hemispheric or commissural (Zhang et al., 2018b, 2017).

2.4. Anatomical Tract Annotation

After obtaining fiber clusters of each subject, a novel method is proposed to automatically assign an anatomical tract annotation to each fiber cluster according to the common brain anatomical regions the fiber cluster passes through across multiple subjects. There are two main steps: anatomical tract structure definitions using WMQL and population-based fiber cluster anatomical annotation.

2.4.1. Anatomical tract definitions using WMQL

We first employ an anatomical definition of a fiber tract using the white matter query language (WMQL) (Wassermann et al., 2016). Each fiber tract definition includes a set of brain anatomical regions through which the fiber tract passes (or does not pass). For example, a fiber belonging to the CST tract can be determined if the fiber passes through the brainstem and the precentral or postcentral cortex regions. Recently, WMQL has been successfully applied in multiple studies to identify anatomical fiber tracts, such as the cingulum bundle (Lee Masson et al., 2017; Olivetti et al., 2016), inferior occipito frontal fascicle (Olivetti et al., 2016), uncinate fascicle (Jolles et al., 2016; Lee Masson et al., 2017; Olivetti et al., 2016), arcuate fascicle (Olivetti et al., 2016; Reddy and Rathi, 2016), and corticospinal tract (Shenton et al., 2015). Detailed WMQL anatomical definitions of the tracts of interest in this study (including Corticospinal Tract (CST), Uncinate Fasciculus (UF), Inferior Longitudinal Fasciculus (ILF), Cingulum Bundles (CB), Thalamo-Frontal fibers (TF), Thalamo-Parietal fibers (TP) and Thalamo-Occipital fibers (TO)) are available online⁴.

2.4.2. Population-based fiber cluster anatomical annotation

We calculate a probability that each fiber cluster belongs to a certain anatomical tract in the population by using the WMQL results for the fibers in that fiber cluster. In this study, the Freesurfer segmentation in DWI (b0) space and each fiber cluster in an individual subject are input into WMQL to identify fibers belonging to particular tracts according to WMQL anatomical definitions of the tracts of interest. We focus on annotation of hemispheric fiber clusters for this study, so we remove the commissural fiber clusters (e.g. corpus callosum) from the cluster annotation process. Let c_k represent the k-th fiber cluster (k = 1…K) in atlas and t_j represent the j-th fiber tract (j = 1…7). We calculate a population-based probability of a fiber cluster c_k belonging to t_j

$$p\left(c_k|t_j\right)=\frac{\sum _{i=1}^n{\widehat{m}}_{ijk}}{\sum _{i=1}^n{m}_{ik}}$$ (1)

where m_ik is the total number of fibers of c_k of subject i, and ${\widehat{m}}_{ijk}$ is the number of fibers in c_k of subject i that passed the WMQL definitions of tract t_j, and the sums are over the total number of subjects, n.

Given the population-based probability, we then determine if a fiber cluster c_k can be assigned to a particular anatomical tract t_j. Here, we define an adaptive probability threshold λ_j; i.e. a fiber cluster c_k is annotated as part of an anatomical tract t_j if it has p(c_k|t_j) greater than λ_j. The adaptive threshold is computed as the sum of the mean and one standard deviation of the population-based probability p(c_k|t_j):

$${\lambda }_j=mean\left(P_j\right)+std\left(P_j\right)$$ (2)

$$P_j=\left\{p\left(c_k|t_j\right)|k=1\dots 800\right\}$$ (3)

This threshold allows us to identify the clusters likely to belong to tract t_j as those with probabilities that are statistically higher among all clusters. One benefit of this adaptive threshold is that it could be commonly used across the multiple tracts of interest. Each cluster passing the threshold for tract t_j is then given an anatomical annotation according to the name of tract t_j (e.g. CST).

2.4.3. Tracts of interest for the study

In this study, we focus on WM tracts related to human emotional processing (Bylsma et al., 2008; Catani et al., 2013; LeDoux, 1995, 2000; Rive et al., 2013; Rolls, 2000). In particular, several tracts of interest were studied, including the inferior longitudinal fasciculus (ILF), uncinate fasciculus (UF) and cingulum bundle (CB) which are related to emotional processing, and the fiber tracts related to the thalamus (thalamo-frontal fibers (TF), thalamoparietal fibers (TP) and thalamo-occipital fibers (TO)). CB has been suggested to be related to emotional processing (Bechara et al., 2000; Catani and De Schotten, 2008; Pugliese et al., 2009), and has been investigated in multiple MDD studies (Arnold et al., 2012; Wang et al., 2013b). The thalamus is an important subcortical structure that receives sensory information and relays it to the appropriate part of the cerebral cortex. Several research studies of MDD (Fava and Kendler, 2000; Korgaonkar et al., 2014; Liao et al., 2013; Osoba et al., 2013; Zhang et al., 2011) have reported alterations of the WM connections related to the thalamus. In addition, the corticospinal tract (CST) is also included in our study to investigate potential alterations of the corticospinal motor tract excitability that are related to emotional states in MDD (Baumgartner et al., 2007; Coombes et al., 2009; Hajcak et al., 2007). Therefore, these comprise a total of 7 fiber tracts of interest.

In this study, we employ the available definitions for WMQL⁵. The definitions are based on human brain anatomy expertise (Breiter et al., 1997; Fischl et al., 2002, 2004; Wassermann et al., 2016). For each of the 7 tracts, fiber clusters from the whole brain fiber clustering (Section 2.3) belonging to the tract are identified as introduced above (Section 2.4).

2.5. Diffusion quantitative measurement and statistical analysis

Diffusion quantitative measurements were computed after the tract annotation to quantitatively describe the fiber tracts. Fractional anisotropy (FA) and mean diffusivity (MD) measures, which have been suggested to be highly affected in MDD (Bergamino et al., 2016; Jenkins et al., 2016; Wise et al., 2016; Yip et al., 2013), were measured in this study. For each fiber cluster, the mean statistic of all points along the fibers of each measure was computed. We note that FA and MD were computed at each point along the fibers during fiber tracking (see Section 2.2.3). Unlike traditional diffusion tensor imaging (DTI) tractography (Basser et al., 2000) that performs tensor estimation in each voxel prior to fiber tracking, the UKF tractography is microstructure based and estimates the microstructure model during fiber tracking, resulting in tensors at each point along the fiber (as in many other microstructure tractography methods (Girard et al., 2015; Daducci et al., 2015)). (This enables the UKF method to use prior information from the previous tracking step.) Therefore, we used the microstructure statistics of all points along the fibers for quantitative tract description as in multiple recent studies (Zhang et al., 2018a,b; Sydnor et al., 2018; Gong et al., 2018; Hong et al., 2018).

To analyze between-group (MDD vs HC) statistical differences in FA and MD, a permutation t-test (Holmes et al., 1996) was conducted for each fiber cluster (left-/right-hemisphere) within each of the identified tracts (10000 permutations, as implemented in Matlab R2016a (The MathWorks, Inc., Natick, Massachusetts, United States)). This was followed by a multiple comparison correction across the clusters within each identified tract using false discovery rate (FDR) (Benjamini and Hochberg, 1995) to determine corrected statistical significance, with a significance level of p = 0.05.

3. Experiments and Results

3.1. Data-driven groupwise whole brain fiber clustering

We first investigated whether the clusters were present or absent in each subject to demonstrate that the white matter connections were consistently identified in the population. Tractography from all subjects from the MDD and HC groups was used for groupwise fiber clustering to obtain a study-specific fiber atlas, and then all fiber clusters were parcellated from all subjects. We then calculated how many fiber clusters could be identified from each subject. We observed that the 800 fiber clusters were highly consistent across all subjects: 798 of 800 clusters (99.75%) were detected in all the subjects, and all 800 clusters were detected in 92 subjects (98.92%). This result suggested that groupwise fiber clustering tended to find highly consistent and corresponding white matter connections across the population in this study.

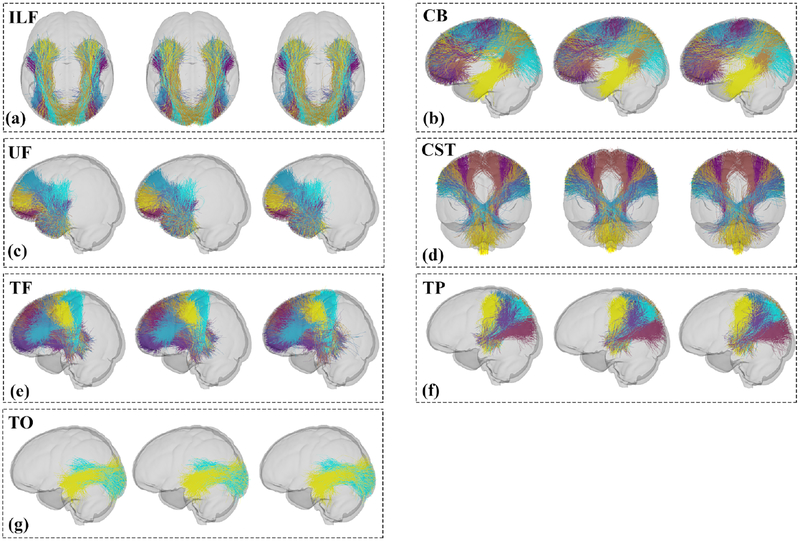
3.2. Annotation of key tracts in fiber cluster atlas

The seven fiber tracts identified by AAFC are displayed in Figure 4, each consisting of multiple fiber clusters. The first image in each box in Figure 4 shows the annotated fiber tracts in the atlas, and the second and third figures show the tracts from the HC and MDD groups, respectively. For the two group-wise visualizations, we appended the corresponding subject-specific fiber clusters across all subjects in each group, then downsampled the fibers for a better visualization. The results of fiber clustering across all subjects showed the method’s ability to identify multiple fiber clusters within each identified tract. This provided fine subdivisions of white matter structures, which corresponded across subjects. Tractography visualization was performed in 3D Slicer⁶ (Fedorov et al., 2012; Gering et al., 2001) via the SlicerDMRI project⁷ (Norton et al., 2017).

Figure 4:

Visualization of the fiber tracts (each cluster has a different color) annotated by AAFC. The first image in each box shows the tract in the atlas. The second and third images show the fiber tracts from the HC and MDD groups, respectively. (a) Inferior Longitudinal Fasciculus (ILF) is the union of 6 fiber clusters; (b) Cingulum Bundle (CB) is the union of 14 fiber clusters; (c) Uncinate Fasciculus (UF) is the union of 8 fiber clusters;(d) Corticospinal Tract (CST) is the union of 7 fiber clusters; (e) Thalamo-Frontal fibers (TF) is the union of 16 fiber clusters; (f) Thalamo-Parietal fibers (TP) is the union of 7 fiber clusters; (g) Thalamo-Occipital fibers (TO) is the union of 2 fiber clusters. A partially transparent model of the brain is displayed as a background to show the relative position of each tract in the brain.

Each tract identified by the proposed AAFC method was composed of the fibers that met and did not meet the WMQL definition. To quantitatively evaluate the fibers uncaught by WMQL, we performed an experiment by measuring their fiber geometric distances (Zhang et al., 2018b) to the fibers that met the WMQL definition. The goal was to show that if the fibers uncaught by WMQL had similar white matter anatomy (small geometric distance) to the fibers caught by WMQL, they were more likely to belong to the same white matter structure. In details, for each of the fibers uncaught by WMQL in a certain tract per subject, we identified the closest fiber within the ones caught by WMQL and recorded this closest distance. Then, a mean closest distance was computed across all fibers uncaught by WMQL. Table 2 shows the mean and the standard deviation of the mean closest distance across all subjects under study for each tract. In general, the geometric distances between the fibers that met and did not meet the WQML definition in our identified tracts were small (around 5mm or 2 to 3 voxels), suggesting a very similar white matter anatomy between these fibers.

Table 2:

The geometric distances between the fibers that met and did not meet the WQML definition in our identified anatomical fiber tracts.

Tracts	CB (mm)	CST (mm)	UF (mm)	ILF (mm)	TF (mm)	TO (mm)	TP (mm)
	5.59 ± 0.40	6.81 ± 0.65	4.27 ± 0.39	5.84 ± 0.57	5.02 ± 0.42	4.36 ± 0.62	5.16 ± 0.57

We then performed a quantitative evaluation to investigate how many fibers were misclassified in our identified anatomical tracts based on all available tract definitions provided in WMQL. Specifically, given a certain identified tract (e.g. CST), we found the fibers that belonged to any other tracts defined in WMQL, and computed the percentage of these fibers given the total number of fibers of the tract of each subject. We note that all available anatomical definitions (including a total of 45 white matter tracts) were used here. Then, across all subjects under study, we calculated a mean percentage of the fibers that were misclassified given all available WMQL tract definitions, as shown in Table 3. In general, a very small percentage of fibers (under 5%) were misclassified.

Table 3:

Percentages of fibers that were misclassified in the anatomical fiber tracts based on all available WMQL tract definitions.

Tracts	CB (%)	CST (%)	UF (%)	ILF (%)	TF (%)	TO (%)	TP (%)
	3.15 ± 1.65	0.01 ± 0.03	1.08 ± 0.94	2.36 ± 2.49	2.74 ± 2.64	1.97 ± 1.91	4.85 ± 2.50

3.3. Visualization and Comparison between AAFC and WMQL methods

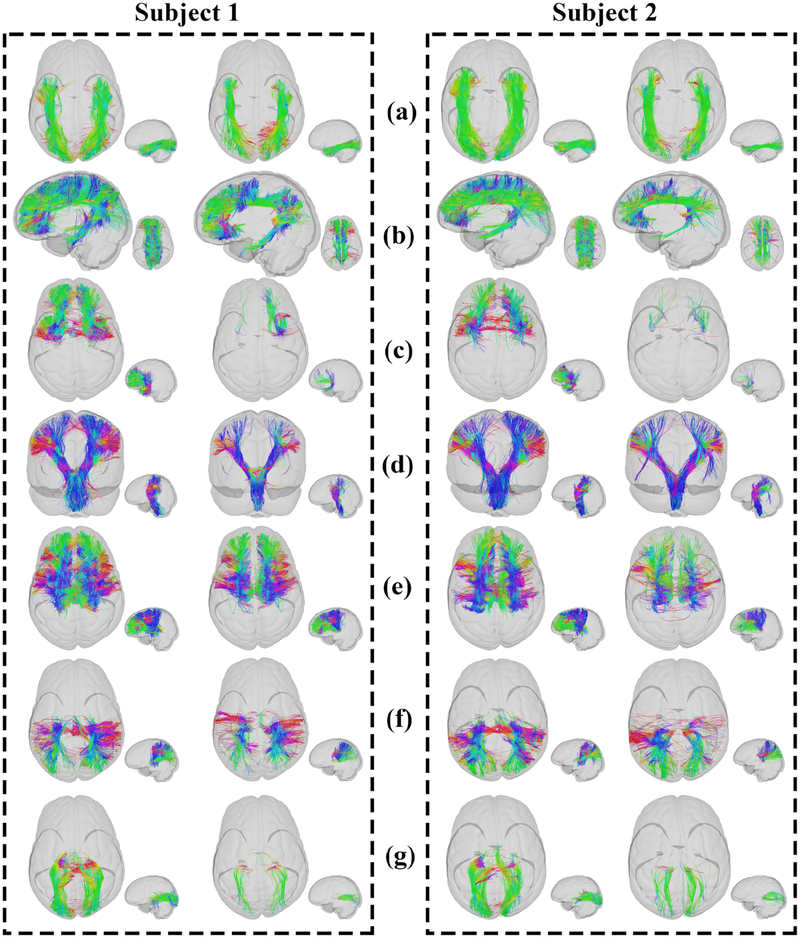
To compare two key tract segmentation strategies, the WMQL and AAFC methods, in identifying the seven tracts in this study, visualizing and quantifying experiments were carried out. Two example subjects (one MDD subject (subject 1) and one HC subject (subject 2)) were randomly selected for visualizing the comparison of the two tract segmentation strategies (Figure 5).

Figure 5:

Visual presentation of the AAFC method (left) and the WMQL method (right) results segmenting fiber tracts, ILF, CB, UF, CST, TF, TP and TO, respectively. Two subjects (one MDD subject (Subject 1) and one HC subject (Subject 2)) were randomly selected for visualization. Fibers in each tract are colored by the fiber orientation.

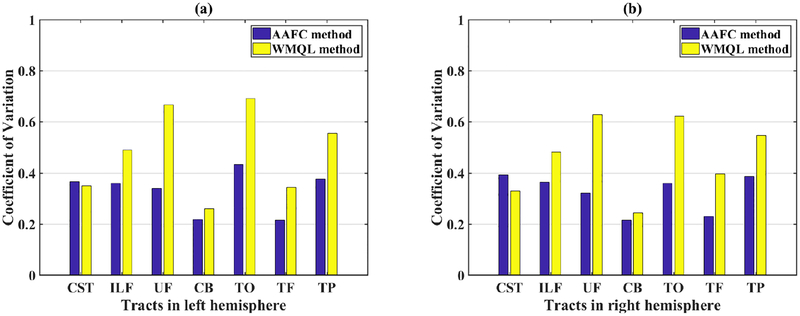
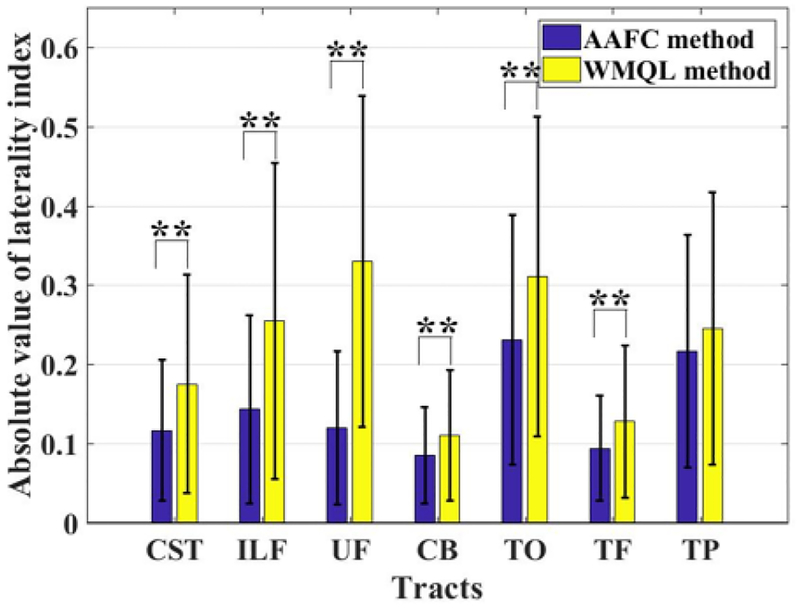
For quantitative comparison of the WMQL and AAFC methods in identifying the tracts of interest across subjects, we calculated the number of fibers in each tract to investigate if the corresponding tracts across subjects represented similar WM connections. Figure 6 shows the coefficient of variation (CV) of the number of fibers (streamline count) from the corresponding tracts across all subjects. (The CV is the ratio of the standard deviation to the mean.) Two-tailed paired t-tests were used to compare the CV from the two methods in the left hemisphere (p = 0.0153) and the right hemisphere (p = 0.0274). The AAFC method obtained a significantly lower mean CV when compared to the the WMQL method. The tracts in this study are expected to be relatively symmetric (Latini et al., 2017; de Schotten et al., 2011) according to studies of the white matter anatomy, so we assessed hemispheric lateralization of the tracts detected by both methods. Figure 7 shows the absolute values of the laterality index (LI) (O’Donnell et al., 2010; Prop-per et al., 2010; de Schotten et al., 2011) of the number of fibers for each tract. The absolute LI of a tract was measured as |(m_R − m_L)/(m_R + m_L)|, where m_L and m_R are the number of fibers in the left and right hemispheres of the tract. Paired t-tests were used to compare mean absolute LIs of the number of fibers (streamlines) for each tract across methods. A significantly lower mean absolute LI was obtained by the AAFC method (Figure 7) in 6 of 7 tracts.

Figure 6:

Coefficient of variation (CV) of the number of fibers from each tract across all subjects, as identified by WMQL and the proposed AAFC method. (a) Left hemisphere (p = 0.0153, two-tailed paired t-test of CV across seven left-hemisphere tracts between AAFC and WMQL); (b) Right hemisphere (p = 0.0274, two-tailed paired t-test of CV across seven right-hemisphere tracts between AAFC and WMQL). Lower CV values indicate lower variability across subjects.

Figure 7:

Absolute value of hemispheric laterality index (LI) of the numbers of fibers for each tract. A lower absolute LI indicates a more symmetric tract identification across hemispheres. The fiber tracts with significant difference between methods (p < 0.01) are highlighted using the two asterisks.

3.4. Statistical analysis

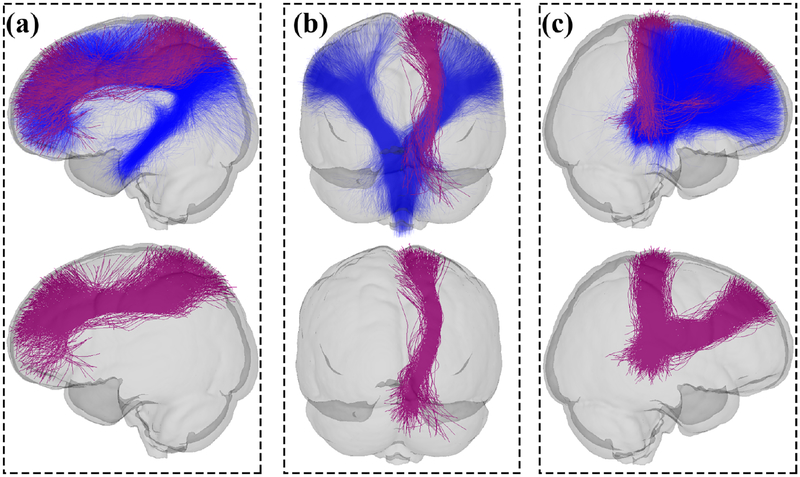
Significant differences between groups in the identified tracts and the fiber clusters of the identified tracts are summarized in Tables 4 and 5, respectively. Table 4 reports the average and standard deviation of FA and MD of each tract of interest. Significant differences between groups identified by the AAFC method at the tract level are highlighted, including the left ILF, the left CB and the right TF based on the MD measure. We also performed a tract level comparison for these three tracts identified using the WMQL method. The average MD values in each tract were as follows: left ILF: MDD (0.702 ± 0.029) vs HC (0.717 ± 0.026, p-value = 0.017; left CB: MDD (0.733 ± 0.023) vs HC (0.744 ± 0.021), p-value = 0.027; right TF: MDD (0.667 ± 0.018) vs HC (0.675 ± 0.016), p-value = 0.048. The results showed that there were significantly increased MD values in the MDD group in these tracts, which were in the same trend as the results obtained using our AAFC method. Table 5 reports the average and standard deviation of FA and MD in each fiber cluster with significant differences between groups. Also, Figure 8 shows selected views displaying the tracts with the significant fiber clusters in red color.

Table 4:

Comparison of group average value of FA and MD for the tracts of interest identified by AAFC in patients with MDD versus HC subjects.

Tracts	FA			MD
	MDD	HC	p-value	MDD (× 1e-3)	HC (× 1e-3)	p-value
ILF (L)	0.554 ± 0.030	0.541 ± 0.031	0.051	0.719 ± 0.029	0.732 ± 0.024	0.043
ILF (R)	0.551 ± 0.032	0.547 ± 0.037	0.634	0.708 ± 0.017	0.712 ± 0.022	0.253
CB (L)	0.477 ± 0.025	0.477 ± 0.030	0.997	0.718 ± 0.025	0.730 ± 0.021	0.032
CB (R)	0.466 ± 0.028	0.464 ± 0.028	0.806	0.712 ± 0.029	0.720 ± 0.020	0.086
UF (L)	0.470 ± 0.036	0.471 ± 0.038	0.843	0.728 ± 0.032	0.726 ± 0.025	0.752
UF (R)	0.472 ± 0.042	0.464 ± 0.035	0.326	0.724 ± 0.028	0.730 ± 0.024	0.263
CST (L)	0.649 ± 0.027	0.638 ± 0.023	0.068	0.683 ± 0.022	0.688 ± 0.020	0.290
CST (R)	0.641 ± 0.022	0.633 ± 0.022	0.126	0.675 ± 0.017	0.679 ± 0.017	0.339
TF (L)	0.536 ± 0.026	0.529 ± 0.021	0.193	0.662 ± 0.021	0.668 ± 0.022	0.191
TF (R)	0.526 ± 0.023	0.520 ± 0.020	0.192	0.665 ± 0.017	0.673 ± 0.016	0.035
TP (L)	0.522 ± 0.035	0.518 ± 0.027	0.639	0.691 ± 0.024	0.700 ± 0.023	0.075
TP (R)	0.523 ± 0.026	0.521 ± 0.024	0.779	0.695 ± 0.021	0.701 ± 0.019	0.168
TO (L)	0.586 ± 0.035	0.578 ± 0.035	0.341	0.745 ± 0.039	0.746 ± 0.031	0.891
TO (R)	0.585 ± 0.045	0.593 ± 0.039	0.385	0.737 ± 0.032	0.738 ± 0.027	0.868

Table 5:

Comparison of group average value of FA and MD for fiber clusters within tracts of interest identified by AAFC in patients with MDD versus HC subjects. Multiple comparison correction is performed across the clusters within each identified tract using the false discovery rate (FDR) method.

Tracts	FA				MD
	MDD	HC	p-value	Cluster	MDD (× 1e-3)	HC (× 1e-3)	p-value	Cluster
ILF (L)	-	-	-	-	-	-	-	-
ILF (R)	-	-	-	-	-	-	-	-
					0.709 ± 0.027	0.728 ± 0.027	0.007	No.299
CB (L)	-	-	-	-	0.738 ± 0.031	0.755 ± 0.026	0.040	No.384
					0.735 ± 0.034	0.759 ± 0.035	0.007	No.449
					0.698 ± 0.025	0.717 ± 0.026	0.005	No.613
CB (R)	-	-	-	-	-	-	-	-
UF (L)	-	-	-	-	-	-	-	-
UF (R)	-	-	-	-	-	-	-	-
CST (L)	-	-	-	-	-	-	-	-
CST (R)	0.662 ± 0.030	0.643 ± 0.033	0.035	No.760	-	-	-	-
TF (L)	-	-	-	-	-	-	-	-
TF (R)	-	-	-	-	0.666 ± 0.024	0.680 ± 0.023	0.048	No.162
					0.668 ± 0.022	0.681 ± 0.017	0.048	No.403
TP (L)	-	-	-	-	-	-	-	-
TP (R)	-	-	-	-	-	-	-	-
TO (L)	-	-	-	-	-	-	-	-
TO (R)	-	-	-	-	-	-	-	-

Figure 8:

Visualization of CST (a), CB (b) and TF (c) tracts showing significant differences in FA (CST) and MD (CB and TF) in the MDD patients compared with the HCs. The first row displays the significant clusters overlaid on the whole tract to show the relative position of the significant clusters. The second row shows only the significant clusters for a better visualization. Red parts represent the fiber clusters with significant difference (1 fiber cluster in the identified right-hemisphere CST had significantly increased FA in MDD, 4 fiber clusters in the identified left-hemisphere CB had significantly decreased MD in MDD, and 2 fiber clusters in the identified right-hemisphere TF had significantly decreased MD in MDD). A partially transparent model of the brain is displayed as a background to show the relative position of each tract in the brain.

4. Discussion

In this paper, we proposed an automatically annotated fiber cluster (AAFC) method to enable robust anatomical fiber tract identification across subjects, and to allow investigations of WM abnormalities specific to local regions (clusters) within the identified tracts. We demonstrated our method with an application to study group WM differences using a dataset of 31 MDD patients and 62 HCs. We have several overall observations about the results, which are discussed below.

The proposed AAFC method was highly consistent in identifying corresponding anatomical fiber tracts across multiple subjects. We found a more consistent performance of the proposed AAFC method when compared to the WMQL method, based on quantitative experiments. We measured a significantly lower mean CV of the number of fibers in each fiber tract across subjects using the AAFC method (Figure 6). We also found a lower absolute LI was obtained using the AAFC method, indicating the identified tracts were more similar across hemispheres. The high consistency of the proposed method can be interpreted from the following aspects. First, the proposed AAFC method relied on a fiber clustering pipeline to enable identification of corresponding WM parcels in the whole brain of all subjects. Given the 800 fiber clusters, 99.75% of fiber clusters were consistently found across all subjects. Second, we applied bilateral clustering that simultaneously clustered fibers in both hemispheres. Due to its ability in finding corresponding white matter structures across the hemispheres (O’Donnell and Westin, 2007), which enables the comparison of these structures across hemispheres, the bilateral clustering is beneficial in investigating potential lateralized microstructural changes in the white matter. When applying this method, although similar structures are bilaterally clustered across hemispheres, the structures may still be asymmetric in the number of fibers. The higher magnitude of asymmetry in the tracts identified by WMQL could potentially relate to the fibers that do not fully reach cortex in individual subjects (Olivetti et al., 2016; Vercruysse et al., 2014), such as in the UF tract of subject 1 (Figure 5). Third, unlike the WMQL method that relied on brain anatomical parcellation of individuals, the proposed AAFC method leveraged information from the whole population, including the group-wise whole brain fiber geometry (via the data-driven fiber clustering) and the population-based cortical parcellation (via the population fiber cluster annotations).

In interpreting our findings, we make the claim that less lateral variation (in terms of the number of fibers) is beneficial, because we feel that it is important to robustly identify each anatomical structure in both hemispheres. It is important to mention that this could potentially reduce findings of lateralization, especially in terms of the number of fibers. However, most tract-specific studies do rely on diffusion properties of the tracts rather than relatively non-anatomical measures such as fiber count (Jones et al., 2013). To our knowledge, to date there have been few studies of brain lateralization specifically in MDD. Prior studies have found lateralized results that are present only in either left or right hemisphere structures (Wise et al., 2016; Jiang et al., 2017). We note that recent meta-analyses of FA studies in MDD have general findings of non-lateralized changes, in both the corpus callosum and bilateral superior longitudinal fasciculus (Wise et al., 2016; Jiang et al., 2017).

One potential benefit of the proposed AAFC method is that it identifies anatomical fiber tracts that are composed of multiple fiber clusters, which allows statistical analyses specific to subdivisions of a WM structure (Table 5). This enables identification of group differences in local WM regions, which could be more affected when compared to the whole tract. In the application of studying MDD, we found that several fiber clusters survived the multiple comparison corrected statistical test in the left CB, the right CST and the right TF. For example, the CB tract consisted of 14 fiber clusters, within which four clusters (Figure 8) were significantly different between the MDD and HC groups when comparing the MD. On the other hand, we also observed that while the whole left ILF tract passed the statistical test at the tract level, none of its fiber clusters survived the fiber-cluster-based comparison of MD (corrected for multiple comparisons). This could be attributed to the fact that the individual clusters had similar or higher t-test-based group statistics (p-values) to the whole tract.

In the application of the AAFC method to study the WM differences between MDD and healthy controls, we found that diffusion properties were affected in left ILF, right CST, left CB and right TF, which suggested potential WM abnormalities in emotional processing and sensorimotor areas in MDD. Similar to our findings, previous studies have reported WM abnormalities in the right CST (Osoba et al., 2013; Sacchet et al., 2014b,a; Wang et al., 2013b), the left CB (Arnold et al., 2012; Emberson et al., 2014; Wang et al., 2013b), the right TF (Lyden et al., 2014; Schnyer et al., 2017; Wang et al., 2013b) and the left ILF (de Diego-Adelino et al., 2014; Kieseppä et al., 2010). In this study, we found generally decreased MD and increased FA in the MDD subjects compared to the healthy controls. While many studies have reported increased MD and decreased FA in MDD compared to HC (Arnold et al., 2012; Benedetti et al., 2011; Osoba et al., 2013; Serafini et al., 2015; Vasavada et al., 2016; Wang et al., 2013b; Zalsman et al., 2017), other works have found different change directions (similar to our results), as follows. Decreased MD values in MDD were found in left-hemisphere CB (Arnold et al., 2012; Lyden et al., 2014; Wang et al., 2013b) and TF (Lyden et al., 2014; Schnyer et al., 2017; Wang et al., 2013b). In addition, significantly increased FA was found in CST in MDD (Osoba et al., 2013; Sacchet et al., 2014b,a; Wang et al., 2013b).

Other research groups have also proposed using a combination of tractography information and other anatomical information for identifying fiber tracts, which can be categorized as hybrid methods (O’Donnell et al., 2013). The earliest work uses the brain parcellation from a gray matter (GM) atlas to initialize the fiber clusters connecting to the same anatomical brain region (Xia et al., 2005). There have also been studies applying WM/GM atlases to guide anatomical tract identification after obtaining fiber clusters in individual subjects (Li et al., 2010; Ros et al., 2013; Wassermann et al., 2016). In addition, works have been conducted by incorporating fiber anatomical information into the fiber distance/similarity computation (Ge et al., 2012; Siless et al., 2018; Tunç et al., 2013; Wang et al., 2013a). These methods in general rely on the anatomical parcellation of individuals under study and thus are limited to the success of applying the voxel-based WM/GM atlases to each individual. In contrast, in our method, we apply a groupwise fiber clustering strategy, which provides a tract-based model that can be highly robust in identifying corresponding WM structures across subjects (e.g. we have successfully applied our fiber clustering atlases to brain tumor patients even though they have very large individual brain anatomy variations (O’Donnell et al., 2017)). A post-hoc fiber cluster anatomical annotation is anatomically computed with respect to the GM and WM information of the entire population that is used for the fiber cluster atlas generation. One benefit of this combination is the potential of applying our annotated fiber cluster atlas to new subjects without requiring individual anatomical prior information. Another benefit is that the proposed method provides an automated way to generate study-specific white matter atlases and corresponding subject-specific white matter parcellations for each subject under study.

Potential limitations of the current work are as follows. We found that the tracts identified in the AAFC method were relatively larger in terms of the number of fibers when compared to those identified in the WMQL method. There are two potential causes leading to this difference. First, we applied a relatively low threshold (Section 2.4.2) which was more inclusive to avoid missing any potential clusters belonging to a certain anatomical fiber tract. While this threshold allowed us to perform cluster annotations across the multiple tracts of interest in an automated manner, certain annotated clusters may not strongly belong to the tract. For example, there are some outlier fibers in our identified UF, CB and TO tracts (Figure 5). Applying a more strict threshold could reduce the possibility of including outliers fibers into the tract, but with the expense of losing part of the tract. To enable a more tract-specific threshold decision, as well as the study of tracts not yet included in WMQL, it would be of interest to enhance the tract annotation by employing expert knowledge. Second, the proposed AAFC method uses a white-matter-centric fiber clustering method that allows identification of the fibers whose endpoints are near the GM, while the WMQL method can only include the fibers ending in or passing through the GM. This is expected to increase the number of detected fibers in AAFC compared to the WMQL method. In this study, we chose a parcellation scale of K = 800 that has been suggested to well separate white matter structures considered to be anatomically different (O’Donnell et al., 2017; Zhang et al., 2018b). We have recently found that, when testing parcellation scales from K = 200 to 4000, K = 800 is a reasonable value to separate different anatomical tracts while providing a good parcellation consistency across subjects (Zhang et al., 2018c). In the present study, our quantitative result (Table 3) showed that with K = 800 only a small percentage of fibers were misclassified based on based on all available WMQL tract definitions, suggesting that the current parcellation provided a good performance in identifying the anatomical tracts. However, because the fiber clusters are white-matter-centric subdivisions according to fiber shape and location, fibers within a cluster may not perfectly correspond to the WMQL definition of a particular tract. For example, the CST, part of the corona radiata (CR) (Jang, 2009), has similar WM anatomy to non-CST CR tracts. Hence, there could be a cluster annotated as CST that includes part of the non-CST CR. To handle this, a potential future research direction could include investigating a finer WM fiber clustering parcellation (K ≥ 800) to obtain clusters more specific to local subdivisions of a WM structure. For example, our currently applied K = 800 WM parcellation subdivided the CST into 7 clusters, but a finer parcellation (e.g. K = 1000) would subdivide the CST into more clusters which could be more specific to local regions of the CST. We note that in our recent work, we found that 800 clusters enabled whole-brain statistical analysis (Zhang et al., 2018b), while fine WM subdivisions (K = 2000) were found to be beneficial for machine learning classification (Zhang et al., 2018a). Third, our quantitative evaluation result about the misclassified fibers in the identified anatomical tracts (Table 3) was based on all currently available tract definitions in WMQL. A comprehensive evaluation would include more tract definitions if they would be available in the future. Another potential limitation is that we applied the mean measurements of the diffusion features (i.e. FA and MD) to investigate local WM abnormality in MDD compared to HC. However, advanced diffusion measurements may provide better tract quantitative descriptions. For example, multi-shell dMRI features, such as return-to-the-origin probability (RTOP) (Zhang et al., 2018b), could be combined with along-tract statistical analysis (Colby et al., 2012; O’Donnell et al., 2009; Yeatman et al., 2012) to study between group white matter alterations.

5. Conclusion

In this study, we have presented an automatically annotated fiber cluster (AAFC) method to identify WM structures from whole brain tractography. The proposed method automatically annotated the anatomical tracts with a high consistency across multiple subjects without requiring any expert selection of fiber tracts. The proposed method allows investigation of local regions of certain fiber tracts. Experimental results suggest that our method in general is more consistent across subjects and hemispheres when compared to the WMQL method, in terms of the number of fibers that are detected. The example application to the study of MDD demonstrates that the proposed method can allow identification of group WM differences specific to subdivisions of anatomical fiber tracts, while enabling whole-tract-based analyses.

Table 6:

List of the Freesurfer regions to which the fiber clusters with significantly different FA or MD measures between HC and MDD groups (Table 5) connect. Abbreviations: hemisphere, L - left; R - right.

Fiber cluster		Connection between areas
CB (L)	No.299	Left superior frontal cortex and left cuneus cortex
	No.384	Left posterior cingulate cortex, left precuneus cortex and left cuneus cortex
	No.449	Left precuneus cortex and left cuneus cortex
	No.613	Left superior frontal cortex and left precuneus cortex
CST (R)	No.760	Brainstem and right precentral cortex
TF (R)	No.162	Right thalamus proper and right precentral cortex
	No.403	Right thalamus proper and right superior frontal cortex