Evaluation of drug combination effect using a Bliss independence dose-response surface model

Abstract

To test the anticancer effect of combining two drugs targeting different biological pathways, the popular way to show synergistic effect of drug combination is a heat map or surface plot based on the percent excess the Bliss prediction using the average response measures at each combination dose. Such graphs, however, are inefficient in the drug screening process and it doesn’t give a statistical inference on synergistic effect. To make a statistically rigorous and robust conclusion for drug combination effect, we present a two-stage Bliss independence response surface model to estimate an overall interaction index (τ) with 95% confidence interval (CI). By taking into all data points account, the overall τ with 95% CI can be applied to determine if the drug combination effect is synergistic overall. Using some example data, the two-stage model was compared to a couple of classic models following Bliss rule. The data analysis results obtained from our model reflect the pattern shown from other models. The application of overall τ helps investigators to make decision easier and accelerate the preclinical drug screening.

1. Introduction

Cancers evolve through various biological pathways involving genetic alterations of multiple driver genes. Many compounds (drugs) targeting specific signaling pathways have been synthesized or are under development. It is well known that single drugs have limited anti-tumor effects because single drugs do not kill all malignant cells and cancer cells frequently develop resistance to single drugs. It is therefore becoming increasingly common to look for drug combinations that produce synergistic effects. Typically, these combinations employ lower doses of each drug than are used when the drugs are delivered as single agents.

In high-throughput drug screening, to test for whether drug combinations have a synergistic effect it is critical to have a precise and efficient statistical analysis method. Over the years, many methods have been proposed (Loewe 1953, Bliss 1956, Carter et al. 1988, Berenbaum 1989, Greco, Par and Rustum 1990, Machado and Robinson 1994, Greco, Bravo and Parsons 1995, Dawson, Gennings et al. 2002, Chou 2006, Fitzgerald et al. 2006, Lee et al. 2007, Whitehead et al 2008). New algorithms have been developed in recent years (Peifer et al. 2010, Harbron 2010, Zhao et al 2012, 2014). Across these efforts, the definitions of synergy are based on two principles: Loewe additivity (Loewe 1953) and Bliss independence (Bliss 1956). In drug combination studies for cancer, the Loewe additivity is appropriate when the drugs target same pathways. In contrast, the Bliss independence principle is more appropriate when two drugs are mutually nonexclusive, i.e. when each target a different signaling pathway. The decision of whether to use Loewe additivity or Bliss independence can be made based on whether each of the combined drugs target the same pathway or not. The biological investigator needs to provide statisticians with the signaling pathway information for the tested drugs. Whether one model or the other is more appropriate is based on our scientific colleague’s current best understanding of a drug’s mechanism of action. However, it should be remembered that both Loewe and Bliss are just models, and as such they are unlikely to reflect the full complexity of any particular drug combination. As more becomes understood about the mechanisms of action of particular drugs, our confidence in a choice of model will correspondingly increase. Both Loewe and Bliss models are often recommended as approaches to explore data, with a major purpose being to identify potential synergistic drug combinations that warrant further mechanistic investigation (Tang, Wennerberg and Aittokallio 2015).

In practice, complex statistical models are not widely applied in preclinical drug screening. Instead, many biologists have become accustomed to using heat maps or surface plots based simply on “excess over Bliss” for determining drug combination effect (Ghosh et al 2015, O’Neil et al 2016, Straussman et al. 2012, Sun et al 2016, Zimmera et al 2016). Such heat maps or surface plots may be helpful for small experiments. However, for high-throughput drug screening, they are inefficient because it is time consuming to make them and look through them. Furthermore, heat maps or surface plots don’t give a statistical inference on synergistic effect if the experiments do not have enough replicates. Even when replicates are available, multiple testing problems arise from repeatedly performing a statistical test across all combination doses (Zhao et al 2014). We propose that an overall interaction index with a 95% confidence interval (CI) is statistically rigorous and can help biological investigators to make conclusions easily and speed up the drug screening process. This manuscript describes how we developed such an overall interaction index.

Models similar to the one we describe here have been developed by other groups. Zhao et al. (2014) proposed analyzing drug combination data using a new Bliss independence model. They proposed a two-stage response surface model that estimates an interaction index with a corresponding 95% CI at each combination dose. We did not consider their proposed method for our drug screening study because we prefer to have an overall interaction index, meaning an index that estimates the summary combination effect across the entire, tested range of doses. Whitehead et al. (2008) provided a response surface model to estimate an overall interaction index using the Bliss Independence principle. Their method applied one-stage modeling using the SAS NLIN procedure. Harbron (2010) proposed a unified approach for Loewe additivity to estimate a uniform interaction index, and separate interaction indexes at each dose of one drug in the combination, with one-stage modeling. In our experience, one-stage modeling sometimes gives unreliable estimates or fail to converge. We also do not favor one-stage modeling because it cannot precisely estimate the single drug’s dose-response parameters solely on the corresponding single drug data, or the interaction index based solely on the drug combination data. Zhao et al (2012) has pointed out that one-stage models may deviate significantly from their true values, and thus potentially lead to wrong conclusions.

To meet the need for our drug screening research, we propose to estimate an overall interaction index with 95% CI based on Bliss independence additivity. This overall interaction index is estimated with a two-stage procedure by applying the bisection scheme algorithm proposed by Harbron (2010). To obtain the details of the combination effect for any particular drug, a series of interaction indexes can be calculated for each dose level of that drug when it is combined with various doses of the other drug.

Below, in Section 2 we introduce the experimental design and procedure used in our drug combination study. Section 3 describes how the overall interaction index is obtained from a global response surface model under the Bliss independence principle. Section 4 shows how our example data can be represented with the overall interaction index and the comparisons with other classic models. We conclude with a discussion and suggestions for future direction.

2. Experimental Design and Procedure

The goal of our drug combination study was to investigate the synergistic, anticancer effect of the combination of Gamitrinib and each of a set of kinase inhibitors. Gamitrinib is a mitochondrially-targeted inhibitor of the molecular chaperone Hsp90. The selected kinase inhibitors target the PI3K pathway. Here we have assumed that Gamitrinib and the kinase inhibitors produce their independent, anticancer effects by targeting different pathways, and that there is no mechanistic connection other than the response outcome.

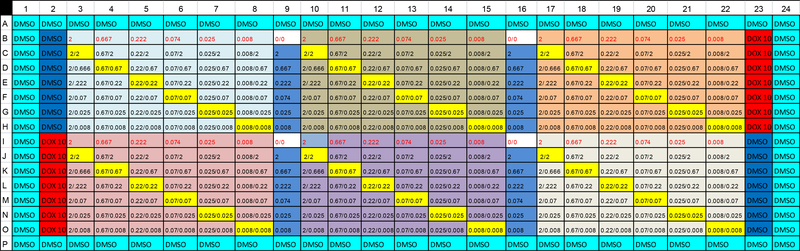
Figure 1 shows the plate map for the drug dosage arrangement. There are six blocks indicated by the different main colors. Each block is used for one set of drug combinations. Using the first block (columns 3 to 9 and rows B to H) as an example, the numbers in column 9 are doses of Gamitrinib (drug A) alone and the numbers in row B are doses for a PI3K inhibitor (drug B) alone. Each of other cells in the block shows two numbers separated by a slash; these cells represent combinations. The number below the slash is the dose for drug A (Gamitrinib) and the number above the slash is the dose for drug B (one of the 6 tested PI3K inhibitors).

Figure 1.

Plate map of drug dosage arrangement for drug combination experiment

For these experiments, cancer cells (LN229 glioblastoma cells) were plated in a 384 well format using 1:3 dilution series with 2.00μM as the highest concentration and 0.008μM as the lowest concentration. LN229 cells were treated with Gamitrinib and selected kinase inhibitors in a 7×7 matrix for 18 h at 37ºC. Cell viability was measured using fluorescence intensity. The fractional viability was determined by normalizing the fluorescence intensity readouts of the individual assay wells to the aggregated average responses obtained with a positive control (10 μM doxorubicin, DOX) and negative control (0.2% dimethyl sulfoxide, DMSO). The fractional growth inhibition rate was calculated as 1–viability, which is the data that was used for the statistical analysis described below. The detailed experimental procedures were described in Ghosh et al. (2015).

3. A Global Response Surface Model under the Bliss Independence Principle

Here we assume that for the given drugs A and B, that each produces its anticancer effect by targeting different pathways, and that these pathways have no mechanistic connection other than the response outcome. The response was measured as the percentage of cancer cells that died following drug treatment, a percentage frequently referred to as the inhibition rate. To determine the combination effect of two drugs, the Bliss independence principle is considered. At designated doses of the component drugs, the Bliss predicted inhibition rate ${\widehat{y}}_{ab}$ can be calculated by equation (1)

$${\widehat{y}}_{ab}=y_a+y_b-y_a{y}_b,{0\le y}_i\le 1,i=a,borab$$ (1)

where y_a and y_b are the observed inhibition rates with drug A alone at dose a and drug B alone at dose b. If the observed inhibition rate y_ab at the combination dose (d_a,d_b) of drug A and drug B is greater than the Bliss predicted inhibition rate ${\widehat{y}}_{ab}$, the drug combination effect is thought of as synergism at that specific (d_a,d_b) dose combination.

Chou and Talalay (1981, 1984) proposed a combination index for two mutually nonexclusive drugs. Using the above symbols, the combination index can be written as:

$$\frac{d_a}{D_{y,A}}+\frac{d_b}{D_{y,B}}+\frac{d_a{d}_b}{D_{y,A}{D}_{y,B}}$$ (2)

Where d_a and d_b are the doses of Drug A and B that, when used in combination, reach the inhibition rate of y. D_y,A and D_y,B are the doses of single drugs A and B that reach the same inhibition rate, y. For equation (2), a value less than 1 indicates synergism. Equation (2) is deducted from equation (3), the summation of the effects of two mutually nonexclusive inhibitors on dose-response systems obeying Michaelis-Menten kinetics or Hill-type kinetics (Chou and Talalay, 1981, 1984).

$$\frac{{\widehat{y}}_{ab}}{1-{\widehat{y}}_{ab}}=\frac{y_a}{1-y_a}+\frac{y_b}{1-y_b}+\frac{y_a{y}_b}{(1-y_a)(1-y_b)}$$ (3)

Equation (3) can be simplified as ${\widehat{y}}_{ab}=y_a+y_b-y_a{y}_b$, which is the Bliss independence model. We thus use equation (2) as the Bliss independence interaction index for our study evaluating the synergism of drug combinations.

The Bliss independence interaction index τ for combination effect of two drugs can be expressed as equation (4) (Chou and Talalay, 1981, 1984)

$$\tau =\frac{d_a}{D_{y,A}}+\frac{d_b}{D_{y,B}}+\frac{d_a{d}_b}{D_{y,A}{D}_{y,B}}\{\begin{array}{cc}<1& Synergism\\ =1& Independent\\ >1& Antagonism\end{array}$$ (4)

To estimate an overall Bliss interaction index, we performed two-stage modeling by extending the one-stage algorithm proposed by Harbron (2010) for Loewe additivity. The overall interaction index can be used to determine if combinations of two drugs produce a statistically significant synergistic effect over the entire range of doses tested.

In the first stage, we estimate dose-response parameters for each drug based on the Hill equation by adding the upper and lower limit of the inhibition rate, which is expressed as equation (5),

$$\mathrm{y}=\frac{U-L}{1+{\left(\frac{IC50}{D_y}\right)}^m}+L$$ (5)

where y is the inhibition rate, and U and L are the upper (top) and lower (bottom) asymptotes of the dose-response curve. IC50 is the dose required to attain half of U − L. D_y is the dose of the single drug that induces response of y. m is the Hill slope.

By natural base (e) log-transformation of the equation (5), we obtain equation (6)

$$\mathrm{y}=\frac{U-L}{1+e^{\left(\mathrm{l}\mathrm{o}\mathrm{g}\left(IC50\right)-\mathrm{l}\mathrm{o}\mathrm{g}\left(D_y\right)\right)m}}+L$$ (6)

Equation (6) is the four-parameter logistic model commonly used for calculating dose-response curves.

In our derivation, the above non-linear dose-response model with homogeneity variance is considered. If there is a notable relationship between the variability of the response and the mean response, a heteroscedastic dose-response model needs to be applied. However, Whitehead et al (2013) indicated that models with homogeneity variance in the presence of heteroscedasticity are robust. When an experiment has replicates, the replicates are used in fitting equation (6). The values for the parameters in equation (6) and their covariance matrix can be estimated using nlsLM() in R. To simplify and get comparable IC50s, U=1 and L=0 were used as fixed values to fit our model.

In the second stage, based on equation (5), for an observed response y in the combination experiment, the dose D_y for a single drug that reaches a response of y can be estimated as

$$D_y=IC50*{(\frac{y-L}{U-y})}^{\frac{1}{m}}$$ (7)

For single drug A, D_y is the parameter of D_y,A, for single drug B it is D_y,B, which are the parameters we need to estimate the interaction index. Using the definition of equation (4), across all combination doses, an overall interaction index τ is estimated from equation (8), a response surface model similar to model (7A) in Harbron’s (2010) paper

$$\frac{d_a}{D_{y,A}}+\frac{d_b}{D_{y,B}}+\frac{d_a{d}_b}{D_{y,A}{D}_{y,B}}=\{\begin{array}{ccc}1& d_a=0or& d_b=0\\ \tau & d_a>0and& d_b>0\end{array}$$ (8)

From equation (8), the response-surface model is further expressed as equation (9), which is used to estimate interaction index τ.

$$\frac{d_a}{{\tau D}_{y,A}}+\frac{d_b}{{\tau D}_{y,B}}+\frac{d_a{d}_b}{{\tau D}_{y,A}{D}_{y,B}}=1$$ (9)

Even though equation (9) does not directly express a function of the response, y, on combination doses of (d_a,d_b) with parameters shown in equations (5) or (6), the fitted y can be exactly calculated using a bisection scheme algorithm proposed by Harbron (2010) and then the interaction index can be estimated using nlsLM() function in R.

When τ <1, and the upper limit of its two-sided 95% CI is also less than 1, we may conclude that the two-drug combination has a statistically significant synergistic effect overall.

To estimate the 95% CI of the overall interaction index, a bootstrapping resampling method is applied. Based on the first-stage estimated $\widehat{log\left(IC50\right)}$ and Hill slope, $\widehat{m}$, for each single drug, bootstrapping samples of ($\widehat{{log\left(IC50\right)}_j},{\widehat{m}}_j$) where j=1, 2, 3, … n, are drawn from a bivariate normal distribution $N(\left(\begin{array}{c}\widehat{log\left(IC50\right)}\\ \widehat{m}\end{array}\right),\widehat{\mathrm{\Sigma }})$ where $\widehat{\mathrm{\Sigma }}$ is the estimated covariance matrix of $\widehat{log\left(IC50\right)}$ and $\widehat{m}$. Each set of n bootstrapping samples are applied to estimate one natural base (e) log-transformed interaction index, $\widehat{log\left(\tau \right)}$ , at the second stage calculation. The mean interaction index, $E(\widehat{\mathrm{l}\mathrm{o}\mathrm{g}\left(\tau \right)}$), and its standard deviation, se(log(τ)), are then estimated. In our experience, these estimates become stabilized after 100 bootstrapping samples and the histograms of $\widehat{log\left(\tau \right)}$ are roughly follow a normal distribution. The 95% CI of the overall interaction index is reported as $e^{E(\widehat{\log (\tau )})\pm 1.96\times se(\mathrm{l}\mathrm{o}\mathrm{g}(\tau ))}$. It will be more robust to use quantiles of the bootstrap samples to form an empirical confidence interval for a non-normal distribution but with a large number (e.g. 1000) of bootstrap samples (Efron and Tibshirani 1994).

Using the above algorithm for the overall interaction index, we can also calculate separate values of interaction indexes for each dose level of each drug in the combination. Such series interaction indexes can be used to show the combination effect when one of the two drugs is given at a fixed dose, and the other drug is given at a series of dosing levels. The R code for this analysis is provided in the Appendix.

4. Data Example and Analysis Results

4.1. Data Example

In this study, we investigated the synergistic, anticancer effect of the combination of Gamitrinib plus selected kinase inhibitors such as BKM120 and BEZ235. Tables 1 and 2 show the example data of fractional growth inhibition generated from the procedures described in Section 2. Each set of combination experiment was carried out twice. Since in each plate with 384 wells (Figure 1), there are quadruplets of dose-response measurements for Gamitrinib treatment alone, these data were averaged for Gamitrinib within each plate (Tables 1 and 2).

Table 1.

The growth inhibition measurements for the experiment Gamitrinib plus BKM120

Dosage of Gamitrinib	Dosage of BKM120
	0	0.008	0.025	0.074	0.222	0.667	2
0		0.036	−0.053	−0.115	0.067	0.303	0.602
		−0.017	−0.033	−0.011	−0.076	0.224	0.532
0.008	0.053	0.215	0.081	0.191	0.184	0.429	0.505
	−0.039	0.002	−0.046	−0.079	0.047	0.294	0.596
0.025	0.012	0.064	0.010	0.031	0.292	0.456	0.483
	−0.020	0.029	0.105	−0.030	−0.002	0.374	0.473
0.074	−0.033	0.088	0.068	0.103	0.069	0.323	0.500
	−0.104	−0.008	−0.090	0.019	0.062	0.190	0.605
0.222	0.028	−0.207	−0.163	−0.149	0.115	0.321	0.499
	0.061	−0.076	−0.125	−0.021	0.025	0.242	0.534
0.667	0.080	0.040	0.031	0.057	0.138	0.364	0.506
	0.058	0.031	0.040	0.008	0.146	0.318	0.458
2	0.494	0.401	0.434	0.435	0.510	0.659	0.949
	0.436	0.359	0.325	0.377	0.432	0.609	0.780

Table 2.

The growth inhibition measurements for the experiment Gamitrinib plus BEZ235

Dosage of Gamitrinib	Dosage of BEZ235
	0	0.008	0.025	0.074	0.222	0.667	2
0		0.129	0.266	0.387	0.399	0.460	0.383
		0.127	0.271	0.313	0.322	0.473	0.457
0.008	0.053	0.426	0.500	0.605	0.595	0.649	0.670
	−0.039	0.325	0.418	0.575	0.533	0.546	0.592
0.025	0.012	0.379	0.448	0.540	0.656	0.511	0.661
	−0.020	0.336	0.365	0.536	0.497	0.500	0.553
0.074	−0.033	0.341	0.429	0.423	0.619	0.568	0.644
	−0.104	0.168	0.280	0.470	0.430	0.466	0.558
0.222	0.028	0.071	0.404	0.443	0.433	0.485	0.520
	0.061	−0.062	0.205	0.317	0.443	0.376	0.447
0.667	0.080	0.290	0.390	0.454	0.537	0.568	0.598
	0.058	0.223	0.347	0.263	0.513	0.457	0.556
2	0.494	0.735	0.668	0.907	0.671	0.846	0.879
	0.436	0.570	0.647	0.829	0.702	0.848	0.885

4.2. Excess over Bliss Scores

Equation (1) is used to calculate the Bliss predicted response (${\widehat{y}}_{ab}$ ) at the combination dose (d_a,d_b) of drug A and drug B. The difference between the observed response (y_ab) and the Bliss predicted response (${\widehat{y}}_{ab}$) at the same combination dose is usually referred to as “excess over Bliss score”, which is widely used to evaluate drug combination effects following these criteria:

$$\mathrm{E}\mathrm{x}\mathrm{c}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{B}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=I=y_{ab}-{\widehat{y}}_{ab}\{\begin{array}{cc}>0& Synergism\\ =0& Independent\\ <0& Antagonism\end{array}$$

With the excess over Bliss score, the drug combination effect is determined at each combination dose. When replicates exist, the average percentage inhibition is usually used in the calculation. The application of excess over Bliss score for the evaluation of drug combination effect is simple but may cause false-positive claims because it does not consider the variability of response measures. To overcome such problems, Zhao et al. (2014) proposed a response surface model to predict the excess over Bliss score at each combination dose using two-stage modeling. They used the letter “I” to represent the “excess over Bliss score”. In the first stage of the model, the average of observed responses and corresponding variance at each dose of drug A and drug B are calculated. In the second stage, 100 random samples of ${\widehat{y}}_{ab}$ are simulated using multivariate normal distributions with first stage estimated means and variances. Conditional on ${\widehat{y}}_{ab}$, a linear model is used to estimate response surface parameters and then the variance of I and the 95% CI of I are calculated.

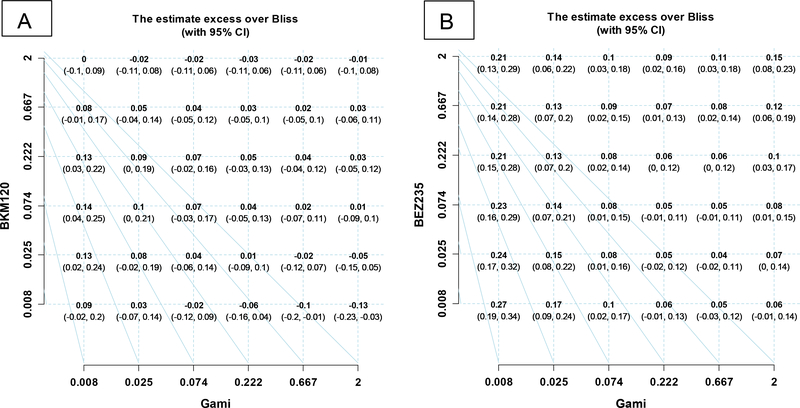
In this section, we applied the method of Zhao et al (2014) to analyze our example data. The estimated I and the 95% CI at each combination dose are listed in the grid plots (Figures 2 A-B). These results will be compared to the results obtained from our proposed model in section 4.3.

Figure 2.

Grid plots with estimated excess over Bliss scores and 95% CI at each combination dose

Figure 2 A shows that the lower bounds of the 95% CI of excess over Bliss scores are many negative across the combination doses of Gamitrinib and BKM120. In contrast, for the combination of Gamitrinib and BEZ235, most of the lower bounds of the 95% CI of excess over Bliss scores are positive, except at dose levels 0.222 and 0.667 of Gamitrinib (Figure 2B). The results in Figure 2 give us a clue that the combination of Gamitrinib and BKM120 does not have impressive synergism, while Gamitrinib and BEZ235 does have a synergistic effect. However, by only looking at the grid plots, it is hard to conclude overall if the two drugs were synergistic or not. From only such results as these, we cannot make a general statistical inference.

4.3. Interaction Indexes

Using the method described in Section 3, we estimated an overall interaction index with 95% CI for the combination of two drugs, and a series of interaction indexes with corresponding 95% CIs for each level of a given drug combined with various doses of the other drug.

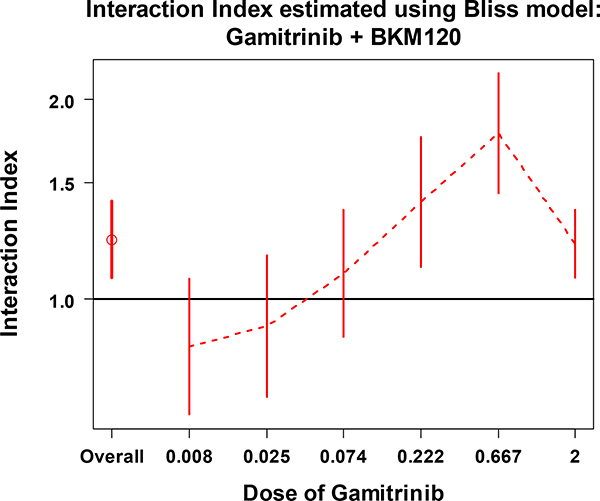
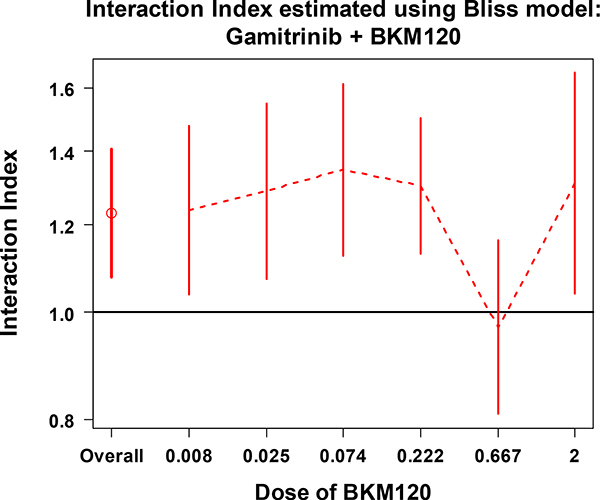
Figures 3 and 4 show the estimates of overall and series interaction indexes with 95% CIs for the combination of Gamitrinib and BKM120. The overall interaction index (the first data point) indicates that combinations of Gamitrinib and BKM120 don’t have a synergistic effect overall. Looking at the series indexes separately, for each dose level of Gamitrinib (Figure 3) or BKM120 (Figure 4), all of the 95% CIs crossed or sit above the line at interaction index of 1. This indicates that there is no significant synergistic effect across the given doses of the two drugs. These results are consistent with the pattern shown in Figure 2A.

Figure 3.

The overall interaction index and the series interaction indexes with 95% CI at each dose of Gamitrinib combined with various doses of BKM120

Figure 4.

The overall interaction index and the series interaction indexes with 95% CI at each dose of BKM120 combined with various doses of Gamitrinib

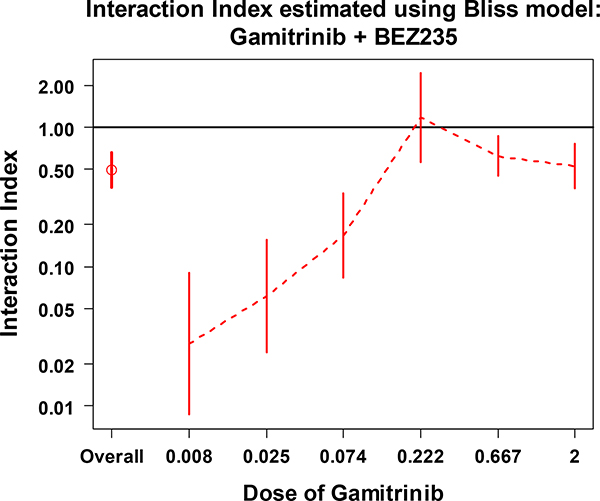
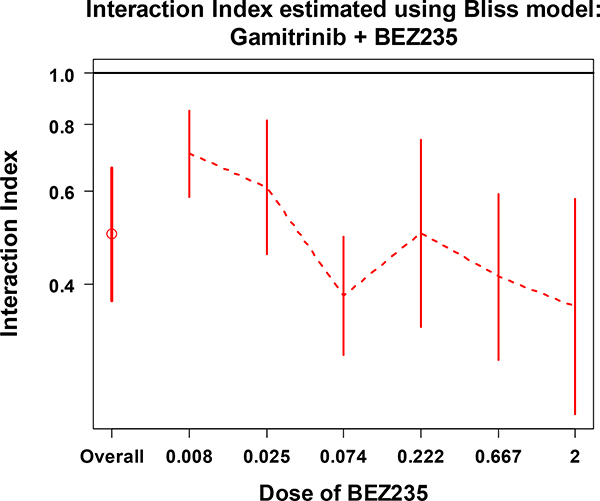
From Figures 5 and 6, we may conclude that the combination of Gaminitrib and BEZ235 has significant synergistic effect overall (first data point). Looking at the series indexes separately, for each dose of Gaminitrib (Figure 5) or BEZ235 (Figure 6), all of the 95% CIs (except the CI for Gamitrinib at dose of 0.222) are under the line at interaction index of 1. This indicates that there is a significant synergistic effect across the given doses of the two drugs. These results are supported by the pattern we saw in Figure 2B.

Figure 5.

The overall interaction index and the series interaction indexes with 95% CI at each dose of Gamitrinib combined with various doses of BEZ235

Figure 6.

The overall interaction index and the series interaction indexes with 95% CI at each dose of BEZ235 combined with various doses of Gamitrinib

4.4 Some Comparisons with One-stage Modeling

Whitehead et al. (2008) proposed a one-stage Bliss model illustrated below. A parameter v is introduced to measure the amount of synergy or antagonism

$$1-\left(\frac{g(x_1,x_2)-\gamma }{\delta }\right)={\left[\left\{1-\left(\frac{g(x_1,0)-\gamma }{\delta }\right)\right\}\left\{1-\left(\frac{g(0,x_2)-\gamma }{\delta }\right)\right\}\right]}^{\nu }$$

The case v = 1 represents Bliss independence. Values of v between 0 and 1 represent antagonism and values greater than 1 represent synergy. Using the four-parameter logistic regression model, with a lower limit γ and an upper limit δ + γ, at a combination dose x₁ of drug 1 and dose x₂ of drug 2 the expected response surface g(x₁,x₂) can be expressed as

$$g\left(x_1,x_2\right)=\delta [1-{\left\{\frac{1}{{\varphi }_1{\varphi }_2}\right\}}^{\nu }]+\gamma$$

where ϕ_i = 1 + exp(α_i + β_ilogx_i), and α_i = −β_ilogD_0.5,i, and β_i and D_0.5,i are the Hill slope and IC50 of drug i, respectively. The parameter v can be estimated using SAS NLIN procedure.

Since the parameter v >1 stands for synergism, and 0 < v <1 for antagonism, 1/v would have the same evaluation rule as the overall interaction index τ in our method. In this section, we report some comparisons obtained by analyzing the same data using the Whitehead et al. (2008) method and our method. For our example data “Gami+BKM120”, both models indicate a non-synergistic effect (Table 3). But for the example data “Gami+BEZ235”, the one-stage method yielded unreliable estimates since it failed to estimate the variance of some parameters, when made the approximate correlation matrix incomplete. The SAS output provided a warning: “Convergence criterion met but a note in the log indicates a possible problem with the model”. A similar issue occurred when the one-stage method was applied to analyze other data such as Chou and Talalay’s (1981) Table 2 data (Table 4). The one-stage modeling failed to converge when we analyzed the data from Lee et al (2007) (Table 4).

Table 3.

Comparison of overall interaction index calculated using our method to that using the method of Whitehead et al, using our example data

Drug combination	τ (95% CI) from our method	1/v (95% CI) from Whitehead et al’s method
Gami+BKM120	1.23 (1.09, 1.40)	1.05 (0.85, 1.28)
Gami+BEZ235	0.51 (0.38, 0.68)	0.68 (0.54, 0.86)*

^*SAS output indicated that the estimates had a problem. No improvement with various initial values.

Table 4.

Comparison of overall interaction index calculated using our method to that using the method of Whitehead et al., using other published datasets

Dataset from	Whitehead et al’s Bliss model	Our method
	1/v (95% CI)	τ (95% CI)
Chou and Talalay (1981) Table 1	1.17 (1.12, 1.23)	1.23 (1.18, 1.27)
Chou and Talalay (1981) Table 2	0.09 (0.01, 0.55)*	0.45 (0.39, 0.53)
Harbron (2010)	0.68 (0.61, 0.76)	0.62 (0.57, 0.68)
Lee et al (2007)	Failed to converge**	0.41 (0.23, 0.73)
Whitehead et al (2008)	1.38 (1.15, 1.67)	1.43 (1.19, 1.72)

^*SAS output indicated that the estimates had a problem. No improvement with various initial values.

^**Failed to converge with default initial values. We tried various initial values but still failed.

Zhao et al (2012) applied a two-stage model using Loewe additivity and compared two-stage modeling to one-stage modeling. They also found that the one-stage modeling sometimes could not converge to proper values or had error messages in the estimating of parameters, but two-stage modeling could overcome these problems. Their simulations indicated that two-stage models gave results almost identical to the true values of the interaction index. The one-stage model, in contrast, gave interaction indexes that deviated from true values. The reason why two-stage modeling would give more precise results was discussed in detail in their paper. From their simulation data, it is worth noting that even though the one-stage method gives less accurate results than the two-stage method, the differences are not large enough to make different conclusions based on the estimated interaction indexes. In our examples shown in Tables 3 and 4, the conclusions about synergism are consistent from both one-stage and two-stage models where a comparison is possible.

5. Discussion

The in vitro drug combination experiments used for drug screening usually generate high-throughput data. Analysis methods such as heat maps or surface plots are not only time consuming, they do not provide a conclusion with statistical confidence overall. In this paper, we have proposed a method for calculating an overall interaction index based on the Bliss independent principle to help our scientists find drugs that reach a statistically significant synergistic effect in combination. This method is easily applied to analyze high-throughput data. The investigator simply needs to order the overall interaction indexes with their 95% CIs to locate those drugs that have a statistically significant synergistic effect in combination. The two-stage modeling we propose here is applicable provided that the dose-response curve of each single drug is well fitted using the Hill equation or the four-parameter logistic model.

In addition to the full factorial experimental design shown in Figure 1, we often see experiments in which the investigators only test for combination effect by adding a fixed dose of one drug to various doses of the other drug. To analyze the data obtained from this kind of experimental design, the proposed overall interaction index is still applicable if we have dose-response data from each single drug and the designed combinations.

When the data have replicates, Harbron’s (2010) algorithm allows estimating an interaction index with 95% CI at each combination dose in the experiment. To assess for a synergistic effect at each combination dose, a grid plot, similar to Zhao et al. (2014), can be generated based on the upper limits of the 95% CIs of the interaction indexes over the combination doses. However, in high-throughput drug screening, it will be more efficient to make decision by looking at the overall interaction indexes like those shown in Figures 3–6.

The two-stage modeling that we describe here is easy to use. One-stage modeling using Harbron’s (2010) algorithm in R with nls function or using Whitehead et al’s (2008) NLIN procedure in SAS does not require, as a starting input, accurate estimates of IC50 and Hill slopes, but it does need appropriate initial values of those parameters. From our experience, some initial values may end as failure of estimation from nls function in R or NLIN procedure in SAS. For some cases, various choices of initial values for the one-stage modeling still failed to converge. Using our model, in contrast, we estimate IC50 and Hill slopes first and use those parameters directly in the second stage; the interaction index can be estimated without problems. In addition, the two-stage modeling achieves more accurate results than one-stage modeling because the parameters accurately estimated from monotherapy data are crucial to precisely estimate an interaction index using combination data. And by incorporating the variance from the first stage into the second stage, the two-stage modeling provides more reliable inference (Zhao et al. 2012).

In the case where the dose-response curve for a single drug cannot be estimated by the Hill equation or the four-parameter logistic regression, we will need to identify other models that can fit the dose-response data in the first stage, and then continue the second stage of the procedure to estimate the interaction index. It is an area for development in the future.

Appendix

R code for estimating Bliss independence interaction index and 95% confidence interval

Read in original data of Gami+BKM120 (full data are shown in table 1):

rep1: Replication 1; rep2: Replication 2

DoseA: dose of drug A, DoseB: dose of drug B, y: response

rep1 <- read.table(header = TRUE, ,sep=“,”,text = “
DoseA,DoseB,y
2.000,2.000,0.949
0.667,2.000,0.506
0.025,0.000,0.012
0.008,0.000,0.053
“)

rep2 <- read.table(header = TRUE, ,sep=“,”,text = “
DoseA,DoseB,y
2.000,2.000,0.780
0.667,2.000,0.458
0.025,0.000,−0.020
0.008,0.000,−0.039
“)

data1 <- rbind(rep1, rep2)
attach(data1)

Core function to estimate Interaction Index, modified based on Harbron’s algorism (2010)

d1: observed dose of drug A; d2: observed dose of drug B

m1: Hill slope estimated from stage I for single drug A

m2: Hill slope estimated from stage I for single drug B

logIC50.1: log_e(IC50) estimated from stage I for single drug A

logIC50.2: log_e(IC50) estimated from stage I for single drug B

U: the upper asymptote of single drugs with the default value of 1

L: the lower asymptote of single drugs with the default value of 0

tau: interaction index

gp: grouping parameter for taus, default is the overall tau for the surface model

niterations: the iteration number on each call of tau.model, default 50

upper & lower: vector of range to estimate response of combined drug at each combination dose level

Y: the estimated response based on current tau value & single drug pamameters from stage I.

tau.model <- function(d1, d2, m1, m2, logIC50.1, logIC50.2,
U=1, L=0, ..., gp=rep(1,sum(d1>0 & d2>0)),
niterations=50) {
Ic50.1 <- exp(logIC50.1) 
Ic50.2 <- exp(logIC50.2)
tau <- exp(unlist(list(...)))
mono <- (d1==0) | (d2==0)
if(length(gp) != sum(!mono)) {
stop(“Incorrect Number Of Grouping Parameters”)
}
if(!all(sort(unique(gp))==1:length(tau))) {
stop(“Numbers Of Parameters & Grouping Parameters Disagree”)
}
upper <- rep(U, length(d1))
lower <- G <- rep(L, length(d1))
for(i in 1:niterations) {
Y <- (upper + lower)/ 2.0
Part1 <- Ic50.1 * ((Y-L)/(U-Y))^(1.0/m1)
Part2 <- Ic50.2 * ((Y-L)/(U-Y))^(1.0/m2)
dPart1 <- d1/Part1
dPart2 <- d2/Part2
dPart3 <- dPart1 * dPart2
dPart1[!mono] <- dPart1[!mono]/ tau[gp]
dPart2[!mono] <- dPart2[!mono]/ tau[gp]
dPart3[!mono] <- dPart3[!mono]/ tau[gp]
G <- dPart1 + dPart2 + dPart3 – 1
if(m1<0) {
lower[G==0] <- upper[G==0] <- Y[G==0]
lower[G<0] <- Y[G<0]
upper[G>0] <- Y[G>0]
} else {
lower[G==0] <- upper[G==0] <- Y[G==0]
upper[G<0] <- Y[G<0]
lower[G>0] <- Y[G>0]
}
}
Y
}

First stage: estimate the Hill Slope and IC50 for drugs A and B, respectively

uppers, lowers: after rescaling, the upper & lower asymptote of both single drugs

Ic50.1 & Ic50.2: selected initial value of IC50 for drug A & B

drugA_est & drugB_est: store the nlsLM estimated Hill slope and IC50 for each single drug

require(minpack.lm)
uppers <− 1; lowers <- 0;
Ic50.1 <- DoseA[DoseB==0][which.min(abs(y[DoseB==0]-.5))] #pick the initial value for IC50, which is the observed single drug dosage produces the response closest to 0.5
drugA_est <- nlsLM(y~(uppers-lowers)/(1+exp(m*logIC50)/DoseA^m) + lowers, 
start=list(m=1,logIC50=log(Ic50.1)), subset=DoseB==0 & DoseA!=0)
Ic50.2 <- DoseB[DoseA==0][which.min(abs(y[DoseA==0]-.5))]    
drugB_est <- nlsLM(y~(uppers-lowers)/(1+exp(m*logIC50)/DoseB^m) + lowers, 
start=list(m=1,logIC50=log(Ic50.2)), subset=DoseA==0 & DoseB!=0)

Bootstrapping the parameters estimated from stage I to estimate the 95% CI of tau estimated from stage II

drugA.para & drug B.para: store each drug’s estimated Hill slope & IC50

drugA.var & drugB.var: store each drug’s estimated variance & covariance of Hill slope & IC50

N: Bootstrapping size

mu1p & mu2p: random samples of Hill slope & IC50 drawn from bivariate-normal distribution for each drug

with corresponding means & variance-covariance estimated from stage I

pars: store the estimated taus based on each mu1p & mu2p.

drugA.para <- summary(drugA_est)$coef[,1] 
drugA.var <- vcov(drugA_est) 
drugB.para <- summary(drugB_est)$coef[,1]
drugB.var <- vcov(drugB_est)
require(mvtnorm)
N <− 100 
mu1p <- mu2p <- NULL
mu1p <- rmvnorm(N, drugA.para, drugA.var) 
mu2p <- rmvnorm(N, drugB.para, drugB.var) 

Second Stage: estimate Interaction Index

To estimate an overall interaction index

pars <- NULL
for (i in 1:N) {
overallTau <- nlsLM(y ~ tau.model(d1=DoseA, d2=DoseB, m1=mu1p[i,1], m2=mu2p[i,1], 
logIC50.1=mu1p[i,2], logIC50.2=mu2p[i,2],
logtau1=logtau1), start=list(logtau1=0)) 
pars <- rbind(pars, summary(overallTau)$coef[,1])
} 
log_tau <- mean(pars)
tau <- unlist(data.frame(est=exp(log_tau), LCL= exp(log_tau-1.96*sd(pars)), HCL= exp(log_tau+1.96*sd(pars))))
print(tau)

To estimate separated interaction indexes at each dose of drug A combining with various doses of drug B

pars <- NULL
gp <- as.numeric(as.factor(DoseA[DoseA*DoseB > 0]))
for (i in 1:N) {
sepTauA <- nlsLM(y ~ tau.model(d1=DoseA, d2=DoseB, m1=mu1p[i,1], m2=mu2p[i,1], 
logIC50.1=mu1p[i,2], logIC50.2=mu2p[i,2], 
logtau1=logtau1, logtau2=logtau2, logtau3=logtau3, logtau4=logtau4, logtau5=logtau5, logtau6=logtau6, gp=gp), start=c(logtau1=0, logtau2=0, logtau3=0, logtau4=0, logtau5=0, logtau6=0)) 
pars <- rbind(pars, summary(sepTauA)$coef[,1])
}
Ataus <- data.frame(cbind(est=exp(apply(pars,2,mean)),LCL=exp(apply(pars,2,mean)-1.96*apply(pars,2,sd)), HCL=exp(apply(pars,2,mean)+1.96*apply(pars,2,sd))))
cat(“The follwing output has been exponentiated”)
print(Ataus)