A Fully-Adjusted Two-Stage Procedure for Rank Normalization in Genetic Association Studies

Abstract

When testing genotype-phenotype associations using linear regression, departure of the trait distribution from normality can impact both Type I error rate control and statistical power, with worse consequences for rarer variants. Because genotypes are expected to have small effects (if any) investigators now routinely use a two-stage method, in which they first regress the trait on covariates, obtain residuals, rank-normalize them, and then secondly use the rank-normalized residuals in association analysis with the genotypes. Potential confounding signals are assumed to be removed at the first stage, so in practice no further adjustment is done in the second stage. Here, we show that this widely-used approach can lead to tests with undesirable statistical properties, due to both a combination of a mis-specified mean-variance relationship, and remaining covariate associations between the rank-normalized residuals and genotypes. We demonstrate these properties theoretically, and also in applications to genome-wide and whole-genome sequencing association studies. We further propose and evaluate an alternative fully-adjusted two-stage approach that adjusts for covariates both when residuals are obtained, and in the subsequent association test. This method can reduce excess Type I errors and improve statistical power.

Introduction

Linear regression-based tests of associations of genetic variants with a quantitative trait can be sensitive to departure of the trait distribution from normality, particularly when testing rare variants. To address this problem, an approach that is widely used in genetic association studies (within the regression framework) is to apply a rank-normalization of trait values, followed by subsequent analysis of the rank-normalized trait as the analysis outcome (see e.g. Ashton and Borecki (1987); X. Wu et al. (2002) and a comprehensive review in Beasley, Erickson, and Allison (2009)). In the context of rare variants, it was shown by Tang and Lin (2015) that applying rank-normalization on traits prior to any analysis and testing helps to control the rate of Type I errors and increase statistical power. However, the factor actually determining the statistical properties of regression-based trait-variant association tests is not the distribution of the trait but instead its distribution after regressing out covariates. Indeed, it was shown in Beasley et al. (2009) that rank-normalizing traits may still result in non-normal residuals, resulting in invalid Type I error rate control, with the problem being most severe when the distribution of the residuals is heavily skewed. Recent Genome-Wide Association Studies (GWASs) have instead used a different approach, applying the rank-normalization to the residuals that were generated by regressing the trait on covariates (Hoffmann et al., 2017; Lange et al., 2014; Shungin et al., 2015; Tajuddin et al., 2016; Wen et al., 2012) in stage 1, and then using these transformed residuals as the outcomes in subsequent analyses, without further adjustment for covariates (stage 2). For GWASs, which primarily address the analysis of common genetic variants, this partly-adjusted two-stage approach has been criticized (Che, Motsinger-Reif, & Brown, 2012; Demissie & Cupples, 2011) due to potential loss of power, and biased estimates when covariates are correlated with genotypes. Pain, Dudbridge, and Ronald (2018) recently argued that these undesirable properties are a result of the residual transformation re-introducing a correlation between the covariates and the normalized outcome. However, some researchers (Auer, Reiner, & Leal, 2016) still suggest that this approach is appropriate for analysis of rare variants. As rare variant analysis is the focus of most Whole Genome Sequencing (WGS) studies, which are currently underway, there is now a strong motivation to better understand why these problems occur and how transformations and covariate associations interplay to affect them, and to provide a comprehensive framework for genetic association analyses for quantitative traits that is appropriate under a wide range of settings.

In this investigation, we propose a fully-adjusted two-stage approach that both provides the protection of rank-normal transformations, and also mitigates the potential for mis-calibrated inference. In Stage 1 we regress the trait on covariates and obtain residuals, which we rank-normalize. In Stage 2 we use these rank-normalized residuals in association analysis with the genotypes, but adjusting for the same covariates used in Stage 1. The covariate adjustment at Stage 2 differentiates the proposed method from the commonly-used partly-adjusted two-stage approach. Here, we show that using the partly-adjusted method can lead to (1) invalid estimates of regression coefficients’ standard errors, and invalid Wald and Score tests; and (2) residual confounding, because rank-normalization interferes with the adjustment for covariate effects. Adjustment for covariates in stage 2 alleviates both of these issues. Surprisingly our approach may increase statistical power compared to the partly-adjusted approach even if the residuals are perfectly Normally distributed. We investigate our approach from two perspectives. First, we separate the issues of covariate adjustment and rank normalization and study, via linear regression theory, the effects of covariate adjustment alone (or lack thereof) on testing associations with the residuals in the absence of rank normalization. Second, we perform simulations mimicking the settings used in Auer et al. (2016), comparing approaches for rank-normalization and covariate adjustment of traits and residuals under normality and deviations from normality, and by the strength of confounding effects. Finally, we demonstrate the undesirable consequences of using rank-normalized residuals in genetic association testing without covariate adjustment in two applications: multiple GWASs in the Hispanic Community Health Study/Study of Latinos, and a WGS analysis of blood hemoglobin levels using three studies from the Trans-Omic Precision Medicine (TOPMed) TOPMed phase 1: the Framingham Heart Study (FHS), Jackson Heart Study (JHS) and Old Order Amish Study (Amish). We show how our fully adjusted two-stage approach addresses these problems.

Materials and Methods

Linear regression and residuals

For person $i$ we assume that a linear regression model holds, in which each individual has quantitative trait $y_i,\text{a}\hspace{0.17em}p\hspace{0.17em}\hspace{0.17em}\times \hspace{0.17em}\hspace{0.17em}1$ covariate vector x_i, and a $k\times 1$ vector of genotypes g_i (in single variant testing $k$ is equal to 1). For simplicity, our derivations assume that the observations are independent with identically distributed (iid) error terms.

According to the linear regression model:

$$y_i=\hspace{0.17em}\hspace{0.17em}{\mathit{x}}_i^T\mathit{\alpha }+{\mathit{g}}_i^T\mathit{\beta }+e_i,$$ (1)

for covariate effects α and genetic effects β, and where the error terms $e_{i,}i=1,\dots ,n$ are independent and iid. In GWAS and WGS analyses the main focus is testing the null hypothesis $H_0:\mathit{\beta }=\mathbf{0}$ This can be done by first obtaining ordinary least squares estimate $\widehat{\mathit{\beta }}$ (in addition to $\widehat{\mathit{\alpha }}$) and a corresponding standard error estimate $\widehat{se}\left(\widehat{\mathit{\beta }}\right),$ and then using these in a Wald test. A popular alternative is the Score test, which does not rely on estimating β (McCullagh & Nelder, 1998), but rather, is based on a model that only estimates $\mathit{\alpha }$ via a `null model’, in which the outcome y_i is regressed on just the covariates ${\mathit{x}}_{\mathit{i}}$ Residuals are obtained from this null model, and their association with genotype is then assessed. We denote these residuals by $\in ={\left({\in }_1,\hspace{0.17em}\mathrm{...}\hspace{0.17em},{\in }_n\right)}^T$, where ${\in }_i=y_i-{\mathit{x}}_i^T\widehat{\mathit{\alpha }}.$. A commonly used Score test in genetic association studies that interrogate rare variants, is the Sequence Kernel Association Test (SKAT, (M. C. Wu et al., 2011)), which tests the association of a set of rare variants with the outcome.

Two-stage approaches for genetic association analysis

In the first stage of a two-stage approach, the null model is fit, the residual vector ϵ calculated, and a rank-normalizing transformation is applied to ∈ This means that entries of ∈ are matched with quantiles of the normal distribution, so that the transformed values maintain the same order (or rank) as the original residuals, but follow the normal $\text{N}\left(0,1\right)$ distribution (Tang & Lin, 2015). In the second stage the transformed residuals, which we denote (∈), are tested for association with the genotypes. It is common in practice to leave this second stage unadjusted for covariates, but in our fully adjusted approach we do adjust for them. This means that the design matrix used when testing a genotype in the second stage differs between the partly- and fully-adjusted approaches. In the partly adjusted approach, the design matrix consists of only an intercept (in addition to the tested genotype), while in the fully adjusted approach, the design matrix is the same as in the first null model. This is crucial, because, as we show in the Appendix, computation of projection matrices used for calculating standard errors rely on this design matrix. The two different design matrices encapsulate different assumptions made on the distributions of the residuals. In the Appendix, we show that in the absence of rank-normalization, a two-stage procedure in which (raw) residuals are used without covariate adjustment can lead to a loss of power. This is true when using rank-normalized residuals as well: to see this, assume that the residuals from the first stage regression are in fact normally distributed. Then rank-normalization has no effect, and our mathematical derivation demonstrates this.

GWASs in the Hispanic Community Health Study/Study of Latinos

To study the effect of using residuals with and without adjusting for covariates, and with and without applying rank-normalization on the residuals, we performed multiple GWASs for each of 19 traits using up to 12,595 individuals from the Hispanic Community Health Study/Study of Latinos (HCHS/SOL). All participants provided informed consent and the study was approved by IRBs in each of the participating institutions. All models were adjusted to age, sex, field center, background group, log-transformed sampling weights, and the five first principle components representing distant genetic ancestry, and some traits were adjusted to additional covariates, such as age², and BMI. We used linear mixed models with correlation matrices corresponding to community, household, and kinship (estimated from the genetic data). Information about the HCHS/SOL, genotyping, imputation, and genetic analysis in the HCHS/SOL, are provided in the Supplementary Material. Genotype and imputed data of the HCHS/SOL can be requested via dbGaP study accession phs000880. Phenotype data can be requested via dbGaP study accession phs000810.

TOPMed hemoglobin WGS association study

We used data from TOPMed Freeze 4, which included 7,486 individuals from the Old Order Amish Study (N=1,102), Jackson Heart Study (JHS, N=3,251 African Americans), and Framingham Heart Study (FHS, N=3,133 European Americans from the offspring and generation 3 studies). All participants provided informed consent and the study was approved by IRBs in each of the participating institutions. Additional information about these studies is provided in the Supplementary Material. For TOPMed WGS data acquisition and QC report see ncbi.nlm.nih.gov/projects/gap/cgi-bin/GetPdf.cgi?id=phd006969.1.

We compared the performance of the SKAT Score statistic for testing the association of hemoglobin (HGB) values with sets of rare variants, under different approaches for rank-normalization and use of residuals, as described below. All analyses used linear mixed models, accounting for genetic relatedness using a genetic relationship matrix (GRM) computed using the GCTA method, (Yang, Lee, Goddard, & Visscher, 2013) where GRM was computed using all variants with MAF≥0.001. Covariates were age, sex, and study. Additionally, to account for heteroscedasticity, we used a study-specific variance model, where we estimated a separate residual variance for each study (Amish, JHS, FHS Offspring, and FHS generation 3). The SKAT test was applied on sets of genotypes formed by taking all genetic variants with alternate allele frequency in the range (0,0.01), and dividing them into non-overlapping sets, defined by running windows across the genome, of length 5, 10, and 50 kilo bases (kb). For comparison, we also report results from analysis of a single permutation phenotype. Specifically, we randomly permuted HGB across participants once, and performed the same association testing as for the unpermuted trait.

GWAS and WGS association studies – model comparisons

For genetic analyses in both the HCHS/SOL and TOPMed, we consider the approaches described in Table 1 and Figure S1 in the Supplementary Material. Table 1 describes the steps taken in each of the two stages (or in a single stage, for one of the approaches). For a given dataset, the covariates (when used) were always the same, as well as the GRM and variance component structure.

Table 1: analysis approaches compared in simulations and applied data analysis.

For each of the compared analysis approaches (left column) the table provides the regression models from the two (or single) stages. Stage 1 is the same for all two-stage approaches. The association tests are general, and could be a single variant Wald, or a variant-set SKAT test, depending on the application.

Approach	Stage 1	Stage 2
Resid-Adj	Regress $Y\sim X,$ giving $\in =Y-X\widehat{\beta }$	Test G association based on the regression $\in \sim X+G$
Resid-Unadj		Test G association based on the regression $\in \sim G$
RN-Resid-Adj		Test G association based on the regression $\left(\in \right)\sim X+G$
RN-Resid-Unadj		Test G association based on the regression $RN\left(\in \right)\sim G$
RN-Trait-Adj	Test G association based on the regression $RN\left(Y\right)\sim X+G$	--

All null models and subsequent association tests were computed in R using the GENESIS package (Conomos et al., 2018). For the HCHS/SOL, we focused on a single-variant Wald test, calculating the p-values of test statistics based on the $\text{N}\left(0,1\right)$ distribution using model-based standard errors, and for TOPMed, we focused on a variant-set SKAT test (Lee, Miropolsky, & Wu, 2017). To quantify inflation, we used the inflation factor ${\lambda }_{gc}$ (Devlin & Roeder, 1999) computed as the ratio between the quantile of the ${\chi }_{\left(1\right)}^2$ distribution corresponding to the median observed p-value $p_{med}$, computed as $t_{med}=\left\{t:\mathrm{Pr}\left({\chi }_{\left(1\right)}^2>t\right)=p_{med}\right\}$ and the median value of the ${\chi }_{\left(1\right)}^2$ distribution, computed as $t_{0.5}=\left\{t:\mathrm{Pr}\left({\chi }_{\left(1\right)}^2>t\right)=0.5\right\}$, i.e. ${\lambda }_{gc}=t_{med}/t_{0.5·}$

Simulation studies

We performed a simulation study mimicking the settings in Auer et al. (2016), with modification to examine the effect of covariate confounding by a genetic principal component. We generated outcomes according to the model $y_i=x_i{\beta }_a+g_i{\beta }_g+{\in }_i$, $i=1,\dots n$, where the residual ${\in }_i$ was sampled from three different distribution settings: ‘normal’ ${\in }_i\sim N\left(0,1\right)$; ‘outlier’ ${\in }_i\sim aN\left(0,1\right)+\left(1-a\right)N\left(0,3\right),$ with $a=1$ with probability 0.99, and 0 otherwise; or ‘non-normal’ ${\in }_i\sim {\chi }_{\left(2\right)}^2.$ There was a single covariate $x_i\sim N\left(0,1\right),$ mimicking a single continuous measure of ancestry, with effect fixed at ${\beta }_a=1.$ Genotype values were simulated under varying minor allele frequencies, and with and without association to the covariate, as follows. A genotype value for each person was sampled in Hardy-Weinberg Equilibrium, i.e. from a binomial distribution, with $g_i\sim Binom\left(p_i,2\right),$ and probability computed as $p_i=\text{exp}\left({\gamma }_0+x_i{\gamma }_x\right)/\left(1+\text{exp}\left({\gamma }_0+x_i{\gamma }_x\right.\right),$ with ${\gamma }_0\in \left\{-2,-3,-4,-5,-6,-7\right\}$ controlling how rare the minor allele is. At the average value of ancestry, i.e. $x_i=0,$ the lowest value ${\gamma }_0=-7$ gives MAF=0.0009, and the highest value ${\gamma }_0=-2$ gives MAF =0.12. Lastly, ${\gamma }_x$ determines the strength of confounding induced by the ancestry covariate, with ${\gamma }_x\in \left\{0,1,2\right\},$ where ${\gamma }_x=0$ corresponds to no confounding. While this model is consistent with confounding due to ancestry, other mechanisms in which the genotype is associated with the covariate (e.g. BMI, age in a cohort of old individuals) are also possible and have the same downstream effect on association analyses. We performed 10⁷ simulations from each combination of parameter settings and ${\beta }_g=0$ (under the null), enabling a good estimation of type 1 error rate at the 10⁻⁴ significance level. Type I error was computed as the proportion of simulations in which the null hypothesis was rejected (p-value <10⁻⁴). For power, we ran 10⁴ simulations for each combination of the aforementioned parameters and with ${\beta }_g\in \left\{0.1,0.15,0.2\right\}$ Power was generally calculated as the proportion of simulations in which the null hypothesis was rejected. In instances in which the Type I error was not control, we calculated the significance level yielding the desired Type I error rate, and used this threshold when determining whether the null hypothesis is rejected.

Results

Simulation studies

Comprehensive simulation results are provided in the Supplementary Material. We here provide a summary of the results, together with selected figures that demonstrate the main results for Type I error rate control and power.

In the ‘normal’ simulation settings (normally distributed errors), all tests always controlled Type I errors appropriately (Supplementary Material, Figures S5a and S6a). Figure 1 provides power estimates for these settings, for varying degrees of confounding and for common (MAF ranged between 0.11 to 0.22) and rare (MAF ranged between 0.002 to 0.02) variants. The power of the unadjusted methods (RN-Resid-Unadj, Resid-Unadj) decreases, compared to the adjusted methods (RN-Resid-Adj, Resid-Adj, RN-Trait-Adj) as the confounding effect increases. All adjusted methods are roughly similar for common variants, however, RN-Trait-Adj loses power compared to Resid-Adj and RN-Resid-Adj when variants become rare. Complete power figures for this setting are provided in the Supplementary Material, Figures S5b and S6b.

Figure 1: Estimated power in selected simulation studies.

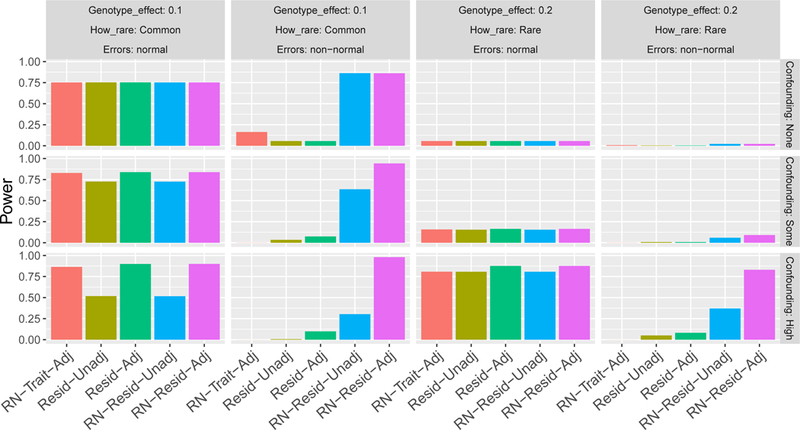
Each of the panels provides the power calculated over 10⁴ replicates of simulations, for each of the compared analysis approaches. Here we consider the ‘normal’ and ‘non-normal’ distribution settings, focusing on rare and common variants (Common: ${\gamma }_0=-2$, with genotype effect size ${\beta }_g=0.1$; Rare: ${\gamma }_0=-5$, with genotype effect size ${\beta }_g=0.2$) and by varying degrees of covariate confounding (None: ${\gamma }_x=0$; Some: ${\gamma }_x=1$; High: ${\gamma }_x=2$). In the displayed results, sample size was n=10,000, p-value threshold for determining significance was set at 10⁻⁴.

Selected results from the `non-normal’ simulation settings (chi-squared distributed errors) are presented in Figure 1 (power) and Figure 2 (type 1 error rates). Type I errors are well controlled when variants are common and there is no confounding. However, alarmingly, Type I error rates are very high for common variants when there is confounding effect, for RN-Resid-Unadj and RN-Trait-Adj. As variants become rare, all methods do not control Type I error under some conditions. Moreover, for rare variants, methods that do not rank-normalize (Resid-Adj and Resid-Unadj), did not control the Type I error rate even under no confounding. While RN-Resid-Adj did not control Type I error rate in the rare variant and strong confounding settings, overall it was the “least bad” approach of those investigated, with lowest observed levels of inflation overall. Figure 1 provides (calibrated) power for the ‘non-normal’ settings. Here, in the common variant and no confounding scenario, where all methods controlled the Type I error rate, only RN-Resid-Adj and RN-Resid-Unadj had high power. The pattern was similar across settings (see Figures S7 and S8 in the Supplementary Material for complete results).

Figure 2: Type 1 error rates in the ‘non-normal’ simulation settings.

Each of the panels provides the (scaled) estimated type 1 error rate over 10⁷ replicates of simulations, respectively, for levels of variant frequency (Common: ${\gamma }_0=-2$; Medium: ${\gamma }_0=-4$; Rarest:${\gamma }_0=-6$), and degree of confounding (None: ${\gamma }_x=0$; Some: ${\gamma }_x=1$; High: ${\gamma }_x=2$). Type 1 errors are scaled by the expected type 1 error rate (ideal value is 1, higher values indicate high rate of false positives, or inflation, lower values indicate deflation, or conservatism). Large values were truncated to 5. In the displayed results, sample size was n=10,000, p-value threshold for determining significance was set at 10⁻⁴.

Finally, the results from the ‘outlier’ simulation settings (errors from a mixture of two normal distributions with different variances) had intermediate results compared to the two more extreme cases of ‘normal’ and ‘non-normal’ simulations. Results from these settings are provided only in the Supplementary Material. The Type I error rate was inflated under some conditions, with, for a given analysis approach, inflation generally higher as a variant becomes rarer and for smaller sample sizes (Supplementary Material Figures S9a and S10a), and with inflation being better controlled with rank-normalization, and power being higher for fully adjusted methods under confounding effect (Supplementary Materials Figures S9b and S10b).

GWASs in the HCHS/SOL

We report results from HCHS/SOL GWASs of 19 traits in the Supplementary Material, and here highlight analyses of 4 traits: height, systolic blood pressure (SBP), ferritin, and number of teeth (N-teeth), in Figure 3. For all traits, Figures S11-S30 in the Supplementary Material demonstrate that Resid-Adj is always had smaller p-values than Resid-Unadj, in agreement with the derivation in the Appendix. Similar patterns are observed when comparing RN-Resid-Adj to RN-Resid-Unadj when the trait residuals are relatively normally distributed. For example, the top left panel in Figure 3 compares the p-values from the GWASs of height in using RN-Resid-Adj and RN-Resid-Unadj, and the patterns is essentially the same as that seen in the analyses without rank-normalization, Resid-Adj and Resid-Unadj (see Figure S13 in the Supplementary Material for distribution of height residuals). When traits are further from normalilty (SBP, ferritin, N-teeth), this pattern changes, and we see some genetic variants with lower p-value in RN-Resid-Unadj compared to RN-Resid-Adj (Figure 3). The most extreme example is N-teeth, for which ${\lambda }_{gc}$ was 1.02 and 1.77 with and without second-stage adjustment for covariates, respectively, i.e. RN-Resid-Unadj was highly inflated. These results are in line with the simulations provided in Figure 2, where in the ‘non-normal’ setting, even a relatively small degree of confounding caused a large inflation of RN-Resid-Unadj.

Figure 3: Computed p-values from the analyses of height, SBP, ferritin, and N-teeth in participants of the HCHS/SOL.

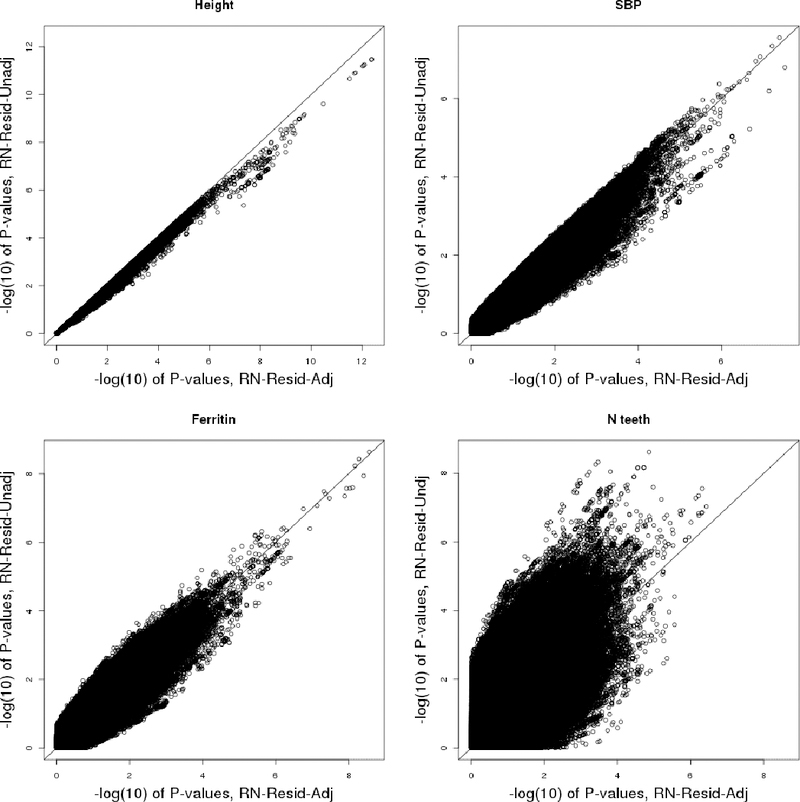
Each of the panels corresponds to a different trait, and compares the (–log) p-values obtained from analyses that tests the association between rank-normalized transformed residuals and common genotypes (MAF≥0.05), with and without adjustment to the covariates that were used in the model that obtained the residuals.

Hemoglobin WGS study in TOPMed

Figure 4 compares the inflation factors across scenarios and sliding window sizes, under true and randomly permuted HGB concentrations. Using Resid-Unadj and RN-Resid-Unadj produced deflated results, compared to Resid-Adj and RN-Resid-Adj, across all settings, as expected. In both real and permuted HGB, the difference in inflation factors between covariates adjusted and unadjusted settings is larger when the residuals were not rank-normalized; and the ${\lambda }_{gc}$ values are about the same in RN-Trait and RN-Resid-Adj settings. In terms of distribution, as seen in Figure S1 in the Supplementary Material, HGB residuals have a few negative outlying values, but otherwise their distribution is relatively normal. This is likely why we primarily see less significant p-values in the unadjusted analyses.

Figure 4: Observed inflation factors in SKAT analyses of the TOPMed Hemoglobin dataset.

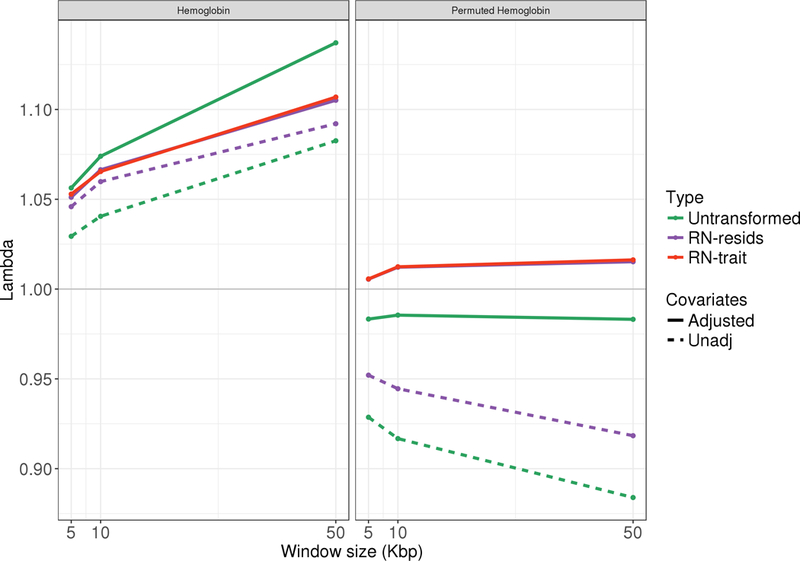
The figure provides the observed inflation factors lambda = ${\lambda }_{gc}$ in testing variants with alternate allele frequencies between 0 to 0.01 in non-overlapping window of sizes 5,10, and 50 Kbp. The left panel corresponds to the true hemoglobin trait, and the right panel correspond to the same analyses applied on permuted values of the observed hemoglobin.

In the Supplementary Material, Figures S2-S4, we provide p-values comparisons for the SKAT tests results obtained using the Resid-Adj, Resid-Unadj, RN-Resid-Adj and RN-resid-Undj. Using residuals without rank-normalization produced very low p-values for some of the tested variant sets. For these sets, there was no difference between Resid-Adj and Resid-Unadj, matching the pattern in Figure 2 (non-normal outcome) under the rarest variant and no confounding, where rank-normalization helped control inflation.

Discussion

The validity of linear regression-based tests of the genetic association with a trait can be sensitive to the trait’s distribution. Some analysis approaches that have been used to counteract this problem include rank-normalization of both trait values and of residuals, which are then used in a partly-adjusted two-stage procedure. Both approaches are known to suffer from drawbacks, albeit some investigators have argued that they are appropriate in the context of rare variants analysis (Tang & Lin, 2015). Here we have proposed a fully-adjusted two-stage approach, which uses the rank-normalized residuals as the outcome in the genetic association testing stage – a stage in which we again adjust for the same covariates used in the first stage. This approach ameliorates the problems of previous methods, for analysis of both common and rare variants. However, as we show in simulations, under non-normality of the trait and confounding by covariates, all the tests of low-count variants we considered may be biased. We separated the roles of adjustment for covariates and rank-normalization and showed theoretically (in the Appendix) that, without rank-normalization, an unadjusted two-stage procedure may result in loss of power, when using either Wald or Score tests. We demonstrated the shortcomings of the partly-adjusted two-stage procedure in both a GWAS, interrogating common variants, and in a WGS study, testing rare variants.

This investigation adds to a large body of research about trait rank-normalization and the partly-adjusted two-stage procedure for rank-normalization of residuals. While we provided mathematical results demonstrating loss of power caused by lack of adjustment at the second, testing stage, when normalization is not performed, more thorough mathematical investigation is needed. First, our mathematical derivations, as well as simulations, considered only the settings of independent observations. While our extensive data analysis supports these results in correlated data settings, mathematical results may be needed to convince some analysts that an issue exists. In addition, mathematical analysis of the rank-normalizing transformation and the association with covariates, potentially elucidating the degree of expected bias of statistical tests under various confounding scenarios, will be very useful, especially for high-throughput settings, where compute costs can be substantially smaller when less covariate adjustment is used.

For common variants, previous criticism of the partly-adjusted two-stage approach showed that it results in biased effect size estimates when covariates confound the genotype-trait associations, (Demissie & Cupples, 2011) and that it loses power (Che et al., 2012; Demissie & Cupples, 2011) compared to a one-stage approach testing the trait directly. The fully-adjusted two-stage approach alleviates both of these concerns: including covariates in the second stage alleviates the confounding problem, because these confounders are accounted for. This is demonstrated in the data analysis example from the GWASs in the HCHS/SOL. We first saw, for all GWASs, that a two-stage procedure of the form Resid-Unadj loses power compared to Resid-Adj, which recovers the same results from the untransformed trait-based analysis. When we applied rank-normalization to the residuals (RN-Resid), we saw that under non-normality, the confounding effects reported by Demissie and Cupples (2011); Pain et al. (2018) are observed. Some of the unadjusted two-stage procedure RN-Resid-Unadj GWASs had many highly significant findings, which could be false positives, compared to the fully adjusted procedure RN-Resid-Adj. The N-teeth GWAS is the most extreme example. As N-teeth is highly skewed, this result agrees with Pain et al. (2018), who showed that when the trait is more skewed, the problems caused by partly-adjusted two-stage procedure, due to correlation between the normalized residuals and covariates, are more severe.

For rare variants, previous work by Tang and Lin (Tang & Lin, 2015) showed in the context of meta-analysis that rank-normalizing the trait in one-stage analysis is useful. However, when pooling multiple heterogeneous studies together in a joint analysis, as in TOPMed, there are strong confounders (e.g., study), so the problems raised by Beasley et al. (Beasley et al., 2009), pointing at biases when residuals are non-normal and there is covariate confounding, are expected, and are demonstrated in our simulation study, in which RN-Trait-Adj analysis did not control Type I error rates. We note that our simulations show that when the trait is highly non-normal and covariate confounding of the genotype-trait association exists, all analysis methods may be inflated, including RN-Trait-Adj. However, RN-Resid-Adj had generally a lower degree of inflation compared to other methods.

Recently, Auer et al. (2016) argued that an unadjusted two-stage procedure is appropriate for rare variants, because the confounding problem pointed out in Demissie and Cupples (2011) is negligible. In our simulations, we see that RN-Resid-Unadj controlled type 1 error in the normal and outlier outcome settings, where it lost some power compared to RN-Resid-Adj in the presence of confounding. In the analysis of TOPMed hemoglobin data set, we tested sets of rare variants using SKAT. Rank-normalizing either trait or residuals reduced overall inflation. Not adjusting for covariates in a partly-adjusted two-stage procedure clearly caused a strong deflation, as measured by inflation factors, i.e. in the median of the distribution. For very low p-values, they remain qualitatively quite similar in the partly- and fully-adjusted two-stage procedures (Figures S3-S6 in the Supplementary Material). We first note we cannot conclude that partly- and fully-adjusted two-stage procedures are equivalent at the low significance level when using SKAT tests. Still, the overall distribution of results is important and serves as a primary tool in evaluating model fit in genetic association studies. Therefore, one should be cautious about using a partly-adjusted approach, and whenever possible, we recommend using the fully-adjusted two-stage procedure, to both control Type 1 error rate and optimize power.

In meta-analysis of GWASs, investigators often apply genomic control (Devlin & Roeder, 1999) on each individual study contributing to the meta-analysis. This differs from our approach, in that genomic control assumes that there is global dispersion in the study, which affects all tested variants in a similar way, and can be globally corrected by a single constant. Instead our method is primarily concerned with the effect of non-normality on association analysis. Non-normality affects different genetic variants in different ways. Similarly, confounding effects, as our GWAS results demonstrate, differ between genetic variants. Therefore, a single global correction cannot account for, or fix, the challenges that we highlighted.

In summary, in this investigation we provide a thorough assessment of the controversial uses of the rank-normalizing transformation which is often used in practice despite several published manuscripts criticizing their use. We demonstrate a proper and beneficial use of such transformations when coupled with a fully adjusted two-stage procedure. In addition to the main investigation, in the Supplementary Material (Figures S12-S30) we provide comparisons of the approaches investigated in this manuscript for GWASs of 19 anthropometric, blood pressure, blood markers, and electrocardiogram traits in the HCHS/SOL, alongside the distribution of their residuals from the ‘null model’. These comparisons suggest that future large consortia meta-analyses may reduce Type I errors and gain power from using the fully-adjusted two-stage approach, compared to the partly-adjusted approach often used.

Appendix

The Wald and score test statistics in a two-stage procedure

Below we provide mathematical details of Wald and score tests, first when using the trait itself as the outcome, and then compare them to the use of residuals with and without adjusting the residuals for covariates. This section is separate from the issue of transformation, and assumes that the residuals are used without transformation. For a clean exposition, we assume here that the genotypes are centered, to that ${\mathit{g}}^T\left(\mathit{I}-\frac{1}{n}{\mathbf{11}}^T\right)\mathit{g}={\mathit{g}}^T\mathit{g}$, where 1 is the n-vector of only ones, representing the intercept in a regression without additional covariates.

The Wald test in a one-step procedure

We first review the usual `one-step’ procedure, in which the trait associations of genotype site and covariates are jointly estimated. Consider the model (1). The Wald test statistic, is the ratio of the effect estimate to its standard error estimate (where usually this ratio is squared). Let $\mathit{X}$ be the $n\times p$ ‘design’ matrix of covariates, and $\left(\mathit{X}\mathit{|}\mathit{g}\right)$ be the $n\times \left(p+1\right)$ matrix with now an additional, rightmost column being the genotype values g (a single variant) of the $n$ study individuals. If model (1) was directly used, the least squares estimator of the combined effect parameter vector ${\left({\alpha }^T,\beta \right)}^T$ would be:

$$(\mathit{\alpha }{\widehat{{}^{\mathit{T}},\mathit{\beta })}}^T={\left[{\left(\mathit{X}\mathit{|}\mathit{g}\right)}^T\left(\mathit{X}\mathit{|}\mathit{g}\right)\right]}^{-1}{\left(\mathit{X}\mathit{|}\mathit{g}\right)}^T\mathit{y}$$ (2)

Applying standard matrix operations, we notice that:

$${\left(\mathit{X}|\mathit{g}\right)}^T\left(\mathit{X}|\mathit{g}\right)=\left(\begin{array}{cc}{\mathit{X}}^T\mathit{X}& {\mathit{X}}^T\mathit{g}\\ {\mathit{g}}^T\mathit{X}& {\mathit{g}}^T\mathit{g}\end{array}\right)$$

and

$${\left[{\left(\mathit{X}|\mathit{g}\right)}^T\left(\mathit{X}|\mathit{g}\right)\right]}^{-1}=\left(\begin{array}{cc}{\left({\mathit{X}}^T\mathit{X}\right)}^{-1}+\frac{1}{k}{\left({\mathit{X}}^T\mathit{X}\right)}^{-1}{\mathit{X}}^T\mathit{g}\hspace{0.17em}{\mathit{g}}^T\mathit{X}{\left({\mathit{X}}^T\mathit{X}\right)}^{-1}& -\frac{1}{k}{\left({\mathit{X}}^T\mathit{X}\right)}^{-1}{\mathit{X}}^T\mathit{g}\\ -\frac{1}{k}{\mathit{g}}^T\mathit{X}{\left({\mathit{X}}^T\mathit{X}\right)}^{-1}& \frac{1}{k}\end{array}\right)$$

Where $k={\mathit{g}}^T\mathit{g}-{\mathit{g}}^T\mathit{X}{\left({\mathit{X}}^T\mathit{X}\right)}^{-1}{\mathit{X}}^T\mathit{g}={\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{g},$ where $\mathit{I}$ is $n\times n$ the identity matrix and $\mathit{H}$ is the ‘hat matrix’. Multiplying as needed, we get that:

$$\widehat{\beta }=\frac{{\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{y}}{{\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{g}}.$$ (3)

The estimated variance of this $\widehat{\beta }$is given by:

$$\widehat{\text{var}}\left(\widehat{\beta }\right)=\frac{\widehat{{\sigma }^2}}{{\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{g}}$$ (4)

Where $\widehat{{\sigma }^2}$ is the estimated variance of an outcome $y_i,i=1,\dots ,n$ and under assumptions of homoscedasticity with respect to the covariates, is by default taken to be the residual variance from the same regression.

The Wald test in an unadjusted two-stage procedure

Suppose now that we first regressed the outcomes $\mathit{y}$ on the design matrix, and obtained the residuals. We will get that:

$$\in \hspace{0.17em}\hspace{0.17em}\text{=}\left(\mathit{I}-\mathit{H}\right)\mathit{y}.$$ (5)

However, because the design matrix will now be only the intercept and the vector $\mathit{g}$, the effect estimate will be

$$\widehat{{\beta }^{\prime }}=\frac{{\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{y}}{{\mathit{g}}^T\mathit{g}}.$$ (6)

The difference from (3) is in the denominator, and is due to the fact that the genotypes are not projected onto the space spanned by $\left(\mathit{I}-\mathit{H}\right).$ Therefore, the effect estimates are slightly different if we use residuals, compared to using the original outcomes $\mathit{y}$ and adjusting for covariates. Moreover, the default standard error estimates of $\widehat{{\beta }^{\prime }}$are wrong. While the true variance of $\widehat{{\beta }^{\prime }}$ is ${\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{g}{\sigma }^2/{\left({\mathit{g}}^T\mathit{g}\right)}^2,$ when we use the residuals as an actual trait, we estimate the variance of $\widehat{{\beta }^{\prime }}$ as

$$\widehat{va{r}^{\prime }}\left(\widehat{\beta }\right)=\widehat{{\sigma }^2}/\left({\mathit{g}}^T\mathit{g}\right).$$ (7)

Therefore, both the effect estimates are not the least squares estimators, and their standard errors are wrong. Note here that if the genotypes were regressed on covariates, as the residuals, the correct effect estimates and standard errors would have been recovered, a result known as the Frisch-Waugh-Lovell theorem. (Puntanen, Styan, & Isotalo, 2011)

The Wald test in a fully-adjusted two-stage procedure

However, we can also use the residuals and adjust for covariates and recover the same effect size estimates given in (3): because we adjust for covariates, the denominator of the expression for $\widehat{\beta }$ is again as in (3), ${\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{g},$, yielding the same effect estimate. In addition, because not only the numerator of $\widehat{\beta }$ stayed the same, but also the matrix $\left(\mathit{I}-\mathit{H}\right)$ is used via the covariates adjustment and its effect on $\mathit{g}$, the variance of $\widehat{\beta }$ is correctly recovered to be (5).

The score statistic

The score statistic is given by the gradient of the log-likelihood with respect to the parameter one wishes to test, and evaluated under the null hypothesis. For analysis of rare variants, the SKAT (M. C. Wu et al., 2011), a score test, is often used for testing associations between a variant site set and a trait. Because score statistics are computed under the null hypothesis, they do not depend on, nor take into account, effect estimates pertaining to the tested genetic variants, and therefore, the regression residuals used by such tests are always those provided in (4). For single variant analysis, the score statistic is given by

$${\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{y},$$ (8)

which under homoscedasticity has variance

$${\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{g}{\sigma }^2.$$ (9)

Considering again the computation of the score statistics, whether the residuals (3) are used directly, or whether they are used with and adjusted to covariates, the score statistics will remain the same, as in (8). However, if we use the residuals as if they are the actual trait without adjusting for covariates, we use the wrong design matrix – i.e. only an intercept and no covariates, and the score variance will be erroneously computed as ${\mathit{g}}^T\mathit{g}{\widehat{\sigma }}^2,$ while if the same design matrix was used as in the null model used for obtaining residuals, the variance will be computed to be as in (9) (with $\widehat{{\sigma }^2}$), as needed. Because we have that ${\mathit{g}}^T\mathit{g}\widehat{{\sigma }^2}\ge {\mathit{g}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{g}\widehat{{\sigma }^2},$ using residuals without accounting for covariates (in an unadjusted two-stage procedure) yields smaller test statistics, and as a result, a global deflation.

The SKAT test

A similar deflation trend holds for the SKAT test when covariates are unaccounted for when computing the test statistics distribution. For an $n\times k$ matrix of $k$ genotypes across $n$ individuals, with residuals (4) obtained via a null model, the SKAT test statistic, in its simplest form (all variant weights equal to 1, linear kernel), is given by:

$$K={\mathit{\in }}^T\mathit{G}{\mathit{G}}^T\mathit{\in }$$ (10)

The distribution of the SKAT statistics is a weighted sum of independent ${\chi }_{\left(1\right)}^2$ variables with weights given by the eigenvalues of $\text{cov}\left(\in \right)\mathit{G}{\mathit{G}}^T,$ or equivalently, of ${\mathit{G}}^T\text{cov}\left(\in \right)\mathit{G}.$ If we do not adjust for covariate at the second (testing) stage, we will not be using the design matrix from the regression that obtained ∈, and instead will use $\text{cov}\left(\in \right)=\widehat{{\sigma }^2}\mathit{I}.$ However, in a fully adjusted two-stage procedure we will set $\text{cov}\left(\in \right)=\left(\mathit{I}-\mathit{H}\right)\widehat{{\sigma }^2}.$ Deflation occurs because${\mathit{G}}^T\mathit{G}\widehat{{\sigma }^2}\ge {\mathit{G}}^T\left(\mathit{I}-\mathit{H}\right)\mathit{G}\widehat{{\sigma }^2},$ i.e. the residual variance of the adjusted covariates may be smaller than that without adjustment.