Estimating causal log-odds ratio using the case-control sample and its application in the pharmaco-epidemiology study

Abstract

One important goal in pharmaco-epidemiology studies is to understand the causal relationship between drug exposures and their clinical outcomes, including adverse drug events. In order to achieve this goal, however, we need to resolve several challenges. Most of pharmaco-epidemiology data are observational and confounding is largely present due to many co-medications. The pharmaco-epidemiology study data set is often sampled from large medical record databases using a matched case-control design, and it may not be representative of the original patient population in the medical record databases. Data analysis method needs to handle a large sample size that cannot be handled using existing statistical analysis packages. In this paper, we tackle these challenges both methodologically and computationally. We propose a conditional causal log-odds ratio (OR) definition to characterize causal effects of drug exposures on a binary adverse drug event adjusting for individual level confounders. Using a case-control design, we present a propensity score estimation using only case samples and we provide sufficient conditions for the consistency of the estimation of the causal log-odds ratio using case-based propensity scores. Computationally, we implement a principle component analysis to reduce high-dimensional confounders. Extensive simulation studies are performed to demonstrate superior performance of our method to existing methods. Finally, we apply the proposed method to analyze drug-induced myopathy data sampled from a de-identified subset of medical record database (close to 5 million patient records), The Indiana Network for Patient Care. Our method identified 70 drug-induced myopathy (p < 0.05) out 72 drugs, which have myoathy side effects on their FDA drug labels. These 70 drugs include three statins who are known for their myopathy side effects.

1. Introduction

One important goal in pharmaco-epidemiology (PE) studies is to investigate the causal relationship between drug exposures and their clinical outcomes. Such clinical outcomes can be either drug efficacy endpoints or adverse drug events (ADEs). For the latter, because it is unethical to conduct randomized trials in studying how drugs cause ADEs, PE studies are currently the best available and effective approaches to understand their causal relationship.¹ For example, in our motivating application, investigators are interested to detect novel drugs and/or drug–drug interaction-induced myopathy, which is defined by either ICD-9 codes or a laboratory claim of serum creatine renal kinase measurement.² Data were obtained from an de-identified subset of The Indianan Network for Patient Care data, which contains coded prescription medications, diagnoses, and observational data for million of patients between 2004 and 2009.^3–6

To estimate the true relationship between drug exposure and ADEs, it is necessary to control potentially systematic difference between drug-exposed and unexposed patients.^7,8 Traditionally, the true causal relationship is defined as the mean difference between potential outcomes associated with exposed or unexposed drug status in a counterfactual outcome framework established by literatures.^8,9 There have been a number of methods to infer this drug effect using observational data after sufficiently controlling potential confounders in analysis. Particularly, propensity scores, which describe the tendency of patient taking the drug of interest, are extensively used in these methods, and they reduce the imbalance of baseline covariates, like age, gender and comorbidity, between subjects who take the drug and who do not in observational studies.¹⁰ The propensity score methods include stratified analysis by propensity scores,¹¹ matching analysis using propensity scores,¹² and inverse probability weighting based on propensity scores.¹³

Since ADEs are measured as whether one specific case event occurs within certain time period, ADE outcomes are usually dichotomous. The standard practice in PE studies is to report log-odds ratios¹⁴ as the true relationship between drugs and ADEs, which has an easy interpretation for dichotomous outcomes, especially when ADEs rate is low. Many methods have been proposed to make inference on log-odds ratios, including frequentist approaches such as the Chi-square test, the Fisher’s exact test, the reporting odds ratio¹⁵ and the proportional reporting ratio,¹⁶ and empirical Bayesian methods including empirical Bayes geometric mean proposed by Bate et al.¹⁷ and DuMouchel.¹⁸ Tatonnetti et al.¹⁹ used the traditional propensity scores to screen the large scale drug-ADEs in Federal Adverse Events Reporting System (FAERS).

Previously, using chi-square and logistic regression methods, we have shown much increase myopathy risk due to simvastatin–loratadine and chloroquine–simvastain interactions.^5,20

However, all these approaches do not fully control potential confounders between drug-exposed and unexposed groups. The obtained log-odds ratios may not reflect the true relationship in terms of odds of having ADE for two exactly same patients except for opposite exposure status.

In fact, estimating odds ratio between drugs and dichotomous ADEs in PE studies encounters several challenges. First, the definition of true causal relationships between drugs and ADEs in terms of odds ratio remains largely unclear even within a potential outcome framework, as this quantity cannot be expressed as the mean difference of potential outcomes. Second, because of the latter, propensity score methods in traditional causal inference, which rely on unbiased estimation separately for each potential outcome, are no longer applicable. Most importantly, in many PE studies, data are usually collected from a big database under some special sampling designs, mainly because of cost and efficiency concerns. In the motivating application of myopathy analysis, a case-control sampling frame was used to obtain patient’s ADE records and corresponding drug use history. Particularly, within the study period, all the case information with at least one ADE occurrence was obtained and for each case, 10 patients who had never experienced ADE within the time period were further sampled as matched controls. Then for each control patient, their drug use information within most recent month was obtained. When data are obtained from biased sampling designs, estimating causal relationship becomes even more challenging since the estimation must account for biased representation of the whole population in addition to potential confounders. For example, since traditional propensity scores are estimated from biased sample and so may not reflect the true tendency of patients taking this drug in the true population, all current methods could lead to artifactual modification and reduced ability to control for potential confounders as studied in Månsson et al.²¹ There have been some recent work attempting to address causal inference in a case-control design, including double robust inverse probability weighted methods by Wang et al.²² and targeted maximum likelihood estimation in Rose,²³ but they both aim to estimate the prevalence of outcomes, instead of odds ratio.

Motivated by the PE study of drug induced myopathy, we develop a novel framework to estimate the log-odds ratios of the true effect of drug on ADE. Our contributions are multi-folds. First, we rigorously define the true causal relationship in terms of log-odds ratios and provide sufficient conditions to show when this quantity is estimable under a case-control design. Second, we propose a case-based propensity score approach for inference. Our method first obtains propensity scores using only case samples so avoids the bias representation when using mixed data from both cases and controls. We then estimate log-odds ratios nonparametrically after matching on this one-dimensional propensity score instead of potentially high-dimensional confounders. We show that the proposed method results in consistent estimators of the log-odds ratios. Finally, when analyzing the PE study of myopathy, we develop effective computation algorithms based on data partition and meta analysis to handle the challenge in this big data analysis of 450,634 cases and 450, 634 × 10 controls.

The paper is structured as follows. Section 2 describes the proposed method and gives theoretical justification for the method. The last part of Section 2 provides detailed algorithms for method implementation. Section 3 summarizes the results from extensive simulation studies and makes comparison with some existing methods, where we consider both the situation of continuous confounders and the situation of dichotomous confounders. Section 4 presents the detail of analyzing the PE study of myopathy. Final remarks are given in Section 5.

2. Method

In this section, we first present a definition of a causal log-odds ratio (OR) for binary outcomes in the framework of counterfactual outcomes. We then provide sufficient conditions such that this quantity is estimable in a case-control design. Finally, we propose a case-based propensity score method to estimate the causal log-OR in the presence of high-dimensional confounders.

2.1. Causal log-odds ratio

Let A be a dichotomous exposure status (A = 1: exposed to a risk; A = 0: not exposed). The outcome of interest is binary, denoted by D. Particularly, in our application, A is the status whether a candidate drug has ever been taken or not and D indicates whether an ADE has occurred in a given study period. To introduce the definition of a causal log-OR, we adopt the counterfactual framework in causal inference so let D(a) be the counterfactual outcome if a subject’s exposure status is A = a, where a is 0 or 1. Thus, every subject has a pair of the counterfactual outcomes {D(0), D(1)}. Traditional causal effect defines the average causal effect of A as E[D(1) – E[D(0), i.e. the risk difference given by P(D(1) = 1) – P(D(0) = 1), so it describes the difference of two ADE probabilities in our application. As ADE rate is usually low, we expect that this difference is small so it may not be scientifically meaningful to discriminate two exposure status. Therefore, a more meaningful quantity with causal interpretation is necessary to characterize the true causal relationship between A and D.

For a binary outcome D, the ORs, which is defined as

$$\frac{P(D=1\left|A=1)/P(D=0\right|A=1)}{P(D=1\left|A=0)/P(D=0\right|A=0)}$$

is extensively used in epidemiology to characterize the relationship between the drug exposure A and the ADE D. However, OR only describes the apparent associations that can be highly different from the actual causal relationship between A and the underlying counterfactual ADE, the one we are interested in. The latter can be especially true due to the presence of confounding, which may result in potentially different compositions of subjects in the drug exposed and unexposed groups. Hence, a proper OR with causal interpretation should be able to describe the effect of A on the potential outcomes within homogeneous subjects. This motivates our definition of the causal log-OR in the following. We let U be the set consisting of all potential confounders which can be either observed or latent. To define a causal log-OR, we assume the following model for the counterfactual ADE given U

$$\text{log}\frac{P(D(a)=1|U)}{P(D(a)=0|U)}=g(U)+\delta a,a=0,1$$ (1)

where g(·) is an unknown and arbitrary function and δ is a constant. We define δ as the causal log-OR. The goodness-of-fit of model (1) defined on the potential outcome can be checked by fitting a generalized partial linear model using existing methods when all potential confounders are collected, although this is usually not the case in practice.

Model (1) assumes that for the finest subpopulation with the same U’s value, the log-odds for the counterfactual ADE D(1) differs from the log-odds for the counterfactual ADE D(0) by a constant independent of U. Equivalently, we assume that the logarithm of the OR for D(1) and D(0) given U is a constant:

$$\text{log}\frac{P(D(1)=1\left|U)/P(D(1)=0\right|U)}{P(D(0)=1\left|U)/P(D(0)=0\right|U)}=\delta$$

Thus, if we can partition the whole population as much as possible so that each partitioned group is perfectly homogeneous in terms of their counterfactual outcomes, then the OR from 2 × 2 table given by D(1) and D(0) is e^δ in this group. Different from the conditional odds ratio that is defined by Robins,²⁴ the U in our definition contains both measured and unmeasured confounders. Particularly, in PE studies, U represents any prognostic factors that can lead to the ADEs. Conditioning on the U, δ is a precise measure of the effect of drug on ADEs. Essentially, for all the subjects with the same confounders, if their exposure levels were 1, as compared to the situation when their exposure status were 0, the odd of having ADE will be increased by a factor of e^δ (δ > 0), or decreased by a factor of e^|δ| (δ < 0), or no change (δ = 0). As a note, our definition is different from the marginal causal log-OR in Rose,²³ which is defined without conditional on U. Since δ reflects the treatment effect for subjects with the same confounders, our causal interpretation is more meaningful than the average causal effect without conditional on U.

2.2. Estimability of causal log-OR in a case-control study

As in our motivating study, practical data are often collected from a case-control study. Suppose that the data consist of observations (D_i, A_i, X_i), i = 1, …, n, where D_i is the ADE, A_i is the drug exposure status, and X_i denotes all other observed covariates for subject i. Our goal is to estimate the causal log-OR using the data from such a biased sampling design.

It is well known that a case-control study can provide a consistent OR of A for the observed ADE D if a logistic regression model also holds for D given (A, X). Therefore, it is natural for one to verify whether this OR is equivalent to the casual OR, δ, as defined previously. Unfortunately, this is no longer true in general. Instead, we need the following estimability conditions:

(C1) (completeness of confounders) A is independent of (D(0), D(1)) given U in the population.

(C2) (consistency) $D=\sum _{a}I(A=a)D(a)$.

Condition (C1) stipulates that U in model (1) should include all possible confounders which explain the dependence between the exposure and the counterfactual ADE. For example, if U contains all the variables accurately predict the drug exposure status, then this assumption holds. This condition is similar to no unobserved confounder assumption in the usual causal inference, but we allow U to contain latent confounders. Condition (C2) is the consistency assumption, which states that the observed ADE is the same as corresponding counterfactual ADE with the same exposure status. This condition is standard in causal inference.

Under (C1) and (C2), for d = 0, 1

$$P(D(a)=d\left|U)=P(D(a)=d\right|A=a,U)=P(D=d|A=a,U)$$

Hence, model (1) also implies that

$$\text{log}\frac{P(D=1|A,U)}{P(D=0|A,U)}=\delta A+g(U)$$ (2)

In other words, if we observed the complete set of potential confounders U, then the causal log-OR δ can be estimated consistently by fitting the logistic regression model (2) with D regressing on both A and U, where g needs to be estimated nonparametrically.

However, U is unlikely to be all observed in practice; instead, only a subset of U, X, is available. Thus, our next question is how to estimate δ using available information X in a case-control design. Specifically, the following theorem provides the feasibility with one additional assumption.

(C3) (conditional independence in the case population) A is independent of U given X in the case population (D = 1).

Theorem 2.1. Under assumptions (C1) to (C3), it holds

$$\text{log}\frac{\tilde{P}(D=1|A,X)}{\tilde{P}(D=0|A,X)}=\alpha +\delta A+\tilde{g}(X)$$ (3)

where $\tilde{P}(D=d|A,X)$ denotes the conditional probability in the case-control sample, and

$$\alpha =\text{log}\frac{\tilde{P}(D=1)P(D=0)}{\tilde{P}(D=0)P(D=1)}$$

$$\tilde{g}(X)=\text{log}\left\{\mathbb{E}\left[\text{exp}\left\{g{(U)}^{-1}\right\}|X,D=1\right]\right\}$$

Condition (C3) gives one key condition such that we can infer the causal log-OR by fitting a partial linear logistic regression model using the case-control observations. In contrast to traditional causal inference, the conditional independence is not assumed for the whole sample. The main reason is that the sample is from a case-control design so the sample is biased. This condition requires that there does not exist latent variable differentiating the exposure status in the case population. In other words, the observed exposure distribution is random within each stratum of X in the case sample. For example, in our motivating example, U, the set of all possible confounders to the drug exposure can be fully captured by X, say the demographical factors, comorbidity or comedication. Or it is very likely that the part of U that is not contained in X is independent to the drug exposure. With this condition, Theorem 1 implies that if we can fit a logistic regression given A and X but allow the effect of X to be nonparametric and additive, then the coefficient of A in the regression is the same as the causal log-OR δ. In addition, the additive effect of X depends on g(U) in model (1) through expression $\text{log}\{\mathbb{E}[\text{exp}\left\{g(U)\right\}|X,D=1]\}$. In general, the independence may not hold between U and A when conditioning on D. But we further condition on X, this independence is more likely to hold. Without this assumption, it is not possible to estimate the causal log-OR theoretically. However, as we will show in the simulation study, when the assumption is slightly violated, our proposed method will still provide good estimates.

Interestingly, the same result holds if we replace the case population by the control population (D = 0). Particularly, we have the following result.

Proposition 2.2. Under (C1) and (C2), condition (C3) is equivalent to (C3′) (conditional independence in the control population) A is independent of U given X in the control population (D = 0).

By our experience, using either only control samples or only case samples lead to similar results and same conclusions in practice. One can choose according computation efficiency and numerical stability. In our motivating example, since drug use is more frequent in case samples, we recommend case samples to estimate propensity scores which is more reliable.

The proofs of Theorem 2.1 and Proposition 2.2 are given in Appendix 1.

2.3. Inference procedure

Recall that we observe (D_i, A_i, X_i), i = 1, …, n, from n independent subjects. Under model (3), the likelihood equals to

$$\prod _{i=1}^n\frac{\text{exp}\left\{D_i\left[\delta A_i+\tilde{g}\left(X_i\right)\right]\right\}}{1+\text{exp}\left\{\delta A_i+\tilde{g}\left(X_i\right)\right\}}$$

where $\tilde{g}$ is a nonparametric function of X, see Theorem 2.1. Our inference shall be based on maximum likelihood estimation where we estimate $\tilde{g}$ nonparametrically via spline approximation. However, the dimensionality of X is often high in practice so the nonparametric estimation of $\tilde{g}$ may not be feasible. To handle this challenge, we introduce a similar propensity score approach as in the usual causal inference in order to reduce dimension in the estimation, but the score will be derived using the case data only.

Specifically, if let Z ≡ π (X) = P (A = 1|X, D = 1), then it is clear that condition (C3) holds if we replace X by π(X). This is because

$$\begin{gathered} P(A=1|\pi (X),U,D=1)=E[P(A=1\left|X,U,D=1)\right|\pi (X),U,D=1] \\ =E[P(A=1\left|X,D=1)\right|\pi (X),U,D=1]=\pi (X) \end{gathered}$$

As a result, model (3) holds if we replace X by Z. Therefore, using the reduced data (D_i, A_i, Z_i), we can maximize the likelihood)

$$\prod _{i=1}^n\frac{\text{exp}\left\{D_i\left[\delta A_i+\lambda \left(Z_i\right)\right]\right\}}{1+\text{exp}\left\{\delta A_i+\lambda \left(Z_i\right)\right\}}$$

to estimate δ and λ. Note that the spline function λ is to nonparametrically estimate the $\tilde{g}$ function and is only a univariate function. Thus, the latter can be well estimated using spline approximation or stratified analysis with moderate sample sizes.

In summary, our estimation procedure can be described as follows.

Step 1. Using the data from the case sample, we estimate the case propensity score Z = π(X) by fitting a logistic regression model regressing A on X. When X is very high dimensional, we will use the first few principal components of X to replace X in the regression. Denote the estimate for π as $\widehat{\pi }$.

Step 2. Reconstruct the data as $\left(D_i,A_i,{\widehat{Z}}_i\right)$ where ${\widehat{Z}}_i=\widehat{\pi }\left(X_i\right)$. We then fit a partial linear logistic regression model by maximizing the likelihood (4) where λ (z) is approximated by a finite sequence of splines. Particularly, we will a histogram spline so λ is approximated by a piece-wise constant function so this step is equivalent to a stratified logistic regression. The number of splines will be determined using a model selection approach such as AIC or BIC.

Denote the estimate for δ as $\widehat{\delta }$ after Step 2. To make inference $\widehat{\delta }$, either direct estimation of the asymptotic variance using an analytic expression,^25,26 or a resampling approach can be used. However, in our experience, the variability in estimating π from Step 1 is often negligible so the variance for $\widehat{\delta }$ can be estimated from the standard logistic regression in Step 2, treating $\widehat{\pi }$ as known.

Finally, under conditions (C1) top (C3) and assuming that the model for estimating the case propensity score π(X) is correct, we can show that $\sqrt{n}\left(\widehat{\delta }-{\delta }_0\right)$ where δ₀ is the true causal log-OR, converges in distribution to a mean-zero normal distribution when the number of splines is chosen to increase with n at a certain rate. The proof follows the similar argument as in Lin and Zeng,²⁵ and,²⁶ since our model (3) is equivalent to the model used in their development. We skip the proof in this paper.

3. Simulation study

In this section, we conduct extensive simulation studies to evaluate the performance of our method and compare with standard propensity score-based methods. We consider a case control design with n cases and m controls. For each subject i, we generate U_i = (X_i,W_i) which contains both observed confounders X_i and unobserved ones W_i. To generate D_i(0) and D_i(1), we use the following models

$$\begin{gathered} \text{log}\frac{P\left(D_i(0)=1|U_i\right)}{P\left(D_i(0)=0|U_i\right)}=g\left(U_i\right) \\ \text{log}\frac{P\left(D_i(1)=1|U_i\right)}{P\left(D_i(1)=0|U_i\right)}=g\left(U_i\right)+\delta \end{gathered}$$ (5)

for some given function g(U) to be determined later. Thus, the true causal log-OR is given by δ. Next, the exposure status for subject i, A_i, is simulated from a Bernoulli distribution with probability b(U_i). Since it only depends on U_i, A_i is independent of D_i(0) and D_i(1), and so condition (C1) is satisfied. Furthermore, to ensure condition (C3) to hold, we particularly choose b(U_i) to be

$$b\left(U_i\right)=\frac{\text{exp}\left\{{\beta }_0+{\beta }^T{X}_i\right\}\left(\text{exp}\left\{g\left(U_i\right)+\delta \right\}+1\right)}{\text{exp}\left\{\delta \right\}\left(\text{exp}\left\{g\left(U_i\right)\right\}+1\right)+\text{exp}\left\{{\beta }_0+{\beta }^T{X}_i\right\}\left(\text{exp}\left\{g\left(U_i\right)+\delta \right\}+1\right)}$$ (6)

for some constant (β₀, β), where β can be a scalar or vector. For this choice of b(U_i), since some algebra gives

$$\frac{P\left(A_i=1|U_i,D_i=1\right)}{P\left(A_i=0|U_i,D_i=1\right)}=\frac{b\left(U_i\right)}{1-b\left(U_i\right)}\frac{\text{exp}\left\{\delta \right\}\left(\text{exp}\left\{g\left(U_i\right)\right\}+1\right)}{\text{exp}\left\{g\left(U_i\right)+\delta \right\}+1}$$

it implies

$$\text{log}\frac{P\left(A_i=1|U_i,D_i=1\right)}{P\left(A_i=0|U_i,D_i=1\right)}={\beta }_0+{\beta }^T{X}_i$$

Therefore, (C3) holds, i.e. A_i is independent of U_i given X_i in the case samples.

We consider two simulation scenarios. In the first scenario, both X_i and W_i are generated from continuous distributions. Specifically, (X_i, W_i) follows a bivariate normal distribution with the mean zeros and covariance matrix $\left[\begin{array}{ll}1\hfill & \rho \hfill \\ \rho \hfill & 1\hfill \end{array}\right]$, where ρ = 0 or 0.2. We then generate (D_i(1), D_i (0)) using model (5), where $g\left(U_i\right)={\gamma }_0+{\gamma }_1{X}_i+{\gamma }_2{X}_i^2+\theta W_i$ The exposure A_i is from a Bernoulli distribution with probability b(Ui) given by equation (6). The true parameter values in both models (5) and (6) are set as γ₀ = −2, γ₁ = 0.3, γ₂ = 0.8,θ = 0.8, β₀ = −4 and β = 2. Finally, to best mimic the real data in our motivating example, we set the ratio of cases and controls, i.e. n: m, as 1 vs. 10. We considered the true causal log-OR to be δ = 1 or 1.5. The number of case samples in the simulation study is 2000 or 4000.

In the second simulation scenario, both X_i and W_i are generated from Bernoulli distribution to mimic drug use variables in the real study. The data U_i = (X_i, W_i) is a multivariate binary random variate marginal probabilities of 0.5 and correlation matrix

$$\left[\begin{array}{cccc}1& \rho & \cdots & \rho \\ \rho & 1& \cdots & \rho \\ ⋮& ⋮& \ddots & ⋮\\ \rho & \rho & \cdots & 1\end{array}\right]$$

where ρ = 0 or 0.2. We then generate (D_i(1), D_i(0)) using model (5), where

$$g\left(U_i\right)={\gamma }_0+\sum _{j=1}^6{\gamma }_j{X}_j+\sum _{j=7}^{10}{\theta }_j{W}_j$$

The exposure A_i is from a Bernoulli distribution with probability b(U_i)given by equation (6). The value of all parameters in equations (5) and (6) is γ₀ = −3, γ₁ = γ₂ = ⋯ = γ₆ = 0.3, θ₇ = ⋯ = θ₁₀ = 0.8 and β₀ = −4. Since X_i is a vector of six elements, we have the corresponding β = (β₁, …, β₆) and β₁ = ⋯ = β₆ = 0.8. Similar to the first scenario, we set the ratio of cases and controls as 1:10. The true value of δ was 1 or 1.5. The number of the cases is 2000 or 4000.

For each simulated data, we apply the proposed method to estimate δ. In the proposed method, we first fit a logistic regression model of A given X using the case data (D = 1). This gives the case-based propensity score Z = π (X) = P (A = 1 | X = x, D = 1) which predicts the probability for each subject. We then construct K strata based on Z’s quantiles and then fit another stratified logistic regression for D regression on A. By stratifying the case-based propensity score, we believe that the population is well stratified with homogeneous prognostic factor. The coefficient of A is used as the estimator for δ. The number of strata K is chosen from {5, 10, 15, 20, 30 }, and the final number of strata is selected by the BIC. The variance for the estimate is obtainedffrom the usualgstratified logistic regression.

For comparison, we also consider the standard logistic regression and the traditional propensity score.¹² For the former, we fit a standard logistic regression for D regression on A and X, and the coefficient of A is used as the estimator for δ. In other words, we assume that logit P(D|A, X) was a linear function of A and X, and regard the estimated OR as the causal log-OR. In the traditional propensity score approach, we fit a logistic regression model of A on X using the entire data to estimate the propensity score Z* = P(A = 1 | X = x). Then we fit a logistic regression for D regression on A and Z*.

Table 1 summarizes the simulation results from 10,000 replicates for both scenarios. The results indicate that the proposed method always performs better than the standard logistic regression and the propensity score adjusted method. For the proposed method, the bias is small and the confidence intervals have proper coverages. Furthermore, the estimated variance from the stratified logistic regression agrees well with the empirical standard deviations the estimates. On the other hand, the standard logistic regression yields the estimate for the causal log-OR with large bias and incorrect inference, mainly because the model in this approach is misspecified. For example, in Appendix 1, we show that the component of X in the logistic regression is nonlinear in the first simulation scenario. The estimates from the propensity score-adjusted method still have larger bias than the proposed method and the confidence intervals constructed in this method tend to have lower coverages. In scenario 2, when the confounders are discrete, the proposed method and logistic regression method perform similarly, and both are better than the propensity score adjusted method. Finally, in the proposed method, the BIC almost always chooses K = 10 in the stratified logistic regression for continuous confounder, and chooses K = 5 or K = 15 for binary confounder.

Table 1.

Summary of estimated δ in the simulation study from 10,000 replicates.

δ	ρ	N	Proposed method				Logistic Reg.				Propensity score
			Bias	Std	ESE	CP	Bias	Std	ESE	CP	Bias	Std	ESE	CP
Scenario 1: continuous confounders
1	0.0	2000	−0.00	0.11	0.11	0.94	1.00	0.10	0.09	0	−0.00	0.11	0.11	0.95
		4000	−0.01	0.08	0.08	0.95	1.00	0.07	0.07	0	−0.00	0.08	0.08	0.94
1.5	0.0	2000	−0.00	0.12	0.12	0.94	1.00	0.11	0.10	0	0.02	0.12	0.12	0.94
		4000	−0.01	0.08	0.08	0.95	1.00	0.08	0.07	0	0.02	0.08	0.08	0.94
1	0.2	2000	0.02	0.11	0.11	0.95	0.90	0.10	0.09	0	0.03	0.11	0.11	0.93
		4000	0.01	0.08	0.08	0.95	0.90	0.07	0.07	0	0.03	0.08	0.08	0.93
1.5	0.2	2000	0.02	0.12	0.12	0.95	0.90	0.11	0.10	0	0.06	0.12	0.12	0.91
		4000	0.01	0.09	0.08	0.95	0.90	0.08	0.07	0	0.06	0.09	0.09	0.88
Scenario 2: binary confounders
1	0.0	2000	0.02	0.06	0.06	0.93	0.00	0.06	0.06	0.95	0.02	0.06	0.06	0.94
		4000	0.01	0.05	0.04	0.94	0.00	0.04	0.04	0.95	0.02	0.04	0.04	0.93
1.5	0.0	2000	0.02	0.07	0.07	0.93	0.00	0.07	0.06	0.95	0.03	0.07	0.07	0.93
		4000	0.01	0.05	0.05	0.94	0.00	0.05	0.05	0.95	0.03	0.05	0.05	0.91
1	0.2	2000	0.01	0.06	0.06	0.95	0.01	0.06	0.06	0.95	0.07	0.07	0.06	0.79
		4000	0.00	0.04	0.04	0.95	0.01	0.04	0.04	0.95	0.07	0.05	0.05	0.64
1.5	0.2	2000	0.01	0.07	0.07	0.95	0.00	0.06	0.07	0.95	0.11	0.07	0.07	0.59
		4000	0.00	0.05	0.05	0.95	0.00	0.05	0.05	0.95	0.12	0.05	0.05	0.32

4. Sensitivity analysis

We also conduct extensive simulation studies to evaluate the performance of our method and compare with standard propensity score-based methods when the assumption of conditional independence is slightly violated. Still, we consider a case control design with n cases and m controls. For each subject i, we generate U_i = (X_i, W_i) which contains both observed confounders X_i and unobserved ones W_i. Again, D_i (0) and D_i (1) are generated using model (5). The true causal log-OR is given by δ. Next, the exposure status for subject i, A_i, is simulated from a Bernoulli distribution with probability b(Ui). Since it only depends on Ui, Ai is independent of D_i(0) and D_i(1) so condition (C1) is satisfied. Furthermore, to ensure condition (C3) to hold, we choose b(U_i) to be

$$b\left(U_i\right)=\frac{\text{exp}\left\{{\beta }_0+{\beta }^T{X}_i+{\zeta }^T{W}_i\right\}\left(\text{exp}\left\{g\left(U_i+\delta \right)\right\}+1\right)}{\text{exp}\left\{\delta \right\}\left(\text{exp}\left\{g\left(U_i\right)\right\}+1\right)+\text{exp}\left\{{\beta }_0+{\beta }^T{X}_i+{\zeta }^T{W}_i\right\}\left(\text{exp}\left\{g\left(U_i+\delta \right)\right\}+1\right)}$$

for some constant (β₀, β, ζ), where β and ζ can be scalars or vectors. For this choice of b(U_i)

$$\text{log}\frac{P\left(A_i=1|U_i,D_i=0\right)}{P\left(A_i=0|U_i,D_i=0\right)}={\beta }_0+{\beta }^T{X}_i+{\zeta }^T{W}_i$$

Therefore, (C3) is violated, i.e. A_i is not independent of U_i given X_i in the case sample.

We consider two simulation scenarios. In the first scenario, both X_i and W_i are generated from continuous distributions. Specifically, (X_i, W_i) follows a bivariate normal distribution with the mean zeros and covariance matrix $\left[\begin{array}{ll}1\hfill & \rho \hfill \\ \rho \hfill & 1\hfill \end{array}\right]$ where ρ = 0 or 0.2. We then generate (D_i (1), D_i (0)) using model (5), where $g\left(U_i\right)={\gamma }_0+{\gamma }_1{X}_i+{\gamma }_2{X}_i^2+\theta W_i$ The exposure A_i is from a Bernoulli distribution with probability b(U_i) given by equation (6). The true parameter values in both models (5) and (6) are set as γ₀ = −2, γ₁ = 0.3, γ₂ = 0.8, θ = 0.8, β₀ = −4 and β = 2. We considered ζ in a range of 0.01–0.05. Finally, to best mimic the real data, we set the ratio of cases and controls, i.e. n: m, as 1 vs. 10. We considered the true causal log-OR to be δ = 1 or 1.5. The number of the cases in the simulation study is 2000 or 4000.

In the second simulation scenario, both X_i and W_i are generated from Bernoulli distribution to mimic drug use variables in the real study. The data U_i = (X_i, W_i) is a multivariate binary random variate marginal probabilities of 0.5 and correlation matrix

$$\left[\begin{array}{cccc}1& \rho & \cdots & \rho \\ \rho & 1& \cdots & \rho \\ ⋮& ⋮& \ddots & ⋮\\ \rho & \rho & \cdots & 1\end{array}\right]$$

where ρ = 0 or 0.2. We then generate (D_i(1), D_i(0)) using model (5), where

$$g\left(U_i\right)={\gamma }_0+\sum _{j=1}^6{\gamma }_j{X}_j+\sum _{j=7}^{10}{\theta }_j{W}_j$$

The exposure A_i is from a Bernoulli distribution with probability b(U_i) given by equation (6). The value of all parameters in equations (5) an (6) are γ₀ = −3, γ₁ = γ₂ = ⋯ = γ₆ = 0.3, θ₇ = ⋯ = θ₁₀ = 0.8, β₀ = −4 and β = (β₁, …, β₆), β₁ = ⋯ = β₆ = 0.8 Since W_i is a vector of four elements, we considered the corresponding coefficients ζ = (ζ₁⋯,ζ₄), ζ₁ = … = ζ₄ from 0.01 to 0.05. Similar to the first scenario, we set the ratio of cases and controls as 1:10. The true value of δ was 1 or 1.5. The number of the cases is 2000 or 4000.

For each simulated data, we apply the proposed method to estimate δ. In the proposed method, we first fit a logistic regression model of A given X using the case data (D = 1). This gives the case-based propensity score Z = π (X) = P(A = 1|X = x, D = 1) which predicts the probability for each subject. We then construct K strata based on Z’s quantiles and then fit another stratified logistic regression for D regression on A. The coefficient of A is used as the estimator for δ. The number of strata K is chosen from {5, 10, 15, 20, 30}, and the final number of strata is selected by the BIC. The variance for the estimate is obtained from the usual stratified logistic regression.

Comparing to the standard logistic regression and the traditional propensity score, our proposed method yields similar results as in the simulation study. Table 2 summarizes the simulation results from 10,000 replicates for both scenarios for different values of β₂. The results indicate that the performance of proposed method is also good even when the drug exposure depends on the unmeasured confounders, if the unmeasure confounders are independent with the measured confounders. For the proposed method, the bias is small and the confidence intervals have proper coverages. We can also notice that the performance of the proposed methods improves as the sample size increasing. In scenario 2 when the confounders are discrete, the proposed method also provides reasonable estimates. We can also notice that under this scenario, the proposed method does perform similarly to the scenario where the drug exposure is independent to the unmeasured confounders conditional on the measured confounders. Finally, for the proposed method, the BIC almost always chooses K = 10 in the stratified logistic regression.

Table 2.

Summary of estimated δ in the sensitivity analysis from 10,000 replicates, where condition C.3 is violated.

δ	ρ	N	ζ = 0.01				ζ = 0.03				ζ = 0.05
			Bias	Std	ESE	CP	Bias	Std	ESE	CP	Bias	Std	ESE	CP
Scenario 1: continuous confounders
1	0.0	2000	0.01	0.11	0.11	0.94	0.02	0.11	0.11	0.94	0.03	0.11	0.11	0.93
		4000	−0.00	0.07	0.08	0.96	0.01	0.07	0.08	0.95	0.03	0.07	0.08	0.94
1.5	0.0	2000	0.01	0.12	0.12	0.94	0.02	0.12	0.12	0.93	0.03	0.12	0.12	0.93
		4000	−0.00	0.08	0.08	0.96	0.01	0.08	0.08	0.96	0.02	0.08	0.08	0.95
1	0.2	2000	0.03	0.11	0.11	0.95	0.04	0.10	0.11	0.94	0.05	0.11	0.11	0.93
		4000	0.02	0.08	0.08	0.95	0.03	0.08	0.08	0.93	0.04	0.08	0.08	0.90
1.5	0.2	2000	0.03	0.12	0.12	0.95	0.04	0.11	0.12	0.95	0.05	0.12	0.12	0.93
		4000	0.02	0.08	0.08	0.94	0.03	0.08	0.08	0.93	0.05	0.09	0.08	0.92
Scenario 2: binary confounders
1	0.0	2000	0.03	0.06	0.06	0.93	0.04	0.06	0.06	0.90	0.05	0.06	0.06	0.87
		4000	0.02	0.04	0.04	0.93	0.03	0.04	0.04	0.89	0.04	0.04	0.04	0.83
1.5	0.0	2000	0.03	0.06	0.06	0.93	0.04	0.06	0.06	0.90	0.05	0.06	0.06	0.87
		4000	0.02	0.05	0.05	0.93	0.03	0.05	0.05	0.90	0.04	0.04	0.04	0.84
1	0.2	2000	0.02	0.06	0.06	0.94	0.03	0.06	0.06	0.91	0.05	0.06	0.06	0.86
		4000	0.01	0.04	0.04	0.94	0.03	0.04	0.04	0.90	0.05	0.04	0.04	0.81
1.5	0.2	2000	0.02	0.07	0.07	0.94	0.03	0.07	0.07	0.92	0.05	0.07	0.06	0.87
		4000	0.01	0.05	0.05	0.94	0.03	0.05	0.05	0.90	0.05	0.05	0.05	0.83

5. Application to myopathy study

The Indiana Network for Patient Care (INPC) is a health information exchange data repository containing medical records for over 15 million patients throughout the state of Indiana. The Common Data Model (CDM) is a derivation of the INPC containing coded prescription medications, diagnoses, and observational data for 2.2 million patients between 2004 and 2009. The CDM contains over 60 million drug dispensing events, 140 million patient diagnoses, and 360 million clinical observations (e.g. laboratory results, diagnose codes, medications). These data were anonymized and architected specifically for research on adverse drug reactions through collaboration with the Observational Medical Outcomes Partnership project.²⁷

Using our previous defined myopathy phenotype,³ 450, 634 myopathy cases were selected from the CDM-5 database. Among patients having a myopathy event, the drug–condition relationship is anchored by its date in the database. In our analysis, any drug exposure occurring within a one-month drug exposure window before the diagnosis of myopathy was considered as a positive exposure. In order to select a control patient and his/her drug exposure window, an index time was first matched with the myopathy case event time. Then control patients were selected from those patients without myopathy. Finally, we randomly selected 10 control patients who are of the same gender and age range for each myopathy case. Anchored by the index time, a one-month drug exposure window was defined; and the exposure to a drug or no drug was defined similarly as for the cases. Eventually for each case, 10 controls that match the index time, gender and age group were selected. As a result, we have a total of 4,956,974 records in the data.

Our goal is to estimate the causal effect of each drug on myopathy. To control for possible confounding due to the other drug usage, it is ideal to include all comedications in this case-based propensity score model. Ideally, all other drug usage information should be used to derive the case-based propensity score. However, one practical challenge is that the drug usage for each drug is often sparse so the regression including these drugs will be numerically unstable. Instead, we use Principal Components (PCs) instead of original drugs usage as condensed information for all the confounding variables when computing the case-based propensity scores. Particularly, we use the first 10 PCs derived from the correlation matrix of drug usage.

To be specific, for each of the drug, we first created a binary variable from the raw data, denoted as d_j for drug j. For each subject i, d_ij = 1 if the drug j has been taken with in one month prior to condition by this subject, and d_ij = 0 otherwise. Then, we checked the frequency of drug use, and we only considered the drugs that have been used more than five times per 10,000 records in the analysis. This was because that including drugs that have few use will lead to the unstable result. We had 100 drugs left after applying the criteria. With these 100 drugs, we did the eigen-decomposition on the correlation matrix of drugs among case samples. We then computed the PCs for case and control samples with the eigenvectors from last step.

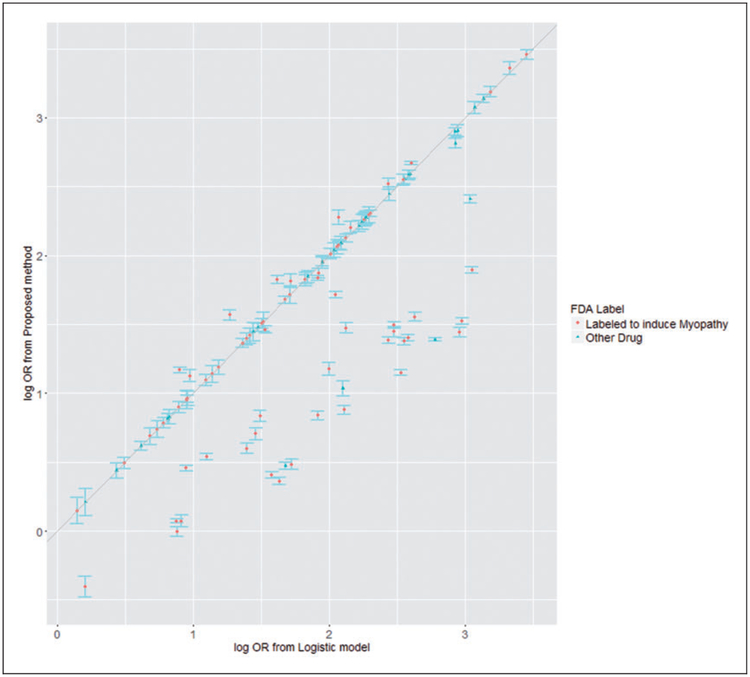
Given the principal components, we then apply the proposed method as described above. Specifically, the occurrence of ADE was treated as D, the use of a specific drug was treated as A, and the PCs, age and gender were treated as X. The results are shown in Figure 1.

Figure 1.

Estimated log OR from proposed method by estimated log OR from marginal logistic model.

The causal associations between 100 drugs and myopathy are analyzed using our proposed method. The estimated log ORs vary from −0.41 to 3.46, with a median of 1.49 and mean 1.54 across 100 drugs. Almost all drugs have significant effect on adverse conditions based on the results. The detailed drug information is given in the Supplementary material. For most of the drugs, the estimated log OR from proposed method is close to the log OR estimated from marginal logistic regression. For the other drugs, our proposed method provides smaller log OR than the marginal logistic regression. We believe that for these drugs, our proposed method provides the log OR closer to their true log OR on myopathy, for we controlled the confounder through case-based propensity score. The log OR from the marginal logistic regression is falsely large because this log OR actually reflected the causal effect on myopathy of confounder rather than the drug. This systematic trend indicates that the actual causal effects of single drug on ADE from the standard logistic regression model are likely to be overestimated, when confounding effects from other drug uses were not well controlled.

Among these 100 drugs, 72 drugs have reported myopathy adverse drug events in their drug labels (www.sideeffects.embl.de), in which 70 drugs have increased myopathy risk (p < 0.05). In particularly, three statins (atorvastatin, lotavastatin, simvastatin) have increased myopathy risk, ORs are (2.61, 1.99, 3.22), respectively. These are highly consistent to the clinical trial data that myopathy are primary statin side effects²⁸. Also, in the top 10 drug-myopathy causal association pairs based on the log OR, 6 of them are reported to have ADE related to myopathy.

6. Discussion

In this paper, we have proposed a new concept called the causal log-OR to evaluate the causal effect of one exposure risk on a dichotomous outcome. This new causal effect differs from the traditional causal effect defined as the marginal mean difference. Since the latter is often small for rare disease such as ADEs in our application, the new causal effect is clinically meaningful and useful to evaluate the exposure risk. We then proposed a set of conditions to describe how such a causal effect can be estimated under a case-control design. Both theoretical results and numerical results showed that the proposed method is valid and performs superior to some naive method. In our applications, we proposed both principal component analysis and meta-analysis techniques to handle the challenges of sparse predictors and the computational challenges due to a vast number of data records. In analyzing the de-identified Indiana medical record database, our method identifies 70 out of 72 drugs that have myopathy side effects in their labels. These 70 drugs including statins are well known for their myopathy side effect.

Our work is not the first attempt to mining drug ADE associations using causal inference model framework in the health record databases. Early work by Tatonnetti et al.¹⁹ used the traditional propensity scores to screen the large-scale drug-ADEs in Federal Adverse Events Reporting System (FAERS). Unlike our longitudinal CDM medical record database, FAERS is a cross-sectional database containing self-reported ADEs and potentially associated drugs. Analyzing drug-ADE associations in FAERS does not need additional sampling and/or case control matching, and the propensity score method implemented in the Tatonnettis paper does not have to worry about the sampling bias. However, in analyzing drug-ADE associations using longitudinal medical record databases, sampling is needed for proper case/control matching. In our motivating data problem, we use the event time of cases as index times, and collect corresponding controls that did not have events before the index time. We collect drug information before one month window before the index time. Our research in this paper shows that potential sampling bias has impact on the propersity score calculation, and its follow-up causal drug-ADE association estimation. Our research moves a significant step forward in developing drug-ADE data mining algorithms using longitudinal medical record database. Though the longitudinal signal is weak in this sample, it would be interesting to incorporate other longitudinal features in the records and challenging to estimate drug effects in this setting in further studies.

Although we only considered a case-control design, our general idea can be extended to other bias-sampling design such as outcome-dependent sampling or stratified sampling, while the outcome of interest can be either continuous or censored survival event. The key condition (C.3) is necessary to be modified to adapt to each specific sampling design. However, one main message is that traditional propensity score methods, which ignore biased sampling designs, may no longer be valid, since the propensity scores estimated from the biased sample do not represent the actual likelihood of being exposed or unexposed in the underlying population.

Our current causal log-OR method cannot differentiate the causal drug-ADE associations from the drug-incidence associations. It is primarily due to our initial pharmaco-epidmiological study design, where the temperal order of drug exposure and ADEs was not restrained. We expect that a more rigorous design will reduce the drug-incidence associations. Our current method is based on additive model, which controls for individual level confounders, and estimates the causal effects of drugs averaged among homogeneous subjects. Our model cannot be used to estimate the interaction among drugs and individual covariates. However, our model can be used to estimate the drug effect in any given defined subpopulation.

We only consider the causal log-OR of one single drug. The approach can be easily generalized to study the causal effect of drug-drug interactions from multiple drugs, after controlling for confounding effects of other comedications. In this case, the case-based propensity scores will be multidimensional to reflect the likelihood of receiving each combination of candidate drugs and will be incorporated into the downstream logistic regression.

Appendix 1: Proof of Theorem 2.1

With loss of generality, we assume U to be discrete. For continuous U, the summation in the following proof will be replaced by integration with respect to certain dominating measure for U’s distribution. Since

$$\text{log}\frac{P(D=1|U,A)}{P(D=0|U,A)}=g(U)+\delta A$$

we obtain

$$\begin{gathered} P(X,A|D=0)=\sum _U\frac{P(U,X,A|D=0)}{P(U,X,A|D=1)}P(U,X,A|D=1) \\ =\sum _U\frac{P(D=0|U,X,A)}{P(D=1|U,X,A)}\frac{P(D=1)}{P(D=0)}P(U,X,A|D=1) \\ =\sum _U{[\text{exp}(g(U)+\delta A)]}^{-1}\frac{P(D=1)}{P(D=0)}P(U,X,A|D=1) \end{gathered}$$

where the summation is over U which is compatible with X. Therefore

$$P(X,A|D=0)=\text{exp}{(\delta A)}^{-1}\frac{P(D=1)}{P(D=0)}\sum _U\text{exp}{[g(U)]}^{-1}P(U,X,A|D=1)$$

From condition (C3), P(U, X, A|D = 1) = P(U|X, D = 1)P(X, A|D = 1) so it gives

$$P(X,A|D=0)=\text{exp}{\left\{\delta A\right\}}^{-1}\frac{P(D=1)}{P(D=0)}P(X,A|D=1)\text{exp}\{\tilde{g}(X)\}$$

where $\tilde{g}(X)=\text{log}\left\{\sum _U\text{exp}{[g(U)]}^{-1}P(U|X,D=1)\right\}=\text{log}\left\{E\left[\text{exp}{\left\{g(U)\right\}}^{-1}|X,D=1\right]\right\}$ In other words

$$\frac{\tilde{P}(D=1|X,A)}{\tilde{P}(D=0|X,A)}=\frac{P(X,A|D=1)}{P(X,A|D=0)}\frac{\tilde{P}(D=1)}{\tilde{P}(D=0)}=\frac{\tilde{P}(D=1)P(D=0)}{\tilde{P}(D=0)P(D=1)}\text{exp}[\delta A+\tilde{g}(X))]$$

Theorem 2.1 holds.

Proof of Proposition 2.2

We only prove one direction and the other direction holds using the same arguments. Assume (C3′) holds. Note that

$$P(U,A|X,D=1)=\text{exp}\{g(U)+\delta A\}\frac{P(D=0)}{P(D=1)}P(U,A|X,D=0)\frac{P(X|D=0)}{P(X|D=1)}$$

Since U and A are independent given X in the control population, then P(U,A|X,D = 1) can be factorized into a production of two parts, one only involving (U, X) and the other part only involving (X, A). This implies that A is independent of U given X in the control population (D = 0).

Analytic expression of the effect of $X(\tilde{g}(X))$ in the first simulation setting

Since in Theorem 2.1 we established

$$\frac{P(D=1|X,A)}{P(D=0|X,A)}=\text{exp}[\delta A+\tilde{g}(X))]$$

We derive the expression of $\tilde{g}(X)$ from the first simulation study. After some algebra, we obtain

$$\begin{gathered} \tilde{g}(X)=\text{log}\int \text{exp}[g(U)]P(W|X,D=0)\text{d}W \\ =\gamma X+\text{log}\left\{\int \text{exp}(\theta W)\frac{P(D=0|U)P(U)}{\int P(D=0|U)P(U)\text{d}W}\text{d}W\right\} \end{gathered}$$

Using the simulation setting for P(D = 1|U, A) and P(A|U), we have

$$\tilde{g}(X)=\gamma X+\text{log}\left\{\int \frac{\text{exp}(\theta W+\left[2\rho XW-W^2\right]/\left[2\left(1-{\rho }^2\right)\right]}{\text{exp}[a(U)]+1+\text{exp}(\beta X)\text{exp}[a(U)+\delta ]+1}\text{d}W\right\}-\text{log}\left\{\int \frac{\text{exp}\left(\left[2\rho XW-W^2\right]\left[2\left(1-{\rho }^2\right)\right]\right)}{\text{exp}[a(U)]+1+\text{exp}(\beta X)\text{exp}[a(U)+\delta ]+1}\text{d}W\right\}$$

Clearly, $\tilde{g}(x)$ is a nonlinear function of x. Thus, fitting a standard logistic regression model with linear effects of X in the regression will result in a biased estimate for δ.