Abstract
Experimental investigations into the field dependence of magnetization and temperature dependences of magnetic susceptibility in Ni2+xMnGa1−x (x = 0.00, 0.02, 0.04) and Co2VGa Heusler alloy ferromagnets were performed following the spin fluctuation theory of itinerant ferromagnetism, called as “Takahashi theory”. We investigated the magnetic field dependence of magnetization at the Curie temperature TC, which is the critical temperature of the ferromagnetic–paramagnetic transition, and also at T = 5 K, which concerns the ground state of the ferromagnetic state. The field dependence of the magnetization was analyzed by means of the H vs. M5 dependence, and the field dependence of the ground state at 5 K was investigated by means of an Arrott plot (H/M vs. M2) according to the Takahashi theory. As for Ni2+xMnGa1−x, the spin fluctuation parameter in k-space (momentum space, TA) and that in energy space (T0) obtained at TC and 5 K were almost the same. On the contrary, as for Co2VGa, the H vs. M5 dependence was not shown at TC. We obtained TA and T0 by means of an Arrott plot at 5 K. We created a generalized Rhodes–Wohlfarth plot of peff/pS versus TC/T0 for the other ferromagnets. The plot indicated that the relationship between peff/pS and T0/TC followed Takahashi’s theory. We also discussed the spontaneous magnetic moment at the ground state, pS, which was obtained by an Arrott plot at 5 K and the high temperature magnetic moment, pC, at the paramagnetic phase. As for the localized ferromagnet, the pC/pS was 1. As for weak ferromagnets, the pC/pS was larger than 1. In contrast, the pC/pS was smaller than 1 by many Heusler alloys. This is a unique property of Heusler ferromagnets. Half-metallic ferromagnets of Co2VGa and Co2MnGa were in accordance with the generalized Rhodes–Wohlfarth plot with a km around 1.4. The magnetic properties of the itinerant electron of these two alloys appeared in the majority bands and was confirmed by Takahashi’s theory.
Keywords: ferromagnetic Heusler alloy, magnetization, itinerant electron ferromagnetism, half-metal
1. Introduction
Spin fluctuation theories have been proposed to explain the physical principles of the itinerant electron system [1,2,3,4,5,6,7]. Takahashi proposed the self-consistent renormalization (SCR) theory according to zero-point spin fluctuations, which assimilated both the transverse and longitudinal components of the fluctuations [4,5,6,7]. An outstanding characteristic of this theory is the magnetization at TC. The theory proposed by Takahashi indicates that the magnetic field dependence, H, is proportional to the magnetization, M5, at the Curie temperature, TC. This property was obtained by the differential calculus of the magnetization of the spin fluctuation free energy [7,8,9].
In this theory, the relation between the magnetic fields H and magnetization M is obtained theoretically by the equation of,
| (1) |
where c (TC) is the constant value at TC (refer to the references for the derivation process of Equation (1) [7,9]). MnSi [10], FexCo1−xSi [11], CoS2 [12], and Ni [13] followed the relationship provided in Equation (1). The Heusler isotropic ferromagnetic alloy Ni2+xMnGa1−x (x = 0.00, 0.02, 0.04) also followed the relationship mentioned in Equation (1) [8,9,13]. From the spontaneous magnetic moment and magnetization at TC, we obtained the spin fluctuation parameter in k-space (momentum space, TA) and in energy space (T0).
The other approach to obtain TA and T0 is the analysis of the field dependence of the magnetization by means of an Arrott plot (H/M vs. M2) at the ground magnetic state, T = 5 K [7,14]. Tateiwa et al. mentioned the derivation method of this approach in detail [14]. The magnetization in the ground state is expressed by the following equation
| (2) |
where is Lande’s g-factor; N0 is Avogadro’s number; and F1 is the mode–mode coupling term defined as
| (3) |
where c is equal to 1/2 and M0 is the spontaneous magnetization. F1 is derived from the slope of the Arrott plot (H/M vs. M2 plot) at low temperatures by Equation (4)
| (4) |
where kB is the Boltzmann constant, and is the slope of the Arrott plot. TA and T0 are obtained by the following relations of
| (5) |
| (6) |
where C4/3 = 1.00608, and pS is the spontaneous magnetic moment at the ground state (T = 0 K). In the Takahashi theory, it is mentioned that the experimental results of the magnetization measurement can be applied to these equations in units of kOe and emu/g for the magnetic fields H and magnetization M, respectively (p. 66 in Reference [7]). Therefore, we used these units to calculate the TA and T0 parameters clearly. Incidentally, the value of the magnetic field H in 10 kOe is equal to the value in T (Tesla), and the value of magnetization M in emu/g is equal to the value in Am2/kg.
Tateiwa et al. evaluated the parameters, TA and T0, of actinide 5f electron systems which were analyzed by means of Equations (4)–(6) [14]. Tateiwa et al. also used the units of kOe and emu/g.
The relation between pS, TC, T0, and the effective magnetic moment peff in the paramagnetic phase was derived from a formula shown in Equation (3.47) in [7], as follows:
| (7) |
Equation (7) can be rewritten as:
| (8) |
When km is 1.4, Equation (8) is equal to Equation (7).
In this study, experimental investigations into the field dependence of magnetization and temperature dependences of magnetic susceptibility in Ni2+xMnGa1−x (x = 0.00, 0.02, 0.04) and half-metallic ferromagnets (HMFs) of Co2VGa and Co2MnGa Heusler alloys were performed following the self-consistent renormalization (SCR) spin fluctuation theory of itinerant electron ferromagnetism by Y. Takahashi [7]. We investigated the magnetic field dependence of magnetization at the Curie temperature TC, which is the critical temperature of the ferromagnetic–paramagnetic transition, and also at T = 5 K, which concerns the ground state of the ferromagnetic phase. We created a generalized Rhodes–Wohlfarth plot of peff/pS versus TC/T0 for the other ferromagnets. The plot indicated that the relationship between peff/pS and TC/T0 followed Takahashi’s theory. We also discussed the magnetism of Heusler alloys by comparing the spontaneous magnetic moment pS at the ground state (T = 0 K) and paramagnetic magnetic moment pC.
2. Materials and Methods
The polycrystalline samples of Ni2+xMnGa1−x (x = 0.00, 0.02, 0.04) were prepared by arc melting the constituent elements, nominally, 4N Ni, 3N Mn, and 6N Ga, several times in an Ar atmosphere. Each ingot was melted several times to ensure good homogeneity. The products from the arc melting process were sealed in an evacuated silica tube and solution heat-treatment was applied at 1123 K for 3 days. After these treatments, the sample was quenched in water. The polycrystalline sample of Co2VGa was fabricated by levitation melting after making a 66.6Co–33.4Ga (at.%) binary alloy by induction furnace melting in order to avoid the reaction of the crucible by the V element. The purity of the starting elements were 99.7% V, 3N Co, and 4N Ga. The obtained ingot was annealed at 1373 K for 3 days and quenched in water.
The magnetization measurements were performed up to 5 T by means of a SQUID magnetometer (Quantum Design Inc., San Diego, USA) at the Institute for Materials Research, Tohoku University. The permeability measurement was performed in AC magnetic fields with a frequency of 73 Hz and maximum field of ± 10 Oe. The AC magnetic fields were measured by a gaussmeter 410 (Lakeshore Cryotronix Inc., Westerville, Ohio, USA). The magnetic susceptibility measurements were performed by means of a vibrating sample magnetometer (VSM, PASCO Co. Ltd, Roseville, CA, USA), which was installed in a water-cooled electromagnet (Tamagawa Seisakusho Co. Ltd., Sendai, Japan) at Ryukoku University. The magnetic susceptibility in the paramagnetic phase was obtained from the temperature dependences of magnetization M, measured at the magnetic fields of H = 0.10 T and the relation of .
3. Results and Discussion
3.1. Results of the Magnetic Measurements of Ni2+xMnGa1−x
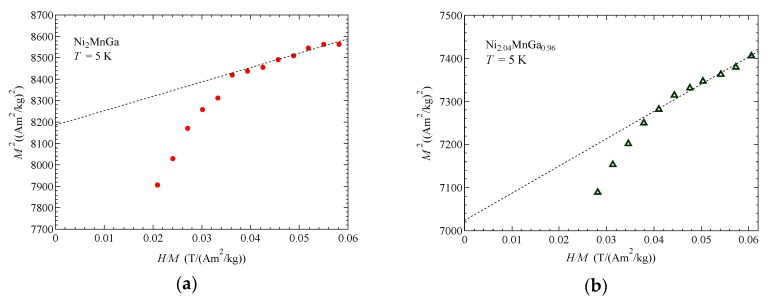
Figure 1 shows the Arrott plot (M2 vs. H/M) of: (a) Ni2MnGa, and (b) Ni2.04MnGa0.96 at T = 5 K. By using the slope value of the Arrott plot, the parameter F1 was derived by Equation (4). The spontaneous magnetic moment, pS; effective moment, peff; Curie temperature, TC; and spin fluctuation parameters TA and T0 are listed in Table 1. The obtained TA and T0 by the relations of Equations (5) and (6) are also listed in Table 1. Errors of TA and T0 were estimated as 10%, which arose from the error of fitting of the Arrott plot. Within these errors, the TA and T0 obtained from a low temperature and the values from TC were the same as each other.
Figure 1.
Arrott plot (M2 vs. H/M) of: (a) Ni2MnGa and (b) Ni2.04MnGa0.96 at T = 5 K.
Table 1.
The magnetic parameters of Ni2+xMnGa1−x (x = 0.00, 0.02, 0.04). The spontaneous magnetic moment, pS; effective moment, peff; Curie temperature, TC; spin fluctuation parameter in k-space (momentum space) TA, and that in energy space, T0. The parameters TA (TC) and T0 (TC) were obtained from the M4 vs. H/M plot at TC [9]. The peff, TA (5 K) and T0 (5 K) were the obtained values in this work.
In a previous study, we analyzed the results of Ni2MnGa by means of the generalized Rhodes–Wohlfarth plot (double logarithmic plot of peff/pS and TC/T0) [9], which was derived to formulate the magnetic moments ratio, peff/pS, and the critical temperature ratio, TC/T0. Takahashi derived an equation for the relationship between pS, TC, T0 and the effective magnetic moment peff as Equation (7). As for Ni2MnGa, the measured effective moment peff, which was measured in this work, was 4.75, which was the same value as the result by Webster et al. [15]. For Ni2MnGa, a value of 1.61 for km was obtained by substituting a peff of 4.75, and pS, TC, and T0 from Table 1 into Equation (8).
In order to investigate the km values of Ni2+xMnGa1−x (x = 0.02, 0.04) and compare them with other ferromagnetic alloy and compounds, we further needed peff values of these alloys. We measured the magnetic susceptibility of these alloys, and peff values were obtained from the Curie constant of the Curie law.
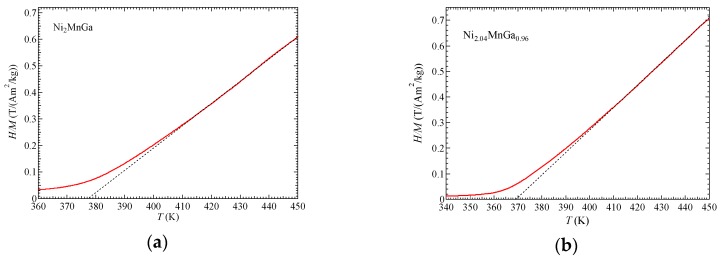
Figure 2 shows the inverse magnetic susceptibilities, . The gradient of vs. T, which is indicated by the dotted lines, is equal to 1/C, where C is a Curie constant.
Figure 2.
Inverse magnetic susceptibilities as: (a) Ni2MnGa and (b) Ni2.04MnGa0.96. Dotted lines are the fitting lines at the paramagnetic phase.
The Curie constant C is written as:
| (9) |
where N is the molecular number per gram. The obtained effective moments peff were 4.72 for Ni2.02MnGa0.98 and 4.68 for Ni2.04MnGa0.96. In Section 3.3, we discuss the itinerant electron ferromagnetism by means of these parameters.
3.2. Results of the Magnetic Measurements of Half-Metallic Ferromagnet Co2VGa
HMFs are comprised of a metallic band for one spin direction. For the other spin direction, a semiconducting band has an energy gap around Fermi energy. Co2VGa is a HMF with a high spin polarization [16]. It has an L21-type cubic crystal structure with a lattice constant a = 0.5782 nm. The spin polarization ratio P is defined as:
| (10) |
where and denote the density of states, DOS, at the Fermi energy, EF, in the majority spin () and minority spin (, respectively. Umetsu et al. calculated the DOS by means of the LTMO method with the atomic spheres approximation (ASA). From the results of this calculation, the P0 value (P value at T = 0 K) was 75% and the P0 value of L21-type Co2(V1−xMnx)Ga alloys ( was also determined. As for x = 1, Co2MnGa, the obtained spin polarization ratio P0 was 48%. This indicates that Co2VGa is a higher polarized HMF. The Curie temperatures of Co2VGa and Co2MnGa were 337 K and 695 K, respectively. We measured the magnetic field dependences of the magnetization to obtain the magnetic moments, ps, and the spin fluctuation parameters, TA and T0, and also measured the magnetic susceptibility to obtain the effective magnetic moment, peff, in the paramagnetic phase. We also obtained TA and T0 of Co2MnGa according to the Takahashi theory by means of the magnetization process at 5 K in Reference [16].
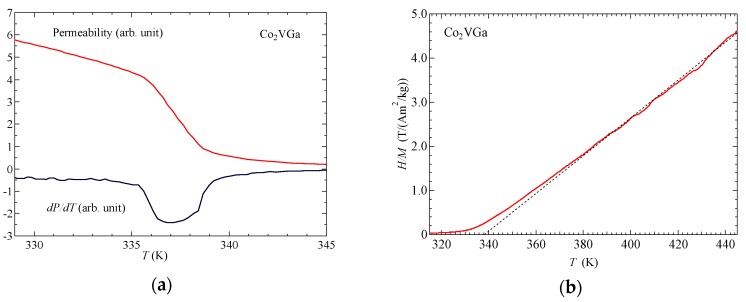
Figure 3a shows the permeability of Co2VGa around the Curie temperature. From the differentiation of the permeability for the temperature, denoted as dP/dT, the Curie temperature was obtained as TC = 337 K. Figure 3b shows the inverse magnetic susceptibility of Co2VGa. The obtained peff was 2.06.
Figure 3.
(a) Permeability of Co2VGa around the Curie temperature. dP/dT indicates the differential of the permeability in the temperature. (b) Inverse magnetic susceptibility 1/χ = H/M of Co2VGa. Dotted line is a fitting line at the paramagnetic phase.
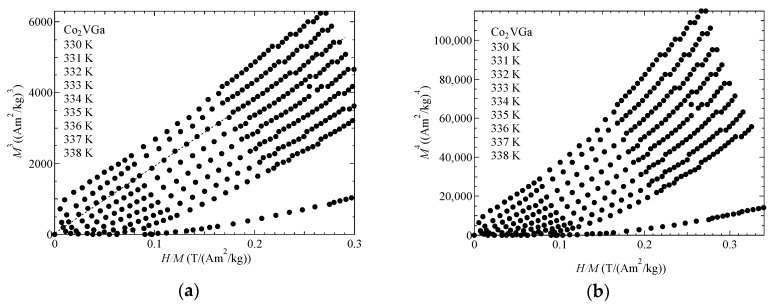
Figure 4 shows the M3 vs. H/M plot and M4 vs. H/M plot of Co2VGa around TC = 337 K.
Figure 4.
The magnetic field dependences of the magnetization of Co2VGa: (a) M3 vs. H/M; (b) M4 vs. H/M. Dotted straight line in (a) is a guide for the eyes.
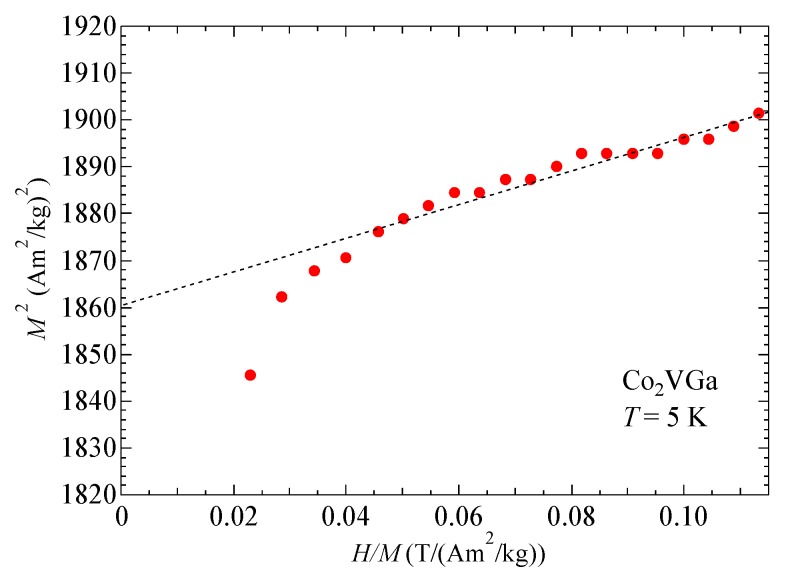
With regard to the Takahashi theory, the magnetization process is expressed as (H/M)M4 by Equation (1) around TC. On the contrary, the H/M was almost proportional to M3 as shown in Figure 4a. Nishihara et al. also measured the magnetization around TC [17]. The magnetization process at TC is expressed as HMD with the index D = 4.15 . Their result was the same as in this study. Nishihara et al. mentioned that the discrepancy between these experimental magnetization results and the Takahashi theory is supposed to arise from the distribution of TC in the sample because the fourth-order expansion of the magnetic-free energy vanishes at the Curie temperature. In this study, we tried again with other ingots from the former sample used by Nishihara et al. As this experiment reproduced the former experiment, there may be an essential reason. Incidentally, other magnetic models have indicated that the molecular field theory denotes the D value as 3.0, the three-dimensional Heisenberg model denotes the D value as 4.8, and the three dimensional Ising model as 4.82 [18]. None of these matched the analysis in this investigation. In order to obtain the spin fluctuation parameters TA and T0 of Co2VGa, we measured the magnetization process of Co2VGa at 5 K. Figure 5 shows the Arrott plot (M2 vs. H/M) of Co2VGa. The parameter F1 was obtained by applying the slope value of the Arrott plot to Equation (4). The parameters TA and T0 were derived by Equations (5) and (6). The obtained TA and T0 were 2258 K and 213 K, respectively.
Figure 5.
The Arrott plot (M2 vs. H/M) of Co2VGa at T = 5 K.
3.3. Analysis According to the Takahashi Theory
Table 2 indicates the Curie temperature TC, the effective magnetic moment peff, the spontaneous magnetization pS, the magnetic moment ratio peff/pS, the spin fluctuation parameters TA and T0, the critical temperature ratio TC/T0, and km, as obtained from Equation (8).
Table 2.
Basic magnetic parameters and km as obtained from Equation (8).
| TC (K) | peff (μB) | pS (μB) | peff/pS | TA (K) | T0 (K) | TC/T0 | k m | Reference 1 | |
|---|---|---|---|---|---|---|---|---|---|
| Ni2MnGa | 375 | 4.75 * | 3.93 | 1.21 | 563 | 245 | 1.53 | 1.61 | This work *, [9] |
| Ni2.02MnGa0.98 | 372 | 4.72 * | 3.79 | 1.25 | 566 | 288 | 1.29 | 1.48 | This work *, [9] |
| Ni2.04MnGa0.96 | 366 | 4.68 * | 3.64 | 1.28 | 567 | 345 | 1.06 | 1.34 | This work *, [9] |
| Co2VGa | 337 | 2.06 | 1.87 | 1.10 | 2258 | 213 | 1.58 | 1.50 | This work |
| Co2MnGa | 695 | 4.16 | 4.09 | 1.02 | 1,037 | 364 | 1.91 | 1.57 | [16,19] |
| Ni | 623 | 3.3 | 0.6 | 5.5 | 1.76 × 104 | 4.83 × 103 | 0.129 | 1.41 | [13] |
| MnSi | 30 | 2.25 | 0.4 | 5.6 | 2.18 × 103 | 155 | 0.194 | 1.88 | [7,10] |
| Ni3Al | 41.5 | 1.3 | 0.075 | 17.3 | 3.67 × 104 | 2.76 × 103 | 0.015 | 1.06 | [7,20] |
| Y(Co0.85Al0.15)2 | 26 | 2.15 | 0.138 | 15.6 | 7.26× 103 | 1.41× 103 | 0.018 | 1.08 | [7,21] |
| ZrZn2 | 21.3 | 1.44 | 0.12 | 12 | 7.4× 103 | 1390 | 0.015 | 0.74 | [7,22] |
| CoS2 | 120 | 1.72 | 0.98 | 1.76 | 2.20× 103 | 294 | 0.41 | 0.96 | [12,23] |
| UCoGe | 2.4 | 1.93 | 0.039 | 49.5 | 5.92 × 103 | 362 | 0.0065 | 1.74 | [7,24] |
| UGe2 | 52.6 | 3.00 | 1.41 | 2.13 | 442 | 92.2 | 0.571 | 1.61 | [14] |
| NpFe4P12 | 23 | 1.55 | 1.35 | 1.15 | 285 | 16.4 | 1.40 | 1.44 | [14,25] |
1 Citations in our published paper [9] are incorrect. The correct citations are listed above. We apologize for this mistake. * These values were obtained by this work.
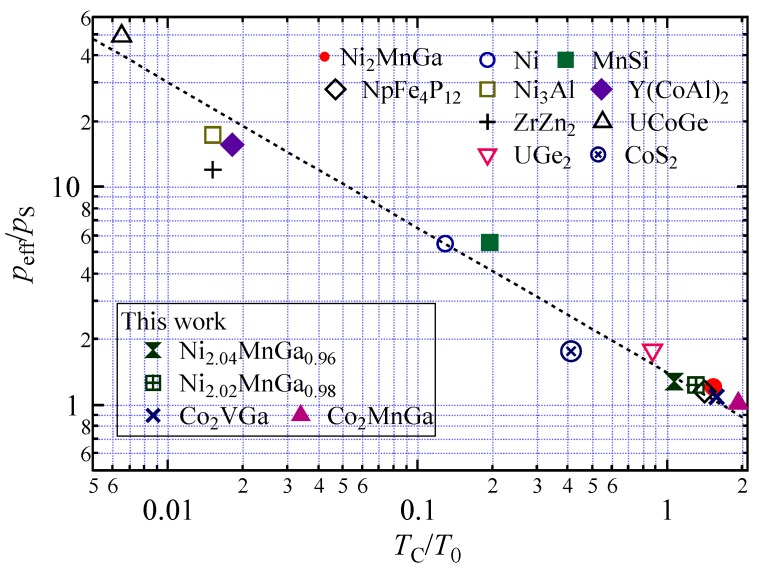
The km value was around 1.4. Figure 6 shows the generalized Rhodes–Wohlfarth plot using the parameters in Table 2 [7,26]. The points of Ni2+xMnGa1−x are in accordance with the dotted line as km = 1.4. It is noteworthy that the HMFs, Co2VGa and Co2MnGa, were also in accordance with this line. Originally, the Takahashi theory was applied to weak ferromagnets. It is interesting that this theory can be applied to strongly correlated 5f electron systems as well as Heusler HMFs.
Figure 6.
The generalized Rhodes–Wohlfarth plot (double logarithmic plot of peff/pS and TC/T0) for this work and other notable alloys and compounds. The dotted line indicates km = 1.4 as obtained from Equation (8).
3.4. Comparison between the Spontaneous Magnetic Moment at the Ground State, pS, and the Paramagnetic Magnetic Moment, pC, for HMFs
In this subsection, we consider the magnetism of Heusler alloys by comparing the spontaneous magnetic moment at the ground state and paramagnetic magnetic moment.
We rewrote the definitions of pS, psat, peff, and pC to make the following argument plain. pS is the spontaneous magnetic moment at the ground state (T = 0 K or T << TC). psat is the saturation magnetic moment at the ground state (T = 0 K or T<< TC). peff is the effective magnetic moment in the paramagnetic phase. pC is the magnetic moment in the paramagnetic phase. These four magnetic moments are defined by the unit of The relation between peff and pC is described as
| (11) |
In HMFs, the band for minority spin electrons has a gap at the Fermi level and indicates semi-metallic bands. On the other hand, for majority spin electrons, the Fermi level intersects the bands and represents metallic bands. Table 3 represents the magnetic parameters of ferromagnetic Heusler alloys, with the paramagnetic moment pC. The notable point of Table 3 is that the pC/ps of Ni2MnGa and many half-metallic Heusler alloys were smaller than 1. From Equation (9) and (11), the pC is calculated by the Curie constant, C = Nμeff2/3kB = Npeff2μB2/3kB = NpC(pC + 2)μB2/3kB. pC refers to the magnetic moment in the paramagnetic phase deduced from the Curie constant C. pc/ps is 1 for the local moment ferromagnetism. For the weak itinerant electron ferromagnetism, the pc/ps is larger than 1 [7].
Table 3.
Magnetic parameters of ferromagnetic Heusler alloys. pC indicates the magnetic moment at the paramagnetic phase. The relation between peff and pC is defined by the equation of .
| Sample | TC (K) | pS (μB/f.u.) | peff (μB/f.u.) | pC (μB/f.u.) | pC/pS | Reference |
|---|---|---|---|---|---|---|
| Ni2MnGa | 375 | 3.93 | 4.75 * | 3.85 | 0.980 | This work *, [9] |
| Ni2.02MnGa0.98 | 372 | 3.79 | 4.72 * | 3.82 | 1.01 | This work *, [9] |
| Ni2.04MnGa0.96 | 366 | 3.64 | 4.68 * | 3.79 | 1.04 | This work *, [9] |
| Co2VGa | 337 | 1.87 | 2.06 | 1.30 | 0.70 | This work |
| Co2MnSi | 1034 | 5.01 | 2.86 | 2.03 | 0.41 | [30] |
| Co2MnGe | 905 | 4.76 | 3.70 | 2.82 | 0.56 | [30] |
| Co2MnSn | 825 | 5.02 | 5.29 | 4.38 | 0.87 | [31] |
| Co2MnGa | 695 | 4.09 | 4.16 | 3.28 | 0.80 | [19] |
| Co2FeSi | 1015 | 5.42 (300 K) | 5.65 | 4.74 | 0.875 | [32] |
| Co2FeGa | 1089 | 5.05 (300 K) | 4.59 | 3.69 | 0.730 | [32] |
| CoMnSb | 478 | 4.2 | 4.0–4.6 | 3.1-3.7 | 0.74–0.88 | [27] |
| NiMnSb | 728 | 4.2 | 2.9–4.2 | 2.1-3.3 | 0.69–0.79 | [27] |
| PtMnSb | 572 | 3.96 | 4.3–4.9 | 3.4-4.0 | 0.86–1.01 | [27] |
| Ni2MnIn | 315 | 4.4 | 4.69 | 3.80 | 0.86 | [33,34] |
| Rh2MnSn | 410 | 4.14 | 4.83 | 3.93 | 0.95 | [31] |
| Pd2MnSn | 189 | 4.23 | 4.70 | 3.81 | 0.90 | [28] |
| Pd2MnSb | 255 | 4.40 | 4.8 | 3.9 | 0.89 | [28] |
* These values were obtained by this work.
As for Ni2MnGa, peff was 4.75, as shown in Table 3. Therefore, the pc obtained was 3.85 from Equation (11), and the pC/pS value was 0.980. As a result, the pC/pS was a little smaller than 1. Webster et al. compared the magnetic moment obtained by the saturation magnetization measurement where psat = 4.17 [15]. Then, the psat/ps was 0.92. The magnetization of Ni2MnGa in the magnetic field of 5.0 T at 5 K was 4.10 μB/f.u. Therefore, the psat/ps was 0.96. Regarding the half-metallic Heusler alloys, Co2VGa and Co2MnGa, which are the focus of this article, the psat/ps were 0.70 and 0.80, respectively. The renowned half-metallic Heusler alloys and compounds listed in Table 3 indicate the property of pC/pS < 1. The magnetic properties of the inter-metallic compounds CoMnSb, NiMnSb, PtMnSb, Pd2MnSn, and Pd2MnSb showed an effective paramagnetic moment above TC, which was also smaller than the spontaneous and saturation moment of the ground state at T = 0 K [27,28].
As above-mentioned, the spin polarization values P0 of Co2VGa and Co2MnGa were 75% and 48%, respectively [16]. This indicates that Co2VGa is a higher polarized HMF. The pC/pS values of Co2VGa and Co2MnGa were 0.70 and 0.80, respectively, as shown in Table 3. The results concerned with these two alloys indicate that the alloy with a larger spin polarization showed a smaller pC/pS value.
Dong et al. studied the spin polarization of Co2MnGe experimentally and analyzed the temperature dependence of the spin polarization [29] where the spin polarization of Co2MnGe was 27% at 2 K. However, the spin polarization decreased with increasing temperature and vanished at 300 K. It is considered that the magnetic moment decreases at a high temperature with the decrease of the spin polarization. Ott et al. also suggested that this effect could be attributed to a decrease of the conduction electron spin polarization in the paramagnetic phase, which has a higher temperature than TC [27]. A simple molecular field model, which took into account both local moments and spin-polarized itinerant electrons, explained that pC/pS < 1 [27]. They introduced an “Enhanced Temperature-independent Pauli susceptibility”, which comes from the itinerant electron bands intersecting the Fermi level, and explained that the Curie constant was reduced if the interactions between local magnetic moments and holes were antiferromagnetic. Therefore, the reduction in the Curie constant indicates that the magnetic moment pC at a high temperature in a paramagnetic phase is smaller than that of the spontaneous magnetization pS as well as the saturation moment psat at the ground phase of T = 5 K. Webster et al. pointed out the electronic and spin phases of Ni2MnGa [15]. In the paramagnetic phase, only the Mn atoms carry a magnetic moment. It is supposed that in the paramagnetic phase a large moment was induced by the electrons around the Mn atom at the Mn site. On the contrary, at the Ni site, the spins fluctuated at high temperature in the paramagnetic phase. Therefore, it is also supposed that pC at a high temperature in the paramagnetic phase is smaller than that of the pS. As for Co2VGa and Co2MnGa, which were treated in this article, it is of interest to investigate the temperature dependence of the spin polarization experimentally.
In Figure 6, the HMFs of Co2VGa and Co2MnGa were in accordance with the generalized Rhodes–Wohlfarth plot with a km around 1.4. The majority of the bands of these two alloys intersected the Fermi level [16]. Therefore, the magnetic property of the itinerant electron appeared in the majority bands and was confirmed by Takahashi’s theory.
4. Conclusions
In this article, experimental investigations and discussions into the field dependence of magnetization and temperature dependences of magnetic susceptibility in Ni2+xMnGa1−x (x = 0.00, 0.02, 0.04), Co2VGa, and Co2MnGa Heusler alloy ferromagnets were performed following the spin fluctuation theory of itinerant electron ferromagnetism by Y. Takahashi.
As for Ni2+xMnGa1−x, the spin fluctuation parameters in k-space (momentum space, TA) and that in energy space (T0) obtained at TC and 5 K were almost the same within 10% error. This consequently indicates that the spin fluctuation parameters can be obtained from the H/M vs. M4 plot at TC and also from an Arrott plot (H/M vs. M2) at a low temperature of T << TC.
As for Co2VGa, the H vs. M5 dependence was not shown at TC. TA and T0 were obtained by means of an Arrott plot at 5 K, which is well below TC = 337 K;
In order to obtain a km value as defined in Equation 8, the magnetic susceptibility was measured, and the peff was obtained by means of Curie law. The km of Co2VGa (1.50) and Co2MnGa (1.57) were around 1.4, which was proposed in Takahashi’s theory. The generalized Rhodes–Wohlfarth plot of peff/pS versus TC/T0 indicated that the relationship between peff/pS and T0/TC for the ferromagnets, including Ni2+xMnGa1−x and HMFs of Co2VGa and Co2MnGa, followed Takahashi’s theory. In HMFs, the band for minority spin electrons has a gap at the Fermi level and indicates semi-metallic bands. On the other hand, for majority spin electrons, the Fermi level intersects the bands and represents metallic bands. The magnetic properties of the itinerant electron of these two HMFs alloys appeared in the majority bands and were confirmed by Takahashi’s theory;
As for Ni2+xMnGa1−x and HFMs, we obtained the spontaneous magnetic moment at the ground state, pS, by an Arrott plot at 5 K, and the high temperature magnetic moment, pC, at the paramagnetic phase. The pC/pS was smaller than 1 for many Heusler alloys, which is a different property from the localized ferromagnets (pC/pS = 1), or, for weak itinerant electron ferromagnets (pC/pS > 1). A comparison between Co2VGa and Co2MnGa indicates that the alloy with a larger spin polarization showed a smaller pC/pS value. Further, an experimental investigation into the temperature dependence of spin polarization is needed to clarify the mechanism of shrinkage of the magnetic moments in the paramagnetic phase at a high temperature.
Acknowledgments
We would like to thank Hironori Nishihara for participating in fruitful discussions. This project was partly supported by the Ryukoku Extension Center (REC) at Ryukoku University. This research was carried out in part at the International Research Center for Nuclear Materials Science, Institute for Materials Research, Tohoku University.
Author Contributions
Sample preparation, D.L., F.H., X.X., R.Y.U, G.O., and T.E.; Investigation, T.S., Y.H., A.F., X.X., R.Y.U., and T.E.; Writing—original draft preparation, T.S, Y.H., and A.F.; Writing—review and editing, T.S. and T.K.; Supervision, T.K.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Moriya T. Spin Fluctuations in Itinerant Electron Magnetism. Springer; Berlin, Germany: 1985. [Google Scholar]
- 2.Moriya T., Kawabata A. Effect of Spin Fluctuations on Itinerant Electron Ferromagnetism. J. Phys. Soc. Jpn. 1973;34:639–651. doi: 10.1143/JPSJ.34.639. [DOI] [Google Scholar]
- 3.Moriya T., Kawabata A. Effect of Spin Fluctuations on Itinerant Electron Ferromagnetism. II. J. Phys. Soc. Jpn. 1973;35:669–676. doi: 10.1143/JPSJ.35.669. [DOI] [Google Scholar]
- 4.Takahashi Y. On the origin of the Curie Weiss law of the magnetic susceptibility in itinerant electron ferromagnetism. J. Phys. Soc. Jpn. 1986;55:3553–3573. doi: 10.1143/JPSJ.55.3553. [DOI] [Google Scholar]
- 5.Takahashi Y. Theoretical Development in Itinerant Electron Ferromagnetism. J. Phys. Conf. Ser. 2017;868:012002. doi: 10.1088/1742-6596/868/1/012002. [DOI] [Google Scholar]
- 6.Takahashi Y., Nakano H. Magnetovolume effect of itinerant electron ferromagnets. J. Phys. Cond. Matter. 2006;18:521. doi: 10.1088/0953-8984/18/2/013. [DOI] [Google Scholar]
- 7.Takahashi Y. Spin Fluctuation Theory of Itinerant Electron Magnetism. Springer; Berlin, Germany: 2013. [Google Scholar]
- 8.Sakon T., Hayashi Y., Fujimoto N., Kanomata T., Nojiri H., Adachi Y. Forced magnetostriction of ferromagnetic Heusler alloy Ni2MnGa at the Curie temperature. J. Appl. Phys. 2018;123:213902. doi: 10.1063/1.5036558. [DOI] [Google Scholar]
- 9.Sakon T., Hayashi Y., Li D.X., Honda F., Oomi G., Narumi Y., Hagiwara M., Kanomata T., Eto T. Forced Magnetostrictions and Magnetizations of Ni2+xMnGa1−x at Its Curie Temperature. Materials. 2018;11:2115. doi: 10.3390/ma11112115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Matsunaga M., Ishikawa Y., Nakajima T. Magneto-volume effect in the weak itinerant ferromagnet MnSi. J. Phys. Soc. Jpn. 1982;51:1153. doi: 10.1143/JPSJ.51.1153. [DOI] [Google Scholar]
- 11.Rizal C., Kolthammer J., Pokharel R.K., Choi B.C. Magnetic properties of nanostructured Fe-Co alloys. J. Appl. Phys. 2013;113:113905. doi: 10.1063/1.4795267. [DOI] [Google Scholar]
- 12.Nishihara H., Harada T., Kanomata T., Wada T. Magnetization process near the Curie temperature of an itinerant ferromagnet CoS2. J. Phys. Conf. Ser. 2012;400:032068. doi: 10.1088/1742-6596/400/3/032068. [DOI] [Google Scholar]
- 13.Nishihara H., Komiyama K., Oguro I., Kanomata T., Chernenko V. Magnetization processes near the Curie temperatures of the itinerant ferromagnets, Ni2MnGa and pure nickel. J. Alloys Compd. 2007;442:191–193. doi: 10.1016/j.jallcom.2006.09.154. [DOI] [Google Scholar]
- 14.Tateiwa N., Pospíšil J., Haga Y., Sakai H., Matsuda T.D., Yamamoto E. Itinerant ferromagnetism in actinide 5f-electron systems: Phenomenological analysis with spin fluctuation theory. Phys. Rev. B. 2017;96:035125. doi: 10.1103/PhysRevB.96.035125. [DOI] [Google Scholar]
- 15.Webster P.J., Ziebeck K.R.A., Town S.L., Peak M.S. Magnetic order and phase transition in Ni2MnGa. Philos. Mag. B. 1984;49:295–310. doi: 10.1080/13642817408246515. [DOI] [Google Scholar]
- 16.Umetsu R.Y., Kobayashi K., Fijita A., Kainuma R., Ishida K., Fukamichi K., Sakuma A. Magnetic properties, phase stability, electric structure, and half-metallicity of L21-type Co2 (V1−xMnx)Ga Heusler alloys. Phys. Rev. B. 2008;77:104422. doi: 10.1103/PhysRevB.77.104422. [DOI] [Google Scholar]
- 17.Nishihara H., Furutani Y., Wada T., Kanomata T., Kobayashi K., Kainuma R., Ishida K., Yamauchi T. Magnetization Process near the Curie Temperature of a Ferromagnetic Heusler Alloy Co2VGa. J. Supercond. Nov. Magn. 2011;24:679–681. doi: 10.1007/s10948-010-0933-3. [DOI] [Google Scholar]
- 18.Seeger M., Kaul S.N., Kronmüller H., Reisser R. Asymptotic critical behavior of Ni. Phys. Rev. B. 1995;51:12585. doi: 10.1103/PhysRevB.51.12585. [DOI] [PubMed] [Google Scholar]
- 19.Ido H., Yasuda S. Magnetic properties of Co-Heusler and related mixed alloys. J. Phys. Colloques (Paris) 1988;49:C8-141–C8-142. doi: 10.1051/jphyscol:1988857. [DOI] [Google Scholar]
- 20.De Boer F.R., Biesterbos J., Schinkel C.J. Ferromagnetism in the intermetallic phase Ni3Al. Phys. Lett. A. 1969;24:355–357. doi: 10.1016/0375-9601(67)90922-X. [DOI] [Google Scholar]
- 21.Yoshimura K., Takigawa M., Takahashi Y., Yasuoka H., Nakamura Y. NMR Study of Weakly Itinerant Ferromagnetic Y(Co1−xAlx)2. J. Phys. Soc. Jpn. 1987;56:1138–1155. doi: 10.1143/JPSJ.56.1138. [DOI] [Google Scholar]
- 22.Ogawa S. Electrical Resistivity of Weak Itinerant Ferromagnet ZrZn2. J. Phys. Soc. Jpn. 1976;40:1007–1009. doi: 10.1143/JPSJ.40.1007. [DOI] [Google Scholar]
- 23.Miyahara S. Magnetic Properties of FeS2 and CoS2. J. Appl. Phys. 1968;39:896–897. doi: 10.1063/1.1656326. [DOI] [Google Scholar]
- 24.Sato N.K., Deguchi K., Imura K., Kabeya N., Tamura N., Yamamoto K. Correlation of Ferromagnetism and Superconductivity in UCoGe. AIP Conf. Proc. 2011;1347:132–137. doi: 10.1063/1.3601803. [DOI] [Google Scholar]
- 25.Aoki D., Haga Y., Homma Y., Sakai H., Ikeda S., Shiokawa Y., Yamamoto E., Nakamura A., Onuki Y. First single crystal growth of the Transuranium filled-Skutterudite compound NpFe4P12 and its magnetic and electrical properties. J. Phys. Soc. Jpn. 2006;75:073073. doi: 10.1143/JPSJ.75.073703. [DOI] [Google Scholar]
- 26.Rhodes P., Wohlfarth E.P. The effective Curie-Weiss constant of ferromagnetic metals and alloys. Proc. Roy. Soc. A. 1963;273:247–258. doi: 10.1098/rspa.1963.0086. [DOI] [Google Scholar]
- 27.Otto M.J., van Woerden R.A.M., van der Valk P.J., Wijngaard J., van Bruggen C.F., Haas C., Buschow K.H.J. Half-metallic ferromagnets. I. Structure and magnetic properties of NiMnSb and related inter-metallic compounds. J. Phys. Cond. Mater. 1989;1:2341–2350. doi: 10.1088/0953-8984/1/13/007. [DOI] [Google Scholar]
- 28.Webster P.J., Ramadan M.R.I. Magnetic order in Palladium-based Heusler alloys Part 1: Pd2MnIn1−xSnx and Pd2MnIn1−xSbx. J. Magn. Magn. Mater. 1977;5:51–59. doi: 10.1016/0304-8853(77)90196-2. [DOI] [Google Scholar]
- 29.Dong X.Y., Adelmann C., Xie J.Q., Palmstrøm C.J., Low X., Strand J., Crowell P.A., Barnes J.-P., Petford-Long A.K. Spin injection from the Heusler alloy Co2MnGe into Al0.1Ga0.9As/GaAs heterostructures. Appl. Phys. Lett. 2005;86:102107. doi: 10.1063/1.1881789. [DOI] [Google Scholar]
- 30.Ido H. Induced magnetic moment on Co below TC in the ferromagnetic Heusler-type alloys Co2MnX (X = Si, Ge and Sn) J. Magn. Magn. Mater. 1986;54–57:937–938. doi: 10.1016/0304-8853(86)90322-7. [DOI] [Google Scholar]
- 31.Uhl E. Magnetization of two new series of Heusler alloys: (Rh1−xCox)2MnSn and (Rh1−xNix)2MnSn. J. Magn. Magn. Mater. 1985;49:101–105. doi: 10.1016/0304-8853(85)90107-6. [DOI] [Google Scholar]
- 32.Deka B., Chakraborty D., Srinivasan A. Magnetic properties of Co2Fe(Ga1−xSix) alloys. Physica B. 2014;448:173–176. doi: 10.1016/j.physb.2014.03.074. [DOI] [Google Scholar]
- 33.Kanomata T., Shirakawa K., Kaneko T. Effect of hydrostatic pressure on the Curie temperature of the Heusler alloys Ni2MnZ (Z = Al, Ga, In Sn and Sb) J. Magn. Magn. Mater. 1987;65:76–82. doi: 10.1016/0304-8853(87)90312-X. [DOI] [Google Scholar]
- 34.Webster P.J. Heusler alloys. Contemp. Phys. 1969;10:559–577. doi: 10.1080/00107516908204800. [DOI] [Google Scholar]