Systematic Coarse-Grained Lipid Force Fields with Semiexplicit Solvation via Virtual Sites

Abstract

Despite the central role of lipids in many biophysical functions, the molecular mechanisms that dictate macroscopic lipid behavior remain elusive to both experimental and computational approaches. As such, there has been much interest in the development of low-resolution, implicit-solvent coarse-grained (CG) models to dynamically simulate biologically relevant spatiotemporal scales with molecular fidelity. However, in the absence of solvent, a key challenge for CG models is to faithfully emulate solvent-mediated forces, which include both hydrophilic and hydrophobic interactions that drive lipid aggregation and self-assembly. In this work, we provide a new methodological framework to incorporate semiexplicit solvent effects through the use of virtual CG particles, which represent structural features of the solvent-lipid interface. To do so, we leverage two systematic coarse-graining approaches, multiscale coarse-graining (MS-CG) and relative entropy minimization (REM), in a hybrid fashion to construct our virtual-site CG (VCG) models. As a proof-of-concept, we focus our efforts on two lipid species, 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), which adopt a liquid-disordered and gel phase, respectively, at room temperature. Through our analysis, we also present, to our knowledge, the first direct comparison between the MS-CG and REM methods for a complex biomolecule and highlight each of their strengths and weaknesses. We further demonstrate that VCG models recapitulate the rich biophysics of lipids, which enable self-assembly, morphological diversity, and multiple phases. Our findings suggest that the VCG framework is a powerful approach for investigation into macromolecular biophysics.

Introduction

Cellular membranes are crucial biological components that regulate many essential biological activities through processes that include compartmentalization, signaling, and transport.^1,2 The main constituent of membranes are lipids, which are amphiphilic molecules with hydrophilic head groups and hydrophobic tails. Collectively, these lipids serve as building blocks for noncovalently assembled fluid membranes.³ As a diverse array of lipid species exists in nature, the properties of these membranes are also highly variable. Hence, we can expect molecular-scale fluctuations to influence the structure and function of these membranes, which, in turn, affect the large-scale macroscopic properties. Understanding the fundamental connection between the microscopic and macroscopic behavior of membranes has widespread implications, which include biophysical insight into cellular activity and design inspiration for biomimetic soft materials.⁴⁻⁶ However, atomistic insight into membrane biophysics has been difficult to probe using experimental techniques, especially at the scales associated with molecular fluctuations. Instead, one may turn toward computer simulation for a detailed investigation of these behaviors, e.g., using classical molecular dynamics (MD).

The use of MD simulations to study membranes contains its own set of challenges. The primary obstacle is to access sufficiently large length- and time-scales in order to capture lipid reorganization and membrane fluctuation, which are inherently slow. In fact, the use of specialized hardware such as the Anton supercomputer has previously been used to study multicomponent lipid bilayers.⁷ An alternative approach is to use coarse-grained (CG) models, in which molecules are represented with reduced (i.e., less than atomistic) detail; here, CG particles correspond to a collective of several or many atoms. The most attractive CG models for studying membranes and a number of other systems are solvent-free as water typically constitutes the majority of the computational burden. Several such CG models already exist, and they are generally categorized into two main groups: top-down and bottom-up CG models. Top-down models are fitted to reproduce macroscopic properties. For example, models for high-resolution CG lipids (∼10–15 CG sites per lipid) have been generated based on experimental partition coefficients,⁸ while low-resolution CG lipids (i.e., 3–6 sites per lipid) have been parametrized to easily tune bending rigidity.⁹⁻¹² Bottom-up models use rigorous statistical mechanics to parametrize models that reproduce microscopic properties. Most models in the bottom-up space are in the high-resolution regime,¹³⁻¹⁶ although some have been reported in the low-resolution regime as well.^17,18 In the case of both top-down and bottom-up CG models, however, the questions of so-called representability and transferability remain important open problems.¹⁹ In particular, the key challenge for implicit-solvent CG models is to faithfully recapitulate the CG physics produced by solvent-mediated effects (i.e., both hydrophilic and hydrophobic interactions) since solvent degrees of freedom are explicitly removed. These missing degrees of freedom represent an inherently many-body lipid-solvent interaction that is the primary driver for lipid self-assembly.^20,21

The ability of a CG model to capture all of the relevant physics of lipids is largely contingent on the expressiveness of the underlying interactions, i.e., based on the CG representation and effective force field. For a variety of CG mappings, some bottom-up methods have been suggested to reproduce the many-body potential of mean force (PMF) in the limit of infinite sampling (i.e., from an all-atom (AA) reference trajectory) when they are allowed to return any possible CG force field.^22,23 However, practical use-cases of these methods necessarily involve limited sampling and finite CG force-field basis sets due to computational cost. An example of a finite basis set is the classical description of molecular energetics using pairwise (i.e., two-body) nonbonded interactions in conjunction with bonded interactions (e.g., two- to four-body).

It is informative to consider an analysis from Rudzinski and Noid, in which two well-known variational bottom-up methods, multiscale coarse-graining²⁴⁻²⁷ (MS-CG) and relative entropy minimization²⁸⁻³⁰ (REM), are compared in this context.²³ Using a general information measure that discriminates the AA and CG ensembles, they showed that REM minimizes the average of this quantity, while MS-CG minimizes the average of its squared gradient. Hence in complex systems, one can expect that effective CG interactions derived from MS-CG or REM may yield considerably different behavior if the CG interaction basis set is not sufficiently descriptive (i.e., fully complete). Conversely, sufficiently descriptive (but not infinite) basis sets that are used for MS-CG and REM have been shown to result in equivalent CG behavior in select cases.²³ Therefore, a comparison between CG models derived from MS-CG and REM may indirectly provide insights into CG force-field expressiveness.

A rich variety of basis sets that describe nonbonded CG interactions have recently been reported. For example, one general direction has been to incorporate many-body effects through higher-order potential energy terms, such as through density- or order-parameter-based interactions; these complex models have been shown to be quite effective for aqueous polymers and simple liquids.³¹⁻³⁴ Nonetheless, one should be mindful of the additional computational cost of these CG force-field variants. Another body of work has been to introduce virtual sites, which are additional particles that have been used for a variety of purposes. In multiresolution simulations, for example, domains that are defined on an atomistic level (with atomistic interactions) may also evolve according to a coupled CG interaction model, in which the simultaneous representation of the atomistic domain as a CG particle may be considered a virtual site.³⁵ Virtual sites have also been used as fictitious particles that impart subtle anisotropic projections of forces acting upon real sites; one prototypical example of this idea is the atomistic TIP4P water model.³⁶ In the context of CG models, these types of virtual sites have been useful for sterols and for aromatic hydrocarbons.^37,38 Overall, virtual sites can be thought of as relatively inexpensive augmentations to conventional pairwise force fields. However, in systems without straightforward geometric symmetry, the general parametrization and use of virtual sites remains unexplored.

In this work, we investigate the use of bottom-up methods to derive CG models for lipids. We consider two lipid species, 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), which adopt liquid-disordered (L_d) and gel-II (L_β) phases at room temperature, respectively.^39,40 We restrict ourselves to low-resolution (i.e., highly CG) mappings that still resolve the two hydrophobic tails as tail-ordering has been implicated for phase behavior.⁴¹ In addition and most importantly, we introduce virtual sites that represent semiexplicit aspects of solvent. As these virtual sites correspond to a nonlinear mapping of solvent, we propose a hybridization of the REM and MS-CG approaches to construct our CG models; given their nature, these virtual sites should be considered a distinct variant from the aforementioned classes of virtual sites. We first compare implicit-solvent (or solvent free) CG models that are derived using either MS-CG or REM in order to emphasize and explore their native differences. These models are then compared to CG models that are augmented by virtual sites (our so-called “VCG” models). In particular, we argue that the virtual representation of structural features at the water–lipid interface greatly enhances the expressivity of our CG models and enables rich behavior, including phase discrimination, robust self-assembly, and morphological diversity, that otherwise cannot be captured, especially at the level of a highly CG model. We anticipate that the proposed methodology may be generalized to other complex macromolecules in the future.

Theory and Methodology

The construction of CG models requires two steps: mapping from atomistic to CG and parametrization of the effective CG interactions. In this work, we utilize six-site center-of-mass mappings of DOPC and DPPC, as depicted in Figure 1(a) and described in detail in Table S1 and Figure S1. The mapping is motivated by physically intuitive groupings: the phosphate and choline groups are represented by the headgroup (HG) CG “bead”, the glycerol backbone and ester group are represented by the middle-group (MG) bead, and the two hydrocarbon tails are represented by the first tail-group (T1) and second tail-group (T2) beads. We select this mapping resolution in an attempt to construct low-resolution CG models (see Figure 1(b)) that maintain tail fidelity, as tail packing and reorganization are likely important for lipid phase behavior.⁴¹

Figure 1.

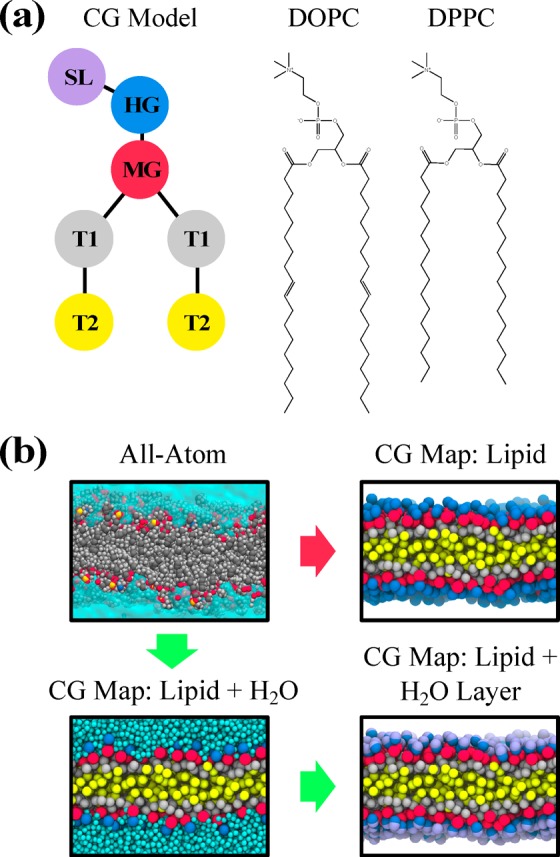
Schematic of the coarse-grained mapping procedure for DOPC and DPPC. (a) The CG model consists of six sites that together represent all lipid atoms, while the virtual SL site represents local structural features of solvent near lipid head groups. (b) The red path indicates conventional implicit-solvent CG mapping procedures, while the green path indicates the procedure used in this work: water is first mapped to single-site particles and used to construct virtual SL sites. Explicit details on mapping can be found in Table S1 and Figure S1.

We also introduce a seven-site CG model, in which an additional site is identified and attached to the six-site model in order to represent a feature of the solvent, namely the solvent-lipid interface, as the SL bead. We hypothesize that the presence of solvent microstructure at the solvent-lipid interface is suggestive of interactions that should be expressed in our VCG model. As depicted in Figure 1(b), we choose to represent the center-of-masses (CoM) of water molecules that are strongly correlated with the hydrophilic region of each lipid, i.e., the HG bead, as the SL bead. This structural correlation can be seen in the radial distribution function (RDF), shown in Figure 2, between HG and the CoM of nearby water molecules; the two peaks (seen below a distance of 6.0 Å) are indicative of preferential aggregation of water molecules, which may arise, for instance, from hydrogen bonding between water and lipid phosphate groups (see inset of Figure 2). These two features may further correspond to recent experimental identification of so-called tightly bound water regimes at the interface of lipid bilayers.⁴² Hence, we identify all water molecules within the first two coordination shells around each HG site, corresponding to a radial cutoff of 6.0 Å (the second minima in the RDFs), and construct the SL site at their CoM; we extended our cutoff to the second coordination shell due to the low coordination number of water molecules within the first shell (∼2 or fewer molecules). We note, however, that adjacent SL beads share water molecules as the hydration shells around adjacent lipids are overlapping. Furthermore, the number of water molecules within the bound regime is inherently dynamic (see Figure S2). These aspects introduce important new challenges for CG interaction parametrization, which we describe next.

Figure 2.

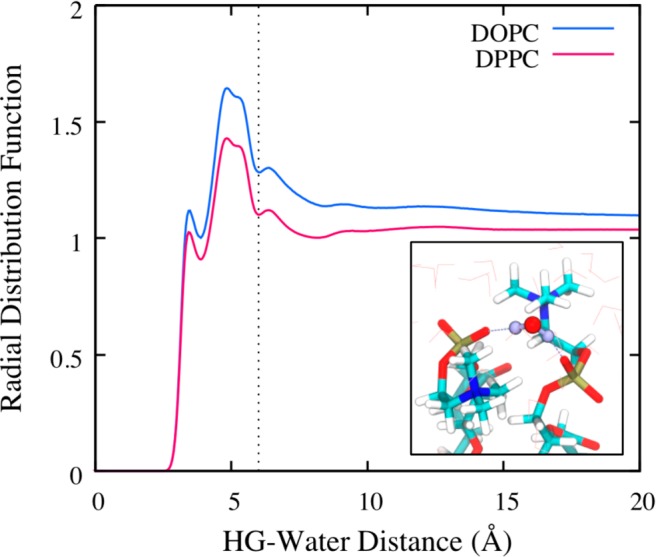
Radial distribution function (RDF) for coarse-grained single-site water around lipid HG (i.e., headgroup) sites. The dashed line indicates the radial distance cutoff that is used to construct the virtual SL sites. The inset shows a representative snapshot of water coordinating between two lipid phosphate groups through hydrogen bonding interactions, which corresponds to the first peak of the RDF.

To parametrize our CG interactions based on our aforementioned mapping, we focus on two variational methods as mentioned earlier, i.e., MS-CG and REM. While full details on both methods can be found elsewhere, we include a brief summary of the two methods as posed in the canonical ensemble.^27,30 The MS-CG method uses the variational principle to find a CG force field (U_CG) based on minimization of the following force-based functional

1

which is the least-squares residual of forces (χ²) with N as the number of CG sites, R^N as the CG-mapped atomistic configuration, f_I as the CG-mapped atomistic forces on site I, F_I as CG-forces on site I given U_CG, and ⟨⟩ indicating an ensemble average over the atomistic ensemble. While this expression is general, it is important to note that defining f_I, i.e., to ensure that global minimization of eq 1 implies phase-space consistency, is trivial only for select choices of mapping operators:²⁶ center-of-mass mappings are a quintessential example as the positions and forces of mapped CG sites are expressed by a linear combination of atomistic positions and forces, respectively, which are commonly assigned to unique CG sites. Generalizations of MS-CG theory for nonlinear mapping functions have also been proposed yet remain difficult to implement in practice.⁴³ Our proposed SL sites fall within the category of nonlinear mappings, e.g., from overlapping water molecules and from variability in the number of water molecules, and a closed form expression for f_I has, to our knowledge, not yet been derived.

The REM method uses a variational procedure to find U_CG based on minimization of the following functional

2

which is known as the relative entropy (S_rel) (i.e., Kullback–Leibler divergence), a measure of the distance between two probability distributions, e.g., the probability of an atomistic configuration (i.e., p) and that of a CG configuration given U_CG (i.e., P); the first term, S_map, only depends on the mapping operator, i.e., rendering S_map effectively constant and negligible with respect to U_CG optimization. Again, while eq 2 is general, it is practical to reformulate this expression in terms of structural or energetic properties. In the canonical ensemble, eq 2 can be formulated as³⁰

3

where E_AA (E_CG) is the atomistic (CG) internal energy (evaluated under AA ensembles), A_AA (A_CG) is the AA (CG) configurational free energy, and β is the Boltzmann factor. In doing so, iterative schemes such as Newton–Raphson minimization can be used to optimize U_CG.³⁰

Both methods yield the correct many-body PMF in a general sense, i.e., in the limit of infinite sampling of reference data and infinite expressivity in the basis set for the CG interactions. However, it is informative to understand the behavior of these two methods in the frame of limited basis sets, which are necessarily employed in molecular simulations. In the infinite sampling limit, it has been shown that n-body potentials that are determined using REM exactly recapitulate specific n-body statistics.²⁹ As an example, two-body potentials, such as Lennard-Jones (LJ) interactions, reproduce particular pairwise structural correlations; in the case of 12-6 LJ, perfect reproduction of pairwise r^–12 and r^–6 correlations is expected. For comparison, two-body potentials that are determined using MS-CG are found to incorporate both two- and three-body correlations based on connections to Yvon-Born-Green liquid-state theory.⁴⁴ Taken further, these subtle differences can be summarized by the following dictum: while the REM method provides a complete fit to reduced statistics, the MS-CG method provides a reduced fit to complete statistics. Hence, CG potentials with finite basis sets that result from these two methods may yield complementary behavior, and one might wish to take advantage of features from both.

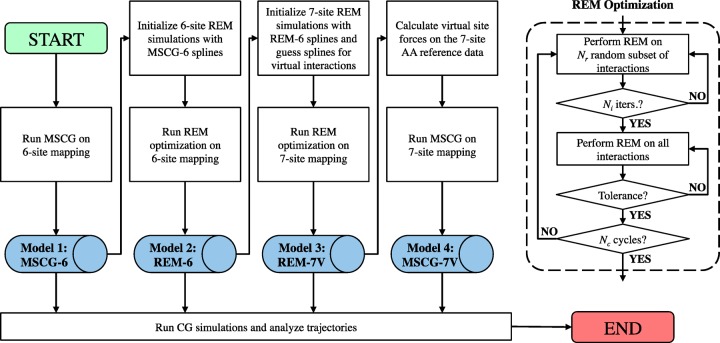
In this work, we report the results of four different CG lipid models, each for two different lipid species (DOPC and DPPC), for a total of eight CG lipid models. Each of the four models is generated using the successive framework shown in Figure 3, which ultimately combines model features from both REM and MS-CG. First, a six-site model is constructed using the MS-CG method, which we denote MSCG-6. The resultant CG potentials are then used as an initial guess for iterative REM optimization for another six-site model, which we denote REM-6. We next turn toward seven-site models by introducing the SL virtual particle (see Figure 1). Recall that a mapping function for mean forces that retains thermodynamic structural consistency is unknown (albeit progress is underway).³⁸ Hence, we use the REM method to optimize a seven-site model, i.e., REM-7V, using the REM-6 model as an initial guess (see the SI for additional details). We then use the generated REM-7V potentials associated with the SL site as a proxy to compute the previously unknown mean forces acting on each SL site in the CG-mapped atomistic trajectory. This, in turn, enables the generation of another seven-site model using the MS-CG method, i.e., MSCG-7V, since the mean forces on both real and virtual CG sites are now defined.

Figure 3.

Flowchart depicting the parametrization strategy used to construct each of the coarse-grained lipid models, which rely on two variational methods: multiscale coarse-graining (MS-CG) and relative entropy minimization (REM). The right block shows the REM optimization subprocedure based on Newton–Raphson minimization, in which a two-part strategy is adopted: initially, stochastically chosen subsets of parameters are refined for each iteration, followed by refinement of all parameters at each iteration.

To summarize, our final CG-mapped forces are obtained from the following two expressions

4

5

where I and J denote CG-mapped sites, i denotes atomistic sites, and U_IJ|REM7 represents the REM-7V pairwise potential between I and J. Note that the final two steps of this procedure can be performed independently of the first two steps; we only use the six-site CG models to accelerate training. Details of each operation are described below.

MS-CG

All calculations were performed using the publicly available MS-CG 1.8 code (https://github.com/uchicago-voth/MSCG-release).⁴⁵ Pairwise nonbonded, bonded, and angle interactions were described by third-order B-splines using resolutions of 0.01 nm, 0.005 nm, and 0.5 degrees, respectively; a radial cutoff of 2.5 (3.0) nm was used for DOPC (DPPC) nonbonded interactions. A down-sampled set of 7,500 MD frames was used for least-squares regression and validated against holdout sets of 7,500 frames. Bayesian regularization for a maximum of 250 iterations was also used.⁴⁶ For nonbonded interactions, the repulsive forces in the exclusion portion of the CG potentials were extrapolated linearly toward r = 0; as this region is rarely sampled, the functional form does not appear to affect the overall behavior of the CG model. All MS-CG calculations are single-iteration computations.

REM

All calculations were again performed using the publicly available MS-CG 1.8 code.⁴⁵ Pairwise nonbonded interactions were described using third-order B-splines using a resolution of 0.03 nm with a radial cutoff of 2.5 (3.0) nm for DOPC (DPPC) models; for simplicity, bond and angle interactions generated by MS-CG were used and held constant. To accelerate training, and due to fast convergence, only 100 frames from the CG trajectory were used. Given the stochastic nature of the optimization and the complexity of the model, we found that unphysical intermediate solutions for the CG potentials were sometimes explored, thereby leading to either divergent behavior or unstable simulations. To mitigate this problem, we adopted a stochastic procedure in which a random subset of the nonbonded interactions was chosen for optimization at every iteration for 50 to 100 iterations. To improve stability, we also used a mixing coefficient of 0.35 during the update step for Newton’s method.³⁰ The entire set of nonbonded interactions was subsequently optimized for 50 to 100 iterations. This procedure was then repeated if convergence was not achieved; convergence was assessed based on a relative tolerance of 0.05 for S_rel, which typically required no more than 400 iterations. A summary of the total required iterations is tabulated in Table S2. Given the stochastic nature of this procedure, we repeated the procedure, which converged to similar solutions. We also repeated the procedure using initial potentials derived from the Cooke-Deserno model.^9,10 Both solution sets are shown in Figure S3 and exhibit consistent potentials. However, it should be noted that other solutions may exist within the same numerical tolerance for S_rel, which would likely depend upon the initial trial potentials.

All-Atom Molecular Dynamics

All atomistic simulations were performed using GROMACS 5.0.7.⁴⁷ An initial configuration of 1152 DOPC (1296 DPPC) lipids in a bilayer, surrounded by around 45,000 (51,000) water molecules and 0.15 M concentration of NaCl, was generated in a periodic box using the CHARMM-GUI membrane builder.⁴⁸⁻⁵⁰ Standard equilibration procedures were employed.^49,50 After energy minimization to a force tolerance of 1000 kJ mol^–1 nm^–1, simulations in the constant NPT ensemble were performed using a Nosé–Hoover thermostat⁵¹ at 300 K and a semi-isotropic Parrinello–Rahman barostat⁵² at 1 atm with coupling times of 2 and 10 ps, respectively. Hydrogen atoms were constrained using LINCS, and electrostatics was calculated using particle-mesh Ewald summation. An integration timestep of 2 fs was used. The CHARMM36 force field⁵³ was used for lipids, and the TIP3P force field³⁶ was used for water; forces were computed up to a radial cutoff of 1.2 nm with a smooth switching function beginning at 1.0 nm. After 300 ns of equilibration under the conditions described above, simulations were run in the constant NVT ensemble (using the average volume over the last 100 ns) for 100 ns and statistics captured every 1 ps.

CG Molecular Dynamics

All CG simulations were performed using LAMMPS 11Aug17⁵⁴ with tabulated CG potentials (accessible from https://github.com/uchicago-voth/MSCG-models). Initial configurations of 1152 DOPC (1296 DPPC) lipids in a bilayer were generated using Moltemplate with a uniform lateral (or xy) spacing of 2.0 nm in a periodic box with vacuum z-spacing of 10 nm. During REM iterations, the simulation domain was rapidly relaxed in the xy-dimensions using a Berendsen barostat⁵⁵ and Langevin thermostat⁵⁶ over 50,000 timesteps, followed by linear deformation to the reference atomistic xy-dimensions over another 50,000 timesteps; here, a timestep of 2 fs was used with coupling constants of 5 and 2 ps, respectively. Simulations were subsequently run for 200,000 timesteps in the constant NVT ensemble with statistics gathered over the final 50,000 timesteps every 500 timesteps; these trajectories were used during the REM optimization procedure.

For CG model validation and characterization, independent simulations were run using a 10 fs timestep and a Langevin thermostat (Nosé–Hoover barostat) with a coupling constant of 10 ps (50 ps); different initial configurations are described throughout the main text. Simulations were run for 750,000 timesteps in the constant NVT ensemble with statistics gathered over the final 500,000 timesteps every 500 timesteps; the analysis performed on these trajectories is described in the main text. Subsequently, constant NPT ensemble simulations were integrated for 300,000 timesteps with statistics from the final 150,000 timesteps (gathered every 150 frames) used for additional analysis (i.e., area per lipid characterization). For all DOPC (DPPC) cases, a radial cutoff of 2.5 (3.0) nm was used with a neighbor-list skin-depth of 0.8 nm.

Results and Discussion

Comparison of Coarse-Grained DOPC Interactions

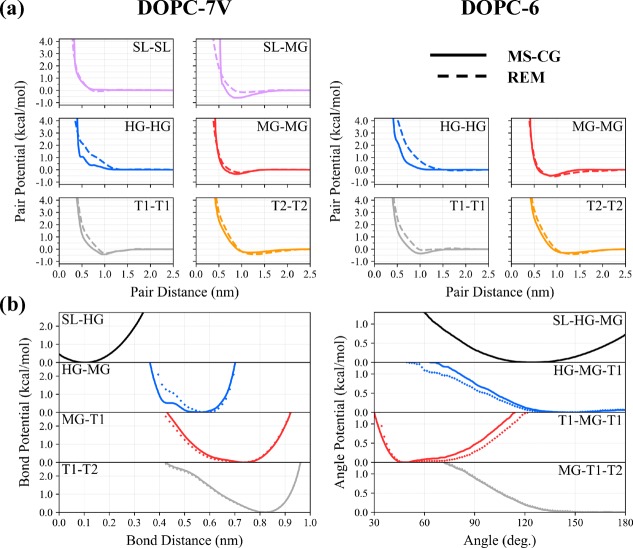
We first examine the effective CG potentials that are determined by MS-CG and REM for the six-site (DOPC-6) and seven-site (DOPC-7V) DOPC models. For simplicity, we will restrict our discussion to the subset of pairwise nonbonded interactions that are shown in Figure 4(a), which depicts the four self-interactions among lipid sites and, in the case of DOPC-7V, two key SL interactions.

Figure 4.

Coarse-grained DOPC interactions. (a) Comparison between seven-site (DOPC-7V) and six-site (DOPC-6) pair potentials for a representative subset of all nonbonded interactions. Models generated using multiscale coarse-graining (MS-CG) and relative entropy minimization (REM) are also denoted by solid and dashed lines, respectively, yielding a total of four different models. Note the emergence of the SL-MG attraction in the DOPC-7V model, which appears to mediate MG-MG attraction (i.e., to maintain surface tension). (b) Bond and angle potentials were computed using MS-CG in the DOPC-7V case (solid) and DOPC-6 case (diamond symbols). For simplicity, the DOPC-6 bonded potentials were used for the two REM models.

It is worth noting the general trends that emerge with respect to the partitioning of attractive and repulsive interactions. It appears that attractive interactions are associated with the MG bead at close range (e.g., a minima of −0.48 kcal/mol when r = 8.7 Å for MSCG-6) and T1 and T2 beads at longer range (e.g., a minima of −0.35 and −0.32 kcal/mol when r = 10 and 12 Å for MSCG-6). Meanwhile, the HG bead is primarily repulsive. We would expect attraction of the MG beads as these are associated with the hydrophobic–hydrophilic interface and are responsible for maintaining the surface tension of the lipid bilayer in the absence of explicit solvent.¹¹ In fact, our results appear to validate certain aspects of previous design principles used for phenomenological CG models, such as that of Brannigan and Brown,¹¹ that adopt this intuition during model construction; these previous models assign repulsion to the headgroup and strong (weak) attraction to the middle (tail) groups. As discussed later, this combination of HG repulsion and MG (and to a lesser extent, T1/T2) attraction effectively enables lipid self-assembly by mimicking hydrophobicity as an enthalpic effect.^15,16

There are a few subtle differences between the CG interactions determined by MS-CG and REM in the DOPC-6 case that are important to mention. The first is that the MG interaction, the primary attraction, appears slightly deeper and longer-range in the REM model (e.g., a minima of −0.54 kcal/mol when r = 9.3 Å for REM-6) compared to that of MS-CG. In contrast, and seemingly to compensate, the REM model also exhibits softer, longer-ranged HG repulsion and weaker tail attraction (e.g., a minima of −0.10 and −0.40 kcal/mol when r = 10.7 and 13.7 Å for T1 and T2, respectively, in REM-6). The implications of these features will be discussed later.

We also find that the inclusion of the virtual SL site has an important effect on the relative partitioning of attractive CG interactions. Both the MS-CG and REM models for DOPC-7V predict slightly weaker and shorter-range MG attraction (e.g., a minima of −0.34 and −0.22 kcal/mol when r = 8.6 and 9.3 Å for MSCG-7V and REM-7V, respectively) compared to that of the DOPC-6 models. Instead, this attraction is now mediated by the presence of the SL bead, i.e., the SL-MG interaction. Hence, while the SL bead is self-excluding, e.g., to represent the space occupied by solvent, the collective aggregation of SL and MG beads is now required to maximize attraction and serves as the primary driver for lipid aggregation. Interestingly, the discrepancy between the interactions determined by MS-CG and REM, and most notably for the MG interactions, appears to be smaller than that of the DOPC-6 case; we evaluate this difference between MS-CG and REM potentials using the relative entropy for the MG interactions which we compute to be 0.0016 and 0.0028 for DOPC-7V and DOPC-6, respectively. As we expect both methods to converge to the same CG model in the limit of infinite basis, we are encouraged by this observation as it suggests that the simple addition of our virtual SL site enhances the expressiveness of our limited (finite) force-field basis set.²³

Finally, we show the predicted bond and angle potentials for DOPC-7V in Figure 4(b). Here, we only show the results from MS-CG, which we found to be nearly indistinguishable from that of DOPC-6. Overall, all of the calculated bond and angle potentials appear to be anharmonic; the use of B-splines is therefore critical to describe these bonded interactions at the CG level. The stiffest segments of the lipid, as indicated by the potentials with the largest curvature, are predicted to be the HG-MG bond and the T1-MG-T1 splay angle. In addition, the predicted potentials are found to be similar to the bonded potentials that are computed from Boltzmann Inversion (BI), which was the strategy used in previous work on solvent free lipid models.^13,14 Hence, in the absence of explicit CG-mapped forces for the SL bead, we approximated the SL-HG bond and SL-HG-MG angle potentials from BI. We should also mention that these bond and angle potentials were used for all REM optimizations, as we only used REM to optimize nonbonded interactions for simplicity.

Evaluation of Coarse-Grained DOPC Behavior

To assess our CG models for DOPC, we consider several illustrative metrics with respect to both reference AA and experimental data. We first investigate structural correlations. Lipid bilayers, by nature, are structurally anisotropic as lateral (i.e., in-plane) lipid packing is distinguishable from normal (i.e., out-of-plane) packing into its two leaflets. As such, we compare the lateral and normal lipid number densities in Figure 5 and restrict ourselves to the five self-pair correlations. In Figure S4, we also provide a comparison of RDFs generated from the two 7V models and the reference AA trajectory; here, we note that the REM-7V model shows expectedly excellent agreement (with an average relative entropy of 0.018 ± 0.007) with our reference data (indicating successful optimization), while the MSCG-7V model exhibits close agreement (with an average relative entropy of 0.076 ± 0.010) with some overstructured features, as indicated by peaks with larger heights and narrower widths.

Figure 5.

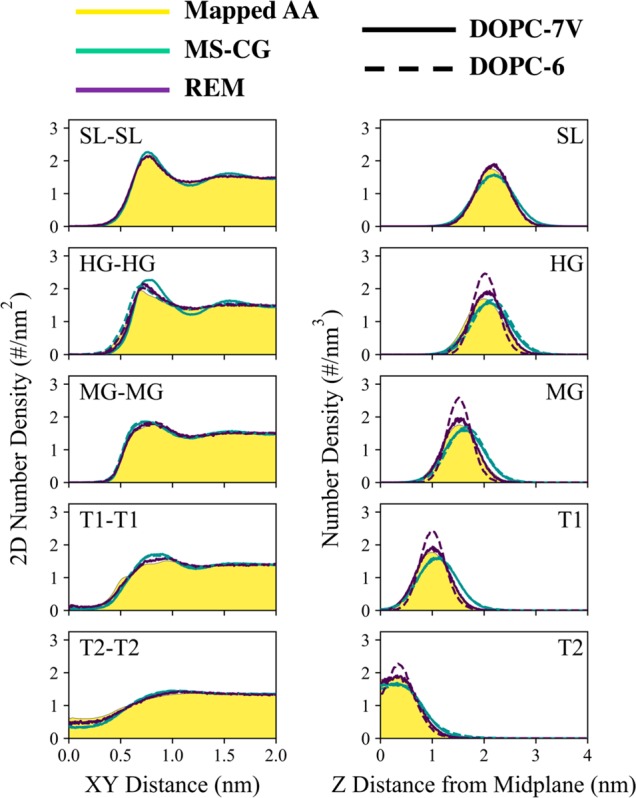
Comparison of structural correlations in coarse-grained DOPC lipid bilayers between mapped all-atom trajectories, multiscale coarse-graining models (MS-CG), and relative entropy minimization (REM) models; here, both DOPC-7V (solid lines) and DOPC-6 (dashed lines) models are shown. The left and right panels are lateral (i.e., xy-direction) and perpendicular (i.e., z-direction) number density profiles between the listed sites. Each of the profiles was averaged over both leaflets and used a bin size of 0.01 nm.

The primary differences between the four CG models are observed when comparing MS-CG against REM results. In the lateral direction (left of Figure 5), good agreement between MS-CG, REM, and the reference AA trajectory is generally seen for all of the profiles, although the MS-CG (REM) model tends to predict overstructuring in the HG (T1/T2) region as evident by the increased maximum density by up to 25% (10%), especially in the DOPC-7V case. In the normal direction (right of Figure 5), more striking differences are seen between MS-CG and REM results. The peak positions predicted by REM in the DOPC-6 model correspond to that of the reference AA trajectory yet also tend to be larger (and narrower) with maximum densities increased by up to 50%; interestingly, the introduction of the virtual SL particle also appears to broaden these peaks and reduces the discrepancy in maximum peak densities to within 15%, thereby indicating a softening effect. On the other hand, the height (and width) of the peaks predicted by both MS-CG models corresponds to that of the reference AA trajectory to within 10% of the maximum peak density, while the peak positions tend to be further away from the midplane by up to 2 Å. This disparity in lateral and normal density profiles is perhaps most representative of the difference between the two methods. While the REM models expectedly match the average radial correlations (e.g., the RDFs in Figure S4), the lateral density distributions appear to be emphasized at the expense of narrower normal density distributions; we speculate that this behavior arises since the lateral pair correlations dominate the radial pair correlations (recall that REM attempts to fit averages of target information). Meanwhile, the MS-CG models have no such guarantee. Instead, the MS-CG models appear to emphasize the shape and curvature of the distributions, especially for the normal density distributions, at the expense of matching the radial distributions (recall that MS-CG attempts to fit gradients of target information).

Our CG models can be assessed further by considering standard membrane properties, summarized in Table 1, which include the area per lipid (APL), bilayer thickness, tail-order parameter (S_TT), head-order parameter (S_HM), and bending modulus (κ_bend). To approximate the bilayer thickness, we laterally divide the membrane into bins with lengths of 1.0 nm and compute the average normal distance between interleaflet HG beads within each grid element; this value is then averaged over the grid and trajectory, which is then reported as d_HG-HG. Order parameters were calculated using the second order Legendre polynomial for cos(θ)⁵⁷

6

in which θ_TT|HM denotes the angle formed between the bilayer normal and the bond vector that connects T1-T2 (or HG-MG); recall that S_TT|HM is 1.0 when the two bond vectors prefer parallel orientation, −0.5 when they prefer orthogonal orientation, and 0.0 when preferential orientation is absent. Area-normalized fluctuation spectra (H_z) were calculated, as described previously,⁵⁸ using large CG simulations that were around 60 × 60 nm² (with 10,368 lipids) and run for 10⁶ timesteps. The spectra (Figure S5) were used to approximate κ_bend by fitting the low-frequency modes with the following:

7

Table 1. Comparison of Properties for DOPC from the Listed CG Models: Area Per Lipid (APL), Distance (or Bilayer Thickness) between HG (d_HG-HG), T1-T2 (S_TT) and HG-MG (S_HM) Order Parameters, and Bending Modulus (κ_bend) at 300 K^c.

property	MSCG-6	REM-6	REM-7V	MSCG-7V	AA	exp
APL (nm2)	0.66	0.46	0.53	0.68	0.67	0.72a
dHG-HG (nm)	4.4	4.1	4.0	4.2	4.0	4.48a
STT [SHM]	0.65 [0.62]	0.63 [0.64]	0.61 [0.62]	0.60 [0.61]	0.56 [0.53]	n/a
κbend (kBT)	56.4 ± 2.2	183.9 ± 10.4	88.0 ± 3.1	29.8 ± 1.7	23.4 ± 2.6, 28.8b	18.3a

^aReference (39).

^bReference (61).

^cStandard errors within the range of listed significant digits are shown.

The stiffness of the flexural modes of the bilayer is a critical descriptor of membrane physics, such as for membrane-mediated protein interactions.^59,60 For comparison, an alternative method is used to compute κ_bend for the reference AA systems as these simulations are not large enough to reliably sample low-frequency modes.⁶¹ We use the relationship between the area compressibility (κ_A) and κ_bend as follows⁶¹

8

where ⟨A⟩ and ⟨ΔA²⟩ are the average membrane area and mean squared area fluctuation, respectively. Note that eq 8 should not be applied to CG systems due to its reliance on compressibility.¹⁹

Given the previous discussion on the fidelity of normal density distributions, it is unsurprising that the d_HG-HG predicted by both REM-6 and REM-7V models agree to within 3% of values computed from AA simulations. Similarly, both MSCG-6 and MSCG-7V models overestimate d_HG-HG by up to 10% compared to AA simulations, yet, coincidentally, agree better with experiments; given the disparity between predictions from AA simulations and experimental values, it would be worthwhile to use sensitivity-based methods⁶² to correct CG potentials in future work, e.g., upon changes to the underlying AA force field. We also find that the APL predicted by both MS-CG models agree within 3% with that of AA simulations, which is within the expected difference between values predicted by simulations and experiments. On the other hand, both REM models predict an additional 20–30% of lateral compression. However, as the APL is computed in the constant NPT ensemble, we must note that the discrepancy between the two methods most likely arises from the representability issues related to pressure.¹⁹ As there is no rigorous correspondence between the naïvely computed CG virial and AA virial, unless the CG interactions are independent of volume (which they are not), we assume that the success of the MS-CG method is partially by chance. A more thorough assessment of APL (and related metrics) would likely require amendments to eqs 1 and 3, which is an active area of research and includes recent extensions to MS-CG and REM for constant NPT ensembles.^19,63−65

The final two metrics, S_TT/S_HM and κ_bend, are particularly informative about the benefit of virtual solvent sites. We find that both DOPC-6 models result in S_TT and S_HM values that are larger by up to 22% compared to our reference AA simulations. In addition, κ_bend is considerably stiffer than that of previous atomistic simulations⁶¹ and experiments³⁹ by at least a factor of 2 (factor of 7) for MSCG-6 (REM-6). We expect that the origin of this rigidity can be attributed to the absence of the entropy-driven hydrophobic effect, i.e., due to the lack of solvent, which is a primary driver for lipid self-assembly.²¹ To compensate, both CG models introduce explicit attraction, which is largely seen in the MG, T1, and T2 interactions (see Figure 4). The DOPC-7V models, on the other hand, result in reduced S_TT and S_HM that are within 17% of reference AA values. A 2-fold reduction in κ_bend is also observed upon introduction of the SL bead, such that the stiffness of the MSCG-7V model recapitulates that of atomistic simulations.⁶¹ This suggests that the effective repartitioning of attractive forces due to the presence of the SL beads (see Figure 4) is important in order to recapitulate the flexible and fluid nature of lipid bilayers.

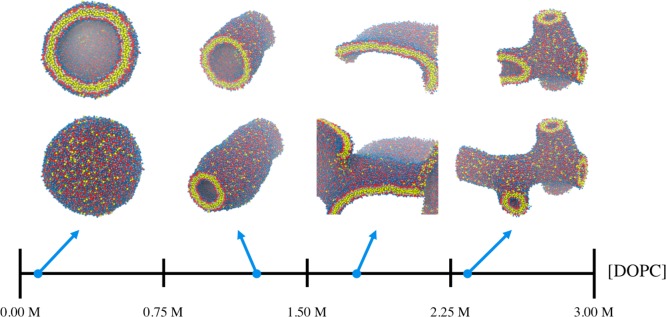
A related but equally important characteristic of lipids is their ability to self-assemble, especially into morphologically diverse structures. Interestingly, we find that both of our DOPC-6 models tend to assemble into various types of defective structures (see Figure S6) when starting from a random configuration. While the stability of preassembled bilayers for both DOPC-6 models suggests that bilayer configurations are represented, at minimum, as a metastable state, kinetic barriers may exist that prevent the accessibility of this state from other configurations, i.e., during self-assembly; for example, in the case of REM-6, the CG lipids aggregate into a disordered ball rather than a bilayer. However, we find that both DOPC-7V models robustly self-assemble into lipid bilayers (see Figure S6). We attribute the success of both 7V models to the presence of the semiexplicit solvent SL bead and, in particular, the effective repartitioning of repulsive and attractive forces. Given the necessity of SL to mediate lipid MG attraction, combined with the self-repulsion of both HG and SL beads and weak attraction at the tail beads, one can imagine that adjoining lipids are now free to sample many collective configurations until the combination of weak interactions is maximized when stacked in a bilayer-like state. Relatedly, we observe that the DOPC-7V lipids readily reorganize, flip flop, and undergo membrane fission during self-assembly simulations (see Movie S1). As an additional test, we investigate the self-assembly of MSCG-7V under different concentrations, in which 9000 lipids are randomly distributed in cubic domains of varying size and integrated over 2 × 10⁷ timesteps. As seen in Figure 6, the morphologies of the self-assembled CG lipids vary between vesicles, tubules, bilayers, and a network of tubules as the concentration increases. The observed morphological diversity is consistent with expected behavior from amphiphiles, such as lipids, which are capable of adopting a hierarchy of topological morphologies that depend upon concentration, as well as additional factors including choice of solvent or mixing with other constituents.⁶⁶ To our knowledge, while top-down implicit-solvent CG lipid models have exhibited the ability to robustly self-assemble through careful design,⁸⁻¹² it is an uncommon attribute for bottom-up implicit-solvent CG lipid models. One notable exception is the CG lipid model from Mirzoev and Lyubartsev,⁶⁷ which assembles into both bilayers and vesicles, yet only for potentials derived from a specific stoichiometric composition of lipids to solvent. However, it should be noted that the CG models reported in this work are only expected to approximate the PMF of lipids when aggregated in a bilayer state, as only these configurations are sampled in the training data. Hence, at present, it is unclear if configurational states beyond bilayers, such as during the observed structural transition from dispersed to self-assembled lipids, are accurately represented, and this issue of transferability in bottom-up CG models is an important subject for future studies.

Figure 6.

Molecular snapshots of self-assembled MSCG-7V for DOPC starting from random configurations at the listed concentrations with colors consistent with Figure 1(a). As concentration increases, the DOPC-7V model adopts morphologies that range between vesicles, tubules, bilayers, and tubule networks. The top row of panels depicts interiors of the same configurations shown in the bottom row of panels through the use of a clipping plane.

Extension to Coarse-Grained DPPC

To further test the importance of virtual solvent sites, we now consider DPPC. This lipid species is particularly interesting as it adopts a L_β (or gel-II) phase at room temperature, although the ripple phase (P_β), which is believed to be a pretransition phase between L_β and L_d phases, may also emerge if cooled starting from the L_d phase.⁴⁰ Our AA simulations appear to emulate this latter case; starting from initially disordered configurations, we observed the formation of the P_β phase in two independent AA simulations. It is possible that with either subcooling or exceptionally long simulation time scales, a slow relaxation to the L_β phase may occur. Nonetheless, as our focus is on systematic CG procedures and the utility of virtual solvent sites, we will consider the prediction of the P_β phase to be sufficient for our purposes as it is distinct from the L_d phase that DOPC adopts at room temperature.

Intriguingly, our early attempts to construct six-site DPPC models revealed significant deficiencies in the absence of a virtual solvent bead. For instance, our MSCG-6 model results in unstable lipid aggregates (i.e., a bilayer is not formed), while our REM-6 model results in stable yet flat bilayers with no evidence of the ripple phase (see Figure S7). In contrast, both MSCG-7V and REM-7V models yield stable bilayers that also spontaneously self-assemble, which we discuss further below.

A comparison between the DPPC-6 and DPPC-7V potentials, as shown in Figure 7, provides insightful hints to understand the notable discrepancy between model behavior. We find that the partitioning of attractive and repulsive potentials is qualitatively similar between the two model resolutions. However, the interfacial bead attraction (i.e., MG-MG) is considerably weaker in the DPPC-7V case, as observed similarly in the DOPC-7V case; the minima in the MG interaction, for example, is around −0.64 and −0.32 kcal/mol at r = 9 Å for the MSCG-6 and MSCG-7V models, respectively. Instead, the presence of virtual solvent beads (i.e., SL-MG) appears to mediate lipid attraction. The effective tail bead interactions (i.e., T1-T1 and T2-T2) are also slightly redistributed such that the T1 (T2) interaction is less (more) attractive in the DOPC-7V case; the minima in the T1 (T2) interaction is around −0.44 and −0.38 (−0.30 and −0.53) kcal/mol at r = 9.6 (12.7) Å for the MSCG-6 and MSCG-7V models, respectively. The observed changes to tail interactions are likely coupled to a similar redistribution of intermolecular forces, which is notably seen in the T1-MG-T1 angle shown in Figure 7(b). Hence, we find that the emergence of SL-mediated attractive interactions is essential for stable bilayer formation, which we further confirm upon observation of bilayer disassembly when the SL interactions are switched to a noninteracting state (see Figure S8).

Figure 7.

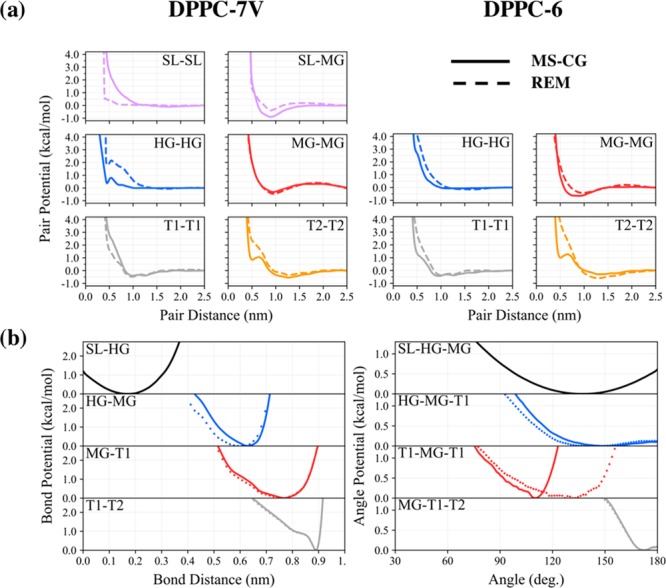
Coarse-grained DPPC interactions. (a) Comparison between seven-site (DPPC-7V) and six-site (DPPC-6) pair potentials for a representative subset of all nonbonded interactions. Models generated using multiscale coarse-graining (MS-CG) and relative entropy minimization (REM) are also denoted by solid and dashed lines, respectively, yielding a total of four different models. Similar to the DOPC-7V case, note the emergence of the SL-MG attraction, which appears to mediate MG-MG attraction for lipid aggregation. (b) Bond and angle potentials were computed using MS-CG in the DPPC-7V case (solid) and DPPC-6 case (diamond symbols). For simplicity, the DPPC-6 bonded potentials were used for the two REM models.

Unlike the DOPC-7V case, we observe several distinct qualitative differences between the effective tail interactions predicted by the MSCG-7V and REM-7V models. The MSCG-7V tail interaction profiles exhibit a greater degree of concavity changes (i.e., commensurate with local minima in the force profiles) compared to that of REM-7V, which is most distinctly seen in the T2-T2 interaction at r = 5.1 Å. Recall that the observed difference between the effective interactions predicted by these two methods suggests that our simple pairwise nonbonded basis is still insufficient for complete convergence. In fact, the T2-T2 interaction predicted by MSCG-7V bears resemblance to previous work on simple CG liquids, in which minimum expressed at short-range (i.e., at 0.5 nm in this case) has been prescribed as a two-body approximation to three-body correlations.⁴⁴ On the other hand, this minimum is absent from the REM-7V model, which instead attempts to capture up to two-body correlations given our current basis set. To investigate the consequences from our choice of a restricted interaction basis, we next turn toward structural characterization of the CG DPPC lipid bilayers.

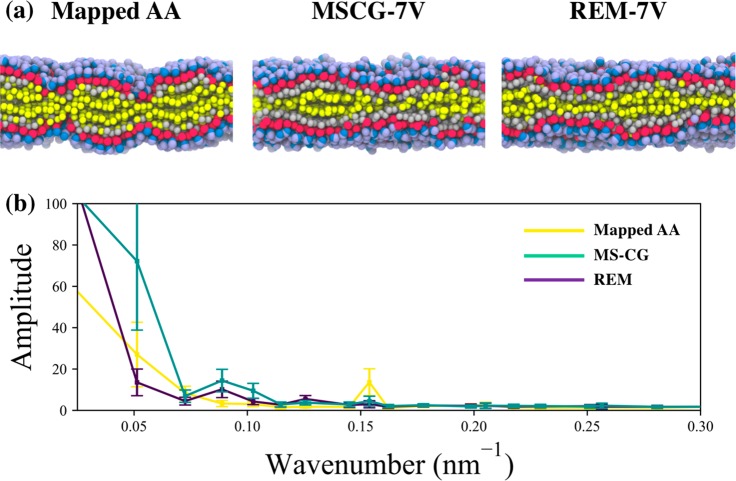
We depict the lateral and normal lipid number densities in Figure 8 and restrict ourselves to the five self-pair correlations. Here, the predicted behavior of the REM-7V and MSCG-7V models with respect to the reference AA trajectory appears to be quite similar to that of DOPC-7V (see Figure 5). In the lateral direction, both methods seem to recapitulate the structure of the hydrophilic region, although the MSCG-7V model results in slight overstructuring, which is evident from the narrowing of the density peak at a distance of 6.9 (6.0) Å for HG-HG (MG-MG) and increase in maximum density by 5%. In the normal direction, the MSCG-7V and REM-7V models both resemble the distribution from the reference AA trajectory yet consistently overpredict maximum densities by up to 15% and 30%, respectively. Both models also predict the mean positions to be within 1 Å of the mean from the reference AA distributions; as a result, the bilayer thickness obtained from both REM-7V and MSCG-7V models is in good agreement with that of the reference AA trajectory, as shown in Table 2. We also note that the normal density distributions are quite skewed compared to that of DOPC (see Figure 5). The skew in these distributions is reflective of the ripple phase that is adopted by DPPC at 300 K, in contrast to the liquid-disordered phase adopted by DOPC. These ripples are clearly seen in the snapshots depicted in Figure 9(a). As depicted in Figure 9(b), we characterize the ripples using the fast Fourier transform of the 2D bilayer height fluctuations (around the mean with respect to the MG bead) using a grid with a 15 Å bin size. We find that the reference AA trajectory exhibits a distinct mode around 0.15 nm^–1, which suggests that the characteristic ripple wavelength is around 6.5 nm. Both MSCG-7V and REM-7V models exhibit a distinct mode around 0.09 nm^–1 (or around 11 nm), which suggests that the ripples predicted by both CG models are broadened by comparison. However, it is interesting to note that the REM-6 model (see Figure S7) predicts the formation of a flat bilayer, as evident by the absence of distinct Fourier modes, and therefore suggests that the addition of the virtual SL bead enables partial structural heterogeneity that is commensurate with the ripple phase.

Figure 8.

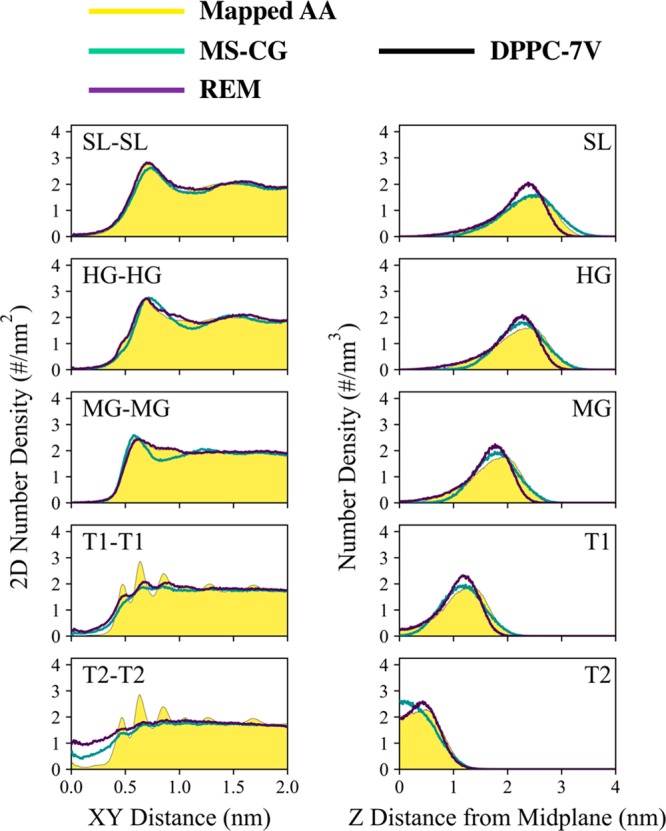
Comparison of structural correlations in coarse-grained DPPC lipid bilayers between mapped all-atom trajectories, multiscale coarse-graining models (MS-CG), and relative entropy minimization (REM) models; here, only DPPC-7V results are shown. The left and right panels are lateral (i.e., xy-direction) and perpendicular (i.e., z-direction) number density profiles between the listed sites. Each of the profiles was averaged over both leaflets and used a bin size of 0.01 nm.

Table 2. Comparison of Properties for DPPC from the Listed CG Models: Area Per Lipid (APL), Distance (or Bilayer Thickness) between HG (d_HG-HG), T1-T2 (S_TT) and HG-MG (S_HM) Order Parameters, and Bending Modulus (κ_bend) at 300 K^d.

property	REM-7V	MSCG-7V	AA	exp
APL (nm2)	0.49	0.46	0.51	0.48–0.52a
dHG-HG (nm)	4.3	4.4	4.4	4.3b
STT [SHM]	0.66 [0.75]	0.63 [0.76]	0.78 [0.48]
κbend (kBT)	180.6 ± 5.8	80.4 ± 10.8	210.1 ± 6.9, ∼240c

^aReference (77).

^bReference (40).

^cReference (78).

^dStandard errors within the range of listed significant digits are shown.

Figure 9.

(a) Lateral view snapshots of DPPC-7V from the mapped all-atom (AA) configuration, the MSCG-7V model, and the REM-7V model. Colors are consistent with Figure 1. (b) Comparison of amplitudes from the fast Fourier transform of the bilayer surface morphologies (taken with reference to the MG bead [red] height) generated by each model.

From Figure 8, it is also clear that recapitulation of the distinct T1/T2 structuring in the lateral direction, which is indicative of hexatic ordering seen in both gel and liquid-ordered phases,⁷ remains a challenge for both the MS-CG and REM methods. Given that both models predict a slight increase in density, and more so by the REM-7V case, in the three peak positions exhibited by the reference AA trajectory, we speculate that our use of a pairwise and spherically symmetric nonbonded basis is simply insufficient to describe the wide variety of tail packing environments seen in ripple phases, which include intralayer ordering, interdigitation, and disordered kinks.⁶⁸ The loss in lateral structure correlation may also explain the relative reduction of S_TT and κ_bend compared to reference AA simulations, as seen in Table 2. In fact, given the more faithful structural correlations exhibited by the REM-7V model compared to that of MSCG-7V, we similarly find that the REM-7V model more closely reproduces the APL, d_HG-HG, S_TT, and κ_bend from simulations and experiments,⁴⁰ although recall that the fidelity of the APL may instead be coincidental due to pressure representability.¹⁹

Our analysis of the behavior of both DOPC and DPPC CG models suggests that inclusion of a semiexplicit representation of the solvent-lipid interfacial microstructure imparts additional interactions (ascribed to both hydrophobic and hydrophilic forces) that may improve representation of both pairwise and higher-order structural correlations in comparison to implicit-solvent CG models. In addition, as none of the VCG models offer complete recapitulation of all of the properties analyzed above, we offer some suggestions for their potential uses. The REM-7V models may be the preferable CG model when distinctions between lipid microstructure is an essential factor, such as in the study of lipid phases. On the other hand, in the context of membrane remodeling in which physical properties, e.g., bending rigidity, are important, the MSCG-7V and REM-7V models may be preferable for liquid-disordered and liquid-ordered/gel-phase species, respectively. It is also important to note that these recommendations are presented on the basis of the currently reported strategy for VCG model generation, and it is unclear if fundamental limitations from the use of semiexplicit solvent sites prevent the derivation of CG models with broader utility. Efforts to both improve VCG model parametrization and to extend VCG models to other lipid species will be necessary to address this open question.

We anticipate several potential directions one may pursue to further improve our VCG models, especially in the context of highly structured lipid phases. One natural extension is to consider a more expressive (and more computationally costly) CG basis set. For example, Gay-Berne potentials have previously been used to capture anisotropy in lipid tail interactions.^69,70 Alternatively, a return to higher resolution models may mitigate the need for a higher-order interaction basis if pairwise nonbonded interactions are preferred due to computational cost. Finally, one intriguing direction is to adopt the ultra-coarse-graining (UCG) framework, in which internal states are associated with CG beads (to represent, for example, metastable configurations within the collective of coarse-grained atoms), in order to greatly enhance the expressiveness of low-resolution CG models.^32,71,72 For example, the ripple phase of DPPC is known to have several types of regions, which have been labeled the major arm, minor arm, and kink region.^53,73 Each of these regions adopts different characteristics of the liquid-disordered and gel phase, as the ripple phase is believed to be a metastable transition between these two states.⁷⁴ Conceivably, a UCG-type VCG model could be constructed that discriminates states based on each of these regions and allows for discrete state transitions and hence modulation of the effective CG interactions. Taken one step further, these types of UCG models may also enable systematic investigation of multicomponent lipids, which are known to have quite complex phase behavior.^75,76 In both scenarios, we predict that the use of virtual solvent sites will be essential to represent solvent-mediated effects, including both hydrophilic and hydrophobic interactions, and to potentially serve as a signal for changes in the local chemical environment.

Conclusions

In this work, we introduce a new framework to generate highly coarse-grained (CG) semiexplicit-solvent lipids through the use of CG virtual particles. The central idea is to capture hydrophobic and hydrophilic driving forces by representing the solvent microstructure at the lipid bilayer interface as explicit CG particles that remain bound to lipids. To parametrize these CG models, we utilize two systematic bottom-up methods known as multiscale coarse-graining (MS-CG) and relative entropy minimization (REM), which we implement within a hybrid procedure to generate our so-called virtual CG (VCG) models. We demonstrate the utility of VCG models for two lipid species, 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), which are liquid-ordered and gel phase, respectively, at room temperature. We show that the introduction of virtual solvent particles greatly enhances the expressivity of our CG models, which notably recapitulate a broad spectrum of lipid properties, including self-assembly, morphological diversity, and phases, that are difficult to preserve in other systematically derived CG models.

As this work is the first study of VCG models, we should briefly mention several aspects of the model generation procedure that have room for additional improvement. The detection of features that are represented by virtual sites, for example, may benefit from classification algorithms and, relatedly, dimensional reduction procedures. A more rigorous procedure to parametrize these VCG models would also be of interest, e.g., through additional development of the current hybrid methodology or alternative procedures to generate mappings and energetics. Nonetheless, our findings suggest that the augmentation of CG models through our VCG framework offers a powerful yet computationally inexpensive means to faithfully represent implicit-solvent lipids. Given the importance of solvent for the function of many biomacromolecules, we anticipate that the VCG approach will have broad applications, which warrant future investigation.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b01033.

• Additional information on CG mapping procedure and initialization of REM and MS-CG model optimization procedures, time series data describing water behavior at lipid-solvent interface, measured two-body structural correlations and fluctuation spectra generated by CG models, and molecular snapshots of lipid aggregation behavior (PDF)

• Movies of lipid aggregation behavior (MPG)

This research was funded in part by the National Institute of General Medical Sciences of the National Institute of Health under award number R01-GM063796 (to G.A.V.). A.J.P. gratefully acknowledges support from the Ruth L. Kirschstein National Research Service Award Postdoctoral Fellowship from the National Institute of General Medical Sciences of the National Institutes of Health under fellowship number F32-GM125218. J.J.M. is grateful for support from the Carlsberg Foundation in the form of a postdoctoral fellowship (CF15-0552, CF16-0639, and CF17-0783). Simulations were performed using resources provided by the University of Chicago Research Computing Center (RCC) and the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation (ACI-1053575).

The authors declare no competing financial interest.