Semiempirical Quantum-Chemical Methods with Orthogonalization and Dispersion Corrections

Abstract

We present two new semiempirical quantum-chemical methods with orthogonalization and dispersion corrections: ODM2 and ODM3 (ODMx). They employ the same electronic structure model as the OM2 and OM3 (OMx) methods, respectively. In addition, they include Grimme’s dispersion correction D3 with Becke–Johnson damping and three-body corrections E^ABC for Axilrod–Teller–Muto dispersion interactions as integral parts. Heats of formation are determined by adding explicitly computed zero-point vibrational energy and thermal corrections, in contrast to standard MNDO-type and OMx methods. We report ODMx parameters for hydrogen, carbon, nitrogen, oxygen, and fluorine that are optimized with regard to a wide range of carefully chosen state-of-the-art reference data. Extensive benchmarks show that the ODMx methods generally perform better than the available MNDO-type and OMx methods for ground-state and excited-state properties, while they describe noncovalent interactions with similar accuracy as OMx methods with a posteriori dispersion corrections.

1. Introduction

Semiempirical quantum chemistry (SQC) methods based on the neglect of diatomic differential overlap (NDDO) integral approximation^1,2 enable computationally efficient calculations of ground-state and excited-state electronic structure properties.^3,4 They are widely used when computational time becomes a major issue, i.e. in calculations of very large systems, e.g. of fullerenes,⁵⁻⁹ nanotubes,^5,8 long polyynes,¹⁰ proteins,^3,11−17 and others,^5,18,19 in real-time quantum chemistry studies,²⁰⁻²⁴ and in simulations requiring a very large number of electronic structure calculations. The latter applications include high-throughput screening in drug^5,25−33 and materials^34,35 design, high-throughput pK_a calculations,^36,37 ground-state molecular dynamics (MD) simulations,^38,39 excited-state nonadiabatic MD simulations,³ quantum mechanics/molecular mechanics (QM/MM) MD and Monte Carlo studies,^3,12−16,40 and mass spectra simulations.⁴¹⁻⁴⁴

There are two classes of modern NDDO-based SQC methods: 1) orthogonalization-corrected methods (OMx),⁴⁵⁻⁵⁰ which account for repulsive orthogonalization effects, attractive penetration effects, and repulsive core–valence interactions via explicit corrections; 2) MNDO-type methods without such corrections, which ignore the overlap matrix while solving the Roothaan–Hall equations and also ignore penetration integrals and core–valence interactions. The first class comprises the OM1,^45,46,50 OM2,^47,48,50 and OM3^49,50 methods; somewhat related is the NO-MNDO method, which solves the Roothaan–Hall equations taking overlap into account explicitly.⁵¹ Generally, the OMx methods are more accurate than the MNDO-type methods both for ground-state and excited-state properties, because they are based on a better physical model.⁵¹⁻⁵⁶ The MNDO-type methods include MNDO,^57,58 MNDO/d,⁵⁹⁻⁶¹ AM1,⁶² RM1,⁶³ AM1*,⁶⁴ PM3,^65,66 the PDDG-variants of MNDO and PM3,^67,68 PM6,⁶⁹ and PM7.⁷⁰ They are popular and useful for many applications, especially because parameters are available for many elements and because they are often reasonably accurate thanks to an elaborate parametrization and fine-tuning via empirical core–core repulsion functions.

A common problem of SQC methods is that they do not properly describe noncovalent complexes with significant dispersion interactions.⁷¹ This problem is often ameliorated by adding explicit empirical dispersion corrections.^18,72−80 OMx methods augmented with such explicit dispersion corrections describe various large noncovalent complexes with an accuracy comparable to density functional theory (DFT) methods with dispersion corrections^18,19 that are computationally much more expensive. Noncovalent interactions with hydrogen bonds are also often described poorly with SQC methods. This issue has been addressed by including special hydrogen bond corrections in MNDO-type methods.^{70,72−75,77} In contrast, the OMx methods treat hydrogen-bonding interactions even without such corrections reasonably well,^50,54,81,82 while inclusion of dispersion corrections generally further improves the accuracy.^50,54 One should note, however, that the addition of empirical attractive dispersion corrections to any semiempirical Hamiltonian parametrized without such corrections will inevitably deteriorate the accuracy of the computed heats of formation (which will become too small), while the computed relative energies may become more or less accurate.^52,54 Hence, it is more consistent to reparametrize the Hamiltonian with inclusion of dispersion corrections. This has so far been done only in PM7,⁷⁰ which however suffers from error accumulation in very large noncovalent complexes,^19,54 and in the proof-of-principle MNDO-F method,⁸³ which still has large errors in heats of formation.

Another problem of modern NDDO-based SQC methods is that all of them conventionally treat atomization energies calculated at the SCF level as atomization enthalpies at 298 K, i.e. heats of formation are obtained without explicitly computing zero-point vibrational energies (ZPVEs) and thermal enthalpic corrections from 0 to 298 K.^50,54,57,84 This convention was useful for parametrizing SQC methods against experimental heats of formation in early times, when accurate theoretical reference data were not yet available and when it was computationally unfeasible to calculate ZPVE and thermal corrections during parametrization. It is debatable whether this convention contributes much to the errors in SQC methods.^84,85 Benchmark studies show that it often has only a small effect on reaction energies,⁵⁴ but it may be problematic when comparing ZPVE-exclusive energies at 0 K with differences in semiempirical heats of formation for reactions with large changes in bonding.⁵⁴ Nowadays this convention is no longer justified, and it should be avoided in new methods.⁸⁴

As already mentioned, general-purpose SQC methods are often used for excited-state calculations, yet they are typically parametrized on ground-state properties only. On the other hand, there are special-purpose semiempirical methods such as INDO/S^86,87 and INDO/X⁸⁸ that were parametrized to reproduce electronic spectra. They can be applied for predicting such spectra but are less suitable for other purposes. It would clearly be desirable to develop general-purpose SQC methods that describe ground-state and excited-state properties in a balanced manner; this will require including both during parametrization.

In this work, we report two new orthogonalization- and dispersion-corrected SQC methods, ODM2 and ODM3 (ODMx). They are based on OM2 and OM3, respectively. They differ from the underlying OMx methods in the following aspects: (a) They include explicit dispersion corrections as an integral part. (b) They are parametrized against much larger sets of diverse, state-of-the-art reference properties, with special emphasis on a balanced treatment of both ground-state and excited-state properties as well as noncovalent interactions. (c) Atomization energies calculated from total energies are treated consistently as ZPVE-exclusive atomization energies at 0 K, while heats of formation are determined by adding ZPVE and thermal corrections obtained within the harmonic-oscillator and rigid-rotor approximations.

This Article is structured as follows. First, we discuss the theoretical formalism of the ODMx methods (Section 2). We then describe the parametrization procedure and present the optimized values of the ODM2 and ODM3 parameters (Section 3). Thereafter, we validate the new methods on a huge collection of benchmark sets and compare their performance to that of the underlying OMx and dispersion-corrected OMx methods (Section 4). Finally, we offer conclusions.

2. Methodology

The ODM2 and ODM3 methods employ the same electronic structure model as OM2^47,48,50 and OM3,^49,50 respectively. The OM2 and OM3 electronic structure models have been described in detail elsewhere⁵⁰ and will therefore not be explained again here. Instead we focus on the formal differences between the ODMx and OMx methods.

The ODMx methods incorporate Grimme’s dispersion correction D3^89,90 with the Becke–Johnson (BJ) damping function⁹¹⁻⁹³ as an integral part (unlike the OMx methods). They also include explicit three-body corrections E^ABC for the Axilrod–Teller–Muto dispersion interaction,⁸⁹ which are necessary for a better description of large dense systems.^54,94,95 We denote these D3(BJ)+E^ABC corrections as D3T in the following. The ODMx total energy (E_tot) is defined as the SCF total energy plus the post-SCF D3T dispersion energy. The same definition holds for OMx methods with a posteriori D3T corrections (the OMx-D3T methods), which have been shown to describe noncovalent interactions well.^50,54

Consistent with the definitions in ab initio methods, the ZPVE-exlusive atomization energy at 0 K (ΔE_at) can be written as the difference between the sum of the total ODMx energies of N_at constituent atoms and the ODMx total energy of a molecule (E_tot):

1

This definition is different from that used in earlier NDDO-based SQC methods (including the OMx methods) where ΔE_at is assumed to be the atomization enthalpy at 298 K (ΔH_at, 298 K) and is directly used in evaluating the heat of formation at 298 K without ever calculating ZPVE and thermal corrections explicitly.^50,54,57,84 By contrast, in the ODMx methods, heats of formation (ΔH_f, T) include ZPVE and thermal corrections from 0 K to a given temperature T computed explicitly within the harmonic-oscillator and rigid-rotor approximations (as in ab initio methods).

More specifically, ΔH_f, T is defined in the ODMx methods as

2

where ΔH_f, T(A) denotes the heats of formation of the constituent atoms at temperature T. At 298 K we use the same experimental heats of formation of atoms as in the OMx methods. The atomization enthalpy at temperature T (ΔH_at, T) is determined from the absolute enthalpies H_T of a molecule and its constituent atoms:

3

Absolute enthalpies are defined as

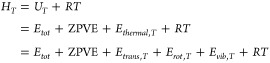4

where U_T is the internal energy, E_thermal,T denotes the thermal corrections from 0 K to T, E_trans,T, E_rot,T, and E_vib,T are translational, rotational, and vibrational contributions at T, and R is the gas constant. For atoms ZPVE, E_rot,T and E_vib,T vanish.

The chosen definition of the ODMx total energy has also implications on how ZVPE-exclusive proton affinities at 0 K (PAs) should be calculated at the ODMx level. The quantities PA^ODMx can be formally expressed as

5

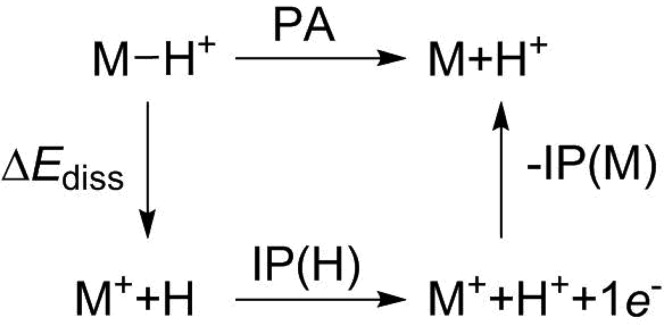
However, eq 5 does not take into account that the electron-accepting properties of the bare proton, which are quantified by the ionization potential of the hydrogen atom IP(H), are often severely underestimated by SQC methods. This is also true for the ODMx methods. The ionization potential of hydrogen at the ODMx level (IP^ODMx(H)) is equal to the negative of the U_ss parameter of hydrogen (−U_ss(H)). This parameter is optimized for molecular reference systems (Section 3.3) and turns out to be much lower than the experimental value of the ionization potential of the hydrogen atom IP^exp(H) of 313.5873 kcal/mol,⁹⁶ by 25–29 kcal/mol. The impact of this underestimation becomes evident when considering the thermochemical cycle in Figure 1, which offers an alternative way to calculate PA^ODMx:

6

Figure 1.

Thermochemical cycle for calculating proton affinities (PAs). IP(H) and IP(M) are the ionization potentials of the hydrogen atom and of molecule M, respectively, and ΔE_diss is the dissociation energy.

It is obvious from eq 6 that PA^ODMx will be strongly underestimated. In a semiempirical context, it is more reasonable to substitute IP^ODMx(H) with IP^exp(H) in this equation to obtain corrected PAs (PA^corr), which do not suffer from the inadequate use of the same hydrogen U_ss parameter in the hydrogen atom and in molecules:

7

The correction ΔPA^corr required to calculate PA^corr from PA^ODMx is thus given by

8

Hence, we use the following expression to calculate corrected ZPVE-exclusive proton affinities at 0 K at the ODMx level:

9

In the following we refer to these quantities simply as proton affinities. We note that this convention is consistent with that adopted in previous MNDO-type and OMx methods, which employ the experimental heat of formation of the proton when converting the computed heats of formation of the molecule and the protonated molecule to the corresponding proton affinity.

3. Parametrization

In this Section we specify the chosen training sets, describe the parametrization procedure, and provide the list of final ODM2 and ODM3 parameters for the elements carbon, hydrogen, nitrogen, oxygen, and fluorine (CHNOF).

3.1. Training Sets

The quality of SQC methods strongly depends on the training sets, which should satisfy two requirements:

• 1. Molecules and properties of interest should be covered in a balanced manner.

• 2. Reference data should be very accurate.

In the present general-purpose parametrization, we aim at covering the entire space of CHNOF-containing molecules with regard to ground-state and excited-state properties as well as noncovalent interactions. Concerning ground-state energies we want to describe both ZPVE-exclusive atomization energies at 0 K and heats of formation at 298 K as accurately as possible. To satisfy these requirements, we have chosen the following training sets with state-of-the-art reference data:

• Our own CHNO set of energies (heats of formation at 298 K, ionization potentials, vibrational energies, relative energies, and barriers), geometries (bond lengths, bond angles, and dihedral angles), and dipole moments.⁵⁰

• Our own FLUOR set of energies (heats of formation at 298 K, ionization potentials, and vibrational energies), geometries (bond lengths and bond angles), and dipole moments.⁵⁰

• The MGAE109 set with ZPVE-exclusive atomization energies at 0 K,^97,98 which is part of the CE345 database.^99,100

• The TAE140 set with ZPVE-exclusive atomization energies at 0 K, which is part of the W4-11 benchmark set.¹⁰¹

• Our own set of vertical excitation energies (called VEE set in the following)¹⁰² with updated theoretical best estimates from ref (55).

• The S66 set of interaction energies and geometries of 66 noncovalent complexes.^103,104

We found it beneficial to also include the ZPVE-exclusive atomization energy at 0 K of cubane calculated at the W2-F12 level.¹⁰⁵

3.2. Parametrization Procedure

Parametrization of SQC methods is a very complicated task in itself and is as much an art as a science. One of the challenges is the large number of parameters (usually more than a dozen per element), which makes it difficult to find the optimum set of parameters. The large parameter space provides enormous flexibility: in the words of John von Neumann, ‘with four parameters I can fit an elephant, and with five I can make him wiggle his trunk’. However, this flexibility should not be mistaken as a sign that the parametrization can achieve perfect accuracy for general-purpose SQC methods. The underlying physical model strongly limits what can be achieved for different sets of molecules and properties. While special-purpose SQC parametrizations can yield highly accurate results for certain classes of molecules and/or specific properties,¹⁰⁶ they will often fail outside their range of validity. Extending the metaphor, one may specifically ‘fit an elephant’, but such ‘an elephant model’ would be useless for describing the locomotion of both an elephant and a car. In our experience, there is plenty of subjective judgment involved in all stages of a general-purpose parametrization, up to evaluating and choosing among a number of reasonable candidate parameter sets. In the present work, we discarded well over 99.9% of the parameter sets considered. This underlines that a general-purpose parametrization is very demanding both in terms of human effort and computational costs.

As already mentioned above, we target a balanced treatment of a large number of diverse molecules and properties. There are two issues:

• 1. Errors in different properties with different units cannot be directly compared, e.g. the numerical errors of heats in formation at 298 K (in kcal/mol) cannot be directly compared to the errors in bond lengths (in Å).

• 2. Errors in different molecules and properties may be chemically of different importance, e.g. parameter sets giving a planar hydrogen peroxide geometry may be deemed unacceptable even if the total error for heats of formation is very low.

Usually, both these problems are addressed by weighting the errors (Err) for the properties and for specific molecules or types of molecules that enter the overall sum of squares (SSQ) of errors

10

where N_set is the number of training sets, N_prop is the number of properties in a training set, N_entry is the number of entries for a property in a training set, and w_sp^prop and w_si are weighting factors that are specific for a property and an entry in a training set, respectively. The error (Err) is defined as

11

where P_si^ODMx is the value calculated for a given property at the ODMx level with the current parameters, and P_si is the corresponding reference value.

In previous general-purpose parametrizations of MNDO-type and OMx methods, the SSQ value of weighted absolute errors was minimized during the optimization. In practice, this was found to be a slow, iterative, trial-and-error procedure, as described in detail elsewhere.^46,48,49,69 In our present work, we initially also applied this conventional approach, which however turned out to be too tedious for our broad diversity of training sets (much broader than in the OMx case). Thus, we designed an alternative parametrization procedure specifically tuned for ODMx methods to reach the following objectives:

• 1. Aim for an accuracy that is better than or close to the accuracy of the corresponding OMx methods after redefining the SQC total energy.

• 2. Aim for an accuracy that is better than or close to the accuracy of the corresponding OMx methods for ground-state properties.

• 3. Aim for an accuracy that is better than or close to the accuracy of the corresponding OMx-D3T methods for noncovalent interactions.

• 4. Improve the accuracy of the ODMx methods in comparison with the corresponding OMx methods for excited-state properties.

In short, our goal is to obtain unified methods, which preserve good and eliminate bad qualities of the OMx and OMx-D3T methods for ground-state properties and noncovalent interactions, while improving the description of the excited-state properties and using the proper definition of SQC total energies.

This clear breakdown of objectives allows for a systematic step-by-step parametrization of the ODMx methods. The key to simplifying the complicated optimization problem is to choose the proper error measure to be minimized. Since we deal with many diverse properties, we have chosen to focus on the ODMx errors relative to the corresponding errors of a reference SQC method (usually the corresponding OMx or OMx-D3T method)

12

where P_si^ref SQC is the value of the property calculated with the reference SQC method.

This approach obviously meets objectives 1–3 in a straightforward manner. Moreover, it also resolves the two issues discussed above: relative errors are unitless and normalized for each individual property by definition, and the parametrization with regard to relative errors will tend to retain the performance of the underlying OMx or OMx-D3T methods for chemically important molecules and properties. To allow for larger flexibility and specific tuning, we still keep the option to adjust the weights for individual properties and molecules, if necessary. These conventions make parameter optimization much easier, because parameter changes that lead to very large errors of ODMx relative to OMx or OMx-D3T are easily identified and avoided by the optimizer. We note that in the final stage of the parametrization, we also ran conventional parameter optimizations minimizing the SSQ value of the absolute errors (starting from the best candidate parameter sets), which however did not lead to further improvement.

Equation 12 requires that the denominator is not close to zero, which was therefore set to a small value (typically 0.1) whenever the reference SQC errors were very small. During the parametrization runs, the SQC calculations sometimes failed due to convergence problems, which is usually an indication of entering an unphysical region of parameter space. In such cases, the SSQ value was set to an arbitrarily huge number, and the parametrization was continued with a modified set of parameter estimates. This procedure was repeated until there were no remaining convergence problems (or otherwise the parametrization was terminated). Such a fail-safe approach is necessary for a numerically stable parametrization algorithm.

A good initial guess for the parameters is very important. In our case, the corresponding standard OMx-D3T parameters are expected to provide an excellent guess. For ODM2 we optimized three element-independent parameters and 17 parameters per element (8 for hydrogen). ODM3 has two less parameters per element. We decided to retain the one-center two-electron integrals derived from experimental atomic spectra, which are used in all OMx methods⁵⁰ and in MNDO.⁵⁷ We also decided to keep the standard OMx parameters for the effective core potentials.⁵⁰ During parametrization we paid special attention to large changes in the parameters to make sure that they do not assume unphysical values. For this purpose we normally imposed strict limits on the allowed range of parameter values.

For parameter optimization we employed our own in-house parametrization program, which calls the development version of the MNDO program¹⁰⁷ for the ODMx calculations.

The detailed step-by-step protocol that was adopted for optimizing the ODMx parameters is documented in the Supporting Information. The final parameter values are presented in the next subsection.

3.3. Parameter Values

The values of the final ODM2 and ODM3 parameters are listed in Tables 1 and 2, respectively. The largest changes relative to the corresponding standard OMx-D3T parameters are found in the orthogonalization correction parameters F₁, F₂, G₁, and G₂. The smallest changes (all below 10%) occur for the U_ss, U_pp, and ζ parameters. The dispersion correction parameters are also changed only slightly in ODM2 relative to OM2-D3T, but there are larger shifts in ODM3 relative to OM3-D3T. However, detailed numerical tests show that the actual values of the dispersion corrections are similar for noncovalent complexes at the ODM3 and OM3-D3T levels. Moderate changes are observed in the resonance integral parameters. In the Supporting Information (SI) we present plots of resonance integrals of various types and for all combinations of diatomics as a function of the internuclear distance (Figures S1–S55 for ODM2 vs OM2 and Figures S56–S110 for ODM3 vs OM3). Inspection of these plots reveals that most of the ODMx resonance integrals are very similar to their OMx counterparts.

Table 1. ODM2 Parameters^a.

	H	C	N	O	F
Orbital Exponent: Scale Factor
ζ	1.38028450	1.38113662	1.29958384	1.49880729	1.48240692
(au)	(−6.3%)	(−2.8%)	(−2.4%)	(−3.4%)	(2.1%)
One-Center One-Electron Energies
Uss	–12.48937475	–51.23186063	–73.38299795	–102.59234481	–117.89864612
(eV)	(−1.3%)	(−0.8%)	(−1.3%)	(0.8%)	(−2.3%)
Upp		–39.34045880	–57.70164912	–78.80113288	–107.04309769
(eV)		(−1.0%)	(0.2%)	(−0.2%)	(−0.2%)
Resonance Integrals
βs	–3.40625426	–7.50866135	–13.71974340	–10.44716267	–3.58269305
(eV bohr–1/2)	(−0.4%)	(4.1%)	(26.5%)	(−1.9%)	(−42.7%)
βp		–4.13979929	–8.25662188	–9.52283396	–13.71612319
(eV bohr–1/2)		(−0.1%)	(8.3%)	(10.3%)	(−1.6%)
βπ		–6.21901456	–10.06577228	–10.00369376	–15.32274646
(eV bohr–1/2)		(4.2%)	(8.5%)	(8.6%)	(−18.2%)
αs	0.06556888	0.09431728	0.12110139	0.13492482	0.25992551
(au)	(−0.8%)	(4.3%)	(34.9%)	(3.3%)	(−2.4%)
αp		0.05372380	0.08742445	0.09874026	0.12102605
(au)		(−1.5%)	(−0.2%)	(2.6%)	(−1.3%)
απ		0.10370542	0.13827427	0.13861427	0.20389243
(au)		(1.6%)	(5.0%)	(6.0%)	(−6.0%)
βs(X–H)		–6.58983035	–9.28605650	–6.12279073	–7.73941491
(eV bohr–1/2)		(4.6%)	(−2.2%)	(−6.4%)	(23.8%)
βp(X–H)		–4.53309066	–9.59598789	–9.78113133	–11.60040200
(eV bohr–1/2)		(12.1%)	(12.7%)	(−3.3%)	(−16.8%)
αs(X–H)		0.10047864	0.11512537	0.13949313	0.74053556
(au)		(3.9%)	(0.7%)	(25.5%)	(65.6%)
αp(X–H)		0.05754390	0.11625375	0.10684454	0.13290605
(au)		(8.9%)	(8.9%)	(−10.2%)	(−15.1%)
Orthogonalization Factors
F1	0.25711330	0.48173972	0.67114023	1.19835125	2.32598335
	(−13.0%)	(−3.6%)	(4.7%)	(−5.2%)	(10.0%)
F2	1.29097121	0.88486717	0.29297257	0.98518300	1.29045770
	(−7.9%)	(22.5%)	(49.6%)	(−14.2%)	(18.2%)
G1	0.64932010	0.18362749	0.12275808	0.53895482	0.66523038
	(−0.5%)	(−13.7%)	(−12.0%)	(90.4%)	(109.8%)
G2	0.46314833	0.99145627	0.76190787	1.80028762	0.02575130
	(−49.0%)	(−0.1%)	(−9.7%)	(129.6%)	(20.3%)
Element-Independent Dispersion-Correction Parameters
s8	0.56467295 (6.3%)
a1	0.66492067 (−3.6%)
a2	3.34510640 (−2.9%)

^aListed are only those parameters whose values differ from the standard OM2-D3T parameters. Relative deviations of the ODM2 from the OM2-D3T parameters are given in parentheses. See ref (50) for the description and the values of OM2-D3T parameters kept in ODM2 without change.

Table 2. ODM3 Parameters^a.

	H	C	N	O	F
Orbital Exponent: Scale Factor
ζ	1.19376951	1.24063783	1.31794708	1.20420353	1.11606475
(au)	(−5.2%)	(−2.9%)	(0.6%)	(−0.3%)	(−7.4%)
One-Center One-Electron Energies
Uss	–12.34522989	–50.53809829	–76.86911508	–105.32281913	–119.94597476
(eV)	(−0.9%)	(0.0%)	(1.2%)	(−0.4%)	(−0.6%)
Upp		–39.18893465	–57.30532511	–78.61741113	–107.72538552
(eV)		(−1.0%)	(−0.1%)	(−0.4%)	(0.2%)
Resonance Integrals
βs	–3.55853909	–7.22299220	–11.27163531	–13.99112485	–6.21626110
(eV bohr–1/2)	(4.6%)	(1.0%)	(−16.0%)	(−3.0%)	(0.3%)
βp		–3.89503707	–5.19814028	–9.57907838	–14.17975990
(eV bohr–1/2)		(−2.9%)	(−8.7%)	(9.2%)	(2.6%)
βπ		–5.98389263	–9.42644204	–13.14461173	–17.97416645
(eV bohr–1/2)		(6.1%)	(14.2%)	(1.5%)	(−5.2%)
αs	0.06732426	0.08775193	0.08380547	0.12829059	0.36826212
(au)	(−2.9%)	(−4.6%)	(−11.4%)	(−1.0%)	(18.3%)
αp		0.05302831	0.06387304	0.09616309	0.12592688
(au)		(0.5%)	(−8.0%)	(3.7%)	(1.2%)
απ		0.10244561	0.12706496	0.16588421	0.21676922
(au)		(3.9%)	(20.9%)	(3.1%)	(0.4%)
βs(X–H)		–6.67027186	–9.43111309	–13.89205019	–10.28397098
(eV bohr–1/2)		(7.6%)	(−17.3%)	(2.4%)	(27.5%)
βp(X–H)		–4.66942670	–7.96127622	–10.28574783	–14.01190662
(eV bohr–1/2)		(10.3%)	(1.1%)	(9.2%)	(0.6%)
αs(X–H)		0.10456205	0.09898195	0.15947641	0.40117629
(au)		(4.3%)	(−12.8%)	(9.9%)	(23.0%)
αp(X–H)		0.06145722	0.09655514	0.11563129	0.15563457
(au)		(11.9%)	(4.4%)	(5.3%)	(0.4%)
Orthogonalization Factors
F1	0.24779546	0.37629902	0.49200495	0.56899924	0.95888963
	(−2.4%)	(−8.6%)	(−15.5%)	(3.0%)	(−7.4%)
G1	0.36151043	0.08125059	0.19511376	0.19048647	0.15019006
	(1.5%)	(−21.9%)	(229.1%)	(205.9%)	(7.0%)
Element-Independent Dispersion-Correction Parameters
s8	0.78131768 (56.0%)
a1	0.69959980 (14.1%)
a2	3.05404380 (−6.3%)

^aListed are only those parameters whose values differ from the standard OM3-D3T parameters. Relative deviations of the ODM3 from the OM3-D3T parameters are given in parentheses. See ref (50) for the description and the values of OM3-D3T parameters kept in ODM3 without change.

4. Validation

In this Section, we compare the ODMx results with the corresponding OMx and OMx-D3T results for our big collection of benchmark sets covering ground-state properties (Subsection 4.1) and noncovalent interactions (Subsection 4.2).^50,54 We also evaluate the results for the most important excited-state benchmark sets from our previous work⁵⁵ (Subsection 4.3). We refer the reader to the cited literature for the description of these sets. Compared with our previous work^50,54 we made only a few minor modifications to the CHNO, OVS7-CHNOF, and PDDG sets to correct some erroneous or outdated reference data (see the SI) or to use more appropriate symmetry definitions of molecules. In the following, we report only a statistical analysis of the performance of the methods considered; the underlying individual numerical results for energies are documented in the SI.

All calculations were done using our developmental version of the MNDO program.¹⁰⁷ We applied the same computational settings as in our previous studies.^50,54,55 Generally we used very tight convergence criteria. In the ground-state calculations, we applied the half-electron (HE) approach for open-shell molecules,¹⁰⁸ because the OMx^46,48,49 and ODMx methods were parametrized using this approach and because it is known that the HE-SQC treatment gives results that are generally superior to those from unrestricted Hartree–Fock SQC calculations.¹⁰⁹ We had to loosen the convergence criteria only in very few difficult cases of ground-state calculations. Excited-state properties were computed using multireference configuration interaction (MRCI) calculations with SQC Hamiltonians including single (S), double (D), and optionally also triple (T) and quadruple (Q) substitutions: specifically, CISDTQ for vertical excitation energies and MRCISD for excited-state geometry optimizations; in some cases, we had to use MRCISDT or MRCISDTQ instead of MRCISD (or different starting geometries) to achieve convergence of the geometry optimizations. The quoted OMx and OMx-D3T results for ground-state properties were taken from our previous benchmarks,^50,54 except those for the updated sets (see above), which were recalculated. We used the same conventions as previously^50,54,55 for relative energies calculated at the OMx and OMx-D3T levels, i.e. they are based on heats of formation at room temperature (rather than ZPVE-exclusive energies at 0 K) unless mentioned otherwise. The quoted OMx/MRCI results for excited-state properties were taken from our previous benchmarks of electronically excited states.⁵⁵

4.1. Ground-State Properties

Ground-state properties in the CHNO and FLUOR sets^{45−50,110,111} were used for training both the ODMx and OMx methods. It is evident from Tables 3 and 4 that the ODMx methods are somewhat better than the OMx methods for heats of formation at 298 K. The inclusion of a posteriori D3T-corrections in the OMx methods significantly increases the mean absolute errors (MAEs) in the heats of formation at 298 K, which become systematically too small because the dispersion corrections are intrinsically negative. This highlights the importance of a consistent parametrization of SQC methods with dispersion corrections as integral part. Other properties including geometries, ionization potentials, dipole moments, relative enthalpies, and activation enthalpies are described similarly well by all SQC methods considered here. We note that ODM2 and ODM3 reproduce the bond lengths and bond angles in the CHNO set statistically somewhat better than their OMx and OMx-D3T counterparts.

Table 3. Mean Absolute Errors in Heats of Formation, Enthalpy Changes, and Activation Enthalpies at 298 K (kcal/mol), Bond Lengths (Å), Bond Angles (deg), Ionization Potentials (eV), and Dipole Moments (D) Calculated with the OMx, OMx-D3T, and ODMx Methods for the CHNO Set and Its Subsets.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
Heats of Formation
overall	138	3.05	5.10	2.64	3.00	6.95	2.74
CH	57	1.72	4.98	1.60	1.63	7.72	1.46
CHN	32	3.92	4.88	2.88	3.80	6.77	3.36
CHO	37	4.40	6.24	4.01	4.05	6.87	3.83
CHNO	4	1.96	2.13	2.38	3.24	3.45	3.39
HNO	8	3.28	3.12	2.86	4.53	4.43	4.01
Bond Lengths
overall	242	0.016	0.016	0.015	0.019	0.019	0.015
CH	113	0.010	0.010	0.009	0.009	0.009	0.009
CHN	49	0.015	0.015	0.014	0.027	0.027	0.015
CHO	57	0.018	0.018	0.018	0.022	0.022	0.021
CHNO	5	0.018	0.018	0.023	0.033	0.033	0.019
HNO	18	0.049	0.049	0.044	0.043	0.043	0.033
Bond Angles
overall	101	2.24	2.24	2.04	1.85	1.86	1.70
CH	38	1.46	1.48	1.48	1.23	1.25	1.27
CHN	22	2.30	2.28	2.11	1.82	1.80	1.64
CHO	31	2.45	2.44	2.11	2.03	2.04	1.96
HNO	10	4.42	4.42	3.85	3.76	3.75	2.69
Ionization Potentials
overall	52	0.26	0.26	0.23	0.44	0.44	0.41
CH	22	0.24	0.24	0.19	0.37	0.37	0.30
CHN	13	0.22	0.22	0.22	0.39	0.39	0.39
CHO	14	0.34	0.34	0.29	0.61	0.61	0.61
HNO	3	0.23	0.23	0.22	0.45	0.45	0.36
Dipole Moments
overall	63	0.25	0.25	0.26	0.26	0.26	0.23
CH	20	0.11	0.11	0.10	0.10	0.10	0.09
CHN	16	0.27	0.27	0.27	0.33	0.33	0.32
CHO	19	0.31	0.31	0.38	0.26	0.26	0.24
HNO	6	0.49	0.49	0.41	0.58	0.58	0.44
Enthalpy Changes at 298 K
overall	17	1.96	1.94	2.05	2.83	2.65	3.34
CH	9	0.52	0.48	0.41	1.08	0.76	0.85
CHN	3	4.09	4.07	3.57	5.65	5.63	8.11
CHO	3	3.63	3.67	4.67	3.91	3.98	4.20
Activation Enthalpies at 298 K
overall	60	1.55	1.55	1.77	1.53	1.48	2.01
CH	20	1.63	1.62	1.88	1.96	1.94	2.33
CHN	10	1.92	1.88	2.06	1.51	1.21	2.63
CHO	25	1.35	1.36	1.49	1.31	3.2	1.52
CHNO	3	1.43	1.44	2.40	0.68	0.68	2.19

Table 4. Mean Absolute Errors in Heats of Formation at 298 K (kcal/mol), Bond Lengths (Å), Bond Angles (deg), Ionization Potentials (eV), and Dipole Moments (D) Calculated with the OMx, OMx-D3T, and ODMx Methods for the FLUOR Set and Its Subsets.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
Heats of Formation
overall	48	3.41	4.12	3.35	3.70	5.15	3.49
CHF	39	3.72	4.61	3.42	3.88	5.71	3.42
HNOF	9	2.08	1.99	3.07	2.93	2.75	3.80
Bond Lengths
overall	125	0.023	0.023	0.021	0.024	0.024	0.022
CHF	104	0.019	0.019	0.018	0.021	0.021	0.019
CHNOF	3	0.020	0.020	0.017	0.014	0.014	0.010
HNOF	17	0.043	0.043	0.040	0.044	0.044	0.040
Bond Angles
overall	69	2.23	2.22	2.15	1.78	1.78	1.87
CHF	56	2.06	2.06	2.04	1.61	1.61	1.71
CHNOF	3	2.44	2.45	89	1.75	1.75	1.86
HNOF	9	2.91	2.91	2.64	2.68	2.67	2.66
Ionization Potentials
overall	39	0.26	0.26	0.25	0.32	0.32	0.36
CHF	29	0.25	0.25	0.26	0.29	0.29	0.33
HNOF	9	0.29	0.29	0.21	0.42	0.42	0.48
Dipole Moments
overall	39	0.31	0.31	0.31	0.25	0.25	0.23
CHF	30	0.33	0.33	0.33	0.24	0.25	0.24
HNOF	8	0.26	0.26	0.26	0.29	0.29	0.21

Turning to the independent OVS7-CHNOF validation set⁵⁴ (Table 5) that was not used for parametrization, the ODMx methods outperform their OMx counterparts for heats of formation of large molecules in the BIGMOL20 subset,^46,112 of anions in ANIONS24,⁴⁶ of various conformers in CONFORMERS30,⁴⁸ and of F-containing molecules in FLUORINE91.¹¹³ They are however inferior for heats of formation of radicals in RADICALS71¹⁰⁹ and of cations in CATIONS41.⁴⁶ The ODMx and OMx methods perform similarly well for heats of formation of isomeric molecules in ISOMERS44.⁴⁸ The OMx-D3T methods again systematically underestimate the heats of formation (because of the uniformly attractive dispersion interactions included a posteriori) and thus suffer from larger errors in the heats of formation. For most other properties considered in the OVS7-CHNOF validation set, the ODMx methods and their OMx counterparts show similar errors; the ODM3 method performs better than OM3 and OM3-D3T for the ionization potentials in RADICALS71.¹⁰⁹

Table 5. Mean Absolute Errors in Heats of Formation and Enthalpy Changes at 298 K (kcal/mol), Bond Lengths (Å), Bond Angles (deg), and Ionization Potentials (eV) Calculated with the OMx, OMx-D3T, and ODMx Methods for the OVS7-CHNOF Set and Its Subsets.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
Heats of Formation
RADICALS71	42	5.07	5.81	6.21	5.75	7.23	6.56
ANIONS24	24	8.37	9.11	8.12	9.56	11.63	8.08
CATIONS41	33	7.20	8.17	8.83	7.21	7.62	8.08
BIGMOL20	20	4.41	10.84	4.03	4.26	15.01	3.51
CONFORMERS30	11	2.95	6.56	2.21	3.05	9.81	1.61
ISOMERS44	27	1.05	4.75	1.16	1.81	7.80	1.77
FLUORINE91	91	7.15	7.59	6.65	7.34	7.49	6.03
Bond Lengths
FLUORINE91	455	0.016	0.016	0.015	0.022	0.022	0.019
Bond Angles
FLUORINE91	355	2.04	2.03	2.02	1.78	1.78	1.92
Ionization Potentials
RADICALS71	25	0.42	0.42	0.44	0.59	0.60	0.47
Enthalpy Changes at 298 K
RADICALS71	4	3.66	3.66	1.76	3.27	3.27	2.15
CATIONS41	5	6.36	6.37	6.11	6.19	6.20	6.56
CONFORMERS30	17	1.00	1.07	1.36	1.10	1.20	1.34
ISOMERS44	17	0.80	0.69	0.70	2.07	1.65	1.99

The MAEs in the heats of formation for the independent G2G3-CHNOF set^{49,54,114−116} and in the enthalpy changes for its ALKANES28 subset^49,116 (Table 6) are in the same range for all methods considered; in the ALKANES28 subset, ODM2 outperforms OM2 in heats of formation, while ODM3 has the lowest MAE. It is also encouraging that the MAEs in the heats of formation at 298 K for the independent PDDG, PM7-CHNOF, and C7H10O2 sets are generally lower at the ODMx levels than at the corresponding OMx levels (Tables S1–S3). Other properties in the PDDG and PM7-CHNOF sets (geometries, ionization potentials, and dipole moments) are described similarly well by all methods.

Table 6. Mean Absolute Errors in Heats of Formation and Enthalpy Changes at 298 K (kcal/mol) Calculated with the OMx, OMx-D3T, and ODMx Methods for the G2G3-CHNOF Set and Its Subsets.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
Heats of Formation
G2	93	3.37	4.01	3.52	3.83	5.04	3.93
G3	52	3.18	6.30	3.11	3.71	9.24	3.06
ALKANES28	22	1.91	9.24	1.15	0.72	15.76	0.63
Enthalpy Changes at 298 K
ALKANES28	6	0.61	0.21	0.34	1.48	0.90	1.06

The benefits of redefining the SQC total energy in the ODMx methods are clearly seen in the evaluation of the W4-11-CHNOF set¹⁰¹ (Table 7). The reference ZPVE-exclusive atomization energies at 0 K and the relative energies derived therefrom are well reproduced by the ODMx methods (without any corrections), while the TAE140, TAE_nonMR124, and BDE99 subsets can be properly described by the OMx and OMx-D3T methods only after removing the ZPVE and thermal contributions from their heats of formation at 298 K.

Table 7. Mean Absolute Errors in ZPVE-Exclusive Atomization Energies at 0 K (kcal/mol) Calculated with the OMx, OMx-D3T, and ODMx Methods for the W4-11-CHNOF Set and Its Subsets.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
TAE140	88	14.93	14.27	4.89	15.21	14.22	6.22
		4.81a	4.64a		6.47a	6.19a
TAE_nonMR124	80	15.63	14.94	4.79	15.25	14.22	5.63
		4.84a	4.66a		6.05a	5.79a
BDE99	79	8.15	7.95	6.46	9.65	9.29	7.31
		6.25a	6.18a		7.51a	7.31a
HAT707	394	8.92	8.91	8.49	9.44	9.40	8.47
		9.17a	9.16a		9.73a	9.68a
ISOMER20	19	8.54	8.56	8.00	8.32	8.35	9.03
		8.34a	8.35a		8.13a	8.17a
SN13	13	5.55	5.35	5.20	4.31	4.15	4.94
		5.36a	5.24a		4.98a	5.13a

^aThe OMx and OMx-D3T energies are corrected by excluding ZPVE and thermal contributions.

The evaluation of the diverse reference data in the large GMTKN30-CHNOF set¹¹⁷ leads to the impression that overall the ODMx methods perform somewhat better than the OMx and OMx-D3T methods (Table 8). Again, in the MB08-165,¹¹⁸ W4-08,¹¹⁹ W4-08woMR,¹¹⁹ and BSR36¹²⁰ subsets, the MAEs can be reduced substantially for OMx and OMx-D3T by removing the ZPVE and thermal contributions, while the ODMx methods have reasonably small MAEs without any need for additional corrections. Encouragingly, the ODMx methods perform better than the other methods for the WATER27¹²¹ subset (with updated reference values for four large complexes from ref (122)). They also outperform their OMx and OMx-D3T counterparts for the RSE43,¹²³ O3ADD6,¹²⁴ and PCONF¹²⁵ subsets but have higher MAEs for the G21IP,¹²⁶ G21EA,¹²⁶ BH76,^127,128 and ACONF¹²⁹ subsets. ODM2 performs better than OM2 and OM2-D3T for the G2RC,¹¹⁴ ISO34,¹³⁰ and SCONF^131,132 subsets, worse for the PA,^133,134 SIE11,¹³² and DARC¹³⁵ subsets, and similarly to OM2 and/or OM2-D3T for the BHPERI,^{119,136−139} BH76RC,^127,128 ISOL22,¹⁴⁰ IDISP,^130,141,142 S22,^143,144 and ADIM6^120,145 subsets. ODM3 performs worse than OM3 and OM3-D3T for the BH76RC and G2RC subsets and similarly to OM3 and/or OM3-D3T for the PA, SIE11, BHPERI, ISO34, ISOL22, DARC, IDISP, S22, ADIM6, and SCONF subsets. All SQC methods considered here fail to reproduce the isomerization energy of C₂₀ in the DC9 subset.^{132,138,146−151}

Table 8. Mean Absolute Errors (kcal/mol) in Properties Calculated with the OMx, OMx-D3T, and ODMx Methods for the GMTKN30-CHNOF Set and Its Subsets.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
overall	480	7.94	7.76	7.33	7.17	7.24	6.88
overall*a	454	6.95	6.77	6.64	6.30	6.35	6.32
MB08-165	25	22.47	22.36	16.10	19.46	20.11	13.55
		12.20b	11.51b		15.03b	15.72b
W4-08	50	4.19b	4.41b	4.60	6.20b	6.26b	6.05
W4-08woMRc	43	4.12b	4.41b	4.34	5.37b	5.51b	5.00
G21IP	15	12.00	12.00	13.74	11.45	11.45	13.61
G21EA	12	11.39	11.39	13.95	9.31	9.31	12.65
PA	8	14.82	14.88	16.62	11.99	11.69	11.56
SIE11	5	7.78	8.07	8.42	4.31	4.70	4.26
BHPERI	22	8.21	6.69	6.49	8.25	6.78	6.80
BH76	54	9.72	9.71	11.08	10.66	10.93	11.24
BH76RC	22	4.29	4.22	4.24	5.37	5.48	6.82
RSE43	34	4.31	4.24	3.64	5.24	5.12	3.94
O3ADD6d	6	12.24	12.61	10.54	10.97	11.38	7.12
G2RC	15	8.23	7.75	5.58	4.16	3.62	4.63
ISO34	34	4.44	4.55	3.88	4.37	4.48	4.35
ISOL22	18	5.31	4.95	5.17	6.05	6.17	6.01
DC9	7	25.02	24.93	26.90	24.69	23.30	23.42
DC9woC20e	6	13.59	13.94	14.43	13.20	12.36	12.06
C20f	1	93.63	90.89	101.74	93.61	88.94	91.61
DARC	14	7.24	9.38	10.08	4.91	9.03	8.36
BSR36	36	10.77	13.99	11.90	3.46	7.05	5.39
	36	7.08b	10.28b		1.90b	3.40b
IDISP	6	7.34	9.86	7.42	6.19	8.00	6.12
WATER27	27	12.28	7.13	5.24	9.19	6.81	7.25
WATER27 (upd)g		11.49	6.34	4.45	8.40	7.38	6.46
S22	22	3.05	0.94	0.84	3.54	0.95	0.93
ADIM6	6	3.13	0.09	0.15	4.09	0.39	0.62
PCONF	10	1.28	1.02	0.73	1.33	1.39	1.12
ACONF	15	0.64	0.22	0.80	0.86	0.31	1.05
SCONF	17	1.67	1.62	1.35	1.32	1.34	1.36

^aWithout MB08–165 and C20.

^bThe OMx and OMx-D3T energies are corrected by excluding ZPVE and thermal contributions.

^cSubset W4–08 without multireference cases.

^dThe adduct O₃+C₂H₂ is treated as an open-shell singlet in all cases.

^eSubset DC9 without C₂₀ bowl/cage isomerization energy.

^fC₂₀ bowl/cage isomerization energy.

^gWATER27 subset with four reference dissociation energies of (H₂O)₂₀ clusters taken from ref (122).

Similar observations are made in the evaluation of the CE345-CHNOF set^99,100 (Table 9). The ODMx methods outperform the corresponding OMx and OMx-D3T methods for the ZPVE-exclusive atomization energies at 0 K for the MGAE109/11^97,98 subset, which has been used in the ODMx parametrization. The ODMx methods are better than their OMx and OMx-D3T counterparts for the IsoL6¹⁵² and HC7/11¹⁵³ subsets but worse for the IP21,^97,154−158 EA13/03,^97,154−156 NHTBH38/08,^{97,128,159,160} and ABDE12^{97,153,161,162} subsets; in the latter case, the OMx and OMx-D3T energies were corrected by removing the ZPVE and thermal corrections. ODM2 is better than OM2 and OM2-D3T for the PA8/06¹³⁴ and NCCE31/05^155,163 subsets but worse for the πTC13^134,154,161 and HTBH38/08^{97,128,159,160} subsets. ODM3 is better than OM3 and OM3-D3T for the πTC13 and HTBH38/08 subsets but worse for the PA8/06 and NCCE31/05 subsets.

Table 9. Mean Absolute Errors (kcal/mol) in Properties Calculated with the OMx, OMx-D3T, and ODMx Methods for the CE345-CHNOF Set and Its Subsets.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
overalla	186	6.40	6.18	6.68	6.89	6.52	6.72
MGAE109/11	74	4.26b	4.19b	3.60	4.73b	4.53b	4.41
IsoL6	6	1.99	2.16	1.40	3.22	3.28	2.52
IP21	4	13.24	13.24	15.59	11.91	11.91	15.92
EA13/03	4	9.80	9.80	12.70	9.18	9.18	13.26
PA8/06	4	25.04	24.97	24.11	17.89	17.77	18.20
ABDE12	12	8.98b	7.78b	9.54	10.52b	8.91b	11.39
HC7/11	7	8.66	7.16	5.37	6.75	3.21	2.83
πTC13	13	2.54	2.73	6.61	5.17	4.77	2.68
HTBH38/08	26	4.96	4.96	5.94	5.99	6.61	5.73
NHTBH38/08	23	13.64	13.58	15.35	14.18	14.07	15.66
NCCE31/05	13	2.15	1.11	0.97	2.61	1.26	1.35

^aThe NH₃···F₂ complex in the NCCE31 subset was excluded from this statistics, because the SCF calculations did not converge with the OM2 and OM3 methods.

^bThe OMx and OMx-D3T energies are corrected by excluding the ZPVE and thermal contributions.

Concerning barrier heights, the performance of the ODMx methods is generally similar to that of the OMx and OMx-D3T methods. For example, the MAEs in 60 activation enthalpies (298 K) in the CHNO set are slightly higher for ODM2 and ODM3 (1.77 and 2.01 kcal/mol) than for the OMx methods (1.53–1.55 kcal/mol). On the other hand, the MAEs in 22 barrier heights of pericyclic reactions (BHPERI subset) are lower for ODM2 and ODM3 (6.49 and 6.80 kcal/mol) than for their OMx counterparts (8.21–8.25 kcal/mol) and of similar magnitude as those for the OMx-D3T methods (6.69–6.78 kcal/mol). Compared to their OMx and OMx-D3T counterparts, ODM2 and ODM3 perform somewhat worse for the BH76 subset (54 barriers of hydrogen and heavy-atom transfers, nucleophilic substitutions, unimolecular and association reactions), comparably bad for the O3ADD6 subset (only 2 barriers of ozone addition to unsaturated hydrocarbons), similarly for the HTBH38/08 (26 hydrogen transfer barriers), and somewhat worse for the NHTBH38/08 subset (23 non-hydrogen transfer barriers). Judging from the single-point results for the GMTKN30-CHNOF and CE345-CHNOF subsets (Tables 8 and 9), the MAEs of the ODMx methods for barriers and reaction energies seem to be overall of similar magnitude, while those for energy differences between conformers and isomers are lower.

4.2. Noncovalent Interactions

The evaluation of the results for the A24-CHNOF,¹⁶⁴ S22,^143,144,165 S66,^103,104 S66×8,¹⁰³ S66a8,¹⁰⁴ JSCH-2005-CHNOF,¹⁴³ S7L,¹⁶⁶ S30L-CHNOF,¹⁹ and AF6¹⁶⁷ benchmark sets for noncovalent interactions shows that statistically ODM2 and ODM3 are rather similar to OM2-D3T and OM3-D3T, respectively, for energies at the reference geometries (Table 10) and for the optimized geometries (Table 11). The OMx methods without dispersion corrections are known to perform much worse (as expected). The ODMx methods are generally somewhat better than their OMx-D3T counterparts for predicting interaction energies in the hydrogen-bonded complexes of the A24-CHNOF, S22, S66, and JSCH-2005-CHNOF sets (Table 10). ODM2 and ODM3 have similar MAEs of 4.36–4.86 kcal/mol for the S30L set with very large noncovalent complexes, which lie within the range of the MAEs for OM2-D3T (5.01 kcal/mol) and OM3-D3T (3.59 kcal/mol). The MAEs for the folding energies of alkanes (AF6 set) are reasonably low at the ODMx level (1.87–3.22 kcal/mol) but still higher than those at the OMx-D3T level (0.34–1.17 kcal/mol). On the other hand, the ODMx methods perform better than their OMx-D3T counterparts for the large stacked complexes in the S7L set (MAE values in kcal/mol: ODM2 1.62, OM2-D3T 2.38, ODM3 0.44, OM3-D3T 0.95).

Table 10. Mean Absolute Errors in Interaction Energies (kcal/mol) for the A24-CHNOF, S22, S66, S66×8, S66a8, JSCH-2005-CHNOF, S7L, and S30L-CHNOF Sets and Their Subsets and in Folding Enthalpies and Folding Energies for the AF6 Set at the Reference Geometries As Calculated with the OMx, OMx-D3T, and ODMx Methods.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
A24-CHNOF
overall	21	0.89	0.56	0.50	1.11	0.67	0.72
hydrogen bonded	5	1.79	1.40	1.15	1.86	1.32	1.28
mixed	10	0.70	0.17	0.13	1.05	0.34	0.43
dispersion	6	0.44	0.52	0.57	0.58	0.67	0.72
S22
overall	22	3.07	0.94	0.82	3.58	0.97	0.94
hydrogen bonded	7	3.63	2.15	1.91	4.20	2.28	1.81
mixed	8	3.68	0.47	0.34	3.92	0.24	0.35
dispersion	7	1.80	0.28	0.29	2.57	0.50	0.74
S66
overall	66	2.66	0.85	0.76	3.11	0.81	0.83
electrostatic	23	2.96	1.80	1.76	3.24	1.75	1.68
mixed	20	1.82	0.27	0.22	2.50	0.39	0.48
dispersion	23	3.10	0.39	0.23	3.52	0.23	0.29
S66×8
overall	528	1.93	0.79	0.75	2.23	0.71	0.72
electrostatic	184	2.27	1.43	1.40	2.39	1.30	1.32
mixed	160	1.31	0.37	0.34	1.78	0.34	0.37
dispersion	184	2.13	0.52	0.47	2.45	0.43	0.42
S66a8
overall	528	1.96	0.61	0.58	2.29	0.60	0.66
electrostatic	184	2.35	1.34	1.32	2.63	1.33	1.42
mixed	160	1.39	0.22	0.19	1.88	0.26	0.29
dispersion	184	2.07	0.21	0.17	2.30	0.18	0.21
JSCH-2005-CHNOF
overall	134	4.97	1.81	1.59	5.15	1.37	1.17
overall*a	128	4.81	1.61	1.39	4.95	1.13	0.91
hydrogen bonded base pairs	31	5.70	3.05	2.93	5.72	2.47	1.33
interstrand base pairs	32	1.73	0.72	0.75	1.80	0.70	0.69
stacked base pairs	54	6.42	1.50	1.02	6.58	0.75	0.89
amino acid pairs	17	5.13	2.55	2.49	5.88	2.62	2.63
amino acid pairs*a	11	3.29	0.65	0.64	3.97	0.52	0.49
S7L
overall	7	9.69	2.38	1.62	10.08	0.79	0.35
π–π	5	10.67	2.72	1.73	10.25	0.95	0.44
S30L-CHNOF
overall	24	21.33	5.01	4.86	24.14	3.59	4.36
π–π stacking	7	31.15	3.04	2.37	32.54	3.17	3.30
hydrogen bondedb	8	16.23	6.49	6.36	20.41	4.62	5.00
charged complexesb	8	16.22	8.41	8.85	19.40	4.56	6.27
AF6
folding enthalpiesc	6	3.38	0.34		5.11	1.00
folding energiesd	6	3.55	0.34	1.87	5.28	1.17	3.22

^aCharged amino acids excluded.

^bTwo complexes are attributed to both H-bonded and charged complexes subsets.

^cFolding enthalpies were not calculated at the ODMx levels, because this would require geometry optimizations at these levels.

^dErrors in folding energies were calculated using uncorrected changes in heats of formation at 298 K calculated at the OMx and OMx-D3T levels.

Table 11. Mean Absolute Errors in Selected Distances (Å) and Angles (deg) for the A24-CHNOF, S22, S66, S7L, and AF6 Sets and Their Subsets As Calculated with the OMx, OMx-D3T, and ODMx Methods.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
A24-CHNOF
Selected Interatomic Distances
overall	23	0.790	0.500	0.261	0.871	0.262	0.274
hydrogen bonded	5	0.189	0.198	0.114	0.336	0.335	0.371
mixed	13	0.419	0.413	0.386	0.254	0.326	0.326
dispersion	5	2.357	1.027	0.083	3.009	0.023	0.040
Selected Angles
overall	40	13.89	9.97	4.91	8.59	8.80	8.94
hydrogen bonded	13	11.47	11.39	4.67	11.50	11.08	11.30
mixed	21	10.78	6.45	6.00	4.27	9.56	9.77
dispersion	6	30.00	19.18	1.60	17.40	1.20	0.88
S22
Selected Interatomic Distances
overall	105	0.708	0.424	0.300	1.996	0.285	0.295
Selected Angles
overall	14	2.50	2.60	2.40	1.76	0.85	1.12
S66
Selected Interatomic Distances
overall	172	1.010	0.348	0.339	1.942	0.317	0.294
electrostatic	28	0.175	0.173	0.226	0.286	0.283	0.313
mixed	63	0.572	0.415	0.383	0.762	0.361	0.327
dispersion	81	1.639	0.356	0.345	3.432	0.295	0.263
Selected Angles
overall	141	21.53	12.32	12.89	20.69	12.99	11.62
electrostatic	28	10.84	13.30	13.74	9.76	9.97	7.31
mixed	52	15.66	14.54	17.21	20.07	19.73	17.92
dispersion	61	31.44	9.97	8.82	26.23	8.63	8.22
S7L
Selected Interatomic Distances
overall	28	15.579	0.420	0.389	10.540	0.393	0.386
C···C	20	21.662	0.421	0.409	14.479	0.468	0.450
H···H	8	0.370	0.416	0.340	0.694	0.207	0.227
AF6
Selected Interatomic Distances
overall	27	0.502	0.168	0.163	0.566	0.165	0.198
Selected Angles
overall	74	15.44	6.42	6.28	16.33	7.03	7.54

The ODM3 method suffers from one particular problem that also plagues OM3 and OM3-D3T:^50,54 geometry optimization of carboxylic acid dimers leads to symmetric cyclic structures with equal O–H bond distances, i.e. the methods fail to differentiate between covalent and noncovalent O–H bonds in these dimers. We did find ODM3 parameter sets that fix this problem, but their overall performance for other properties was less satisfactory than that of OM3 or OM3-D3T, and hence they were discarded. This underlines again how difficult it is to achieve an overall balanced treatment of a large variety of target properties during parametrization.

Another problem common to many SQC methods⁵⁴ is the bad description of the HF dimer. The OMx and OMx-D3T methods give a cyclic structure with two equal H···F hydrogen bonds and strongly underestimate the interaction energy. ODM3 suffers from the same problem, while ODM2 yields a qualitatively correct geometry (Figure 2) and an interaction energy of −2.2 kcal/mol that is still too small but much closer to the reference value of −4.6 kcal/mol than the values obtained otherwise (−1.2, −1.4, 0.5, 0.2, and 0.3 kcal/mol at OM2, OM2-D3T, OM3, OM3-D3T, and ODM3). Mainly because of the improved description of the HF dimer geometry, the MAE for selected angles in the A24-CHNOF set is much lower at the ODM2 level (4.9°) than at any other level (more than 8.5°).

Figure 2.

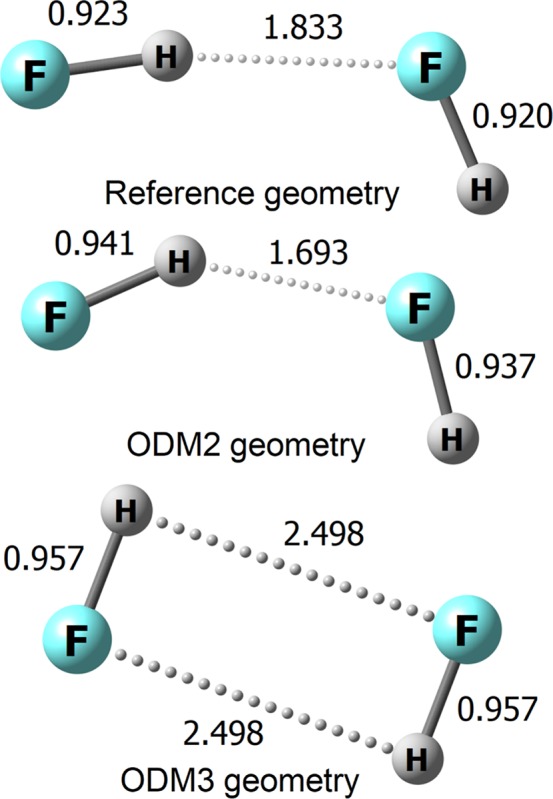
Geometries of the HF dimer at the reference coupled cluster level (CCSD(T) with complete basis set extrapolation) and at the ODM2 and ODM3 levels. Distances in Å.

Since the above sets contain only a few fluorine-containing noncovalent complexes, we also performed benchmarking on the X40×10-CHNOF set. This set is the subset of the X40×10 set constructed by excluding complexes containing elements beyond CHNOF. Reference geometries and interaction energies were taken from the original publication¹⁶⁸ and from subsequent higher-level calculations,¹⁶⁹ respectively. It is clear from the statistical analysis of the errors (Table S4) that all tested methods have similar accuracy with MAEs of 1.37–1.89 kcal/mol (lowest for ODM2, highest for OM3).

4.3. Excited-State Properties

In Table 12 we provide a statistical evaluation of the results for the vertical excitation energies of the VEE set that was included in the ODMx parametrization. The OMx/MRCI and OMx-D3T/MRCI results are trivially identical since the D3T-correction term does not affect the excitation energy at a given geometry. The ODMx/MRCI results are generally superior to their OMx/MRCI counterparts: the overall MAE for the excitation energies is reduced by ca. 25% in the ODM2 case (0.35 vs 0.47 eV) and by ca. 20% in the ODM3 case (0.33 vs 0.42 eV). Singlet and triplet excitations are described with similar accuracy by all methods considered.

Table 12. Mean Absolute Errors in Vertical Excitation Energies (eV) for the VEE Set and Its Subsets As Calculated with the OMx/MRCI, OMx-D3T/MRCI, and ODMx/MRCI Methods.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
overall	167	0.47	0.47	0.35	0.42	0.42	0.33
singlet	104	0.47	0.47	0.35	0.41	0.41	0.32
triplet	63	0.46	0.46	0.35	0.44	0.44	0.35

We also performed benchmarking on a previously introduced set of excited-state equilibrium geometries (called ExGeom)⁵⁵ and compared the results from the ODMx/MRCI, OMx/MRCI, and OMx-D3T/MRCI methods with reference results from time-dependent density functional theory (TDDFT) and coupled cluster theory (CC2). ODM2/MRCI performs very similarly to OM2/MRCI as seen from the MAEs in bond lengths and bond angles given in Table 13 (comparison to TDDFT; see Table S5 for comparison to CC2). ODM3/MRCI is slightly superior to OM3/MRCI for bond lengths, consistent with the observations for ground-state covalent bonds computed at the ODM3/SCF and OM3/SCF levels. The accuracy for bond angles is similar across all methods. As expected, dispersion corrections have practically no effect on the excited-state geometries of these small molecules (compare the OMx/MRCI with the OMx-D3T/MRCI results in Table 13).

Table 13. Mean Absolute Errors in Bond Lengths (Å) and Bond Angles (deg) Calculated with the OMx/MRCI, OMx-D3T/MRCI, and ODMx/MRCI Methods for the ExGeom Set and Its Subsets Relative to the TDDFT Level of Theory.

subset	N	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
Bond Lengths
overall	527	0.016	0.016	0.016	0.022	0.022	0.019
singlet	394	0.018	0.018	0.018	0.025	0.025	0.021
triplet	133	0.013	0.013	0.011	0.016	0.016	0.013
C–C bonds	291	0.016	0.016	0.015	0.018	0.018	0.017
C–H bonds	71	0.011	0.011	0.011	0.017	0.017	0.015
C–O bonds	58	0.017	0.017	0.015	0.020	0.020	0.019
C–N bonds	68	0.025	0.025	0.024	0.040	0.039	0.032
N–H bonds	33	0.009	0.009	0.017	0.030	0.029	0.008
Bond Angles
overall	278	1.88	1.89	1.78	1.85	1.86	1.92
singlet	201	1.82	1.83	1.76	1.81	1.82	1.93
triplet	77	2.04	2.04	1.82	1.96	1.97	1.88

Some brief remarks on specific molecules that had been addressed in our previous benchmarking are as follows:⁵⁵ The singlet and triplet excited-state geometries of formaldehyde are better described by the ODMx/MRCI methods than by their OMx/MRCI counterparts (Table S86). More generally, the excited-state C=O bond lengths in formaldehyde, acetaldehyde, and acetone from ODMx/MRCI are closer to the experimental and TDDFT values than those from OMx/MRCI (Table S87), but they are still underestimated. The pyramidalization of these carbonyl compounds upon excitation is reproduced well by the ODMx/MRCI, similarly to TDDFT, CC2, and OMx/MRCI (Table S88). The nonlinear equilibrium geometries of acetylene in several excited states are qualitatively well described both at the ODMx/MRCI and OMx/MRCI levels (see the ∠CCH angles in Table S89); for two states (2 ¹A₂ and 2 ³A₂) acetylene is still predicted to be linear, whereas the reference TDDFT and CC2 calculations give slightly bent structures. Both the ODMx/MRCI and OMx/MRCI methods give excited-state structures of 9H-adenine, aniline, cytosine, and 9H-guanine with out-of-plane bending angles of the amino groups that are much too small compared to the reference TDDFT and CC2 results (Table S90).

Finally, we assess the performance of the ODMx/MRCI methods on the SKF (Send–Kühn–Furche) set of experimental 0–0 transition energies.¹⁷⁰ In view of the technical problems encountered in MRCI calculations of ZPVEs,⁵⁵ we compare theoretical values without ZPVEs to experimental values back-corrected using ΔZPVEs from (TD)DFT calculations.^55,170 As seen from Table 14 the ODM2/MRCI method is marginally better than OM2/MRCI for the 0–0 transition energies of the SKF set, while ODM3/MRCI performs statistically basically the same as OM3/MRCI. Again, as expected, the dispersion corrections do not have any significant effect for this set.

Table 14. Mean Absolute Errors (MAEs) in 0–0 Transition Energies (eV) Calculated with the OMx/MRCI, OMx-D3T/MRCI, and ODMx/MRCI Methods for the SKF Set Relative to Back-Corrected Experiment^a.

	OM2	OM2-D3T	ODM2	OM3	OM3-D3T	ODM3
countb	68	67	65	66	66	65
MAE	0.26	0.26	0.25	0.27	0.27	0.27

^aExperimental values were back-corrected with (TD)DFT ΔZVPE values to directly compare them with theoretical calculations, which do not include ZPVE-corrections, see ref (55) for the reasons.

^bSome calculations could not be converged which reduces the total count of successful computations to less than 68. Tests have confirmed that this practically does not affect the overall statistics.

To conclude, we note that our current excited-state validations employ an MRCI treatment, which may no longer be feasible for larger active spaces that are often required for larger molecules. To deal with such cases, our code includes efficient implementations of the CIS and SF-XCIS (spin-flip extended CIS) methods^171,172 that allow for practical SQC explorations of large systems (with little loss of accuracy).

5. Conclusions

In this work we present two new semiempirical quantum-chemical methods with integrated orthogonalization and dispersion corrections, ODM2 and ODM3 (ODMx). The electronic structure formalism is the same as in the established NDDO-based orthogonalization-corrected methods (OMx). In addition, the ODMx methods include D3-dispersion corrections with Becke–Johnson damping and with three-body corrections E^ABC as an integral part, for proper description of noncovalent interactions. Moreover, the total energy in the ODMx methods is defined in complete analogy to ab initio methods, and the traditional convention in NDDO-based methods of using SQC total energies directly in calculating heats of formation at room temperature is abandoned. Instead, ODMx heats of formation at 298 K are determined by explicitly computing ZPVE and thermal corrections within the harmonic-oscillator and rigid-rotor approximations.

Compared with the previous OMx development, the parametrization of the ODMx methods targeted a much broader range of reference properties, covering in particular also vertical excitation energies. To ensure a balanced description of a large variety of ground-state and excited-state properties as well as noncovalent interactions, we employed a novel robust parametrization procedure and a carefully chosen selection of representative training sets.

The performance of the ODMx methods was evaluated for a large and diverse collection of accurate reference data. The ODMx methods are found to perform overall somewhat better than the OMx methods for ground-state and excited-state properties, while their accuracy is similar to that of the dispersion-corrected OMx-D3T methods for noncovalent interactions. They are also formally more consistent: since they were parametrized with integrated dispersion corrections, there are no problems arising from the a posteriori addition of attractive dispersion terms to SQC methods parametrized without them. Therefore, heats of formation at 298 K are well described by the ODMx methods but are systematically too small for the dispersion-corrected OMx-D3T methods. Moreover, the redefinition of the total energy (in analogy to ab initio methods) removes ambiguities caused by associating them directly with heats of formation at 298 K (as traditionally done in the NDDO-based SQC methods). Thus, we recommend the ODM2 and ODM3 methods as standard tools for fast electronic structure calculations. To widen their scope we plan to extend them to heavier main-group elements.

The ODM2 method is the most complete model, shows good performance in our benchmarks, and would thus normally be the method of choice. Of course, SQC application studies should generally begin with a careful validation, and it may turn out that another SQC method is more appropriate for a particular problem, which should then be chosen for the actual production work. The benchmark results reported here and in our previous studies^50,54,55 may be helpful for choosing the most appropriate method.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b01265.

• Parametrization details, plots of resonance integrals, and tables with additional validation results and with reference and calculated property values for individual items in the benchmark sets (PDF)

We thank the European Research Council for financial support through an ERC Advanced Grant (OMSQC).

The authors declare no competing financial interest.