Anatomically constrained tractography facilitates biologically plausible fiber reconstruction of the optic radiation in multiple sclerosis

Abstract

Diffusion-weighted magnetic resonance imaging (dMRI) enables the microstructural characterization and reconstruction of white matter pathways in vivo non-invasively. However, dMRI only provides information on the orientation of potential fibers but not on their anatomical plausibility. To that end, recent methodological advances facilitate the effective use of anatomical priors in the process of fiber reconstruction, thus improving the accuracy of the results. Here, we investigated the potential of anatomically constrained tracking (ACT), a modular addition to the tractography software package MRtrix3, to accurately reconstruct the optic radiation, a commonly affected pathway in multiple sclerosis (MS). Diffusion MRI data were acquired from 28 MS patients and 22 age- and sex-matched healthy controls. For each participant, the optic radiation was segmented based on the fiber reconstruction obtained using ACT. When implementing ACT in MS, it proved essential to incorporate lesion maps to avoid incorrect reconstructions due to tissue-type misclassifications in lesional areas. The ACT-based results were compared with those obtained using two commonly used probabilistic fiber tracking procedures, based on FSL (FMRIB Software Library) and MRtrix3 without ACT. All three procedures enabled a reliable localization of the optic radiation in both MS patients and controls. However, for FSL and MRtrix3 without ACT it was necessary to place an additional waypoint halfway between the lateral geniculate nucleus and the primary visual cortex to filter out anatomically implausible tracks. In the case of ACT, the results with and without an additional waypoint were virtually identical, presumably because the employed anatomical constraints already prevented the occurrence of the most implausible tracks. Irrespective of the employed tractography procedure, increased diffusivity and decreased anisotropy were found in the optic radiation of the MS patients compared to the controls.

Highlights

• •Anatomical constraints improve tractography of the optic radiation in MS.
• •In MS, lesion mapping is essential to implement sensible anatomical constraints.
• •Patients showed increased diffusivity and decreased anisotropy in the OR.

1. Introduction

Diffusion-weighted magnetic resonance imaging (dMRI) can be used to assess microstructural tissue properties in vivo, since these properties influence diffusion measures such as the mean diffusivity (MD) or the fractional anisotropy (FA; Basser, 1995). In multiple sclerosis (MS) research, dMRI is an important technique complementing more conventional MR imaging modalities in studying pathological changes, such as inflammation, demyelination, or axonal loss, within the white matter (Cercignani and Wheeler-Kingshott, 2018).

In the current study, we focused on the optic radiation (OR), which is regularly affected in MS (Gabilondo et al., 2014; Klistorner et al., 2014). Alterations within the OR might be explained by its transitional position within the visual pathway, which renders it vulnerable to both anterograde (originating from optic nerve or primary retinal pathology) and retrograde (originating from lesions within the OR) trans-synaptic neurodegeneration (Kuchling et al., 2017; Jenkins et al., 2011; Audoin et al., 2006). Moreover, regional cortical as well as global brain atrophy affects the OR structure and leads to vision deficits that are often among the first symptoms of MS (Klistorner et al., 2014; Pietroboni et al., 2017).

Most dMRI studies on MS employed diffusion tensor imaging (DTI). However, as the diffusion tensor cannot represent more than one independent orientation, it is a poor model of more complex local fiber configurations. Therefore, DTI is most useful when applied to large WM bundles like the corticospinal tract, which is characterized by high myelination with many axially directed axons and few crossing and kissing fibers (Jeurissen et al., 2013). Higher order diffusion models are better suited to describe complex local fiber configurations, but high angular resolution diffusion imaging (HARDI) data are required to reliably fit them. As modern HARDI protocols are gaining currency, even in clinical settings, the diffusion tensor is increasingly superseded by higher order models. For example, in MRtrix spherical harmonics are used to model the fiber orientation distribution in a given voxel (Tournier et al., 2012, Lilja et al., 2016). In contrast, in FSL (FMRIB3 Software Library) the principal diffusion or fiber directions present in a given voxel are modeled based on Bayesian probability theory (Woolrich et al., 2009; Lilja et al., 2014). These and other methods have proven useful in representing tissue-specific diffusion properties, particularly in the presence of crossing fibers (Tournier et al., 2011; Wilkins et al., 2015).

Although DTI-based diffusion measures, such as FA, MD, axial (AD), and radial diffusivity (AD), are inherently limited by the underlying tensor model, alternative non-DTI-based measures like the multi-directional anisotropy (MDA), the generalized FA (GFA; Tuch, 2004), or the fiber density (FD) and cross section (FC; Gajamange et al., 2017) are not yet well established, especially in clinical settings. Thus, DTI-based diffusion measures are still the most widely used method for the analysis of WM changes (Balk et al., 2015). In the current study, we rely on higher order models for fiber tractography but use tensor-based diffusion measures for within-tract statistical analyses. In doing so, we make full use of the high angular resolution of the data to obtain more accurate fiber reconstructions while maintaining comparability with tensor-based results reported in other studies.

Previous dMRI studies in MS often relied on post-processing based on additional filtering to remove false or excessive paths and enhance the anatomically plausibility of the final tractography results. This is necessary because dMRI provides only limited information about the different underlying tissue types (Sbardella et al., 2013). Here, we investigate a new framework for anatomically constrained tractography (ACT; Smith et al., 2012) that is designed to integrate anatomical information extracted from additional T1-weighted MRI data during tracking. More specifically, a T1-based tissue-type segmentation is used in conjunction with a fixed set of rules based on anatomical and biological a priori knowledge to influence the termination and acceptance/rejection criteria for each probabilistic fiber track. However, disease-related pathologies can cause tissue-type misclassifications upon using the T1-weighted data to inform tractography. To avoid this, it is therefore important to integrate lesion information, e.g., derived from FLAIR hyperintensities (e.g., Schmidt et al., 2012), into the procedure as well.

Compared to commonly used ad-hoc approaches, e.g., based on study-specific filtering regions, ACT provides a more principled attempt to constraint imposition based on anatomical images. As we show here, this approach is also effective in the case of the OR, as it facilitates biologically plausible reconstructions in both healthy controls (HCs) and MS patients. Both of the other approaches required the addition of a study-specific filtering region to exclude implausible results. However, some minor problems, e.g., regarding tracks passing through the lateral ventricles were still observed, whereas this was not the case using ACT.

2. Methods

2.1. Participants

The study involved 28 patients diagnosed with MS according to the McDonald criteria 2010 (Polman et al., 2011) and 22 age- and sex-matched HCs. Participants were prospectively recruited at the Department of Neurology, Otto-von-Guericke University Magdeburg, Germany. Visual acuity measurements were carried out by an ophthalmologist (M.W.). Participants with ophthalmological diseases other than a history of optic neuritis or a refractive error exceeding +/− 5.0 dpt. were not included. Further exclusion criteria were other neurological diseases (e.g., stroke or epilepsy), any immunosuppression (e.g., diabetes or hematological diseases), and any MRI contraindication. Moreover, MS patients had not presented with an acute clinical relapse or received any steroids within the preceding 4 weeks. Clinical disability was quantified using the Expanded Disability Status Scale (EDSS; Kurtzke, 1984). Disease duration was defined as the time between diagnosis and study inclusion. The study was approved by the local ethics committee (Reference No. 7414) and all participants gave their written informed consent prior to inclusion. Demographic data are summarized in Table 1.

Table 1.

Subject characteristics.

	MS (n = 28)	HC (n = 22)	p-value
Age (y), mean ± SD (range)	42.0 ± 10.6 (25–66)	40.3 ± 11.8 (20–60)	0.580
History of optic neuritis, N (%)	14 (50)	–	–
Disease duration (y), mean ± SD (range)	8.5 ± 6.45 (1–26)	–	–
Female, N (%)	21 (75)	12 (54.5)	0.147
EDSS, median ± (IQR)	1.75 (1.125–4.0)	–	–

Between-group differences were assessed using the independent samples t-test (age) and the Chi² test (sex); EDSS: Expanded disability status scale; HC: healthy controls; MS: multiple sclerosis; N: number, SD: standard deviation; y: years.

2.2. OCT data acquisition

Optical coherence tomography (OCT) was used to measure each patient's retinal nerve fiber layer (RNFL) thickness around the optic nerve head based on a peripapillary ring scan (angle 12°, diameter 3.4mm) acquired without pupillary dilation. All measurements were performed by an experienced ophthalmologist (M.W.) using a spectral domain OCT (SD-OCT) device (Heidelberg Spectralis, Heidelberg Engineering, Heidelberg, Germany). The acquired scans underwent rigid quality control according to the validated OSCAR-IB criteria (Schippling et al., 2015; Tewarie et al., 2012) at the Neuro-OCT Reading Centre at the University Hospital Zurich, Zurich, Switzerland (S.S.). The RNFL measurements of each patient were averaged to obtain one mean RNFL value per patient.

2.3. MRI data acquisition

All imaging data were acquired on a Siemens MAGNETOM Prisma 3 Tesla MRI scanner with syngo MR D13D software and a twenty-channel head coil. For anatomical reference, each scanning session included a high-resolution, T1-weighted structural scan acquired using a 3D-MPRAGE sequence (TE/TR = 2.82/2500 ms, TI = 1100 ms, flip angle = 7°, voxel size = 1 mm³, FoV: 256 × 256 mm²; image matrix: 256 × 256, 192 sagittal slices) (Mugler and Brookeman, 1990). Parallel imaging (GRAPPA) with an acceleration factor of 2 was used (Griswold et al., 2002), yielding a scan duration of 5 min and 18 s. For detection of WM lesions, a T2-weighted 3D-FLAIR scan was acquired (TE/TR = 284/6000 ms, TI = 2100 ms, variable flip angle, voxel size = 0.49 × 0.49 × 1.0 mm³, FoV = 250 × 250 mm², image matrix = 512 × 512, 160 sagittal slices, GRAPPA acceleration factor = 2, scan duration = 10 min 30 s). Diffusion-weighted images (DWI) were obtained based on a single-shot, single-refocused echo planar imaging (EPI) pulse sequence (TE/TR = 51/8200 ms, voxel size = 1.6 × 1.6 × 1.6 mm³, FoV = 220 × 220 mm², image matrix = 138 × 138, 86 axial slices parallel to the AC-PC line, receiver bandwidth = 1812 Hz/pixel, echo spacing = 0.66 ms, GRAPPA acceleration factor = 3, 36 reference lines, scan duration = 19 min 8 s) using 60 non-collinear diffusion gradients (Jones, 2004; Jones et al., 1999) with two b-values (b1/b2 = 800/1200 s/mm²) and 16 scans without diffusion weighting (b = 0 s/mm²). For each of the two b-values, data were acquired in six blocks. Each block consisted of one b = 0 volume and 10 diffusion-weighted volumes. Before the first and after the last block, an additional b = 0 volume was obtained. All volumes were registered to the first b = 0 volume. To be able to address the problem of geometric distortions in EPI caused by magnetic field inhomogeneities, a field map was acquired prior to the EPI sequence using a double-echo gradient recalled echo (GRE) sequence (TE 1/2 = 4.92 ms/7.38 ms, TR = 600 ms, flip angle = 60°, voxel size = 2.0 × 2.0 × 3.0 mm³, FoV = 220 × 220 mm², 54 slices parallel to the AC-PC line, scan duration = 2 min 13 s). For all data, image reconstruction was carried out using Siemens' “Adaptive Combine”.

2.4. MRI data preprocessing

The FMRIB software library (FSL, University of Oxford, https://fsl.fmrib.ox.ac.uk) version 5.0.9 was used for preprocessing (Jenkinson et al., 2012). To correct for eddy-current-induced distortions, the DWI images were registered to a corresponding b = 0 image based on a 12-dof affine transformation using eddy_correct with spline interpolation (Graham et al., 2015). To account for head movement, we computed an affine transformation from each block's non-diffusion-weighted volume to the first b = 0 image using FLIRT (Jones and Cercignani, 2010; Smith et al., 2004). The DWI images of each block were then realigned based on these transformations. Geometric distortions induced by magnetic field inhomogeneities were corrected based on the GRE field map, and the diffusion data were registered to the corresponding T1-weighted structural scan. These steps (EPI distortion correction and EPI-to-MPRAGE registration) were performed simultaneously using epi_reg. Diffusion tensors were fitted with dtifit to obtain the eigenvalues and eigenvectors for each voxel, from which the fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD), and radial diffusivity (RD) were calculated. The cortical thickness of V1 was determined based on the T1 data using Freesurfer version 5.3 (Fischl and Dale, 2000).

2.5. WM lesion mapping

WM lesions were identified using the lesion prediction algorithm (LPA) implemented in the LST toolbox version 2.0.154 for SPM125 (University College London). The DWI co-registered MPRAGE image was used as reference image. LPA is based on a binary classifier in the form of a logistic regression model trained on the data of 53 MS patients with lesions from the Department of Neurology, Technische Universität München (Munich, Germany). We used LPA to compute a voxel-wise estimate of lesion probability for each subject (Schmidt et al., 2012). The resulting subject-specific lesion probability maps were binarized using a probability threshold of 0.3 to obtain binary lesion maps.

2.6. Seed and target selection

The OR is a fiber bundle between the lateral geniculate nucleus (LGN) and primary visual cortex (V1). Individual segmentation of the LGN and V1 was done automatically based on the Juelich Brain Atlas (Eickhoff et al., 2007) included in FSL. Each of the resulting ROIs was visually inspected to ensure its anatomical plausibility. In doing so, the LGN (seed) and V1 (target) ROIs were considered to be adequately placed lateral to the transition between the cerebral peduncle and the posterior limb of the internal capsule, and in the posterior pole of the occipital lobe and the cortex next to the calcarine sulcus, respectively (Brodmann, 1909).

The left LGN, as defined in MNI space by the Juelich Histological Atlas, is about 20% larger than the right LGN. The final LGN and V1 ROIs (after transformation to native space and thresholding based on the median) were consistent in volume with previous measurements (Schmitt et al., 2014; Wang et al., 2015) and differed by approx. 10% between hemispheres. The volumes of the ROIs are shown in Table 2.

Table 2.

Volume of seed and target ROIs.

ROI	Side	Mean ± SD	Paired T-test
			∆ (L-R)	T	p-value
LGN (Atlas)	R	2576	720 (21%)
	L	3296
V1 (Atlas)	R	53,488	696 (1.3%)
	L	54,184
LGN (final)	R	355 ± 47	36.82 (9.4%)	7.1	0.000
	L	392 ± 61
V1 (final)	R	3,046 ± 546	−305 (9.9%)	−6.8	0.000
	L	2,742 ± 452

Mean volume (in mm³) for seed (LGN) and target (V1) ROIs. Atlas: ROIs as defined in MNI space based on the Juelich Histological Atlas; final: ROIs after transformation to native space and median-based thresholding; L: left; R: right. Paired t-tests were conducted to compare the corresponding ROIs of the left and right hemisphere; p-values ≤ 0.05 were deemed to be statistically significant.

2.7. Tractography

We compared three different fiber tracking methods: two well-established methods (FSL, MRtrix) and the newer anatomically constrained fiber tracking (ACT), which is a modular addition to MRtrix.

2.7.1. FSL

The first procedure we considered is based on the FMRIB Diffusion Toolbox (FDT version 3.0) which is included in FSL (Behrens et al., 2003; Smith et al., 2004; Woolrich et al., 2009). First, the FSL Brain Extraction tool (BET) was used to remove non-brain tissue (Smith, 2002; Smith et al., 2004). The preprocessed diffusion-weighted images were used to model three fibers per voxel using bedpostx. The use of multiple shells improves the modeling of crossing fibers within each voxel (Jbabdi et al., 2012). Here, we used two shells with b1 = 800 s/mm² and b2 = 1200 s/mm², respectively. The sampling results from bedpostx were used to generate connectivity distributions from user-specified seed voxels with probtrackx2 (Behrens et al., 2007). The following settings were used: simple Euler streamlining, number of samples per voxel = 10,000, number of steps per sample = 2000, step length = 0.5mm, loop check, curvature threshold = 90°, way-point conditions to each half tract separately, subsidiary fiber volume threshold = 0.01, seed sphere sampling = 0 and a stop option when V1 is reached. In the resulting map, each voxel's value represents the degree of connectivity between it and the seed voxels.

2.7.2. MRtrix

The second tracking procedure is based on the MRtrix3 software package (http://www.mrtrix.org, Tournier et al., 2012). Using dwi2response (with the “dhollander” algorithm for multi-shell data (Dhollander et al., 2016), we estimated response functions from the preprocessed diffusion-weighted images. These were then used to estimate fiber orientation distributions (FOD) based on 8th order constrained spherical deconvolution (CSD) using dwi2fod (Tournier et al., 2004). Specifically, we used the msmt_csd algorithm (Jeurissen et al., 2014), which facilitates the computations of three separate FODs for WM, gray matter (GM) and cerebrospinal fluid (CSF) based on multi-shell data. For fiber tracking, we then used tckgen with the iFOD2 (improved 2nd order integration over fiber orientation distributions) algorithm. This algorithm facilitates more accurate fiber reconstruction in heavily curved regions such as the Meyer's loop and thus enhances the anatomical plausibility of the results (Tournier et al., 2010). During tracking, the direction for each step is obtained by sampling from the FOD at the current position, such that the probability of a particular direction being produced is proportional to the amplitude of the FOD along that direction. The following additional tckgen settings and inputs were used: default step size of 0.8 mm, max. angle between successive steps = 90°, max. length = 160 mm, min. length value set the min. length 8 mm, cutoff FA value = 0.1, b-vectors and b-values from the diffusion-weighted gradient scheme in the FSL format, b-value scaling mode = true, maximum number of fibers = 10,000, and unidirectional tracking.

2.7.3. MRtrix/_ACT

The third procedure (MRtrix/_ACT) extends the second procedure by employing additional anatomical constraints. The settings were the same as described above for MRtrix (without ACT). Using ACT, an image segmentation derived from additional MRI data is combined with prior anatomical knowledge to influence the termination and acceptance/rejection criteria during fiber tracking with MRtrix (Smith et al., 2012). The segmentation is supplied to the software via a so-called 5TT (five tissue types) file, which contains the tissue types “cortical GM”, “subcortical GM”, “WM”, “CSF”, and optionally “pathological tissue”. We used the command 5ttgen fsl, which, in turn, uses the FSL segmentation tools FIRST and FAST, to generate segmentations of the four mandatory tissue types based on the T1-weighted data. To avoid tissue-type misclassifications due to WM lesions, we used 5ttedit to add the previously determined lesion maps to the 5TT files using the optional 5th tissue type (pathological tissue). To enhance the anatomical plausibility of the reconstructed fibers based on prior information, Smith et al. (2012) devised the following six rules, which pertain to the mandatory four tissue types in the segmentation. (1) If a streamline enters cortical GM, it is terminated and accepted. (2) If a streamline enters CSF, it is rejected. (3) If a streamline leaves the FOV of the diffusion image or the segmentation, or a pre-defined tracking mask, it is terminated and accepted. This is necessary to facilitate, for example, tracking to the spinal column. (4) If a streamline reaches a WM area of poor directionality, as indicated by a very low FOD amplitude, or exhibits excessive curvature while in WM, it is terminated and rejected. (5) If this occurs within subcortical GM, the streamline is instead terminated and accepted. (6) Streamlines are not allowed to exit subcortical GM, and are instead truncated based on the minimum FOD amplitude within the subcortical structure. As a result, tracks will typically terminate upon entering cortical GM or within subcortical GM, which is in line with known properties of the corresponding neuronal axons. Since the condition of pathological tissue is unclear, the anatomical priors implemented by the above rules are temporarily suspended, if a streamline passes through such tissue.6 Until the streamline either terminates, for example, due to poor directionality, or exits the pathological tissue, tractography is conducted based on the diffusion data alone. To better understand how the incorporation of lesion maps influences the tractography results in practice, we conducted an additional comparison between ACT as described above (5TT) and ACT using only the four mandatory tissue types (4TT).

2.7.4. Waypoint-based filtering of tractography results

An additional ROI, to be used as a waypoint for the tracking procedures, was placed inside the OR, lateral to the posterior ventricle above the superior colliculus. Using a waypoint ROI, any generated track that does not pass through the waypoint is essentially filtered out and discarded. The waypoint ROI was defined in MNI152 space and then transformed to the individual MPRAGE images using FSL's FLIRT and FNIRT for linear and non-linear registrations, respectively (Andersson et al., 2007). To presage the results, many implausible tracks, passing, e.g., through the corpus callosum and parahippocampal regions, are generated by MRtrix and FSL without such a waypoint ROI. In the case of MRtrix/_ACT, the results with and without waypoint ROI were virtually identical (see Results section, Fig. 4). Therefore, the waypoint ROI was used with FSL and MRtrix (without ACT) but not with MRtrix/_ACT in all subsequent analyses.

Fig. 4.

OR tracking results from one representative subject for each of the three procedures: FSL, MRtrix, and MRtrix/_ACT with and without an additional filtering waypoint. FSL density map in jet colormap, both MRtrix procedures direction encoded (anterior-posterior - green, left right – red, superior inferior - blue), filtering waypoint in hot colormap. In the case of FSL and MRtrix w/o ACT, tracking without the additional filtering waypoint resulted in anatomically implausible tracks parahippocampal and via the corpus callosum.

2.8. Construction and anatomical validation of OR segments

In the cases of MRtrix and MRtrix/_ACT, a tract density image was computed from the generated tracks using tckmap. FSL's output already consisted in a comparable map. The FSL, MRtrix and MRtrix/_ACT density images were then divided by its maximum and thresholded at 0.1, so that the set of suprathreshold voxels forms an OR segment.

All OR segments were inspected by two raters (M.H., J.K.) to assess their anatomical plausibility. While all OR segments appeared generally reasonable, the OR segments generated by MRtrix appeared to be larger and more extensive than those generated by FSL. Therefore, we measured the average distance between the anterior Meyer's loop (aML) and the temporal pole (TP) in MNI space (Lilja et al., 2014), which confirmed this observation (see Results section, Fig. 1).

Fig. 1.

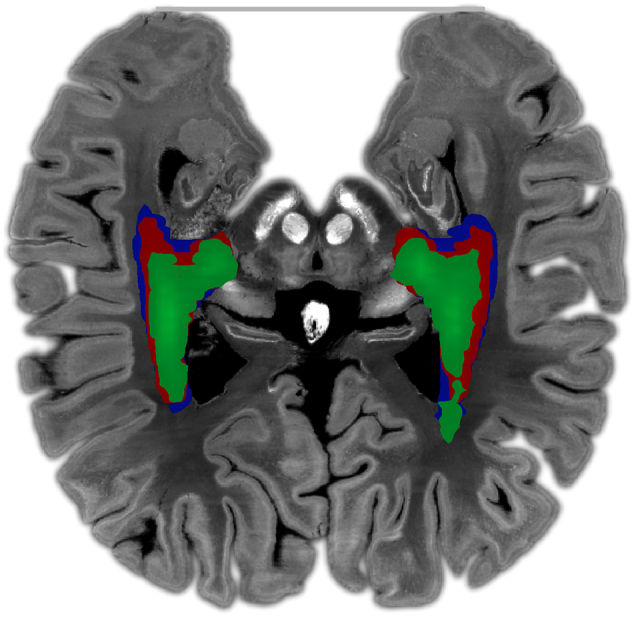
Mean normalized tract density maps for FSL (green), MRtrix (red), and MRtrix/_ACT (blue). The distances reported in the text were measured between the anterior Meyer's loop (aML, determined separately for each of the procedures based on the OR segments) and the temporal pole (TP, gray line). Maps were registered to the Big Brain MNI template (https://bigbrain.loris.ca/main.php) (200 μm voxel size) for visualization purposes.

2.9. Within-tract diffusion measures

After construction of the OR segments via thresholding of the normalized tract density maps, the within-tract diffusion measures (FA, MD, AD, RD) were computed as weighted averages based on the suprathreshold voxels. In doing so, areas with a higher tract density have a greater influence on the final average, which seems reasonable.

2.10. Statistical analyses

Statistical analyses were conducted using SPSS 21 (IBM). Comparisons of categorical (sex) and continuous variables (e.g., age) were performed using a Chi²-test and an independent-samples t-test. We analyzed both hemispheres separately to prevent reduction of variance by averaging. The left and right data were compared using paired t-tests. For lesion burden estimation, only lesions inside the OR ROI with a probability > 0.3, were considered.

Two-way repeated measures ANOVA was used to test for between-subject factor “group” (MS, HCs) and within-subject factor “tracking procedure” (FSL, MRtrix, MRtrix/_ACT). All results were Greenhouse-Geisser corrected to account for violations of sphericity. For a more detailed description of the differences between the three methods, paired sample t-tests were applied for controls and patients separately. Bonferroni-corrected p-values < 0.0125 (0.05/4) were deemed to be statistically significant.

To assess intra-individual differences and variance homogeneity for two different procedures, Bland-Altman plots were used. To inspect measurement deviations, such as scale or location shift, we used scatter plots with calibration and orthogonal regression lines (Koch and Spörl, 2007). Intraclass correlation coefficient (ICC) was used to evaluate the reproducibility between the procedures.

We used Spearman's ⍴ to assess dependencies between the OR diffusion measures (FA, MD, AD, RD) corresponding to each procedure and the OR lesion volume. Bonferroni-corrected p-values < 0.008 (0.05/6) were deemed to be statistically significant. Pearson's correlation coefficient was used to correlate the visual acuity, RNFL and V1 thickness with the FA values of each procedure; p-values < 0.008 (0.05/6) were deemed to be statistically significant.

3. Results

3.1. Anatomical validation

Since the aML is the most anterior section of the OR, a smaller distance between it and the TP indicates a more accurate representation of this highly curved section. The mean distances for the left and right hemisphere were 55 and 56 mm (FSL), 50 and 47 mm (MRtrix), and 47 and 44 mm (MRtrix/_ACT). As illustrated in Fig. 1, the average distance in our study was smallest for MRtrix/_ACT, so that the corresponding OR segments appear more accurate with regard to the above argument than those constructed based on the other two procedures. Nevertheless, Ebeling and Reulen (1988), who performed a high-quality dissection in formalin fixed tissue, reported even smaller distances (between 22 and 37 mm).

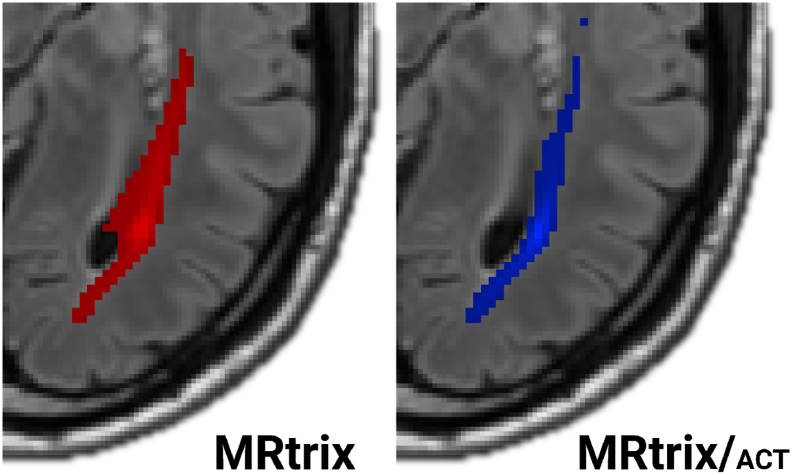
A comparison of individual cases showed that MRtrix without ACT sometimes produced OR ROIs that overlapped with the side ventricles (Fig. 2). MRtrix/ACT produced more reasonable results.

Fig. 2.

MRtrix/ACT often produced more accurate OR reconstructions than plain MRtrix. As illustrated by a representative patient, MRtrix results (left) sometimes included parts of the lateral ventricles. In contrast, MRtrix/ACT results did not exhibit these problems. OR segments (red: MRtrix; blue: MRtrix ACT) are shown on top of the corresponding FLAIR images.

To better understand how the incorporation of lesion maps influences the tractography results in practice, we conducted an additional comparison between ACT using only the four mandatory tissue types (4TT) and ACT using all five tissue types (5TT). For some patients, especially those with an exceptionally high lesion burden, the 4TT results contained a lot of errors due to lesion-related tissue-type misclassifications. Using 5TT, such problems can be circumvented by temporarily suspending ACT's anatomical priors, leading to much more reasonable results (Fig. 3).

Fig. 3.

If lesions are present, MRtrix/_ACT needs to be provided with corresponding maps to work as expected. The case of a patient with prominent FLAIR WM hyperintensities (A) illustrates how tissue-type misclassifications in lesional areas lead to erroneous results when only the four mandatory tissue types are used (B). To avoid this, lesional tissue can be marked as such using the optional fifth tissue type. This locally disables the use of ACT's rules, so that only the actual diffusion data is used to inform tractography in the affected areas. As a result, a much more useful reconstruction of the OR is achieved (C).

3.2. Waypoint-based filtering of tractography results

To enhance the anatomical plausibility of fiber reconstructions, a waypoint ROI was placed inside the OR, lateral to the posterior ventricle above the superior colliculus. Using a waypoint ROI, any generated track that does not pass through the waypoint is filtered out and discarded. As it turned out, many implausible tracks, passing, e.g., through the corpus callosum and parahippocampal regions, were generated by MRtrix and FSL without such a waypoint ROI. In the case of MRtrix/_ACT, the results with and without waypoint ROI were virtually identical. Therefore, the waypoint ROI was used with FSL and MRtrix (without ACT) but not with MRtrix/_ACT in all subsequent analyses. Fig. 4 illustrates the effect of the waypoint ROI on the results generated by the different procedures.

3.3. Statistical analyses

3.3.1. Repeated measures ANOVA

For all diffusion values, significant within-subject effects were found between all three procedures (F_FA(1.20) = 13.93, p < 0.001, Greenhouse-Geisser p < 0.001; F_MD(1.35) = 6.42, Greenhouse-Geisser p = 0.002; F_AD(1.29) = 3.77, Greenhouse-Geisser p = 0.044 and F_RD(1.34) = 8.66, p < 0.001, Greenhouse-Geisser p = 0.002). There were no significant group × procedure interactions.

3.3.2. Per-procedure differences between groups

DTI metrics (FA, MD, AD, RD) of the ORs from the different groups are summarized in Table 3 and significant FA differences are shown in Fig. 5A–C. All procedures detected significant between-group differences (p < 0.001). No significant between-group differences were found in visual acuity (p = 0.243) or V1 thickness (p = 0.2). Significant differences were found in RNFL ( = 0.04) and lesion volumes (OR: p < 0.001, whole brain: p = 0.011).

Table 3.

dMRI metrics of the ORs, optical and structural metrics from multiple sclerosis (MS) patients and healthy controls (HC).

	MS	HC	p-values
FA OR	0.52 ± 0.05	0.55 ± 0.03	0.000
FSL
FA OR	0.50 ± 0.04	0.54 ± 0.02	0.000
MRtrix
FA OR	0.50 ± 0.04	0.54 ± 0.03	0.000
MRtrix/ACT
MD OR	0.81 ± 0.10	0.75 ± 0.05	0.000
FSL
MD OR	0.83 ± 0.10	0.76 ± 0.03	0.000
MRtrix
MD OR	0.81 ± 0.09	0.75 ± 0.02	0.000
MRtrix/ACT
AD OR	1.32 ± 0.11	1.26 ± 0.07	0.001
FSL
AD OR	1.32 ± 0.10	1.27 ± 0.05	0.001
MRtrix
AD OR	1.31 ± 0.09	1.25 ± 0.03	0.000
MRtrix/ACT
RD OR	0.67 ± 0.10	0.59 ± 0.05	0.000
FSL
RD OR	0.68 ± 0.10	0.61 ± 0.03	0.000
MRtrix
RD OR	0.67 ± 0.09	0.60 ± 0.02	0.000
MRtrix/ACT
Visual acuity, median (IQR; range)	1.0 (1–1; min-max)	1.0 (1–1; min-max)	0.243
RNFL in μm	90.9 ± 11.4	97.4 ± 7.7	0.04
Primary visual cortex in mm	1.7 ± 0.1	1.6 ± 0.1	0.2
Mean FLAIR whole lesion burden in ml ± SD	8.22 ± 11.8	1.47 ± 1.5	0.011
Mean FLAIR OR lesion burden in ml ± SD	0.47 ± 0.7	0.03 ± 0.05	0.000

Mean (standard deviation) is given. ACT: MRtrix/ACT; AD: axial diffusivity; FA: fractional anisotropy; FSL: FSL probtrackx2 tracking; HC: healthy controls; IQR: interquartile range; MD: mean diffusivity; MRtrix: MRtrix without ACT; MS: multiple sclerosis; OR: optic radiation; RD: radial diffusivity; RNFL: Retinal nerve fiber layer; SD: standard deviation; mean lesion burden and intracranial volumes are given in ml; mean MD, AD and RD are expressed in 10⁻³ mm²/s; FA is a dimensionless index. For continuous variables, independent samples t-tests were conducted; p-values < 0.05 were deemed to be statistically significant.

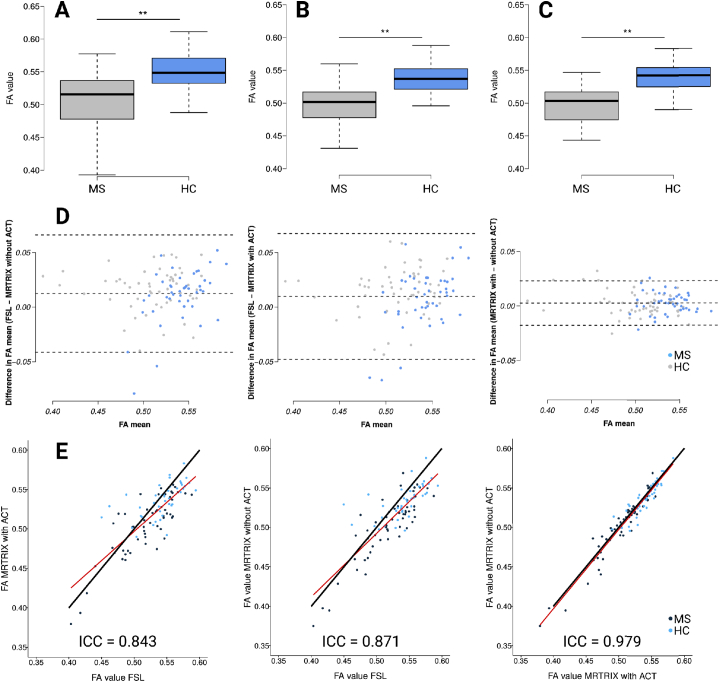
Fig. 5.

Boxplots of the mean fractional anisotropy (FA) for MS patients and HCs; A: FSL; B: MRtrix; C: MRtrix/_ACT; differences were significant (p < 0.001 and 95% confidence interval for all comparisons) D: Bland-Altman plots for FSL and MRtrix (left), FSL and MRtrix/_ACT (middle), and MRtrix/_ACT and MRtrix (right); biggest variances and values of outliers are shown in comparison to FSL, variances of MRtrix/_ACT with MRtrix are much lower, upper and lower dashed line: +/− 1.96 x standard deviation, middle dashed line: mean; outliers are described in the text. E: Scatter plots show multiplicative scale differences (scale shift) for FSL/MRtrix (left) and FSL/MRtrix_ACT (middle) and nearly no differences for MRtrix/MRtrix_ACT(right); black line: 45° calibration line, red line: orthogonal regression line; ICC: intraclass correlation coefficient.

Between-group differences in FA values are shown separately for each procedure using boxplots (Fig. 5A–C).

3.3.3. Per-group differences between procedures

We observed significant differences between FSL and MRtrix for FA (p = .007), MD (p = .004) and RD (p = .001) values in HCs and for FA (p = .001) and RD (p = .012) in MS patients. No significant differences were found between FSL and MRtrix/_ACT except for FA (p = .010) in MS patients. Comparing MRtrix and MRtrix/_ACT, we observed significant differences for all diffusion measures with the exception of FA values in HCs (p = .049) and in MS patients (p = .110, Table 4).

Table 4.

Summary of per-group differences between tracking procedures.

Measure	Group	p-values
		FSL vs. MRtrix	FSL vs. MRtrix/ACT	MRtrix vs. MRtrix/ACT
FA	MS	0.001	0.010	0.110
	HC	0.007	0.059	0.049
MD	MS	0.086	0.996	0.000
	HC	0.004	0.863	0.001
AD	MS	0.979	0.111	0.000
	HC	0.342	0.495	0.002
RD	MS	0.012	0.273	0.003
	HC	0.001	0.410	0.003

Significant differences (bold), Bonferroni-corrected, p-values < 0.0125 (0.05/4); FA: fractional anisotropy; FSL: FSL probtrackx2; HC: healthy controls; MD: mean diffusivity; AD: axial diffusivity; MRtrix: MRtrix without ACT; MRtrix/_ACT: MRtrix with ACT; MS: multiple sclerosis; RD: radial diffusivity. MD, AD and RD are given in 10⁻³ mm²/s.

The Bland-Altman plots (Fig. 5D) showed that the differences between MRtrix and MRtrix/_ACT FA values were lower compared to the differences between MRtrix or MRtrix/_ACT and FSL. Fig. 5E shows scatter plots to facilitate pairwise comparisons between the three procedures. Several outliers indicated differences between the procedures. The similarity of MRtrix/_ACT and MRtrix w.r.t. the FA values was evident (ICC = 0.979). The comparison of FSL with MRtrix (ICC = 0.871) and FSL with MRtrix/_ACT (ICC = 0.843) showed a similar scale shift especially in the higher FA values, with a point of intersection of the regression lines with the identity line on 0.47.

3.4. Relationship between OR lesion volume and OR diffusivity

Table 5 shows correlations between lesion volume and diffusion parameters for each procedure. In the MS patients, we found strong dependencies, which were very similar for the different procedures (FA: negative correlation; MD, AD, RD: positive correlation). Of note, the absolute correlation values were greatest for MRtrix/_ACT for all diffusion parameters. No correlations were found in the HCs.

Table 5.

Correlations of dMRI metrics of the ORs from multiple sclerosis (MS) patients and healthy controls (HC) with the optic radiation (OR) specific FLAIR lesion volume.

		FSL		MRtrix		MRtrix/ACT
		Spearman's ⍴	p-value	Spearman's ⍴	p-value	Spearman's ⍴	p-value
OR FLAIR lesion volume
FA	HC	−0.164	0.288	−0.156	0.313	−0.229	0.135
	MS	−0.488	0.000	−0.650	0.000	−0.692	0.000
MD	HC	0.388	0.009	0.263	0.084	0.377	0.012
	MS	0.715	0.000	0.738	0.000	0.818	0.000
AD	HC	0.133	0.026	0.192	0.211	0.262	0.086
	MS	0.680	0.000	0.683	0.000	0.703	0.000
RD	HC	0.222	0.147	0.102	0.512	0.306	0.044
	MS	0.704	0.000	0.761	0.000	0.819	0.000

p-values < 0.00625 (0.05/8) were deemed to be statistically significant (bold).

3.5. ROC curves and AUC

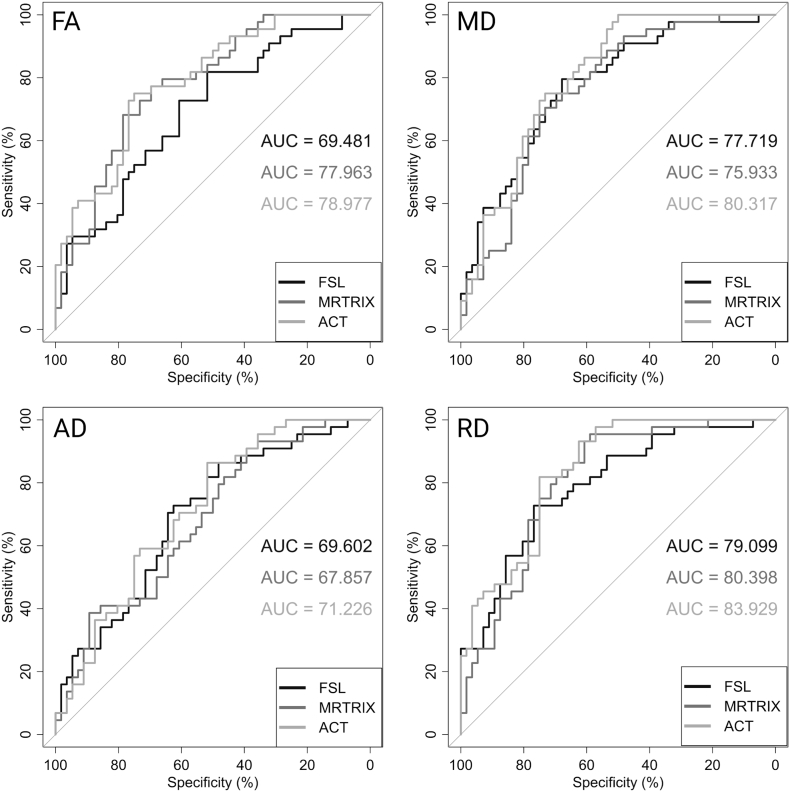
Fig. 6 shows the ROC curves of each diffusivity parameter (FA, MD, AD, RD) for all three fiber tracking procedures. Here, the MRtrix/_ACT method exhibited the highest AUC values (from RD: AUC = 83.929 to AD: AUC = 71.226) for all four diffusion parameters to distinguish both groups (HC and MS patients). The lowest AUC values (from RD: AUC = 79.099 to FA: AUC = 69.481) were reached by the MRtrix (without ACT) procedure.

Fig. 6.

ROC curves and AUC values for each diffusion parameter and all procedures. The ROC curves and AUC values were calculated comparing HC and MS patients based on fractional anisotropy (FA), axial (AD), mean (MD) and radial diffusivity (RD). ROC: receiver operating characteristics; AUC: area under the curve.

3.6. Relationship between clinical, OCT and MRI values

We did not find any significant correlations between visual acuity, RNFL thickness, V1 thickness, lesion and FA (independently from the tracking procedure used; Table 6).

Table 6.

Correlations for the FA of the ORs from multiple sclerosis (MS) patients and healthy controls (HC) with the Visus, RNFL (μm) and V1 (mm).

		Visual acuity	p-value	RNFL	p-value	V1	p-value
FA
FSL	HC	−0.057	0.757	−0.056	0.752	0.199	0.455
	MS	0.090	0.511	0.025	0.867	0.304	0.023
MRtrix	HC	−0.050	0.786	−0.114	0.522	0.199	0.207
	MS	0.168	0.216	0.281	0.059	0.252	0.061
ACT	HC	−0.093	0.613	−0.045	0.799	0.212	0.177
	MS	0.222	0.100	0.292	0.049	0.290	0.030

Pearson correlation and the p-values are given. ACT: MRtrix/ACT; FA: fractional anisotropy; mean lesion burden is given in ml. p-values ≤.008 ≅ 0.05/6 were deemed to be statistically significant.

4. Discussion

The aim of our study was to compare the performance of MRtrix/_ACT with two other probabilistic fiber tracking procedures (MRtrix and FSL) regarding their localization precision and characterization of the OR, especially in MS patients with WM lesions. All three methods enabled a reliable localization of the OR in both MS patients and controls. With regard to the anatomical accuracy of the reconstructed ORs, both visual inspection and a comparison of the distances between the anterior Meyer's loop and temporal pole showed that ACT provides more anatomically plausible pathways compared to the other two procedures. Furthermore, all procedures detected increased MD, AD and RD as well as decreased FA within the OR in MS patients compared to controls, indicative of the MS-induced WM damage (Horsfield and Jones, 2002). However, the observed between-group differences were most pronounced when using ACT. Similarly, in a ROC curve analysis based on the within-tract diffusion parameters, the ACT-based procedure showed the highest discriminatory performance. As a result, ACT also appears to improve the diagnostic value of OR tractography as compared to the other two procedures.

4.1. Clinical background

WM changes are thought to reflect additional WM pathologies, such as trans-synaptic degeneration induced by retinal damage after optic neuritis (Kolbe et al., 2016; Tur et al., 2016; Oertel et al., 2019) or by primary V1 thinning (Balk et al., 2015). Overall, the observed MS-related RNFL thickness and WM changes in the OR are in good agreement with previous studies (see Supplementary Material, Table 7). Such changes are associated with visual disability (Reich et al., 2010; Lennartsson et al., 2014), but are often analyzed in conjunction with the OR lesion burden (Wang et al., 2018; Klistorner et al., 2015; Rocca et al., 2013; Sinnecker et al., 2014). However, in contrast to previous investigations (Jenkins et al., 2011; Pfueller et al., 2011; Gabilondo et al., 2014; Balk et al., 2015), we did not observe V1 atrophy. Such conflicting findings regarding regional cortical changes may be explained either by a larger WM lesion burden within the OR (Jenkins et al., 2011) or a larger sample size (Balk et al., 2015).

4.2. Anatomical constraints in fiber tractography

Traditionally, to enhance the anatomical plausibility of fiber reconstructions, the generated tracks are often filtered using waypoint ROIs based on anatomical knowledge relevant to the fiber tracts studied (Conturo et al., 1999; Catani et al., 2002; Hagmann et al., 2003; Wakana et al., 2007). User-defined constraints can also be placed on other tract-specific parameters such as path length or curvature to filter tractography results (Sherbondy et al., 2008). These techniques enable highly customized filtering, tailored to the application, research question, or data set. However, significant additional efforts are often necessary to define appropriate ROIs and adjust the constraints and parameters with regard to the targeted fiber tracts (Jones and Cercignani, 2010). For example, the high curvature of the Meyer's loop requires an angle of at least 90° to facilitate its reconstruction in an anatomically plausible manner (Lilja et al., 2014).

In contrast, ACT is a more general technique improving the overall anatomical plausibility independent of application-specific considerations and in a fully automated fashion. In many cases, ACT obviates the need for additional filtering based on constraints tailored to the targeted fiber tract. For example, waypoint ROIs were employed in the current study to filter out implausible streamlines, e.g., extending into the CSF or parahippocampal regions, that would otherwise occur when using FSL or MRtrix without ACT. In the case of ACT, this was not necessary, as the results with and without an additional waypoint ROI were virtually identical. It appears that the anatomical constraints employed by ACT were very successful in preventing the generation of implausible fiber tracks. In fact, the ACT-based fiber reconstructions appeared anatomically more accurate, even, than the results from the other two procedures, which employed filtering. At the same time, the avoidance of such filtering improves the usability and also removes a source of rater-dependence, if the filtering ROIs are not defined in a fully automated fashion. Still, it may be beneficial in some cases to employ target-specific filtering in addition to ACT.

For example, Martinez-Heras et al. (2015) used MRtrix3 with ACT to reconstruct the OR. In sharp contrast to our results, they report that many implausible streamlines were generated despite using ACT, which they remedied using a post-processing routine based on anatomical exclusion criteria designed to filter out anatomically implausible streamlines. In addition to the difference in sample size (Martinez Heras et al.: 5 MS patients and 10 controls; the current study: 28 MS patients and 22 controls), there are a number of important methodological differences, some of which may be responsible for the substantially different performance of ACT. First, there are differences in the dMRI acquisition hardware (Martinez-Heras et al.: Siemens MAGNETOM Trio 3 T; this study: Siemens MAGNETOM Prisma 3T) and protocols (Martinez-Heras et al.: one b-value 1500 s/mm², 1 .5mm isotropic voxel, high resolution acquisition with TE/TR = 110/16600 ms, 32 channel coil; this study: two b-values 800 and 1200 s/mm², 1 .6mm isotropic voxel, TE/TR = 51/8200 ms, 64 channel coil) used. The much higher gradient strength (80 mT/m for the Prisma vs. 45 mT/m for the Trio) allowed us to use a much lower TE, which, in turn, results in a significantly higher signal-to-noise ratio. Second, a different segmentation method was used (Martinez-Heras et al.: 5ttgen freesurfer; this study: 5ttgen fsl). Third, the version of MRtrix3 that was used for the analysis may have been older than the one used in the current study. Therefore, potential improvements to the relevant code in MRtrix3 are another possible source for the observed differences in ACT performance. Note, in this context, that Martinez-Heras et al. apparently did not use ACT's option to specify lesion probability maps, which may have had undesirable effects on the tractography due to tissue type misclassifications in the affected areas. Finally, the definition of seed and target ROIs were also substantially different. While Martinez-Heras et al. used the entire thalamus (including the LGN) to define the start ROIs, we used only the LGN. We believe that the substantially larger seed ROIs used by Martinez-Heras et al. may be the most likely reason for the poor performance of ACT in their study.

Filtering of tracts during post-processing was successfully employed to enhance the anatomical plausibility of OR reconstructions in MS (Klistorner et al., 2015; Klistorner et al., 2016; Martinez-Heras et al., 2015; Kuchling et al., 2018) and in other applications (Winston et al., 2011; Lim et al., 2015; Renauld et al., 2016; Oertel et al., 2017). However, as mentioned above, a potential disadvantage of the ROI-based filtering arises if ROIs are defined in a user-dependent fashion, which can hamper both usability and reproducibility. Since MRtrix/_ACT is a fully automated method, we would recommend the evaluation of its performance in a given application first. If it performs reasonably well, the development of more targeted, potentially user-dependent methods may prove unnecessary. In the case of the OR, our results, in contrast to those of Martinez-Heras et al. (2015), indicate that ACT (by itself) is, in fact, sufficient to ensure the anatomical plausibility of the reconstructed tracts.

4.3. Other methods for OR localization

At the moment, we are not aware of any commonly accepted standard to perform the tractography of the OR (Lilja et al., 2014). Upon defining OR segments for each data set, one faces the problem of the multitude and heterogeneity of options and settings in each software package (Jones and Cercignani, 2010; Jones et al., 2013). Where possible, the same or equivalent settings were chosen across procedures to enhance comparability.

Kuchling et al. (2018) compared two TBSS-based atlas procedures and two tractography based procedures (ConTrack (Sherbondy et al., 2008) and constrained spherical deconvolution tractography). No lesions were included into the fiber tracking procedure, which could be very important in patients with great lesional tissue. Interestingly, Kuchling et al. come to the conclusion that there is no clearly superior method. Depending on the group of patients acquired, false-positive or false-negative results may result in group assignment. To assess correlations between T2 lesions and diffusion values, TBSS-based procedures appear most promising, while CSD-PROB (MRtrix3 without ACT modified after Martinez-Heras) offers the best performance for between-group comparisons. As another aspect, Wang et al. (2018) compared probabilistic tractography-based and template-based OR segmentation in MS patients. Compared to the former, the latter yielded larger OR segments, which also encompassed more lesional tissue. In line with this, the template-based OR segments resulted in higher OR lesion load estimates than the tractrography-based OR segments.

4.4. Impact of regional WM lesions and the diagnostic value

Interestingly, both the correlation between the patients' OR lesion burden and within-tract diffusion values and the discriminatory power between groups were greater in the case of MRtrix/_ACT as compared to the other two procedures. Although the main focus of this work was to assess the ability of different procedures to accurately reconstruct the OR in MS patients, these results underline the favorable role of ACT in enhancing the ability to distinguish between MS patients and controls as a diagnostic approach (Kuchling et al., 2018).

4.5. Problem of ROI comparability

Another challenge in comparing different fiber tractography procedures lies in appropriately thresholding the corresponding density maps to obtain comparable OR segments. It appears that smaller differences in ROI size between procedures are acceptable when computing within-tract statistic based on density-weighted averaging. In doing so, the influence of marginal areas, in which most of the differences are usually located, is limited, thus facilitating more sensible comparisons of the average diffusion parameters. In addition to considering other thresholding strategies, e.g., to match the ROIs in size, a further alternative would consist in a voxel-based analysis of the density maps, thus avoiding the thresholding problem altogether. However, this would require to spatially normalize either the diffusion data or the density maps (Raffelt et al., 2017. Gajamange et al., 2017). Since the spatial normalization is adversely affected by the abovementioned MS-related pathologies, we decided to forego this option for the current study.

5. Conclusion

In this study, we found that ACT facilitates biologically plausible reconstructions of the OR in both HCs and MS patients. It provides a more realistic basis for the assessment of between-group differences and higher discriminatory performance as compared to two more commonly used fiber tracking methods.

Ethical publication statement

We confirm that we have read the Journal's position on issues involved in ethical publication and affirm that this report is consistent with those guidelines.

Conflicts of interest

Marc Pawlitzki received research grants from Novartis and Genzyme, speaker honoraria and travel/accommodations/meeting expenses and speaker honoraria by Novartis, Biogen Idec., MERCK Serono.

The other authors declare that there is no conflict of interest.

Appendix A. Supplementary data

Supplementary Material