“Physiological Dysregulation” as a Promising Measure of Robustness and Resilience in Studies of Aging and a New Indicator of Preclinical Disease

Abstract

Recently suggested novel implementation of the statistical distance measure (D_M) for evaluating “physiological dysregulation” (PD) in aging individuals (based on measuring deviations of multiple biomarkers from baseline or normal physiological states) allows reducing high-dimensional biomarker space into a single PD estimate. Here we constructed D_M using biomarker profiles from FRAMCOHORT (Framingham Heart Study) and CHS (Cardiovascular Health Study) Research Materials obtained from the NHLBI Biologic Specimen and Data Repository Information Coordinating Center, and estimated effect of PD on total survival, onset of unhealthy life (proxy for “robustness”) and survival following the onset of unhealthy life (proxy for “resilience”). We investigated relationships between PD and declines in stress resistance and adaptive capacity not directly observed in data. PD was more strongly associated with the onset of unhealthy life than with survival after disease suggesting that declines in robustness and resilience with age may have overlapping as well as distinct mechanisms. We conclude that multiple deviations of physiological markers from their normal states (reflected in higher PD) may contribute to increased vulnerability to many diseases and precede their clinical manifestation. This supports potential use of PD in health care as a preclinical indicator of transition from healthy to unhealthy state.

Human longitudinal studies of health and aging available nowadays have collected repeated measurements of numerous biomarkers, along with follow-up information on mortality, onset of diseases and other health and aging-related variables. This provides opportunity for analyses of dynamics of biomarkers in relation to mortality and other time-to-event outcomes. Such analyses can use different analytic approaches, based on individual biomarkers, as well as on cumulative measures combining the information on multiple biomarkers, see recent review in (1). Recently suggested novel implementation of the statistical distance measure (denoted as D_M) allows for estimating the level of “physiological dysregulation” (PD) in aging individuals based on the information about multiple biomarker profiles (2,3). D_M reduces the high-dimensional biomarker space into a single measure of PD that summarizes the information about biomarker deviations from a specified “physiological norm” or a baseline state. D_M is a continuous measure, and therefore, it conceptualizes PD differently than, for example, allostatic load which can also be considered as an index of PD (4) and which counts “high-risk” values of biomarkers based on either empirical or clinical practice thresholds. Available longitudinal data can be used to study the relationships between PD and longevity and other health and aging-related outcomes, including those representing declines in physical resilience and robustness, which are key characteristics of biological aging (5–7).

Physical (or biological) resilience could be defined as one’s ability to bounce back after a deviation from a normal or baseline physiological state, or quickly and completely recover after stress, damage or an adverse health event (5–7). Physical resilience declines during aging, meaning that elderly individuals are able to survive and recover after an adverse health event less quickly and completely than they were able to do at younger ages. The decline in resilience is a universal feature of aging, which contributes to an increase in vulnerability to death with age even in apparently healthy individuals, and to longevity limits (a.k.a. maximum longevity). Phenotypes characterizing resilience can be studied at different levels of biological organization (cell, tissue, organ, system, body), as well as may represent more than one such level (6,8,9). For instance, the speed and quality of DNA repair would characterize resilience at the cellular level; the ability to restore blood pressure back to normal after a deviation caused by cold stress, or the ability to quickly heal a hip fracture, would represent resilience at the tissue or organ levels; and the ability to survive following an adverse health event would characterize resilience at the whole body level. Given the integrated nature of body functioning, the latter type of resilience will be the focus of this article. Indeed, a localized damage (such as hip fracture) may affect not only the resilience of respective tissue but sometimes lead to weakening of the whole body, so that even successful healing of the specific body part (hip) may not necessarily mean a full recovery at the whole body level. It is well known that elderly people with fractures continue to have a significant mortality excess many years after the injury (10,11), suggesting additional factors (besides the fracture per se) that may negatively affect resilience. We thus decided to investigate resilience at an aggregated level, as the ability to survive following the onset of unhealthy life, and will use this definition as a proxy for the whole body physical resilience in this study, being fully aware of limitations of this (and any other) definition of resilience.

Physical robustness could be defined as the ability to resist the deviation from the baseline or the “normal” physiological state and shield oneself from an adverse health event by preventing it from happening in first place, thus avoiding its destructive consequences whatsoever (5). As with resilience, robustness can be studied at different levels of biological organization (cell, tissue, organ, system, body). For instance, the ability of skin cells to avoid UV-induced DNA damage may represent robustness at the cell level; the ability to prevent a large deviation of blood pressure from its baseline after a cold stress would characterize robustness at the tissue or organ level; and the ability to protect oneself from a disease occurrence would characterize robustness at the whole body level. In this article, we will focus on an aggregated indicator of the whole body robustness, “onset of unhealthy life,” which refers to the onset of any disease belonging to this group: cancer, cardivascular diseases (CVDs), diabetes. The whole body robustness declines during aging; it, however, may improve in specific health domains. For instance, vulnerability to particular infectious disease (eg, flu) may diminish following the immunization against this disease, so the robustness in relation to such disease may become better later in life. Some internal exposures may also change during aging in a way improving the robustness in relation to particular health disorder. For example, the drop in internal exposure to estrogens during menopause may favor the decline in risk of endometrial cancer later in life, which means an improved robustness in relation to this cancer (12,13).

Aging changes in robustness and resilience are obviously mutually connected and may affect each other, eg, through the use of the same body resource (reserve). For instance, getting sick too often would be an indicator of low robustness. In order to recover from the illness, the body needs to use its resources, such as stem and immune cells reserves. When an appropriate portion of the body reserves is spent on the recovery process (resilience) and restoration of health (robustness), this partial loss of the reserves may diminish the organism’s ability to respond to and recover from the next health problem, which in the long-term may contribute to the decline in resilience limiting longevity of this organism.

Analysis of the dynamics of D_M in relation to the proxies for physical robustness and resilience, such as disease onset and survival after disease, respectively, can be performed using appropriate analytical techniques such as the Cox regression model with time-dependent covariates or a recently developed biodemographic model of aging known as the stochastic process model (SPM) (14). The latter approach can provide additional insights relevant in research on aging as the model conceptualizes several aging-related mechanisms in its structure which allow evaluation of “hidden” characteristics of aging-related changes not otherwise available in the data. D_M has recently been implemented in the framework of SPM (15). Application of D_M in SPM allows for investigation of relationships between PD and other aging-related characteristics, not directly observable in data (such as decline in stress resistance and adaptive capacity), in the context of proxies for resilience, robustness, and total mortality.

The goal of this study was to measure PD in aging individuals, based on D_M, and investigate relationships between the level of PD and onset of unhealthy life (proxy for robustness), survival following the onset of unhealthy life (proxy for resilience), and total mortality, using data on dynamics of biomarkers available from two large longitudinal human studies: Framingham Heart Study (original cohort) and Cardiovascular Health Study (CHS), and applying two approaches: the Cox proportional hazards model, and the SPM.

Data and Methods

Data

In this study, we used the FRAMCOHORT (Framingham Heart Study Cohort) Research Materials (version 2017b) and the CHS Research Materials (version 2015a) provided by the National Heart, Lung, and Blood Institute’s (NHLBI) Biologic Specimen and Data Repository Information Coordinating Center (BioLINCC) resource (https://biolincc.nhlbi.nih.gov/home/). Details are provided in Supplementary Material.

Proxies for Robustness and Resilience

As mentioned, physical robustness and resilience can be described by various biomarkers representing different levels of biological organization (cell, tissue, organ, system, body; see Introduction for detail). In this study, we focus on the robustness and resilience at the whole body level, and use “onset of unhealthy life” as a proxy indicator of the robustness, and “survival following the onset of unhealthy life” as the proxy indicator of the resilience.

We define the “age at onset of unhealthy life,” as the age of first occurrence of any disease from this group of major complex diseases: cancer, CVD (including coronary heart disease, CHD, stroke or congestive heart failure, CHF), and type 2 diabetes. If the individual did not contract any of these diseases during the observation period, then she or he was considered censored at the age of the last follow-up or death. Individuals who have cancer or CVD before the first exam, or diabetes at the first exam, were excluded from the analyses. The analyses of survival after disease onset were limited to the individuals who acquired any of respective diseases during the follow-up period.

In addition, we analyzed data on all-cause mortality as the ultimate outcome. Note that in ref. (15) we reported results of analyses of D_M and mortality in the Framingham Heart Study original cohort using SPM. These results are different from those reported in this paper because the present study uses more recent data with longer follow up and more examinations (physiological measurements).

Table 1 shows sample characteristics of FRAMCOHORT and CHS. The numbers related to the entire follow-up period correspond to the analyses using the Cox regression models and the continuous-time SPM. The numbers during the specific period since the last observation of D_M (2 years for FRAMCOHORT and 1 year for CHS) correspond to analyses of the discrete-time SPM.

Table 1.

Characteristics of Framingham Heart Study Original Cohort (FRAMCOHORT) and Cardiovascular Heart Study (CHS) Used in the Analyses

Characteristics	FRAMCOHORT			CHS
	Females	Males	Total	Females	Males	Total
Number of individuals	2,785	2,294	5,079	3,329	2,466	5,795
Number of deaths during entire follow-up period	2,653	2,252	4,905	2,469	2,112	4,581
Number of individuals with onset of “unhealthy life” during entire follow-up period	2,015	1,841	3,856	2,192	1,756	3,948
Number of individuals with onset of “unhealthy life” who died during entire follow-up period	1,535	1,467	3,002	1,178	1,182	2,360
Number of deaths since last observation of DMa	1,335	1,286	2,621	749	863	1,612
Number of individuals with onset of “unhealthy life” since last observation of DMa	1,583	1,524	3,107	1,313	1,242	2,555
Number of individuals with onset of “unhealthy life” who died since last observation of DMa	982	974	1956	495	579	1,074
Number of observations of DM in the total sample	35,142	26,586	61,728	9,986	7,404	17,390
Number of individuals in the “reference population”	1,103	908	2,011	1,330	854	2,184
Number of observations of DM in the “reference population”	1,039	858	1,897	1,319	847	2,166

Note: ^aFRAMCOHORT numbers reflect 2 y after last observation of the measure of physiological dysregulation (D_M); CHS numbers reflect 1 y after last observation of D_M.

Mahalanobis Distance (D_M) as Measure of PD

We used D_M (the Mahalanobis distance, see refs. (16,17)) to evaluate deviations of multiple biomarkers from a baseline physiological state and reduce the high-dimensional biomarker space into a single estimate representing the level of PD in the aging body. Details about the rationale of the use of the D_M as a measure of PD and its characteristics are given in works by Cohen and colleagues (2,3,18,19). In this study, we are interested in effects of longitudinal dynamics of D_M. Therefore, for our analyses, we selected physiological variables measured at a sufficient number of exams in both datasets and whose dynamic characteristics have been shown to be related to the outcomes of our interest (mortality risk and risk of onset of “unhealthy life”) in our earlier applications of SPM to the Framingham data, see eg, (20–24). Eight physiological variables were used in calculations of D_M: blood glucose (BG), body mass index (BMI), total cholesterol (TC), diastolic blood pressure (DBP), hematocrit (HC), pulse pressure (PP), systolic blood pressure (SBP), and ventricular rate (VR). As there is a linear relationship between DBP, SBP, and PP, three different D_M variants were constructed which contain two out of these three: D_M1: BG, BMI, TC, DBP, HC, SBP, VR; D_M2: BG, BMI, TC, DBP, HC, PP, VR; and D_M3: BG, BMI, TC, HC, PP, SBP, VR. We repeated all computations using these three D_M variants. The results were similar in all three variants; thus, we keep those with D_M1 in the main text and show D_M2 and D_M3 in Supplementary Material. Supplementary Material also contains more details about calculations of D_M.

Statistical Analysis

We ran the Cox proportional hazards model with D_M as the time-dependent covariate. Sex (coded as 0 – females, 1 – males) was used as an additional covariate in FRAMCOHORT. In CHS, we also adjusted for race (coded as 0 – whites; 1 – all other). Age at the first exam was used as the left truncation variable in analyses of mortality and robustness. Time since onset of “unhealthy life” was used as the time variable in the model for resilience and age at onset of “unhealthy life” was included as a covariate in such analyses. Analyses with the Cox model were done using SAS 9.4.

We also applied the SPM (14) to investigate the dynamic relationships between D_M and other aging-related characteristics, not directly observable in data (such as declines in stress resistance and adaptive capacity), in the context of proxies for resilience, robustness and total mortality. We used specification of SPM as in (15). Analyses with SPM were performed using the discrete-time specification of the model (25) in MATLAB R2017b and using the continuous-time specification in a recently developed R-package stpm (https://cran.r-project.org/web/packages/stpm/index.html) (26) (Supplementary Material).

Results and Discussion

The average D_M is 3.19 (SD: 1.15) in FRAMCOHORT and 2.6 (0.87) in CHS. Note that the age range in reference populations is different in the two studies hence D_M variables are on a different scale. This is also reflected in the dynamics of these variables with age in the two studies. On average, D_M changes 0.048 per year in FRAMCOHORT and 0.029 in CHS.

To check whether D_M adds anything in terms of predictive accuracy compared to calendar age, we computed areas under the receiver operating characteristic curves (AUC) for the models with and without D_M (using the last observed value before respective event in logistic regression adjusted also for age, sex and race [in CHS only]). Comparisons revealed significantly better predictive accuracy of the models with D_M for all outcomes in both studies: 0.674 versus 0.645 (p = .013) for mortality in FRAMCOHORT; 0.65 versus 0.642 (p = .017) for “robustness” in FRAMCOHORT; 0.719 versus 0.681 (p = .008) for “resilience” in FRAMCOHORT; 0.762 versus 0.741 (p < .0001) for mortality in CHS; 0.576 versus 0.552 (p = .0002) for “robustness” in CHS; and 0.643 versus 0.583 (p < .0001) for “resilience” in CHS. We note that such analyses, even though they indicated a significant improvement in predictive accuracy, are limited in scope as they do not take the dynamic characteristics of D_M into account and also are based on a limited number of biomarkers. More detailed analyses based on a larger panel of biomarkers in a different study will be reported elsewhere.

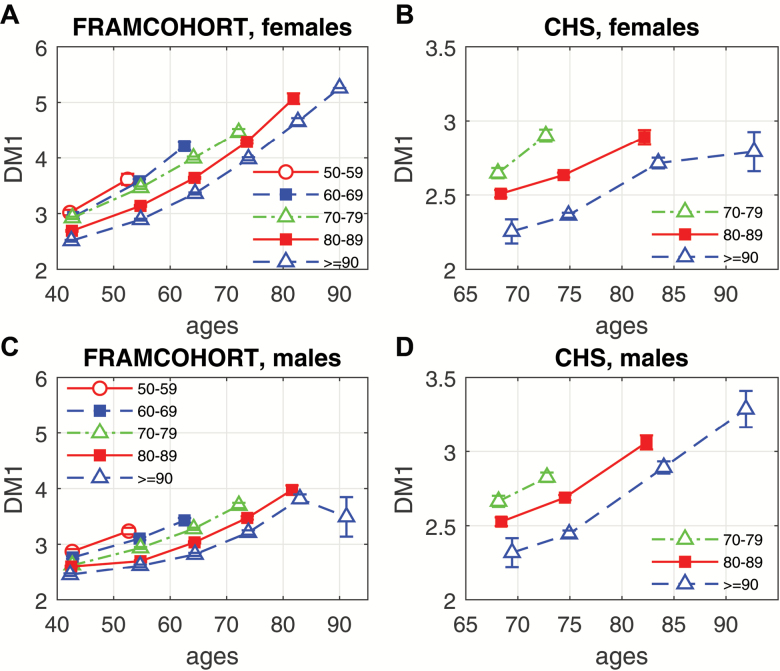
We also compared average age-trajectories of PD (represented by D_M) for longer- versus shorter-lived study participants (Figure 1). One can see from this figure that those individuals who survived to the oldest old age (ie, lifespan ≥ 90) may have a better (lower) initial level of PD, or slower increase of PD over the life course, or both. The figure also shows that the shorter- and longer-lived people may sometimes have similar initial levels of the dysregulation (see, eg, D_M trajectories for lifespan = 50–59 vs lifespan = 80–89 in Framingham males around the age 45) but different rates of their changes with age. This indicates the importance of considering both baseline D_M and its age-dynamics as predictors of longevity.

Figure 1.

Average age-trajectories of physiological dysregulation (represented by D_M) for longer- vs shorter-lived study participants: (A) females in FRAMCOHORT; (B) females in CHS; (C) males in FRAMCOHORT; (D) males in CHS. Each trajectory presents average values (±SE) of D_M in 10-y age intervals for individuals dying at different ages shown in the legend (“50–59” to “80–89”) or surviving until age 90 (“≥90”).

Table 2 summarizes the results of analyses of D_M in the Cox regression model. The results indicate that measures of PD (D_M) constructed using data on biomarkers in two longitudinal studies (FRAMCOHORT and CHS) and two distinct reference populations (ages at baseline below 40 in FRAMCOHORT and 65–70 in CHS) show significant negative effect on onsets of “unhealthy life” (proxy for robustness), survival following onset of “unhealthy life” (proxy for resilience; however, it is only marginally significant in CHS), and total mortality in the Cox regression analyses. In FRAMCOHORT, hazard ratios (for a unit increase in D_M) tend to be highest for robustness and lowest for resilience with mortality in between. In CHS, the hazard ratios for total mortality are the highest, followed by those for robustness and resilience. There was also a marked similarity between results obtained in FRAMCOHORT and CHS, specifically associations between PD and “robustness” were of much higher significance and effect size than the associations between PD and “resilience” (Table 2).

Table 2.

Results of Analyses of the Measure of Physiological Dysregulation (D_M) in the Cox Regression Model in Applications to Mortality, Onset of “Unhealthy Life” (Considered as a Proxy for Robustness) and Survival Since Onset of “Unhealthy Life” (Considered as a Proxy for Resilience) in Framingham Heart Study Original Cohort (FRAMCOHORT) and Cardiovascular Heart Study (CHS)

Study	Trait	Beta	SE	p-value	HR (95% CI)
FRAMCOHORT	Mortality	0.209	0.022	7.2E-21	1.23 (1.18, 1.29)
	Robustness	0.297	0.017	6.3E-72	1.35 (1.3, 1.39)
	Resilience	0.136	0.03	7.6E-06	1.15 (1.08, 1.22)
CHS	Mortality	0.404	0.05	8.1E-16	1.5 (1.36, 1.65)
	Robustness	0.277	0.036	2.0E-14	1.32 (1.23, 1.42)
	Resilience	0.212	0.099	3.2E-02	1.24 (1.02, 1.5)

Note: Beta is the estimate of respective regression coefficient in the Cox model (adjusted for sex in FRAMCOHORT, sex and race in CHS, plus age at onset of “unhealthy life” in case of “resilience” in both studies); results shown in the table are for D_M1 (results for D_M2 and D_M3 are in Supplementary Material); HR is hazard ratio for a unit increase in D_M (95% confidence interval in brackets) which roughly corresponds to SD of D_M in the samples (1.15 and 0.87 in FRAMCOHORT and CHS, respectively).

These results indicate that simultaneous deviations of multiple physiological markers from their normal or baseline states may reflect a systemic (whole-body) level of vulnerability to a transition from healthy to diseased state (rather than the vulnerability to a particular disease), and to a lesser extent influence recovery from such diseased state.

The analyses by the Cox model provide general evidence that D_M is an important variable affecting robustness, resilience, and total mortality. Applications of SPM to these data allow investigation in more detail of how this measure can be related to hidden aging-related processes in an organism. Table 3 presents results of analyses of D_M in SPM showing parameter estimates and the results of testing of different hypotheses (see Notes after the table for explanations of symbols, or the absence of those, used in different columns of the table, and Supplementary Material for description of parameters of the model).

Table 3.

Results of Analyses of the Measure of Physiological Dysregulation (D_M) in the Stochastic Process Model (SPM) in Applications to Mortality, Onset of “Unhealthy Life” (Considered as a Proxy for Robustness) and Survival Since Onset of “Unhealthy Life” (Considered as a Proxy for Resilience) in Framingham Heart Study Original Cohort (FRAMCOHORT) and Cardiovascular Heart Study (CHS) (see footnotes [a-c] below)

Study	Trait	ln aµ0	b µ0	b Sex	b Race	a Q	b Q	a Y	b Y	σ0	σ1	a f1	b f1
FRAMCOHORT	Mortality	−11.05	0.105	1.99		−1.76†	0.63†	−0.19	1.04†	0.95	0.58	2.12†	0.05†
	Robustness	−7.71	0.07	1.46		−10.94†	3.91†	−0.2	1.17†	0.91	0.55	2.18†	0.04†
	Resilience	−6.9	0.048	1.13		7.76†	−0.53	−0.18	0.6	1.22	1.39	2.44†	0.04†
CHS	Mortality	−13.4	0.121	2.36	1.39	−4.92†	1.76*	−0.27	0.002	0.91	0.58	1.41†	0.03†
	Robustness	−5.54	0.033	0.94	0.09	−1.67†	3.81	−0.28	0.03	0.9	0.56	1.43†	0.03†
	Resilience	−9.97	0.12	0.7	0.36	30.87*	0.08	−0.29	0.03	0.9	1.03	1.91†	0.02§

Notes: (a) The estimates of some parameters are rescaled for better visibility in the table: $a_Q$ are multiplied by 10⁴; $b_Q$ are multiplied by 10⁵; $b_Y$are multiplied by 10³.

(b) The symbols after the numbers in the following columns of Table 1 denote p-values (evaluated by the likelihood ratio test) for different null hypotheses:

Column “$a_Q$” : null hypothesis – zero quadratic part of the hazard, ie, $Q(t)=0$ ($a_Q=0$ and $b_Q=0$);

Column “$b_Q$” : null hypothesis – age-independent J-shape of the hazard, ie, $Q(t)=a_Q(b_Q=0)$;

Column “$b_Y$” : null hypothesis – no aging-related decline in the adaptive capacity, ie, $a(t)=a_Y(b_Y=0)$;

Column “$a_{f_1}$” : null hypothesis – systemic dysregulation in an organism, ie, $f_1(t)=0$ ($a_{f_1}=0$ and $b_{f_1}=0$

Column “$b_{f_1}$” : null hypothesis – age-independent level of systemic physiological dysregulation, ie, $f_1(t)=a_{f_1}(b_{f_1}=0)$

The symbols in these columns denote: ^†p < .0001; ^§.0001 ≤ p < .001; ^#.001 ≤ p < .01; *.01 ≤ p < .05, for respective null hypotheses. The absence of symbols after the numbers in these columns means that respective p-values exceed .05. Note that all other columns in the table, except the columns mentioned above, are not used to represent information on testing any null hypotheses and therefore they do not contain any symbols.

(c) Results shown in the table are for D_M1 (results for D_M2 and D_M3 are in Supplementary Material).

The table shows that the null hypotheses H0: $Q(t)=0$ (see symbols in column “a_Q”) is rejected for all traits in both datasets (p < .0001 for all cases except resilience in CHS where p = .04). This indicates that there is an additional quadratic term in the hazard rate (equation S3 in Supplementary Material) so that respective traits are not entirely represented by the baseline Gompertz rate ${\text{μ}}_0(t)$ for all variants of D_M. This confirms that D_M captures effects of deviations of physiological variables on respective traits in these two datasets so that non-zero values of D_M result in higher hazard rates for these outcomes compared to the baseline rates at a given age.

The null hypothesis H0: $Q(t)=a_Q$ (see symbols in column “b_Q”) is rejected for mortality and robustness in FRAMCOHORT (p < .0001) and for mortality in CHS (p = .046). In these cases (taking into account that the parameter $b_Q$ is positive), we may conclude that the effect of PD (represented by D_M) on respective risks is age-dependent and that the J-shape of the risk function (ie, as a function of D_M at any fixed age) narrows with age. This pattern indicates that the same level of PD (ie, the same value of D_M) induces a larger increase in the risk at old ages than it does at younger ages (compared to the baseline hazard rate for respective age) so that the organism becomes more vulnerable to deviant dynamics of respective physiological variables in terms of total mortality and onset of “unhealthy life” (“robustness”) (see also refs. (14) and (22)). The results for the resilience trait and for robustness in CHS (ie, older reference population) were nonsignificant which means that in such cases there is not sufficient evidence that the J-shapes change with age.

The null hypotheses H0: $f_1(t)=0$ (see symbols in column “a_f1”) and H0: $f_1(t)=a_{f_1}$(see symbols in column “b_f1”) are rejected in all cases (p < .0001, except resilience in the latter case for CHS where p = .0003). Such deviations of D_M from zero with age indicate the presence of a systemic dysregulation in an organism that forces the trajectories of physiological variables to move away from their “normal values” (as specified in respective reference populations in calculation of D_M). The effect of such dysregulation is that, on average, the values of physiological variables are different from the “normal” values minimizing respective risks so that the resulting hazard rates are higher than they could be in case of physiological variables at the “normal” level (ie, the baseline hazard rates corresponding to zero D_M). The positive and significant values of $b_{f_1}$ indicate that the trajectories of D_M tend to deviate further from zero with age which results in an additional increase in the respective risks at older ages.

The null hypothesis H0: $a(t)=a_Y$(see symbols in column “b_Y”) is rejected (p < .0001) for mortality and robustness in FRAMCOHORT. This means that respective feedback coefficient in equation S2 (see Supplementary Material) becomes smaller (in absolute value) with age. This is interpreted as decline in adaptive capacity in an organism (14,22,27) so that more time is needed for the trajectories of physiological variables to go back to their mean allostatic trajectories $f_1(t)$ at old ages compared to the time needed at younger ages. The results are not significant for the resilience trait in both datasets and for mortality and robustness in CHS. Thus, in this case there is not sufficient evidence to make such conclusion in relation to these traits (still, the estimates of $b_Y>0$ in most cases). As discussed in ref. (15), such mixed results can be partly explained by the inherent complexity of representation of the concept of adaptive capacity in SPM and this stimulates further developments of the methodological framework to address this topic.

Note that in the situation, in which the reference population represents much younger ages, the D_M may not necessarily reflect the level of PD, in a biological sense, but might instead be related to a change in the biological norm with age. Indeed, the “normal” values of a biomarker may be age-specific (see an example of BG in ref. (20)), so that the difference between values of such biomarker in an older versus younger age may potentially be due to the difference between normal age-values of that biomarker. This could be addressed by, for example, selecting the age-specific mean value (or the value corresponding to a lowest mortality risk in a given age) as the reference value, and analyze deviations from this value in the sample of the same age individuals. We are going to apply this alternative approach in our future analysis, and compare it with the current results.

Deviations of biomarkers’ trajectories to higher and lower values may influence the studied outcomes differently which is not considered in the definition of D_M. We note, however, that we use age interval at younger ages to define D_M before such effects can start producing noticeable differences (20). In principle, SPM can accommodate non-symmetric U-shapes of the hazard rate and age-dependent “optimal ranges” (1) to alleviate such situations. Also, for biomarkers that change non-monotonically with age, such as BMI, TC and HC, the D_M between the middle-aged and the oldest old individuals (eg, between 40 and 90 years old) may in principle be less than between the middle-aged and the old individuals (eg, between 40 and 65 years old). This does not mean that the level of PD in the body diminishes towards extreme ages, and people become physiologically more stable but may simply reflect the non-monotonic nature per se of the aging changes in such biomarkers. This could be addressed by selecting the age intervals, at which the biomarkers change monotonically, which generally happens at ages 70+ for the biomarkers used in this study (for examples of the age-trajectories of these biomarkers see ref. (28)).

We note also that the article reports on two types of analyses, the Cox model and SPM. The former does not model the dynamics of the longitudinal variables whereas the latter does using the stochastic differential equation. The actual relationship between the longitudinal variables and time-to-event outcomes can be even more complicated and involve time lag effects, cumulative effects (ie, integrals), rate of change (ie, derivatives), etc. Such effects can be analyzed using, for example, the joint models (29,30), or extensions of SPM which are left for future work.

It is also important to stress that D_M based on multiple biomarkers (which is the focus of this article), as compared to values of individual biomarkers, or D_M values based on a single biomarker—represent conceptually different components of the vulnerability to death, which is a highly heterogeneous trait. That is, D_M based on deviations of multiple biomarkers from their baseline states characterizes level of systemic dysregulation in the body, which does not specifically require a biomarker to be abnormal or take value typical of a pathological state. For the D_M based on multiple biomarkers, each deviation from baseline may in principle lie within a clinically normal range, so that quantity and variety of biomarkers play more of a role in this estimate than manifestation of any individual marker in regard to a particular pathology. Predictive effects of the composite D_M, and the D_M based on individual biomarkers, should not, therefore, be directly compared since they represent different contributors to the heterogeneity of longevity (ie, systemic dysregulation that increases overall vulnerability vs specific metabolic change that increases risk of particular disease). Due to its systemic nature, the D_M based on multiple biomarkers is conceptually closer to the idea of “deficits indices” that represent overall burden of physiological and health problems in the body, no matter how small each problem might be, which together may influence the overall vulnerability to disease and death, see, for example, refs. (31,32).

Concluding Remarks

We found that the level of PD increases with aging in both males and females. Measures of PD (D_M) constructed using data on biomarkers in two longitudinal human studies (FRAMCOHORT and CHS) show significant negative effects on transition from healthy to unhealthy state (proxy for robustness), and to a lesser extent on survival following the onset of unhealthy life (proxy for resilience), and on total mortality in the Cox regression analyses. Analyses of D_M using SPM confirmed its significant effect on mortality, robustness, and resilience and revealed significant relationships with other aging-related characteristics.

This implies that robustness and resilience may have overlapping as well as distinct biological mechanisms, which warrants exploration of genetic background of the PD and its relevance to longevity and disease-related pathways, in subsequent analysis.

Our results also support a potentially important application of PD, or its equivalent, in clinical settings that regularly collect information about repeated measures of patients’ blood tests and results of physical exams over the years (which refers to most primary care facilities in the United States). Currently, health care professionals pay more attention to values of individual biomarkers that correspond to clinical or preclinical manifestations of particular disease (eg, a fasting blood glucose level over 125 mg/dL indicates diabetes, and the range of 110 to 125 mg/dL indicates prediabetes). A more sophisticated approach includes using a cluster of abnormal values of the different biomarkers that occur together, to predict disease risk. Metabolic syndrome could be an example, in which a combination of abnormally increased blood pressure, blood sugar, body fat around the waist and cholesterol and triglyceride levels, is treated as a composite risk factor for heart disease, stroke, and diabetes. The use of PD measures represents an additional step forward because it allows to utilize not only clinically “abnormal” values of biomarkers, but also those deviations from the baseline physiological state, which “individually” would not be considered strong risk factors for disease, but together may significantly contribute to the transition from healthy to unhealthy state.

Our results suggest that such “multiple” deviations of biomarkers from their baseline physiological states (reflected in higher PD levels) may precede clinical manifestation of not just one but many diseases, even if some deviations are small and not clearly abnormal for individual markers. The main informative value of PD for clinicians could, therefore, be in “quantity” rather than in quality of the biomarker deviations. The multiple deviations of biomarkers may signal that regulatory mechanisms are broadly compromised across tissues and systems of the body, which could make a person more susceptible to a variety of diseases (with specific manifestations dependent on individual genetic predisposition and history of exposures). Thus, measures of PD might be used by the primary care physicians as new preclinical indicators of a person’s transition from a healthy to an unhealthy state even in the absence of strong clinical diagnostic markers pointing out to specific pathology.

Funding

This work was supported by the National Institutes of Health (grant numbers R01AG046860, P01AG043352, P30AG034424, and 5P30 AG028716-11). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Conflict of Interest

None declared.