AICM: A Genuine Framework for Correcting Inconsistency Between Large Pharmacogenomics Datasets

Abstract

The inconsistency of open pharmacogenomics datasets produced by different studies limits the usage of such datasets in many tasks, such as biomarker discovery. Investigation of multiple pharmacogenomics datasets confirmed that the pairwise sensitivity data correlation between drugs, or rows, across different studies (drug-wise) is relatively low, while the pairwise sensitivity data correlation between cell-lines, or columns, across different studies (cell-wise) is considerably strong. This common interesting observation across multiple pharmacogenomics datasets suggests the existence of subtle consistency among the different studies (i.e., strong cell-wise correlation). However, significant noises are also shown (i.e., weak drug-wise correlation) and have prevented researchers from comfortably using the data directly. Motivated by this observation, we propose a novel framework for addressing the inconsistency between large-scale pharmacogenomics data sets. Our method can significantly boost the drug-wise correlation and can be easily applied to re-summarized and normalized datasets proposed by others. We also investigate our algorithm based on many different criteria to demonstrate that the corrected datasets are not only consistent, but also biologically meaningful. Eventually, we propose to extend our main algorithm into a framework, so that in the future when more datasets become publicly available, our framework can hopefully offer a “ground-truth” guidance for references.

1. Introduction

One goal of precision medicine is to select optimal therapies for individual cancer patients based on individual molecular biomarkers identified from clinical trials.^1–3 Molecular biomarkers for many cancer drugs are currently quite limited, and it takes many years to identify and validate a biomarker for a single drug in clinical trials.^4,5 Recent pharmacogenomics studies, where drugs are tested against panels of molecularly characterized cancer cell lines, enabled large-scale identification of various types of molecular biomarkers by correlating drug sensitivity with molecular profiles of pre-treatment cancer cell lines.^6–10 These biomarkers are expected to predict the chance that cancer cells will respond to individual drugs.

There have been a handful of similar pharmacogenomic studies since Cancer Cell Line Encyclopedia (CCLE)⁷ and Genomics of Cancer Genome Project (CGP)¹¹ were published in 2012 by the Broad Institute and Sanger Institute, respectively. CCLE included sensitivity data for 1046 cell lines and 24 compounds; CGP included data for almost 700 cell lines and 138 compounds. The following Broad Institute’s Cancer Therapeutics Response Portal (CTRPv2) dataset included 860 cell lines and 481 compounds.^8,12,13 The dataset from the Institute for Molecular Medicine Finland (FIMM) included 50 cell lines and 52 compounds.¹⁴ The new version of Genomics of Drug Sensitivity in Cancer (GDSC1000) dataset included 1001 cell lines and 251 compounds. There have also been similar pharmacogenomics studies specific to particular cancers including acute myeloid leukemia.^15–17

Each dataset is essentially a data matrix, where each row represents one drug, each column represent one cell line, and values are sensitivity measures derived from dose-response curves. IC50 (concentration at which the drug inhibited 50% of the maximum cellular growth) and AUC (area under the activity curve measuring dose response) are commonly used as sensitivity measures. However, recent re-investigation of published pharmacogenomics data has revealed the inconsistency of drug sensitivity data among different studies, raising the concern of using them for biomarker discovery.^18,19 In the recent comparison of drug sensitivity measures between CGP and CCLE for 15 drugs tested on the 471 shared cell lines, the vast majority of drugs yielded poor concordance (median Spearman’s rank correlation of 0.28 and 0.35 for IC50 and AUC, respectively).¹⁸

There have been numerous attempts to address this issue. Mpindi et al. proposed to increase the consistency through harmonizing the readout and drug concentration range.²⁰ They re-analyzed the dose–response data using a standardized AUC response metric. They found high concordance between FIMM and CCLE and reasoned that similar experimental protocols were applied, including the same readout, similar controls. Bouhaddou et al. calculated a common viability metric across a shared log10-dose range, and computed slope, AUC values and found the new matrix could lead to better consistency.²¹ Hafner et al. proposed another metric called GR50 to summarize drug sensitivity and demonstrated its superiority in assessing the effects of drugs in dividing cells.²² Most proposed ideas focused on forming better summarization metric and/or standardizing experiments and data processing pipeline. Unfortunately, standardization methods cannot address the inconsistency issues of existing datasets. Re-summarization methods rely heavily on the assumption that the raw data is correct. But since datasets produced under similar experimental protocols are more consistent with each other, there surely exists some technical noises on the raw data.²⁰ Hence when the overlapping part between datasets grows bigger and the noise sources become more complex, these methods might not work well. Note that most of the studies have focused on the overlaps between CCLE and other datasets, which only contain very limited number of drugs. Novel computational methods correcting large-scale summarized data are therefore in urgent need.

Studies confirmed that drug-wise correlation is poor, but the cell-wise correlation is considerably strong (for example: overlapping cell lines between CTRPv2 and GDSC1000 have a median Spearman’s correlation of 0.553), suggesting the underlying consistency of pharmacogenomics datasets. Inspired by this observation, we developed a novel computational method Alternating Imputation and Correction Method (AICM). Through purely correcting data based on their cell-wise correlation, AICM significantly improves the drug-wise correlation and hence makes the datasets more credible in future work. Furthermore, since AICM works on summarized data, it can easily concatenate with all previous methods proposed to improve the summarization of raw data — just run on the re-summarized data. To the best of our knowledge, this is the first method that leverages cell-wise information into correcting data to address such challenge. We release the code and corrected datasets to the community^a.

2. Method

2.1. Method overview

The main goal is to increase the drug-wise correlation between two datasets, denoted as $A,B\in {ℝ}^{n\times p}-n$ drugs and p cell lines — for convenience. We denote the ith row of matrix A as A_[i,:], then the goal can be formalized into the following problem:

$$\underset{f,g}{\text{max}}\sum _{i=1}^n\text{Corr}(f{(A)}_{[i,:]},g{(B)}_{[i,:]})$$ (1)

This is a more generalized idea than Renyi’s correlation as we define f, g not functions but operations such that $f,g:{ℝ}^{n\times p}\to {ℝ}^{n^{\prime }\times p^{\prime }}$, where $n^{\prime },p^{\prime }\in {\mathbb{Z}}_{+}$. Operations include using a new summarization metric to re-summarize raw data and subsampling the data.

Now, since cell-wise correlation is consistently more concordant across different studies than drug-wise correlation, we can raise one natural question: can we rely on the cell-wise information to correct the datasets so that the drug-wise correlation will also be improved? We denote A^j as the jth column of A and A^J as the union of all column A^j such that j ∈ J, then more precisely, we want to develop some operation f, g such that

$$\underset{f,g}{\text{max}}\sum _{i=1}^n\text{Corr}(f{(A|A^J,B^J)}_{[i,:]},g{(B|A^J,B^J)}_{[i,:]})J\subseteq \underset{k=1}{\overset{p}{\cup }}\left\{k\right\}$$ (2)

$$\text{s.t. }\Vert f(A)-A\Vert \le {ϵ}_A,\Vert g(B)-B\Vert \le {ϵ}_B$$ (3)

where $(\cdot |A^J,B^J),J\subseteq {\cup }_{k=1}^p\left\{k\right\}$ means either partial or all corresponding column information of A and B is given. ‖ · ‖ in (3) denotes an arbitrary matrix norm, and ϵ_A, ϵ_B are some arbitrary tolerance that we allow maximum departure from the original values. We have found that there are considerably large amount of missing data in these datasets. Surprisingly, with some simple linear regression based imputation of these missing data based solely on the cell-wise information, we found increase in drug-wise correlation. This confirmed our hypothesis that cell-wise information can be utilized to correct the datasets. Thus, AICM is developed to accomplish this goal by randomly dropping the parts of one dataset’s column and re-fit based on another dataset’s corresponding column with a simple linear regression with ℓ_∞ norm regularization. ℓ_∞ norm is leveraged to regularize large departure from the original data as it bounds the maximum departure of fitted values from original values. The corrected values are subject to a hard threshold assuming that the data are not completely destroyed by noises, so that the corrected data shall not depart too far from the original value. By repeating such regression process interactively between two datasets, AICM hopes to reveal the true information shared in between these datasets and hence increase the drug-wise consistency.

2.2. Algorithm

The main idea is as described above: we uniformly randomly drop the values from one matrix (response matrix) and use the other matrix’s column (variable matrix) to impute dropped values. We then threshold the imputed values into the final correction by some proportional threshold with respect to the original values of the response matrix. We iteratively repeat this process by swapping the role of response and variable between two matrices. Below are the hyperparameters for the algorithm:

• max iterations ($iter\in {\mathbb{Z}}_{+}$): how many iterations the alternating imputation and correction need to be run.

• dropping rate (r ∈ (0, 1)): what percent of the data from the response matrix should be dropped each iteration

• regularization term (${\lambda }_r\in {ℝ}_{+}$): how much the original value should be taken into account during the regression process

• hard proportional constraint (λ_h ∈ (0, 1)): how many percentage points percent the imputed data can depart from the original value absolutely

And the full algorithm is described in detail as in Algorithm 1. We use a simple linear regression with ℓ_∞ norm (Eq 4) regularization for fitting process. Besides this, one can always use other fitting methods. For example, if one believes sparsity needs to be incorporated, one can use more weights and an ℓ₁ norm, or if one believes there needs to be some group effects across cell lines, one can use an ℓ₁ and ℓ₂ norm penalty. These ideas are similar to the idea of Lasso and Elastic Net.^23,24 However, it is suggested that the objective function of this fitting process should remain convex, since solving non-convex problems would highly likely lead to a local extrema (or even a saddle point) and thus cause disastrous variations among trials.

2.3. Remarks

Although the whole iterative procedures are not convex, the main objective function (4) is convex and hence the solution of this function would be a global minimum with an appropriate solver. Thus (4) can be solved efficiently and accurately by various methods such as proximal gradient algorithm and alternating direction of multipliers (ADMM).^25,26 They have well-established convergence theorems and are available in many open-source (i.e. SCS²⁷) and industrial solvers.²⁸

In the next section, we will show the results of our algorithm on real datasets, as well as synthetic datasets to demonstrate our method significantly increases drug-wise correlation remarkably and does not artificially increase the correlation under certain assumption. We will also show the result is indeed biologically meaningful.

3. Results and Discussion

3.1. Synthetic datasets

The alternative correction procedure (Swap) in AICM essentially agglomerates two datasets. It inevitably gives rise to the concern that the corrected datasets are forced to be similar regardless of the ground truth. For example, one easily questions whether AICM improves the between-group correlation of placebo – it functions as white noise, thus is expected to be uncorrelated between one dataset and another. In addition, the induced randomness (Drop) in AICM might well shake one’s confidence in the stability and reliability of this method. In this section, we utilize synthetic datasets to demonstrate that AICM are free of these hypothetical troubles.

Algorithm 1.

Alternating Imputation and Correction Method (AICM)

Hyperparameter: Dropping rate r, maximum iteration iter, regularization term λr, and hard constraint term λh.

Input: Two data matrices, of both n drugs and p cell-lines with summarized sensitivity data, denote as $A,B\in {ℝ}^{n\times p}$. We denote jth column of two matrices as aj; bj, j ∈ {1, 2,…,p} respectively. We denote the entry at ith row and jth column as Aij and Bij respectively, {i, j} ∈ {1, 2,…,n} × {1, 2,…, p}.

Initialization: For each j ∈ {1, 2,…,p} for all i ∈ {1, 2,…,n} such that Bij is missing while Aij is not, we denote such set as $B_{ij}^{\text{NA}}$, we fit a linear model such that αj, βj maximizes ${\Vert b^j-{\alpha }_j{a}^j+{\beta }_j\Vert }_2$ and then impute the missing values as $B_{ij}^{\text{NA}}={\alpha }_j{A}_{ij}+{\beta }_j$. Then swap the role of A and B and repeat the above process. Now we have two matrices with same missing indices.

for k in {1, 2,… Iter} do

Swap: A → B, B → A.

Drop: Randomly drop r × n × p data uniformly from A, we denote the indices of the dropped data as $\mathcal{D}\subseteq \{1,2,\dots ,n\}\times \{1,2,\dots ,p\}$, and hence dropped data as a set $A^{\text{DR}}:=\left\{{\cup }_{\{i,j\}\in \mathcal{D}}{A}_{ij}\right\}$. In a similar fashion, we denote dropped data of column k as $a_{\text{DR}}^k:=\left\{{\cup }_{\{i,j\}\in \mathcal{D},\forall i\text{ s.t.}j=k}{A}_{ij}\right\}$, we denote the corresponding data in kth column of B as $b_{\text{ADR}}^k$. We fit a set of parameters ${\alpha }_j\in ℝ$, ${\beta }_j\in ℝ$ for each j with the following objective function:

$\underset{{\alpha }_j,{\beta }_j}{\text{min}}\frac{1}{n}{\Vert b^j-\left({\alpha }_j{a}^j+{\beta }_j\right)\Vert }_2+{\text{λ}}_r{\Vert a_{\text{DR}}^j-\left({\alpha }_j{b}_{\text{ADR}}^j+{\beta }_j\right)\Vert }_{\infty }\text{(4)}$

Correction: Set $a_{\text{DR}}^j={\alpha }_j{b}_{\text{ADR}}^j+{\beta }_j$ or each j. We denote the set of corrected value as $\left\{A^{\text{IMP}}\right\}={\cup }_{j=1}^p\left\{a_{\text{DR}}^j\right\}$.

Threshold: For $\{i,j\}\in \mathcal{D}$, we set{AIMP}ij to

${\left\{A^{\text{IMP}}\right\}}_{ij}=\text{max}\left(\text{min}\left(A_{ij},\left(1-{\text{λ}}_h\right)A_{ij}\right),\left(1+{\text{λ}}_h\right)A_{ij}\right)\text{(5)}$

end for

In the most ideal scenario, where there exist no technical or biological noises, the drug sensitivity matrices are expected to be the same across distinct research teams. For simplicity, we assume that the ground truth can be separated into the drug part and the cell part. Then, the observed matrix can be modelled as

$$M=\alpha 1\cdot 1^T+a\cdot b^T+W,$$ (6)

where α is the baseline, $a\in {ℝ}^n$ contains the information about the n drugs, $b\in {ℝ}^p$ summarizes the structure of the cell lines. The matrix α1 · 1^T + a · b^T represents the ground truth of the drug sensitivities. We simulate the ineffective drugs as uncorrelated rows by setting the top m entries of a to 0’s while the other rows associated with non-zero values (hence correlated) in a are regarded as effective drugs. $W\in {ℝ}^{n\times p}$ is a random matrix from a matrix normal distribution which reflects the composite of noise. In this study, we set n = 50, p = 40, m = 10. The details of the data generation process are deferred to supplementary material.

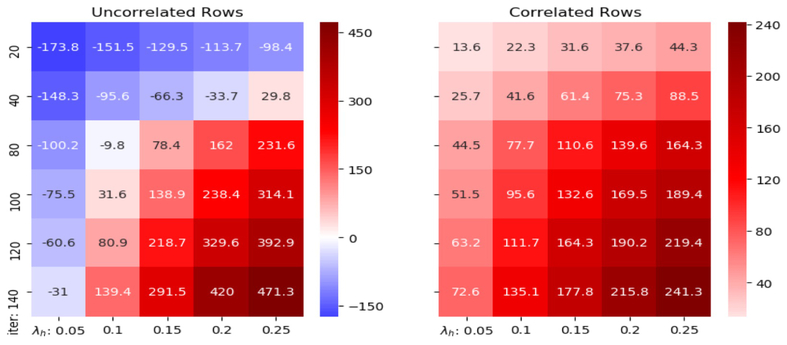
We apply AICM to the synthetic datasets with 30 different combinations of hyperparameters iter and λ_h: iter ∈ {20, 40, 80, 100, 120, 140} and λ_h ∈ {0.05, 0.1, 0.15, 0.2, 0.25}, and repeat the method for 20 times for each combination. With careful selection, we take (iter, λ_h) = (80, 0.1) because this combination gives acceptable reduction on correlations between first ten uncorrelated rows and strong increase of correlations between correlated rows as demonstrated (see Figure 1). In addition, λ_h = 0.1 is a conservative control of the correction step. Note that the normalized distances between the two matrices and the ground truth are reduced to 1.188 and 1.170 respectively after correction (the distances are 1.272 and 1.267 before correction). The decrease in distance is relatively significant, given the fact that we put a hard proportional threshold at 10% for each individual value. Therefore, AICM does help reduce the noise in the observed matrices. Furthermore, the Spearman’s correlation median of the correlated rows is increased to 0.390 from 0.219 with standard deviation 0.021, while the Spearman’s correlation median of uncorrelated rows is reduced to 0.084 from 0.095 with standard deviation 0.010. It indicates that the result is insensitive to the randomness of the dropping procedure in AICM. In Figure 2, the actual shift of the correlation distributions is displayed. On top of incremental correlations of correlated rows, there appear to be reduced correlations of uncorrelated rows after using AICM. It implies that our method not only enhances the real signals, but also exposes the fake ones. Thus, the original concern is eliminated on indiscriminately blending signals between datasets.

Fig. 1:

The percentage change (%) of the medians of the correlations on synthetic datasets with different parameters. x-axis is iter and y-axis is λ_h.

Fig. 2:

Distribution of drug-wise correlations between the synthetic datasets before AICM is applied and after. Note that the darker green bars denote overlap of uncorrelated rows and correlated rows in this histogram.

3.2. Real datasets

We choose the three largest datasets in PharmacoGX: CTRPv2, GDSC1000, and FIMM as case studies.^8,11,13,19 Drug names are compared by first converting to InChIKey via the webchem R package.²⁹ For the GDSC1000 dataset, 60 InChIKeys are subsequently manually retrieved from PubChem. A Python script is prepared and used to retrieve generic cell line “Accession numbers” from Cellosaurus.³⁰ Given that not all cell lines returned Accession numbers, we remove symbols, spaces, and case from the names of the remaining cell lines for improved matching between datasets. For each of the three datasets, their respective IC50 and AUC data are obtained from PharmacoGx. Duplicate experiments are removed from CTRPv2 and GDSC1000 by removing all instances of a certain culture medium. Finally, the six dataframes are filtered for matching cell lines and drugs between each other, yielding 12 dataframes which contain IC50 and AUC between all 3 datasets.

With the optimal hyperparameters fetched from synthetic data, we demonstrate the shift of Spearman’s correlation between 90 drugs overlapping between GDSC1000 and CTRPv2 after AICM is deployed in Figure 3a. The data uses AUC summarization. It is clear that after AICM is deployed, the two datasets become more concordant with each other — this can be observed from both individual drug scatter plot and overall distribution. We also demonstrate two similar graphs between 30 overlapping drugs between CTRPv2 and FIMM, 29 overlapping drugs between GDSC1000 and FIMM with AUC summarization in Figure 3b and 3c.

Fig. 3:

The shift of Spearman’s correlation, both individually and as a distribution, of common drugs between specified datasets before and after AICM is run.

Note that when we calculate the correlation, the original values that are missing are discarded from both matrices for fair comparison. Brief statistics of the original and post-correction drug-wise Spearman’s correlation can be found in Table 1. For significance, we used the cutoff of one-sided test at p-value 0.05 using the significance test of Spearman’s correlation proposed by Jerrold Zar.³¹ The values present what percentage of drugs is significant across two datasets.

Table 1:

Brief statistics of the original and post-correction drug-wise Spearman’s correlation

Datasets	Mean		Median		Significant		Size
	Before	After	Before	After	Before	After	Drug	Cell
CTRPv2 & GDSC1000	0.261	0.410	0.249	0.411	63.33%	90.00%	90	566
CTRPv2 & FIMM	0.485	0.624	0.468	0.585	70.00%	93.33%	30	41
GDSC1000 & FIMM	0.250	0.352	0.278	0.380	27.59%	55.17%	29	47

We demonstrate the scatter plots of some individual drug’s effect on cell lines before and after AICM correction in Figure 4, we can indeed see the scatter plots become more concordant across datasets. We color the plots in a similar fashion as Safikhani et al.: we use blue (sensitive) to denote both datasets ≥ 0.2 and red (resistant) for both ≤ 0.2; orange denotes inconsistency.¹⁹ We pay particular interest to drugs that show significant improvement and drugs that show little improvement. We can see that drugs such as ZSTK474. Rapamycin, JQ1, OSI027 and PIK93 show significant improvement. Although Velaparib shows little improvement, it is known to be a very selective PARP inhibitor; it is not effective in any of cancer cell lines examined in this study. Thus it would be meaningless and artificial to increase the correlation across two datasets.

Fig. 4:

Individual drugs with respect to individual cell lines before and after AICM is deployed. First five demonstrate drugs whose correlations are significantly improved and the last one demonstrates a drug whose correlation is poorly improved.

We also present the scatter plots of some drugs shared by all three datasets: CTRPv2, GDSC1000 and FIMM. We can see that in both 5a and 5b, the two graphs on the right consistently demonstrate more similar pattern than the two graphs on the left, which confirms that the variation across multiple datasets is alleviated after AICM is deployed – AICM indeed recovers some meaningful signals.

4. Conclusions and Future Work

In this work, we develop a genuine algorithm by alternatively dropping and fitting cell-wise data and succeeds in improving the drug-wise correlation. The algorithm is flexible to incorporate different ideas. For example, one can replace the fitting process with other regression methods if one had different assumptions in mind. We have shown that with appropriate hyperparameters chosen, AICM can improve the drug-wise correlation across different studies and that the increase in correlation is indeed concordant and biologically meaningful.

We realize the limitation of AICM’s dependence on the overlapping of existing data, while such data is rather rare. We did not include experiment on CCLE dataset primarily because it has very limited drug overlap with other existing datasets. Also, AICM currently does not purport to correct sensitivity data of new drugs. Future work will be to extend such algorithm into a complete framework. AICM is able to scale to reasonable amount of datasets. When a new dataset is coming in, say X, we can conduct AICM procedure between this dataset and each existing dataset, say Y₁, Y₂, … Y_n, yield n corrected datasets, ${\tilde{X}}_1,{\tilde{X}}_2,\dots ,{\tilde{X}}_n$. Afterward, we can do an average on corrected to specify the corrected new dataset, i.e. $\tilde{X}{=}_n^1{\sum }_{i=1}^n{\tilde{X}}_i$. We will maintain a database of corrected existing drugs and cells, and when more data comes in, we will be able to incorporate it. We hope as more data comes in, the database would asymptotically become more accurate of reflecting true relationship between drugs and cell lines and can thus serve as a ground-truth guidance. As for new drugs, we will develop either a generative algorithm or a clustering algorithm, i.e. getting the latent distribution where drug is “generated” or cluster it based on existing features, and find similar existing drugs in hope of some practical guidance. We believe our corrected datasets will facilitate biomarker discovery.

Fig. 5:

Overlapping drugs across three datasets.