A fast imputation algorithm in quantile regression

Abstract

In many applications, some covariates could be missing for various reasons. Regression quantiles could be either biased or under-powered when ignoring the missing data. Multiple imputation and EM-based augment approach have been proposed to fully utilize the data with missing covariates for quantile regression. Both methods however are computationally expensive. We propose a fast imputation algorithm (FI) to handle the missing covariates in quantile regression, which is an extension of the fractional imputation in likelihood based regressions. FI and modified imputation algorithms (FIIPW and MIIPW) are compared to existing MI and IPW approaches in the simulation studies, and applied to part of of the National Collaborative Perinatal Project study.

1. Introduction

Quantile regression (Koenker and Bassett 1978; Koenker 2005) has emerged as a promising and flexible modeling tool to capture the complex associations between a response variable and its covariates. When some covariates are missing, the complete-case (CC) analysis can be underpowered or lead to biased quantile estimation (Little 1992). How to handle the missing data has been well discussed in econometrics and statistics. Under the missing at random assumption, multiple imputation methods (Little and Rubin 1987) are particularly popular among practitioner due to its simplicity and intuitive appeal. The fundamental step is to simulate missing covariates from the density f (x|z, y), and assemble a full likelihood or estimating equations with both observed and imputed values. Wei et al. (2012) proposed the first multiple imputation (MI) algorithm for quantile regression, assuming the covariates are missing at random, but the missingness is unrelated to the outcome Y. Their proposed MI methods fully utilize the entire data, are asymptotically more efficient than the CC analyses, and are robust against possible model misspecification. However, they are computationally expensive, partly due to the lack of parametric likelihood in quantile regression. As recent statistical applications often involve complex and massive data, computational efficiency becomes a crucial measure of any statistical method. The goal of this paper is to propose a faster imputation algorithm to relieve the computation burden of the quantile regression imputation methods. The new imputation algorithm partly extends the fractional imputation in Kim (2011) to quantile regression.

We consider the following linear quantile regression model,

$$Q_Y(\tau )=x^T{\mathit{\beta }}_{1,\tau }+x^T{\mathit{\beta }}_{2,\tau },\forall \tau \in (0,1)$$ (1)

where Q_Y (τ) stands for the τth quantile of a response variable Y, and (x, z) are both covariate vectors. We assume that the conditional quantile functions of Y given (x, z) is a linear function of (x, z) with quantile specific coefficients (β_1,τ, β_2,τ ). Without the loss of generosity, we assume that the covariate x may be missing, but z is always observed. We assume that z contains the constant 1, hence the intercept term is not written out separately.

In this paper, we first considered the same setting as in Wei et al. (2012), where the covariates are missing at random, and the missingness is unrelated to the outcome Y. We show that the estimates from the new algorithm is as efficient as the MI estimation, but computationally much faster. We then extend to a more general case where the missingness of the covariates could relate to the response variable. In this more general setting, the CC analyses could be seriously biased. Wei and Yang (2014) proposed an EM-like algorithm to correct such bias, but is computationally undesirable. In contrast, we considered inverse probability weighting to correct the bias in imputation estimations, and investigated and compared its performance when combined with MI estimation and when combined with faster fractional imputation estimates.

The rest of the paper is organized as follows. We described our imputation algorithms in Sect. 2, and conducted a simulation study in Sect. 3. Finally, we applied the proposed methods to part of the National Collaborative Perinatal Project (NCPP) study in Sect.4.

2. Estimation with imputation methods

2.1. Notation

Suppose (x_i, z_i, y_i), i = 1, … , n is an i.i.d. random sample of sample size n following the Model (1), but n₁ (out of n) x_i are missing. We denote δ_i as the binary indicator for the existence of x_i. That is, x_i is observed when δ_i 1 for i 1, … , n₁ and is missing when δ_i = 0 for i = n₁ + 1, … , n. Let n₀= n − n₁ be the number of complete cases, we further assume that 0 < lim_n→∞ (n₀/n₁) = λ < ∞, so that the proportion of the missing observations are non-negligible non-dominating.

2.1.1. A fast imputation (FI) algorithm when δ_i is conditionally independent with y_i

We first considered the same setting as in Wei et al. (2012), where the missingness indicator δ_i are conditionally independently with the response variable y_i given z_i. Same as in any MI approaches, a fundamental step is to simulate missing covariates from the density f (x|z, y). One can decompose the imputation density f (x|z, y) by f (x|z, y) ∝ f (y|x, z) f (x|z), and estimate the two density components separately. Under the conditional independence assumption, the density f (x|z) can be easily estimated by maximizing a parametric likelihood over the observed (x_i, z_i. However, we do not have a parametric density f (y|x, z) following the quantile model (1). To circumvent this difficulty, Wei et al. (2012) considered model the entire quantile process Q_Y (τ|x, z), and derive the model-induced density f (y|x, z). The underlying rational is as follows. Since quantile function is the inverse function of the cumulative distribution function, the density component f (y|x, z) can be rewritten as the first derivative of the the conditional quantile function Q_y(τ|x, z) at τ_y, where τ_y is the quantile level of y, i.e. pr(Y ≤ y|x, z) = τ_y. Following this direction, we model the entire conditional quantile process Q_y(τ|x, z) = β₀(τ) + x^T β₁(τ) z^T β₂(τ) on a fine grid of $0<{\tau }_1<\cdots <{\tau }_k<\cdots <{\tau }_{k_n}<1$ and approximate the density f (y|x, z) by

$$\widehat{f}\{y|x,z,{\widehat{\mathit{\beta }}}_{n1}(\tau )\}=\sum _{k=1}^{K_n}\frac{\left\{{\tau }_{k+1}-{\tau }_k\right\}\mathit{I}\left\{\left(x^T,z^T\right){\widehat{\mathit{\beta }}}_{n_1,{\tau }_k}\le y<\left(x^T,z^T\right){\widehat{\mathit{\beta }}}_{n_1,{\tau }_{k+1}}\right\}}{\left(x^T,z^T\right){\widehat{\mathit{\beta }}}_{n_1,{\tau }_{k+1}}-\left(x^T,z^T\right){\widehat{\mathit{\beta }}}_{n_1,{\tau }_k}}.$$ (2)

With the estimated f (y|x, z) and f (x|z), one can assemble the imputation density f (x|z, y), and simulate the missing covariates from there. This joint modeling makes MI possible for quantile regression. However, due to the nonparametric nature of f (y|x, z), evaluating and simulating the imputation density f (x|z, y) for each missing value is extremely computationally expensive. We propose to avoid this step completely by simulating the missing covariates from the parametric f (x|z), instead of the complicated f (x|z, y), and adjust the bias through a re-weighting algorithm. Similar idea was investigated in (Kim 2011) with fully parametric likelihoods. In order to understand the underlying rational of the proposed algorithm, we define the following unbiased estimating function with missing covariates.

$$S_n^{*}(\mathit{\beta })=\sum _{i=1}^n{\delta }_i{\phi }_{\tau }\left(y_i-x_i^T\mathit{\beta }-z_i^T\beta \right)+\sum _{i=1}^n\left(1-{\delta }_i\right){\mathit{E}}_x\left\{{\phi }_{\tau }\left(y_i-x_i^T\mathit{\beta }-z_i^T\mathit{\beta }\right)|y_i,z_i\right\},$$ (3)

where φ_τ (u) = u(τ −I{u < 0}) is the standard estimating function for quantile regression. Using basic double expectation formula, one can easily show $S_n^{*}(\mathit{\beta })$ is unbiased estimating function for regression quantiles with covariates missing at random. Based on the bayesian theory, f (x|z, y) can be written as $\frac{f\left(y_i|x,z_i\right)f(x|z_i)}{{\int }_{x}f\left(y_i|x,z_i\right)f(x|z_i)dx}$ Consequently, one can rewrite the conditional expectation $E_x\{{\phi }_{\tau }(y_i-x^T\mathit{\beta }-z_i^T\mathit{\beta }|y_i,z_i\}$ in (3) by

$$\frac{{\int }_x{\phi }_{\tau }\left(y_i-x^T\mathit{\beta }-z_i^T\mathit{\beta }\right)f\left(y_i|x,z_i\right)f(x|z_i)dx}{{\int }_{x}f\left(y_i|x,z_i\right)f(x|z_i)dx}$$ (4)

Both of the numerator and denominator of (4) can be approximated by Monte-carlo integrations, i.e.,

$$\begin{gathered} {\int }_x{\phi }_{\tau }\left(y_i-x^T\mathit{\beta }-z_i^T\mathit{\beta }\right)f\left(y_i|x,z_i\right)f(x|z_i)dx \\ =\frac{1}{M}\sum _{k=1}^M{\phi }_{\tau }\left(y_i-{\tilde{x}}_{i,k}^{*T}\mathit{\beta }-z_i^T\mathit{\beta }\right)f\left(y_i|{\tilde{x}}_{i,k}^{*},z_i\right) \end{gathered}$$

and

$${\int }_{x}f\left(y_i|x,z_i\right)f(x|z_i)dx=\frac{1}{M}\sum _{k=1}^{M}f\left(y_i|{\tilde{\mathit{x}}}_{i,k}^{*T},z_i\right)$$

where ${\tilde{\mathit{x}}}_{i,k}^{*T}$ is random draw from f (x|z_i). Replacing the conditional expectation in (3), we can approximate the estimating function $S_n^{*}(\mathit{\beta })$ by

$$S_n(\mathit{\beta })=\sum _{i=1}^{n_1}{\phi }_{\tau }\left\{y_i-\left(x_i^T,z_i^T\right)\mathit{\beta }\right\}+\sum _{i=n_1+1}^n\sum _{k=1}^M{w}_{i,k}{\phi }_{\tau }\left\{y_i-\left({\tilde{x}}_{i,k}^{*T},z_i^T\right)\mathit{\beta }\right\}$$ (5)

where

$$w_{i,k}=\frac{f\left(y_i|{\tilde{\mathit{x}}}_{i,k}^{*},z_i\right)}{{\sum }_{k=1}^{M}f\left(y_i|{\tilde{\mathit{x}}}_{i,k}^{*},z_i\right)}.$$ (6)

Consequently, one can obtain an unbiased imputation estimator by solving the weighted estimation equations S_n(β) = 0. In what follows, we outline the proposed fast imputation algorithm for quantile regressions.

Remark 1 One can also approximate the conditional expectation in equation (3) by ${\int }_x{\phi }_{\tau }\left(y_i-x_i^T\mathit{\beta }-z_i^T\mathit{\beta }\right)\frac{f(x|y_i,z_i)}{f(x|z_i)}\mathit{f}(x|z_i)dx$, and use importance sampling to approximate the conditional expectation. However, importance sampling needs to simulate x from f (x|z_i) and estimate the f (x|y_i, z_i) at the same time, which makes the imputation process more complex.

Algorithm 1.

Fast Imputation Algorithm Step

Step 1: Quantile regression with the complete data on a fine grid of quantile levels $0<{\tau }_1<\cdots <{\tau }_k<\cdots <{\tau }_{k_n}<1$.

Step 2: Model the conditional density f (x|z) parametrically as f (x | z, η), and estimate η based on the complete data.

Step 3: Simulate M x from the estimated $f(x|z,\widehat{\eta })$ for each missing xi, 1 ≤ i ≤ n1.

Step 4: Calculate the weights using the model induced density from Step 1, and assemble the weighted estimating function as in (5) to get the final estimator.

2.1.2. Fast imputation algorithm with inverse probability weighting

When the missingness in the covariates x is related with y, the outlined faster imputation (FI) algorithm as well as the standard MI algorithm are biased. To correct the bias, one could incorporate the inverse probability weighting (IPW) as in Seaman and White (2011), which is a commonly used method to correct the bias induced by missing data or biased sampling. The implementation of IPW is easy and generally applicable. It weights each completely observed data by 1/prob(δ_i = 1|y_i, z_i), the reciprocals of the probabilities of missing x_i given y_i and z_i. In our case, we need to re-weight the regressions in both Steps 1 and 3 of the FI and MI algorithms. We call such modified FI and MI algorithms by FIIPW and MIIPW algorithms. The missing probability prob(δ_i = 1| y_i, z_i) can be easily estimated by logistically regressing δ_i against y_i and z_i.

3. Simulations

3.1. Models and settings

We use Monte-Carlo simulations to investigate the performance of our estimators. We first consider the following location-scale model

$$y_i=1+x_i+z_i+\left(0.5x_i+0.5z_i\right)e_i$$ (7)

where the covariates (x_i, z_i) are jointly normal with mean vector (4, 4)^T, variances (1, 1)^T and correlation 0.5. The true intercept equals 1 at every quantile level, but the two slope coefficients equal to 1 + 0.5Q_τ (e_i) at quantile level τ.

Remark 2 Quantile function does not have scale-equivlance when the scaler is negative, i.e. Q_τ (aX) = aQ_1−τ (X). Hence, in our location scale model, we assume that X is a positive covariate, and follows a normal distribution with mean 4 and variance 1.

We also consider the two missing mechanisms. In Setting 1, we define p(δ_i|z_i) max[0, {(z_i − 3)/10}^1/20], such that approximately 25% observations miss x_i’s, and the missingness is independent with Y. While in Setting 2, we allow the missingness to be related with Y and define p(δ_i|y_i, z_i) = 1/(1+exp(1, z_i, y_i)∗c(−6, −0.5, 0.6)). Approximately 20% observations missing x_i’s in Setting 2. Furthermore, we consider two distributions for the random errors e_i1, either standard normal or chi-square. In what follow, we denote Setting S1–1 as Setting 1 with normal e_i, and Setting S1–2 is that with chi-square e_i. Likewise, we denote Setting S2–1 and Setting S2–2 as the Setting 2 with normal and chi-square random errors.

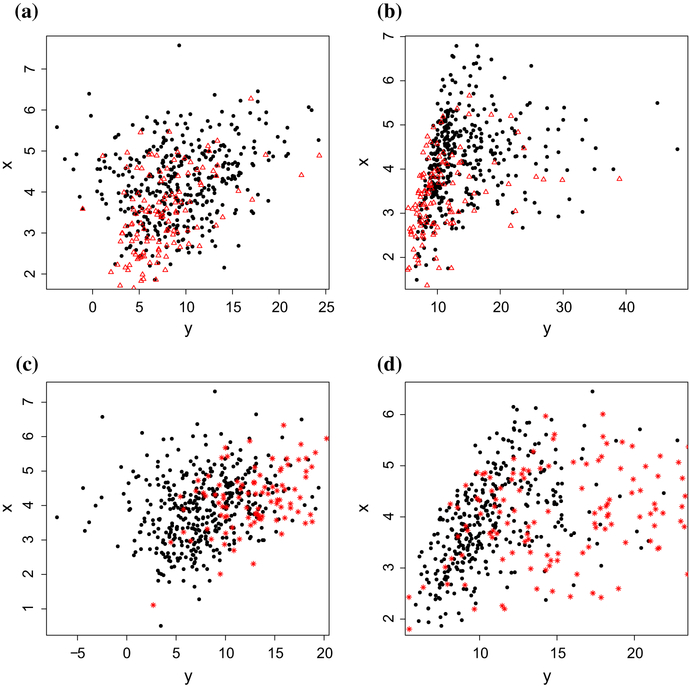
Figure 1 shows the missing data distribution under the four settings with sample size 500. One can see that missing data is evenly distributed in the plot S1–1, while the missing data tends to locate in the bottom-left corner in S1–2 and in top-right corner in S2–1 and S2–2

Fig. 1.

Missing data distributions under S1–1, S1–2, S2–1 and S2–1 with sample size 500. S1–1 means the missingness is independent with Y and e_i is normal. S1–2 means the missingness is independent with Y and e_i is chi-square. S2–1 means the missingness is related with Y and e_i is normal. S2–2 means the missingness is related with Y and e_i is chi-square. Filled points represent observed x_i ‘s under all four settings. Open triangle points represent the missing x_i ‘s under S1–1 and S1–2, star points represent the missing x_i ‘s under S2–1 and S2–2. There are 500 points (for example, Filled points and Open triangle points in S1–1) in total in each setting. For S1–1, there are 125 missing x_i ‘s and the missing percentage is 25%. For S1–2, there are 120 missing x_i ‘s and the missing percentage is 24%. For S2–1, there are 95 missing x_i ‘s and the missing percentage is 19%. For S2–2, there are 160 missing x_i ‘s and the missing percentage is 32%. a S1–1, b S1–2, c S2–1, d S2–2

Based on these settings, we conducted the following numerical investigations. In all the investigations, we choose the Monte-Carlo sample size as 200.

1. We compared the estimation accuracy and efficiency of MI and FI estimates under the Setting 1 with sample size 500. We choose m = 10 in MI and M = 20 in FI.

2. In Setting 2 where the CC analysis is biased, we compared the estimation accuracy and efficiency of the estimates from five algorithms including IPW, MI, MIIPW, FI, FIIPW. To assess the level of uncertainty brought in by estimated weights, we also compared both MIIPW and FIIPW to their counterparts using true weights calculated from true density f (y|x, z), which we denote as FIP and MIP.

3. To understand the impact of the number of imputations (M) in FI, we considered various number of imputation replicates (M = 10, 20, 50, 100) in the FI algorithms.

4. Under all the settings, we compared the computing times between FI and MI with various number of imputation replicates (M = 10, 20) and various sample sizes (N = 500, 1000).

3.2. Results

3.2.1. Comparisons of estimation accuracy and efficiency

Table 1 presents the mean biases, standard errors and mean square errors of the 200 estimated MI and FI coefficients (from the 200 Monte-Carlo replicates) at the quantile levels 0.1, 0.5 and 0.9 under the Settings S1–1 and S1–2. We add subscripts MI and FI to $\widehat{\beta }$ to indicate which algorithm $\widehat{\beta }$ is estimated from. The estimates from the two algorithms are fairly comparable in their biases, variances and mean square errors, while FI algorithm slightly outperforms the MI algorithm at quantile level 0.5 and at the estimated Z coefficients.

Table 1.

Mean biases (“M.B.”), standard errors (“S.E.”) and mean squared errors (“MSE”) of the estimated MI and FI coefficients at quantile levels 0.1, 0.5 and 0.9 under the settings S1–1 and S1–2 with sample size 500 and 200 Monte-Carlo replicates

Quantile levels			M.B.			S.E.			MSE
			0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9
S1–1	x	${\widehat{\mathit{\beta }}}_{1,MI}$	0.032	0.008	−0.061	0.362	0.283	0.374	0.132	0.080	0.144
		${\widehat{\mathit{\beta }}}_{1,FI}$	0.003	−0.018	−0.065	0.366	0.276	0.388	0.134	0.077	0.155
	z	${\widehat{\mathit{\beta }}}_{2,MI}$	−0.023	−0.009	0.032	0.343	0.267	0.378	0.118	0.071	0.144
		${\widehat{\mathit{\beta }}}_{2,FI}$	−0.007	0.013	0.021	0.341	0.258	0.371	0.116	0.067	0.138
S1–2	x	${\widehat{\mathit{\beta }}}_{1,MI}$	−0.062	−0.170	−0.560	0.111	0.298	1.001	0.016	0.118	1.315
		${\widehat{\mathit{\beta }}}_{1,FI}$	−0.036	−0.134	−0.480	0.069	0.265	0.998	0.006	0.088	1.227
	z	${\widehat{\mathit{\beta }}}_{2,MI}$	0.091	0.130	0.288	0.138	0.266	0.967	0.027	0.088	1.019
		${\widehat{\mathit{\beta }}}_{2,FI}$	0.059	0.097	0.240	0.098	0.247	0.972	0.013	0.070	1.003

S1–1 means the missingness is independent with Y and e_i is normal. S1–2 means the missingness is independent with Y and e_i is chi-square. MI stands for the multiple imputation algorithm in Wei et al. (2012), FI stands for the proposed fast imputation algorithm

Tables 2 and 3 display the mean biases, standard errors and mean squared errors of the estimated quantile coefficients under Setting 2 with 200 Monte-Carlo replicates and sample size 500 at quantile levels 0.1, 0.5 and 0.9. As expected, FI and MI estimates are biased, while the IPW adjustments (FIIPW and MIIPW) help reduce the bias, especially at quantile level 0.9. Although the direct IPW approach does a good job in correcting the bias, the variances are much larger than those of FIIPW and MIIPW, which make it under-performed in mean square errors. We also notice that there are very small differences between FIIPW and FIP, and between MIIPW and MIP. These suggest the weights are well estimated in this study. We also run the same simulation process with increased sample size 1000, and reach very similar results (not reported in the paper).

Table 2.

Mean biases (“M.B.”), standard errors (“S.E.”) and mean squared errors (“MSE”) of the estimated coefficients from various methods at quantile levels 0.1, 0.5 and 0.9 under the setting S2–1 with sample size 500 and 200 Monte-Carlo replicates

Quantile levels		M.B.			S.E.			MSE
		0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9
x	${\widehat{\mathit{\beta }}}_{1,FI}$	0.028	−0.028	−0.234	0.336	0.263	0.416	0.114	0.070	0.228
	${\widehat{\mathit{\beta }}}_{1,FIIPW}$	0.032	−0.029	−0.171	0.341	0.274	0.452	0.117	0.076	0.234
	${\widehat{\mathit{\beta }}}_{1,FIP}$	0.035	−0.022	−0.162	0.341	0.269	0.450	0.118	0.073	0.229
	${\widehat{\mathit{\beta }}}_{1,IPW}$	0.050	0.037	0.080	0.342	0.292	0.635	0.120	0.087	0.409
	${\widehat{\mathit{\beta }}}_{1,MI}$	0.026	−0.031	−0.244	0.337	0.270	0.430	0.114	0.074	0.245
	${\widehat{\mathit{\beta }}}_{1,MIIPW}$	0.034	−0.015	−0.133	0.339	0.269	0.457	0.116	0.073	0.227
	${\widehat{\mathit{\beta }}}_{1,MIP}$	0.033	−0.011	−0.130	0.336	0.270	0.461	0.114	0.073	0.229
z	${\widehat{\mathit{\beta }}}_{2,FI}$	−0.010	0.011	0.106	0.345	0.254	0.378	0.119	0.065	0.154
	${\widehat{\mathit{\beta }}}_{2,FIIPW}$	−0.014	0.012	0.079	0.345	0.256	0.393	0.119	0.066	0.160
	${\widehat{\mathit{\beta }}}_{2,FIP}$	−0.015	0.011	0.083	0.342	0.257	0.402	0.117	0.066	0.169
	${\widehat{\mathit{\beta }}}_{2,IPW}$	−0.020	−0.030	−0.066	0.350	0.268	0.588	0.123	0.072	0.351
	${\widehat{\mathit{\beta }}}_{2,MI}$	−0.009	0.013	0.106	0.342	0.255	0.370	0.117	0.065	0.148
	${\widehat{\mathit{\beta }}}_{2,MIIPW}$	−0.015	0.008	0.056	0.341	0.256	0.380	0.116	0.066	1.148
	${\widehat{\mathit{\beta }}}_{2,MIP}$	−0.014	0.004	0.063	0.340	0.255	0.392	0.116	0.065	1.157

FI stands for the proposed fast imputation algorithm, IPW stands for inverse probability weighting, FIIPW is the FI algorithm with IPW adjustment, FIP stands for the fast imputation algorithm using true weights calculated from the true density f (y|x, z); Likewise, MI, MIIPW and MIP respectively stand for the multiple imputation algorithm in Wei et al. (2012), and its adjustment with IPW and true weights

Table 3.

Mean biases (“M.B.”), standard errors (“S.E.”) and mean squared errors (“MSE”) of the estimated coefficients from various methods at quantile levels 0.1, 0.5 and 0.9 under the setting S2–2 with sample size 500 and 200 Monte-Carlo replicates

Quantile levels		M.B.			S.E.			MSE
		0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9
x	${\widehat{\mathit{\beta }}}_{1,FI}$	−0.009	−0.123	−1.968	0.024	0.266	0.998	0.001	0.086	4.868
	${\widehat{\mathit{\beta }}}_{1,FIIPW}$	−0.007	−0.109	−1.333	0.023	0.286	1.854	0.001	0.094	5.213
	${\widehat{\mathit{\beta }}}_{1,FIP}$	−0.008	−0.098	−1.280	0.023	0.296	1.844	0.001	0.097	5.037
	${\widehat{\mathit{\beta }}}_{1,IPW}$	0.005	0.078	−1.032	0.075	1.657	2.483	0.006	2.752	7.231
	${\widehat{\mathit{\beta }}}_{1,MI}$	−0.004	−0.086	−1.918	0.019	0.264	0.901	0.000	0.077	4.488
	${\widehat{\mathit{\beta }}}_{1,MIIPW}$	−0.005	−0.075	−1.200	0.021	0.287	1.989	0.000	0.088	5.396
	${\widehat{\mathit{\beta }}}_{1,MIP}$	−0.006	−0.087	−1.247	0.022	0.290	2.010	0.001	0.092	5.595
z	${\widehat{\mathit{\beta }}}_{2,FI}$	0.008	0.071	0.896	0.023	0.212	1.011	0.001	0.050	1.826
	${\widehat{\mathit{\beta }}}_{2,FIIPW}$	0.006	0.058	0.423	0.022	0.218	1.210	0.001	0.051	1.643
	${\widehat{\mathit{\beta }}}_{2,FIP}$	0.007	0.052	0.434	0.022	0.220	1.191	0.001	0.051	1.608
	${\widehat{\mathit{\beta }}}_{2,IPW}$	−0.002	−0.100	−0.654	0.079	1.384	2.452	0.001	1.926	6.440
	${\widehat{\mathit{\beta }}}_{2,MI}$	0.003	0.057	0.882	0.019	0.209	0.903	0.000	0.047	1.593
	${\widehat{\mathit{\beta }}}_{2,MIIPW}$	0.005	0.058	0.390	0.021	0.213	1.309	0.000	0.049	1.865
	${\widehat{\mathit{\beta }}}_{2,MIP}$	0.005	0.062	0.433	0.021	0.217	1.313	0.000	0.051	1.912

FI stands for the proposed fast imputation algorithm, IPW stands for inverse probability weighting, FIIPW is the FI algorithm with IPW adjustment, FIP stands for the fast imputation algorithm using true weights calculated from the true density f (y|x, z); Likewise, MI, MIIPW and MIP respectively stand for the multiple imputation algorithm in Wei et al. (2012), and its adjustment with IPW and true weights

3.2.2. Comparison of computing time

Table 4 displays the average computing time (in seconds) of MI and FI algorithms with various sample sizes under all the four settings.

Table 4.

Average computing times on all quantile levels from 200 Monte-Carlo simulations in Model (7) under all settings (Seconds)

	S1–1		S1–2
	N = 500	N = 1000	N = 500	N = 1000
FI (M = 10)	0.826	1.313	0.789	1.357
FI (M = 20)	0.903	2.883	1.775	2.972
MI (m = 10)	8.353	21.929	18.079	22.355
	S2–1		S2–2
	N = 500	N = 1000	N = 500	N = 1000
FI (M = 10)	0.519	1.365	1.237	2.354
FI (M = 20)	0.986	1.972	1.550	3.533
FIIPW (M = 10)	0.509	1.404	1.316	2.345
FIIPW (M = 20)	0.995	2.020	1.635	3.535
IPW	0.062	0.112	0.049	0.079
MI (m = 10)	9.469	14.622	23.649	38.588
MIIPW (m = 10)	9.744	15.301	25.685	40.350

Here FI, FIIPW, IPW, MI, MIIPW are the imputation approaches. N stands for sample size and M stands for the number of x we simulate from the estimate function f (x|z_i). m stands for the repeated imputation-estimation times in MI and MIIPW

In S1–1, sample size 500 and 1000 reach very similar results, so we only report sample size 500 here. The average computing time of FI (M = 10) is 0.826s and the average computing time of FI (M = 20) is 0.903s. FI (M = 20) costs a little more time than FI (M = 10). The average computing time of MI (m = 10) is 8.353s, which cost more than ten times of FI’s (M = 10) computing time. This conclusion can also be confirmed in S1–2.

In both S2–1 and S2–2, we add FIIPW and MIIPW algorithms. Compared with FI and MI, the IPW adjustments in both FIIPW and MIIPW have little impact on the computing time. The differences of the average computing time between FI(MI) and FIIPW(MIIPW) are negligible. We also find that FI and FIIPW only need one tenth of MI and MIIPW’s average computing time.

Based on all these settings, the proposed fast imputation algorithm FI almost costs only one tenth of MI’s average computing time. It concludes that FI is able to greatly relieve the computation burden in MI algorithm.

3.2.3. The selection of M in FI

In this subsection, we investigate how the number of imputation replicates M affects the estimation accuracy and computation time of the proposed FI method. We repeated the FI estimation in settings S1–1 and S1–2 with M =10, 20, 50, 100, respectively. Table 5 displays the resulting relative biases, standard errors and mean squared errors of the estimated FI coefficients with different M at quantile levels 0.1, 0.5 and 0.9. We found that, when M increases, the standard errors and mean squared errors remain nearly unchanged. A small M between 10 and 20 is sufficient to stabilize the estimated coefficients. Bigger M does not further improve the accuracy in our simulations.

Table 5.

Relative biases (“R.B.”), standard errors (“S.E.”) and mean squared errors (“MSE”) of the estimated coefficients at quantile levels 0.1 and 0.5 from 200 Monte-Carlo simulations in Model (7)

Quantile levels			M = 10		M = 20		M = 50		M = 100
			0.1	0.5	0.1	0.5	0.1	0.5	0.1	0.5
S1–1	R.B. (%)	${\widehat{\mathit{\beta }}}_{1,FI}$	1.000	−2.600	0.300	−1.800	2.400	0.500	2.100	0.400
		${\widehat{\mathit{\beta }}}_{2,FI}$	−0.500	2.200	−0.700	1.300	−1.800	−0.200	−1.500	−0.300
	S.E.	${\widehat{\mathit{\beta }}}_{1,FI}$	0.364	0.275	0.366	0.276	0.362	0.283	0.358	0.283
		${\widehat{\mathit{\beta }}}_{2,FI}$	0.342	0.253	0.341	0.258	0.344	0.262	0.346	0.260
	MSE	${\widehat{\mathit{\beta }}}_{1,FI}$	0.133	0.076	0.134	0.077	0.131	0.080	0.129	0.080
		${\widehat{\mathit{\beta }}}_{2,FI}$	0.117	0.064	0.116	0.067	0.119	0.069	0.120	0.068
S1–2	R.B. (%)	${\widehat{\mathit{\beta }}}_{1,FI}$	−2.800	−12.800	−3.600	−13.400	−4.100	−13.600	−4.400	14.200
		${\widehat{\mathit{\beta }}}_{2,FI}$	4.700	7.600	5.900	9.700	6.600	10.200	7.000	11.500
	S.E.	${\widehat{\mathit{\beta }}}_{1,FI}$	4.700	0.248	0.069	0.265	0.079	0.277	0.085	0.282
		${\widehat{\mathit{\beta }}}_{2,FI}$	0.078	0.240	0.098	0.247	0.110	0.253	0.115	0.259
	MSE	${\widehat{\mathit{\beta }}}_{1,FI}$	0.003	0.078	0.006	0.088	0.008	0.095	0.009	0.100
		${\widehat{\mathit{\beta }}}_{2,FI}$	0.008	0.063	0.013	0.070	0.016	0.074	0.018	0.100

Relative bias is defined as the ratio between the bias and the true value. Here S1–1 means the missingness is independent with Y and e_i is normal. S1–2 means the missingness is independent with Y and e_i is chi-square. FI stands for the proposed fast imputation algorithm. The estimated coefficients at quantile level 0.9 are just similar to the case at quantile level 0.1

4. Application to real data study

In this section we illustrate the performance of our methods using part of a prospectively collected data from families who are part of the National Collaborative Perinatal Project (CPP). The children are all American race, born from 1959 to 1966 at 14 centers in United States and followed until 7years of age. Their infancy physical measurements (weight and height) were taken at fixed intervals (birthdates, 4, 8months and 1years).

In these data, we find that mothers’ smoking years and education years are weekly correlated with 7-year-old children’s BMI. The correlation coefficients are − 0.002 and − 0.026 respectively. Thus we build a model with y_i being the 7-year-old −child’s BMI for the ith person, x_i,1 baby’s birth weight, x_i,2 baby’s 4-month weight, x_i,3 baby’s 8-month weight, x_i,4 baby’s 1-year weight and x_i,5 mother’s pregnancy BMI. Considering the the distributions of the variables are commonly skewed, we use quantile regression and the model can be written as

$$y_i={\beta }_{0,\tau }+{\beta }_{1,\tau }{x}_{i,1}+{\beta }_{2,\tau }{x}_{i,2}+{\beta }_{3,\tau }{x}_{i,3}+{\beta }_{4,\tau }{x}_{i,4}+{\beta }_{5,\tau }{x}_{i,5}+e_i.$$ (8)

We use 200 bootstraps among the 1554 subjects. The covariate a baby’s 8-month weight is missing, while other covariates are completely observed. Here we apply complete-case analysis (CC), IPW, FI, FIIPW, MI, MIIPW to obtain the estimated coefficients β_i,τ , i = 1, … , n, with x as baby’s 8-month weight, and z as baby’s birth weight, baby’s 4-month weight, baby’s 1-year weight and mother’s pregnancy BMI. We set m = 10 in MI and MIIPW, and M = 10 in FI and FIIPW. The estimated coefficients and their standard errors from different approaches at quantile levels 0.1, 0.5 and 0.9 are listed in Table 6, and the average computing times are listed in Table 7.

Table 6.

The estimated coefficients before 200 bootstraps (Raw), Standard errors (“S.E.”), relative efficiencies (“RE”) and P value of the estimated coefficients from 200 bootstraps in Model (8)

	birthwt			wt4mon			Wt8mon			Wt1yr			MatBMI
	0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9	0.1	0.5	0.9
cc
Raw	0.110	−0.058	−0.609	0.085	−0.198	−0.484	−0.128	0.145	0.571	0.508	0.650	0.820	0.014	0.049	0.182
S.E.	0.173	0.108	0.326	0.149	0.122	0.373	0.129	0.181	0.363	0.104	0.117	0.222	0.018	0.012	0.052
P	0.525	0.591	0.062	0.570	0.105	0.194	0.322	0.422	0.116	0.000	0.000	0.000	0.435	0.000	0.001
IPW
Raw	0.088	−0.050	−0.561	0.110	−0.248	−0.607	−0.107	0.189	0.674	0.471	0.652	0.814	0.021	0.047	0.184
S.E.	0.171	0.105	0.388	0.158	0.133	0.427	0.134	0.189	0.411	0.111	0.118	0.243	0.018	0.012	0.055
P	0.606	0.637	0.148	0.486	0.061	0.155	0.424	0.316	0.101	0.000	0.000	0.001	0.250	0.000	0.001
RE	103%	104%	71%	89%	85%	76%	93%	92%	78%	87%	99%	84%	96%	99%	90%
MI
Raw	0.057	−0.051	−0.312	0.122	−0.144	−0.207	−0.083	0.192	0.628	0.499	0.603	0.796	0.024	0.054	0.157
S.E.	0.111	0.073	0.256	0.104	0.093	0.265	0.103	0.171	0.378	0.084	0.107	0.266	0.015	0.009	0.046
P	0.607	0.483	0.223	0.242	0.122	0.434	0.421	0.262	0.097	0.000	0.000	0.003	0.101	0.000	0.001
RE	244%	216%	163%	206%	173%	198%	158%	112%	92%	151%	119%	70%	152%	180%	131%
MIIPW
Raw	0.075	−0.040	−0.354	0.130	−0.124	−0.146	−0.088	0.153	0.491	0.496	0.615	0.894	0.024	0.057	0.158
S.E.	0.109	0.075	0.251	0.105	0.094	0.280	0.102	0.167	0.396	0.083	0.105	0.276	0.014	0.009	0.045
P	0.493	0.591	0.159	0.217	0.189	0.602	0.388	0.360	0.215	0.000	0.000	0.001	0.094	0.000	0.000
RE	251%	205%	169%	202%	169%	178%	162%	118%	84%	157%	123%	65%	154%	187%	134%
FI
Raw	0.090	−0.038	−0.377	0.120	−0.139	−0.124	−0.129	0.194	0.490	0.529	0.596	0.877	0.024	0.055	0.157
S.E.	0.111	0.075	0.248	0.103	0.097	0.267	0.110	0.180	0.390	0.087	0.111	0.269	0.014	0.009	0.045
P	0.418	0.613	0.129	0.245	0.152	0.642	0.239	0.280	0.209	0.000	0.000	0.001	0.103	0.000	0.000
RE	245%	207%	173%	210%	160%	195%	139%	102%	86%	142%	111%	68%	155%	185%	137%
FIIPW
Raw	0.069	−0.047	−0.375	0.120	−0.140	−0.161	−0.108	0.188	0.572	0.519	0.603	0.829	0.023	0.055	0.159
S.E.	0.110	0.075	0.248	0.103	0.098	0.270	0.107	0.180	0.403	0.085	0.110	0.274	0.014	0.009	0.045
P	0.529	0.536	0.130	0.245	0.154	0.550	0.312	0.297	0.156	0.000	0.000	0.003	0.116	0.000	0.000
RE	50%	204%	173%	211%	156%	190%	146%	101%	81%	150%	113%	66%	155%	191%	138%

RE is defined as the ratio between the estimated variances of the CC estimator and the other estimators. The variables birthwt, wt4mon, wt8mon, wt1yr and MatBMI stand for baby’s birth weight, baby’s 4-month weight, baby’s 8-month weight, baby’s 1-year weight and mother’s pregnancy BMI respectively. CC, IPW, FI, FIIPW, MI and MIIPW are imputation approaches

Table 7.

Average computing times (ACT) of six imputation approaches (CC, IPW, MI, MIIPW, FI and FIIPW) at 50 evenly-spaced quantile levels from 200 bootstraps based on 1554 subjects (Seconds)

Methods	CC	IPW	MI	MIIPW	FI	FIIPW
ACT	0.146	0.162	60.814	60.817	5.884	5.910

Table 6 consists of six layers. The first layer is CC estimators, including the estimated coefficients (raw estimation) before bootstrap, standard errors from 200 bootstraps and P value. The latter five layers present the same information from the other estimators. In addition, we also list the relative efficiency comparing to the CC estimates. Based on Table 6, we find that all the imputation methods (FI, FIIPW, MI and MIIPW) have smaller estimated standard errors (S.E.) than the CC and IPW estimates. These are expected as both of CC and IPW only use the completely observed data.

Based on Table 7, FI and FIIPW are much more faster than MI and MIIPW. On average, CC and IPW cost less than 0.2s (0.146 and 0.162s) for each estimation process. MI and MIIPW cost more than one minute (60.814 and 60.817s) for each estimation process. FI and FIIPW only need less than 6s (5.884 and 5.910s) to finish one estimation process. Thus in our real data, both FI and FIIPW’s average computing times are about 10% of MI and MIIPW’s.

5. Discussion

In this paper, we propose a fast imputation algorithm to handle the missing covariates in quantile regression. The proposed algorithm FI greatly reduces the computation burden of MI estimator (Wei et al. 2012). And we use IPW adjustment to modify FI and MI to deal with the second missing mechanism when the missingness in the covariates x is related with y. Under this missing mechanism, the modified algorithm FIIPW also runs very fast when compared with MIIPW.

We assume that all the quantile regression models in this paper belong to linear conditional quantile functions. In the future, we will consider arbitrary nonlinear functions or nonparametric functions. Although we focus on cross-section data missing problems, it is still possible to carry out longitudinal data researches. In that case, we can use a similar algorithm with the longitudinal quantile regression objective function based on the assumption that the quantiles of y is linear in x and z. Another future work is about the weighting methods we choose to modify the algorithms such FIIPW and MIIPW when the missingness in the covariates is related with the response. Instead of inverse probability weighting method (IPW), we will try other weighting methods such as augmented inverse probability weighting method (AIPW) and do more investigation work in the properties of different imputation methods. Last but not least, theoretical derivation in large number properties is needed in the future research.