Abstract
Molecular dynamics simulations of intrinsically disordered proteins (IDPs) can provide high resolution structural ensembles if the force field is accurate enough and if the simulation sufficiently samples the conformational space of the IDP with the correct weighting of sub-populations. Here, we investigate the combined force field–sampling problem by testing a standard force field as well as newer fixed charge force fields, the latter specifically motivated for better description of unfolded states and IDPs, and comparing them with a standard temperature replica exchange (TREx) protocol and a non-equilibrium Temperature Cool Walking (TCW) sampling algorithm. The force field and sampling combinations are used to characterize the structural ensembles of the amyloid-beta peptides Aβ42 and Aβ43, which both should be random coils as shown recently by experimental nuclear magnetic resonance (NMR) and 2D Förster resonance energy transfer (FRET) experiments. The results illustrate the key importance of the sampling algorithm: while the standard force field using TREx is in poor agreement with the NMR J-coupling and nuclear Overhauser effect and 2D FRET data, when using the TCW method, the standard and optimized protein-water force field combinations are in very good agreement with the same experimental data since the TCW sampling method produces qualitatively different ensembles than TREx. We also discuss the relative merit of the 2D FRET data when validating structural ensembles using the different force fields and sampling protocols investigated in this work for small IDPs such as the Aβ42 and Aβ43 peptides.
INTRODUCTION
Intrinsically disordered proteins (IDPs) are a class of biomolecules that do not adopt a well-defined equilibrium structure in solution, instead sampling an ensemble comprised of sub-populations of fully and/or partially disordered structures.1,2 A classic IDP example is the amyloid-β (Aβ) peptide associated with Alzheimer’s disease,3 for which recent state-of-the-art solution-based nuclear magnetic resonance (NMR) and Förster resonance energy transfer (FRET) experiments have shown that the monomeric forms of the Aβ40 and Aβ42 peptides are largely random coils.4–6 Roche and co-workers performed multiple types of J-coupling measurements on Aβ40 and Aβ42 to show there were no overt differences from random coil signatures for both peptides.5 They further supported this result with very high resolution Nuclear Overhauser effect (NOE) spectra that showed that both Aβ40 and Aβ42 are dominated by short (i, i + 1 contacts) and to a lesser extent medium range (i, i + 2 to i, i + 4 contacts) NOEs, and thus, any longer-range helical or β−hairpin formation would only be expected to appear at levels below the detection limit.5 Conicella and Fawzi employed 1HN and 15N chemical shift data and HN-Hα J-couplings, as well as 15N R2, 15N R1, and heteronuclear 15N−1H NOE measurements, to show that there are no structural differences in the N-terminus and central hydrophobic core (CHC) between the Aβ42 and Aβ43 peptides, with only small structural differences in the C-terminus.4 Since the two peptides differ only by a threonine residue at the C-terminus, it implies that the Aβ43 monomer is also largely random coil-like in structure, albeit with a greater propensity for aggregation.4 Finally, using a single molecule and 2D FRET, Meng et al.6 showed that both Aβ40 and Aβ42 have ensembles that are dominated by expanded conformations with no persistent sub-populations of secondary or tertiary structure (i.e., no long helices or β sheets above ∼5%-10% population), in general agreement with the NOE spectra of Roche et al.
Computational techniques are often combined with such experimental information to create the structural ensemble and to characterize the sub-populations of an IDP of interest.7–10 A complementary approach is to generate IDP ensembles using molecular dynamics (MD) simulation without experimental information as input, which therefore requires an accurate force field and a sampling method that can describe the conformational substates of the IDP ensemble. In early simulation studies of IDPs, research groups relied on off-the-shelf and pairwise-additive protein and water force fields,11 such as the Amber,12 GROMOS,13 OPLS-AA,14,15 and CHARMM16 protein force fields in combination with TIP3P,17 TIP4P,18 and TIP4P-Ew19 water models. But since standard pairwise additive force fields are parameterized using mostly folded protein crystallographic data,20 they have been thought to be insufficient for modeling of IDPs because they exhibit a bias toward overly collapsed and ordered structural ensembles or poorly reproduce the equilibrium between unfolded and native conditions for globular proteins.21–23
Furthermore, multiple groups have shown that unfolded and IDP structural ensembles generated using different standard force fields vary considerably in terms of secondary structure content.24–27 For example, in studies of the Aβ16-22 peptide, Nguyen et al. have demonstrated that Amber99 predicts more helical structures and GROMOS9628 favors more β-strand structures, whereas OPLS-AA demonstrates no particular secondary structure preference.24 As we have discussed before, the quality of the water model is also critical for accurate molecular simulations of peptides and proteins by balancing the relative strengths of water-water and water-solute interactions.29 Several groups including Song and co-workers,30 Amini and co-workers,31 and Viet and co-workers32 have conducted straight MD simulations on Aβ peptides on the order of microseconds with standard protein force fields and using a variety of three-site and four-site water models and multiple starting structures. Using brute force MD, Robustelli and co-workers simulated Aβ40 using a single 30 µs trajectory of a standard protein force field Amber99ffsb-ildn* and TIP3P and found close to 90% β−sheet structure in different regions of the sequence.33 In general, all of these simulations produce overstructured ensembles, in disagreement with the experimental results of Roche et al.5 and Meng et al.6 for Aβ peptides. One might surmise from the accumulation of evidence that the standard force fields for the protein and water are failing to describe disordered or unfolded protein ensembles.
To make better and more uniform predictions across different IDPs, as well as more accurate models for protein folding equilibrium, a number of research labs have modified the parameters used in standard force fields.21–23,27,34,35 These force field modifications include adjusting the water-protein London dispersion interactions to be more favorable,21,22 refining the peptide backbone parameters to produce more expanded structures22,23,34 or reduce propensity to certain ordered conformations,21 and/or changing the salt-bridge interactions.21 Skepö and co-workers, using long MD simulations, have shown that some of these modified force fields produce better agreement with experimental small-angle x-ray scattering (SAXS) data in terms of radius of gyration, Rg, for the disordered histatin 5 peptide.36,37 Huang et al.21 also found better agreement with the SAXS profile for the RS peptide using the modified CHARMM force field. However, Robustelli et al. simulated Aβ40 with a single 30 µs trajectory for the recently modified A03ws force field by Best and co-workers38 and found close to 25%-60% α−helix in large regions of the sequence that indicate that the newer IDP force fields may also be experiencing problems.33
But the other important and often not enough emphasized aspect of generating IDP structural ensembles is the sampling technique itself. Because IDPs have a relatively flat energy landscape with many local minima, it takes substantial sampling efficiency to determine all relevant configurations with the correct weighting of multiple small sub-populations. Enhanced sampling methods are therefore generally applied for the simulation of IDPs, as they accelerate the rate of convergence to time scales that are significantly less than possible with a brute force MD simulation.39,40 The most common enhanced sampling technique used in the IDP field at present is the temperature replica exchange (TREx) method.39–43 In fact, TREx simulations were used to identify perceived errors in standard force fields, which led to some of the modified force fields developed to improve modeling of unfolded proteins and IDPs.26,27,38,44
However, a noted deficiency of TREx for large systems is the diffusiveness of barrier crossing due to many closely spaced intermediate replicas when energy landscapes are dominated by entropic barriers.39,45,46 Several alternative enhanced sampling methods with better performance than TREx have been developed and applied to the study of IDPs, including replica exchange with solute tempering (REST),47 metadynamics,48 and MD combined with the Markov State Model (MSM) analysis.49 More specifically, Lin et al.49 performed ∼200 µs MD simulations over many initial conditions, and combined it with MSM to reach even longer time scales, to characterize the Aβ42 structural ensemble using the Amberff99SB protein force field and the TIP3P water model. Over this much longer sampling time scale, they obtained far higher quantities of extended, largely unstructured conformations, with the only noteworthy structural component being ∼10%–20% observed helical content between residues 12-18. While there may be concerns that the clustering protocols may have introduced error in secondary structure populations, and improved clustering methods are now available,88 it is evident that the full weighted ensemble based on the MSM is equivalent to the raw α-helix and β propensities from their production MD runs (as seen in their supplementary material). Thus, this more extensive sampling produced a significant improvement in generating random coil ensembles using a standard peptide-water force field, in good agreement with the experimental results of Roche et al.5 and Meng et al.6 for Aβ peptides and in significant disagreement with previous shorter MD runs33 and TREx studies.26,27,38,44
We have developed the temperature cool walking (TCW) technique,46,50 a non-equilibrium alternative to TREx, which uses only one high temperature replica to generate trial moves for the target temperature replica. In previous studies, we have shown that TCW converges more quickly to the proper equilibrium distribution than TREx, and at much lower computational expense, for a 1D rough surface46 and for alanine dipeptide and met-enkephalin—sufficiently small systems where well-defined and quantitative metrics of convergence are available.50 More recently, we have been able to apply TCW to larger systems such as Aβ through its implementation in OpenMM.50,51 In this work, we address both dimensions of the IDP problem by comparing different combinations of enhanced sampling techniques, TREx and TCW, and protein-water force fields, unmodified and newly optimized, testing combinations of each on Aβ42 and Aβ43. Again summarizing the recent experiments,4–6 the structural ensembles of Aβ42 and Aβ43 peptides should be largely the same and exhibit no persistent structural ordering or long-range contacts. Thus, one would expect the computationally generated structural ensembles to be highly similar for Aβ42 and Aβ43 in terms of back-calculations to experimental observables such as chemical shifts or J-couplings4,5 and that both peptides would display largely random coil configurations, lacking stable populations of organized structures such as β−hairpins and extended helices, to agree with reported NOE4,5 and 2D FRET6 data for Aβ.
Among our set of results, we attain the biggest improvement in IDP ensemble generation by switching the sampling method from TREx to TCW, since the latter sampling algorithm provides much better agreement with the full range of NMR J-coupling and NOE data4,5 as well as with the 2D FRET data,4–6 compared to the same force fields simulated with TREx. More specifically, the unmodified force field when sampled with TCW yields Aβ ensembles that are largely unstructured, in qualitative agreement with the robust MD/MSM simulation49 of the Aβ42 peptide using a similar unmodified force field, with only small populations of structures containing longer-range contacts at levels (∼5%-10%) that would be undetectable by the NOE and 2D FRET experiments. We believe that the presented evidence supports the conclusion that TCW is more capable than TREx of sampling the disordered protein energy landscape and is in support of recent work by Granata and co-workers that have shown that disordered conformations are lower in free energy than ordered structures.52 Finally, using the TCW sampling protocol, we find that the newly modified force fields do produce more extended ensembles that are in better quantitative agreement with the 2D FRET data, whereas the standard force field is in better quantitative agreement with the NMR J-coupling data. We conclude that more work is needed in regard to interpreting FRET data6,53–57 and more extensive testing in general is needed before standard force fields are abandoned or more force field changes are pursued for IDPs.
METHODS
Peptide simulations
The starting Aβ42 and Aβ43 configurations were created using the tleap module in Amber,58 and the peptides were subsequently minimized and equilibrated in the NPT ensemble at 1 bar to obtain the correct density. Structures at the density of maximum probability were selected as initial structures for production, producing boxes that were approximately 60 Å on each side. The Ewald summation was used for the long-range with a cutoff of 9.0-9.5 Å for the real space electrostatics and Lennard-Jones forces. Trajectories were analyzed for results at 287 K.
TREx simulation protocol
The Amber14 molecular dynamics package58 was used to perform 100 ns TREx simulations with 58 temperature replicas in the temperature range 287-450 K, testing both peptides with (1) the Amber ff99SB12 force field with TIP4P-Ew19 water and (2) the CHARMM36m21 force field with CHARMM-TIP3P water.16 The temperature schedule was chosen such that the exchange probability between each pair of replicas was in the range 18%-22%, which has been shown to be optimal for TREx.59 Exchanges between neighboring replicas were attempted every 0.5 ps. The TREx simulations were performed in the NVT ensemble with a time step of 1 fs and with constraints on the heavy atom hydrogen bonds. A Langevin thermostat was used to maintain a constant temperature. Each set of conditions—peptide + force field + water model—was run in duplicate. The first 50 ns of data was discarded as equilibration, with the last 50 ns being analyzed and presented, averaged across the two independent simulations. TREx simulations with this setup were also attempted for the Amber ff99SB-ILDN22,60 force field with TIP4P-D22 water, but using the same temperature ladder and simulation package, we were unable to obtain similar exchange probabilities across the entire temperature span. As we could not run an optimal TREx simulation with this force field combination, no data are presented for this simulation setup.
Over the last several years, several groups have run much longer TREx simulations for IDPs, on the order of 750–1000 ns, noting that even when optimally run, structural properties such as the radius of gyration and secondary structure propensities can take several hundred ns to reach apparent equilibration in TREx.6,44,61,62 To evaluate this difference, we additionally performed one 800 ns TREx simulation each for Aβ42 and Aβ43 using Amber ff99SB + TIP4P-Ew water using the Amber16 molecular dynamics package.63 All parameters were kept the same as in the original 100 ns TREx simulations with the exception of using a 2 fs time step and attempting exchanges between adjacent pairs of replicas every 1 ps. For these simulations, the first 300 ns of data was discarded as equilibration, with the last 500 ns of data at 287 K analyzed. Averaging over two 250 ns blocks was done to mimic the averaging over two independent simulations performed for the 100 ns TREx simulations and the TCW simulations.
TCW protocol
The TCW enhanced sampling method uses only two temperature replicas to generate an equilibrium ensemble at the target temperature.46,50 Starting with expanded structures at the high temperature, sequential cooling is performed to obtain structures at the low temperature such that detailed balance is satisfied. The same set of maximum and minimum temperatures and cooling schedule was used as for all TREx simulations. The temperature was regulated using an Andersen thermostat. Trial moves were initiated every 8 ps. The cooling rate was set such that the peptides spent 40 fs on average at each intermediate temperature, with the first trial exchange per cooling run occurring after having annealed through 40 of the 56 intermediate temperature steps on average. Additional high temperature replica propagation was performed to further decorrelate subsequent configurations at a ratio of 8:1 to each fs of annealing performed. TCW simulations were performed using modifications to the OpenMM software package,64 and a code is available upon request from the authors. TCW simulations were performed with the (1) Amber ff99SB force field + TIP4P-Ew water model, (2) CHARMM36m force field + CHARMM-TIP3P water, and (3) Amber ff99SB-ILDN force field + TIP4P-D water. Simulations were run in duplicate for 200 ns, with the first 50 ns of each discarded as equilibration and results from the remaining 150 ns of each simulation averaged together.
Trajectory analysis
The structural ensembles were analyzed using both the cpptraj65 module of Amber and in-house codes. Contact maps were generated by calculating the fraction of structures where pairs of residues had at least one pair of heavy atoms within 5 Å of each other. The DSSP criterion was used to assign secondary structures.66 Details about the back calculation of NMR observables have been reported in previous publications by our group,10,29,67,68 including chemical shifts from ShiftX269 and J-coupling constants.70 In this work, we focus primarily on J-couplings using the Karplus equation
| (1) |
where ⟨…⟩ denote ensemble averages. We calculate the χ2 parameter from the simulated J-coupling constants ( JHN-Hα) for each ensemble as compared to the experiment,
| (2) |
where Ji is the scalar coupling constant for the ith residue, N is the total number of experimental JHN-Hα observables, subscripts sim and expt refer to the simulated and the experimental values, respectively, and σ2 is the RMSD error when using the Karplus parameters introduced by Vögeli et al.71 We additionally perform a Bayesian analysis on the scalar couplings, Experimental Inferential Structure Determination (EISD),72 that accounts for uncertainties in the values of the Karplus parameters as well as the individual per-coupling experimental uncertainties. The relative magnitudes of ensemble scores for a peptide represent the relative likelihood of that structural ensemble matching the experimental data against which they are compared with a larger score corresponding to a higher probability.
The observable directly obtained in MD simulations of the FRET experiments, the efficiency distribution E(t),
| (3) |
and its average EFRET, is back-calculated from the simulated end-to-end distance, Ree of the untagged peptide across the ensemble, with a Förster radius R0 = 5.2 nm for the dye pair of Alexa 488 and 647.6 As in the work of Meng et al., the Ree is first calculated as the distance between the Cα atoms of the first and last residue of each peptide and then scaled up to approximate the additional distance between the two fluorophores, relative to the distance between the first and last residues.
RESULTS
We tested five different force field-sampling combinations for each of the two peptides: (1) duplicate TREx simulations using the standard Amber ff99SB12 protein force field and the TIP4P-Ew19 water model, (2) duplicate TREx simulations using the modified CHARMM36m21 protein force field and the CHARMM-TIP3P16 water model, (3) duplicate TCW simulations using the standard Amber ff99SB protein force field and the TIP4P-Ew water model (4) duplicate TCW simulations using the modified CHARMM36m protein force field and the CHARMM-TIP3P water model, and (5) duplicate TCW simulations using the Amber ff99SB-ILDN60 protein force field and the TIP4P-D22 water model.
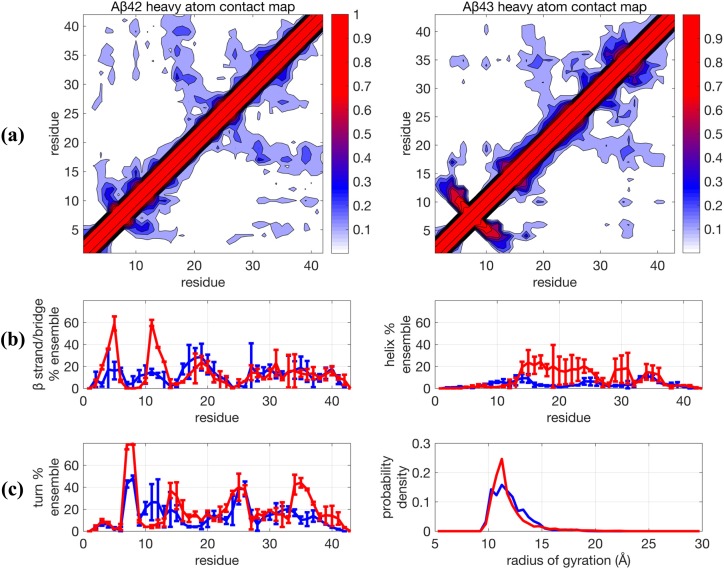
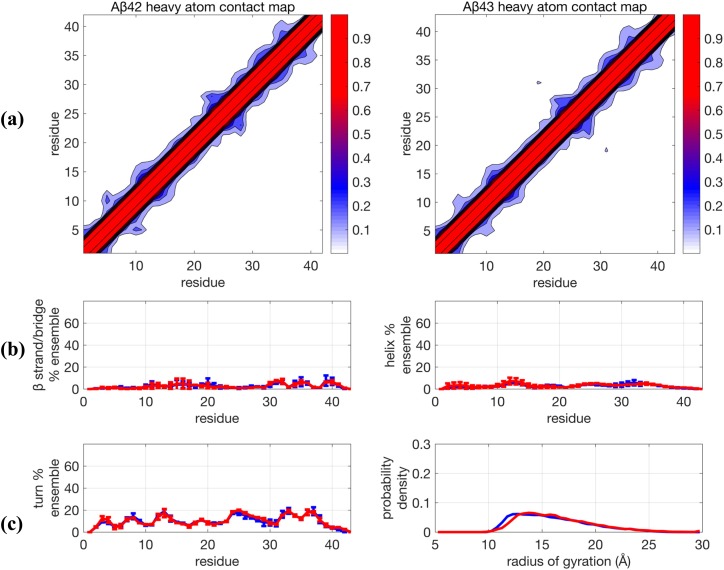
Figure 1 shows that the 0.1 µs TREx + Amber ff99SB + TIP4P-Ew simulations predict that both peptides are very collapsed, as evidenced by their contact maps and Rg distributions, which originate from the abundance of organized backbone structure that underlies the secondary structure propensities (Fig. 1 and Table I). In addition, the Aβ42 and Aβ43 ensembles show significant differences, with the Aβ43 ensemble exhibiting an increased α−helical structure in the central hydrophobic cluster (CHC) of residues 16-30, as well as increases in the turn populations at residues 36-38 and the 6-9 region with a simultaneous increase in the β strand formed by residues 3-5 and 10-12, structural sub-populations that are greatly diminished (but still present) in the Aβ42 ensemble. This result is in direct contradiction with results reported by Conicella and Fawzi,4 which showed that there are no major structural differences in the N-terminus and CHC region for the two peptide monomers.
FIG. 1.
Comparison of structural properties for Aβ42 and Aβ43 using the force field Amber99SB + TIP4P-Ew and using TREx simulated at 0.1 µs/replica. (a) Contact maps, (b) β−strand and helix propensities, and (c) turn propensity and radius of gyration distribution. For (b) and (c), blue lines are for Aβ42 and red lines are Aβ43 and represent the average for two independent trajectories. Error bars are plus and minus one standard deviation of the calculated propensity at the given residue for the two trajectories and generally represent the degree of agreement between the two trajectories.
TABLE I.
Simulated properties for the Aβ42 and Aβ43 peptides for each sampling method-force field combination. Mean and standard deviation averaged over two independent trajectories, except for the 0.8 µs TREx simulation, where block averaging over two 250 ns blocks was used. We noted a systematic shift in J-couplings between the two experimental datasets from Conicella and Fawzi4 and Roche et al.; we have applied a −0.4 Hz shift to the Aβ43 Ji values from Conicella and Fawzi before comparison which would bring the Aβ42 results in line with each other to the simulated J-couplings.
| Sampling method and force field combination | ||||||
|---|---|---|---|---|---|---|
| TREx (0.1 µs) | TREx (0.1 µs) | TREx (0.8 µs) | TCW (0.2 µs) | TCW (0.2 µs) | TCW (0.2 µs) | |
| + TIP4P-Ew | + CHARMM36m | + Amberff99SB | + Amberff99SB | + CHARMM36m | + Amber99SB-ILDN | |
| Peptide | + Amberff99SB | + CHARMM-TIP3P | + TIP4P-Ew | + TIP4P-Ew | + CHARMM-TIP3P | + TIP4P-D |
| χ2 between simulated and experimental4,5 J-coupling constants | ||||||
| Aβ42 | 3.70 | 4.65 | 3.70 | 2.70 | 3.01 | 2.89 |
| Aβ43 | 4.75 | 3.76 | 3.65 | 2.47 | 2.96 | 2.71 |
| EISD score | ||||||
| Aβ42 | 39.479 | 3.858 | 40.014 | 57.833 | 47.741 | 54.937 |
| Aβ43 | 23.234 | 25.090 | 36.530 | 47.488 | 39.328 | 45.338 |
| Mean and standard deviation of the end-to-end-distance, ⟨Ree⟩ (in Å) | ||||||
| Aβ42 | 24.3 0.6 | 39.3 3.0 | 20.5 1.7 | 28.4 0.9 | 36.8 1.3 | 33.5 7.9 |
| Aβ43 | 26.5 3.5 | 44.4 1.1 | 20.3 0.7 | 29.1 2.0 | 38.2 1.3 | 31.9 0.9 |
| Mean and standard deviation of FRET efficiencies, ⟨EFRET⟩ | ||||||
| Aβ42 | 0.93 0.002 | 0.64 0.084 | 0.96 0.007 | 0.88 0.009 | 0.71 0.031 | 0.77 0.150 |
| Aβ43 | 0.92 0.049 | 0.56 0.001 | 0.97 0.007 | 0.87 0.034 | 0.69 0.020 | 0.82 0.004 |
| Mean and standard deviation of the radius of gyration, ⟨Rg⟩ (in Å) | ||||||
| Aβ42 | 12.0 0.3 | 17.2 2.2 | 11.3 0.0 | 12.9 0.1 | 15.9 0.5 | 14.9 1.6 |
| Aβ43 | 11.8 0.6 | 17.8 0.4 | 11.8 0.1 | 13.2 0.4 | 16.4 0.2 | 15.7 2.0 |
When using the same TREx sampling method for 0.1 µs, but changing to the CHARMM36m + CHARMM-TIP3P force field, there is significant reduction in long-range structure and secondary structure propensities for the two peptides, and hence, the ensembles are less collapsed compared to the standard force field combination for the two peptides (Table I and Fig. S1). However, the TREx simulations using the newer protein-water force field produce ensembles that still predict differences in the sub-populations of structure for both Aβ42 and Aβ43 that are not observed in the experiment,4 such as the relative enrichment in β content for Aβ42. The long-range structure evident in the contact maps shown in Fig. S1 directly contradicts the NOE data of Roche et al., which found no evidence for long-range contacts.5 The large error bars indicate that the two independent trajectories did not converge to the same result, a sign that one or both of the independent trajectories were stuck in local minima on the 0.1 µs/replica time scale of the TREx simulation. We show this data to emphasize the point that TREx simulations on these non-converged time scales were used to identify errors in standard force fields and thus informed the development of modified force fields for unfolded proteins and IDPs.27,38
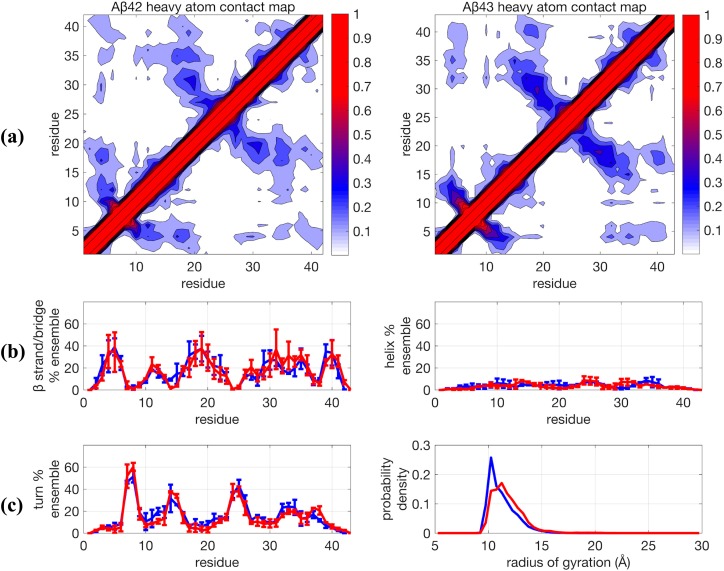
Since more recently it has become standard to perform TREx simulations using on the order of 1 µs/replica in recent IDP studies,6,21,44,61,62 we conducted one additional trajectory using a TREx simulation out to 800 ns/replica for each peptide using Amberff99SB + TIP4P-Ew, with the resulting structural data in Fig. 2. Our TREx simulation of 0.8 µs is generally consistent with the 1.0 µs/replica TREx simulations performed by Rosenman et al.44 With longer simulation time scales, the previously significant differences between Aβ42 and Aβ43 are reduced to being within statistical error for all secondary structure categories. While there is a clear improvement in some structural properties at this longer time scale using TREx, such as reduction in the population of α−helices, the β−sheet propensities still show a large variability of ±20% at residues 5-6, 19, and 31. As a result, their structural ensembles are in stark disagreement with the available NMR and 2D FRET data by being too collapsed and highly structured. It is therefore very understandable why one would continue to conclude that there is a deficiency in the standard force fields based on evidence such as Fig. 2.
FIG. 2.
Comparison of structural properties for Aβ42 and Aβ43 using the force field Amberff99sb + TIP4P-Ew and using Temperature Replica Exchange (TREx) simulated at 0.8 µs/replica. (a) Contact maps, (b) β−strand and helix propensities, and (c) turn propensity and radius of gyration distribution. For (b) and (c), blue lines are Aβ42 and red lines are Aβ43. Further details are given in the caption of Fig. 1.
Furthermore, the TREx + Amberff99SB + TIP4P-Ew Aβ ensembles strongly disagree with the Aβ42 ensemble generated by Lin et al.49 In their more extensive MD/MSM simulation, they found negligible β-sheet content, with the only persistent secondary structure being ∼10%–20% α-helical content for residues 12-18. While the MD/MSM study used the same peptide force field as in this work (Amber ff99SB), they performed their simulations with the TIP3P water model17 instead of TIP4P-Ew, which likely accounts for some quantitative differences in the Aβ ensembles. A study of the folding of Trp-cage using Amber ff99SB found that TIP3P enriched the sampling of helical content by ∼10% and reduced the sampling of β-sheet content by a similar amount when compared to TIP4P-Ew.73 These relatively minor population shifts are too small to explain the large discrepancies between the TREx and MD/MSM results; so much of the differences between the ensembles must result from the sampling efficiency. We believe this demonstrates that even on the μs time scale, TREx simulations are not able to fully capture the structural ensemble of Aβ peptides.
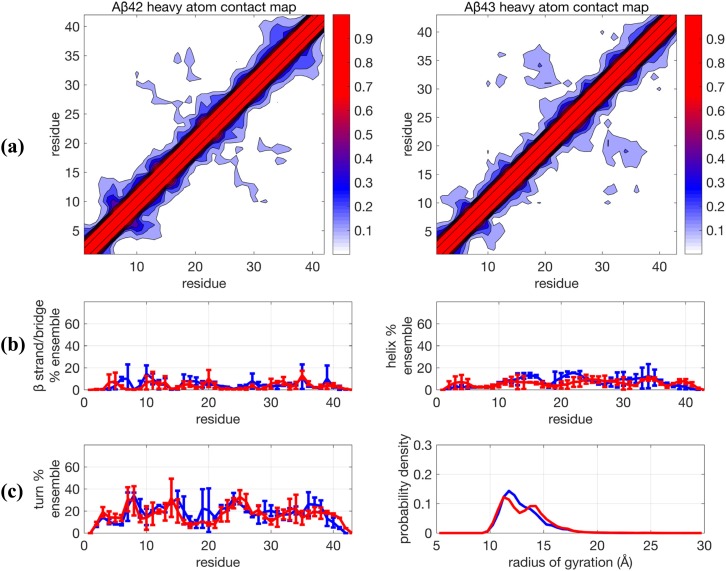
We next consider, whether an alternative sampling, namely, the TCW method, would converge faster on the ∼0.1-0.2 µs/replica time scale to evaluate the different force field combinations (Fig. 3 and Table I). We have established in previous work that TCW is superior to the TREx approach using test systems where quantitative measures of convergence are available.46,50 In addition, Figs. S2 and S3 show that the TCW method on the ∼0.2 µs time scale reaches comparable convergence to the ∼0.8 µs TREx simulation for all secondary structure categories. But as seen when comparing Figs. 2 and 3, the TREx and TCW enhanced sampling methods yield very different Aβ peptide ensembles using the same unmodified protein-water force field combination. More specifically, the TCW + ff99SB + TIP4P-Ew result is far less structured than that found with TREx and is much more similar to the MD/MSM results by Lin et al.49 Although there are regions of the sequence that exhibit larger uncertainties in the turn population, this variation in turn content suggests the transient sampling of still overall unstructured conformations since the sampling of β and helical conformations is consistently low rather than the more significant sampling of highly structured conformations seen in the TREx simulations. For the unmodified force field combination using TCW, there is a very small amount (∼5%-10%) for the contact region formed by residues 16-20 and 30-37 for both Aβ42 and Aβ43. It is unlikely that the experimental NOEs could absolutely rule out the presence of such a small population of long-ranged structure, and in fact the simulated NOEs would support this conclusion since the average NOE distance for these residues would be dominated by the ∼90% of the unstructured populations.
FIG. 3.
Comparison of structural properties generated for Aβ42 and Aβ43 using the force field combination Amber99SB + TIP4P-Ew and using Temperature Cool Walking (TCW). (a) Contact maps, (b) β−strand and helix propensities, and (c) turn propensity and radius of gyration distribution. For (b) and (c), blue lines are Aβ42 and red lines are Aβ43. Further details are given in the caption of Fig. 1.
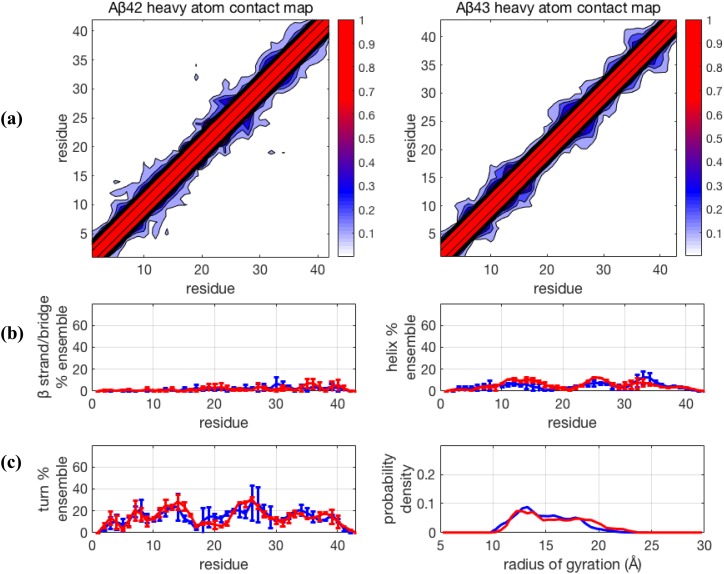
For completeness, we consider the newer force fields that have been shown to improve descriptions of IDP ensembles using TREx but now simulated with TCW. We first consider the Amber ff99SB-ILDN + TIP4P-D combination (Fig. 4), where the force field optimization is centered on increasing the strength of attractive London dispersion forces on the water oxygen atoms by ∼50% relative to that of other four-site water models. Using TREx simulations, this has been reported to produce less structured IDP ensembles by increasing the strength of protein-water attractions relative to protein-protein attractions using standard Lennard-Jones mixing rules.22 The results for TCW shown in Fig. 4 also confirm that this recently introduced water model generally reduces structural order and maintains structural similarity between the ensembles of the two peptides, with ⟨Rg⟩ ∼ 14.9 Å and 15.7 Å for Aβ42 and Aβ43, respectively (Table I). There is again, as in the TCW + ff99SB + TIP4P-Ew result, some variability in the turn population, suggesting the sampling of some different unstructured substates in the different trajectories, but the β−sheet and α−helical populations are consistently small.
FIG. 4.
Comparison of structural properties generated for Aβ42 and Aβ43 using the force field Amber99SB-ILDN + TIP4P-D and using Temperature Cool Walking (TCW). (a) Contact maps, (b) β−strand and helix propensities, and (c) turn propensity and radius of gyration distribution. For (b) and (c), blue lines are Aβ42 and red lines are Aβ43. Further details are given in the caption of Fig. 1.
Similar structural results are obtained for the CHARMM36m + CHARMM-TIP3P force field combination using the TCW sampling method (Fig. 5), predicting more expanded structures as evidenced by a shifted and broader Rg distribution, with ⟨Rg⟩ ∼ 15.9-16.4 Å for the two peptides (Table I), with no long-range contacts found using TREx as demonstrated through the absence of secondary structure signatures as well as the contact maps, in agreement with the NOEs for Aβ42.5,6 Furthermore, the structural ensemble of the Aβ42 and Aβ43 free monomers is seen to be nearly identical, in agreement with the experimental results of Conicella and Fawzi.4
FIG. 5.
Comparison of structural properties generated for Aβ42 and Aβ43 using the force field CHARMM36m + CHARMM-TIP3P and using Temperature Cool Walking (TCW). (a) Contact maps, (b) β−strand and turn propensities, and (c) α−helix propensity and radius of gyration distribution. For (b) and (c), blue lines are Aβ42 and red lines are Aβ43. Further details are given in the caption of Fig. 1.
Experimental validation of simulated ensembles
In order to better validate these results for the different force fields, and to better understand the differences found between TREx and TCW, we consider back-calculations of the NMR and FRET data as a metric for comparing Aβ42 and Aβ43 ensembles to the experiment (Table I). Unfortunately, current state-of-the-art chemical shift calculators developed specifically for protein applications have large associated intrinsic back-calculation errors, making quantitative comparisons problematic for IDPs. For example, the RMS error for 1HN chemical shifts in the SHIFTX2 calculator is 0.17 ppm,69 which is much larger than the experimental difference (<0.05 ppm) between the Aβ42 and Aβ43 ensembles.4 Thus, chemical shifts are not an ideal metric to distinguish between the different simulated ensembles, and as expected, the simulations are unable to capture the subtle differences in the 1HN chemical shifts in the C-terminus of the two peptides (examples given in Fig. S4).33
Table I shows the calculated χ2 parameter from the simulated J-coupling constants (JHN-Hα) for each ensemble as compared to the experiment, in which lower values of the χ2 metric indicate better agreement with experimental J-coupling constants, with values near one indistinguishable from the scalar coupling back-calculation error. We compare to the Roche et al. experimental dataset5 consisting of 38 Ji values for Aβ42 and the Conicella and Fawzi4 experimental dataset consisting of 22 Ji values for Aβ43. The simulated J-couplings from the computational ensembles support the general conclusion that the TCW sampling method is in better agreement with the NMR J-couplings than found for TREx, regardless of force field for both Aβ42 and Aβ43 peptides, with the standard force field in best quantitative agreement.4 We note that the χ2 values appear to be commensurate with the results of Meng et al. for Aβ42 using 750 ns TREx simulations with Amber ff99SBws (χ2 = 2.89) and Amber ff03ws (χ2 = 4.58), two IDP-optimized force fields, using the same experimental data and set of Karplus parameters. However, their χ2 values include a block-averaging error due to variance within the trajectories that depresses the value of the χ2 (up to ∼10%). We did not apply this block averaging error since this hides the intrinsic sampling problem we are investigating.
The conclusion that the TCW method yields better agreement with J-couplings is bolstered when using a Bayesian analysis we have developed, the Experimental Inferential Structure Determination (EISD) method.72 The EISD method is designed to assess agreement given the available experimental J-coupling data (as well as chemical shifts, which we ignore here given their low predictive value) that take into account the intrinsic experimental and back-calculation uncertainties through optimization. In this case, the optimization occurs within the variance of the Gaussian distributed model for the back-calculation error for Karplus parameters A, B, and C in Eq. (1). We analyze each ensemble with EISD against the same set of experimental data used for the χ2 analysis and find that the ranking of the ensembles does not change from the χ2 analysis (Table I), i.e., the available J-coupling data are sufficient for concluding that the TCW ensembles are in better agreement with the NMR data, with significant better agreement for the standard force field.
Although we do not invoke a full scale simulation of NOE data as we have done in previous studies,10,29,67,68 we can make some qualitative comparisons to the NOE data for Aβ425 using the contact maps. Clearly, the newer force fields are in excellent agreement with the NOE data. Furthermore, the standard force field using the TCW simulations is also in good agreement with the NOE data, unlike the TREx simulations that contain a very high percentage of long-range contacts. For the unmodified force field combination using TCW, there is a very small amount (∼5%-10%) for the contact region formed by residues 16-20 and 30-37 for both Aβ42 and Aβ43, but as we have already stated above, it is unlikely that the experimental NOEs could absolutely rule out the presence of such a small population of transient long-ranged structure.
Next, we consider the comparison of the different sampling and force field combinations to 2D FRET that have been reported recently for Aβ42;6 we again make the reasonable assumption that FRET efficiencies, EFRET, for Aβ43 will be nearly identical based on the results of Conicella and Fawzi.4 In principle, EFRET should be calculated for all conformations using the end-to-end distance between the dyes or tags, , i.e., the simulations should use the same sequence construct as the experiment that includes additional residues and the chemical specifics of the covalently bound dye molecules. The possibility that the IDP ensemble will be perturbed to some degree by these tags, as we have seen previously for the MTSL tag used in EPR studies,51 obscures the means to compare from the simulation data of untagged peptides, with experimentally derived values of . Hence, a model for the missing tags must be developed to make contact with the 2D FRET data.
It is useful to consider the FRET model used by Meng et al.6 in which the distance between the dyes is implicitly accounted for by scaling the with an approximation that the effect of the dyes is equivalent to adding Ntag additional residues to the sequence length,74
| (4) |
The origin of the scaling model used for the missing tags [Eq. (4)] and value for Ntag has precedent in the literature from a study by McCarney and co-workers, who conducted 1 ns standard MD simulations on a model of Alexa 488 attached to a single cysteine residue; they obtained an ensemble average that does provide support for Ntag = 12 for a pair of dyes.75 However, they also noted that this average conceals the chemical nature of the bimodal distribution, which results from an extended conformation corresponding to Ntag ∼ 16, and a collapsed conformation due to hydrophobic interactions between the dye and its linker, with Ntag ∼ 4.4. While McCarney et al. noted that the collapsed conformation would not likely persist in experiments with sufficient denaturants present, as is the case in many FRET studies including their own,75 that would not be and is not the case for native, denaturant-free studies, as in the experiments of Meng et al.6 for Aβ42 that study the peptide in more native-like conditions.
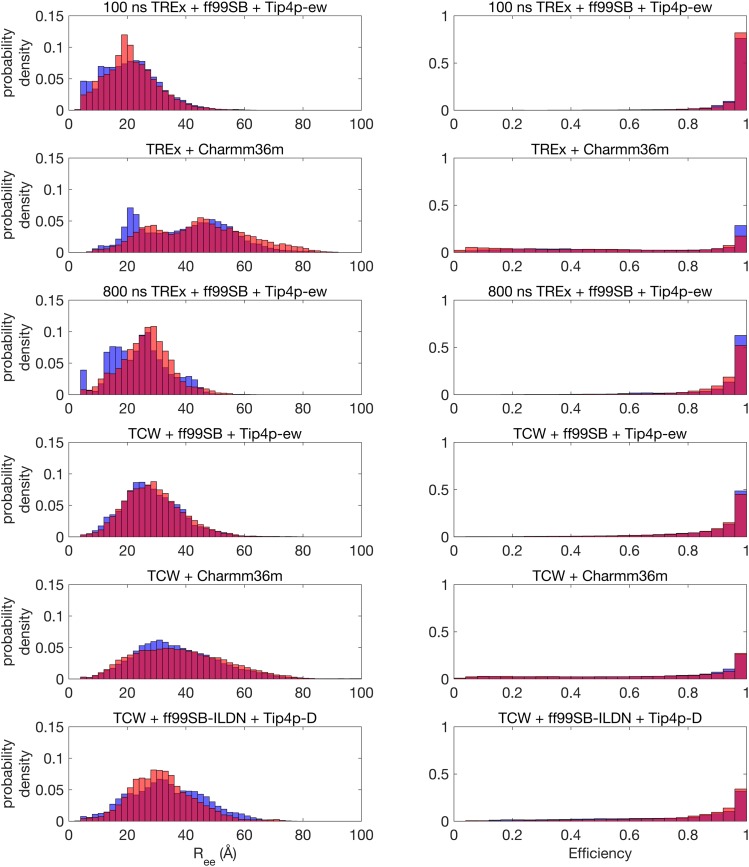
The resulting untagged peptide simulations that have been scaled using Eq. (4) with Ntag = 12 show a highly skewed distribution with a dominant peak at EFRET = 1 (Fig. 6) that is in disagreement with the experiment which is peaked around the average FRET efficiency of ∼0.63 for Aβ42. This same difference between the experimental and simulated result is also evident in the supplementary material in the work of Meng et al.6 using the new IDP force fields developed by Best and co-workers.23,27,38 The extremely high FRET efficiency is as expected given the relatively short length of the Aβ peptides and the large Förster radius for the dye pair of Alexa 488 and 647, i.e., as per Eq. (3), all conformations with the scaled values of less than ∼40 Å will yield EFRET ∼ 1.
FIG. 6.
Simulated end-to-end distance histograms (left) and corresponding FRET efficiency histograms using Eq. (3) (right) for all force field- sampling combinations. For all plots, blue bars are for Aβ42 and red bars are for Aβ43. All simulations are for the untagged peptides, with the results shown having incorporated a shift to model the additional residues and tags.
Even so, the TCW simulations using the different force fields yield FRET efficiencies for Aβ42 of ⟨EFRET⟩ = 0.71–0.88 (Table I); to compare to the work of Meng et al. for Aβ42, the range of simulated FRET efficiencies they found using two different force fields designed for IDPs with the same value of Ntag = 12 gave values of EFRET = 0.68–0.83 which they state is in good agreement with the experimental results.6 By contrast, the 0.8 µs TREx simulation using a standard force field yields EFRET = 0.96–0.97. Increasing Ntag to 16 or even 20 would only reduce EFRET by a few percent; hence, this general difference between sampling methods would remain the same. Among the TCW simulations, those using modified force fields produce values of EFRET that are lower and closer to the experimental values of Meng et al., consistent with those force fields producing more expanded ensembles than standard ones.
Given the complete summary of the experimental validation, we also must conclude that the secondary structure propensities for the standard force field for the Aβ peptides are not as egregiously incorrect as ascertained from the TREx sampling method using a standard 0.8 µs/replica simulation. There is no question that the newer force fields agree well with the experimental data, but the TCW + Amber ff99SB + TIP4P-Ew also agrees as well and in fact even slightly better for the NMR J-coupling χ2 and EISD evaluation. Given the uncertainties in the 2D FRET models, we can only conclude that the TCW simulations for the standard force fields are acceptable based on the upper bound value reported by Meng et al.6 (EFRET = 0.83) for one of their modified force fields. Using TCW, the standard force field yields negligible β-sheet and α-helical content, and the only observed long-range contacts are at very low population, and hence qualitatively consistent with the 2D FRET and NOEs taken on the Aβ42 peptide, where the 5%-10% population of long-range contacts will likely not be captured in the experiment.5,6 As a result, the structural ensemble of both peptides generated using the TCW sampling method is more extended than what was found under the TREx protocol for the standard force field, with ⟨Rg⟩ ∼ 12.9–13.2 Å for the two peptides (Table I).
DISCUSSION
Given the better agreement with all of the experimental data using the TCW protocol over the TREx simulations, we use the TCW results to next address the question as to whether the new modified force fields introduce a genuine improvement over the standard force field. One assessment is whether the force fields are yielding structural ensembles consistent with a random coil ensemble modeled as a Gaussian random chain or a self-avoiding random walk (SARW). Although the Aβ ensemble using the standard force field does contain a small amount of residual structure, a rapidly interconverting unfolded or IDP ensemble will sample both extended and compact conformations containing regions of secondary structure seen in folded proteins that are still consistent with a random coil ensemble.76
The chain length scaling exponents for polymer models used to interpret SAXS, NMR, and FRET measurements for unfolded proteins and IDPs have been shown to be dependent on sequence characteristics such as charge and hydrophobicity.77,78 Given that Aβ has both a net positive and relatively high hydrophobicity in the CHC region of its sequence, the scaling exponent might be expected to reduce to the Θ-limit for this IDP,6
| (5) |
where R0 = 2.0 Å as given by Fitzkee and Rose79 and ν = 0.5 for the Θ-limit which would yield ⟨Rg⟩ ∼ 13 Å that is consistent with the value calculated from the unmodified force field results simulated with TCW given in Table I. Under the Gaussian random coil model, we would conclude that the modified force fields have resulted in an over-correction by producing much more expanded ensembles than is warranted. However, if we assume a SARW model, we determine a larger value for Rg, i.e., using ν = 0.54–0.6 in a good solvent56 would yield ⟨Rg⟩ ∼ 15–19 Å, in better agreement with the modified force fields, thereby suggesting that the standard force fields are in fact too collapsed. Furthermore, for a Gaussian random chain, we would expect the following relationship to hold:
| (6) |
But this correlation between Rg and Ree is poor given the simulated data in Table I, except for the TCW + CHARMM36m + CHARMM-TIP3P combination, which is inconsistent with the Gaussian model based on Rg.
Thus, we view polymer physics models and analyses as largely inconclusive for differentiating the quality of force fields for this IDP system for several reasons. First is that the differences between the Gaussian and SARW models are better differentiated for much longer polymers than the small Aβ peptides investigated here. Furthermore, Fuertes et al. have presented some novel analytical techniques on a set of IDPs and denatured proteins using a variety of dyes and denaturant conditions to evaluate the relationship between FRET and SAXS.57 They suggest that one should generally decouple Rg from Ree and thus avoid using a simple scaling law such as Eq. (6) that is independent of peptide chemistry.57 Finally, the field is in need of new heteropolymer-centric theoretical models that are able to capture sequence details to extend beyond simple scaling laws and empirical relations, models which are now starting to be developed in recent work for the IDP class of proteins.80,81
We next turn to a more quantitative assessment using the 2D FRET data to ascertain the differences in force fields. The simulation of FRET efficiencies, especially for IDPs, involves a series of assumptions that introduce uncertainty that must be acknowledged when comparing to the FRET observable given the presence of the fluorescent dyes. As of late 2018, there is active debate on the perturbations introduced by fluorophore tags.53–57 Fuertes et al.54 assert that there is no perturbation of the structural ensemble across a series of disordered peptides upon addition of dye labels. Part of the basis of their conclusion is that they did not find significant shifts in the SAXS profiles or ⟨Rg⟩ of tagged and untagged peptides at high denaturant conditions.57 If this is the case, then our 2D FRET results and analysis support the view that the standard force field for the untagged Aβ ensembles and tags modeled using Eq. (4) is in adequate to good agreement with the experiment, with the modified force fields performing only slightly better.
By contrast, Riback et al. concluded that at native conditions with no denaturant, the addition of tags in FRET experiments leads to interactions with the IDP that will contribute to FRET signals that overemphasize its contraction and thus artificially increases its FRET efficiency under denaturant-free conditions.56 Furthermore, the perturbative effect of the dyes was seen to be larger for the smaller peptides in their experiments, where the addition of labels and the residues to which they are bonded has a greater effect on the mass and resulting dynamics and structure of the peptide. For example, the addition of the tags produced shifts from −0.3 to +0.5 nm in the average Rg of the two smallest peptides studied, N49 and NLS, which are natively 36 and 44 residues.56 Even the results of Meng et al. found an increase in EFRET upon explicit representation of the Alexa fluorescent tags using a standard MD calculation for Aβ42,6 which is consistent with greater compaction of the ensemble. Our own recent work demonstrated that addition of a hydrophobic MTSL-Cys tag to Aβ42 can perturb the structural ensemble through interactions between the dye and the peptide that in turn leads to more a collapsed structural ensemble compared to the original peptide.51 The simulations of Fuertes et al., however, modeled the unlabeled peptide using implicit solvent and then built up an ensemble of structures of the labeled peptide by stochastically adding the dyes to the unlabeled conformers.57 While this produces a useful test for verifying that many different values of Ree can be obtained from an ensemble with the same Rg, it does not address the potential phenomenon of the dyes affecting the chain dynamics and structure directly. If the tags do induce an artificial compaction of the ensemble, then the true experimental ensembles would be more expanded with even lower FRET efficiencies than reported for Aβ42. If that is the case, then the standard force fields yield IDP ensembles that are in fact too collapsed, and force field modifications are warranted, especially for small Aβ42 and Aβ43 peptides studied in this work.
CONCLUSION
We have simulated the disordered structural ensembles of the Aβ42 and Aβ43 peptides, which according to recent experiments4–6 should be largely the same and exhibit no persistent structural ordering or long-range contacts. But two types of error can occur during computational studies of IDP structural ensembles that prevent connections to such experiments, namely, statistical sampling error and systematic error in energy and forces. Statistical sampling error occurs when the simulations have not been run sufficiently long to achieve convergence, while systematic error happens when the energy surface of the peptide-water system is not modeled with accurate molecular interactions. Not surprisingly, these two potential errors are intertwined, and hence, we have attempted to consider them both by comparing two sampling methods, TREx and TCW, as well as comparing a standard protein-water force field and those that have been recently modified to yield better modeling of disordered states. We have also attempted to validate the various simulated ensembles by comparing to recent state of the art NMR and 2D FRET experiments.4–6
While it is starting to become established that long MD trajectories of ∼100 µs–1 ms are often necessary to reveal force field deficiencies,11,49 simulation time scales that are largely routine only on specialized hardware such as Anton82 or Folding@home,83 the hope is that better enhanced or accelerated sampling methods might converge more quickly, i.e., with one to two orders of magnitude less effort. In this work, we have shown that even at μs time scales there appear to be limitations in the TREx sampling method, producing far more structured ensembles that are in disagreement with NMR and 2D FRET validation data on Aβ peptides. Changing the sampling method from TREx to TCW produces ensembles that are qualitatively in agreement with J-couplings, NOEs, and FRET efficiencies, regardless of the force field that is simulated. The TCW results for Aβ42 are also in very good agreement with the very long sub-millisecond MD/MSM results by Lin and co-workers.49 Thus, our evidence has shown that what was thought to be primarily a force field problem was masked by what is at least in part a problem of poor sampling. This work establishes that the TCW method is more effective than TREx when entropic barriers dominate and, when applied to IDPs, supports the recent hypothesis that IDPs have an inverted free energy landscape in which disordered conformations are lower in free energy than ordered structures.52
Sampling is an important consideration for establishing the transferability of any force field, by demonstrating that appropriate conformational equilibria are reached across a range of thermodynamic conditions in order to describe folded and unfolded states of globular proteins as well as IDP sequences. For example, some standard protein and water force field combinations have proven robust for understanding mechanistic questions about protein folding,84 which requires a good model of the structure and internal dynamics of the unfolded states in addition to the folded state of a globular protein.85 But historically, it was the ability to sample multiple folding and unfolding events using these standard force fields which allowed them to gain validation through direct comparisons to robust folding experiments.86,87 This work rescues some of these standard force fields in the sense that they require extensive sampling to definitively show whether they are also capable of simulating accurate IDP ensembles.
The modified force fields may have had the effect of inherently lowering the entropic barriers and, in the best case, still maintaining the folded-unfolded equilibrium. However, unlike the case of protein folding, experimental validation is more limited and underdetermined for IDPs for a variety of reasons. At present, there is an impedance mismatch for chemical shifts and FRET data; for chemical shifts, the fault is on the theoretical side because of the reduced capability to back-calculate shifts from structure,72 whereas for FRET measurements on very small IDPs, there remains the possibility that the presence of the fluorescent tags might perturb the IDP ensemble from its equilibrium state.56 However, the impedance match between theory and experiment for scalar couplings and NOEs has provided strong support for the conclusion that, when simulated with TCW or using a very long MD/MSM simulation, the Amberff99SB + TIP4P-Ew, CHARMM36m + CHARMM-TIP3P, and Amberff99SB-ILDN + TIP4P-D are all appropriate force fields for IDPs. While clearly some of the new force field modifications can promote more expanded monomer ensembles to reproduce many experimental IDP properties more expediently, it is important to remember that the IDP-specific force fields38 and other modified force fields may come with their own limitations, such as now manifesting native state instability,33 thereby forgoing the ability to simulate disorder to order transitions in folding upon binding events that are part of the greater functional repertoire of proteins with intrinsic disorder.2
SUPPLEMENTARY MATERIAL
See supplementary material for comparison of other sampling methods and force fields, end-to-end distance and FRET efficiency histograms, simulated chemical shifts, and EISD results between the Aβ43 and Aβ42 structural ensembles.
ACKNOWLEDGMENTS
We would like to thank Ad Bax, Robert Best, Nick Fawzi, Julie Forman-Kay, Alex MacKerell, Stefano Piana-Agostinetti, and Kevin Plaxco for helpful discussions. We thank Reviewer 1 for very helpful comments and David H. Brookes for early calculations using EISD. S.S. and T.H.-G. were supported by the National Institutes of Health (NIH) Grant No. U01GM121667-02, and J.L. was partially supported on No. 5R01GM127627-01. J.L. also acknowledges partial support from an NIH Molecular Biophysics Training Grant No. T32-GM008295 during early stages of this study. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This research also used GPU resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725.
REFERENCES
- 1.Dunker A. K., Silman I., Uversky V. N., and Sussman J. L., Curr. Opin. Struct. Biol. 18(6), 756–764 (2008). 10.1016/j.sbi.2008.10.002 [DOI] [PubMed] [Google Scholar]
- 2.Dyson H. J. and Wright P. E., Nat. Rev. Mol. Cell Biol. 6(3), 197–208 (2005). 10.1038/nrm1589 [DOI] [PubMed] [Google Scholar]
- 3.Goedert M. and Spillantini M. G., Science 314(5800), 777–781 (2006). 10.1126/science.1132814 [DOI] [PubMed] [Google Scholar]
- 4.Conicella A. E. and Fawzi N. L., Biochemistry 53(19), 3095–3105 (2014). 10.1021/bi500131a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Roche J., Shen Y., Lee J. H., Ying J., and Bax A., Biochemistry 55(5), 762–775 (2016). 10.1021/acs.biochem.5b01259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Meng F., Bellaiche M. M. J., Kim J.-Y., Zerze G. H., Best R. B., and Chung H. S., Biophys. J. 114(4), 870–884 (2018). 10.1016/j.bpj.2017.12.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Marsh J. A. and Forman-Kay J. D., Proteins: Struct., Funct., Bioinf. 80(2), 556–572 (2012). 10.1002/prot.23220 [DOI] [PubMed] [Google Scholar]
- 8.Krzeminski M., Marsh J. A., Neale C., Choy W.-Y., and Forman-Kay J. D., Bioinformatics 29(3), 398–399 (2013). 10.1093/bioinformatics/bts701 [DOI] [PubMed] [Google Scholar]
- 9.Bhowmick A., Brookes D. H., Yost S. R., Dyson H. J., Forman-Kay J. D., Gunter D., Head-Gordon M., Hura G. L., Pande V. S., Wemmer D. E., Wright P. E., and Head-Gordon T., J. Am. Chem. Soc. 138(31), 9730–9742 (2016). 10.1021/jacs.6b06543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ball K. A., Wemmer D. E., and Head-Gordon T., J. Phys. Chem. B 118, 6405–6416 (2014). 10.1021/jp410275y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nerenberg P. S. and Head-Gordon T., Curr. Opin. Struct. Biol. 49, 129–138 (2018). 10.1016/j.sbi.2018.02.002 [DOI] [PubMed] [Google Scholar]
- 12.Hornak V., Abel R., Okur A., Strockbine B., Roitberg A., and Simmerling C., Proteins: Struct., Funct., Bioinf. 65(3), 712–725 (2006). 10.1002/prot.21123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Christen M., Hünenberger P. H., Bakowies D., Baron R., Bürgi R., Geerke D. P., Heinz T. N., Kastenholz M. A., Kräutler V., Oostenbrink C., Peter C., Trzesniak D., and van Gunsteren W. F., J. Comput. Chem. 26(16), 1719–1751 (2005). 10.1002/jcc.20303 [DOI] [PubMed] [Google Scholar]
- 14.Jorgensen W. L., Maxwell D. S., and Tirado-Rives J., J. Am. Chem. Soc. 118(45), 11225–11236 (1996). 10.1021/ja9621760 [DOI] [Google Scholar]
- 15.Kaminski G. A., Friesner R. A., Tirado-Rives J., and Jorgensen W. L., J. Phys. Chem. B 105(28), 6474–6487 (2001). 10.1021/jp003919d [DOI] [Google Scholar]
- 16.MacKerell A. D., Bashford D., Bellott M., Dunbrack R. L., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., Reiher W. E., Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiórkiewicz-Kuczera J., Yin D., and Karplus M., J. Phys. Chem. B 102(18), 3586–3616 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- 17.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79(2), 926–935 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 18.Jorgensen W. L. and Madura J. D., Mol. Phys. 56(6), 1381–1392 (1985). 10.1080/00268978500103111 [DOI] [Google Scholar]
- 19.Horn H. W., Swope W. C., Pitera J. W., Madura J. D., Dick T. J., Hura G. L., and Head-Gordon T., J. Chem. Phys. 120(20), 9665–9678 (2004). 10.1063/1.1683075 [DOI] [PubMed] [Google Scholar]
- 20.Wang W., Ye W., Jiang C., Luo R., and Chen H.-F., Chem. Biol. Drug Des. 84(3), 253–269 (2014). 10.1111/cbdd.12314 [DOI] [PubMed] [Google Scholar]
- 21.Huang J., Rauscher S., Nawrocki G., Ran T., Feig M., de Groot B. L., Grubmüller H., and A. D. MacKerell, Jr., Nat. Methods 14, 71 (2016). 10.1038/nmeth.4067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Piana S., Donchev A. G., Robustelli P., and Shaw D. E., J. Phys. Chem. B 119(16), 5113–5123 (2015). 10.1021/jp508971m [DOI] [PubMed] [Google Scholar]
- 23.Best R. B. and Mittal J., J. Phys. Chem. B 114(46), 14916–14923 (2010). 10.1021/jp108618d [DOI] [PubMed] [Google Scholar]
- 24.Nguyen P. H., Li M. S., and Derreumaux P., Phys. Chem. Chem. Phys. 13(20), 9778–9788 (2011). 10.1039/c1cp20323a [DOI] [PubMed] [Google Scholar]
- 25.Siwy C. M., Lockhart C., and Klimov D. K., PLoS Comput. Biol. 13(1), e1005314 (2017). 10.1371/journal.pcbi.1005314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rauscher S., Gapsys V., Gajda M. J., Zweckstetter M., de Groot B. L., and Grubmüller H., J. Chem. Theory Comput. 11(11), 5513–5524 (2015). 10.1021/acs.jctc.5b00736 [DOI] [PubMed] [Google Scholar]
- 27.Best R. B. and Mittal J., Proteins: Struct., Funct., Bioinf. 79(4), 1318–1328 (2011). 10.1002/prot.22972 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Scott W. R. P., Hünenberger P. H., Tironi I. G., Mark A. E., Billeter S. R., Fennen J., Torda A. E., Huber T., Krüger P., and van Gunsteren W. F., J. Phys. Chem. A 103(19), 3596–3607 (1999). 10.1021/jp984217f [DOI] [Google Scholar]
- 29.Fawzi N. L., Phillips A. H., Ruscio J. Z., Doucleff M., Wemmer D. E., and Head-Gordon T., J. Am. Chem. Soc. 130(19), 6145–6158 (2008). 10.1021/ja710366c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Song W. L., Wang Y. Y., Colletier J. P., Yang H. Y., and Xu Y. C., Sci. Rep. 5, 11024 (2015). 10.1038/srep11024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Amini Z., Fatemi M. H., and Rauk A., Can. J. Chem. 94(10), 833–841 (2016). 10.1139/cjc-2016-0267 [DOI] [Google Scholar]
- 32.Viet M. H., Nguyen P. H., Derreumaux P., and Li M. S., ACS Chem. Neurosci. 5(8), 646–657 (2014). 10.1021/cn500007j [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Robustelli P., Piana S., and Shaw D. E., Proc. Natl. Acad. Sci. U. S. A. 115(21), E4758–E4766 (2018). 10.1073/pnas.1800690115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nerenberg P. S. and Head-Gordon T., J. Chem. Theory Comput. 7(4), 1220–1230 (2011). 10.1021/ct2000183 [DOI] [PubMed] [Google Scholar]
- 35.Nerenberg P. S., Jo B., So C., Tripathy A., and Head-Gordon T., J. Phys. Chem. B 116(15), 4524–4534 (2012). 10.1021/jp2118373 [DOI] [PubMed] [Google Scholar]
- 36.Henriques J., Cragnell C., and Skepö M., J. Chem. Theory Comput. 11(7), 3420–3431 (2015). 10.1021/ct501178z [DOI] [PubMed] [Google Scholar]
- 37.Henriques J. and Skepö M., J. Chem. Theory Comput. 12(7), 3407–3415 (2016). 10.1021/acs.jctc.6b00429 [DOI] [PubMed] [Google Scholar]
- 38.Best R. B., Zheng W., and Mittal J., J. Chem. Theory Comput. 10(11), 5113–5124 (2014). 10.1021/ct500569b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Abrams C. and Bussi G., Entropy 16(1), 163 (2014). 10.3390/e16010163 [DOI] [Google Scholar]
- 40.Bernardi R. C., Melo M. C. R., and Schulten K., Biochim. Biophys. Acta 1850(5), 872–877 (2015). 10.1016/j.bbagen.2014.10.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sugita Y. and Okamoto Y., Chem. Phys. Lett. 314(1-2), 141–151 (1999). 10.1016/s0009-2614(99)01123-9 [DOI] [Google Scholar]
- 42.Hansmann U., Chem. Phys. Lett. 281, 140–150 (1997). 10.1016/s0009-2614(97)01198-6 [DOI] [Google Scholar]
- 43.Zuckerman D. M. and Lyman E., J. Chem. Theory Comput. 2, 1200–1202 (2006). 10.1021/ct0600464 [DOI] [PubMed] [Google Scholar]
- 44.Rosenman D. J., Wang C., and García A. E., J. Phys. Chem. B 120(2), 259–277 (2016). 10.1021/acs.jpcb.5b09379 [DOI] [PubMed] [Google Scholar]
- 45.Nymeyer H., J. Chem. Theory Comput. 4(4), 626–636 (2008). 10.1021/ct7003337 [DOI] [PubMed] [Google Scholar]
- 46.Brown S. and Head-Gordon T., J. Comput. Chem. 24(1), 68–76 (2003). 10.1002/jcc.10181 [DOI] [PubMed] [Google Scholar]
- 47.Hicks A. and Zhou H.-X., J. Chem. Phys. 149(7), 072313 (2018). 10.1063/1.5027409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Do T. N., Choy W.-Y., and Karttunen M., J. Chem. Theory Comput. 12(1), 395–404 (2016). 10.1021/acs.jctc.5b00868 [DOI] [PubMed] [Google Scholar]
- 49.Lin Y. S., Bowman G. R., Beauchamp K. A., and Pande V. S., Biophys. J. 102(2), 315–324 (2012). 10.1016/j.bpj.2011.12.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lincoff J., Sasmal S., and Head-Gordon T., J. Chem. Phys. 145(17), 174107 (2016). 10.1063/1.4965439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sasmal S., Lincoff J., and Head-Gordon T., Biophys. J. 113(5), 1002–1011 (2017). 10.1016/j.bpj.2017.06.067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Granata D., Baftizadeh F., Habchi J., Galvagnion C., De Simone A., Camilloni C., Laio A., and Vendruscolo M., Sci. Rep. 5, 15449 (2015). 10.1038/srep15449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Riback J. A., Bowman M. A., Zmyslowski A., Knoverek C. R., Jumper J., Kaye E. B., Freed K. F., Clark P. L., and Sosnick T. R., Science 361(6405), eaar7949 (2018). 10.1126/science.aar7949 [DOI] [PubMed] [Google Scholar]
- 54.Fuertes G., Banterle N., Ruff K. M., Chowdhury A., Pappu R. V., Svergun D. I., and Lemke E. A., Science 361(6405), eaau8230 (2018). 10.1126/science.aau8230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Best R. B., Zheng W., Borgia A., Buholzer K., Borgia M. B., Hofmann H., Soranno A., Nettels D., Gast K., Grishaev A., and Schuler B., Science 361(6405), eaar7101 (2018). 10.1126/science.aar7101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Riback J. A., Bowman M. A., Zmyslowski A. M., Knoverek C. R., Jumper J. M., Hinshaw J. R., Kaye E. B., Freed K. F., Clark P. L., and Sosnick T. R., Science 358(6360), 238 (2017). 10.1126/science.aan5774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fuertes G., Banterle N., Ruff K. M., Chowdhury A., Mercadante D., Koehler C., Kachala M., Estrada Girona G., Milles S., Mishra A., Onck P. R., Gräter F., Esteban-Martín S., Pappu R. V., Svergun D. I., and Lemke E. A., Proc. Natl. Acad. Sci. U. S. A. 114(31), E6342 (2017). 10.1073/pnas.1704692114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Case D. A., Cheatham T. E., Darden T., Gohlke H., Luo R., Merz K. M., Onufriev A., Simmerling C., Wang B., and Woods R. J., J. Comput. Chem. 26(16), 1668–1688 (2005). 10.1002/jcc.20290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Rathore N., Chopra M., and de Pablo J. J., J. Chem. Phys. 122(2), 024111(2004). 10.1063/1.1831273 [DOI] [PubMed] [Google Scholar]
- 60.Lindorff-Larsen K., Piana S., Palmo K., Maragakis P., Klepeis J. L., Dror R. O., and Shaw D. E., Proteins: Struct., Funct., Bioinf. 78(8), 1950–1958 (2010). 10.1002/prot.22711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sgourakis N. G., Yan Y. L., McCallum S. A., Wang C. Y., and Garcia A. E., J. Mol. Biol. 368(5), 1448–1457 (2007). 10.1016/j.jmb.2007.02.093 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rosenman D. J., Connors C. R., Chen W., Wang C. Y., and Garcia A. E., J. Mol. Biol. 425(18), 3338–3359 (2013). 10.1016/j.jmb.2013.06.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Case D. A., Betz R. M., Cerutti D. S., Cheatham T. E. III, Darden T. A., Duke R. E., Giese T. J., Gohlke H., Goetz A. W., Homeyer N., Izadi S., Janowski P., Kaus J., Kovalenko A., Lee T. S., LeGrand S., Li P., Lin C., Luchko T., Luo R., Madej B., Mermelstein D., Merz K. M., Monard G., Nguyen H., Nguyen H. T., Omelyan I., Onufriev A., Roe D. R., Roitberg A., Sagui C., Simmerling C. L., Botello-Smith W. M., Swails J., Walker R. C., Wang J., Wolf R. M., Wu X., Xiao L., and Kollman P. A., AMBER 2016, University of California, San Francisco, 2016. [Google Scholar]
- 64.Eastman P., Friedrichs M. S., Chodera J. D., Radmer R. J., Bruns C. M., Ku J. P., Beauchamp K. A., Lane T. J., Wang L.-P., and Shukla D., J. Chem. Theory Comput. 9(1), 461 (2013). 10.1021/ct300857j [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Roe D. R. and Cheatham T. E., J. Chem. Theory Comput. 9(7), 3084–3095 (2013). 10.1021/ct400341p [DOI] [PubMed] [Google Scholar]
- 66.Kabsch W. and Sander C., Biopolymers 22(12), 2577–2637 (1983). 10.1002/bip.360221211 [DOI] [PubMed] [Google Scholar]
- 67.Ball K. A., Phillips A. H., Nerenberg P. S., Fawzi N. L., Wemmer D. E., and Head-Gordon T., Biochemistry 50(35), 7612–7628 (2011). 10.1021/bi200732x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Ball K. A., Phillips A. H., Wemmer D. E., and Head-Gordon T., Biophys. J. 104(12), 2714–2724 (2013). 10.1016/j.bpj.2013.04.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Han B., Liu Y., Ginzinger S. W., and Wishart D. S., J. Biomol. NMR 50, 43–57 (2011). 10.1007/s10858-011-9478-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Vuister G. W. and Bax A., J. Am. Chem. Soc. 115, 7772–7777 (1993). 10.1021/ja00070a024 [DOI] [Google Scholar]
- 71.Vögeli B., Ying J., Grishaev A., and Bax A., J. Am. Chem. Soc. 129(30), 9377–9385 (2007). 10.1021/ja070324o [DOI] [PubMed] [Google Scholar]
- 72.Brookes D. H. and Head-Gordon T., J. Am. Chem. Soc. 138(13), 4530–4538 (2016). 10.1021/jacs.6b00351 [DOI] [PubMed] [Google Scholar]
- 73.Paschek D., Day R., and García A. E., Phys. Chem. Chem. Phys. 13(44), 19840–19847 (2011). 10.1039/c1cp22110h [DOI] [PubMed] [Google Scholar]
- 74.Zheng W., Borgia A., Borgia M. B., Schuler B., and Best R. B., J. Chem. Theory Comput. 11, 5543 (2015). 10.1021/acs.jctc.5b00778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.McCarney E. R., Werner J. H., Bernstein S. L., Ruczinski I., Makarov D. E., Goodwin P. M., and Plaxco K. W., J. Mol. Biol. 352(3), 672–682 (2005). 10.1016/j.jmb.2005.07.015 [DOI] [PubMed] [Google Scholar]
- 76.Smith L. J., Fiebig K. M., Schwalbe H., and Dobson C. M., Folding Des. 1(5), R95–R106 (1996). 10.1016/s1359-0278(96)00046-6 [DOI] [PubMed] [Google Scholar]
- 77.Aznauryan M., Delgado L., Soranno A., Nettels D., Huang J.-r., Labhardt A. M., Grzesiek S., and Schuler B., Proc. Natl. Acad. Sci. U. S. A. 113(37), E5389–E5398 (2016). 10.1073/pnas.1607193113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Hofmann H., Soranno A., Borgia A., Gast K., Nettels D., and Schuler B., Proc. Natl. Acad. Sci. U. S. A. 109(40), 16155–16160 (2012). 10.1073/pnas.1207719109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Fitzkee N. C. and Rose G. D., Proc. Natl. Acad. Sci. U. S. A. 101(34), 12497–12502 (2004). 10.1073/pnas.0404236101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Lin Y.-H. and Chan H. S., Biophys. J. 112(10), 2043–2046 (2017). 10.1016/j.bpj.2017.04.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Firman T. and Ghosh K., J. Chem. Phys. 148(12), 123305 (2017). 10.1063/1.5005821 [DOI] [PubMed] [Google Scholar]
- 82.Lindorff-Larsen K., Maragakis P., Piana S., Eastwood M. P., Dror R. O., and Shaw D. E., PLoS One 7(2), e32131 (2012). 10.1371/journal.pone.0032131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Pande V. S., Baker I., Chapman J., Elmer S. P., Khaliq S., Larson S. M., Rhee Y. M., Shirts M. R., Snow C. D., Sorin E. J., and Zagrovic B., Biopolymers 68(1), 91–109 (2003). 10.1002/bip.10219 [DOI] [PubMed] [Google Scholar]
- 84.Piana S., Klepeis J. L., and Shaw D. E., Curr. Opin. Struct. Biol. 24, 98–105 (2014). 10.1016/j.sbi.2013.12.006 [DOI] [PubMed] [Google Scholar]
- 85.Echeverria I., Makarov D. E., and Papoian G. A., J. Am. Chem. Soc. 136(24), 8708–8713 (2014). 10.1021/ja503069k [DOI] [PubMed] [Google Scholar]
- 86.Soranno A., Buchli B., Nettels D., Cheng R. R., Müller-Späth S., Pfeil S. H., Hoffmann A., Lipman E. A., Makarov D. E., and Schuler B., Proc. Natl. Acad. Sci. U. S. A. 109(44), 17800–17806 (2012). 10.1073/pnas.1117368109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Eaton W. A. and Wolynes P. G., Proc. Natl. Acad. Sci. U. S. A. 114(46), E9759–E9760 (2017). 10.1073/pnas.1716444114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Husic B. E. and Pande V. S., J. Am. Chem. Soc. 140(7), 2386–2396 (2018). 10.1021/jacs.7b12191 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for comparison of other sampling methods and force fields, end-to-end distance and FRET efficiency histograms, simulated chemical shifts, and EISD results between the Aβ43 and Aβ42 structural ensembles.