Understanding Dyslexia Through Personalized Large-Scale Computational Models

Abstract

Learning to read is foundational for literacy development, yet many children in primary school fail to become efficient readers despite normal intelligence and schooling. This condition, referred to as developmental dyslexia, has been hypothesized to occur because of deficits in vision, attention, auditory and temporal processes, and phonology and language. Here, we used a developmentally plausible computational model of reading acquisition to investigate how the core deficits of dyslexia determined individual learning outcomes for 622 children (388 with dyslexia). We found that individual learning trajectories could be simulated on the basis of three component skills related to orthography, phonology, and vocabulary. In contrast, single-deficit models captured the means but not the distribution of reading scores, and a model with noise added to all representations could not even capture the means. These results show that heterogeneity and individual differences in dyslexia profiles can be simulated only with a personalized computational model that allows for multiple deficits.

Learning to read is foundational for literacy development, yet a large percentage of children in primary school (~5%–17%) fail to become efficient and autonomous readers despite normal intelligence and schooling, a condition referred to as developmental dyslexia (Snowling, 2000). Research on developmental dyslexia has documented deficits in vision (Stein & Walsh, 1997), attention (Vidyasagar & Pammer, 2010), auditory and temporal processes (Vandermosten et al., 2010), and phonology and language (Hulme, Nash, Gooch, Lervåg, & Snowling, 2015; Snowling, 2001). It remains a challenge to link the various deficits to the precise learning mechanisms that cause atypical reading development.

Computational models provide a unique tool for understanding how deficits in component skills affect the mechanisms or representations that underlie reading development. Harm and Seidenberg (1999) were the first to use a computational modeling approach to understand developmental dyslexia. They assumed, in line with mainstream theories of reading acquisition (Ziegler & Goswami, 2005), that learning to read consisted of mapping an orthographic code onto a preexisting phonological system, modeled with an attractor neural network that learned phonological structure from phonetic input. Then, following the dominant view of dyslexia as being caused by a core phonological deficit (Vellutino, Fletcher, Snowling, & Scanlon, 2004), they impaired the phonological network to create impoverished representations and trained the model to map orthography onto them. A mild phonological impairment resulted in impaired nonword reading (e.g., blorf ) but not irregular word reading (e.g., aisle, yacht, pint), a moderate impairment resulted in strong deficits in nonword reading but smaller deficits in irregular word reading, and a severe deficit caused very strong deficits in both nonword and irregular word reading. These simulations provided a proof of concept that one can impair a model such that it reflects impaired reading performance. However, they did not investigate how the size of the phonological deficit for any given child would affect his or her reading outcomes. Moreover, they did not investigate how different types of impairments, including nonphonological deficits, affect reading outcomes. This issue is of great importance because it has become increasingly clear that the causes of developmental dyslexia are multifactorial (Menghini et al., 2010).

In the present research, we went a major step further. First, we implemented a developmentally plausible computational model of reading acquisition that learns to read in the same way children do, that is, through a combination of explicit teaching (i.e., direct instruction), phonological decoding, and self-teaching (Share, 1995). Second, we used real data from one of the biggest dyslexia samples (Peterson, Pennington, & Olson, 2013; 622 children, 388 of whom have dyslexia) to set up 622 individual models, in which the efficiency of key mechanisms and representations was set up using individual measures in tasks that tap these component skills. Third, we simulated the real reading performance of these 622 children using exactly the same words that the children read. Fourth, we investigated whether a multideficit model was superior to three alternative models that represent different major theories of developmental dyslexia: the core phonological-deficit model (Vellutino et al., 2004), a visual-deficit model (Stein, 2014), and a noisy computation model (Hancock, Pugh, & Hoeft, 2017). Finally, we investigated how changing the efficiency of a given component skill affects individual learning outcomes for word and nonword reading.

Model Description and Method

The model is presented in Figure 1a. The basic architecture was taken from the connectionist dual-process model (Perry, Ziegler, & Zorzi, 2007, 2010, 2013), but new dynamics and mechanisms were introduced to capture reading acquisition within a realistic learning environment. It is assumed that the phonological lexicon is largely in place prior to reading, although its size can vary from one child to another. The grapheme–phoneme mapping system (i.e., the decoding network) is initially taught with a small number of grapheme–phoneme correspondences (e.g., b → /b/) in a supervised fashion using a simple associative-learning rule (for these correspondences, see the Supplemental Material available online). This process reflects the explicit teaching of grapheme–phoneme correspondences, as it occurs during early reading instruction (e.g., see the statutory requirements of the National Curriculum in England; U.K. Department for Education, 2013; Hulme, Bowyer-Crane, Carroll, Duff, & Snowling, 2012).

Fig. 1.

Schematics illustrating how a developmentally plausible computational model of reading development can be used to predict learning outcomes. After initial explicit teaching on a small set of grapheme–phoneme correspondences (GPCs), the decoding network (a) is able to decode words that have a preexisting representation in the phonological lexicon but no orthographic representation. If the decoding mechanism activates a word in the phonological lexicon, an orthographic entry is created, and the phonology is used as an internally generated teaching signal (red arrows) to refine and strengthen letter–sound connections, thereby improving the efficiency of the decoding network. In the individual-deficit simulation approach (b), the efficiency of various components of the reading network can be estimated individually for each child (N = 622) through performance on component tasks that map directly onto model components. The performance of each child in the three component tasks is used to individually set the parameters of the model in order to predict individual learning outcomes.

From there on, however, learning becomes unsupervised, and most of the correspondences are picked up via implicit statistical-learning procedures. That is, when presented with a new word, the initially rudimentary decoding network generates a phoneme sequence that potentially activates entries in the phonological lexicon. If the correct word is in the phonological lexicon and passes a critical threshold, it is selected, and a representation is set up in the orthographic lexicon (i.e., orthographic learning), which is connected to its phonological representation. Importantly, the internally generated phonological representation is then used as a teaching signal (i.e., self-teaching) to improve the decoding network. That is, every successful decoding of a new word provides the child (and the network) with an opportunity to set up an orthographic representation and improve the decoding network without an external teacher or teaching signal. Indeed, we showed in previous simulations that 80% of words from an English corpus of more than 32,000 words can be learned through decoding alone (Ziegler, Perry, & Zorzi, 2014). The remaining 20% are too irregular (e.g., yacht, aisle, chef ) to be learned through decoding.

To simulate irregular word learning and reading—that is, words that were not able to be learned via decoding—we added a mechanism that specifies how irregular words would get into the orthographic lexicon. The basic idea is that children learn these words via direct instruction (e.g., flash cards). Direct instruction of irregular words is explicitly listed as one of the statutory requirements up to Grade 4 in the National Curriculum in England (U.K. Department for Education, 2013). Direct instruction on irregular words is also achieved in the context of teaching word spelling. Thus, each time a word was not lexicalized via phonological decoding, we allowed for the possibility that it might be lexicalized via direct instruction. We made this a probabilistic process in which the chance that a word would enter the orthographic lexicon varied as a function of the orthographic ability of each child (see Simulation Methods in the Supplemental Material).

We used this computational model to investigate how deficits in the underlying components of the reading network can predict interindividual differences in reading performance. The general approach is outlined in Figure 1b. We used the data of all children included in the study by Peterson et al. (2013) and additional children tested by the same group, which included accuracy in reading aloud (on regular words, irregular words, and nonwords) as well as performance measures in other nonreading tasks for 622 English-speaking children, including 388 children with dyslexia. We selected three component tasks that map relatively directly onto processes and processing components of the model (i.e., orthographic lexicon, phonological lexicon, phonemes). Orthographic choice was taken as a measure of processing efficiency in the orthographic lexicon, phoneme deletion was taken as a measure of the efficiency of activating phonemes correctly, and vocabulary score was taken as a measure of the size of a child’s phonological lexicon.

For each child, we used performance on these three tasks to create individual models, one for each child, in which the parameterization of the models’ components and processes was changed using a simple linear function based on the child’s performance on the three component tasks. In particular, performance in the orthographic-choice task was used to parameterize the amount of noise in the orthographic lexicon and the probability that a word would be lexicalized if successfully decoded or found through direct instruction. Performance in the phoneme-deletion task was used to parameterize the amount of noise in the decoding network during training, in which noise was used probabilistically to swap correct phonemes with phonetically similar ones (see Ziegler et al., 2014). Finally, the vocabulary score was used to set the size of the phonological lexicon, that is, how many words a child knows when he or she begins the task of learning to read. Importantly, model parameters were not optimized to fit the individual reading scores, thereby preventing overfitting (see Materials and Methods in the Supplemental Material).

A full learning simulation was performed for each individual model, and its performance after learning was assessed by presenting the same words and nonwords used by Peterson et al. (2013). This allowed a direct comparison between learning outcomes in the simulation and actual reading performance of the child that the simulation was meant to capture. It is important to point out that the three component tasks do not map directly onto the three word types (e.g., orthographic choice for irregular words, phoneme deletion for nonwords), but rather, they affect different aspects of processing in the model and thus the way activation is generated and combined in the model before a final output is produced.

Results

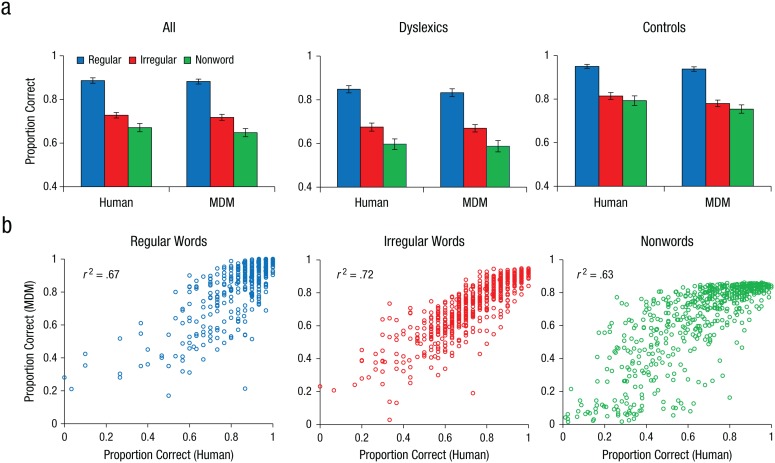
Overall reading performance (proportion of correct responses) averaged across the 622 simulations (model) and 622 children (human) is presented in Figure 2a. These data are further broken down for dyslexic and normally developing readers. As can be seen in Figure 2a, the overall means of the children and the predicted means of the model for the very same children are highly similar, for both the normally developing readers and the readers with dyslexia. That is, the model accurately simulated normal and impaired reading development on the basis of performance in three component tasks. To investigate how well the model captured interindividual differences and reading outcomes, we plotted the actual versus predicted reading performance for the 622 children on the three reading outcome measures (see Fig. 2b). The fit was very good, as indexed by r² values ranging from .63 to .72. That is, knowing a child’s performance on only three component tasks of reading allows the model to predict his or her learning outcomes on regular words, irregular words, and nonwords with high accuracy.

Fig. 2.

Predicted versus actual reading performance. The bar graphs (a) show the proportion of correct responses for regular words, irregular words, and nonwords by the multideficit model (MDM) and humans, separately for all children (N = 622), children with dyslexia (n = 388), and normally developing children (controls; n = 234). Error bars show 95% confidence intervals. The scatterplots (b) show the relationship between predicted and actual individual reading scores for regular words, irregular words, and nonwords for all children.

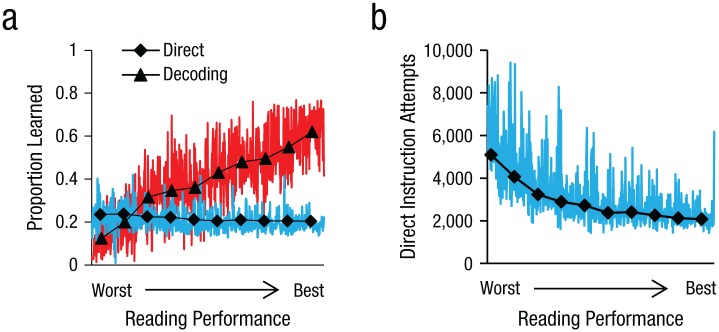
In addition to examining the accuracy of the model, we examined its reliance on decoding versus direct instruction for word learning. This is an interesting analysis because a large number of studies have suggested that good readers are initially efficient decoders and poor readers tend to be poor decoders (e.g., Gentaz, Sprenger-Charolles, Theurel, & Colé, 2013; Juel, 1988). Poor readers are thus more reliant on direct instruction when learning to read than are good readers. The results of our simulations show that the predictions of the multideficit model are consistent with these findings. In particular, Figure 3a presents the proportion of words that entered the lexicon through decoding or direct instruction as a function of overall reading skill (the average performance of each child across all word types). Figure 3b complements the analysis by presenting the number of direct instruction attempts as a function of overall reading skill. As can be seen from the simulations of poor readers, only a small proportion of the words were learned through decoding compared with direct instruction, and there were far more attempts at direct instruction compared with the simulations of good readers. Alternatively, in the simulations of good readers, most of the words were learned via decoding.

Fig. 3.

The use of decoding versus direct instruction as a function of reading skill. Simulations show (a) the proportion of words that were learned via self-generated decoding and via direct instruction and (b) the number of direct instruction attempts. Both are plotted as a function of the average reading performance of each child. Colored lines represent the individual data, and the black overlaid lines are the results in deciles. The proportions of words in (a) do not add up to 1.0 because they refer to a full-size phonological lexicon, which includes words that were not learned by either decoding or direct instruction for most of the simulated individuals.

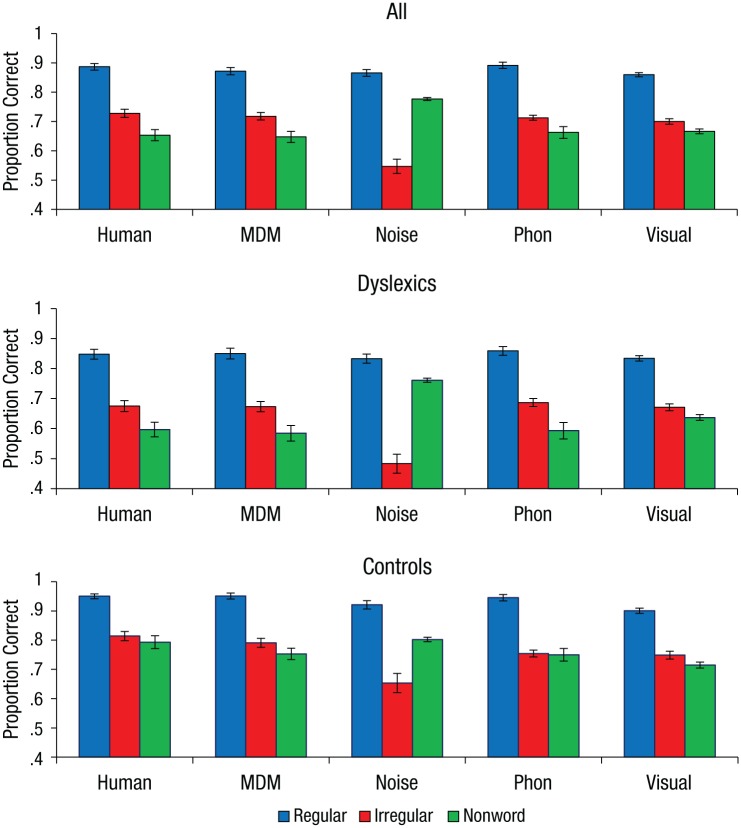
The performance of the multideficit model in simulating the whole distribution of reading deficits in children with dyslexia was then compared with that of three alternative models: (a) a phonological-deficit model, which assumes deficits in activating correct phonemes (i.e., deficits in phonological awareness, phoneme discrimination, and categorical perception of phonemes); (b) a visual-deficit model, which assumes impoverished orthographic processing due to poor letter-position coding (e.g., letter reversals); and (c) a global-noise model, which assumes general processing inefficiency (set as a function of the child’s overall level of performance) due to noisy computations (Hancock et al., 2017; Sperling, Lu, Manis, & Seidenberg, 2005). For all models, the vocabulary score was used to set the size of the individual phonological lexicon (with the same procedure used for the multideficit model). These simulations were designed to examine whether simpler models could account for the distribution of reading scores and to investigate how single deficits may affect different aspects of reading (for further details, see the Supplemental Material). The mean results appear in Figure 4.

Fig. 4.

Reading performance for regular words, irregular words, and nonwords for all children, dyslexic children, and control children, compared with performance of the multideficit model (MDM), the global-noise model (noise), the phonological-deficit model (phon), and the visual-deficit model (visual). Error bars show 95% confidence intervals.

As can be seen, the mean results from the multideficit, phonological-deficit, and visual-deficit models were very similar to the mean results found with the human data. Only the global-noise model was not parameterizable in such a way as to allow it to capture the mean results. Despite the similarities in the mean results across models, however, only the multideficit model captured the distribution of reading scores across word types, as can be seen in Figure 5, in which the data from all children with dyslexia are displayed (see also Fig. S2 in the Supplemental Material for the whole data set and Fig. S3 in the Supplemental Material for only the normally developing children). To quantitatively compare the predictive accuracy of the different models, we calculated the residual sum of squares between the simulated data and the empirical data (i.e., scores for regular words, irregular words, and nonwords for each child) and computed the Bayesian information criterion (BIC) for each model.

Fig. 5.

Predicted mean dyslexic reading performance (bar graphs) and the association between predicted and actual reading performance of individual dyslexics (scatterplots) of the multideficit, global-noise, phonological-deficit, and visual-deficit models. A Bayesian information criterion (BIC) difference of 10 corresponds to a posterior odds of about 150:1 (Raftery, 1995), and a larger negative value is an index of better fit. Error bars show 95% confidence intervals.

On the full set of data, although the multideficit model was penalized for its larger number of free parameters—four (orthographic noise, phoneme switching, lexicalization threshold, and vocabulary) versus two for the single-deficit models (one specific parameter and vocabulary)—it yielded a markedly lower BIC score (−2,630) than all alternative models (the global-noise, phonological-deficit, and visual-deficit models had scores of −316, −2,244, and −2,027, respectively); the size of the difference between BIC scores represents very strong evidence in favor of the multideficit model (a BIC difference of 10 corresponds to a posterior odds of about 150:1; Raftery, 1995). The same pattern was found when the comparison was restricted to the dyslexic children, with the multideficit model having the lowest BIC score (−1,398) compared with all alternative models (−19, −1,189, and −1,074 for the global-noise, phonological-deficit, and visual-deficit models, respectively), as well as when the comparison was restricted to the normally developing children (−1,288 for the multideficit model; −321, −1,101, and −985 for the global-noise, phonological-deficit, and visual-deficit models, respectively).

A potential problem with the model comparison is that a systematic search of the optimal parameter set for each model was computationally unfeasible despite our use of supercomputing facilities. However, there is no reason to believe that the alternative models were penalized with respect to the multideficit model because it is much easier to find suitable values in a two-parameter space (for the single-deficit models) than in a four-parameter space (for the multideficit model). Our hand-search approach was to explore the parameter space of each model until the overall means in the simulations were close to the empirical means. As can be seen in Table S2 in the Supplemental Material, apart from the global-noise model, the fit of all models with respect to the overall means was indeed rather good. Thus, it is only when it comes to explaining the individual distributions (i.e., interindividual differences) that the phonological-deficit and visual-deficit models go off track. Further inspection of the results showed that the single-deficit models were worse because there were no parameters that could be changed to fix this (for further discussion, see the Supplemental Material).

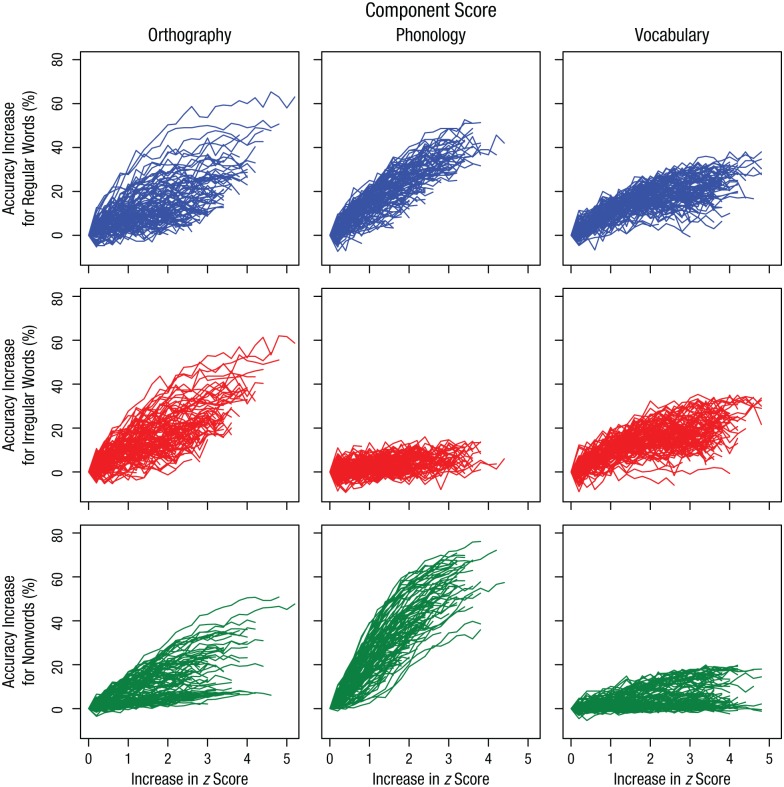
Finally, we used the multideficit model as a tool to predict how the increase in the efficiency of a single component would change reading performance on regular words, irregular words, and nonwords. This was done by first selecting the 100 children with the worst average deficit scores (i.e., the most negative z scores averaged across the three types of deficit). Then, each deficit score of each child was increased in 0.2 z-score steps until it reached a level corresponding to unimpaired processing (for orthographic and phonological deficits) or a full vocabulary size. Thus, each z score was increased as much as it could be, and the other two z scores were held constant. Predicted reading scores were generated at each step using the same method as in the previous simulations. The results appear in Figure 6.

Fig. 6.

Predicting learning outcomes as a function of improvements in orthography, phonology, and vocabulary. The scores of each child were normalized to start at 0, and the component scores were increased by 0.2 of a z score until they were at their maximum. Thus, the start of a line represents a child’s initial state, and the end of a line represents how a child was predicted to perform when a single component score was increased as much as possible. Thus, the length of the line represents the potential gain (in z scores) for a given child.

The results of the simulations show that increasing vocabulary tends to be more beneficial for irregular word reading (i.e., sight word reading) than nonword reading (i.e., decoding), whereas increasing the efficiency of phonological processing shows the opposite pattern. Increasing orthographic efficiency helps all word types. However, Figure 6 shows important interindividual differences, which suggest that the choice of an optimal intervention depends on the initial conditions, that is, the individual starting point in the 3-D deficit space. The validity of these models’ predictions should be tested in future empirical studies.

Conclusion

Our results show that large-scale simulations with a developmentally plausible computational model of reading acquisition allow us to predict learning outcomes for individual children and reading profiles of children with dyslexia on the basis of performance on three component tasks (orthographic choice, phoneme deletion, vocabulary). The multideficit model is superior to alternative single-deficit models in all respects, which suggests that future research needs to take into account the multidimensional nature of the deficits that cause dyslexia. This novel computational approach establishes causal relations between deficits and outcomes that can be used to make long-term predictions on learning outcomes for at-risk children. Importantly, the model can be used to predict how changing the efficiency of one component might change reading performance for an individual child. One limitation is that the present simulations were based on a cross-sectional sample of children rather than on data from a longitudinal study. In particular, it would be of great interest to validate the model’s predictions of intervention outcomes in future intervention studies. Confirming the validity of the model’s predictions would pave the way for developing personalized computer models to guide the design of individually tailored remediation strategies.