Object-Feature Binding Survives Dynamic Shifts of Spatial Attention

Abstract

Visual object perception requires integration of multiple features; spatial attention is thought to be critical to this binding. But attention is rarely static—how does dynamic attention impact object integrity? Here, we manipulated covert spatial attention and had participants (total N = 48) reproduce multiple properties (color, orientation, location) of a target item. Object-feature binding was assessed by applying probabilistic models to the joint distribution of feature errors: Feature reports for the same object could be correlated (and thus bound together) or independent. We found that splitting attention across multiple locations degrades object integrity, whereas rapid shifts of spatial attention maintain bound objects. Moreover, we document a novel attentional phenomenon, wherein participants exhibit unintentional fluctuations—lapses of spatial attention—yet nevertheless preserve object integrity at the wrong location. These findings emphasize the importance of a single focus of spatial attention for object-feature binding, even when that focus is dynamically moving across the visual field.

Our visual environment contains a multitude of objects, each composed of multiple visual features (e.g., color, shape, texture) that must be integrated into a cohesive object-level representation, forming the basis for effective perception, memory, and action (e.g., Kahneman, Treisman, & Gibbs, 1992). Spatial attention is thought to be crucial for this binding process, acting as the glue that binds an object’s features together (Nissen, 1985; Reynolds & Desimone, 1999; Treisman & Gelade, 1980). Thus, attending to a given location selects all of the nonspatial features coinciding at that location and binds them into an integrated object representation (e.g., Schoenfeld et al., 2003).

Visual object integrity is critical for interacting with the world. Successful object-feature binding requires integration between different nonspatial features (i.e., feature-feature binding) and between nonspatial features and spatial location (i.e., feature-location binding). Failures of binding can be both detrimental and revealing (Treisman, 1996; Wolfe & Cave, 1999). For example, limited attention can produce illusory conjunctions, such as when one views a green square and a red circle but reports a green circle (Treisman & Schmidt, 1982). Patients with unilateral deficits in spatial attention also report more illusory conjunctions, which suggests that object integrity depends on intact spatial extent (Robertson, 2003). Other studies have demonstrated that spatial crowding can induce greater swap errors (see Bays, 2016), that is, misreporting features from another location altogether (e.g., Emrich & Ferber, 2012). One candidate model of object-feature binding posits that nonspatial features are randomly sampled from a probabilistic window of spatial attention (Vul & Rich, 2010)—when the attentional window is narrower and more precise, features are veridically bound as an integrated object, but when the focus of spatial attention is more diffuse and encompasses multiple object locations, features are encoded independently, resulting in inaccurate groupings of features and thus failures of object integrity. The strong consensus is that the ability to maintain a precise spatial focus of attention is critical for preserving object integrity.

Visual attention, however, is rarely singular or static—nor do we want it to be. In the real world, multiple objects with multiple features are simultaneously present in the environment, and attention must dynamically shift and split across multiple goals and locations. How do these dynamic changes in spatial attention impact visual object integrity?

Here, we examined object-feature binding while manipulating dynamic attention. We applied a recent paradigm measuring distortions in feature perception under different conditions of spatial attention (Golomb, L’Heureux, & Kanwisher, 2014), adapted to probe binding between multiple feature dimensions. Participants were presented with an array of multifeature objects and were asked to reproduce both the color and the orientation of a target object (i.e., joint-continuous-report paradigm; Bays, Wu, & Husain, 2011; Wilken & Ma, 2004). In Experiment 1, we manipulated attention with a spatial precue that remained stable, shifted from one location to another, or was split across two locations simultaneously. Experiment 2 replicated these conditions with the further addition of a continuous location report. We applied probabilistic mixture models to assess whether errors in recalling multiple features of the same object would be correlated, indicating that features were bound together (Bays et al., 2011). This modeling approach allowed us to evaluate the fate of object integrity under common conditions of dynamic attention (Experiment 1) and, moreover, to directly examine the three-way conjunction of feature-feature-location binding (Experiment 2).

We predicted that object-feature binding would be contingent on the spatial extent of attention (Cohen & Ivry, 1989; Vul & Rich, 2010), such that splitting attention simultaneously across two locations would expand the attentional window and disrupt object integrity. But what happens during shifts of spatial attention? Previous studies have demonstrated that spatial attention does not update immediately but, rather, may take 100 ms to 200 ms to fully disengage from one location, move, and reengage attention at a new location (e.g., Müller, Teder-Sälejärvi, & Hillyard, 1998). More recent work suggests that attention can be allocated to a new location before it disengages from the previously attended location, resulting in a transient period in which both locations are simultaneously attended (e.g., Eimer & Grubert, 2014; Khayat, Spekreijse, & Roelfsema, 2006). Here, we probed binding during this critical period of spatial updating and tested two contrasting theories: If spatial attention shifts as a single “spotlight” from location A to location B (Posner, Snyder, & Davidson, 1980), then the spatial extent of attention should remain narrow, and object-feature binding should survive—for either object A or object B. Alternatively, a shift might result in temporarily highlighting both locations—for example, spreading to encompass both locations (zooming out; Eriksen & St. James, 1986) or briefly activating both A and B simultaneously (e.g., Golomb, Marino, Chun, & Mazer, 2011; Khayat et al., 2006)—and then we should expect greater independent feature errors.

We found that dynamic shifts and splits of attention led to distinct patterns of object-feature binding: Rapid shifts of attention preserved object integrity, whereas splitting attention resulted in failures of object integrity. We also document a novel attentional phenomenon, wherein participants exhibited unintentional fluctuations—or lapses—of spatial attention, akin to momentary fluctuations of sustained attention (Reason, 1984). Although lapses of sustained attention are typically defined as slowed responses in a vigilance task (e.g., Rosenberg et al., 2016), lapses of spatial attention are here defined as identifying an incorrect location as the target. By simultaneously modeling color, orientation, and location responses in Experiment 2, we showed that the vast majority of feature reports were correlated across all three dimensions, demonstrating that fully bound objects survive both intentional shifts and inadvertent lapses of spatial attention. Thus, object integrity is preserved when there is a single focus of spatial attention, even if attention is at the wrong location.

General Method

Participants

Twenty-three participants were recruited for Experiment 1 (ages 18 to 30 years; 11 male), and 25 new participants were recruited for Experiment 2 (ages 18 to 21 years; 13 male). On the basis of an a priori power analysis using effect sizes from previous studies (Golomb et al., 2014), we estimated that we would need at least 22 participants to detect feature errors with 80% power, given a .05 criterion of significance. We collected a few extra participants per experiment in anticipation of dropout related to poor eye-tracking or task performance. Additional participants were excluded for not completing the full experimental session (2 from Experiment 1; 3 from Experiment 2) or not successfully performing the task (< 50% probability of pT_CT_O from the simple model described below; 2 from Experiment 2). All participants reported normal or corrected-to-normal visual acuity and color vision, received course credit or a payment of $10 per hour, and provided informed consent in accordance with The Ohio State University Institutional Review Board.

Stimuli and procedure

Stimuli were presented on a 21-in. flat-screen CRT monitor with a refresh rate of 85 Hz and screen resolution of 1,280 × 1,024 pixels, using MATLAB (The MathWorks, Natick, MA) and the Psychophysics Toolbox (Brainard, 1997). Participants’ heads were positioned with a chin rest approximately 60 cm from the monitor, and eye position was tracked using an EyeLink 1000 eye-tracking system (SR Research, Kanata, Ontario, Canada). The monitor was color calibrated with a Minolta CS-100 colorimeter.

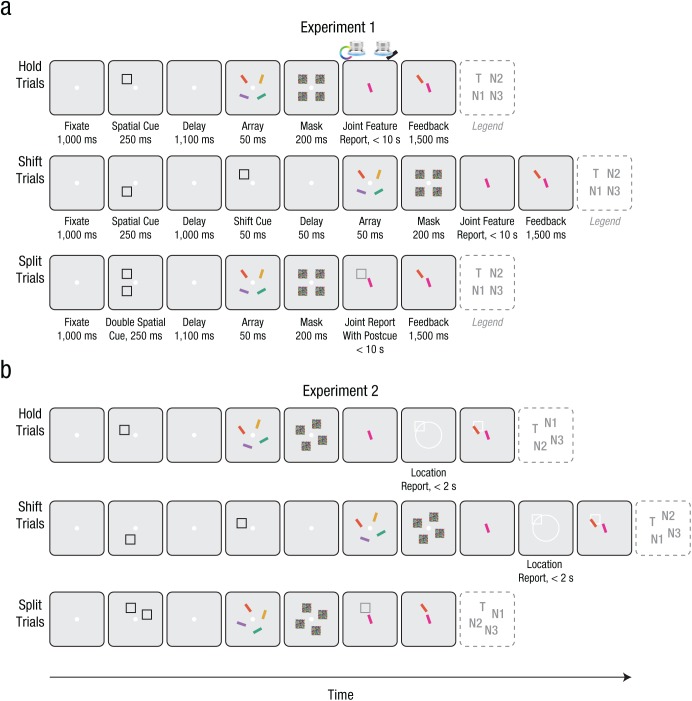
Figure 1 illustrates an example trial sequence for the three critical conditions (hold, shift, and split) for both experiments. In Experiment 1, each trial began with the presentation of a white central fixation dot (diameter of 0.6°). After participants were accurately fixating for 1,000 ms, as determined by real-time eye tracking, the trial continued as follows.

Fig. 1.

Example trial sequences for (a) Experiment 1 and (b) Experiment 2. Participants were cued to covertly attend to a spatial precue that remained stable (hold trials) or dynamically shifted from one location to another (shift trials), before providing a joint continuous report of both the color and orientation of the cued target item. In split trials, participants were precued to attend to two locations simultaneously before reporting the features of the postcued target item. In Experiment 2, the four array positions could be rotated, and participants additionally reported the location of the target item (on hold and shift trials only). For each trial sequence shown here, the final panel (dotted outline) denotes which array position corresponds to the target (T), critical nontarget (N1), adjacent nontarget (N2), and diagonal nontarget (N3). On hold trials, N1 and N2 were arbitrarily assigned.

For hold and shift trials, a single spatial cue (a black 4° × 4° square outline) was presented at one of four possible stimulus locations (the corners of an imaginary square centered on fixation, 7.4° eccentricity) for 250 ms. For hold trials, the spatial cue was followed by a 1,100-ms delay period in which only the fixation dot was visible on the screen. For shift trials, the cue was followed by a similar 1,000-ms delay, after which a second cue appeared in a different, adjacent location (never the diagonal location) for 50 ms, followed by a 50-ms delay. Participants were instructed to covertly attend to the cued location and shift their attention if a second location was cued, so they were always attending to the most recently cued location. For split trials, two spatial cues were presented simultaneously at two adjacent locations for 250 ms, followed by a 1,100-ms delay period. Participants were instructed to attend to both cued locations in split trials.

After the spatial precue(s) and delay period, an array of four colored and oriented bars (0.75° × 4°) appeared for 50 ms. One of these stimuli was the target (T), which appeared at the most recently cued location for hold and shift trials or at one of the two cued locations for split trials (randomly selected and indicated by a postcue at the time of response). Of the three nontarget items, the critical nontarget (N1) appeared at a location adjacent to the target, which was either initially cued in shift trials or simultaneously attended in split trials; the other adjacent nontarget (N2) and the diagonal nontarget (N3) were considered control items. In hold trials, both adjacent nontargets were never cued, so they were arbitrarily assigned as the critical N1 or control N2.

The color of the target item was chosen randomly on each trial from 180 possible colors, which were evenly distributed along a 360° circle in Commission Internationale de l’Éclairage (CIE) L*a*b* coordinates with constant luminance (L* = 70, center at a* = 20, b* = 38, and radius 60; Zhang & Luck, 2008). The colors of the remaining stimuli were chosen so that the adjacent items (N1 and N2) were equidistant in opposite directions (90° clockwise or counterclockwise deviation along the color wheel, with direction randomly varying from trial to trial), and the item at the diagonal location (N3) was set 180° away in color space. The orientation of the target item was also chosen randomly on each trial from a range of angles from 0° to 180°, and N1 and N2 were likewise equidistant in opposite directions (45° clockwise or counterclockwise deviation), with N3 set 90° away. Feature values for color and orientation were set independently, as was the direction of deviation for each feature. The stimulus array was followed by 200 ms of masks (squares colored with a random color value at each pixel location, covering each of the four stimulus locations).

Participants then made a joint continuous-report response indicating the color and orientation of the target item. A single probe bar with random initial values for color and orientation was presented at the center of the screen. For split trials, the probe stimulus was accompanied by a spatial postcue (white 4° × 4° square outline) indicating which of the two precued locations was the target. Participants were instructed to adjust the color and orientation of the probe item to match the features of the target. The probe’s features were adjusted using two input dials (PowerMate USB multimedia controllers; Griffin Technology, Irvine, CA), one operated with each hand (left for color, right for orientation). Turning one dial caused the probe to rotate through the 180° range of possible orientations (steps of 1°); turning the other dial caused the probe’s color to cycle through the 360° space of possible colors (steps of 2°). Participants could adjust the two dials in any order or simultaneously. To input their response, participants pressed down on either dial. Participants were told to be as accurate as possible, and there was a time limit of 10 s.

At the end of the trial, participants were shown feedback for 1,500 ms: The reported color-orientation response was shown in the center of the screen, and the actual target item was displayed in its original location. Eye-tracking feedback was presented as the percentage of deviant fixation samples (i.e., when the participant’s eye position deviated more than 2° from the central fixation location) between initial cue onset and probe onset. Eye-tracking feedback was intended to motivate participants to maintain central fixation; they were not told about trial exclusion criteria.

Experiment 2 was identical to Experiment 1 except for two key changes (see Fig. 1b). First, we increased the possible range of stimulus locations, although only 4 locations were ever chosen on each trial. For each trial, the target location was randomly selected from 1 of 16 possibilities (along an imaginary circle centered on fixation, 7.4° eccentricity), and the other 3 locations were arranged 90°, −90°, and 180° away (four corners of an imaginary rotated square). Second, we added a location report at the end of hold and shift trials. (Split trials already included an explicit spatial postcue, rendering a subsequent location report uninformative.) The location report was presented after the joint color-orientation report but also as a continuous response: A single location probe (white 4° × 4° square outline) was displayed at a random location along a white circle outline (7.4° eccentricity), and turning the right-hand dial rotated the placeholder through the 360° space of possible locations (steps of 2.25°). Participants were instructed to adjust the location of the probe to match the location of the target (i.e., the most recently cued location). Participants input their location response by pressing down on the dial, with a time limit of 2 s. For location feedback on hold and shift trials, the reported location was displayed as a white outline on the same screen as color-orientation and eye-tracking feedback.

In Experiment 1, each participant completed 7 to 10 blocks of intermixed hold and shift trials (112–160 trials of each condition) and 4 to 5 blocks of split trials (128–160 trials), although the order of hold/shift or split blocks was counterbalanced between participants. In Experiment 2, participants completed 5 to 8 blocks of intermixed hold and shift trials (80–128 trials of each condition), always followed by 3 to 4 blocks of split trials (96–128 trials). Hold and shift trials were intermixed to ensure that participants had to attend to the first cue and could not simply wait for the second cue; split trials were presented in separate blocks for ease of instruction. Both experiments began with fixation training and 8 hold practice trials, as well as 12 shift practice trials before the hold/shift blocks and 12 split trials before the split blocks. Trials were discarded if they contained more than 15% deviant fixation samples between initial cue onset and probe onset (Experiment 1: 3.3%; Experiment 2: 8.8%)¹ or if participants made no dial adjustments before inputting their response (Experiment 1: 0.1%; Experiment 2: 2.5%).

Joint-feature analyses

On each trial, response error was calculated as the angular deviation between the continuous probe report and the cued target item, for each feature separately (${\theta }_{\mathrm{C}}$ = color error, range = −180° to 180°; ${\theta }_{\mathrm{O}}$ = orientation error, range = −90° to 90°; θ_L = location error, range = −180° to 180°). In shift and split trials, although the direction of N1 varied randomly in relation to T (clockwise or counterclockwise in terms of spatial location, color, or orientation space), we aligned the responses on each trial so that errors toward the N1 feature were always coded as positive deviations (+90° or +45°), and errors toward N2 were always coded as negative deviations (−90° or −45°).

To quantify the amount of object-feature binding, we employed a mixture-modeling approach (Bays, Catalao, & Husain, 2009; Bays et al., 2011; Golomb et al., 2014; Zhang & Luck, 2008). Within each single feature dimension (see Table 1), responses could be attributed to either reporting T (a von Mises distribution centered on the target feature value), misreporting one of the three nontargets (N1, N2, N3; separate von Mises distributions centered on each nontarget feature value), or random guessing (U, a uniform distribution across all feature values). Critically, we modeled color and orientation as joint probability distributions, fitting responses from both feature dimensions simultaneously (see Bays et al., 2011).

Table 1.

Mixture-Model Response Distributions Within a Single Feature Dimension

Response type	Color (C)	Orientation (O)	Location (L)
Target (T)	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}$	${\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}$	${\mathrm{\varphi }}_{{\mu }_{\mathrm{L}},{\kappa }_{\mathrm{L}}}$
Critical nontarget (N1)	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}$	${\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Adjacent nontarget (N2)	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}$	${\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Diagonal nontarget (N3)	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}$	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}$	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{L}}}$
Random (U)	${\gamma }_{\mathrm{C}}$	${\gamma }_{\mathrm{O}}$	${\gamma }_{\mathrm{L}}$

Note: In the top four rows, φ is a von Mises probability density function, with concentration ${\kappa }_C$, ${\kappa }_O$, or ${\kappa }_{\mathrm{L}}$ (standard deviation $\sigma =\sqrt{1/\kappa }$) and means of ${\mu }_C$ or ${\mu }_{\mathrm{L}}$, 90°, −90°, and 180° (color or location) or ${\mu }_{\mathrm{O}}$, 45°, −45°, and 90° (orientation) for the T, N1, and N2 and N3 features, respectively. In the bottom row, ${\gamma }_{\mathrm{C}}$, ${\gamma }_{\mathrm{O}}$, and ${\gamma }_{\mathrm{L}}$ are uniform distributions that reflect the probability of responding to the respective feature at random (guessing).

For Experiment 1, we evaluated two types of joint color-orientation mixture models: In the full joint model, we modeled the five types of feature reports described above (T, N1, N2, N3, and U) for each dimension, resulting in 25 response combinations of color (5) and orientation (5; see Table 2). This resulted in a model with 29 parameters (including parameters for the concentrations κ_C and κ_O, $\sigma =\sqrt{1/\kappa }$, and means µ_C and µ_O of the target). Because of this large number of parameters, the full model required data to be collapsed across participants to achieve reliable model fits. Thus, to conduct within-subjects statistics for our primary analyses, data from individual participants were fitted with the simple joint model, which attributes responses only to T, N1, or U within each dimension, resulting in nine response combinations of color (three) and orientation (three; see Table 2) plus four parameters for concentrations and means. Because our focus here was on the effects of dynamic attention involving the T and critical N1 locations, the simple model dropped parameters that involved N2 or N3 (which were theoretically less relevant and had very low probabilities in the full model results; see Table S2 in the Supplemental Material available online). In the simple model, the few responses to N2 or N3 items should be absorbed by U. Indeed, the results reported using the simple joint model were confirmed at the population level with the full joint model (see Section S5 in the Supplemental Material).

Table 2.

Response Distributions From the Simple and Full Joint Mixture Models, Combined Across Both Nonspatial-Feature Dimensions

Item and response type	m simple	m full	Response combination	Joint probability density
Correlated
Correlated target	1	1	TCTO	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}$
Correlated swap	2	2	N1CN1O	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Correlated swap		3	N2CN2O	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Correlated swap		4	N3CN3O	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}$
Independent T*
Illusory conjunction	3	5	TCN1O	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Illusory conjunction	4	6	N1CTO	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		7	TCN2O	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		8	N2CTO	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		9	TCN3O	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		10	N3CTO	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}$
Unbound guess	5	11	TCUO	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\gamma }_{\mathrm{O}}$
Unbound guess	6	12	UCTO	${\gamma }_{\mathrm{C}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}$
Independent N*
Illusory conjunction		13	N1CN2O	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		14	N2CN1O	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		15	N1CN3O	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		16	N3CN1O	${\mathrm{\varphi }}_{\pi ,\kappa \mathrm{C}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		17	N2CN3O	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}$
Illusory conjunction		18	N3CN2O	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Unbound guess	7	19	N1CUO	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\gamma }_{\mathrm{O}}$
Unbound guess	8	20	UCN1O	${\gamma }_{\mathrm{C}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Unbound guess		21	N2CUO	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\gamma }_{\mathrm{O}}$
Unbound guess		22	UCN2O	${\gamma }_{\mathrm{C}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$
Unbound guess		23	N3CUO	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\gamma }_{\mathrm{O}}$
Unbound guess		24	UCN3O	${\gamma }_{\mathrm{C}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}$
Random guessing	9	25	UCUO	${\gamma }_{\mathrm{C}}{\gamma }_{\mathrm{O}}$

Note: The simple joint model includes only 9 parameters, as numbered by m_simple, where m indicates the index of each response combination; the full joint model includes all 25 parameters, as numbered by m_full. In the column for joint response combinations, the color response is always written first. In the rightmost column, φ is a von Mises probability density function, with concentration ${\kappa }_{\mathrm{C}}$ or ${\kappa }_{\mathrm{O}}$ (standard deviation $\sigma =\sqrt{1/\kappa }$) and means of ${\mu }_{\mathrm{C}}$, 90°, −90°, and 180° (color) or ${\mu }_{\mathrm{O}}$, 45°, −45°, and 90° (orientation) for the target (T), critical nontarget (N1), adjacent nontarget (N2), and diagonal nontarget (N3), respectively; ${\gamma }_{\mathrm{C}}$ and ${\gamma }_{\mathrm{O}}$ are uniform distributions that reflect the probability of responding at random. Rows 1 to 4 describe correlated responses: reporting both features of the target object or misreporting both features of the same nontarget (correlated swap errors). Rows 5 to 12 describe independent T* errors: reporting one target feature and one nontarget feature (illusory conjunctions) or reporting one target feature and guessing the other feature (unbound guesses). Rows 13 to 25 describe the remaining errors (e.g., misreporting features from different nontargets and guessing).

For both models, the joint distribution of responses was modeled as follows:

$$p\left({\theta }_{\mathrm{C}},{\theta }_{\mathrm{O}}\right)={\Sigma }_m{\alpha }_m{p}_m,$$

where ${\theta }_{\mathrm{C}}$ and ${\theta }_{\mathrm{O}}$ are the reported feature errors, m is the number of joint color-orientation response combinations, with m_full = 1:25 or m_simple = 1:9, αm is the probability of each response combination, and $p_m$ represents the joint probability density distribution for that combination. Table 2 lists each of the m combinations and associated probability density functions. For example, the joint probability distribution of reporting the target color and the N1 orientation would be pT_CN1_O $={\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}$.

For both models, joint-feature response distributions were fitted using the Markov chain Monte Carlo procedure, as implemented through custom MATLAB scripts (available at osf.io/h2xpu/) using the MemToolbox (Suchow, Brady, Fougnie, & Alvarez, 2013) through the Ohio Supercomputer Center (https://www.osc.edu/). We used the Markov chain Monte Carlo procedure to sample three parallel chains across as many iterations as necessary to achieve convergence, according to the method of Gelman and Rubin (1992). We collected 15,000 postconvergence samples and used the posterior distributions to compute the maximum-likelihood estimates of each parameter as well as its 95% highest-density interval (HDI). For our primary analyses using the simple model, we adopted a standard within-subjects analytical approach: Parameter estimates were obtained separately for each individual participant and each trial type and then evaluated with frequentist significance testing. Post hoc tests were evaluated with the appropriate Bonferroni correction for multiple comparisons. These standard statistical comparisons were corroborated by analyses using the full model: Data were collapsed across all participants within each experiment, and parameter estimates were obtained separately for each trial type. Parameter estimates from the full model were considered significantly different if their 95% HDIs did not overlap (Kruschke, 2011).

For Experiment 2, we first evaluated the joint color-orientation feature reports with both the simple model and the full model, as described above. With the inclusion of the continuous-location report, we also fitted single-participant data with a single-dimension location model, which attributed location responses to T_L, N1_L, N2_L, N3_L, or U_L, with flexible κ_L and µ_L of the target. We then took the joint modeling approach a step further, modeling the continuous responses from color, orientation, and location simultaneously as three-way joint probability distributions. Because a full triple joint model including all possible response types for all three dimensions would include an unwieldy number of parameters (131), we simplified the triple joint model to focus on parameters of theoretical interest. Specifically, we examined whether reporting both the color and orientation of a specific item (feature-feature binding; e.g., N1_CN1_O) was also bound to the location of that specific item (feature-feature-location binding; e.g., location N1_L). Thus, the triple model included parameters only for correlated feature-feature responses (i.e., T_CT_O, N1_CN1_O, N2_CN2_O, N3_CN3_O) or guessing (U_CU_O), crossed with the different types of location responses. Location reports were attributed to T_L, N1_L, N2_L, or N3_L; we did not include a random guessing component U_L because the corresponding pU_L parameter from the single-dimension location model was found to be negligible (see Table S8 in the Supplemental Material). Similarly, we did not include flexible parameters for means µ_C, µ_O, and µ_L because the corresponding parameters in the simple and location models were not significantly different from 0 (see Tables S1 and S8 in the Supplemental Material). Consequently, the triple model included 20 response combinations of color-orientation (5) and location (4) and 3 parameters for concentrations κ_C, κ_O, and κ_L (see Table 3). The joint distribution of responses was modeled as follows:

Table 3.

Response Distributions From the Triple Joint Mixture Model, Combined Across Color, Orientation, and Location Dimensions

Location response and nonspatial-feature response	m triple	Response combination	Joint probability density
Target location
Correlated target	1	TCTOTL	${\mathrm{\varphi }}_{0,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{L}},{\kappa }_{\mathrm{L}}}$
Correlated N1	2	N1CN1OTL	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{L}},{\kappa }_{\mathrm{L}}}$
Correlated N2	3	N2CN2OTL	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{L}},{\kappa }_{\mathrm{L}}}$
Correlated N3	4	N3CN3OTL	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{L}},{\kappa }_{\mathrm{L}}}$
Other	5	UCUOTL	${\gamma }_{\mathrm{C}}{\gamma }_{\mathrm{O}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{L}},{\kappa }_{\mathrm{L}}}$
Nontarget N1 location
Correlated target	6	TCTON1L	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Correlated N1	7	N1CN1ON1L	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Correlated N2	8	N2CN2ON1L	${\mathrm{\varphi }}_{-\mathrm{\pi },{\mathrm{\kappa }}_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\mathrm{\pi }}{2},{\mathrm{\kappa }}_{\mathrm{O}}}{\mathrm{\varphi }}_{\mathrm{\pi },{\mathrm{\kappa }}_{\mathrm{L}}}$
Correlated N3	9	N3CN3ON1L	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Other	10	UCUON1L	${\gamma }_{\mathrm{C}}{\gamma }_{\mathrm{O}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Nontarget N2 location
Correlated target	11	TCTON2L	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Correlated N1	12	N1CN1ON2L	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Correlated N2	13	N2CN2ON2L	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Correlated N3	14	N3CN3ON2L	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Other	15	UCUON2L	${\gamma }_{\mathrm{C}}{\gamma }_{\mathrm{O}}{\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$
Nontarget N3 location
Correlated target	16	TCTON3L	${\mathrm{\varphi }}_{{\mu }_{\mathrm{C}},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{{\mu }_{\mathrm{O}},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{L}}}$
Correlated N1	17	N1CN1ON3L	${\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{4},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{L}}}$
Correlated N2	18	N2CN2ON3L	${\mathrm{\varphi }}_{-\frac{\pi }{2},{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{-\frac{\pi }{4},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{L}}}$
Correlated N3	19	N3CN3ON3L	${\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{L}}}$
Other	20	UCUON3L	${\gamma }_{\mathrm{C}}{\gamma }_{\mathrm{O}}{\mathrm{\varphi }}_{\pi ,{\kappa }_{\mathrm{L}}}$

Note: The triple joint model includes 20 parameters, as numbered by mtriple, where m indicates the index of each response combination. In the rightmost column, φ is a von Mises probability density function, with concentration ${\kappa }_{\mathrm{C}}$, ${\kappa }_{\mathrm{O}}$, or ${\kappa }_{\mathrm{L}}$ (standard deviation $\sigma =\sqrt{1/\kappa }$) and means of 0°, 90°, −90°, and 180° (color or location) or 0°, 45°, −45°, and 90° (orientation) for the target (T), critical nontarget (N1), adjacent nontarget (N2), and diagonal nontarget (N3), respectively; ${\gamma }_{\mathrm{C}}$ and ${\gamma }_{\mathrm{O}}$ are uniform distributions that reflect the probability of responding at random.

$$p\left({\theta }_{\mathrm{C}},{\theta }_{\mathrm{O}},{\theta }_{\mathrm{L}}\right)={\Sigma }_m{\alpha }_m{p}_m,$$

where ${\theta }_{\mathrm{C}}$ and ${\theta }_{\mathrm{O}}$ are the reported color and orientation errors,${\theta }_{\mathrm{L}}$is the reported location error, ${\alpha }_m$ is the probability of each response combination, and $p_m$ represents the combined probability density, with m_triple = 1:20. For example, the probability distribution of reporting the color and orientation of the target with the location of the critical nontarget (N1) would be pT_CT_ON1_L $={\mathrm{\varphi }}_{0,{\kappa }_{\mathrm{C}}}{\mathrm{\varphi }}_{0,{\kappa }_{\mathrm{O}}}{\mathrm{\varphi }}_{\frac{\pi }{2},{\kappa }_{\mathrm{L}}}$. Given the large number of parameters (23), the triple model was fitted with data collapsed across all participants and analyzed in the same way as the full model described above. Parameter estimates were obtained separately for hold and shift trial types. (Split trials were not included in these analyses because there was no location report on these trials.)

Results

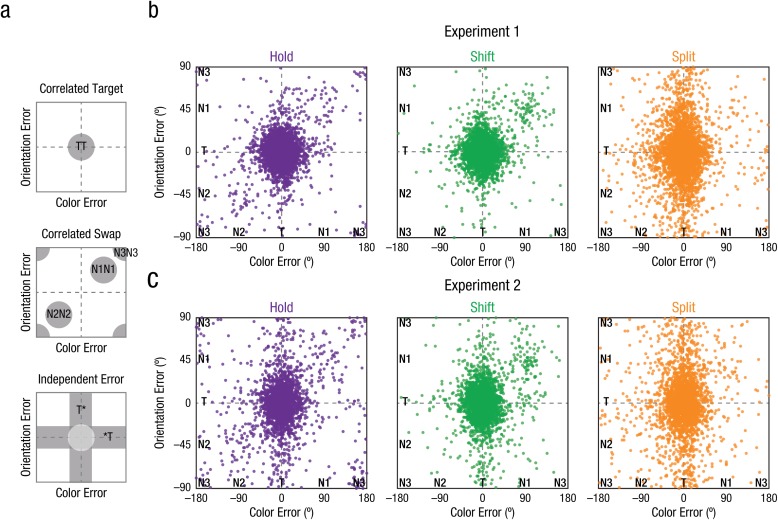
By probing both color and orientation on each trial, we examined whether errors in recalling multiple features of the same object were correlated (and thus bound together) or independent (and unbound) under different conditions of covert spatial attention. Figure 2 visualizes the joint distribution of responses by plotting individual trials in joint-feature space, in which the vertical and horizontal axes correspond to the color and orientation errors, respectively. Figure 2a illustrates the predicted distributions for different types of hypothetical responses, and Figures 2b and 2c show the actual response distributions for each attention condition.

Fig. 2.

Visualizations of color-orientation reports in joint-feature space, plotted as error relative to actual target feature values. Color responses are shown along the x-axis, and orientation responses are shown along the y-axis. For visualization purposes, we have flattened the joint-feature space; both feature dimensions are in fact circular, such that +180° is identical to −180° in color space. The schematics in (a) show predicted distributions for possible response types: Correlated target responses (TT) reflect reporting both features of the target item. Correlated swaps reflect reporting both features of the same nontarget; see the legends in Figure 1 for placement of the critical nontarget (N1), adjacent nontarget (N2), and diagonal nontarget (N3) across different conditions. Independent errors reflect reporting only one target feature (with the missing feature replaced by an asterisk). The scatterplots show trial-by-trial error distributions separately for hold, shift, and split trials, for Experiment 1 (b) and Experiment 2 (c). Each dot represents the corresponding color and orientation response for a single trial, aggregating across participants.

Object integrity was inferred from contrasting correlated responses (i.e., reporting both the color and orientation of the same item) with independent responses (i.e., reporting only one feature of the target item; see Fig. 2a). Correlated responses could stem from (a) reporting both features of the correct target item (correlated target, T_CT_O), which would be represented as a 2-D Gaussian density centered on the origin (0° error), or (b) misreporting both features of the same nontarget item (correlated swap, denoted N1_CN1_O, N2_CN2_O, and N3_CN3_O), which would be represented as 2-D Gaussian densities along the positive-slope diagonal of joint-feature space. Failures in object-feature binding, on the other hand, would result in independent target errors, represented as a distribution of responses along the horizontal and vertical axes of joint-feature space (i.e., centered on zero error in one dimension but not the other). Independent target errors could be due to misbinding the features of a target and a nontarget item (illusory conjunction; e.g., T_CN1_O) or reporting only one feature of the target and guessing the other (unbound guess; e.g., T_CU_O). Finally, pure guessing (U_CU_O) would be represented as a 2-D uniform distribution of responses across the entire joint-feature space.

We quantified each of the error types above with joint-feature probabilistic models (see Table 2). The probabilistic models also allow for independent nontarget errors, such as reporting the color of one nontarget and the orientation of a different nontarget (e.g., N1_CN2_O) or reporting only one feature of a nontarget and guessing the other (e.g., N1_CU_O); however, such errors were relatively rare and not discussed further, but see Tables S1 and S2 for all parameter estimates. Scatterplots of the empirical data for each experiment, collapsed across all participants, for hold, shift, and split trials, are presented in Figures 2b and 2c. The corresponding parameter estimates from the simple model are shown in Figure 3; below, we report within-subjects statistics for the simple model, but comparisons of 95% HDIs from the full model confirm these results and are reported in Table S2 (see also Section S5).

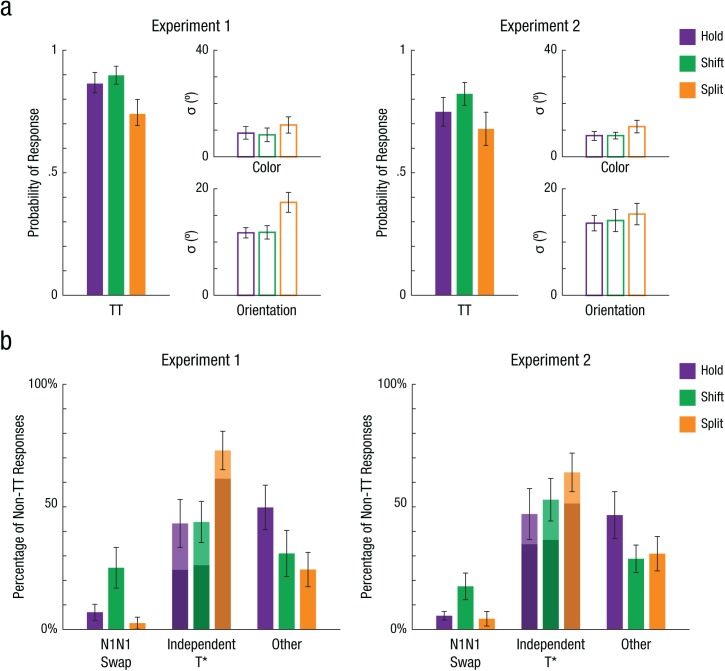
Fig. 3.

Simple joint model maximum-likelihood parameter estimates for both experiments. The graphs in (a) present best-fitting estimates for the probability of a correlated color (C) and orientation (O) target response (T_CT_O) and the standard deviations of the T_CT_O distribution for color (σ_C) and orientation (σ_O) for each condition. The graphs in (b) present the percentage of erroneous responses (i.e., non-T_CT_O) that can be attributed to correlated critical nontarget (N1_CN1_O) swaps, independent target errors (illusory conjunctions in light shading or unbound guesses in darker shading), and other errors (e.g., random guessing) for each condition. The simple model was fitted separately for each participant and each condition, and then parameter estimates were averaged across participants. Error bars represent 95% confidence intervals. Results are shown separately for Experiment 1 (N = 23) and Experiment 2 (N = 25).

Experiment 1

Across all trial types, the vast majority of responses were attributed to reporting both features of the correct target item (correlated target responses; see Fig. 3a), as reflected in the scatterplots as a central density of responses at the origin (see Fig. 2b). However, the patterns of errors outside that central density differed as a function of attention condition. As predicted, split attention degraded performance. Splitting attention across two locations resulted in greater feature errors, with significantly lower correlated target responses (pT_CT_O, simple model) in split trials compared with hold trials, t(22) = 4.20, p = .001, d = 0.88, and shift trials, t(22) = 6.78, p < .001, d = 1.42. The standard deviations of both color (σ_C) and orientation (σ_O) responses were also greater for split trials, ps < .001 (for all comparisons, see Table S3 in the Supplemental Material), indicating less precise feature reports when splitting spatial attention (see Fig. 3a). In contrast, shifts of attention from one location to another did not impact pT_CT_O or feature precision; pairwise t tests revealed that these parameters were not significantly different between hold and shift trials, ps > .5 (see Table S3).

Next, we compared the different types of errors produced by shifts or splits of attention, examining the probability of correlated N1_CN1_O swap errors (simple model) versus independent T* errors (e.g., T_CN1_O, U_CT_O, simple model). Because split trials produced more non-T_CT_O responses overall, to compare across conditions, we calculated these as proportions of “all errors” (non-T_CT_O responses) for each attention condition (see Fig. 3b). A repeated measures analysis of variance (ANOVA) across condition (hold, shift, split) and error type (correlated N1_CN1_O swap, independent T*) revealed a significant interaction, F(2, 44) = 23.3, p < .001, η² = .515. Split trials had the greatest percentage of independent T* errors (M = 72.8% of non-T_CT_O responses, SD = 17.4%) compared with hold trials (M = 44.8%, SD = 22.9%) and shift trials (M = 44.2%, SD = 19.6%), ps < .001 (for all comparisons, see Table S4 in the Supplemental Material). In contrast, shift trials had the greatest percentage of correlated N1_CN1_O swaps (M = 25.1% of non-T_CT_O responses, SD = 18.9%) compared with hold trials (M = 6.5%, SD = 7.4%) and split trials (M = 2.4%, SD = 5.4%), ps < .001 (see Table S4). This interaction is illustrated in the Figure 2b scatterplots, in which a sizeable cluster of errors is visible around N1_CN1_O for shift trials, whereas for split trials, errors are reflected as noise around the vertical and horizontal axes. In other words, dynamic splits of spatial attention resulted in failures of object-feature binding (more independent T* errors), whereas dynamic shifts of attention were more likely to maintain object integrity (more correlated T_CT_O responses and correlated N1_CN1_O swaps).

When splits of spatial attention break down object-feature binding, what kinds of independent errors do participants make? In split trials, unbound guesses (M = 60.2% of non-T_CT_O responses, SD = 19.8%, simple model) occurred significantly more often than illusory conjunctions between T and N1 (M = 12.7%, SD = 13.7%, simple model), t(22) = 7.78, p < .001, d = 1.62. This suggests that participants were not simply encoding and reporting both features of both cued objects independently, as might be expected if the constituent features were processed as loose bundles of features and illusorily misbound (Vul & Rich, 2010). Instead, splitting attention across multiple objects seemed to induce a feature-load strategy in which one feature dimension was prioritized (e.g., Fougnie, Asplund, & Marois, 2010; Woodman & Vogel, 2008) such that participants reported only one feature of the target and guessed the other (see Section S6 in the Supplemental Material).

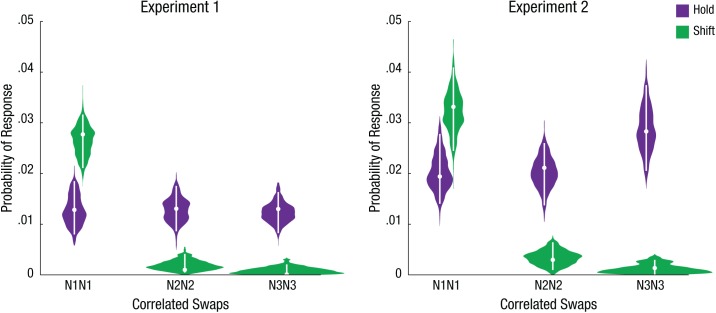
In shift trials, we found a greater percentage of correlated N1_CN1_O swap errors, consistent with the hypothesis that spatial attention had not yet shifted from the initially cued N1 location to the correct target location on some trials. To confirm that correlated swap errors in shift trials were specific to N1_CN1_O, we used the full-model parameter fits to compare correlated swaps across all possible nontarget locations (i.e., N1_CN1_O, N2_CN2_O, N3_CN3_O). In shift trials, participants were indeed more likely to misreport the entire feature-bound object at the initially cued location (pN1_CN1_O = .028, 95% HDI = [.021, .032]) compared with the other nontarget locations (pN2_CN2_O = .001, 95% HDI = [0, .004]; pN3_CN3_O < .001, 95% HDI = [0, .002]); parameter estimates were considered significantly different if their 95% HDIs did not overlap (Kruschke, 2011). In contrast, in hold trials, correlated swaps were distributed equally across the three nontargets (see Fig. 4; 95% HDIs overlapped).

Fig. 4.

Full-joint model maximum-likelihood estimates for both experiments. For each correlated color (C) and orientation (O) swap (N1_CN1_O, N2_CN2_O, N3_CN3_O), a violin plot illustrates the posterior distribution of each parameter over 15,000 postconvergence samples. The white dots mark each parameter’s best-fitting estimate, and the whiskers represent the 95% highest-density interval. The full model was fitted for each condition separately, collapsed across all participants. Results are shown separately for Experiments 1 and 2. N1 = critical nontarget; N2 = adjacent nontarget; N3 = diagonal nontarget.

We had expected hold trials to have very few errors overall because those trials involved only a single relevant spatial location. However, surprisingly, the full model parameter fits revealed that in hold trials, participants made just as many total correlated swap errors (pN1_CN1_O + pN2_CN2_O + pN3_CN3_O = .039, 95% HDI = [.029, .046]) as in shift trials (.029, 95% HDI = [.023, .035]). Why would hold trials produce substantial correlated swap errors? One possible explanation is that participants occasionally made inadvertent attentional shifts on hold trials; because all nontarget locations were equally irrelevant, these random lapses of spatial attention should lead to correlated swap errors for all nontarget locations. To directly probe possible lapses of spatial attention and their impact on object-feature binding, we added a continuous location report to Experiment 2.

Experiment 2

In Experiment 2, we directly evaluated the role of spatial attention in the binding of nonspatial visual features. Specifically, is an integrated object (i.e., intact feature-feature binding) anchored to its spatial location (i.e., intact feature-feature-location binding)? In addition to reporting the target’s color and orientation, participants also reported the target’s location on hold and shift trials. When participants correctly reported both features of the target, we expected them to correctly report its location. But when participants made a correlated swap error (i.e., reporting the color and orientation of a nontarget), would they also report the incorrect location of that same nontarget?

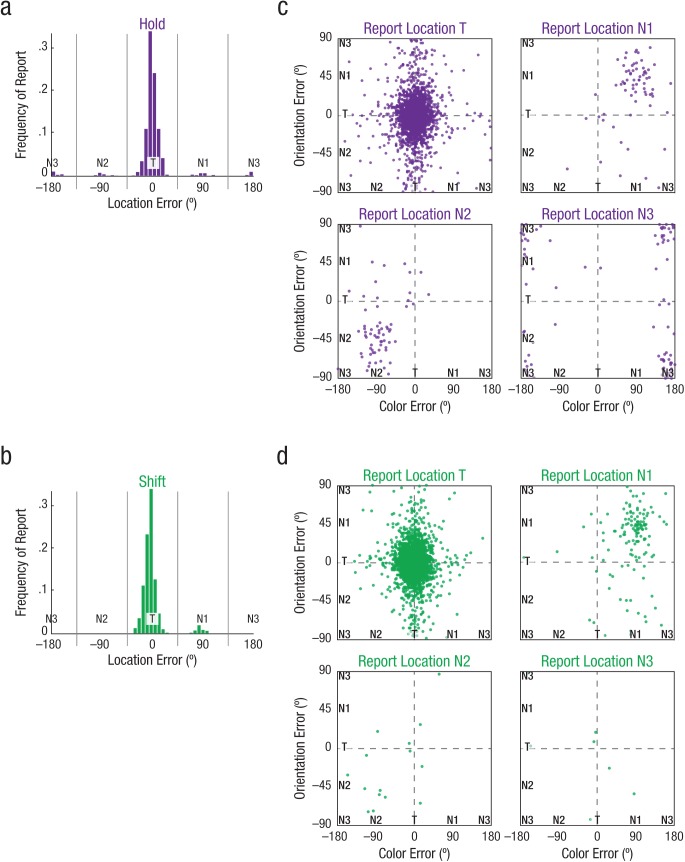
For color and orientation feature reports, Experiment 2 replicated the same pattern of results as reported for Experiment 1 (see Figs. 2c, 3, and 4; see also Fig. S5 in the Supplemental Material). Figures 5a and 5b depict the response distributions for the location reports that followed hold and shift trials; split trials did not include a location report because location was already postcued. A single-dimension location model (see Table S8) revealed that participants primarily reported the target location (hold: pT_L = .887, shift: pT_L = .920) with high precision (hold: σ = 9.0°, shift: σ = 9.3°). Even on shift trials, when the second cue was flashed for only 50 ms, participants were highly accurate at reporting that second location, indicating that participants were able to perceive the shift cue. Neither the probability of reporting the target location nor standard deviation was significantly different between hold and shift trials, t(24) = 1.20, p = .240, d = 0.24, and t(24) = 1.07, p = .293, d = 0.22. However, the difference in the pattern of location errors was evident: A repeated measures ANOVA across condition (hold, shift) and error type (N1, N2, N3, U) revealed a significant interaction, F(3, 72) = 8.40, p < .001, η² = .259. Post hoc paired-samples t tests confirmed that in shift trials, participants were more likely to misreport the initially cued N1 location compared with N2, t(24) = 3.66, p = .001, d = 0.73, or N3, t(24) = 3.74, p = .001, d = 0.75, whereas in hold trials, participants were equally likely to misreport any of the three nontarget locations, ps > .14 (for all comparisons, see Table S9 in the Supplemental Material). Thus, the pattern of location report errors mimicked the pattern of correlated swap errors for nonspatial features.

Fig. 5.

Visualization of color (C), orientation (O), and location (L) report errors. The graphs on the left show the location report data from Experiment 2, plotted as histograms showing frequency of report as a function of location errors relative to target location values, separately for hold trials (a) and shift trials (b). For both conditions, each trial was then coded into separate response bins (vertical gray lines) to produce the scatterplots on the right, which plot the trial-by-trial color and orientation error distributions of hold trials (c) and shift trials (d) in joint-feature space, split by each trial’s coded location. Data are combined across participants. T = target; N1 = critical nontarget; N2 = adjacent nontarget; N3 = diagonal nontarget.

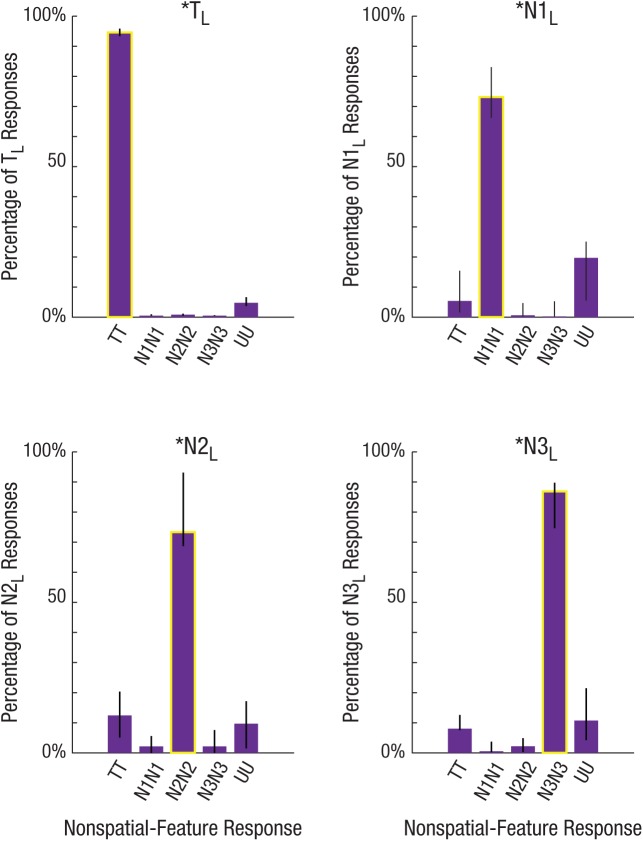
Next, we directly investigated how these lapses of spatial attention (using reports of nontarget locations as a proxy) impact object-feature binding. We jointly modeled the three-way conjunction of color, orientation, and location with the triple model (for all parameter estimates, see Table S10 in the Supplemental Material) to test whether reporting both the color and orientation of a specific item (e.g., N1_CN1_O*) was bound to the location of that specific item (e.g., N1_CN1_ON1_L). Figure 5c illustrates the joint color and orientation reports for hold trials in the same scatterplot form as in Figure 2, but here plotted separately according to location response (coarsely coded as T, N1, N2, or N3) on that trial. Figure 6 shows the parameter estimates from the triple model, also grouped by their shared location component (e.g., *N1_L), such that each feature-feature response type is plotted as a percentage of all the responses containing that location component.

Fig. 6.

Triple joint model maximum-likelihood estimates. Color, orientation, and location (L) responses from hold trials in Experiment 2 were fitted simultaneously as joint distributions. Parameter estimates are plotted separately, grouped according to each parameter’s location component: target (T_L), critical nontarget (N1_L), adjacent nontarget (N2_L), and diagonal nontarget (N3_L). For each graph, each nonspatial-feature response type (N1_CN1_O, N2_CN2_O, N3_CN3_O, U_CU_O) is calculated as a percentage of all responses specific to that location component. For each graph, the bar with the yellow outline signifies reporting the fully bound color, orientation, and location of the same object. The triple model was fitted for each condition separately, collapsed across all participants. Error bars represent 95% highest-density intervals. T = target; N1 = critical nontarget; N2 = adjacent nontarget; N3 = diagonal nontarget; U = random guessing.

As suggested by the scatterplots and confirmed with the triple model, the vast majority of all responses were attributed to fully bound objects: correlated color-orientation-location reports (yellow outlined bars; see Fig. 6). When the correct target location was reported, participants overwhelmingly reported both nonspatial features of the target object (pT_CT_OT_L = 95.1% of T_L responses, 95% HDI = [93.4%, 96.0%]; see Fig. 5c). Whereas there was a small percentage of random feature guessing (pU_CU_OT_L), participants did not make correlated swap errors when spatial attention was properly maintained (e.g., pN1_CN1_OT_L).

But what about during lapses of spatial attention? When participants incorrectly reported the location of a nontarget, the color and orientation errors appear to systematically cluster around that specific nontarget’s features (see Fig. 5c). Thus, when spatial attention lapsed to a nontarget location, the nonspatial-feature reports reflected these location errors, with participants mostly reporting both the color and orientation of the item at the lapsed spatial location (pN1_CN1_ON1_L = 73.5% of all *N1_L responses, 95% HDI = [66.2%, 83.1%]; pN2_CN2_ON2_L = 73.4% of all *N2_L responses, 95% HDI = [61.4%, 85.8%]; pN3_CN3_ON3_L = 86.9% of all *N3_L responses, 95% HDI = [74.7%, 89.8%]; see Fig. 6). On these lapse trials, although there were small percentages of correct target reports (pT_CT_O*) and random guesses (pU_CU_O*), there were almost never correlated swap errors associated with another location. In other words, after lapses of spatial attention, participants still primarily reported fully bound properties (color, orientation, and location), but for the lapsed nontarget item instead of the correct target item.

By simultaneously modeling all feature dimensions (i.e., color, orientation, location), we demonstrated that the locus of spatial attention seems to drive object-feature binding, even when spatial attention mistakenly shifts to or lingers at an incorrect, nontarget location. How important, then, is the precision of spatial attention for successful object-feature binding? A strong interpretation of a spatially driven binding mechanism would predict that the degree of successful feature-feature binding should increase with the precision of spatial attention. To test this, we performed a supplementary analysis that took location response error as a proxy for the precision of spatial attention on a given trial and then fitted data from an expanding window of location error with a basic joint-feature mixture model (see Section S11 in the Supplemental Material). As the magnitude of location error increased, correlated target responses decreased and independent target errors increased, suggesting that the degree of nonspatial object-feature binding was indeed related to spatial precision, which could provide further support for the idea that the spatial extent of visual attention is critical to the successful integration of nonspatial features.

Discussion

Our fundamental question was whether visual object integrity survives conditions of dynamic attention, which we induced by cuing covert spatial attention to shift and split across multiple objects with multiple features. We observed distinct patterns of object-feature binding: Splitting attention across multiple locations degrades object integrity, whereas rapid shifts of spatial attention maintain bound objects, even when reporting the wrong features. These reliable effects were consistent across both simple and full models and replicated across two independent experiments with large effect sizes. Moreover, we document a novel attentional phenomenon: Inadvertent shifts, or lapses of spatial attention, result in erroneous feature reports, but object integrity is still preserved at the wrong location. Together, these findings emphasize the importance of a single focus of spatial attention for object-feature binding, even when that focus is dynamically moving across the visual field.

When spatial attention was cued to shift to a new task-relevant location, object-feature binding for the newly cued target item was generally successful. We probed binding amid the dynamic process of shifting attention by presenting the arrays almost immediately (50 ms) after shifts were cued; thus, intact object integrity for the target suggests that attention had rapidly shifted and fully updated to the new task-relevant location by the time the array appeared on those trials. Critically, on trials with feature errors, there was an increase in reporting both features of the nontarget that appeared at the initially cued location (i.e., correlated N1_CN1_O swap errors). Although these swap errors could stem from never seeing the shift cue on those trials, overall performance for location reports was highly accurate, with participants reporting the newly cued location on 92% of shift trials. In other words, participants were very good at seeing the shift cue. Thus, a more likely explanation is that these errors reflect the dynamic process of attentional updating: Attention had not yet fully disengaged from the initially cued location and re-engaged at the newly cued location. For instance, previous work has demonstrated that incomplete shifts of attention can result in misreporting a single visual feature of a nontarget (e.g., Golomb et al., 2014), but single-feature swaps could present as either correlated or independent errors when multiple features are probed. Here, we show that an incomplete shift of spatial attention preserves object integrity at the initially attended location. There was no increase in independent errors, such as illusory conjunctions (i.e., swapping just one feature), contrary to what might be expected if attention spread across the two locations (Cohen & Ivry, 1989) or briefly activated both locations simultaneously (e.g., Khayat et al., 2006). Instead, spatial attention seems to shift rapidly from one discrete location to another, binding together the visual features at each single, attended location (Nissen, 1985; Treisman & Gelade, 1980).

In contrast, splitting attention across two locations resulted in more independent feature errors (i.e., reporting only one target feature) rather than correlated feature errors. The lack of correlated feature errors suggests that participants were not simply attending to one of the two cued locations, in hopes that it would be postcued as the target, nor were they rapidly shifting attention back and forth between the two cued locations, which would have also been unlikely given that the stimulus array was presented for only 50 ms (Jans, Peters, & De Weerd, 2010). Eye movements were also restricted throughout presentations of the cue, array, and mask. Instead, participants likely attended to both locations simultaneously (Cave, Bush, & Taylor, 2010), perhaps as separate and parallel foci (e.g., Eimer & Grubert, 2014) or within a larger, diffuse attentional window (e.g., Eriksen & St. James, 1986). Contrary to probabilistic accounts of independent feature sampling (Vul & Rich, 2010), binding errors here consisted primarily of unbound guesses rather than illusory conjunctions, as if only one feature dimension were prioritized (e.g., Woodman & Vogel, 2008). Even when participants did report both features of the target item, the cost of splitting attention was decreased precision for both color and orientation. These results are consistent with previous findings in visual working memory (which employ longer encoding and delay periods), in which remembering multiple multifeature objects also results in feature independence (e.g., Bays et al., 2011; Fougnie & Alvarez, 2011) and decreased feature precision (e.g., Bays et al., 2011; Fougnie et al., 2010; Park, Sy, Hong, & Tong, 2017).

Surprisingly, even when only one location was cued (hold trials), participants sometimes failed to sustain spatial attention at that target location. By including a continuous location report in Experiment 2, we demonstrated that participants had occasional lapses of spatial attention and mistakenly identified a random nontarget location as the true target location. We emphasize that these lapses of spatial attention are not simply lapses of sustained attention (i.e., momentarily disengaging from the task at hand; Reason, 1984); indeed, the systematic pattern of correlated swap errors during lapses of spatial attention demonstrates that participants remained on task and were not simply mind wandering. In other words, participants were attending to a location, just to the wrong location. Thus, simply seeing a spatial cue does not mean that spatial attention is perfectly maintained at that cued location. For example, when you are waiting for a red traffic light to turn green, a lapse of sustained attention might cause you to miss the light change and react more slowly, but it does not mean that you forgot the task or never understood the task. Likewise, a lapse of spatial attention does not necessarily mean that participants forgot or never saw the cue but, rather, that there was a momentary spatial fluctuation away from the actual cue’s location. Although it is possible that they never saw the cue and randomly picked a location to attend to, this seems unlikely because the initial cue was presented for 250 ms. It seems more likely in the current task that lapses of spatial attention may have been anticipatory in nature; because hold and shift trials were randomly intermixed within blocks, participants may have inadvertently but proactively shifted covert attention to a noncued location in anticipation of a second spatial cue. The lapses of spatial attention in the current task may also reflect the rhythmic nature of visual attention (see VanRullen, 2016). For instance, Fiebelkorn, Saalmann, and Kastner (2013) demonstrated that when participants were cued to attend to a single location, they periodically monitored an uncued location at a frequency of 4 Hz. Importantly, rhythmic spatial attention in that study may have also been anticipatory in nature, as cue validity was 75% (i.e., the uncued location was still relevant).

Importantly, the joint-feature errors that arose from these lapses of spatial attention were predictable: Participants systematically reported both the color and orientation of the nontarget (i.e., correlated swap error) corresponding to that misidentified location. Just as correlated swap errors occurred after intentional shifts of spatial attention, correlated swap errors also occurred after inadvertent shifts—or lapses—of spatial attention. Lapses of spatial attention may, however, differ mechanistically from cued shifts of attention in this paradigm, given that inadvertent shifts in hold trials were self-directed, whereas intentional shifts in shift trials were exogenously cued. The attentional effects of exogenous cuing are thought to be more transient and efficient, although the sustained effects of endogenous cuing may have more time to become more precise and focused (see Jans et al., 2010). Future work could investigate how exogenously and endogenously cued shifts of spatial attention might differentially affect object-feature binding.

Importantly, these fully bound (feature-feature-location) object errors do not reflect traditional failures of feature binding (cf. Bays, 2016) but instead reflect the stubborn persistence of object-feature binding whenever any single location is attended, regardless of spatial relevance. Previous studies have argued that spatial location serves as the anchor for object-feature binding (e.g., Nissen, 1985; Pertzov & Husain, 2013; Reynolds & Desimone, 1999; Schneegans & Bays, 2017; Treisman & Gelade, 1980; see also Wolfe & Cave, 1999). For example, Nissen (1985) presented color-shape-location combinations and cued either location (i.e., report color and shape) or color (i.e., report shape and location), whereas more recently, Schneegans and Bays (2017) presented colored and oriented bars in a continuous-report visual working memory task and cued the target item by either orientation (i.e., report color and location) or color (i.e., report orientation and location). In both of these studies, when participants reported the incorrect location (i.e., a swap error), their reports of the nonspatial feature were strongly linked to that incorrect location. Although the current study was not designed to examine the specific mechanism by which binding occurs, the results of Experiment 2 reinforce the critical role of spatial location in feature binding, in addition to revealing the consequences for binding when spatial attention is dynamic. We also found little evidence of correlated feature-feature reports without also reporting their corresponding location, consistent with a spatial-binding mechanism in which the nonspatial features of an object are each bound to its location and only transitively bound to each other via that shared location (e.g., Schneegans & Bays, 2017). Interestingly, some studies have reported feature-feature representations unbound from spatial location in visual working memory (e.g., Logie, Brockmole, & Jaswal, 2011; Saiki, 2016; but see Pertzov & Husain, 2013). Combined with our results, this suggests that when multifeature objects are perceived and encoded, object integrity is initially anchored to spatial location, but as object representations are uploaded to memory, direct feature-feature binding may survive without the location information.

These findings may have broad implications for object perception, memory, and attentional mechanisms, shedding light on how we manage coherent representations of objects in the world. As spatial attention shifts from location to location, the visual features at each location can be rapidly bound together as cohesive objects. However, object integrity depends on a single and precise focus of spatial attention; splitting attention across multiple locations or increasing the spatial extent of attention comes at a cost. Thus, to avoid potential failures of object integrity, we may default to processing the visual world rapidly and serially (Jans et al., 2010). An intriguing question is whether such processing strategies might be adaptively learned. Our results raise potential implications for other types of dynamic attention (e.g., remapping across eye movements; Golomb et al., 2014) as well as individual differences in attentional abilities (Rosenberg et al., 2016) and attentional deficits (e.g., attention-deficit/hyperactivity disorder, cognitive aging).