Convolutional Mixture of Experts Model: A Comparative Study on Automatic Macular Diagnosis in Retinal Optical Coherence Tomography Imaging

Abstract

Background:

Macular disorders, such as diabetic macular edema (DME) and age-related macular degeneration (AMD) are among the major ocular diseases. Having one of these diseases can lead to vision impairments or even permanent blindness in a not-so-long time span. So, the early diagnosis of these diseases are the main goals for researchers in the field.

Methods:

This study is designed in order to present a comparative analysis on the recent convolutional mixture of experts (CMoE) models for distinguishing normal macular OCT from DME and AMD. For this purpose, we considered three recent CMoE models called Mixture ensemble of convolutional neural networks (ME-CNN), Multi-scale Convolutional Mixture of Experts (MCME), and Wavelet-based Convolutional Mixture of Experts (WCME) models. For this research study, the models were evaluated on a database of three different macular OCT sets. Two first OCT sets were acquired by Heidelberg imaging systems consisting of 148 and 45 subjects respectively and set3 was constituted of 384 Bioptigen OCT acquisitions. To provide better performance insight into the CMoE ensembles, we extensively analyzed the models based on the 5-fold cross-validation method and various classification measures such as precision and average area under the ROC curve (AUC).

Results:

Experimental evaluations showed that the MCME and WCME outperformed the ME-CNN model and presented overall precisions of 98.14% and 96.06% for aligned OCTs respectively. For non-aligned retinal OCTs, these values were 93.95% and 95.56%.

Conclusion:

Based on the comparative analysis, although the MCME model outperformed the other CMoE models in the analysis of aligned retinal OCTs, the WCME offers a robust model for diagnosis of non-aligned retinal OCTs. This allows having a fast and robust computer-aided system in macular OCT imaging which does not rely on the routine computerized processes such as denoising, segmentation of retinal layers, and also retinal layers alignment.

Introduction

Retinal disorders, especially those involving macula, such as diabetic macular edema (DME) and age-related macular degeneration (AMD), are among the major ocular diseases.[1,2] Having one of these diseases can lead to permanent blindness in a not-so-long time span. Today, the progression rate of these diseases in industrialized and developing countries has become a growing concern that can endanger the vision of people.[3] Based on clinical evaluations in modern societies, these diseases are trending toward becoming the most important causes of blindness and visual impairment. Vision impairments or blindness due to the chronic retinal diseases can be averted if they are detected and treated early via screening programs.[4] Hence, the early diagnosis and effective treatment of these diseases are the main goals of eye researchers in the field of health.[5]

One of the main methods for detecting macular diseases and monitoring response to treatment is the optical coherence tomography (OCT) imaging of the eye. OCT, as a non-invasive three-dimensional (3-D) imaging technique, can effectively visualize intraocular microscopic structures such as the retina and the optic nerve head.[6] Hence, it has the ability to diagnose intrinsic diseases in macula such as AMD and DME. As OCT images are produced at higher sampling rates and resolution, there is a strong need for the analysis of their images with helpful computer-aided diagnosis (CAD) systems to diagnose diseases early and to examine how the response to treatment occurs.[3]

Most software research studies that have been performed for the automatic analysis of OCT images include various algorithms for image preprocessing, enhancement, and segmentation processes. However, limited work has been reported for automatic diagnosis of ocular diseases via OCT imaging.[7] Most commonly used methods for classifying OCT images rely on a precise retinal layer segmentation step. Since there has been no effective method for the segmentation of pathological retinal layers in OCT images, relying on segmentation as the main step for classification of OCT images can greatly affect the performance of the diagnostic systems. In the following, some recent works on macular OCT CAD systems are briefly reviewed.

In,[3] the authors proposed a multiscale local binary pattern (LBP) feature extraction step and a non-linear support vector machine (SVM) method for the diagnosis of macular pathologies including macular edema, macular hole, and AMD from normal ones using a dataset of 326 OCT scans. With the help of a retinal alignment preprocessing step based on morphological operations and using the receiver operating characteristic (ROC) analysis, the algorithm reached an average area under the ROC curve (AUC) of 0.93.

Farsiu et al.[8] developed a semi-automatic classification method for AMD diagnosis in a dataset of 384 retinal Bioptigen spectral domain OCTs (SD-OCTs). Given manually-corrected segmentations of Bruch's membrane (BM), the retinal pigment epithelium (RPE) and inner limiting membrane layers, they calculated a number of metrics: Total thickness of the retina; thickness between drusen apexes and the RPE; abnormal thickness score; abnormal thinness score. Then, they trained linear regression models using different combinations of these metrics. Using the best combination and the leave-one-out validation approach, the method achieved an AUC of 0.99.

In another study,[9] the authors employed a feature extraction method based on the histogram of oriented gradients (HOG) and fed the features to three linear SVM classifiers for the purpose of discrimination among DME, AMD, and normal SD-OCT volumes. The research utilized a preprocessing stage composed of block matching and 3-D-filtering (BM3D) denoizing,[10] and retinal curvature flattening steps. Based on a threshold of 33% of abnormal B-scans for decision-making on a dataset of 45 OCTs. This method achieved a classification rate of 86.67%, 100%, and 100% for normal, DME and AMD classes, respectively.

In Sugmk et al.,[11] after the segmentation of the RPE layer, binary features were computed from the RPE layer to identify AMD and DME pathologies. The experimental results showed an accuracy of 87.5% through a dataset of 16 OCT images.

With the same OCT set as Farsiu et al.,[8] an automatic AMD identification method was proposed Apostolopoulos et al.[12] based on convolutional neural networks (CNNs) with an AUC of 0.997. For this purpose, the method remapped the OCT volumes to large image mosaics and trained a two-dimensional (2-D) CNN, called RetiNet-C, for the classification of retinal OCTs.

In Hassan et al.,[13] proposed a feature extraction methodology based on structural tensors. They extracted three thickness profiles, and two cyst fluids features for the classification of macular edema, central serous retinopathy, and healthy OCTs. The algorithm correctly classified 88 out of 90 subjects with the accuracy, sensitivity, and specificity of 97.77%, 100%, and 93.33%, respectively.

In addition, Sun et al.,[14] proposed a macular pathology detection algorithm in OCT images using sparse coding and dictionary learning. After using the BM3D denoizing and retinal curvature correction, the authors performed a dictionary learning technique on shift invariant feature transform features on partitioned B-scans. Then, they used three binary linear SVM classifiers for discrimination between normal, DME, and AMD OCT volumes with a classification rate of 93.33%, 100%, and 100%, respectively on a dataset of 45 OCTs.[9]

Recently, in[15] the authors proposed a CAD in macular OCT diagnosis including two learning stages: (I) adaptive feature learning through a new Wavelet-based CNN, and (II) random forests (RF) classifier learning. With the application of the algorithm on a set of 45 OCT volumes[9] and 10 repetitions of 5-fold cross-validation (CV), the proposed scheme obtained an average precision of 98.67% on the dataset as a three-class classification task (AMD/DME/normal).

Most recently, Rasti et al. introduced two novel convolutional mixture of experts (CMoE) models called multiscale convolutional mixture of experts (MCMEs),[16] and wavelet-based convolutional mixture of experts (WCMEs)[17] for the diagnosis of macular abnormalities. The MCME ensemble using the prior multiscale spatial pyramid (MSSP) decomposition method was developed to incorporate multiple CNNs with special fields of view same as the attention models to represent the aligned macular region at multiple scales. The information fusion in this model was conducted through a Gaussian mixture objective function benefiting from a new cross-correlation penalty term. The WCME ensemble was designed to impose the spatial-frequency information fusion in multiple CNNs with special receptive fields. Using a prior 2D-Daubechies wavelet decomposition, this model tries to represent the non-aligned macular region at multiple frequency maps.

The present study is designed to perform a comparative analysis on the recent MCME[16] and WCME[17] models for distinguishing normal macular OCT from DME and AMD using three different SD-OCT datasets. The rest of the paper is structured as follows: Section 2 describes the OCT database and data pre-processing steps. It also introduces evaluated baselines and the methods. Section 3 presents the experimental setup and results of the evaluated CMoE ensembles. Sections 4 and 5 give the research discussion and conclusion, respectively.

Materials and Methods

In this section, we first introduce the retinal OCT image database and present a general data preprocessing pipeline used for retinal OCT image analysis. We briefly review the architecture and mathematical model of regular CNNs. Then, the evaluated CMoE model are presented and described in detail.

Optical coherence tomography database

For this research study, the proposed algorithms were designed and evaluated on three different SD-OCT datasets acquired by Heidelberg and Bioptigen OCT imaging systems.

Dataset 1: Local\Heidelberg dataset

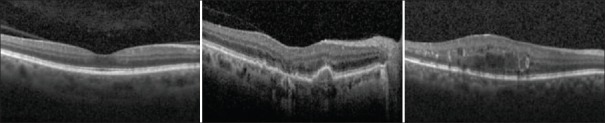
The first macular dataset was acquired at Noor Eye Hospital in Tehran consisting of 50 normal, 48 dry AMD, and 50 DME OCTs from Heidelberg device (Heidelberg Engineering Inc., Heidelberg, Germany). For this dataset, the number of A-scans varied among 512 or 768 scans where 19-61 B-scans per volume were acquired from different patients. Figure 1 illustrates example B-scans from different SD-OCT volumes of each class in Dataset 1.

Figure 1.

Example B-scans from normal (left), age-related macular degeneration (middle), and diabetic macular edema (right) subjects in Dataset1

Dataset 2: Duke-Harvard-Michigan Heidelberg dataset

The second dataset was a collection of Heidelberg acquisitions that contains 45 OCTs.[9] This dataset included volumetric scans (nonunique protocols) of control, AMD, and DME classes with 15 subjects for each class. The OCT B-scans in this dataset varies in a range of 31 to 97 slices with the size of 512 × 496 or 768 × 496 pixels.

In addition to the provided case labels, all B-scans in the two Heidelberg research datasets were annotated by an expert ophthalmologist experienced in OCT imaging. Therefore, all B-scans in Dataset1 and Dataset2 (4142 and 3247 respectively) were annotated as normal, AMD or DME images. The B-scans and annotations were used for training and evaluating the proposed models. In total, Dataset1 included 862 DME and 969 AMD B-scans. These samples were 856 and 711 B-scans for Dataset2. In addition, other B-scans were taken as healthy images.

Dataset 3: Duke Bioptigen Dataset

The third dataset was a set of Bioptigen SD-OCT data, which totally includes 384 retinal OCTs (269 AMD, 115 control volumes).[8] The control group consisted of healthy subjects who had no evidence of macular drusen or AMD signs in both eyes. One hundred foveal B-scans for each volume were obtained with a resolution of 1000 × 512 pixels. Since manual analysis and annotating of this dataset (including 38,400 B-scans) is a very time-consuming task and demanding for days of hard-work by ophthalmologists, therefore we consider and call this OCT set as an unseen data for validation purposes.

Optical coherence tomography data preprocessing

A general pipeline of the preprocessing algorithm is shown in Figure 2.

Figure 2.

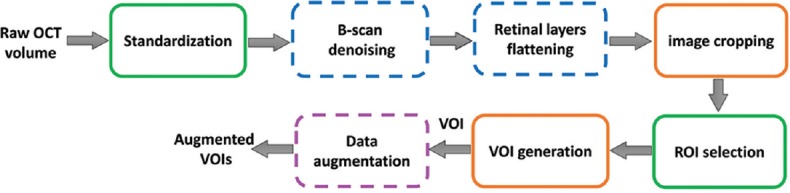
A general overview of the data preprocessing algorithm

Standardization

All B-scans in the database were first resized to 512 × 496 pixels and the possible missing regions in the background were compensated using the “imfill” morphological operation[18] with an intensity value of zero. In addition, a normalization step was done to remove the intensity mean value of each B-scan and to scale it so that we could have a standard deviation of one.

B-scan denoising

In general, OCT images are corrupted by speckle noise in imaging step.[5] Since CNNs are rather robust to image noise; however, it seems beneficial to denoize their input images to facilitate the learning process of classifiers. Therefore, by denoizing individual B-scans in the OCT volumes, the quality of the database was improved. For this purpose, the BM3D method, according to Fang et al.,[19] was used in which the standard deviation of the noise (corresponding to image intensities in the range (0,255)) was adaptively estimated for each B-scan. Hence, 4 different 10 × 10 window boxes were considered at the corners of each raw image, and the minimum value of these four noise standard deviations was selected as the sigma value in the BM3D algorithm.

Retinal layers flattening

In ocular OCT images, due to the imaging distortion and anatomical structures, the retinal layers may be randomly translated or rotated in the B-scans. To counteract these variations, a graph-based curvature correction algorithm[20] was performed. As for the main idea in the flattening block [Figure 3], the hyper-reflective complex (HRC) band is detected, then a convex second-order polynomial curve is fitted on the HRC band. Consequently, the retina layers are wrapped up in a way that the HRC points can be placed horizontally.[20]

Figure 3.

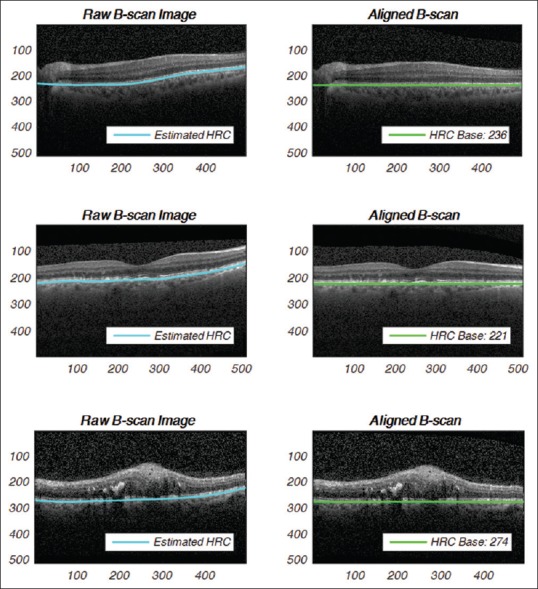
Retinal layers flattening on noisy B-scans: (top row) normal, (middle row) age-related macular degeneration, (bottom row) diabetic macular edema B-scan instances

Image cropping

Nonaligned data

To crop raw retinal B-scans, middle row position of the maximum intensity values in B-scans of current OCT volume was selected as the central row of the case. Hence, for each B-scan, 135 rows above and 120-row pixels below the calculated central row were selected as the cropped image. In severely misaligned cases with very low or high central row, 256 rows located on the top or bottom of the image were selected for image cropping purpose.

Aligned data

Here, to focus on the retina and reduce image sizes, each B-scan was first cropped at 200 pixels higher and 35 pixels lower than the detected HRC band. These values were selected through visual inspection over the datasets to maintain all retinal information. Finally, the cropped images were downsampled to 128 × 512 pixels as the aligned fields of view (FOVs) for further processes.

Volume of interest generation and augmentation

Nonaligned data

Here, in the first step, a centered 256 × 470 pixels bounding box was defined as a FOV in a cropped B-scan. This FOV was used to generate the central region of interests (ROIs) for a given volume of interest (VOI). In the training phase for generalization of the problem and to have an effective training process, the selected FOVs in training cases were horizontally flipped, translated by (±10, ±20) pixels, and rotated by (±3°, ±5°) angles. This augmentation trend increased the number of the nonaligned samples with a factor of 18 in our training process. Furthermore, all the extracted ROIs were resized to 128 × 256 pixels for subsequent processes. In the testing phase, only the resized central ROIs in a given volume were considered for the evaluation purpose.

Aligned data

In the case of aligned B-scans, the ROI was selected with a limited and centered box of 128 × 420 pixels in each B-scan. In the next step, all extracted ROIs in all B-scans were downsampled to 128 × 256 pixels and were concatenated to produce the case VOI. In the training phase, the centered bounding box was flipped horizontally and/or translated by ± 20 pixels to produce augmented ROI training sets. The number of training examples was increased by a factor of 6 using this strategy. Basically, the augmentation technique helps to reduce the chance of overfitting by degrading the data bias with respect to the number of right and left eyes.[12]

Regular convolutional neural networks

CNN is a deep neural network model that captures spatial information of the input image data.[21] The typical CNN consists of a cascade of several convolutional (C or CONV) layers, nonlinearity, pooling (P or POOL) layers, and fully connected (FC) layers. Other CNN layers exist for recent published CNNs such as batch-normalization layers (BN layers)[22] and dropout layers[23] for creating more efficient convolutional models.

Convolutional neural network signal forward propagation

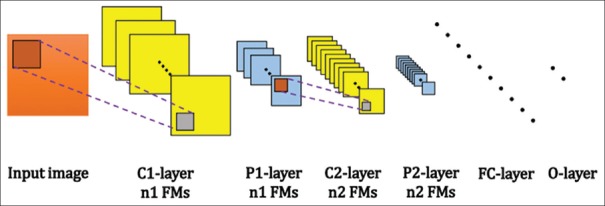
As shown in Figure 4, in a regular CNN model, layers are arranged in a feed-forward structure: Stacks of hidden C-P layers (CONV-POOL), some hidden FC layers, and a final FC-layer called output layer (O-layer). In CNNs, C and P-layers have several extracted planes which called output feature maps (FMs).

Figure 4.

An example of layers configuration in a regular 6-active layer convolutional neural network

Convolutional layer

In a typical convolutional layer or C-layer for short, a set of 2-D neural kernels (filters) are learned to fuse local spatial information of the preceding layer output(s). For this purpose, several convolutional kernels, which are 2-D arrays of neuron weights, are convolved with the 2-D input FMs. By conducting the multiple convolution operations between the input FMs and the kernels, the C-layer can represent the visual features at input pixel locations adaptively and efficiently. Figure 5 demonstrates a typical C-layer. In this figure, the output of the layer is a 2-D FM which is then connected to exactly one plane in the next P-layer.[24]

Figure 5.

A typical convolutional layer in convolutional neural network

In C-layer l, n^th output feature map is calculated mathematically as:

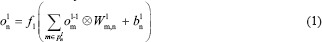
Where f_l is the activation function of layer, o^l-1_m is output FM of the previous layer, W^l_m,n is the convolutional 2-D kernel of weights from m^th FM in layer (l − 1) to n^th FM in layer l. Indeed, b^l_n is the bias term associated with n^th FM and p^l_n denotes the list of all planes in layer (l − 1) that are connected to n^th FM. The ⊗ indicates the 2-D convolution operation without any zero-padding.

Pooling layer

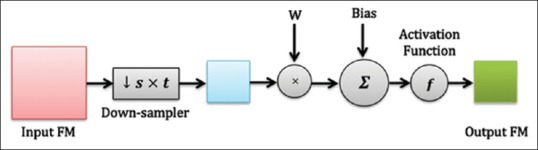
An s × t pooling layer (P-layer) is usually applied after convolutional layers. To reduce computational complexity and also to improve translation invariance, a pooling layer fuses local spatial information in a small window in the same FM with the max operation. For this purpose, this layer performs a down-sampling function (Max-Pooling in this study) over the nonoverlapping patches of size s × t pixels. As shown in Figure 6, for P-layer l, n^th output FM is calculated as:

Figure 6.

A typical pooling layer in convolutional neural networks including an s × t sub-sampler

The pool (.) is a max-pooling operator, reduced dimension of input FMs by a factor of s × t. Here, w^l_n and b^l_n are the scalar weights and the bias term related to n^th FM in this layer.

Fully connected layer

This layer consists of some FC neurons. The inputs of these FC neurons are flattened feature maps provided by the previous layer. These FC units map the input values to a vector of scalar features. In the O-layer, the outputs of FC neurons are considered as the network outputs which indicate the predicted classes. Figure 7 shows a FC O-layer in CNN. Sometimes, in multiclass problems, this layer is followed by a “Softmax” operator to generate probabilistic outputs.

Figure 7.

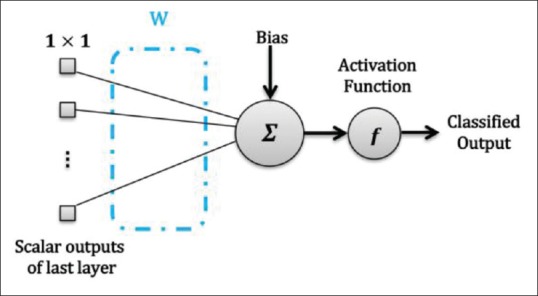
Output layer with one neuron in convolutional neural network

The output relation for an FC layer is expressed as:

Where p^l denotes the collection set of all planes in the previous layer that is connected to output neurons.

Convolutional neural network signal error backpropagation

In literature, for the training of the regular CNN models, batch error back-propagation (BP) method is used with mean square error objective function. Suppose that the training set has K input images and K desired outputs. Let X (K) be the k^th image of training pattern, d (k) be the corresponding desired output vector, and that o^L be the actual network output. The error function is defined as:

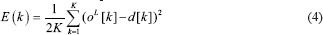
This is an error function of all network free parameters such as weights, kernels, and biases. By following the partial derivative of the CNN output error, the error sensitivities and gradient equations of free parameters in different layers are summarized in Table 1.

Table 1.

Error sensitivity and error gradient computations for n^th forward path in different layers in a typical CNN model

Layer	Error sensitivity: δl,kn	Weight error gradient:	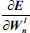Bias error gradient: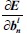
O-layer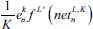
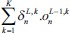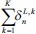C-layers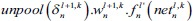
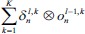P-layers

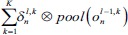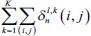In this table, net and k are weighted-sum of the active layer and the number of 2-D input pattern, respectively. W^l is the layer weights’ tensor and o^l is the vector of output scalar feature maps of the layer. Since n is the number of error BP paths in the layer, W^l_n is n^th 2-D kernel of the layer, and O^l,k_n is corresponding output 2-D FM of the layer for k^th sample. Indeed, δ^l_n and net^l_n are matrices of the layer error sensitivity and weighted-sum of the active layer feature maps through n^th error BP path. Moreover, in the table, unpool(.) is a dimension double size increasing operator according to the repetitions of the rows and columns of the input delta map. ⊗ indicates the 2-D convolution operation without any zero-padding. ** operator is the conventional 2-D convolution, and p indicates kernels’ collection that is defined between two consecutive layers.

Convolutional mixture of experts model

Mixture ensemble of convolutional neural networks model

CNN-Mixture ensemble model[25] works based on the idea of the divide-and-conquer approach using the MoE combination method. The traditional structure of the MoE was introduced by Jordan and Jacob in 1991.[26] The MoE is an adaptive and dynamic information fusion method in machine learning literature. In CNN version of the MoE model, using a convolutional gating network (CGN), the output decision of different local CNNs (experts) are adaptively weighted to generate the overall result. Technically, this model benefits from an inherent competitive behavior for input space partitioning by CNN sub-modules.[6] As illustrated in Figure 8, CGN in this model combines the output of several local CNNs. In fact, the CGN performs an adaptive weighting role that makes the overall model run a competitive learning process over the local CNN expert modules.[26] For this purpose, MoE maximizes the probability function based on the Gaussian mixture model (GMM) in which each Gaussian term corresponds with a local CNN expert.[16]

Figure 8.

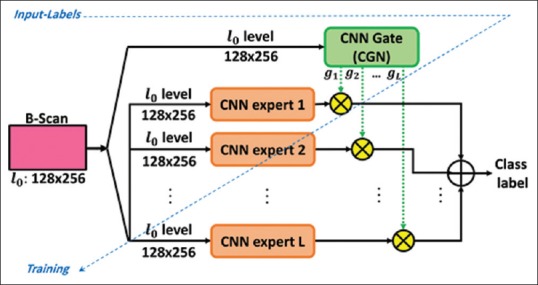
The conventional mixture of L experts (classifiers) structure: a common signal supplies the input of all modules i.e., the experts and the gating network

Multi-scale convolutional mixture of expert model

As demonstrated in Figure 9, the MCME model performs a mechanism for combining several multi-scaled CNN sub-modules. Inspired by visual attention systems, this design enables the MoE model to perform a multi-scale analysis of input patterns.[16] For this purpose, MCME includes a prior multi-scale spatial pyramid (MSSP) decomposition[27] layer in which a symmetric Gaussian kernel is employed for input image decomposition. Subsequently, the pyramid scales are delivered to the local CNN experts and CGN for information abstraction.

Figure 9.

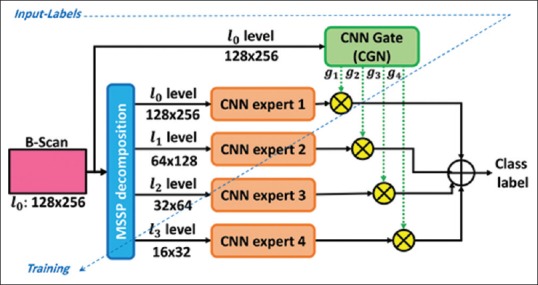
The multiscale convolutional mixture of expert structure: the convolutional neural network experts and gating network are fed by specific scales of the input pattern through a multiscale spatial pyramid decomposition block

In contrast to the traditional MoE, suggesting a prior decomposition of the inputs would be useful for reducing the computational complexity of the overall model by dividing the task among simpler and scaled CNNs. For this, the CGN tries to integrate key information of different scales. In this model, total error cost function for k^th input image is defined as:

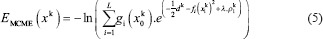
Where g_i(x^k₀) is a probabilistic weight to expert's output f_i which assigned by the CGN. In addition, d_k, ρ_i, and L are the desire output of the input sample x^k, a cross-correlation penalty term, and the number of CNN experts in the model, respectively. Here, ρ_i is defined as follows:

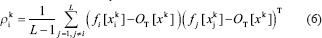
Here, O_T is the overall output of the model. In addition, the strength of the above penalty is adjusted explicitly with the parameter 0≤ λ ≤1.

Wavelet-based convolutional mixture of expert model

The WCME model[17] is an ensemble model based on the MoE mechanism in the spatial-frequency domain. This model forces the CNN experts to consider different level frequency maps of the input data directly and tries to reduce the computational effort by the model to build high-level representations. Using the wavelet transform (WT),[28] the analysis of the image spatial and frequency characteristics at multiple resolutions is possible in this model. This model includes a one-level decomposition block of the 2-D Daubechies WT to partition the input space and to produce low pass approximation (LL), horizontal detail (LH), vertical detail (HL), and diagonal detail (HH) sub-bands, respectively. Figure 10 shows the WCME model.

Figure 10.

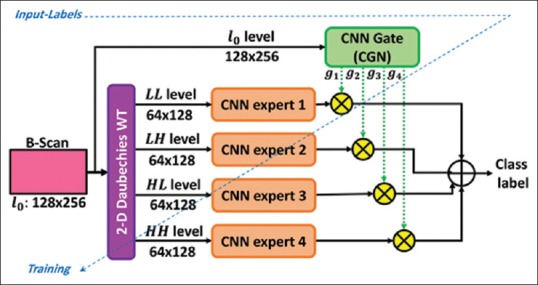
The proposed wavelet-based convolutional mixture of expert model for retinal optical coherence tomography B-scan analysis. In this structure, all modules are trained simultaneously based on an end-to-end learning procedure

In forward pass, given a pattern, wavelet-based CNN experts perform distinct classifications over the spatial-frequency maps. Moreover, the outputs of the CGN represent specific confidences in local CNNs. For this, CGN simultaneously analyzes spatial information of the original input image and the performance of the experts. Finally, WCME presents an overall output based on the weighted sum of the all estimated probabilities by local experts.

Convolutional neural network training algorithm

Training of the CNN models is based on error BP technique. Numerous optimization algorithms can be applied to minimize the error gradients of different layers in the model.[11] In this work, for training the proposed ensemble models, the mini-batch Root Mean Square Propagation (RMSprop) was evaluated as the state-of-the-art optimization methods on CNN models. This optimization algorithm was introduced by Hinton et al.[29] to train neural structures. The main idea here is to divide the learning rate for network weights using average magnitudes of the recent and correspondent gradients. Therefore, the following training parameters were considered for training the CNN structures: lr = 0.001, ρ = 0.9, batch size = 32, epoch = 50, and decay = 0.00005.

Performance measures

In the present paper, diagnostic performance is calculated and reported based on the confusion matrix and ROC analysis at the patient level which are: accuracy, recall, F1 score and average AUC values. For this purpose, we computed precision, recall, F1-score, and AUC values for each class, which were defined in a binary classification problem for the target classes (one-vs.-the-rest). In a three-class classification problem, the negative samples were considered as the samples that do not exist in the considered class. Therefore, the overall precision, recall, F1-score, and AUC values were averaged over the three class labels and reported as the final performance measures. The measures were defined as follows:

• The Precision (or positive predictive value) is defined as:

  Precision =

  where TP is the number of true positives and FP the number of false positives[30]

• The recall (or sensitivity, or true positive rate) is the below ratio:

  Recall =

Here FN the number of false negatives

• The F₁ score which can be defined as:[30]

  

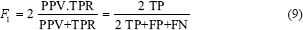
• The area under the ROC curve, or “AUC” or “A_z”. A reliable and valid AUC estimate can be interpreted as the probability that the classifier will assign a higher score to a randomly chosen positive example than to a randomly chosen negative example[31]

• Normalized cross-correlation: The strength and direction of a linear relationship between CNN experts in an ensemble model can be indicated by the normalized cross-correlation factor:

  

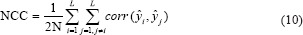
  In the above formula, ŷ_i is a 1 × N vector of predicted output values generated by i^th CNN expert module in a trained ensemble model

• Cohen's kappa (κ): −1≤ κ ≤1 is a statistical measure of classifiers agreement between each pair of different estimators.[32]

Computer equipment and setup

All convolutional models in this study were implemented in Python 2.7 using the Theano v0.8.2[33] and Keras v1.2[34] Toolkits. Training of the networks was executed on an NVIDIA GTX 1080-8GB graphic card, Cuda Toolkit v8.0, and accelerating cuDNN library v5.1. Main codes and other CPU-based toolboxes were run with Corei7 CPU at 3.4GHz (Intel 6800K: 15M), and 32 GB of RAM.

Optical coherence tomography diagnostic strategy

For test VOIs, the diagnostic decision was made by this role: if more than 15% of the B-scans were predicted as abnormal by the trained model, the maximum vote according to AMD /DME scores, determined the type of retinal disease at the patient level.

Experimental Design and Results

Baselines

In this research study, the following baselines were considered to demonstrate the proficiency of the evaluated strategies. This experimental setup obtains a benchmark for comparing the performance and complexity of models in retinal OCT image classification.

• Feature-Based Methods: As the first baseline study, two commonly used feature-based approaches were implemented. These two approaches extract LBP[3] and HOG[9] features at multiple scales and then use SVM classifier.

• Mixture ensemble of convolutional neural network (ME-CNN) model: ME-CNN, as the basic model of convolutional MoE[25], was considered to challenge the performance of the MCME and WCME models in our problem. This comparative analysis gets better insight into the suggested prior multiscale decomposition in the convolutional MoE model, and the proposed cost function as well. For this purpose, ME-CNN was studied using the full-scale combination of 2, 3, and 4 CNN experts [CNN1 in Table 2].

Table 2.

Structural details of scale-dependent convolutional experts

Module	Input scale	Input size	Number of layers	First conv- mask size	Other conv- mask size	Max-pooling size	Number of FMs in C and P layers	Number of FC1 neurons	Number of FC2 neurons	Number of free parameters
CNN1	l0	128×256	19	5×5	3×3	2×2	3	15	3	2993
CNN2	l1	64×128	16	5×5	3×3	2×2	3	15	3	1901
CNN3	l2	32×64	13	5×5	3×3	2×2	3	15	3	1381
CNN4	l3	16×32	10	5×5	3×3	2×2	3	15	3	997

CNN – Convolutional neural networks; FM – Feature maps

Multi-scale convolutional mixture of expert model

Here, in order to evaluate the MCME model, a low-to-high-resolution strategy was performed to assess the number of scales influencing the performance of the convolutional MoE. Following this goal, different scale-dependent CNNs were considered for local expert modules according to [Table 2]. Additionally, CGN was designed based on the CNN1 structure and “Softmax” output layer.

In this experiment, the MCME model was evaluated considering any combination of 2, 3, or 4 scales. So, four different structures were considered using CNNs in Table 2. All regular CNNs were made using the CONV-BN-POOL composite sequence and connected to two FC-BN layers. In addition, in order to reduce the probability of over-fitting, an optimized dropout factor of 70% was set for the entire FC1 layers.

In Table 2, FM, C, P and FC stand for the featured map, convolutional layer, pooling layer, and fully-connected layer. Output activation functions for experts and CGN were considered as “Sigmoid” and “Softmax”, respectively where the “ReLU” function was selected for hidden layers thoroughly. All modules were initialized with the “Glorot Uniform” method.[35] In addition, the MoE cost function was optimized by monitoring the control parameter λ between 0 and 1 with a step of 0.1 in the Eq. 5.

Multiscale convolutional mixture of expert analysis

Table 3 reports the average results of the best structures on Dataset1 obtained with the 5-fold CV method. According to the table, the MCME model with l3-l2-l1-l0 combination at λ = 0.2 performed better than the other methods. For this configuration, the AUC, precision, and recall were 0.998, 99.39%, and 99.36% in Dataset1 respectively. In this experiment, the best multi-scale structure was evaluated by exploring the optimal λ parameter at τ = 15% in Dataset2. As a result, the l₃- l₂- l₁- l₀ MCME model performed with a precision of 96.67%.

Table 3.

Details and the average performance of the baselines and the multi-scale convolutional mixture of experts structures on Dataset1 according to the 5-fold cross-validation, the threshold of 15% for decision-making, and optimum λ values for mixture of experts models

Method	Configuration	Best λ	Precision (%)	Performance
				Recall (%)	F1-score (%)	AUC	NCC	κ	Training time (s/ROI)
Feature based	LBP + RBF.SVM[3]	−	84.24±7.25	83.41±7.97	83.55±7.77	0.895	−	−	−
	HOG + L.SVM[9]	−	85.35±9.51	82.56±11.2	82.09±11.1	0.903	−	−	−
ME-CNN[25]	l0−l0−l0	0.1	98.83±1.48	98.64±1.63	98.67±1.64	0.992	0.11	−0.02	0.193
MCME[16]	l3−l2−l1−l0	0.2	99.39±1.21	99.36±1.33	99.34±1.34	0.998	−0.04	0.03	0.170

l_i – Indicates the multiscale spatial pyramid decomposition level of the input ROI for CNNs in the models. MCME – Multiscale convolutional mixture of experts; ME-CNN – Mixture ensemble of convolutional neural networks; AUC – Area under the ROC curve; NCC – Normalized cross-correlation; ROC – Receiver operating characteristic; LBP – Local binary pattern; SVM – Support vector machine; RBF – Radial basis function; HOG – Histogram of oriented gradients; ROI – Regions of interest

Performance evaluation of the multi-scale convolutional mixture with respect to the role of image denoizing and retinal flattening steps

In this experiment, to evaluate the reliability of the performance of the proposed MCME model to the preprocessing steps, retinal OCT ROIs/VOIs were prepared in four different categories, and the MCME model was evaluated according to the following OCT data categories: (I) denoized and aligned, (II) denoized and non-aligned, (III) without noise elimination but with alignment, and (IV) without any noise elimination and alignment.

As shown in Figure 11, the MCME model with retinal alignment process and without denoizing step (i.e., the case of “No. D-Yes. A” in the figure) outperformed the other configurations with a precision of 99.39% ± 1.21%. It follows that the prior MSSP decomposition in the MCME model is practically efficient when the model analyzes aligned retinal B-scans. When we used a prior denoizing step by the BM3D method, the model resulted in a precision of 96.02% ± 1.40%.

Figure 11.

The effects of the BM3D denoizing and the graph-based alignment processes on the precision measure for the l₃– l₂– l₁– l₀ multiscale convolutional mixture of expert model at λ = 0.2 on Dataset1. In this figure, the letters “D” and “A” indicate “Denoizing” and “Alignment” preprocesses, respectively. The results were calculated at the patent level based on the thresholding technique for decision-making considering τ = 15%

It should be noted that the model's precision for Dataset1 without any denoizing and retinal alignment was 92.79% ± 2.92% at λ = 0.2. By exploring the λ parameter in the interval of [0,1], the precision value recomputed at the optimal value of λ = 0 reached to 94.23% ± 2.53%.

Wavelet-based convolutional mixture of expert analysis

In this experiment, two different structures were considered according to Table 4. Same as the MCME experimental settings, to reduce over-fitting probability during the learning process, a dropout factor of 70% is considered for all FC1 layers too.

Table 4.

Details of the wavelet-based convolutional mixture of experts modules structures

Module	Input scale	Input size	Number of layers	First convolutional - mask size	Other convolutional - mask size	Max-pooling size	Number of FMs in C and P layers	Number of FC1 neurons	Number of FC2 neurons	Number of parameters
CGN	l0	128×256	19	5×5	3×3	2×2	3	15	4	3988
Expert 1, 2, 3, 4	LL−LH−HL−HH	64×128	16	5×5	3×3	2×2	3	15	3	1901

FM – Feature maps

For the comparison purpose, the ME-CNN model was also considered to evaluate the WT decomposition proficiency for feeding relevant nonaligned information to the WCME model. For this purpose, the ensemble of ME-CNN without any WT decomposition and retinal alignment was analyzed as the benchmark study. Table 5 summarizes the diagnosis performance of the evaluated methods at the patient level on Dataset1.

Table 5.

Test performance comparison of the proposed wavelet-based convolutional mixture of experts and the mixture ensemble of convolutional neural networks models on Dataset1 (without denoizing and alignment) using τ=15% for decision-making

Method	Configuration	Best λ	Precision (%)	Performance
				Recall (%)	F1-score (%)	AUC	NCC	κ	Training time (s/ROI)
ME-CNN[25]	l0−l0−l0−l0	0.2	94.41±4.38	93.03±5.76	92.94±5.81	0.986	0.15	0.06	0.228
WCME[17]	LL−LH−HL−HH	0.1	95.90±2.97	95.17±3.40	95.09±3.62	0.993	0.06	0.05	0.141

MCME – Multiscale convolutional mixture of experts; ME-CNN – Mixture ensemble of convolutional neural networks; AUC – Area under the ROC curve; NCC – Normalized cross-correlation; ROC – Receiver operating characteristic; ROI – Regions of interest

For Dataset2 (without denoising and alignment), the WCME resulted in a precision and AUC values of 97.78% ± 4.44% and 0.999, respectively at λ = 0.1 and τ = 15% where it often misestimated a normal subject as AMD in this dataset.

Comparative analysis of the multiscale convolutional mixture of expert and wavelet-based convolutional mixture of expert models

In this experiment, to get a general insight into the performance of the evaluated CNN-ensemble models, 10 repetitions of the unbiased 5-fold CV method were applied at the patient level. Hence, the generated VOIs were used to train and to evaluate the diagnostic efficacy of MCME and WCME schemes. For evaluation purpose, in each repetition, the Heidelberg datasets were reshuffled initially and partitioned into five case folds. By applying the augmentation methods (for aligned and non-aligned B-scans), training of these convolutional MoE models were executed. Moreover, test folds were considered and analyzed to get average performance results.

Table 6 reports average results of the evaluated ensemble models. In this table, Ave. λ for a specific model and configuration indicates to the mean value of the best Lambdas in 10 repetition of the 5-fold CV method.

Table 6.

Comparison of average classification performance for multiscale convolutional mixture of experts and wavelet-based convolutional mixture of experts on the research Heidelberg datasets based on 10 repetitions of 5-fold cross-validation method with τ=15% for decision-making

Model	Configuration	Dataset	Curvature correction	Average λ	Performance
					Precision (%)	AUC	Average testing time (s/VOI)
MCME[16]	l3−l2−l1−l0	Set 1	×	0.08	94.68±1.47	0.961	10.9
			√	0.21	99.01±0.41	0.998
		Set 2	×	0.17	94.63±2.45	0.974
			√	0.26	97.11±0.96	0.994
WCME[17]	LL−LH−HL−HH	Set 1	×	0.12	95.91±1.56	0.976	9.34
			√	0.18	97.40±0.78	0.995
		Set 2	×	0.21	96.03±2.14	0.986
			√	0.24	96.33±1.29	0.990

MCME – Multiscale convolutional mixture of experts; AUC – Area under the ROC curve; ROC – Receiver operating characteristic; WCME – Wavelet-based convolutional mixture of experts; VOI – Volume of interest

Furthermore, Dataset3 was also tested as an unseen retinal OCT database to evaluate the generalization ability of the proposed models in a comparative manner. For this purpose, the models’ topologies were modified to be consistent with a 2-class classification problem according to the nature of the Bioptigen dataset (Dataset3). Hence, CNN experts were modified to include 2-output neurons in the MCME and WCME models. Subsequently, the transfer-learning technique was considered to retrain the models for diagnosis of AMD-vs-normal classes on a combined dataset. The combined dataset was composed of the AMD and normal cases from the Dataset1 and Dataset2 (the Heidelberg datasets). For transfer-learning, only the output neurons of the convolutional structures and the RF classifier were retrained according to the grand truths where all the hidden layers’ weights and the biases were frozen. Table 7 summarizes the performance results of the evaluated ensemble models on Dataset3.

Table 7.

Comparison of classification performance for multiscale convolutional mixture of experts and wavelet-based convolutional mixture of experts on the unseen Dataset3 with τ=15% for decision-making

Model	Configuration	Dataset	Curvature correction	λ	Performance
					Precision (%)	Recall (%)	F1	AUC	Average testing time (s/VOI)
MCME[16]	l3−l2−l1−l0	Set 3	×	0.125*	92.54	93.94	93.23	0.965	0.51
			√	0.235*	96.64	97.37	97.01	0.986
WCME[17]	LL−LH−HL−HH		×	0.165*	94.74	94.38	94.56	0.974	0.45
			√	0.210*	94.44	95.51	94.97	0.971

*λ values were considered based on the average Lambdas in Table 7 for each model and configuration. In addition, OCT volumes including 64 retinal B-scans were analyzed to report average testing time. MCME – Multiscale convolutional mixture of experts; AUC – Area under the ROC curve; ROC – Receiver operating characteristic; WCME – Wavelet-based convolutional mixture of experts; OCT – Optical coherence tomography; VOI – Volume of interest

Discussion

As the experimental showed in Section 3, the MSSP decomposition was not an effective processing block in the CMoE models to represent nonaligned OCT data. One suitable strategy for achieving this goal was to apply the wavelet decomposition and using WCME ensemble model on spatial-frequency domain sub-bands. From the details in Table 5 in Sub-sections 3.2.2, the spatial-frequency decomposition in the WCME model (provided by 2D Daubechies DWT) caused a promising performance and time-complexity versus the comparable ME-CNN model.

Results showed that the WCME model at optimal λ = 0.1 outperformed the ME-CNN ensemble (at optimal λ = 0.2) with a precision rate of 1.49% on non-aligned Dataset1. This indicates that WCME performs more high-level representation than the ME-CNN. Most likely the analysis of the spatial-frequency domain of input data in the WCME model can directly and effectively solve the input partitioning problem in the MoE model. Additionally, the prior decomposition strategy is a way of defining the architecture of the convolutional MoE, where the number of local CNN experts should be the same as the number of WT sub-bands. In fact, according to the prior wavelet decomposition, there is a straightforward distinction between the responsibilities of the local CNN experts in the WCME model.

The WCME outperformed the MCME model in the diagnosis of non-aligned retinal OCTs in Dataset1. However, it could not yield a considerable performance same as the MCME on aligned OCTs in this dataset. The difference was due to the prior decomposition and partitioning. The experimental finding showed that, for analyzing aligned OCT data, the MSSP was a more effective unsupervised decomposition approach than the DWT to partition input space and to feed scale-dependent CNNs in convolutional MoE models.

In Section 3.3, we also analyzed the proposed models in a comparative manner. Hence, the convolutional MoE models were evaluated according to the two different study schemes: (I) the diagnosis of AMD, DME, and normal cases on the Heidelberg datasets using 10 repetition of the 5-fold CV method, and (II) the diagnosis of AMD, and normal (control) cases in an unseen Bioptigen dataset of 384 subjects. In study (I), the MCME model presented average precisions of 98.14% and 93.95% for aligned and non-aligned Heidelberg OCTs, respectively. Table 6 showed that the WCME model performance outperformed the other ensemble models on nonaligned OCT on average. It offered a robust method against retinal curvatures for the analysis of macular OCT data. Indeed, regarding the training time, the WCME model located in the first place before the MCME and ME-CNN models.

Through this study, we found that in the MoE ensemble models (i.e., MCME and WCME models), best λ values for nonaligned OCT data were less than those ones for aligned retinal OCTs in general. This is probably because of the input variations (reduced correlation between data) that the non-aligned data add to the models. In this way, the model requires a smaller λ parameter to differentiate among CNN experts in the intrinsic competitive process for information fusion.

For unseen dataset in study (II) in Section 3.3, although the best performance was obtained by the MCME for aligned OCTs with a precision of 96.64%, the WCME model presented the same precision on aligned and nonaligned data on average where its average precision was 94.59%. As expected, the test speed of the WCME model was lower than the MCME too.

By and large, spatial frequency decomposition in the WCME ensemble provided by the Daubechies WT caused the framework to have a high potential for fast and discriminative feature representation and diagnosis of macular diseases with minimum OCT image preprocessing requirements.

Conclusion

The goal of this paper was to explore different convolutional mixture ensemble methods for learning hierarchical features from retinal OCT images. Following this purpose, we considered three recent convolutional ensemble models called ME-CNN, MCME, and WCME networks. In addition, the ME-CNN model was evaluated on our database as the basic convolutional mixture ensemble model. To represent macular region at multiple scales, the MCME ensemble using the prior MSSP decomposition method tried to incorporate multiple CNNs with special fields of view same as the attention models. Although the MCME model yielded promising diagnostic performance on flattened and registered (aligned) retinal OCT images, its performance was improved intuitively on nonaligned data in WCME model using the 2D-Daubechies wavelet decomposition instead of the prior MSSP. Imposing the spatial-frequency information fusion was the key concept used in WCME model. To provide better performance insight into the proposed convolutional ensemble networks, we extensively analyzed and discussed the models. Comparative analysis showed that although the MCME model outperformed the other proposed models on aligned retinal OCT analysis, the WCME offers a promising performance and robust model on nonaligned retinal OCT data diagnosis. This allows having a CAD algorithm in macular OCTs which does not rely on the routine computerized processes such as denoizing, segmentation of retinal layers, and also retinal curvature correction (flattening). This is a significantly important feature when dealing with severe retina diseases where segmentation and alignment of pathological retinas are very challenging tasks.

Finally, we investigated ways to improve the performance of convolutional mixture ensemble models for macular diagnosis while showing indirectly the impact of prior unsupervised decomposition for the features learned at the subsequent layers of the models. We hope this study will enable future work on better modeling of the macular OCT abnormalities for developing useful clinical CAD systems.

Financial support and sponsorship

This work was supported in part by the Isfahan University of Medical Sciences, vice-chancellor of Research and Technology under Grant No. 395645.

Conflicts of interest

There are no conflicts of interest.

BIOGRAPHIES

Reza Rasti is a Postdoctoral Research Associate at Duke University Pratt School of Engineering. He received his B.Sc. degree in Electronics from Shahid Rajaee University, Tehran, Iran, and the M.Sc. and Ph.D. degrees in Biomedical Engineering from K. N. Toosi University of Technology, and Isfahan University of Medical Sciences, respectively. His current research interests include Deep Learning, Pattern Recognition, Medical Image/Signal Analysis, and Computer-Aided Diagnosis.

Email: reza.rasti@duke.edu

Hossein Rabbani received the B.Sc. degree in Electrical Engineering from Isfahan University of Technology, Isfahan, Iran, in 2000, and the M.Sc. and Ph.D. degrees in Bioelectrical Engineering from Amirkabir University of Technology, Tehran, Iran, in 2002 and 2008, respectively. He is now a Full Professor in Biomedical Engineering Department at Isfahan University of Medical Sciences, Isfahan. His research interests are medical image analysis and modeling, signal processing, sparse transforms, and image restoration

Email: h_rabbani@med.mui.ac.ir

Alireza Mehridehnavi received the B.Sc. degree in Electronic Engineering from Isfahan University of Technology in 1988. He had finished M.Sc. in Measurement and Instrumentation at IIT Roorkee in India in 1992, and his Ph.D. in Medical Engineering at Liverpool University in 1996. He is a Full Professor in Biomedical Engineering Department at Isfahan University of Medical Sciences, Isfahan. Iran. His research interests are Medical Optics, Devices and Signal and Image processing

Email: mehri@med.mui.ac.ir

Fedra Hajizadeh received the M.D. degree from Tehran University of Medical Sciences, Tehran, Iran, in 1995 and completed the Ophthalmology Residency and Vitreo-Retinal Fellowship both at Farabi Eye Hospital of Tehran University of Medical Sciences in 1999 and 2004, respectively. Since 2008, she has been a Consulting Surgeon of Vitreo-Retinal diseases and Research Scientist at Noor Eye Hospital, Tehran, Iran. Her current research includes retinal optical coherence tomography (OCT), ocular trauma, and retinal fluorescein angiography

Email: fedra_hajizadeh@yahoo.com