Abstract
Motivation
Validation of variable selection and predictive performance is crucial in construction of robust multivariate models that generalize well, minimize overfitting and facilitate interpretation of results. Inappropriate variable selection leads instead to selection bias, thereby increasing the risk of model overfitting and false positive discoveries. Although several algorithms exist to identify a minimal set of most informative variables (i.e. the minimal-optimal problem), few can select all variables related to the research question (i.e. the all-relevant problem). Robust algorithms combining identification of both minimal-optimal and all-relevant variables with proper cross-validation are urgently needed.
Results
We developed the MUVR algorithm to improve predictive performance and minimize overfitting and false positives in multivariate analysis. In the MUVR algorithm, minimal variable selection is achieved by performing recursive variable elimination in a repeated double cross-validation (rdCV) procedure. The algorithm supports partial least squares and random forest modelling, and simultaneously identifies minimal-optimal and all-relevant variable sets for regression, classification and multilevel analyses. Using three authentic omics datasets, MUVR yielded parsimonious models with minimal overfitting and improved model performance compared with state-of-the-art rdCV. Moreover, MUVR showed advantages over other variable selection algorithms, i.e. Boruta and VSURF, including simultaneous variable selection and validation scheme and wider applicability.
Availability and implementation
Algorithms, data, scripts and tutorial are open source and available as an R package (‘MUVR’) at https://gitlab.com/CarlBrunius/MUVR.git.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
State-of-the-art ‘omics’ technologies, such as genomics, proteomics and metabolomics, generate large and/or high-dimensional data (Meng et al., 2016; Patti et al., 2012) that can be used to identify biomarkers (Shi et al., 2018), characterize biochemical systems (Fondi and Liò, 2015; Li, 2013) and reveal insights into the mechanisms of pathophysiological processes (Smith et al., 2014; Tanaka and Ogishima, 2011). Supervised multivariate modelling, e.g. partial least squares analysis (PLS) and random forest (RF), is often used to cope with complex data and assess the importance of variables, thereby facilitating selection of relevant variables into biologically meaningful interpretations (Afanador, 2016; Yi et al., 2016). Although designed for multivariate analyses, these methods could benefit from a compact data structure with non-redundant predictors, by offering decreased computation time, improving the predictive performance and avoiding overfitting, as well as simplifying data interpretation (Fox et al., 2017; Mehmood et al., 2012). Variable selection is an important, albeit challenging, element which contributes to construction of parsimonious models, meaning simple models with great and robust explanatory predictive power (Saeys et al., 2007; Vandekerckhove et al., 2014).
Most variable selection techniques are designed to identify a minimal set of strongest predictors associated with a research question, i.e. the minimal-optimal problem (Nilsson et al., 2007). This strategy may be particularly useful to identify potential diagnostic, predictive or prognostic biomarkers of disease or exposures (Saeys et al., 2014). Only a limited number of algorithms have been tailored for identifying all variables of relevance to the analytical problem, i.e. the all-relevant problem, including weak and redundant attributes, but avoiding inclusion of noisy, uninformative variables (Nilsson et al., 2007; Rudnicki et al., 2015). This strategy is of particular interest to understand complicated biochemical systems and to uncover mechanisms of e.g. pathophysiological or metabolic processes. All-relevant algorithms are mostly designed based on ensembles of decision trees, e.g. Boruta (Kursa and Rudnicki, 2010) and VSURF (Genuer et al., 2015).
Existing variable selection techniques are mainly dedicated to regression and/or classification tasks applied to independent data structures (e.g. Hapfelmeier and Ulm, 2013; Mehmood et al., 2012; Saeys et al., 2014). However, in many situations, e.g. in clinical and nutritional cross-over or time-series studies, multilevel data analysis could deal with dependent data structures (Velzen et al., 2008; Westerhuis et al., 2010) and helps to better dissect the treatment effects within subject separately from the biological variation between subjects. To date, multilevel data analysis has been limited to PLS modelling and, to the best of our knowledge, has not been performed using RF. In addition, no previous study has investigated how implementation of variable selection affects multilevel modelling performance.
It is also noteworthy that many existing variable selection techniques may suffer from selection bias, consequently inducing underestimation of error rates and leading to general model overfitting (Krawczuk and Łukaszuk, 2016). Such selection bias occurs when variable selection is carried out based on some or all of the samples used to estimate the prediction error in cross-validation scheme, which is frequently applied to optimize model parameters and to evaluate model performance (e.g. Ambroise and McLachlan, 2002; Baumann and Baumann, 2014; Christin et al., 2013; Filzmoser et al., 2009). Although a few variable selection-within-validation schemes have been proposed to reduce selection bias (Boulesteix, 2007; Correa and Goodacre, 2011; Gregorutti et al., 2015), the number of freely available, easy-to-use algorithms is limited. Moreover, no algorithm has implemented variable selection within repeated double cross validation (rdCV), a procedure that was shown to give more reliable estimations of prediction errors than several other commonly used validation approaches, such as k-fold and leave-n-out (Filzmoser et al., 2009; Krstajic et al., 2014).
We therefore introduce an algorithm for multivariate modelling with minimally biased variable selection in R (MUVR), an easy to use variable selection-within-rdCV framework for multivariate modelling. MUVR is particularly useful for underdetermined data, i.e. where the number of variables outweigh the number of observations. It allows for both PLS and RF core modelling and supports regression and classification, as well as multilevel modelling to manage data with dependent structures. The aims of the present study were: i) to describe the working principle of MUVR; ii) to compare MUVR with rdCV without variable selection in terms of model performance and degree of model overfitting; and iii) to compare MUVR with Boruta and VSURF.
2 Materials and methods
2.1 Datasets
Freelive. Detailed information on study design and metabolomics data acquisition is provided elsewhere (Hanhineva et al., 2015). In brief, free-living participants with no diagnosed or perceived gastrointestinal diseases or symptoms were invited to participate and instructed to adhere to their habitual diet. Untargeted LC-qTOF-MS metabolomics was performed on urine samples. The dataset consisted of reported wholegrain rye consumption (continuous Y variable) from 112 observations (58 unique participants; two individuals had samples from one occasion available), codes for individual (numerical ID variable) and 1, 147 features as X matrix (a molecular entity with a unique m/z and retention time as measured by an LC-MS instrument).
Mosquito. This dataset is described in detail by Buck et al. (2016). Anopheles gambiae mosquitoes were collected from three villages in western Burkina Faso and whole-body bacterial flora was analyzed by 16S amplicon sequencing. In total, 29 observations were available for village of capture (categorical Y variable; three levels) and 1678 16S operational taxonomic units (OTU, X matrix). For each sample, the number of reads per OTU was rarefied to the lowest number of reads per sample. However, owing to the non-continuous nature of 16S data, leading to a high degree of data scarcity, 940 OTUs showed near-zero variance. PLS was therefore performed on a subset with 738 OTUs only.
Crisp. The study design is described elsewhere (Zamaratskaia et al., 2017). In brief, rye and wheat crispbreads were consumed as part of isocaloric breakfast interventions in a cross-over design. Untargeted UHPLC-qTOF-MS metabolomics was performed on plasma samples from 20 randomly selected individuals and six time points. Feature signals were numerically integrated using the trapezoidal rule to obtain area-under-the-curve values (AUCs) for all features. This dataset contained 20 subjects (Y, sample ID) and AUCs of 1587 features as X matrix.
2.2 Algorithm description
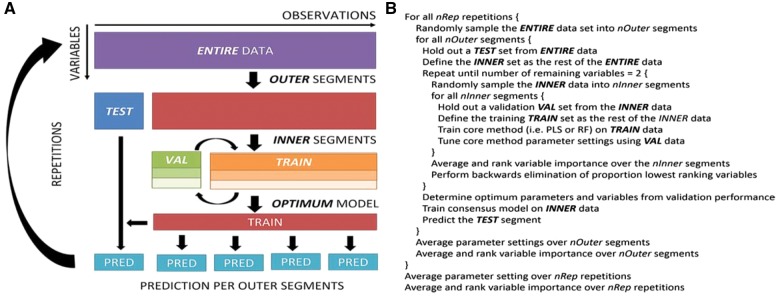
The MUVR algorithm is based on nesting a recursive variable ranking and backward elimination at an intermediate level between the outer and inner cross-validation loops of an rdCV procedure (Fig. 1).
Fig. 1.
Working principle of MUVR. (A) Graphical representation of the MUVR algorithm. The original data are randomly subdivided into OUTER segments. For each outer segment, the remaining (INNER) data are used for training and tuning of model parameters, including recursive ranking and backward elimination of variables. Each outer segment is then predicted using an optimized consensus model trained on all inner observations, ensuring that the holdout test set is never used for training or tuning modelling parameters. The procedure is then repeated for improved modelling performance. (B) Pseudocode of the MUVR algorithm
2.2.1 Sample independence within MUVR
To reduce risk of model overfitting and false positive discoveries in the validation scheme, it is crucial to ensure sample independence between testing, validation and training data segments (Varoquaux et al., 2017), particularly for studies with repeated measures or a cross-over design. For instance, it is often seen in clinical studies that multiple measurements are taken per participant. These measurements are then dependent and should therefore be co-sampled during segmentation. To meet this demand, the MUVR algorithm allows a subject identifier (‘ID’) as input parameter. If not specified, observations are considered independent, which is the default and usually the only available option in commercial and conventional software and packages.
2.2.2 Variable selection procedure
Variable ranking and selection are performed in the inner validation loop and final model performance is then assessed using observations in the test segment that is never used for model training or tuning.
In each of the inner training models, variables are ranked by de facto standard techniques, i.e. variable importance of projection (VIP) for PLS analysis (Mehmood et al., 2011) and mean decrease in Gini index (classification) or mean decrease in accuracy (regression) for RF analysis (Strobl et al., 2007). For each iteration of the variable tuning, variable ranks are averaged between the inner models. After averaging, a user-specified proportion (varRatio) of the variables is maintained from the data matrix before the next iteration, where inner segments are again randomly sampled to decrease bias to individual segments. Model performance is then estimated from predictions of the untouched test segments, using the number of selected variables (and optimal number of components for PLS modelling) determined by consensus from all inner observations. Arbitration of model performance in variable tuning within the inner validation loop is performed using different fitness functions specifically adapted to the problem type: Root mean square error of prediction (RMSEP) for regression and number of misclassifications (MISS) for multilevel or general classification analysis (two or more classes). The area under the receiver operation characteristics curve (AUROC) and balanced error rate (BER) are supported as optional fitness metrics for classification.
For each inner segment, three different consensus models (i.e. ‘min’, ‘mid’ and ‘max’) with similar model fitness are returned. The ‘min’ and ‘max’ models correspond to the minimal-optimal and all-relevant predictors, respectively, while ‘mid’ corresponds to the geometric mean of the max and min number of variables. The number of variables for ‘min’ and ‘max’ model is determined based on averaged validation performance per repetition and overall. Using misclassifications as a fitness metric, all three models share the same optimum fitness response during validation. However, to obtain robust results while taking into account the higher resolution and random variability in RMSEP and AUROC metrics, the criterion for finding ‘min’ and ‘max’ models includes a permitted 5% deviation from optimum fitness. The ‘min’, ‘mid’ and ‘max’ models thus share the same (or similar) prediction performance within permitted deviation during validation. These models are created nRep (number of repetitions) × nOuter (number of outer test segments) times for prediction of test segment observations, ensuring that test segment observations are never used for model training or tuning. For final estimation of fitness and model predictive ability, Q2 is used for regression analysis, facilitating interpretation of modelling fitness, regardless of the scale of the original dependent variable (upper bounded by 1 for perfect prediction). This is in contrast to the inner validation loop, where RMSEP estimates fitness in the original response scale and is thus suitable for averaging. The number of misclassifications is used for classification and multilevel analysis.
2.2.3 Key parameters of MUVR
Key parameters of MUVR include nRep, nOuter, nInner (number of inner validation segments) and the ratio of variables maintained in the data per iteration during variable elimination (varRatio). All these parameters can easily be tuned by users. Filzmoser et al. (2009) suggested nRep = 100, nOuter = 7, nInner = 4 for rdCV. Since the MUVR algorithm is more computationally demanding than rdCV, due to the nested recursive variable elimination, an increasing number of segments will increase computation time and thus compromises are necessary. As a general principle in classification analysis, it is advisable to ensure that each class is represented in each segment at least once, effectively resulting in an upper bound of the number of segments. We thus suggest 6≤nOuter≤8 and nInner=nOuter-1 for MUVR, which tends to result in robust modelling. However, it is likely that parameter settings are dependent on context and the nature of the data, and more research is needed to extend parameter recommendations to full generalizability.
Since the MUVR framework is built upon repeated random segmentation of observations in combination with recursive elimination of the least informative variables, key parameters of MUVR such as nRep and varRatio may introduce variability into modelling and thus potentially influence final modelling outputs, such as number and order of selected variables and goodness-of-fit (Filzmoser et al., 2009). We therefore investigated the effects of nRep and varRatio on modelling performance using 0.50≤varRatio ≤ 0.95 and up to 100 repetitions.
In addition, the user can easily select the core multivariate modelling technique [‘PLS’ or ‘RF’ (default)] and fitness function for model tuning. When the multilevel function (parameter ‘ML=TRUE’) is used, core modelling applies on the within-subject variation matrix (Velzen et al., 2008).
2.2.4 Evaluation of stability of variable selection using MUVR
A permutation-by-class approach was designed to examine the stability of variable selection, not only in terms of separating informative variables from noisy data, but also for successfully distinguishing optimal from informative but redundant variables. We investigated stability of selection for variables in the minimal-optimal (‘min’) and all-relevant (‘max’) sets using MUVR-PLS modelling of the ‘Mosquito’ data (classification). Variables of the original model were classified as ‘optimal’ if belonging to the ‘min’ model, ‘redundant’ if belonging to the ‘max’ but not the ‘min’ model and ‘noisy’ otherwise. Four new analyses were then performed to investigate the effect of permuting distinct variable classes on variable classifications. These were: i) permuted optimal variables substituted for the original optimal variables; ii) permuted redundant variables substituted for the original redundant variables; iii) permuted noisy variables substituted for the original noisy variables; and iv) permuted optimal variables added to all the original data. The variables from the four new models were then reclassified into optimal, redundant and noisy and cross-tabularized against their original classes.
2.3 Other variable selection methods
Boruta and VSURF were compared with MUVR. Boruta is an all-relevant wrapper variable selection that determines variable relevance by comparing the relevance of the real variables with that of random probes. Variable selection using VSURF performs a stepwise forward selection of variables for interpretation (VSURF-I) or prediction (VSURF-P). Boruta and VSURF were applied using default parameter settings. The final choices of variables selected by Boruta and VSURF for optimum model performance were assessed by rdCV, i.e. Boruta-rdCV and VSURF-rdCV.
2.4 Assessment of model performance and overfitting
Each of the investigated variable selection methods was applied on the three authentic datasets designed to i) identify urinary biomarkers of wholegrain rye intake using regression analysis (‘Freelive’ data); ii) classify mosquitoes into village of capture according to their microbiome makeup using classification analysis (‘Mosquito’ data); and iii) discover intra-individual differences in the metabolome between consumption of whole-grain rye crispbread and refined wheat bread in a cross-over intervention using multilevel analysis (‘Crisp’ dataset). Multilevel analysis was performed on an effect matrix calculated as EM = XRye – XWheat, where X denotes the AUC of plasma metabolites measured for each intervention (Velzen et al., 2008; Westerhuis et al., 2010). This Crisp EM was then provided as the X argument in MUVR. In the present work, the ‘Mosquito’ OTU counts were log-transformed, mean centred and autoscaled per sample, using the ‘preProcess()’ function implemented in MUVR, while ‘Freelive’ and ‘Crisp’ metabolomics data were autoscaled internally to the training data in each PLS submodel. The ‘preProcess’ function allows for various data pre-processing options, e.g. transformation, scaling and centreing (see tutorial at https://gitlab.com/CarlBrunius/MUVR.git).
MUVR, Boruta-rdCV, VSURF-rdCV and rdCV were each applied on the three omics datasets. To simplify interpretation, results from the ‘mid’ model of MUVR, representing a compromise between minimal-optimal and all-relevant variable selections, were used for between-model comparisons. For fitness estimation, Q2 was used for regression analysis, whereas number of misclassifications was used for classification and multilevel analysis. Permutation tests were used for assessing modelling performance (Lindgren et al., 1996). Permutations were obtained by repeated random sampling of the original Y variable and thereafter modelling original X matrix on permuted Y responses, thus obtaining a population of fitness metrics corresponding to a null hypothesis distribution. It was then assumed that the population of fitness metrics from random permutations had a Gaussian t-distribution and permutation P-values were calculated as the cumulative 1-tailed probability of achieving the actual model fitness in the t-distribution. In cases where the assumption of Gaussianity was refuted by e.g. visual inspection of the null hypothesis distribution and/or frequentist tests such as Shapiro-Wilk test and Anderson-Darling test, fitness metrics of actual model and null hypothesis distribution were rank-transformed prior to calculations, thus resulting in non-parametric P-values. The MUVR package provides functions for permutation analyses, including plotPerm (plots to inspect assumption of Gaussianity) and pPerm (to calculate P-values).
2.5 Software and hardware
The MUVR algorithm is available in the R package ‘MUVR’, which is freely available together with data, scripts and tutorial at https://gitlab.com/CarlBrunius/MUVR.git. The algorithm currently supports PLS and RF core methods as implemented in the ‘mixOmics’ and ‘randomForest’ R packages. All model calculations except permutation analyses were performed on a HP Elitebook with an Intel i7-3687U processor. Permutation analyses were performed using resources provided by the Uppsala Multidisciplinary Centre for Advanced Computational Science (https://www.uppmax.uu.se/). A function for rdCV is available at https://gitlab.com/CarlBrunius/rdCV.git, of which key parameters and variable ranking approaches are the same as in MUVR, but without ‘varRatio’.
3 Results and discussion
The MUVR algorithm is a novel and easy-to-use statistical validation framework, incorporating a recursive variable selection procedure within an rdCV scheme, to cope with datasets where the number of variables outweighs the number of observations. MUVR allows for PLS and RF core modelling, effectively selects both minimal-optimal variable sets and all-relevant variables for regression, classification and multilevel analyses, and yields parsimonious models with minimal variable selection bias and model overfitting.
3.1 MUVR identified all-relevant and minimal-optimal predictors
Variables are first ranked in the inner training model by de facto standard ranking techniques for both PLS and RF. By averaging variable ranks over the inner segments before variable reduction in each recursive backwards elimination step, potential overfitting that may occur during model training and variable ranking is minimized. This recursive variable elimination is reflected in the validation curve (Fig. 2). Regardless of the problem type (i.e. regression, classification and multilevel) and core modelling applied (i.e. PLS and RF), variable reduction from the entire data to the ‘max’ model effectively resulted in removal of noise until optimal validation performance, as measured by the fitness function, was obtained. In PLS modelling, the proportion of noisy variables removed represented more than 90% of variables in the original dataset. For RF modelling, these proportions were even higher (Fig. 2, Supplementary Table S1). Further variable reduction from the ‘max’ (all-relevant) model down to the ‘min’ model (removal of ‘redundant’ variables), maintaining validation performance, indicates dismissal of informative but redundant variables. This could correspond to a maximum of biologically relevant information carried by the optimal variables that can therefore be considered to provide maximum information density. The ‘min’ model of the datasets investigated represented a further reduction of about 60–95% of the variables from the ‘max’ model (Fig. 2, Supplementary Table S1). Further variable reduction increased model prediction errors, probably due to elimination of genuinely relevant, non-redundant information. It should be noted that although validation curves per segment may fluctuate, validation curves per repetition and overall are based on averaging segmentation curves for higher resolution to better describe the actual validation performance.
Fig. 2.
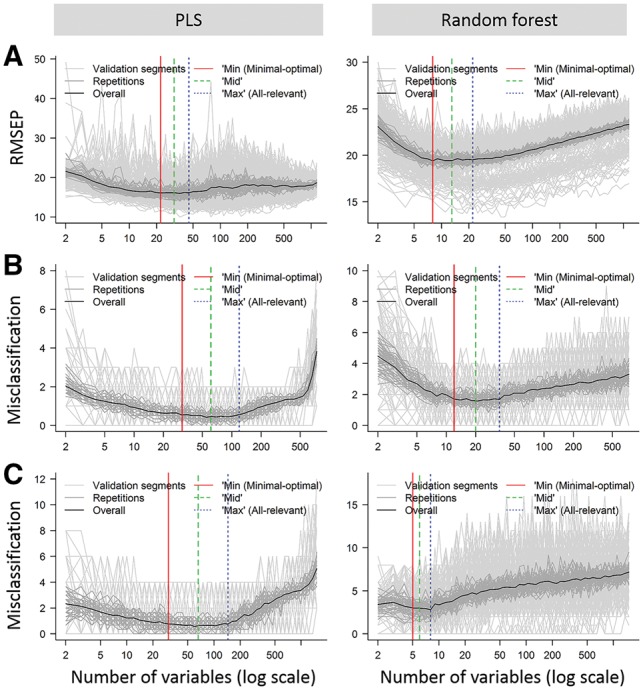
MUVR validation plots for identification of the all-relevant (‘max’ model) and minimal-optimal (‘min’ model) variables on three datasets: (A) ‘Freelive’, regression; (B) ‘Mosquito’, classification; (C) ‘Crisp’, multilevel. Results are presented for PLS (left) and random forest (right). Validation plots can be generated using the MUVR ‘plotVAL’ function
MUVR also provides a ‘mid’ model solution, which represents a compromise between the minimal-optimal and all-relevant solutions. On a theoretical curve representing the true modelling performance during recursive variable removal (Fig. 2), the ‘min’ and ‘max’ models represent limits outside which the prediction accuracy rapidly decreases. From a practical perspective, the ‘mid’ model consists of strong predictors but with some redundancy, and may be useful e.g. in situations where alternatives to the strongest individual predictors may be desired. This may occur e.g. when identifying biomarkers of exposure, if the strongest individual predictors (from the ‘min’ model’) are known to be perturbed by several different factors and are thus not specific to the research question. It is noteworthy that the variable ranking technique is not used primarily to identify the single most predictive variables, but rather as a tool to identify variables that contribute least to modelling performance and should therefore be removed prior to the next iteration. Consequently, the final choice of variables is based on the validation performance of the constructed models, rather than ranking techniques. Moreover, variable selection is not at all performed on a per-variable basis and should thus be considered a truly multivariate variable selection technique. It could therefore be argued that the effects of the choice of variable ranking technique are diluted in the selection procedure, but this remains to be investigated in detail.
In addition, the ‘max’ model offers an all-relevant solution corresponding to a maximum of biologically relevant information. It should, however, be noted that ‘optimal’ and ‘redundant’ in this sense refer to the data analysis and that instrumental or other artifacts may introduce discrepancies between data analysis and underlying biology. The redundant variable set does not imply less important from a biological point of view. But rather, that the information contained in the variable was already present in the model in the ‘optimal’ set, thereby failing to provide additional information in model prediction (Supplementary Figs S1 and S2).
Importantly, MUVR identified biologically relevant signals from the analytically optimal variables (Buck et al., 2016; Hanhineva et al., 2015; Shi et al., 2017, 2018). Specifically, metabolites selected from the ‘Freelive’ data were found to be putative dietary biomarkers of rye consisting of e.g. phenolic acids that are mainly bound to arabinoxylans in the bran, phenolic lipids (e.g. alkylrecorcinols) found in the outer cuticle of testa/inner curricula of pericarp, phenylacetamides previously suggested as potential biomarkers of rye‐rich diet, as well as novel carnitine structures reflecting the metabolic impact of rye consumption (Supplementary Table S2) (Hanhineva et al., 2015). The top OTUs selected from the mosquito data contributed to 90% successful classification (Supplementary Table S1), reflecting different life stages of the An. Gambiae mosquito: Wolbachia was maternally inherited via the egg and thus reflected the locality of females (mothers) from the previous generation; Shewanella and Massilia sequences were likely obtained in breeding sites during the larval stage, whereas the Acinetobacter sequences suggest that the nectar sources for the adults differ (Buck et al., 2016). Moreover, using the ‘Crisp’ data, 66 out of 1584 metabolomics features successfully discriminated rye intake from wheat crispbreads intake (MUVR-PLS, ‘min’ model) in a study material which had already shown differences in appetite, plasma glucose and insulin concentrations after consumption of rye crispbread versus wheat crispbread (Zamaratskaia et al., 2017). Further studies are needed to identify these discriminative metabolites to gain mechanistic insights into appetite and glucose regulation. In addition, MUVR was applied to identify predictive biomarkers of type 2 diabetes in a large-scale nested case–control study, providing biologically meaningful results and interpretation (Shi et al., 2018). These findings confirm that MUVR has extracted biologically meaningful information from massive OMICs data and addressed specific biological problems in various studies.
3.2 Stability of variable selection using MUVR
Regardless of varRatio setting, modelling outcomes showed variability between repetitions (Supplementary Fig. S3). After 10–20 repetitions, fluctuations in output parameters were attenuated and stability was seemingly obtained after 50–100 repetitions, as shown for the ‘min’ PLS model of the classification problem. The stability included fitness (number of misclassifications), number of selected variables and the actual variables selected. The number of misclassifications was not noticeably affected by the varRatio setting. Interestingly, there was a negative correlation between varRatio and the number of selected variables in the ‘min’ model even after 50 repetitions, where stability of outcomes was assumed, although the variables selected at the higher varRatio setting were always present at lower varRatio settings (‘Proportion of selected variables’ in Supplementary Fig. S3). These results indicate that a higher varRatio may result in a higher degree of parsimony for the minimal-optimal solution. By removing smaller proportions of variables per iteration, the variable ranking is limited to identifying only the poorest predictors. Then, by using model fitness for arbitration, the effects of the method for ranking are diluted. The same general trend of increased parsimony with higher varRatio was observed for all data types and for both PLS and RF core modelling (data not shown). In addition, with increasing varRatio, smaller proportions of poorer predictors would be removed per iteration and the computation time would thus increase. Therefore, our general recommendation is therefore to use nRep ≈ 15 and 0.5≤varRatio ≤ 0.75 for initial analysis and, if showing results of relevance to the analytical problem (i.e. high Q2 or low number of misclassifications), later increase nRep ≥ 50 for reproducible results and varRatio ≈ 0.9 for a higher degree of parsimony for the minimal-optimal solution.
To further examine the stability of variable selections, variables from the MUVR-PLS classification problem were permuted by class (i.e. optimal, redundant or noisy) (Fig. 3). Replacing optimal variables with permuted variables was expected to promote the strongest predictors from the redundant to the optimal category: With the removal of the 31 strongest predictors (i.e. the optimal variables) from the data, 36 out of 52 redundant variables were expectedly promoted to the optimal category (Fig. 3). In contrast, permuting redundant or noisy variables resulted in only limited migration of variables between categories in most cases, indicating the robustness of MUVR in variable selection. Migration of variables between categories occurred primarily between the redundant and noisy categories, most likely reflecting borderline status of some variables, which may contain relevant information, but have low signal-to-noise ratio. As expected, adding permuted optimal variables (n = 31) did not influence the original classification of variables. Moreover, 26 out of 31 permuted variables were classified as noisy, while 5 were classified as redundant. This might be attributed exclusively to random permutations causing systematic patterns due to the small sample size (n = 29; Supplementary Fig. S4). Substitution of permuted variable categories for the original variables showed similar effects as above on the distribution of permuted variables between classes, i.e. with a minor amount of additional optimal and redundant permuted variables due to random effects from resampling. Our results highlight the potential impact of false positive findings in small datasets and indicate that even the most careful cross-validation scheme may not be able to fully safeguard against overfitting in under-determined systems with a low number of samples (Rao and Fung, 2006; Varoquaux, 2017).
Fig. 3.
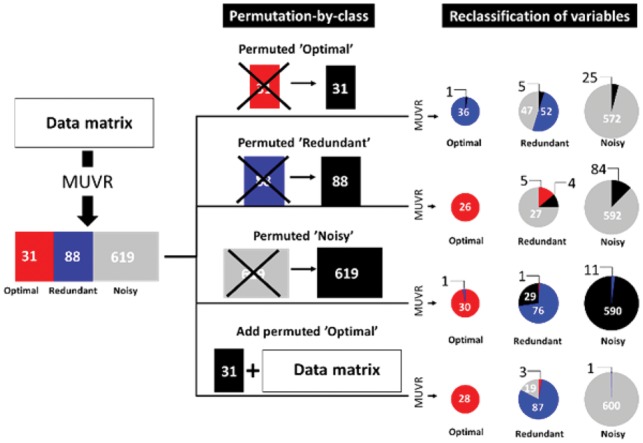
Flowchart of the permutation-by-class approach and the reclassification of variables from the MUVR-PLS classification on ‘Mosquito’ data using permutations-by-class approach. The ‘Optimal’ variable set is selected in the MUVR ‘min’ model. The ‘Redundant’ variable set belongs to the all-relevant variable set selected in the MUVR ‘max’ model, but not belonging to the minimal-optimal variable set. The ‘Noisy’ variable set contains presumably uninformative variables that are not selected in the MUVR ‘max’ model. The permuted variable refers to the distinct variable class after permutation. Details are given in 2.2.4 Evaluation of stability of variable selection using MUVR
3.3 MUVR improved model performance without increasing overfitting
Selection bias has been reported when a given dataset is used for both variable selection and assessment of model performance, in turn leading to biased estimates and an increasing risk of false-positive discoveries due to overfitting (Ambroise and McLachlan, 2002; Castaldi et al., 2011; Cawley and Talbot, 2010; Krawczuk and Łukaszuk, 2016). Benefitting from the rdCV scheme, MUVR minimizes selection bias by performing variable selection and tuning of model parameters in the inner segments, followed by assessment of modelling performance using outer loop data held out of model construction and variable reduction. The risk of overfitting to individual validation segments is thus effectively minimized by averaging variable ranks among inner models.
Despite this, all observations from the inner data are used to fit the consensus model per outer segment, which may theoretically induce selection bias and model overfitting during variable selection. However, such overfitting was not observed (Fig. 4). In contrast, MUVR compared with rdCV markedly improved model performance (higher Q2 for regression or lower number of misclassifications for classification and multilevel analyses), without increasing the risk of general model overfitting, as demonstrated by increased distance between actual model fitness and random permutation (Fig. 4). This was further confirmed by an additional analysis: MUVR was performed on a training-set (n = 40 samples) randomly selected from the ‘Freelive’ data, and was validated on the rest of samples (n = 18). No difference in Q2 was observed between models constructed using all samples (n = 58, Q2=0.61) or the subset of samples (Q2=0.60), supporting the robustness of MUVR (Supplementary Table S3). Taken together, our findings confirmed that MUVR resulted in minimal selection bias, in practice leading to potentially unbiased variable selection, as indicated by the lack of overfitting examined from the extensive series of permutation tests.
Fig. 4.
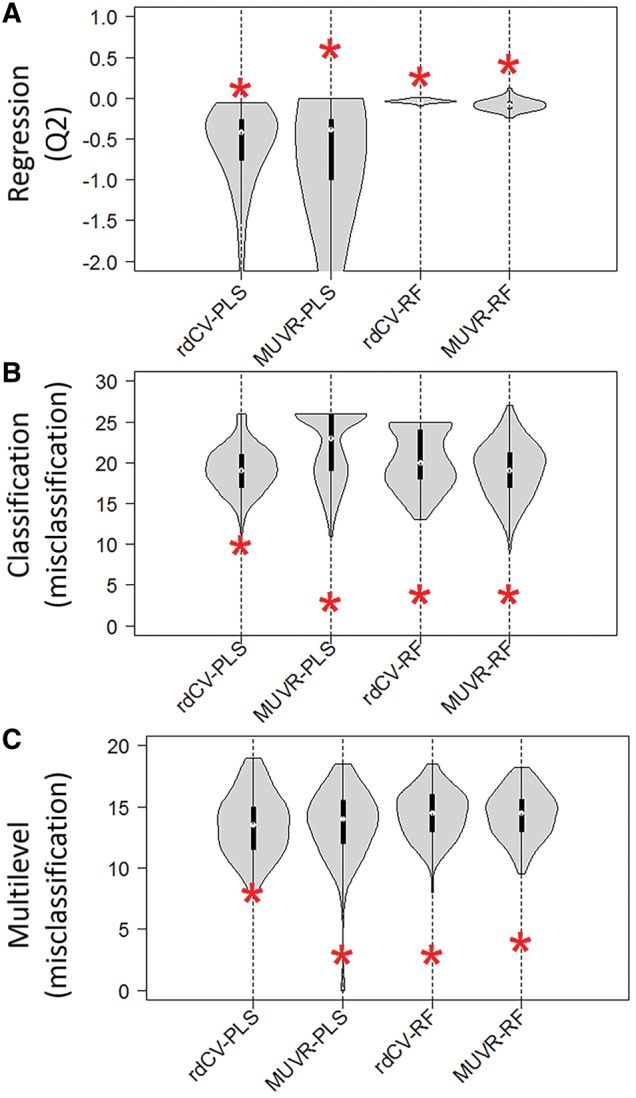
Performance of MUVR or repeated double cross-validation models (rdCV) built from actual data and random permutations for three datasets: (A) ‘Freelive’, regression; (B) ‘Mosquito’, classification; (C) ‘Crisp’, multi-level. The performance distributions of random permutations are represented as violin plots, with the asterisks representing actual model performance (Q2 for regression, number of misclassifications for classification and multilevel analysis)
Notably, modelling performance was not improved for MUVR-RF classification and multilevel, which gave similar (or slightly worse) results than those obtained using rdCV-RF, but with a dramatic reduction in the variable space (see ‘MUVR-PLS versus MUVR-RF’ section for details).
3.4 MUVR-PLS versus MUVR-RF
MUVR currently supports PLS and RF as core modelling techniques, which have been extensively applied in omics and in biostatistics (Gorrochategui et al., 2016; Gromski et al., 2015). The strengths and weakness of PLS and RF are well summarized elsewhere (see e.g. Gromski et al., 2015). It should be noted that RF is scale-invariant and is also insensitive to monotonous variable transformations, such as log- or square root transformation. In contrast, PLS is sensitive to data pre-processing. At present, we autoscaled data internally to the training data in each PLS sub-model (the default in MUVR PLS core modelling), thereby potentially decreasing risk of overfitting. MUVR also allows the user to perform any other scaling procedures priori to modelling (i.e. by manually scaling according to user preference and then setting internal scaling to ‘FALSE’.).
Although PLS may have benefits over RF for visualization and interpretation of results, the RF core modelling yielded more robust and parsimonious models without compromising model performance for all three datasets tested in the present work, corresponding to the three problem types most frequently encountered in biostatistical analysis, i.e. regression, classification and multilevel analysis (Fig. 4, Supplementary Fig. S5; Supplementary Table S1). For the data investigated, the number of variables selected by MUVR-RF was smaller than for MUVR-PLS, but with considerable overlap between the variable sets (Supplementary Fig. S6). Strong correlations between the variable sets selected by PLS and RF were also observed (Supplementary Figs S7–S9).
Even though MUVR-PLS showed higher Q2 for the regression task than MUVR-RF, a much larger discrepancy between R2 and Q2 was obtained, indicative of a higher degree of general overfitting (Supplementary Table S1, Supplementary Fig. S5). Our findings indicate that the developed variable selection procedure effectively minimizes model overfitting, but cannot fully optimize variable selection if the core modelling technique applied is prone to overfitting and up-weighing a large number of redundant variables with a high degree of inter-correlations, as is the case with component-based methods like PLS (Gromski et al., 2014, 2015). RF does not assume latent variables or linear dependencies of variables with the response. Instead, it gives priority to information complementarity between variables, which may explain the increased parsimony compared with PLS. Moreover, to the best of our knowledge, multilevel data analysis combined with RF modelling has not been performed previously. Compared with multilevel MUVR-PLS, MUVR-RF did not improve actual classification results. However, the distance between actual model fitness and random permutations was increased, thus indicating decreased general overfitting and increased confidence in observed findings (Fig. 4).
In addition, RF makes no assumptions about underlying Gaussian variable distributions and thus effectively manages discontinuous and near-zero variance variables frequently present in e.g. microbiota data (such as the ‘Mosquito’ data). However, the RF algorithm was computationally more intensive, which becomes especially noticeable in complex validation schemes (Supplementary Table S1). The computational efficiency is of course highly dependent not only on core methodology, but also on implementation (Wright and Ziegler, 2015) and future generations of the MUVR algorithm may thus improve on computational efficiency. It is worth mentioning that we base our comparison between PLS and RF on limited data and our results and interpretations can therefore not be extended to the general case before extensive validation on multiple other datasets.
3.5 MUVR versus Boruta and VSURF
Boruta and VSURF resulted in selection of much fewer variables compared with MUVR (Supplementary Table S4), regardless of dataset. Considerable overlap between variables selected by MUVR-RF and those chosen by Boruta and VSURF was observed for regression and classification analyses (Supplementary Fig. S10). It is likely that Boruta and VSURF could successfully identify informative variables, but these methods may be over-stringent, potentially increasing the risk of false-negative findings. This was also supported by the fact that both Boruta and VSURF were unable to select any variables at all in over 80% of permutations in classification (data not shown) and Boruta failed to identify any variables in multilevel data structure. For the regression task, permutation analysis strongly suggests increased overfitting using Boruta compared with MUVR, since the distance between actual model performance and the random permutation distribution was markedly reduced (Supplementary Fig. S11). Moreover, the VSURF algorithm was extremely computationally intensive for high-dimensional datasets in regression tasks, so permutation analysis could not be undertaken and investigation into model overfitting was consequently not possible. The applicability of these algorithms in omics research might be limited.
It is also worth noting that Boruta and VSURF enable variable selection, but some form of cross-validation is still required to avoid selection bias and to assess prediction performance. In this respect, MUVR is more easy to use and efficient, allowing for simultaneous variable selection and validation with minimized selection bias. It should be mentioned that we applied Boruta and VSURF with default parameters on limited datasets and tuning of key parameters of algorithms, e.g. number of decision trees and measures of variable importance may affect variable selection performance. A more thorough comparison between different types of optimized methods for variable selection is highly warranted, but was beyond the scope of the present work.
4 Concluding remarks
We developed the MUVR algorithm, a novel cross-validation framework incorporated with variable selection. MUVR provides effective, stable and minimally biased selection of biologically meaningful variables in multivariate modelling. MUVR currently supports PLS and RF core modelling techniques and allows for regression, classification and multilevel modelling, which are the most frequent data analysis tasks from different study designs. Using authentic omics datasets, we showed that the MUVR algorithm provides advantages over state-of-the-art rdCV in terms of prediction accuracy, general overfitting and selection of informative variables. Although applicable to several types of data, MUVR is especially useful for data where the number of variables outweighs the number of samples, as often obtained in ‘omics’ studies.
Declaration
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards and were approved by the Regional Ethics Review Board in Uppsala. Informed consent was obtained from all individual participants included in the human studies from where samples taken to this study are originating.
Funding
This work was financially supported by Swedish University of Agricultural Sciences (SLU) through a young investigators’ quality grant held by RL. RL’s salary was provided by SLU, Chalmers University of Technology (since 2016), a Vetenskapsrådet medicine grant and a Swedish Research Council Formas grant. LS obtained a stipend from the China Scholarship Council (file no. 201306300047).
Conflict of Interest: none declared.
Supplementary Material
References
- Afanador N.L. (2016) Unsupervised random forest: a tutorial with case studies. J. Chemom., 30, 231–241. [Google Scholar]
- Ambroise C., McLachlan G.J. (2002) Selection bias in gene extraction on the basis of microarray gene-expression data. Proc. Natl. Acad. Sci. USA, 99, 6562–6566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baumann D., Baumann K. (2014) Reliable estimation of prediction errors for QSAR models under model uncertainty using double cross-validation. J. Cheminform., 6, 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boulesteix A.L. (2007) WilcoxCV: an R package for fast variable selection in cross-validation. Bioinformatics, 23, 1702–1704. [DOI] [PubMed] [Google Scholar]
- Buck M. et al. (2016) Bacterial associations reveal spatial population dynamics in Anopheles gambiae mosquitoes. Sci. Rep., 6, 22806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castaldi P.J. et al. (2011) An empirical assessment of validation practices for molecular classifiers. Brief. Bioinform., 12, 189–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cawley G.C., Talbot N.L.C. (2010) On over-fitting in model selection and subsequent selection bias in performance evaluation. J. Mach. Learn. Res., 11, 2079–2107. [Google Scholar]
- Christin C. et al. (2013) A critical assessment of feature selection methods for biomarker discovery in clinical proteomics. Mol. Cell. Proteomics, 12, 263–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Correa E., Goodacre R. (2011) A genetic algorithm-Bayesian network approach for the analysis of metabolomics and spectroscopic data: application to the rapid detection of Bacillus spores and identification of Bacillus species. BMC Bioinformatics, 12, 33–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filzmoser P. et al. (2009) Repeated double cross validation. J. Chemom., 23, 160–171. [Google Scholar]
- Fondi M., Liò P. (2015) Multi -omics and metabolic modelling pipelines: challenges and tools for systems microbiology. Microbiol. Res., 171, 52–64. [DOI] [PubMed] [Google Scholar]
- Fox E.W. et al. (2017) Assessing the accuracy and stability of variable selection methods for random forest modeling in ecology. Environ. Monit. Assess, 189, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genuer R. et al. (2015) VSURF: an R package for variable selection using random forests. R J. Journal., 7, 19–33.
- Gorrochategui E. et al. (2016) Data analysis strategies for targeted and untargeted LC-MS metabolomic studies: overview and workflow. TrAC Trends Anal. Chem., 82, 425–442. [Google Scholar]
- Gregorutti B. et al. (2015) Grouped variable importance with random forests and application to multiple functional data analysis. Comput. Stat. Data Anal., 90, 15–35. [Google Scholar]
- Gromski P.S. et al. (2014) A comparative investigation of modern feature selection and classification approaches for the analysis of mass spectrometry data. Anal. Chim. Acta, 829, 1–8. [DOI] [PubMed] [Google Scholar]
- Gromski P.S. et al. (2015) A tutorial review: metabolomics and partial least squares-discriminant analysis – a marriage of convenience or a shotgun wedding. Anal. Chim. Acta, 879, 10–23. [DOI] [PubMed] [Google Scholar]
- Hanhineva K. et al. (2015) Discovery of urinary biomarkers of whole grain rye intake in free-living subjects using nontargeted LC-MS metabolite profiling. Mol. Nutr. Food Res., 59, 2315–2325. [DOI] [PubMed] [Google Scholar]
- Hapfelmeier A., Ulm K. (2013) A new variable selection approach using Random Forests. Comput. Stat. Data Anal., 60, 50–69. [Google Scholar]
- Krawczuk J., Łukaszuk T. (2016) The feature selection bias problem in relation to high-dimensional gene data. Artif. Intell. Med., 66, 63–71. [DOI] [PubMed] [Google Scholar]
- Krstajic D. et al. (2014) Cross-validation pitfalls when selecting and assessing regression and classification models. J. Cheminform., 6, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kursa M.B., Rudnicki W.R. (2010) Feature selection with the Boruta Package. J. Stat. Softw., 36, 1–13. [Google Scholar]
- Li H. (2013) Systems genetics in ‘-omics’ era: current and future development. Theory Biosci., 132, 1–16. [DOI] [PubMed] [Google Scholar]
- Lindgren F. et al. (1996) Model validation by permutation tests. J. Chemom., 10, 521–532. [Google Scholar]
- Mehmood T. et al. (2011) A Partial Least Squares based algorithm for parsimonious variable selection. Algorithms Mol. Biol., 6, doi: 10.1186/1748-7188-6-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehmood T. et al. (2012) A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst., 118, 62–69. [Google Scholar]
- Meng C. et al. (2016) Dimension reduction techniques for the integrative analysis of multi-omics data. Brief Bioinform., 17, 628–641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson R. et al. (2007) Consistent feature selection for pattern recognition in polynomial time. J. Mach. Learn. Res., 8, 589–612. [Google Scholar]
- Patti G.J. et al. (2012) Metabolomics: the apogee of the omics trilogy. Nat. Rev. Mol. Cell Biol., 13, 263–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao R.B., Fung G, (2006) On the dangers of cross-validation an experimental evaluation. Solutions, 588, 596. [Google Scholar]
- Rudnicki W.R. et al. (2015) All Relevant Feature Selection Methods and Applications. In: Stańczyk,U. and Jain,L. (eds) Feature Selection for Data and Pattern Recognition. Studies in Computational Intelligence, Vol. 584. Springer, Berlin, Heidelberg. [Google Scholar]
- Saeys Y. et al. (2007) A review of feature selection techniques in bioinformatics. Bioinformatics, 23, 2507–2510. [DOI] [PubMed] [Google Scholar]
- Saeys Y. et al. (2014) Robustness of Random Forest-based gene selection methods. Bioinformatics, 23, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi L. et al. (2018) Plasma metabolites associated with type 2 diabetes in a Swedish population: a case–control study nested in a prospective cohort. Diabetologia, 61, 849–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi L. et al. (2017) Targeted metabolomics reveals differences in the extended postprandial plasma metabolome of healthy subjects after intake of whole-grain rye porridges versus refined wheat bread. Mol. Nutr. Food Res., 61, 1600924. [DOI] [PubMed] [Google Scholar]
- Smith R. et al. (2014) Proteomics, lipidomics, metabolomics: a mass spectrometry tutorial from a computer scientist’s point of view. BMC Bioinformatics, 15, S9.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strobl C. et al. (2007) Bias in random forest variable importance measures: illustrations, sources and a solution. BMC Bioinformatics, 8, 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka H., Ogishima S. (2011) Omics-based identification of pathophysiological processes. Methods Mol. Biol., 719, 499–509. [DOI] [PubMed] [Google Scholar]
- Vandekerckhove J. et al. (2014) Model Comparison and the Principle of Parsimony. In Oxford Handbook of Computational and Mathematical Psychology. UC Irvine. [Google Scholar]
- Varoquaux G. et al. (2017) Assessing and tuning brain decoders: cross-validation, caveats, and guidelines. Neuroimage, 145, 166–179. [DOI] [PubMed] [Google Scholar]
- Varoquaux G. (2017) Cross-validation failure: small sample sizes lead to large error bars. arXiv:1706.07581. Preprint submitted to NeuroImage. [DOI] [PubMed] [Google Scholar]
- Van Velzen E.J.J. et al. (2008) Multilevel Data Analysis of a Crossover Designed Human Nutritional Intervention Study research articles. J. Proteome Res., 7, 4483–4491. [DOI] [PubMed] [Google Scholar]
- Westerhuis J. a. et al. (2010) Multivariate paired data analysis: multilevel PLSDA versus OPLSDA. Metabolomics, 6, 119–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright M.N., Ziegler A. (2015) ranger: a fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw., 77, 1–17. [Google Scholar]
- Yi L. et al. (2016) Chemometric methods in data processing of mass spectrometry-based metabolomics: a review. Anal. Chim. Acta, 914, 17–34. [DOI] [PubMed] [Google Scholar]
- Zamaratskaia G. et al. (2017) Impact of sourdough fermentation on appetite and postprandial metabolic responses – a randomised cross-over trial with whole grain rye crispbread. Br. J. Nutr., 118, 686–697. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.