Penalized co-inertia analysis with applications to -omics data

Abstract

Motivation

Co-inertia analysis (CIA) is a multivariate statistical analysis method that can assess relationships and trends in two sets of data. Recently CIA has been used for an integrative analysis of multiple high-dimensional omics data. However, for classical CIA, all elements in the loading vectors are nonzero, presenting a challenge for the interpretation when analyzing omics data. For other multivariate statistical methods such as canonical correlation analysis (CCA), penalized least squares (PLS), various approaches have been proposed to produce sparse loading vectors via l₁-penalization/constraint. We propose a novel CIA method that uses l₁-penalization to induce sparsity in estimators of loading vectors. Our method simultaneously conducts model fitting and variable selection. Also, we propose another CIA method that incorporates structure/network information such as those from functional genomics, besides using sparsity penalty so that one can get biologically meaningful and interpretable results.

Results

Extensive simulations demonstrate that our proposed penalized CIA methods achieve the best or close to the best performance compared to the existing CIA method in terms of feature selection and recovery of true loading vectors. Also, we apply our methods to the integrative analysis of gene expression data and protein abundance data from the NCI-60 cancer cell lines. Our analysis of the NCI-60 cancer cell line data reveals meaningful variables for cancer diseases and biologically meaningful results that are consistent with previous studies.

Availability and implementation

Our algorithms are implemented as an R package which is freely available at: https://www.med.upenn.edu/long-lab/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Recently, there has been rapid progress in high-throughput technologies to generate various -omics datasets (e.g. gene expression data and metabolomics data) from same biological subjects or samples. As a result, there has been increasing interest in an integrative analysis of multiple omics datasets. Such analysis integrates and concatenates information from multiple datasets leading to a better understanding of biological underpinnings of diseases.

There are several statistical techniques to conduct an integrative analysis of multivariate datasets. In specific, methods for two multivariate datasets include canonical correlation analysis (CCA), partial least squares (PLS), canonical correspondence analysis and multiple factor analysis (MFA). For example, CCA (Hotelling, 1936) is one of the popular statistical multivariate methods, which finds linear transformations of two multivariate datasets so that the correlation between transformed datasets is maximized. PLS (Wold, 1966) is similar with the CCA, which is widely used in chemometrics. Estimated loading vectors of PLS maximize a covariance between two linearly transformed multivariate data. However, a number of multivariate methods are not applicable if datasets lie in a high-dimensional space, which is also one of the natural features that -omics data have. For example, the CCA typically requires an inverse of a sample covariance matrix, which can be singular because the number of variables exceeds the sample size. To overcome this drawback of the CCA, researchers adopt a regression framework (Lykou and Whittaker, 2010; Parkhomenko et al., 2009; Waaijenborg et al., 2008) or assume that a covariance matrix as an identity matrix (Witten et al., 2009). Those analysis methods also suffer from a lack of interpretability. Typically estimators from high-dimensional datasets combine thousands of variables in a linear fashion and there is no zero coefficient. This causes difficulties on interpreting the results. There have been recent works in the literatures that propose a sparsity-constrained approach as a remedy for the high dimensionality of the data, such as sparse CCA (Hardoon and Shawe-Taylor, 2011; Parkhomenko et al., 2009; Safo et al., 2018; Waaijenborg et al., 2008; Witten et al., 2009) and sparse PLS (Chun and Keleş, 2010; Chung et al., 2012; Lee et al., 2011).

Co-inertia analysis (CIA) is another multivariate statistical analysis technique proposed by Dolédec and Chessel (1994), which can be considered as a generalized CCA or PLS. Co-inertia analysis takes two multivariate datasets as an input and seeks for multiple sets of axis pairs that maximize the concordance between two datasets projected on those new axis pairs. This goal is achieved by maximizing the global measure called ‘co-inertia’ that calculates the degree of the co-variability between two heterogeneous datasets. This analysis approach has been widely used in the ecology area (Dray et al., 2003; Thioulouse, 2011) to uncover the relationship between species and environment. CIA can be applied directly to the high dimensional datasets without any constraints or problems since CIA does not require inverting covariance matrices. Due to this advantage of the CIA, it has been used to the analysis of various biological datasets such as gene expression and proteomics data (Culhane et al., 2003; Fagan et al., 2007; Lê Cao et al., 2009). Culhane et al. conducted a cross-platform comparison of two gene expression datasets using CIA and Fagan et al. used CIA to conduct an integrative analysis of proteomic and gene expression data. In Lê Cao et al. (2009), they consider three methods, sparse PLS, sparse CCA and CIA for the integrative analysis of two datasets. They pointed out that objective goals of three methods are different so that it is difficult to compare them directly. As means of an indirect comparison, they focused on the biological interpretation of the selected genes and graphical outputs from the real data analysis results of each method. In that process, it is pointed out that lack of sparsity is one of weaknesses of the CIA since nonsparse estimated loading vectors make hard to interpret the analysis results and identify robust biomarkers (Lê Cao et al., 2009; Meng et al., 2016). Lê Cao et al. (2009) apply hard thresholding on estimated loading vectors to select important variables as a heuristic approach. Recently Tenenhaus et al. (2017) proposed regularized generalized canonical correlation analysis framework, which includes many methods as its special cases. The CIA also can be regarded as a special case of the RGCCA framework, but this framework cannot includes the sparse CIA as its special case. To the best of our knowledge, there has been no work on combining penalization with CIA to obtain sparse loading vectors.

In this paper, we propose two novel penalized CIA methods conducting estimation and features selection simultaneously to improve interpretability of analysis result and get enhanced identification of significant biomarkers from analysis result. By converting the CIA problem into a penalized regression problem, we achieve the sparsity of estimators. Also, we adopt another penalty that uses network information among genes such as those from functional genomics data so that the estimated model is expected to select relevant genes guided by the prior knowledge about relationships between genes. All penalty parameters are selected by cross-validation, and the performance of our algorithms is investigated by extensive simulation studies. We illustrate our methods by analyzing the NCI60 cell line data, gene expression and proteomics datasets on 57 cell lines.

The rest of this paper is organized as follows. In Section 2, we first review the CIA problem starting from the case dealing with one dataset to the case with two datasets. In Section 3, we present two proposed methods namely the sparse CIA (sCIA) and the structured sparse CIA (ssCIA) the latter of which incorporates biological/structural information. In Section 4, we conduct simulation studies to investigate the performance of our proposed algorithms in comparison with the CIA. We apply our methods to the NCI-60 cancer cell line data in Section 5 and some discussions and remarks are addressed in Section 6.

2 Co-inertia analysis

Suppose that we have a given dataset $\mathit{X}\in {\mathbb{R}}^{n\times p}$ observed from n subjects and assume that $\mathit{X}$ is centered without loss of generality. Let $\mathit{D}=\text{diag}\{d_1,\dots ,d_n\}\in {\mathbb{R}}^{n\times n}$ be the positive weights for samples (row space) of $\mathit{X}$ and ${\mathit{Q}}_x=\text{diag}\{q_1,\dots ,q_p\}\in {\mathbb{R}}^{p\times p}$ be the positive weights for variables (column space) of $\mathit{X}$. Define the inner product of $\mathit{X}$ in the column space of $\mathit{X}$ as ${\langle \mathit{X},\mathit{X}\rangle }_Q=\mathit{X}{\mathit{Q}}_x{\mathit{X}}^T$. Based on the above notations, the inertia of $\mathit{X}$ is defined as ${\mathit{I}}_x={\sum }_{i=1}^n{d}_i\left|\right|{\mathit{x}}_i|{|}_{Q_x}^2=trace(\mathit{X}{\mathit{Q}}_x{\mathit{X}}^T\mathit{D})$. The inertia ${\mathit{I}}_x$ is a global measure of the variability of the data $\mathit{X}$, which has a variance as its specific case. If $\mathit{X}$ is centered, ${\mathit{Q}}_x$ is the Euclidean metric, and $\mathit{D}$ is the $\frac{1}{n}{\mathit{I}}_n$, the inertia ${\mathit{I}}_x$ is the sum of variances of n data points of $\mathit{X}$. There are several approaches to construct $\mathit{D}$ and ${\mathit{Q}}_x$. For example, $\mathit{D}$ can be used to adjust possible sampling bias or duplicated observations. Specifically, we can estimate the probability of selection for each individual in the sample using available covariates in the data and use the inverse of the estimated probability as a weight for each individuals to adjust sampling bias. Also $\mathit{D}$ can be used to put strong emphasis on some reliable samples compared to the other samples. ${\mathit{Q}}_x$ can be used to give weights for specific variables, a column sum is one of the choice for the diagonal elements of ${\mathit{Q}}_x$ (Dray et al., 2003). As another approach, ${\mathit{Q}}_x$ can be chosen such that genes in $\mathit{X}$ that are known to be associated with a clinical phenotype of interest have larger weights. It may be also a good approach to compute ${\mathit{Q}}_x$ based on functional annotation following some recent proposed methods, originally proposed for rare-variant test for integrative analysis (Byrnes et al., 2013; He et al., 2017).

Let $\mathit{X}{\mathit{Q}}_x\mathit{u}$ denote the projection of $\mathit{X}$ to the vector $\mathit{u}$ normalized with ${\mathit{Q}}_x$, where $\mathit{u}$ is known as the inertia axis (Culhane et al., 2003; Dray et al., 2003) or the inertia loading vector (Lê Cao et al., 2009). Following the latter, we call $\mathit{u}$ the loading vector. The projected inertia ${\mathit{I}}_x(\mathit{u})$ is defined as ${\mathit{I}}_x(\mathit{u})={\mathit{u}}^T{\mathit{Q}}_x{\mathit{X}}^T\text{DX}{\mathit{Q}}_x\mathit{u}$. There exists p orthogonal vectors ${\mathit{u}}_i$ that are normalized with ${\mathit{Q}}_x$ such that sum of projected inertias becomes the total inertia ${\mathit{I}}_x$. Those orthogonal vectors are the eigenvectors of the matrix ${\mathit{X}}^T\text{DX}{\mathit{Q}}_x$, which also can be calculated sequentially by solving the following problem,

$$\begin{array}{cc}{\displaystyle \underset{{\mathit{u}}_i}{maximize}}\hfill & \hspace{1em}{\mathit{u}}_i^T{\mathit{Q}}_x{\mathit{X}}^T\text{DX}{\mathit{Q}}_x{\mathit{u}}_i\hfill \\ \mathit{s}.\mathit{t}.\hfill & \hspace{1em}{\mathit{u}}_i^T{\mathit{Q}}_x{\mathit{u}}_i=1,{\mathit{u}}_i^T{\mathit{Q}}_x{\mathit{u}}_j=0,1\le j<i.\hfill \end{array}$$ (1)

Suppose that there is another set of data $\mathit{Y}\in {\mathbb{R}}^{n\times q}$ collected from the same subjects. Analogous to the definition of the inertia, we define the ‘co-inertia’ that measures the concordance between two datasets (Dray et al., 2003) as $I_c=trace(\mathit{X}{\mathit{Q}}_x{\mathit{X}}^T\text{DY}{\mathit{Q}}_y{\mathit{Y}}^T\mathit{D})$. For two projections $\mathit{X}{\mathit{Q}}_x\mathit{u}$ and $\mathit{Y}{\mathit{Q}}_y\mathit{v}$, where a ${\mathit{Q}}_x$-normed vector $\mathit{u}$ and a ${\mathit{Q}}_y$-normed vector $\mathit{v}$, the co-inertia between two projections is defined as $I_c(\mathit{u},\mathit{v})={({\mathit{u}}^T{\mathit{Q}}_x{\mathit{X}}^T\text{DY}{\mathit{Q}}_y\mathit{v})}^2$. In addition to the centering the data, it is recommended to scale both datasets if variables in each data are measured on different scales (Dolédec and Chessel, 1994; Dray et al., 2003).The goal of CIA is to find the optimal loading vector pair $(\mathit{u},\mathit{v})$ that maximizes the projected co-inertia. Pairs of optimal co-inertia loading vectors can be obtained simultaneously via eigenvalue decomposition of the matrix ${\mathit{Q}}_x^{1/2}{\mathit{X}}^T\text{DY}{\mathit{Q}}_y{\mathit{Y}}^T\text{DX}{\mathit{Q}}_x^{1/2}$. First R co-inertia loadings are ${\mathit{U}}_R={\mathit{Q}}_x^{-1/2}{\mathit{A}}_R\in {\mathbb{R}}^{p\times R},\hspace{0.17em}{\mathit{V}}_R={\mathit{Y}}^T\text{DX}{\mathit{Q}}_x^{1/2}{\mathit{A}}_R{\Lambda }_R^{-1/2}\in {\mathbb{R}}^{q\times R}$ with respect to $\mathit{X}$ and $\mathit{Y}$, where ${\mathit{A}}_R\in {\mathbb{R}}^{p\times R}$ is set of eigenvectors and ${\Lambda }_R\in {\mathbb{R}}^{R\times R}$ is corresponding eigenvalues. By solving following optimization problem, the first loading vectors can be acquired,

$$\begin{array}{cc}\underset{\mathit{u},\mathit{v}}{maximize}\hfill & \hspace{1em}{({\mathit{u}}^T{\mathit{Q}}_x{\mathit{X}}^T\text{DY}{\mathit{Q}}_y\mathit{v})}^2\hfill \\ subject\hspace{0.17em}to\hfill & \hspace{1em}{\mathit{u}}^T{\mathit{Q}}_x\mathit{u}={\mathit{v}}^T{\mathit{Q}}_y\mathit{v}=1.\hfill \end{array}$$ (2)

We can reformulate problem (2) as follows,

$$\underset{\mathit{a},\mathit{b}}{maximize}\hspace{1em}{\mathit{a}}^T{\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}\mathit{b}\hspace{1em}subject\hspace{0.17em}to\hspace{1em}\left|\right|\mathit{a}|{|}_2=1,|\left|\mathit{b}\right|{|}_2=1,$$ (3)

where $\mathit{a}={\mathit{Q}}_x^{1/2}\mathit{u},\mathit{b}={\mathit{Q}}_y^{1/2}\mathit{v},\tilde{\mathit{X}}={\mathit{D}}^{1/2}\mathit{X}{\mathit{Q}}_x^{1/2}$ and $\tilde{\mathit{Y}}={\mathit{D}}^{1/2}\mathit{Y}{\mathit{Q}}_y^{1/2}$, which is a singular decomposition (SVD) problem. Subsequent pairs of orthogonal loadings $({\mathit{u}}_r,{\mathit{v}}_r)=({\mathit{Q}}_x^{-1/2}{\mathit{a}}_r,{\mathit{Q}}_y^{-1/2}{\mathit{b}}_r),r=2,\dots ,R$ can be estimated by applying SVD to the deflated data with respect to all previously estimated loading vector pairs $({\mathit{U}}_{r-1},{\mathit{V}}_{r-1})=([{\mathit{u}}_1,\dots ,{\mathit{u}}_{r-1}],[{\mathit{v}}_1,\dots ,{\mathit{v}}_{r-1}])$. In following sections, we will develop our methods based on above problem representation (3).

3 Penalized co-inertia analysis

3.1 Sparse co-inertia analysis (sCIA)

To get a sparse loading vector, we impose the l₁-constraint on the optimization problem (3) as follows.

$$\begin{array}{cc}{\displaystyle \underset{\mathit{a},\mathit{b}}{maximize}}\hfill & \hspace{1em}{\mathit{a}}^T{\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}\mathit{b}\hfill \\ subject\hspace{0.17em}to\hfill & \hspace{1em}\left|\right|\mathit{a}|{|}_2\le 1,|\left|\mathit{b}\right|{|}_2\le 1,\hspace{1em}\left|\right|\mathit{a}|{|}_1\le c_1,|\left|\mathit{b}\right|{|}_1\le c_2,\hfill \end{array}$$ (4)

where c₁, c₂ are pre-defined constants. Note that we relax the l₂-equality penalty on $\mathit{a}$ into inequality penalty to achieve the convexity of the problem following Witten et al. (2009). The problem (4) has constraints on $\mathit{a}$ and $\mathit{b}$, which are transformed $\mathit{u}$ and $\mathit{v}$, not directly on $\mathit{u}$ and $\mathit{v}$. However, the sparsity that $\mathit{a}$ and $\mathit{b}$ achieved is transferred to $\mathit{u}$ and $\mathit{v}$ because ${\mathit{Q}}_x$ and ${\mathit{Q}}_y$ are diagonal matrices. Lagrangian formulation of the problem (4) is

$$\begin{array}{cc}{\displaystyle \underset{\mathit{a},\mathit{b}}{maximize}}\hfill & -{\mathit{a}}^T{\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}\mathit{b}+\frac{1}{2}\left|\right|\mathit{a}|{|}_2^{\mathrm{2}}+{\lambda }_1|\left|\mathit{a}\right|{|}_1+\frac{1}{2}\left|\right|\mathit{b}|{|}_2^{\mathrm{2}}+{\lambda }_2|\left|\mathit{b}\right|{|}_1,\hfill \end{array}$$ (5)

where λ₁ and λ₂ are Lagrangian multipliers. The objective function of the problem (5) is a biconvex function in $\mathit{a}$ and $\mathit{b}$ such that we can use iterative approach. By fixing one loading vector at a time, the problem (5) can be reformulated into the iterative algorithm that consists of two penalized least squares problem as follows,

$$\begin{array}{cc}(1)\hspace{1em}\hfill & \mathit{a}\leftarrow \underset{\mathit{a}}{\arg \min }\hspace{1em}\frac{1}{2}\left|\right|{\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}\mathit{b}-\mathit{a}|{|}_2^{\mathrm{2}}+{\lambda }_1|\left|\mathit{a}\right|{|}_1,\hfill \\ (2)\hspace{1em}\hfill & \mathit{b}\leftarrow \underset{\mathit{b}}{\arg \min }\hspace{1em}\frac{1}{2}\left|\right|{\tilde{\mathit{Y}}}^T\tilde{\mathit{X}}\mathit{a}-\mathit{b}|{|}_2^{\mathrm{2}}+{\lambda }_2|\left|\mathit{b}\right|{|}_1.\hfill \end{array}$$ (6)

We can get the optimal pair of $(\mathit{a},\mathit{b})$ by solving iterative problem (6) until it converges. More than two orthogonal sCIA loading vector pairs can be estimated by applying the above iterative procedure to the deflated data with respect to all previous estimated loading vector pairs. The complete overall procedure for the sCIA is summarized in Algorithm 1.

Algorithm 1: Sparse Co-Inertia Analysis

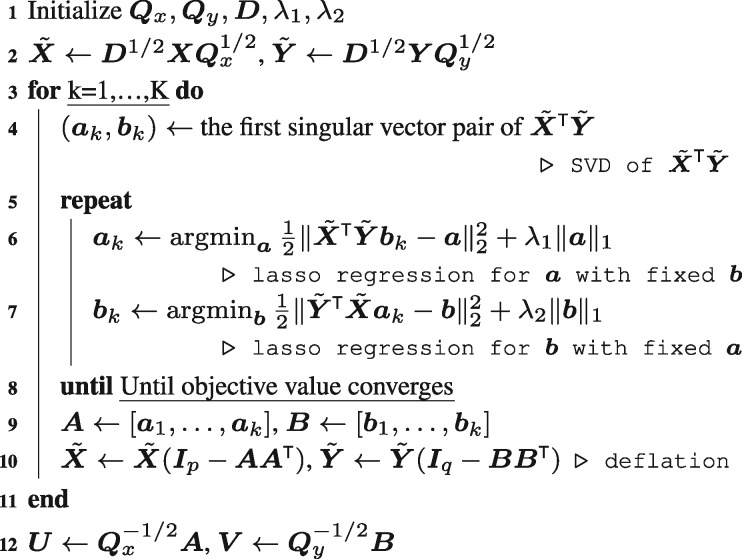
3.2 Structured sparse co-inertia analysis (ssCIA)

In this section, we extend the proposed sCIA method by incorporating prior knowledge about the network information among variables so that relevant variables can be identified more efficiently. To this end, we adopt the Laplacian penalty function proposed by Li and Li (2008). Let ${\mathcal{G}}_x=\{\mathit{C},\mathit{E},\mathit{W}\}$ contains a weighted undirected graph information of variables in $\mathit{X}$, where $\mathit{C}$ is the set of vertices corresponding to the p features (or nodes), $\mathit{E}=\{i\sim j\}$ is the set of edges showing that features i and j are direct neighbors in the network, and $\mathit{W}$ is the weight of each node. Using ${\mathcal{G}}_x=\{\mathit{C},\mathit{E},\mathit{W}\}$, the (i, j)th element of the normalized Laplacian matrix ${\mathit{L}}_x$ is defined by

$$\begin{array}{c}{\mathit{L}}_x(i,j)=\{\begin{array}{cc}1-w_x(i,j)/d_i,\hfill & \text{if} i=j \text{and} d_i\ne 0,\hfill \\ -w_x(i,j)/\sqrt{d_i{d}_j},\hfill & \text{if} i \text{and} j \text{are} \text{adjacent},\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\hfill \end{array}$$ (7)

where $w_x(i,j)$ is the weight of the edge $e=(i\sim j)$ and d_i is the degree of the vertex i defined as $\sum _{i\sim j}{w}_x(i,j)$. The normalized Laplacian matrix ${\mathit{L}}_y$ for the data $\mathit{Y}$ can be defined in the same way. With definitions of ${\mathit{L}}_x$ and ${\mathit{L}}_y$ and given positive constants $c_1,c_2,c_3$ and c₄, we propose the following structured sparse CIA (ssCIA) criterion that is the extended model of the sCIA problem (4),

$$\begin{array}{cc}{\displaystyle \underset{\mathit{a},\mathit{b}}{maximize}}\hfill & \hspace{1em}{\mathit{a}}^T{\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}\mathit{b}\hfill \\ subject\hspace{0.17em}\hspace{0.17em}to\hfill & \hspace{1em}\left|\right|\mathit{a}|{|}_2\le 1,|\left|\mathit{b}\right|{|}_2\le 1,\hspace{1em}\left|\right|\mathit{a}|{|}_1\le c_1,|\left|\mathit{b}\right|{|}_1\le c_2\hfill \\ \hfill & \hspace{1em}{\mathit{a}}^T{\tilde{\mathit{L}}}_x\mathit{a}\le c_3,{\mathit{b}}^T{\tilde{\mathit{L}}}_y\mathit{b}\le c_4,\hfill \end{array}$$ (8)

where ${\tilde{\mathit{L}}}_x={\mathit{Q}}_x^{-1/2}{\mathit{L}}_x{\mathit{Q}}_x^{-1/2}$ and ${\tilde{\mathit{L}}}_y={\mathit{Q}}_y^{-1/2}{\mathit{L}}_y{\mathit{Q}}_y^{-1/2}$. Like as the sCIA problem, the sparsity that $\mathit{a}$ and $\mathit{b}$ achieved is transferred to $\mathit{u}$ and $\mathit{v}$ due to the diagonality of ${\mathit{Q}}_x$ and ${\mathit{Q}}_y$. Also, the Laplacian penalty in the problem (8) smoothes the estimated loading vectors such that variables within a same network can be selected or neglected together. Our structure penalty function uses the Laplacian matrices that ${\mathit{Q}}_x^{-1/2}$ and ${\mathit{Q}}_y^{-1/2}$ are pre-/post-multiplied respectively. Thus, this penalty function encourages smoothness of the $\mathit{u}$ and $\mathit{v}$. Smaller values of c₃ and c₄ result in smoother estimates of loading vectors $\mathit{a}$ and $\mathit{b}$ respectively. Lagrangian formulation of the problem (8) is

$$\begin{array}{cc}\underset{\mathit{a},\mathit{b}}{minimize}\hfill & \hspace{1em}-{\mathit{a}}^T{\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}\mathit{b}+\frac{1}{2}\left|\right|\mathit{a}|{|}_2+{\lambda }_1|\left|\mathit{a}\right|{|}_1+\frac{{\lambda }_2}{2}{\mathit{a}}^T{\tilde{\mathit{L}}}_x\mathit{a}\hfill \\ \hfill & \hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{2}\left|\right|\mathit{b}|{|}_2+{\lambda }_3|\left|\mathit{b}\right|{|}_1+\frac{{\lambda }_4}{2}{\mathit{b}}^T{\tilde{\mathit{L}}}_y\mathit{b},\hfill \end{array}$$ (9)

which is a biconvex problem for $\mathit{a}$ and $\mathit{b}$ such that we can find the optimal $\mathit{a}$ and $\mathit{b}$ using an iterative algorithm. By fixing one loading vector at a time, the problem (9) can be recast into the following iterative algorithm that consists of two simple lasso regression problem as in Li and Li (2008) and Chen et al. (2013),

$$\begin{array}{ccc}(1)\hspace{1em}\mathit{a}\leftarrow \hfill & \underset{\mathit{a}}{\arg \min }\hfill & \hspace{1em}\frac{1}{2}\left|\right|{\mathit{N}}_x\mathit{a}-\tilde{\mathit{b}}|{|}_2^{\mathrm{2}}+{\lambda }_1|\left|\mathit{a}\right|{|}_1,\hfill \\ (2)\hspace{1em}\mathit{b}\leftarrow \hfill & \underset{\mathit{b}}{\arg \min }\hfill & \hspace{1em}\frac{1}{2}\left|\right|{\mathit{N}}_y\mathit{b}-\tilde{\mathit{a}}|{|}_2^{\mathrm{2}}+{\lambda }_3|\left|\mathit{b}\right|{|}_1,\hfill \end{array}$$ (10)

where

$${\mathit{N}}_x=\left[\begin{array}{c}{\mathit{I}}_p\\ \sqrt{{\lambda }_2}{\mathit{M}}_x^T\end{array}\right],{\mathit{N}}_y=\left[\begin{array}{c}{\mathit{I}}_q\\ \sqrt{{\lambda }_4}{\mathit{M}}_y^T\end{array}\right],\tilde{\mathit{b}}=\left[\begin{array}{c}{\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}\mathit{b}\\ 0_p\end{array}\right],\tilde{\mathit{a}}=\left[\begin{array}{c}{\tilde{\mathit{Y}}}^T\tilde{\mathit{X}}\mathit{a}\\ 0_q\end{array}\right],$$

$$\begin{array}{ccc}{\mathit{M}}_x={\mathit{Q}}_x^{-1/2}{\mathit{E}}_x{\Gamma }_x^{1/2},\hfill & {\tilde{\mathit{L}}}_x={\mathit{Q}}_x^{-1/2}{\mathit{L}}_x{\mathit{Q}}_x^{-1/2},\hfill & {\mathit{L}}_x={\mathit{E}}_x{\Gamma }_x{\mathit{E}}_x^T,\hfill \\ {\mathit{M}}_y={\mathit{Q}}_y^{-1/2}{\mathit{E}}_y{\Gamma }_y^{1/2},\hfill & {\tilde{\mathit{L}}}_y={\mathit{Q}}_y^{-1/2}{\mathit{L}}_y{\mathit{Q}}_y^{-1/2},\hfill & {\mathit{L}}_y={\mathit{E}}_y{\Gamma }_y{\mathit{E}}_y^T,\hfill \end{array}$$

and ${\mathit{E}}_x,{\Gamma }_x,{\mathit{E}}_y,{\Gamma }_y$ are eigenvectors and eigenvalues of ${\mathit{L}}_x$ and ${\mathit{L}}_y$ respectively. More than two orthogonal ssCIA loading vectors can be derived by applying above iterative procedure again to the deflated data that is projected to the orthogonal space of all previously estimated pairs of loading vectors. The complete overall procedure for the ssCIA is summarized in Algorithm 2.

Algorithm 2: Structured Sparse Co-Inertia Analysis

4 Numerical studies

4.1 Generative model for synthetic data

We generate the simulation data following the model presented in Parkhomenko et al. (2009), which assumes the existence of a latent variable to make the dependency between two sets of random variables. Consider a pair of random variable vectors $\mathit{x}\in {\mathbb{R}}^p$ and $\mathit{y}\in {\mathbb{R}}^q$. Suppose that μ from $N(0,{\sigma }_{\mu }^2)$ is a latent variable that generates dependency between two random variables. We construct two random variables $\mathit{x}=\mu \mathit{u}+{\mathit{e}}_x\in {\mathbb{R}}^p$ and $\mathit{y}=\mu \mathit{v}+{\mathit{e}}_y\in {\mathbb{R}}^q$ where ${\mathit{e}}_x\sim N(0_p,{\Sigma }_x),\hspace{0.17em}{\mathit{e}}_y\sim N(0_q,{\Sigma }_y)$ and $\mathit{u}={[u_1,\dots ,u_{p\prime },0,\dots ,0]}^T\in {\mathbb{R}}^p,\mathit{v}={[v_1,\dots ,v_{q\prime },0,\dots ,0]}^T\in {\mathbb{R}}^q$ are pre-defined true sparse co-inertia loading vectors such that ${\mathit{u}}^T{\mathit{Q}}_x\mathit{u}={\mathit{v}}^T{\mathit{Q}}_y\mathit{v}=1$. Then the covariance matrix of $\mathit{x}$ and $\mathit{y}$ have a block matrix structure, and we can show that ${\mathit{Q}}_x^{1/2}\mathit{u}$ and ${\mathit{Q}}_y^{1/2}\mathit{v}$ are left and right singular vectors of ${\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}={\mathit{Q}}_x^{1/2}{\mathit{X}}^T\text{DY}{\mathit{Q}}_y^{1/2}$, which maximize the objective function of the CIA. Detailed description of the covariance matrix and the simple proof that $\mathit{u}$ and $\mathit{v}$ be the singular vectors of ${\tilde{\mathit{X}}}^T\tilde{\mathit{Y}}$ can be found in the Section A.1 of the Supplementary Material.

4.2 Design of experiments

One hundred Monte Carlo (MC) datasets are generated, where $\mathit{x}\in {\mathbb{R}}^{400}$ and $\mathit{y}\in {\mathbb{R}}^{500}$ are drawn for n = 200 times for each. We make $\mathit{D}$ as an identity matrix without loss of generality, and diagonal weight matrices ${\mathit{Q}}_x$ and ${\mathit{Q}}_y$ are randomly generated. To mimic networks existing in the omics data, we assume that the first 300 variables each of $\mathit{x}$ and $\mathit{y}$ form 30 networks. Each network has 10 variables and the first one of them within each network is the main variable connected to the rest of 9 variables. Variance matrices for $\mathit{x}$ and $\mathit{y}$ are generated so as to contain each assumed network information.

For the construction of the true loading vectors, we assume that the most of the genes have no effects to the relationship between two datasets and only small portion of genes affects to that relationship. Thus true loading vectors are sparse across all simulations. We consider seven scenarios by changing three conditions, a number of networks affecting on dependency between two datasets, different signal direction of genes within each network, and degree of sparsity within each network. The first condition decides the sparsity of the true loading vector. There are more nonzero elements in the true loadings if there are more effective networks we have. The second and third conditions decide whether the ssCIA can benefits from the prior network information. If signals of coefficients vary or there are zero coefficients within a network, that scenario is not favorable to the ssCIA since true loading vectors cannot make the network penalty zero. Specific values of the constructed variance matrices and true sparse loading vectors for each scenario design are described in Section A.2 and A.3 of the Supplementary Material.

4.3 Tuning parameter selection and performance measures

We use five-fold cross validation (CV) method for selecting the optimal tuning parameters. For each data, we divide the data into five subgroups and calculate CV objective values, $\text{CV}(\lambda )=\frac{1}{K}\sum _{k=1}^K({\widehat{\mathit{u}}}_{-k}(\lambda {)}^T{\mathit{Q}}_x{\mathit{X}}_k^T\mathit{D}{\mathit{Y}}_k{\mathit{Q}}_y{\widehat{\mathit{v}}}_{-k}^T(\lambda ){)}^2$, where ${\mathit{X}}_k,\hspace{0.17em}{\mathit{Y}}_k$ are kth subgroup of the data, ${\widehat{\mathit{u}}}_{-k}(\lambda ),\hspace{0.17em}{\widehat{\mathit{v}}}_{-k}^T(\lambda )$ are estimators from the data except the kth subgroup using tuning parameter λ. We select the optimal tuning parameters that maximize the above cross validation criteria. For the grid search of sparsity tuning parameters of both methods, we use evenly spaced grid points between the maximum and minimum value of the sparsity parameter that gives almost zero loading vectors to almost non-sparse loading vectors. For the network penalty parameters of the ssCIA, we conduct preliminary analyses to obtain a rough guess for the range containing tuning parameter values. After narrowing down the ranges, evenly distributed grid points are used in the simulation. According to the case-specific situation, different grid density generated using different gaps can be used instead.

We assess the feature selection performance of our methods using sensitivity, specificity, Matthews correlation coefficient (MCC), and the estimation performance using the angle between the true and an estimated loading vector. Each measure is defined as $\text{sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}},\hspace{0.17em}\text{specificity}=\frac{\text{TN}}{\text{FP}+\text{TN}},\hspace{0.17em}\text{angle}(\widehat{\mathit{a}})=\frac{{\widehat{\mathit{a}}}^T{\mathit{a}}^{*}}{\left|\right|\widehat{\mathit{a}}|{|}_2\times |\left|{\mathit{a}}^{*}\right|{|}_2}$ and $\text{MCC}=\frac{\text{TP}\times \text{TN}-\text{FP}\times \text{FN}}{\sqrt{(\text{TP}+\text{FP})(\text{TP}+\text{FN})(\text{TN}+\text{FP})(\text{TN}+\text{FN})}}$, where TP, TN, FP and FN are true positives, true negatives, false positives and false negatives and $\widehat{\mathit{a}}$ are the estimator of the true loading vector ${\mathit{a}}^{*}$.

4.4 Results

Simulation results are shown in Table 1. The loading estimators from sCIA having better angles in all scenarios compared to the classical CIA. Since the estimators from sCIA have better angles with fewer nonzero elements in the estimated loadings, we can think that the sCIA shows improvements in interpretability and precision. Also, the ssCIA shows higher angle values in most of the cases, which indicates that the ssCIA shows improvements in the interpretability and precision in most cases.

Table 1.

Simulation results of sCIA and ssCIA

		$\mathit{a}$ in $\mathit{X}$				$\mathit{b}$ in $\mathit{Y}$
		Sens	Spec	MCC	Angle	Sens	Spec	MCC	Angle
Scen1	CIA	–	–	–	$0.940(0.013)$	–	–	–	$0.928(0.015)$
	sCIA	$0.956(0.091)$	$0.478(0.258)$	$0.358(0.214)$	$0.948(0.014)$	$0.784(0.173)$	$0.720(0.306)$	$0.481(0.225)$	$0.943(0.017)$
	ssCIA	$1.000(0.000)$	$0.765(0.314)$	$0.628(0.244)$	$0.968(0.015)$	$0.884(0.062)$	$0.781(0.338)$	$0.579(0.236)$	$0.955(0.015)$
Scen2	CIA	–	–	–	$0.943(0.011)$	–	–	–	$0.927(0.015)$
	sCIA	$0.808(0.039)$	$0.962(0.113)$	$0.731(0.120)$	$0.981(0.010)$	$0.752(0.134)$	$0.866(0.245)$	$0.617(0.245)$	$0.959(0.015)$
	ssCIA	$1.000(0.000)$	$0.933(0.021)$	$0.647(0.064)$	$0.985(0.006)$	$0.920(0.027)$	$0.964(0.010)$	$0.678(0.049)$	$0.973(0.008)$
Scen3	CIA	–	–	–	$0.944(0.011)$	–	–	–	$0.933(0.013)$
	sCIA	$0.956(0.090)$	$0.477(0.265)$	$0.362(0.224)$	$0.952(0.011)$	$0.825(0.173)$	$0.654(0.316)$	$0.444(0.237)$	$0.944(0.014)$
	ssCIA	$0.924(0.017)$	$0.907(0.023)$	$0.694(0.042)$	$0.953(0.010)$	$0.778(0.035)$	$0.934(0.091)$	$0.642(0.072)$	$0.952(0.012)$
Scen4	CIA	–	–	–	$0.954(0.008)$	–	–	–	$0.932(0.012)$
	sCIA	$0.881(0.048)$	$0.952(0.177)$	$0.731(0.211)$	$0.982(0.009)$	$0.769(0.140)$	$0.828(0.286)$	$0.604(0.275)$	$0.960(0.016)$
	ssCIA	$0.882(0.051)$	$0.952(0.016)$	$0.643(0.057)$	$0.935(0.010)$	$0.858(0.023)$	$0.971(0.008)$	$0.679(0.048)$	$0.958(0.011)$
Scen5	CIA	–	–	–	$0.945(0.011)$	–	–	–	$0.932(0.013)$
	sCIA	$0.934(0.082)$	$0.569(0.343)$	$0.456(0.309)$	$0.953(0.013)$	$0.817(0.166)$	$0.700(0.290)$	$0.458(0.230)$	$0.948(0.014)$
	ssCIA	$0.989(0.014)$	$0.882(0.124)$	$0.693(0.097)$	$0.957(0.013)$	$0.786(0.047)$	$0.928(0.088)$	$0.608(0.068)$	$0.952(0.012)$
Scen6-1	CIA	–	–	–	$0.937(0.016)$	–	–	–	$0.921(0.019)$
	sCIA	$0.804(0.028)$	$0.972(0.073)$	$0.731(0.091)$	$0.981(0.008)$	$0.760(0.137)$	$0.858(0.246)$	$0.604(0.247)$	$0.957(0.018)$
	ssCIA	$1.000(0.000)$	$0.930(0.020)$	$0.639(0.060)$	$0.984(0.007)$	$0.919(0.024)$	$0.962(0.012)$	$0.670(0.053)$	$0.972(0.008)$
Scen6-2	CIA	–	–	–	$0.833(0.036)$	–	–	–	$0.800(0.046)$
	sCIA	$0.766(0.074)$	$0.937(0.133)$	$0.596(0.117)$	$0.932(0.031)$	$0.564(0.089)$	$0.946(0.124)$	$0.454(0.089)$	$0.922(0.042)$
	ssCIA	$0.957(0.135)$	$0.892(0.097)$	$0.553(0.109)$	$0.931(0.043)$	$0.752(0.131)$	$0.905(0.157)$	$0.456(0.010)$	$0.913(0.044)$
Scen7-1	CIA	–	–	–	$0.949(0.010)$	–	–	–	$0.929(0.012)$
	sCIA	$0.822(0.063)$	$0.933(0.170)$	$0.736(0.192)$	$0.982(0.007)$	$0.740(0.120)$	$0.887(0.243)$	$0.655(0.234)$	$0.962(0.013)$
	ssCIA	$0.895(0.052)$	$0.950(0.015)$	$0.643(0.059)$	$0.934(0.009)$	$0.860(0.027)$	$0.972(0.009)$	$0.681(0.050)$	$0.958(0.011)$
Scen7-2	CIA	–	–	–	$0.825(0.052)$	–	–	–	$0.797(0.048)$
	sCIA	$0.725(0.079)$	$0.947(0.120)$	$0.617(0.123)$	$0.929(0.034)$	$0.547(0.078)$	$0.958(0.098)$	$0.470(0.087)$	$0.929(0.032)$
	ssCIA	$0.680(0.137)$	$0.930(0.055)$	$0.491(0.098)$	$0.893(0.041)$	$0.613(0.142)$	$0.951(0.034)$	$0.461(0.070)$	$0.896(0.042)$

Note: As a measure for the performance of proposed algorithms, sensitivity (Sens), specificity (Spec), Mattews correlation coefficient (MCC), and the angle between estimated loadings and true loadings are shown. Numbers inside the parenthesis are Monte Carlo standard deviation.

We evaluate the performance of the ssCIA compared to the CIA and the sCIA when the true underlying loadings do not agree with the graph structure assumed by comparing results of the first, second and sixth scenarios to the rest. Scenario 1, 2 and 6 are favorable designs to the ssCIA, because the true loading vectors in those simulation settings agree with the network information incorporated in the model. The ssCIA outperforms the CIA and the sCIA in those favorable scenarios. The estimators from ssCIA have higher values in sensitivity, specificity and MCC in general compared to estimators from the sCIA. In the first and second scenario, the ssCIA finds all effective variables while it keep showing high specificity. Also, measured angle values of the ssCIA are higher in every cases compared to that of the sCIA. Based on the above observations, we conclude that our ssCIA shows better feature selection performance compared to the CIA and the sCIA with a help of graph information if incorporated graph information agrees with true loading vectors.

In the other settings such as scenario 3, 4, 5 and 7, the penalty function has nonzero value when the input is the true loading vector. Thus in those simulation settings, the ssCIA cannot enjoy the benefit of incorporated prior information. However, the ssCIA still shows comparable values in all measures even though those designs are not favorable to them. The difference of four measures between the ssCIA and the CIA/sCIA are relatively small. We conclude that still our ssCIA shows competitive performance, especially in specificity, despite of the discordance between some elements of the true loading vectors and incorporated graph information.

From the comparison between results of scenario 1, 3 and scenario 2, 4, we compare the performance of our penalized CIA compared to the classical CIA when the true loading vectors become more sparse. The classical CIA performs better if the true loading vectors are less sparse, which is expected result. For our proposed methods, there is a trade off between sensitivity and specificity. Our algorithms lose some sensitivity but get a lot more specificity so that MCC and angle are improved. This observation implies that our proposed methods shows better performance when the true loading is sparse that fits with our original purpose.

We also generate averaged ROC curves and corresponding approximated AUC values. Those results are presented in Section B of the Supplementary Material. Figure 1 and Table 1 in the Supplementary Material confirms the above simulation results.

5 Real data analysis

5.1 NCI-60 cell line data

The NCI-60 is a panel of 60 diverse human cancer cell lines used by the Developmental Therapeutics Program (DTP) of the U.S. National Cancer Institute (NCI) to screen over 100 000 chemical compounds and natural products. It consists of 10 kinds of cancerous cell lines, leukemia, lymphomas, melanomas, ovarian, renal, breast, prostate, colon, lung and CNS origin. There are various -omics datasets available for those cell lines including gene expression data from various platforms, protein abundance data and methylation data. We use the gene expression data used in the CIA application (Culhane et al., 2003), which contains 1517 probes that have the minimum change in gene expressions greater than 500 units across all cell lines. For the other data, we use the protein abundance data generated by Nishizuka et al. (2003) using the high-density RP lysate arrays (Paweletz et al., 2001), which can be downloaded from CellMiner (http://discover.nci.nih.gov/cellminer/) web application for the NCI-60 data (Reinhold et al., 2012). In this study, abundance levels of 162 proteins are available for the NCI-60 cell lines. After matching labels of cell lines of two datasets, 57 of 60 matched cell line data were used for the analysis. For the weight matrices in the CIA, sCIA and the ssCIA, we use the identity matrix for $\mathit{D}$ and the column sum divided by total sum of the absolute values of the data each as diagonal values of the weight matrix following Culhane et al. (2003). Network information incorporated in the ssCIA method are collected from KEGG pathway database (Kanehisa et al., 2017).

5.2 Analysis results

To compare the performance of proposed algorithms with the classical CIA, the number of nonzero elements in the first two estimated loading vectors and the cumulative percentage of explained variance of data by the estimated loading vectors are calculated in Table 2. Cumulated percentage of the explained variability is the ratio of sum of estimated co-inertia to the total co-inertia. Since the total co-inertia between $\mathit{X}$ and $\mathit{Y}$ does not change (Dray et al., 2003), we can use the cumulated percentage of explained variability as a measure to compare the performance of the CIA, sCIA and the ssCIA how much they explain the co-variability between two datasets. We can observe that our penalized algorithms select much fewer elements in loading vectors but still explains almost same portion of the data variability explained by the CIA. The ssCIA collects more variables compared to the sCIA, but it explains more variability than the sCIA, and much fewer variables compared to the CIA to explain the similar percentage of the data variability explained by the CIA.

Table 2.

Analysis results of CIA, sCIA and ssCIA for the NCI60 cell line data

Result of the CIA, sCIA and ssCIA
	Number of nonzero elements				Cumul % explained by estimated loadings
	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{b}}_1$	${\mathit{b}}_2$	1st loading	1st, 2nd loadings
CIA	1517	1517	162	162	0.359	0.641
sCIA	1038	573	92	153	0.336	0.598
ssCIA	1206	1036	113	132	0.348	0.624

Note: First four columns are number of nonzero elements in the estimated first two co-inertia loadings for each $\mathit{X}$ and $\mathit{Y}$, next two columns are cumulated percentage of explained variability of the data.

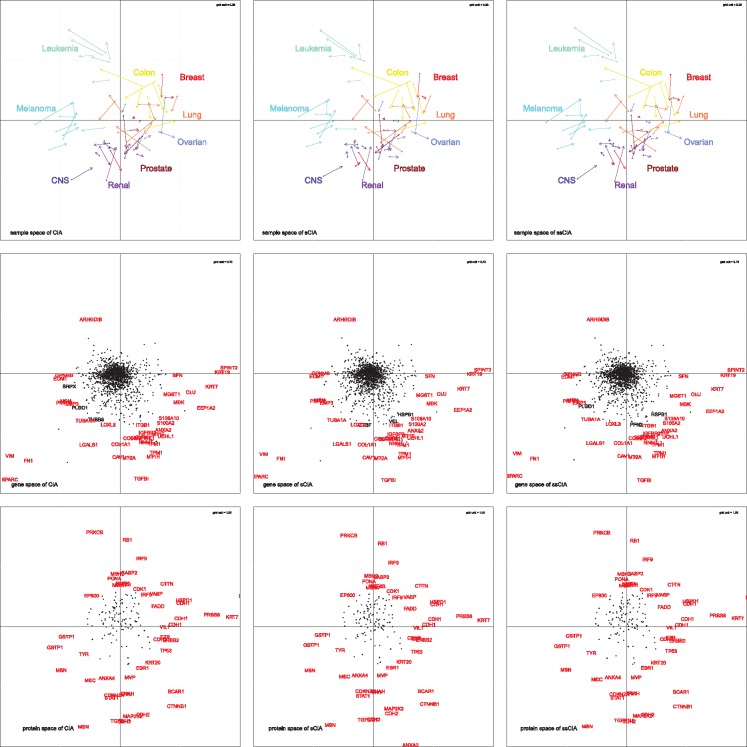
Following Culhane et al. (2003), Fagan et al. (2007) and Meng et al. (2014), we generate three figures for each method and shown in Figure 1. The figures in the first row show the sample space of the gene expression and protein abundance data. The arrow base pointed as a dot is the projection of the cell line from the gene space while the tip of the arrow is the projected coordinate of the cell line from the protein space. The length of the arrow indicates the degree of the concordance between two datasets, the shorter arrow stands for the higher consensus between two datasets. For example, the arrows of the CNS cell line data exhibits relatively short-length compared to others, which suggests that consensus between the gene expression and the protein abundance data of the CNS cell line is higher compared to that of leukemia, melanoma, or lung cell lines. This plot also shows the global pattern of the data, the distance between the tip and the origin tells us which cell line contributes more and have higher weights on the specific co-inertia axis. Gene space (arrow base) of the melanoma cell lines is projected further than its protein space in the direction of the first co-inertia axis, which suggests that the gene expression data contributes more to the trend of the first axis compared to the protein abundance data. Similarly, the protein abundance data of the leukemia cell lines may contributes more to the first axis compared to the gene expression data. Clustering pattern is another information that we can get from the figures in the first row. First we observed is that samples are clustered by their cell lines, especially, samples from leukemia, melanoma and colon cell lines are well clustered compared to others. We notice that both datasets from lung carcinomas and breast cancer are more dispersed than others, which may suggest that datasets for those disease is more heterogeneous than others. In second, we can observe that cell lines are separated by their characteristics. Cell lines clustered to the right of the second axis are colon, breast, lung, ovarian, prostate and renal cell lines. All those cell lines are from epithelial cell tissues (Marshall et al., 2017) while lueukemia, melanoma and CNS are not from that origin of tissues.

Fig. 1.

NCI60 Cell Line data analysis result from the CIA, the sCIA and the ssCIA, left to right respectively at each row. The first row shows the sample space of analysis result. The starting point of an arrow is a normalized score of a sample in the gene data, while the endpoint of arrow is a normalized score of a sample in the protein data. The figures second row show the distribution of samples in the gene space by the first and second scores of estimated CIA axis for the gene space, while the figures in the third row show the distribution of samples in the protein space by the first and second score of estimated CIA axis. The value of d in the upper right part of each figure is the unit length of the grid in each figure

The plots in the second and the third row in Figure 1 show the gene and protein projections in their respective spaces. Labeled genes in each plot are top 50 genes that are the most extreme from the ends of each co-inertia axis and red color-labeled ones are commonly chosen in all three methods (Culhane et al., 2003). We observe that the sCIA and the ssCIA select similar sets of significant genes and proteins while their estimators are sparse compared to estimators of CIA. This suggests that our methods perform well in feature selection, important features are selected while less important features are neglected. Also, we observe that there is a group of genes and proteins projected onto the same direction in those plots across the methods and spaces. For example, the gene TGFBI is located in the bottom-end of the second axis in all figures in the second and third rows. Another observation we make is that the mesenchymal biomarker VIM is located in the left-end of the first axis while epithelial markers KRT7 and KRT19 are located at the right-end of the first axis of the gene space figures. Also, another epithelial maker CDH1 has high positive weight on the first axis of the protein space figures. These observations agree with the results from the figures in the first row. Those findings suggest that our penalized CIA methods give us biologically meaningful results.

We also conduct the pathway enrichment analysis for each selected genes and proteins in each method using ToppGene Suite (Chen et al., 2009). In general, both sCIA and ssCIA finds biologically meaningful results, while the ssCIA can detect more enriched pathways compared to the sCIA. The most highly enriched diseases in the selected genes from the sCIA and the ssCIA are neoplasma, tumor progression, glioma, non-small cell lung carcinoma, ovarian carcinoma, colon carcinoma and a number of other cancers such as leukemia, renal cell carcinoma and malignant tumor of colon. All those listed diseases are included in the list of diseases selected for the NCI60 cell line data. Pathways in cancer (Bonferroni adjusted q-value for sCIA: $5.07e^{-12}$, ssCIA: $5.26e^{-14}$), non-small cell lung cancer (Bonferroni adjusted q-value for sCIA: $4.48e^{-09}$, ssCIA: $1.03e^{-11}$) and many other cancers related pathways are enriched among the selected genes of results from our methods. We also find GO terms that are significantly enriched in the selected genes and proteins. In both the sCIA and the ssCIA results, highly enriched GO term include RNA binding (ID GO: 0003723), enzyme binding (ID GO: 0019899) and structural constituent of the ribosome (ID GO: 0003735) (Ross et al., 2000). GO terms related tissue development, metastasis are expected to be detected in the enrichment analysis of the first estimates since the first axis separates epithelial cancers. And we find that cell adhesion (GO: 0007155), extracellular matrix structural constituent (GO: 0005201) are enriched from both results of the sCIA and the ssCIA. There exists some other GO term such as structural molecule activity (GO: 0005198), structural constituent of cytoskeleton (GO: 0005200) that are related to cell structure but only enriched in the results of the ssCIA. From this, we confirm that the ssCIA enjoys the benefits of network information incorporated via network penalty.

6 Discussion

We proposed two sparse CIA methods that impose penalties on the CIA loading vectors. We use the l₁ penalty and the network penalty that utilizes the prior knowledge about relationships among variables. Our approach is useful when data is high dimensional, since estimated loading vectors from our model are sparse while explaining a similar amount of variation between two datasets as the CIA, particularly when the ssCIA is used and our methods are computationally efficient and scalable to analysis of high-dimensional -omics data. Regarding the scalability, computational complexity of our algorithms are discussed in Section B of the Supplementary Material. Numerical studies prove that our proposed penalized CIA methods achieve close performance compared to the CIA, with small number of selected variables. For the future research, we plan to extend the methods to multiple co-inertia analysis (MCIA) for analysis of more than two datasets.

Funding

This work is partly supported by NIH grants P30CA016520, R21NS091630 and R01GM124111. The content is the responsibility of the authors and does not necessarily represent the views of NIH.

Conflict of Interest: none declared.