Modeling the multi-scale mechanisms of macromolecular resource allocation

Abstract

As microbes face changing environments, they dynamically allocate macromolecular resources to produce a particular phenotypic state. Broad “omics” data sets have revealed several interesting phenomena regarding how the proteome is allocated under differing conditions, but the functional consequences of these states and how they are achieved remain open questions. Various types of multi-scale mathematical models have been used to elucidate the genetic basis for systems-level adaptations. In this review, we outline several different strategies by which microbes accomplish resource allocation and detail how mathematical models have aided in our understanding of these processes. Ultimately, such modeling efforts have helped elucidate the principles of proteome allocation and hold promise for further discovery.

Introduction

Microbes face transiently changing environments that require the expression of new proteins and the dilution or degradation of others. To adapt to these environmental changes, cells preferentially allocate these macromolecular resources to achieve certain objectives, a process typically referred to as “resource allocation.” The total amount and allocation of these proteins is fundamentally limited by constraints such as enzyme kinetics, cell size, and nutrient availability [1–4]. Therefore, microbes are regularly under selection pressure to optimize their resource allocation.

The macromolecular state of a cell can be measured using “omics” technologies, allowing insights into how resource allocation changes in a given condition. Omics data have revealed a highly skewed distribution of macromolecular resource allocation. For example, the most abundant 190 proteins in E. coli are estimated to account for about 60% of the total protein mass [5]. The functional consequences of such skewed macromolecular compositions—and how microbes regulate their state—are open questions. Over the past few years, studies that integrate omics and mathematical modeling have increased our knowledge of how microbes allocate macromolecular resources and of the genetic basis of these allocation strategies.

In this review, we summarize the current understanding of microbial resource allocation based on recent omics measurements from the perspective of biochemical networks. We discuss how computational models have been used to elucidate the functional significance of a cellular state and how these functions are linked to a genetic basis. We close with perspectives on promising directions for future modeling studies and the potential for examining resource allocation in the context of human health.

Proteome pre-allocation provides fitness benefits at a cost

The most direct way for microbes to alter the proteome is to synthesize proteins as needed. The maximum translation rate in E. coli is 16–20 amino acids per second per ribosome [6–8], implying synthesis in ~15 seconds for a copy of protein. However, protein abundances range from ~1 to >100,000 copies per cell [9], and ribosome abundances from ~7,000 to >70,000 per cell [7]. Therefore, during a nutrient shift where hundreds of thousands of additional protein copies can be needed [9], cells must utilize efficient strategies to dynamically allocate expression machinery resources. One strategy to minimize the delay of protein synthesis is to constitutively express proteins even when they are not immediately beneficial. This pre-allocation strategy incurs the cost of using up expression machinery that could be used to express immediately useful proteins, and a metabolic (energetic) cost of expression. Combined omics and modeling analyses have been used to test the hypothesis of pre-allocation.

In E. coli, up to half of expressed protein mass potentially provides no immediate benefit for a given growth condition [10]. Even when grown on glucose minimal medium, at least 13% of the proteins expressed confer no immediate fitness benefit based on ribosomal profiling and transposon mutagenesis [11]. Genome-scale model computations suggested that pre-allocating the E. coli proteome toward alternative carbon sources may provide a fitness benefit when alternative carbon sources are encountered [10].

Pre-allocation also applies to expressing more expression machinery than immediately needed to ensure fast expression rates when needed in a new environment. For example, when growing E. coli under feast-famine cycles, growth recovery during the feast phase was maximized by strategically allocating a ribosomal protein reserve [12].

These results suggest that omics data contain information both on the immediate response to the current environment and the regulatory program shaped by the organism’s evolutionary history. Computational models help to distinguish environment-specific response from pre-programmed responses shaped by evolutionary history.

Hierarchical regulation of resource allocation robustly improves fitness

Cellular metabolism has long been recognized to be regulated through a hierarchical network of regulatory processes [13]. The slow processes of transcriptional regulation and post-translational modifications act together with fast metabolite-level allosteric regulation to control metabolic fluxes [14,15]. Metabolites also modify transcription factors (TFs), leading to a coupling between metabolism and transcriptional regulation.

Recently, there has been increasing recognition of the importance of growth rate-associated global transcriptional regulation for resource allocation. For example, a recent study [16] showed that over 90% of transcriptional changes in 100 E. coli genes across 26 environments could be explained by a surprisingly small number of metabolite-TF interactions along with global regulation. In response to nutrient shifts, E. coli was found to use a global proteome reallocation strategy [17] instead of a theoretically optimal strategy of sequentially de-bottlenecking the rate limiting enzymes [18]. This apparently conservative strategy was hypothesized to be robust by confining metabolic bottlenecks to central precursors that drive global regulatory control [17].

However, growth rate-dependent regulation is not always dominant and appears to be context specific. A recent study subjected E. coli to a transient nutrient stress by starvation or by switching to a lower quality carbon source [19]. The study revealed a central role for proteome allocation in triggering the “persister” phenotype, a metabolically active but non-growing state with increased antibiotic tolerance [20]. Analysis of time-course proteomics from the nutrient-stressed cells (including persisters) and proteomics from other stress conditions (pH, temperature, and osmotic) revealed that proteome allocation was mainly driven by ppGpp-mediated regulation rather than a global growth rate effect [19]. Interestingly, a recent modeling study [21] showed that the optimal control strategy for E. coli to dynamically allocate resources during environmental changes involves an iterative on-off control strategy that resembles the structure of ppGpp-mediated regulation of ribosomal RNA transcription [22]. It thus appears that resource allocation under a variety of stresses may be mediated through overlapping mechanisms that are distinct from those of unstressed conditions.

Laboratory evolution aids in understanding the genetic basis of cellular resource allocation

Adaptive laboratory evolution (ALE) is an experimental method of serially passaging cells under a selection pressure. The outcome of ALE is a set of strains possessing adaptive mutations. ALE has now been automated [23], enabling large-scale production of evolved strains, followed by phenotyping and system-level characterization by DNA re-sequencing, RNA-Seq, ¹³C-metabolic flux analysis, etc. ALE has been used to reveal the genetic basis of growth rate-selection under various conditions: different carbon sources [24], thermal stress [25], osmotic and chemical stress [26,27], oxidative stress [27], and gene knockouts [28].

Multiple studies have connected the systems-level adaptations in an evolved strain to a genetic basis. For example, strains of E. coli were evolved for fast aerobic growth on glucose minimal media, yielding frequent key mutations in genes including rpoB and hns. Despite the potentially broad effects of mutations in these global regulators, the strains showed little change in intracellular metabolic pathway usage. Rather, the mutations enabled higher fluxes for glucose uptake, oxygen uptake, and central carbon metabolism [29]. Interestingly, TCA cycle enzymes have been reported to be transcriptionally repressed under similar selection pressure, yet TCA cycle metabolic flux did not decrease [29]. This result suggests potential nonlinearities between transcriptome abundance, proteome allocation, and flux capacity. A genome-scale model-based analysis further suggests that this nonlinearity arises in part from the flexibility of metabolic states that support optimal growth under these conditions [29]. Specifically, simulations showed that growth at 99% of the computed maximum rate could be supported by TCA cycle fluxes at 19% of the glucose uptake rate (GUR) but also as low as 8% of the GUR.

A recent study performed ALE under dynamic switching carbon sources, which led to either generalists or co-existing specialist subcommunities [30]. Transcriptomics and genome-scale modeling showed that the evolution of generalists versus specialists could be explained by the distance between computed metabolic states for two substrates [30]. Indeed, generalists evolved when the alternating substrates were metabolically “closer” and specialists evolved when metabolic states were more “distant.”

Network models capture the molecular basis of cellular resource allocation strategies

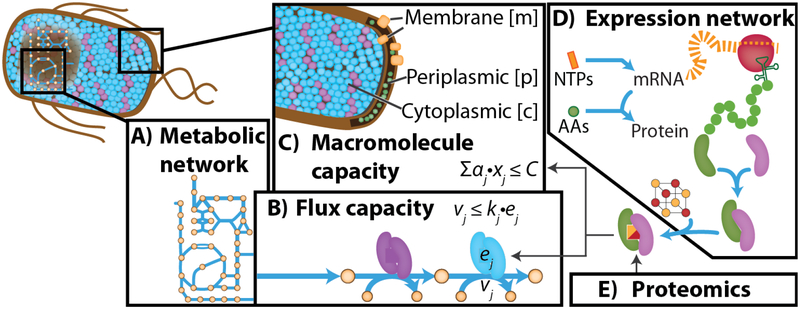
Biochemical network models, including genome-scale models of metabolism (M-models) [31,32] have traditionally been used to compute resource allocation at the level of small molecules and currency metabolites, such as NAD(P)(H) and ATP. GEMs were then extended to account for macromolecular resource allocation along two paths of development: (i) phenomenological (coarse-grained), and (ii) multi-scale (fine-grained) extensions to GEMs (Fig. 1). Here, we briefly review each category of models, followed by the new knowledge they have contributed.

Fig 1 |.

Network models of metabolism and macromolecule expression. (A) a metabolic network is reconstructed from the microbe’s annotated genome. (B) Metabolic flux (v_j) is constrained by catalytic efficiency (k_j) and enzyme abundance (e_j). This general form can be reformulated [34]. (C) Macromolecule (x_i) capacity is constrained based on its physical properties (a_j) such as molecular weight and a total cell capacity (C). Macromolecule abundance can be computed using a macromolecule expression network (D), which can vary in level of detail, or from proteomics data (E). To constrain total mRNA, RNA-Seq is used instead.

Beginning with FBAwMC (flux balance analysis with molecular crowding) [33], a series of methods have been developed to extend M-models with macromolecular resource allocation constraints [34–38]. While these models do not explicitly compute the cost of expressing proteins based on the expression machinery network, they have been effective for integrating omics data to address many specific questions in different microbes: e.g., the basis of hierarchical substrate uptake [33], overflow metabolism [36,38,39], and metabolic states at sub-optimal growth rates [34]. One method extended an M-model of E. coli by integrated growth laws and proteome sector constraints [39]. The proteome sectors were derived from previous studies showing that the E. coli proteome can be partitioned into five coarse sectors whose total mass abundance correlates linearly with growth rate [5]. This coarse-grained model had been used previously to show that overflow metabolism occurs because the proteome cost of energy biogenesis by respiration exceeds that by fermentation [1].

In S. cerevisiae, an M-model extension named GECKO was developed [38]. This method constrains metabolic fluxes based on enzyme abundances that are bounded by proteomics measurements, and turnover rates obtained from BRENDA [38]. GECKO enabled prediction of new phenotypes and reduced flux variability in over 60% of metabolic reactions.

Multi-scale models of metabolism and macromolecular Expression

In a parallel effort, multi-scale models of Metabolism and macromolecular Expression (ME models) have been developed. A multi-scale biological model has been defined as one that includes components from two or more levels of biological organization (length scales) or processes occurring much faster than others (time scales) while conserving information across scales [40–42]. ME models integrate reconstructions of the macromolecule expression machinery with metabolism, enabling simultaneous computation of these two temporally and organizationally distinct but coupled processes [43,44]. These models compute steady states of the integrated system using linear or nonlinear optimization; therefore, they face technical challenges (i.e., ill-conditioning [45–47]) that are distinct from dynamic multi-scale models (e.g., stiff systems of differential equations [41]) or agent-based models [48]. ME models account for up to 80% of protein mass under fast growth conditions [44]. Protein complex stoichiometry is available for 95% of complexes in the E. coli ME model, iOL1650 [49]. ME models have been expanded to account for protein translocation [4], the proteostasis network, and temperature dependence of protein activity and stability [50]. ME models have been used to improve in silico strain performance predictions [51] and for a variety of fundamental studies. We highlight some of these studies below.

ME models have been used to identify a core set of proteins that must be expressed (resources must be allocated) to sustain microbial growth by simulating growth across 333 conditions [52] Methods have been developed to calibrate ME models to improve prediction accuracy. One method defined constraints on the mass fraction of proteome sectors, and calibrated these sectors using proteomics from 15 carbon sources [9] to improve growth rate and flux predictions [53]. Further refinement of ME model parameters was achieved using an optimization pipeline that integrated proteomics, RNA-Seq, and fluxomics [54]. This pipeline enabled a genome-wide estimation of in vivo enzyme turnover rates, based on simulated reaction fluxes and measured protein abundances across four growth conditions. Intriguingly, 284 estimated turnover rates corresponding to high-flux metabolic reactions were relatively invariant across growth conditions [54]. This result suggests that once accurately measured, the turnover rates for these reactions may be applicable across many conditions. Prioritizing the measurement of these relatively invariant kinetic parameters may be one way to approach the larger challenge of measuring the entire “kinetome” (i.e., kinetics of all enzymes) [55].

ME models have enabled deeper investigation of limitation in micronutrients or stress responses. A ME model of E. coli correctly predicted shifts in fermentation versus oxidative phosphorylation pathways in response to iron availability [56]. This simulation provided a possible explanation for why Fur regulates acnA (a TCA cycle enzyme) in a dual-mode manner of direct activation under iron-replete conditions and indirect repression under iron starvation. In a study of acid stress response in E. coli, a ME model was used to compute the fitness benefit of three alternative stress relief systems [57]. The model predicted that the active proton transporter, ndh-cbo system was more efficient than gadABC or adiC, which was consistent with up-regulation of ndh-cbo under acid stress.

Very recently, the ME model of E. coli was extended to include part of the cytoplasmic proteostasis network, and to account for temperature-dependent protein stability and activity [50]. The model, called FoldME, recapitulated changes in growth rate as a function of temperature in three different media conditions. Additionally, the model computed the change in abundances for the approximately 450 proteins that were predicted to be expressed at a given temperature (ranging between 28°C to 45°C). Despite the lack of high-quality protein thermostability data for the majority of the 1,554 modeled proteins, temperature-dependent growth rate predictions were robust against parameter uncertainty [50].

Macromolecular expression networks have also been reconstructed for other organisms besides E. coli and T. maritima. A genome-scale model of the plant pathogen Ralstonia solanacearum was recently reconstructed, and it included macromolecule biosynthesis and secretion, host interaction, and DNA modification [58]. The macromolecule network included 135 reactions for macromolecule biosynthesis, and 165 reactions for secretion processes. The model could compute the cost of synthesizing virulence factors, including exopolysaccharides.

A genome-scale model of Bacillus subtilis integrated 72 cellular processes including metabolism, protein translation and folding, ribosome maturation, and flagella synthesis [37]. The model included 614 reactions, 467 metabolites and ions, and 672 protein-coding genes, and was solved using a new method called Resource Balance Analysis (RBA) [59]. While the metabolic and expression machinery networks are less detailed than a typical ME model, the RBA model parameters could be calibrated using proteomics data, enabling quantitative prediction of protein abundance in new environments. RBA showed that protein allocation for most cellular processes in B. subtilis agrees well with the growth rate maximization objective but that a few processes integrate more complex objectives such as stress or survival [37].

Models can identify simple biological principles and connect them back to biomolecular mechanisms

Mathematical models aid knowledge expansion by distilling complex data into simple principles that may be transferable to other biological systems or contexts. Examples include phenomenological models that describe bacterial growth laws that dictate the allocation of proteome sectors [5,60]https://paperpile.com/c/ZDFrmo/j1wl+3H60. Computational models of microbes have been increasing in detail, with detailed models such as the whole-cell model of Mycoplasma genitalium [61] and ME models for T. maritima [62] and E. coli [43,44] being examples of detailed biomolecular and biochemical network models. We posit that such models help to reveal principles from complex interactions and data with the added benefit of connecting these principles back to biomolecular mechanisms and specific genes that can be validated using omics.

For example, Chen et al. [50] simulated growth, metabolism and response of the chaperone network under thermal stress and recovered a simple, linear “growth law.” This linear relationship described the mass fraction of ribosomes, molecular chaperones, and metabolic enzymes as a function of temperature and growth rate. The study additionally showed that thermosensitivity of growth was attributable not to a few rate-limiting enzymes but to many enzymes. Thus, in addition to computing the global consequences of thermal stress, the model also could enumerate plausible biomolecular responses.

Conclusions and Outlook

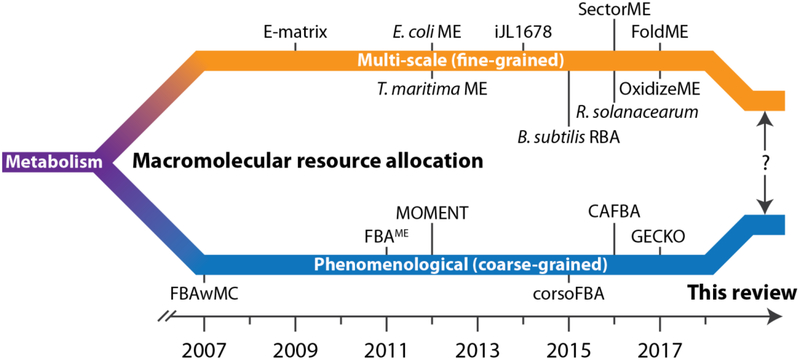
Our current understanding of cellular resource allocation has expanded toward a deeper appreciation of the coupling between regulatory processes across multiple biological scales. Fast metabolite-level regulation feeds back into slow transcriptional regulation, which in turn is hierarchically organized into general growth-associated regulation, global transcriptional programs, and local regulons. Advances in omics technologies and accumulation of multi-omics data have provided readouts of cellular state at these multiple biological scales. More than ever, there is a need for multi-scale network models that integrate these scales. Genome-scale models have risen to this challenge from two directions (Fig. 2). One is developing multi-scale reconstructions of macromolecular expression networks that are integrated with metabolism. This approach, while powerful, is time-consuming and has led to reconstructions for two different organisms so far. Research to accelerate reconstruction of these networks is ongoing [63]. The second approach is extending existing metabolic reconstructions with coarse-grained (phenomenological) constraints and variables that incorporate macromolecular abundance and catalytic efficiency. Based on these advances, we suggest two parallel, near-term efforts.

Fig 2 |.

Developmental paths of genome-scale resource allocation models. Models or algorithms listed are: FBAwMC [33], FBA^ME (Membrane Economics) [36], MOMENT [35], corsoFBA [34], CAFBA [39], GECKO [38], E-matrix [64], E. coli ME [43,44], T. maritima ME [62], iJL1678 (E. coli ME with the protein translocation network) [4], B. subtilis RBA [37], R. solanacearum [58], SectorME [53], FoldME [50], and OxidizeME [65].

First, there is a need to continue detailed reconstruction of non-metabolic processes. For the E. coli ME model, ~20% of protein mass is not modeled for rapidly growing cells [44]. Approximately half of this mass is allocated toward proteostasis and stress response [10]. The recent study of E. coli thermosensitivity has taken first steps toward a detailed reconstruction of the proteostasis network and thermal stress response [50]. Reconstructing periplasmic protein homeostasis and response to additional key stresses (oxidative, acid, osmotic, etc.) are likely to be achievable in the near future.

Second, we suggest a systematic interplay between detailed macromolecule expression reconstructions and coarse-grained resource allocation models as an attractive direction for future modeling studies. In principle, a model’s scope and scale should match the requirements (biological question and available data) of a specific study but this selection process is not trivial and often iterative [48]. ME models currently provide highly detailed reconstructions of expression networks integrated with metabolism. While reliable methods are now available to solve these multi-scale and nonlinear models [46,47], they are still computationally expensive. Methods for metabolic network reduction [66–68] may be adopted to macromolecular networks to reduce complexity. Additionally, methods to systematically coarse-grain selected parts of complex models into phenomenological constraints having few parameters may benefit future studies [69–71].

Cellular resource allocation has applications for microbial cell factory design [51] and also in the context of infectious disease. For example, recent evidence suggests that the persister cellular state, which contribute to chronic infection, may be regulated by a limitation in certain metabolic fluxes that triggers resource reallocation from growth to stress protection [19,72]. Another study used M-models to show that the environment alters the cost-benefit tradeoff of antibiotic resistance mutations through a change in metabolic state [73]. Additionally, antibiotic lethality by certain bactericidal antibiotics directly or indirectly affect macromolecular processes but the mechanisms of lethality are not fully known [74]. Future modeling studies of cellular resource allocation may thus provide new directions for therapeutic interventions against infectious disease.

Highlights.

• Microbes allocate macromolecular machinery to perform different tasks

• Proteome pre-allocation and hierarchical regulation give fitness benefits at a cost

• Examining evolution helps elucidate the genetic basis of cellular resource allocation

• Macromolecular resource allocation can be modeled by coarse-grained constraints

• Detailed reconstructions of macromolecular expression networks are growing in number