A Bayesian model-free approach to combination therapy phase I trials using censored time-to-toxicity data

Summary

The product of independent beta probabilities escalation (PIPE) design for dual-agent phase I dose-escalation trials is a Bayesian model-free approach for identifying multiple maximum tolerated dose combinations of novel combination therapies. Despite only being published in 2015, the PIPE design has been implemented in at least two oncology trials. However, these trials require patients to have completed follow-up before clinicians can make dose-escalation decisions. For trials of radiotherapy or advanced therapeutics, this may lead to impractically long trial durations due to late-onset treatment-related toxicities. In this paper, we extend the PIPE design to use censored time-to-event (TITE) toxicity outcomes for making dose escalation decisions. We show via comprehensive simulation studies and sensitivity analyses that trial duration can be reduced by up to 35%, particularly when recruitment is faster than expected, without compromising on other operating characteristics.

1. Introduction

The majority of anti-cancer therapeutic strategies consist of giving patients two or more treatments together to provide improved treatment effects relative to individual therapies given alone. In phase I trials of novel combination therapies, the aim is to identify one or more Maximum Tolerated Dose Combinations (MTDCs); that is one or more dose combinations with an expected probability of causing a severe drug-related adverse event equal to or close to a target of interest, known as the Target Toxicity Level (TTL). Once identified, larger comparative trials are conducted to compare the efficacy of the MTDC(s) of the new combined treatment regimen to standard care, in the hope of improving patient response and survival outcomes.

Similar to phase I trials for monotherapies, trials of two treatments combined are conducted as dose-escalation studies. In these, patients are allocated to a dose combination and observed over time, with the number and severity of adverse events recorded. Based on these data, the next cohort of patients may receive the same combination or a different combination; if the current dose combination is considered tolerable (e.g. no adverse events reported), the next cohort may receive a combination with only one drug increased, or both drugs increased simultaneously. By gradually exploring the dose-toxicity grid, we aim to identify MTDCs whilst minimising the chance of overdosing patients in the trial.

Several approaches for designing phase I dose-escalation studies on drug combinations have been proposed (Harrington et al., 2013); these include rule-based and model-based trials. Mander and Sweeting (2015) proposed a probabilistic model-free approach, the product of independent beta probabilities escalation (PIPE) design. The PIPE design does not assume a model for the dose-toxicity surface; each dose combination is assigned a beta prior distribution, independent of all other combinations, which is updated with trial data. The tail probabilities of each combination being above the TTL are calculated and used to estimate the chance that a particular contour dividing the dose-toxicity surface into two areas of tolerable and intolerable combinations is the true Maximum Tolerated Contour (MTC). This approach gives sensible estimation of toxicity risks when the dose toxicity surface can not be well-approximated by a model (e.g. if the surface is asymmetric) and, unlike many rule-based designs, allows borrowing of information across dose combinations. The PIPE design has been implemented in practice in trials: a study of the monoclonal antibody Emactuzumab and RO7009789 in combination in participants with advanced solid tumours (ClinicalTrials.gov Identifier: NCT02760797); and ORCA-2, a dose-and-schedule finding trial of olaparib given with cisplatin-based chemoradiotherapy to patients with advanced squamous cell head and neck cancer (ClinicalTrials.gov Identifier: NCT02308072). Since radiotherapy is used in the ORCA-2 trial, late-onset treatment related toxicities are expected and the DLT observation window is 14 weeks from the first administration of olaparib.

One requirement of many phase I trials is that the endpoint (often binary DLT outcome of Yes or No) has to be observed before making dose-escalation decisions. Trials with a long DLT observation window, for example radiotherapy trials such as ORCA-2, may have a long planned duration and therefore a large cost. Furthermore, the underlying patient population may change over time if the trial is planned to last a long time; patient drift may affect which combinations are considered to be tolerable and intolerable (Villar et al., 2015). In addition, rapid recruitment may mean that we cannot assign suitable patients to trial treatments because we must wait for outcomes to be obtained from current patients. Patients waiting may have their treatment delayed, or in the worst case may never receive treatment due to death. To overcome these problems, time-to-event (TITE) outcomes have been proposed for use in single-agent dose-escalation studies (Cheung and Chappell, 2000; Braun, 2006; Ivanova et al., 2016). Rather than an outcome of 0 or 1, a patient’s outcome measured at any point during their DLT observation window is a function of the time for which they have yet to be observed, conditional on the patient not yet experiencing a DLT. Wages et al. (2013) applied the time-to-event continual reassessment method (TITE-CRM) (Cheung and Chappell, 2000) to dual-agent trials by exploiting partial orders of dose-toxicity probabilities per dose combination. They were able to shorten trial durations by 84% – 89% in several scenarios, in which only one combination was the MTDC and patients were treated when they arrived. However, multiple MTDCs may exist when combining treatments and a one-parameter CRM model is insufficient to identify multiple MTDCs. Furthermore, the number of possible partial orders increases exponentially as the number of dose levels per agent is increased.

We propose an approach for extending the model-free PIPE design by using a TITE outcome measure. We use the proportion of a patient’s DLT observation window that has passed since the time of treatment administration, with DLT unobserved, as a form of censored toxicity response. Even if some patients have not completed follow-up, dose-escalation decisions can still be made and trial duration can be reduced. We call this proposed method TITE-PIPE. Section 2 outlines the TITE-PIPE methodology and in Section 3 we describe and present comparative simulation studies to compare the performance of TITE-PIPE against PIPE with respect to experimentation, recommendation and trial duration. In Section 5 we conclude with a discussion of our findings and provide practical considerations as well as areas for future research.

2. Methodology

Consider a dual-agent phase I trial of J dose levels of agent A, {a₁, . . . , a_J}, and K dose levels of agent B, {b₁, . . . , b_K}. Let Y_i,t be a binary random variable that takes value 1 if at time t′ ≤ t patient i has experienced a DLT, and 0 otherwise. Note that if Y_i,t = 1, then Y_i,t′ = 1 ∀t′ ≥ t. Let t_i0 be the time at which patient i begins treatment, and let U_i ≥ 0 be a random variable denoting the time from t_i0 at which patient i experiences a DLT. We assume that each patient’s DLT observation window is T time units. Then, for DLT observation period [t_i0, t_i0 + T], the random variable Y_{i,ti0 +T} |U_i, that is the indicator of whether patient i has had a DLT by the end of their DLT observation period conditional on their time to DLT being equal to U_i, is

$$Y_{i,t_{i0}+T}|U_i=\{\begin{array}{ll}1\hfill & \text{if}{U}_i\in [0,T]\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$

and therefore the distribution of Y_i,ti0+T is Bernoulli with probability ℙ(U_i ∈ [0, T]). Ultimately our aim is to estimate the risk of a patient experiencing a DLT in their DLT observation window [t_i0, t_i0 + T]. However, we would also like to consider what the risk of Y_i,ti0+T equalling 1 is when we have only observed data up to any time t ∈ [t_i0, t_i0 + T] without observing U_i, i.e. ℙ(U_i ∈ [t − t_i0, T]|U_i ≥ t − t_i0). Therefore, we may use the censored time to DLT for patient i part-way through their DLT observation period to help us in this end.

2.1. Weighted outcomes

Let w_i,t be the weighted outcome for patient i who begins treatment at time t_i0 and is observed at time t ∈ [t_i0, t_i0+ T ]. We may define w_i,t as

$$w_{i,t}=\{\begin{array}{ll}1\hfill & \text{if}{y}_{i,t}=1\text{and}t\le t_{i0}+T\hfill \\ \varphi (t;t_{i0},T)\hfill & \text{if}{y}_{i,t}=0\text{and}t\le t_{i0}+T,\hfill \end{array}$$ (1)

where 0 ≤ ϕ(t; t_i0, T) ≤ 1 ∀t and ϕ(t; t_i0, T) is decreasing with increasing t. So if patient i has a DLT by time t ∈ [t_i0, t_i0+ T], then w_i,t = 1. Conversely, if patient i has not had a DLT observed by time t_i0 + T, then w_{i,tio +T} = 0. Otherwise, non-observance of a DLT at time t ∈ [t_i0, t_i0+ T] gives w_i,t = ϕ(t; t_i0, T) → 0 as t → t_i0 + T. At time t_i0 + ξ for small ξ, we may want to have w_i,t close to 1, as we are assigning patient i to dose combination (a_j, b_k) with the belief that at time t_i0, dose combination (a_j, b_k) has DLT probability close to the TTL, and escalation to higher dose combinations for patient i + 1 is not yet advisable. In the TITE-CRM, Cheung and Chappell (2000) proposed using a uniformly decreasing weight function, i.e.

$$\varphi (t;t_{i0,}T)=1-\frac{t-t_{i0}}{T},$$ (2)

such that in the absence of a DLT, the rate of change in the weighted outcome is constantly decreasing with time, i.e. $\frac{d}{dt}\varphi (t;t_{i0},T)=-1/T,\forall t\in [t_{i0},t_{i0}+T].$ An alternative weight function proposed by Cheung and Chappell (2000) adapted weighted outcomes dependent on whether previous DLTs had been observed towards the start or end of the observation window. If more DLTs are observed towards the end of the interval, then a higher weight is given to a patient who has yet to have a DLT and not reached the latter part of the observation window (relative to the uniform case in equation 2). Similarly, if the majority of DLTs are observed at the start of the observation window, a patient’s weighted outcome towards the end of the DLT observation window will be lower relative to the uniform case. Specifically, for the set of z ordered DLT times ${𝒰}_z$ = {u₍₁₎, u₍₂₎, … , u_(z)} that occur in the DLT observation window such that 0 ≡ u₍₀₎ < u₍₁₎ ≤ ⋯ ≤ u_(z) < u_(z+1) ≡ T,

$$\varphi (t;t_{i0},T,{𝒰}_z)=1-\frac{1}{z+1}\left(\kappa +\frac{t-t_{i0}-u_{(\kappa )}}{u_{(\kappa +1)}-u_{(\kappa )}}\right),$$ (3)

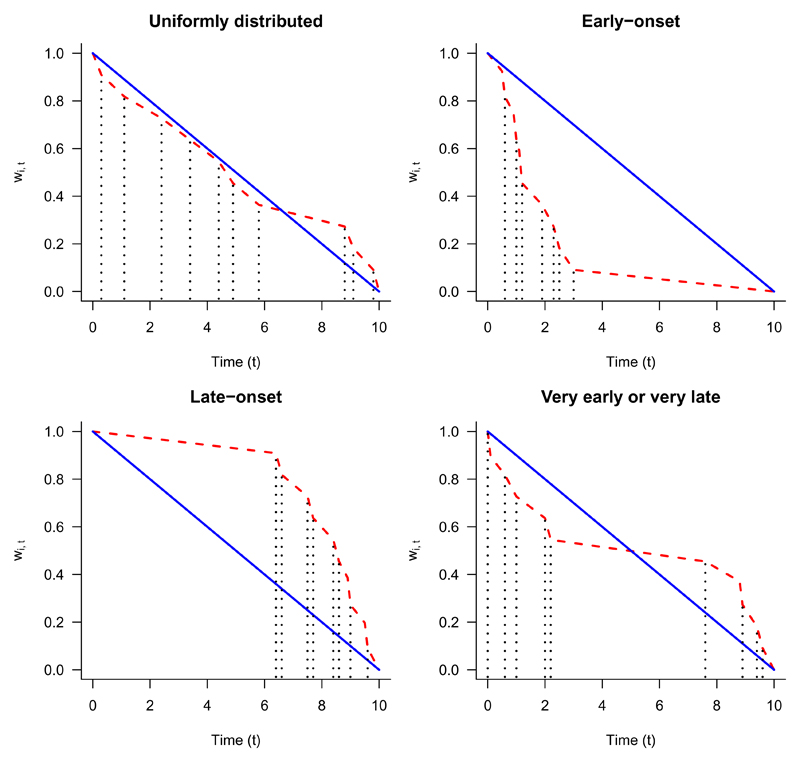
where κ = max_0≤h≤z{h : t − t_i0 ≥ u_(h)}. Figure 1 shows examples of both the uniformly decreasing and adaptive weight functions based on different time-to-toxicity distributions during the DLT observation window.

Fig. 1.

Adaptive weight function (red dashed line) and Uniform weight function (blue solid line). DLT times (vertical black dotted lines) alter slope of adaptive weight function.

2.2. Posterior DLT probabilities

Regardless of the choice of weighting function, we may use the following approach to incorporate censored DLT outcomes into posterior estimates for the probability of DLT per dose combination. Assume our prior uncertainty of the probability of DLT π_jk for dose combination (a_j, b_k) can be represented by a Beta(r_jk,0, s_jk,0) distribution. As per Mander and Sweeting (2015), we specify r_jk,0 and s_jk,0 such that the prior median is equal to a pre-specified value ${\widehat{\pi }}_{jk}$ (i.e. for Beta cumulative distribution function ℬ(υ; r_jk,0, s_jk,0), $ℬ({\widehat{\pi }}_{jk};r_{jk,0,}{s}_{jk,0})=0.50)$ and the effective sample size at dose combination (a_j, b_k) is r_jk,0 + s_jk,0 = 1/(J ×K). Therefore, the effective sample size across all dose combinations is equal to one patient. Assume n_jk,t patients, have been assigned to dose combination (a_j, b_k) at time t, and these patients’ identifiers are contained in the indexing set ℐ_jk,t. Let R_jk,t = ∑_i∈ℐjk,t w_i,t and S_jk,t = ∑_i∈ℐjk,t (1 − w_i,t) = n_jk,t − R_jk,t be the total number of weighted DLTs and weighted non-DLTs observed for patients in ℐ_jk,t. The likelihood function arising from these data is binomial, specifically

$$L({\pi }_{jk}|R_{jk,t,}{S}_{jk,t})\propto {\pi }_{jk}^{R_{jk,t}}{(1-{\pi }_{jk})}^{S_{jk,t}}.$$

Since the beta prior is conjugate for the binomial likelihood function, the posterior probability distribution of π_jk at time t is also beta distributed, i.e. π_jk ~ Beta(r_jk,0 + R_jk,t, s_jk,0 + S_jk,t). This provides a working model for each π_jk, which are independent. Therefore no assumptions are made regarding the marginal dose-toxicity relationship of each agent, specifically that the marginal probabilities are monotonically increasing; i.e. π_jk ≤ π_(j+1)k and π_jk ≤ π_j(k+1). Monotonicity is introduced through the maximum tolerated contour.

2.3. Posterior contour probabilities

As proposed by Mander and Sweeting (2015), we may use the posterior distributions of π_jk to construct a Maximum Tolerated Contour (MTC), which satisfies the assumption of monotonicity. A monotonic contour C can be defined by a J × K binary matrix, such that C[j, k] = 1 if dose combination (a_j, b_k) is above the contour (i.e. it is considered intolerable) and C[j, k] = 0 if it is below (i.e. it is considered tolerable). Let ℱ_t be the set of all trial data available at time t, with ℱ_jk,t ⊆ ℱ_t being the set of all data available at dose combination (a_j, b_k) at time t (i.e. ℱ_jk,t = {∪_i∈ℐjk,t(w_i,t, y_i,t)}; ℱ_t = ∪_j,k ℱ_jk,t). Let p(ℱ_jk,t) be the posterior probability that the toxicity risk at dose combination (a_j, b_k) at time t is less than TTL θ, i.e.

$$p\left({ℱ}_{jk,t}\right)=\mathbb{P}\left({\pi }_{jk}\le \theta |{ℱ}_{jk,t},r_{jk,0},s_{jk,0}\right)=F\left(\theta ;{ℱ}_{jk,t},r_{jk,0},s_{jk,0}\right).$$ (4)

Let r₀ and s₀ be the vectors of prior hyperparameters. A general formula for the probability that the MTC is the contour defined by matrix C_l is

$$q_l\left(F_t\right)=\mathbb{P}\left(MTC=C_l|F_t,{\mathit{r}}_0,{\mathit{s}}_0\right)={{\displaystyle \prod _{j,k}{\left[1-p\left({ℱ}_{jk,t}\right)\right]}^{C_l\left[j,k\right]}\left[p\left({\mathit{\text{ℱ}}}_{jk,t}\right)\right]}}^{1-C_l\left[j,k\right]}.$$ (5)

Here C_l belongs to $𝒞=\left\{C_l:l=1,\dots ,\left(\begin{array}{c}J+K\\ J\end{array}\right)\right\},$ the set of all contours that do not violate the marginal assumptions of monotonicity. Assuming the MTC must be one of these monotonic contours, the q_l(F_t) are rescaled to form a distribution function, i.e.

$${\tilde{q}}_l\left(F_t\right)=\frac{ql\left(F_t\right)}{{\displaystyle {\sum }_{g=1}^{\left(\begin{array}{c}J+K\\ J\end{array}\right)}{q}_g\left(F_t\right)}},$$ (6)

and we may, for simplicity, select the MTC $C_t^{*}$ to be the modal contour at time t, i.e. $C_t^{*}=\arg {\max }_{C_l\in 𝒞}\left\{{\tilde{q}}_l\left(F_t\right)\right\}.$

2.4. Dose allocation

Patient allocation to a dose combination can follow similar procedures as specified by Mander and Sweeting (2015). However, with TITE-PIPE we do not necessarily need to wait for a patient’s follow-up to be complete before allocating doses for the next patient(s). We shall assume the following setup. The study starts at time t = 0, when the first patient enters. A minimum of c patients must be dosed at a combination before experimentation elsewhere can take place, and patients are followed up for a maximum of T time units (e.g. week, month). Under TITE-PIPE, though patients enter the study on their arrival time, regardless of whether previous patients have completed follow up or not, we employ a constraint that the first c patients in the trial (who are given the lowest dose combination (a₁, b₁)) must have completed follow-up before new patients can enter the study. For each variant of TITE-PIPE, we specify two allocation criteria that may be used:

• a)completed dose: at least c patients must have completed their follow-up on a particular dose-combination before any more patients can be assigned to other dose combinations. We denote this as TITE-PIPE-C;
• b)on dose: at least c patients must have been assigned to a dose combination before any more patients can be assigned to other dose combinations. We denote this as TITE-PIPE-O.

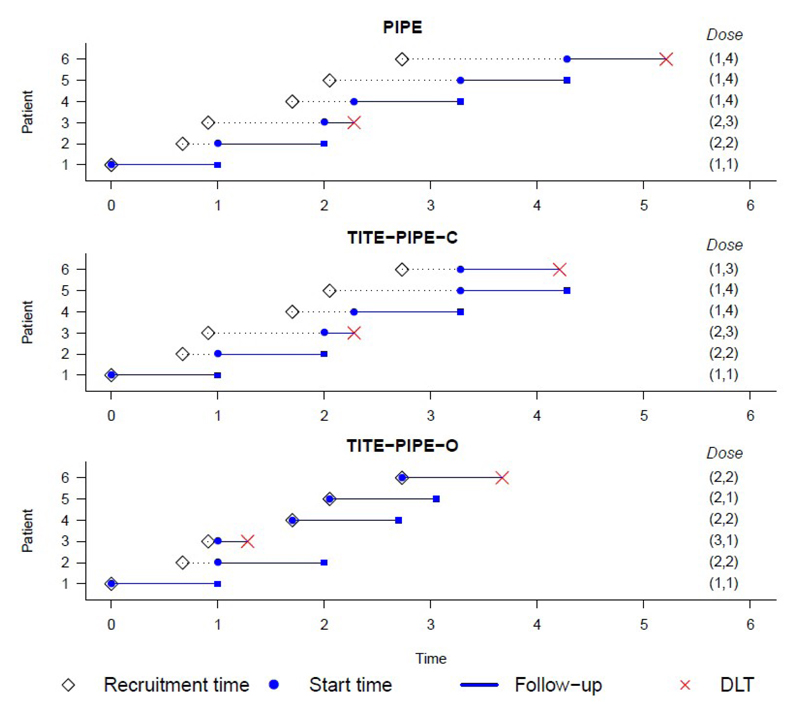
Under TITE-PIPE-O, c patients may be assigned to a dose combination and then immediately after, a decision can be made on where to dose the next patient; this may not be ethical, but is worthy of investigation (Senn et al., 2007; Bird et al., 2017). Under TITE-PIPE-C, though we cannot make a dose-escalation decision for the next patient until c patients have completed their follow-up, if another patient is recommended to the same combination (i.e. c + 1 patients are now on the current dose combination), we may make decisions on where to dose future patients mid-way through the follow-up of patient c + 1. This satisfies ethical constraints (i.e. we have at least c patients’ worth of complete follow-up data on the combination), but trial duration may be reduced relative to the PIPE design where all patients must have completed follow-up before escalation decisions are made. Under both TITE-PIPE-C and TITE-PIPE-O, if two or more patients arrive at the same time, then admissible dose assignments are calculated after each individual patient has been assigned to treatment; this was also undertaken in a trial of clofarabine in combination with fractionated gemtuzumab ozogamicin in patients with refractory or relapsed acute myeloid leukaemia (Foster et al., 2012; Ivanova et al., 2016). Figure 2 illustrates how the trial entry and arrival process works under each design (PIPE, TITE-PIPE-C, TITE-PIPE-O) for a cohort size of one patient.

Fig. 2.

Example arrival and trial entry times from one simulated trial (patients arriving as Poisson process with mean = 1.25; same random number seed used across designs). For PIPE, each patient must have completed follow-up or have a confirmed DLT reported before the next patient (if one has been recruited) can enter the study. For both TITE-PIPE designs, the first patient on study is required to have completed follow-up before more patients are assigned to dose combinations. For TITE-PIPE-C design, at least one patient per combination must have completed follow up before future patients can be assigned to dose combinations. Otherwise (and for TITE-PIPE-O design), patients can enter the trial upon arrival.

When we are ready to allocate patients to a combination, dose combinations are selected based on the following rules (Mander and Sweeting, 2015):

• a)Neighbouring dose combinations; escalation can be to doses that are within at most one dose level of the previously experimented combination;
• b)Diagonal dose escalation (increasing doses of both drugs simultaneously) is permitted;
• c)Closest dose combinations to the estimated MTC; admissible dose combinations for the next cohort are those that are closest to the MTC (see Mander and Sweeting (2015) for further details);
• d)Minimum sample size for ties; if multiple dose combinations are permitted, then choose the one with the fewest patients assigned to it. If there are still multiple combinations to choose from after these rules, the next patient is randomly assigned to one such combination with equal probability.

2.5. Early termination

The trial is terminated either when the maximum sample size is reached, or if one of the following stopping rules is satisfied.

Let ${𝓖}_{jk\text{,}t}$ be the set of all available trial data collected from patients that have completed their follow up (either had a DLT, or not had a DLT during their entire DLT observation window) at dose combination (a_j, b_k), i.e. ${𝓖}_{jk\text{,}t}$ = {∪_i∈ℐjk,t (w_i,t, y_i,t) : (w_i,t, y_i,t) = (0, 0) ∪ y_i,t = 1}. Let ${𝓖}_t$ = ∪_j,k ${𝓖}_{jk\text{,}t}$ and ${\tilde{q}}_{\text{unsafe}}({𝓖}_t)$ be the probability that the monotonic contour defining all dose combinations as unsafe, denoted C_unsafe, is the MTC (computed using Equation 6, conditional on complete follow-up data only). The trial is terminated early if ${\tilde{q}}_{\text{unsafe}}({𝓖}_t)\ge ϵ,$ where ϵ is some threshold to be calibrated before the trial. In words, the trial is terminated early if, using completed follow-up data only, the probability that the lowest dose combination is above the MTC is at least ϵ. Only data from patients who have completed follow-up are used to mitigate stopping early when several patients are still in observation; if they were to not experience DLT, the trial could have continued.

Furthermore, we adopt a safety rule similar to that of Ivanova et al. (2016); if the trial is deemed safe to continue by the aforementioned stopping rule $({\tilde{q}}_{\text{unsafe}}({𝓖}_t)<ϵ),$ but the inclusion of data from patients currently in observation means that all combinations are inadmissible for the next patient, we wait until all patients currently under observation have completed their follow-up. Mathematically, we say dose combination (a_j, b_k) is inadmissible if ${\zeta }_{jk}(F_t)={\sum }_{C_l\in 𝒞}{C}_l[j,k]{\tilde{q}}_l(F_t)\ge ϵ;$ if ζ_jk (F_t) ≥ ϵ ∀j, k, recruitment is suspended until all patients on trial have completed follow-up. We may then reassess whether to terminate the trial or not using ${\tilde{q}}_{\text{unsafe}}({𝓖}_t)$ and if the trial is to continue, decide what combination the next patient should receive. This prevents stopping the trial based on incomplete data, and allows for a thorough assessment of the safety of the dose combinations before enrolling future patients.

2.6. Maximum Tolerated Dose Combinations (MTDCs)

At the end of the trial, say time t = t*, the modal MTC $C_{t^{*}}^{*}=\arg {\max }_{C_l\in 𝒞}\{{\tilde{q}}_l({𝓖}_{t^{*}})\}$ is estimated. All dose combinations that lie closest to $C_{t^{*}}^{*}$ from below that have been experimented on are declared as MTDCs (Mander and Sweeting, 2015).

3. Simulation study

We now compare the original PIPE design, where new patients are admitted either once a DLT has been observed in the previous patient, or the previous patient has completed their follow-up period, with TITE-PIPE-C and TITE-PIPE-O via simulation. In our studies patients will be observed for T = 1 time unit; if patient i enters the study at time 13.2 they will be followed up until time 14.2, or until a DLT is observed, whichever occurs first.

For our simulations we use the seven dose-toxicity scenarios presented as Simulation 2 in the original PIPE paper (Mander and Sweeting, 2015) (4-by-4 dose-toxicity grids also used by Braun and Jia (2013)). We assume a priori median dose-toxicity values are those shown in Scenario A (Table 1). The TTL θ is 0.20. The threshold ϵ at which doses are considered inadmissible (and also for early termination of the trial) is calibrated to be 0.80, such that the trial is terminated if the first two patients, who are both treated at combination (a₁, b₁), experience DLTs.

Table 1.

Dose-toxicity scenarios for simulation study. Combinations marked in bold have DLT probability of 20% ± 2%. Maximum Tolerated Contour (MTC) shown as solid line bisecting dose-toxicity grid.

	Drug A		Drug A
Scenario A		Scenario E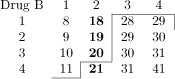
	Drug A		Drug A
Scenario B		Scenario F
	Drug A		Drug A
Scenario C		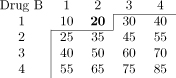Scenario G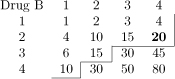
	Drug A
Scenario D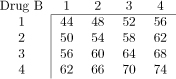

3.1. Dose toxicity models

We consider three models for dose-toxicity, which simulate toxicity onset as uniformly distributed, early-onset or late-onset. Similar to work by Cheung and Chappell (2000) and Braun (2006), these are as follows:

• a)Uniform (conditional uniform model): 1) generate a random variable to determine if patient i has a DLT; 2) if patient i does have a DLT, generate that patient’s time from treatment initiation to DLT, U_i, from a Uniform distribution over the interval [0, T];
• b)Early-onset (Pareto model): time from treatment initiation to DLT for patient i is Pareto-distributed with a mode of 0.20 time units and scale parameter chosen per dose combination so that the cumulative distribution function at time T is that combination’s toxicity probability;
• c)Late-onset (Weibull model): time from treatment initiation to DLT for patient i is Weibull-distributed with a fixed shape parameter of 4 and scale parameters chosen per combination so that the cumulative distribution function at time T is that dose combination’s toxicity probability.

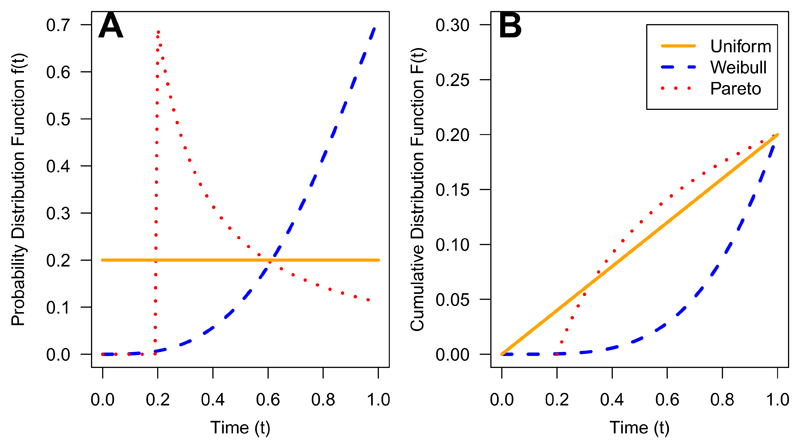
Figure 3 shows the probability distribution functions and cumulative distribution functions for the time-to-toxicity distributions under the uniform, Pareto and Weibull models specified above.

Fig. 3.

Probability Distribution Function (A) and Cumulative Distribution Function (B) of Uniform, Weibull and Pareto distributions for time to toxicity over DLT observation window [0, 1](true DLT probability at dose combination of 0.20).

Arrival times of patients are generated from a Poisson process with rate λ (the average number of patients expected per time unit), with λ ∈ {0.5, 1, 2}. With three arrival rates and three toxicity generation models, we have nine simulation environments per dose-toxicity scenario. For each simulation environment, we investigate the performance of PIPE, TITE-PIPE-C and TITE-PIPE-O; for each TITE-PIPE approach we compare the uniform weighting function (equation 2) and the adaptive weighting function (equation 3). We simulate 2000 trials per simulation environment using a maximum sample size of 40 patients.

3.2. Operating characteristics to compare

We compare the three designs and allocation rules using the following operating characteristics:

• a)Experimentation percentages, i.e. the percentage of patients assigned to dose combinations within a specific DLT probability range;
• b)MTDC recommendation percentages, i.e. the probability that at the end of the trial, dose combinations within a specific DLT probability range are identified as MTDCs (multiple combinations may be recommended);
• c)Trial duration (time until trial is terminated or last patient completes their followup);
• d)Sample size (since some trials may terminate early).

3.3. Computational set-up

Simulations were undertaken in R using code adapted from the pipe.design package (Sweeting, 2016) (functions incorporated into latest version of package). We use the same sequence of random seeds between each simulation environment to provide comparable operating characteristics.

4. Results

4.1. Illustrative single trial

Before presenting the results from the simulation study, we provide a single illustrative trial of 40 patients (Figure 4). Sixteen dose combinations formed from four dose levels each of Drug A and Drug B were under investigation, with the aim of targeting one or more MTDCs with θ = 0.20. Patient arrival times were simulated as a Poisson process with rate λ = 2 (i.e. an average arrival rate of 2 patients per time unit), and patients were followed up for T = 1 time units. DLTs and their times were simulated from Scenario A under a conditional uniform model, with uniform weighting assigned to unobserved DLTs. We conducted this trial using TITE-PIPE-C, and required two patients to have completed treatment on a dose combination before another combination may be considered for exploration.

Fig. 4.

A single illustrative trial using TITE-PIPE simulated over Scenario A, with θ = 0.20. At least two patients were required to have completed treatment on a dose combination before a new combination could be considered for future patients. Combinations marked m(n) + r(s) indicate that of m patients with complete follow-up, n have experienced DLT, and of r that have been assigned to the same combination, s patient-time units are unobserved and therefore count as DLTs at time t. MTC denoted by solid black contour. Safety threshold denoted by dashed red contour. True MTC denoted in MTDC recommendations figure by blue dot-dashed line.

No DLTs were observed in the first four patients (two on (a₁, b₁), two on (a₂, b₂)). Combination (a₃, b₂) was given to two new patients, one of whom experienced DLT. The modal MTC and safety constraint were updated and patients 7 and 8 were given (a₄, b₁); this combination is closest to the MTC and admissible. At t = 4.93, patients 7 and 8 completed their follow-up (with no DLTs occurring), and patients 9 and 10 are allocated to (a₄, b₁) and (a₃, b₁) respectively. Since two patients are required at each dose level in our example trial, patient 11 also received (a₃, b₁). After these three patients completed their DLT follow-up at t = 5.93 (n = 11), patient 12 was allocated to (a₃, b₂); this combination was below the safety contour after 11 patients and closest to the modal MTC.

At t = 12.37, 20 patients have been treated. Due to rapid recruitment, two patients were available for treating at this time. Therefore patient 21 was administered (a₁, b₄) and the MTC re-estimated (similar to that of the clofarabine plus fractionated gemtuzumab ozogamicin trial (Foster et al., 2012)). Patient 22 was given (a₁, b₃), as it was admissible and at least two patients had previously completed treatment at that dose. By t = 12.78, just before patient 25 begins treatment, patients 23 and 24 had been dosed at (a₁, b₃) and (a₂, b₂) respectively, and four patients had partially completed their DLT follow up (patients 21-24). Therefore, based on the best estimate of the MTC and safety constraints, patient 25 was assigned to (a₃, b₁). This procedure was repeated until all 40 patients had received treatment. Three MTDCs, (a₁, b₃), (a₃, b₂) and (a₄, b₁) were recommended at the end of the trial, with true DLT probabilities of 0.16, 0.18 and 0.16 respectively. Nine patients out of 40 (22.5%) experienced DLTs, and 17 patients (42.5%) were treated at the recommended MTDCs. The trial duration was 19.55 time units. We also simulated a trial (using the same random number seed) that waited for complete follow-up from patients, as per the original PIPE design (cohort size of two patients per combination). This trial lasted 32.43 time units, and recommended (a₂, b₃) and (a₄, b₁) as MTDCs (true DLT probabilities 0.20 and 0.16 respectively). Eight patients out of 40 (20%) experienced DLTs, and 17 patients (42.5%) were treated at the recommended MTDCs. Using TITE-PIPE-C here reduced the trial duration by 12.88 time units (39.7%) and recommended dose combinations with similar true DLT risks. Figure 4 shows the trial progression with the estimated MTC and the inadmissible dose contour, as well as the true MTC at the trial end (blue dotted line).

4.2. Experimentation and Recommendation percentages

Tables 2 shows the experimentation percentages respectively, for each simulation, assuming uniformly distributed toxicity times and uniform weight function. Experimentation percentages are dependent on λ, with increasing λ (more rapid arrival of patients) associated with more experimentation at combinations with lower true probabilities of DLT. This is due to the conservative assumption that an unobserved portion of a patient’s observation window is attributed to a DLT outcome. Under TITE-PIPE-O, a new patient is treated at a dose under the assumption that the previous patient, who has been followed up for a short amount of time, contributes more to the number of DLTs rather than non-DLTs. However, under TITE-PIPE-C, a new patient may have to wait until the minimum number of patients have completed treatment at a particular dose. As a result, the average observed DLT rates per scenario decrease both with increasing λ and as we move from PIPE to TITE-PIPE-C to TITE-PIPE-O; TITE-PIPE-C generally offers experimentation operating characteristics that sit between the PIPE approach and TITE-PIPE-O.

Table 2. Experimentation percentages using uniform weight function (assuming uniformly distributed DLT model).

Arrival rate (λ)	Design	Probability of DLT (%)					Mean Sample Size	Mean DLTs (%)
		0-14	15-24	25-34	35-45	46+
	Scenario A
0.5	PIPE	20	63	17	-	-	40.0	19
	TITE-PIPE-C	21	63	16	-	-	40.0	19
	TITE-PIPE-O	23	62	15	-	-	39.9	19
1	PIPE	20	63	17	-	-	40.0	19
	TITE-PIPE-C	22	62	15	-	-	39.9	19
	TITE-PIPE-O	27	61	12	-	-	39.9	18
2	PIPE	20	63	17	-	-	40.0	19
	TITE-PIPE-C	27	60	13	-	-	39.9	18
	TITE-PIPE-O	34	58	7	-	-	39.9	17
	Scenario B
0.5	PIPE	76	24	-	-	-	40.0	12
	TITE-PIPE-C	77	23	-	-	-	40.0	12
	TITE-PIPE-O	80	20	-	-	-	40.0	11
1	PIPE	76	24	-	-	-	40.0	12
	TITE-PIPE-C	79	21	-	-	-	40.0	11
	TITE-PIPE-O	84	16	-	-	-	40.0	11
2	PIPE	76	24	-	-	-	40.0	12
	TITE-PIPE-C	83	17	-	-	-	40.0	11
	TITE-PIPE-O	91	9	-	-	-	40.0	10
	Scenario C
0.5	PIPE	14	15	27	33	11	39.5	31
	TITE-PIPE-C	14	16	27	32	10	39.4	31
	TITE-PIPE-O	15	16	27	33	10	39.1	31
1	PIPE	14	15	27	33	11	39.5	31
	TITE-PIPE-C	15	16	27	32	10	39.4	31
	TITE-PIPE-O	16	16	29	31	8	39.1	30
2	PIPE	14	15	27	33	11	39.5	31
	TITE-PIPE-C	18	16	27	29	9	39.3	30
	TITE-PIPE-O	19	18	29	28	6	39.1	28
	Scenario D
0.5	PIPE	-	-	-	57	43	19.4	61
	TITE-PIPE-C	-	-	-	60	40	19.4	61
	TITE-PIPE-O	-	-	-	61	39	19.2	61
1	PIPE	-	-	-	57	43	19.4	61
	TITE-PIPE-C	-	-	-	63	37	19.5	61
	TITE-PIPE-O	-	-	-	64	36	19.1	61
2	PIPE	-	-	-	57	43	19.4	61
	TITE-PIPE-C	-	-	-	66	34	19.5	61
	TITE-PIPE-O	-	-	-	69	31	19.1	60
	Scenario E
0.5	PIPE	30	31	39	1	-	39.8	21
	TITE-PIPE-C	30	31	39	0	-	39.8	21
	TITE-PIPE-O	32	31	37	0	-	39.7	21
1	PIPE	30	31	39	1	-	39.8	21
	TITE-PIPE-C	31	31	38	0	-	39.8	21
	TITE-PIPE-O	34	32	35	0	-	39.7	20
2	PIPE	30	31	39	1	-	39.8	21
	TITE-PIPE-C	33	30	36	0	-	39.8	20
	TITE-PIPE-O	38	32	30	0	-	39.7	19
	Scenario F
0.5	PIPE	20	55	-	14	11	39.5	25
	TITE-PIPE-C	21	53	-	14	11	39.5	25
	TITE-PIPE-O	22	53	-	14	10	39.3	25
1	PIPE	20	55	-	14	11	39.5	25
	TITE-PIPE-C	23	52	-	14	11	39.4	25
	TITE-PIPE-O	25	52	-	14	9	39.3	24
2	PIPE	20	55	-	14	11	39.5	25
	TITE-PIPE-C	28	48	-	14	10	39.4	24
	TITE-PIPE-O	32	49	-	14	6	39.3	23
	Scenario G
0.5	PIPE	38	35	21	3	3	40.0	17
	TITE-PIPE-C	40	35	20	3	2	40.0	17
	TITE-PIPE-O	42	34	19	3	2	40.0	17
1	PIPE	38	35	21	3	3	40.0	17
	TITE-PIPE-C	41	34	19	3	2	40.0	17
	TITE-PIPE-O	45	32	18	3	2	40.0	16
2	PIPE	38	35	21	3	3	40.0	17
	TITE-PIPE-C	46	33	17	2	2	40.0	16
	TITE-PIPE-O	53	30	15	2	1	40.0	14

Table 3 shows the chance of recommending combinations with true DLT probabilities within different intervals per design and scenario, as well as the mean number of MTDCs recommended, the percentage of trials that did not recommend any MTDCs, and the percentage of trials that were terminated early. TITE-PIPE approaches and PIPE have similar recommendation percentages within the 15% – 24% DLT risk interval (where the TTL lies), with any differences between designs becoming more pronounced as λ increases. Performance can be slightly improved, or slightly reduced by using TITE-PIPE over PIPE; in Scenario A with λ = 2, the chance of choosing combinations with true DLT risk of 15% – 24% increases from 73% to 76% under TITE-PIPE, whereas in Scenario B it decreases from 27% to 18%.

Table 3.

Recommendation percentages using uniform weight function (assuming uniformly distributed DLT model).

Arrival rate (λ)	Design	Probability of DLT (%)					Mean No. MTDCs	Trials with no MTDC (%)	Trials that stopped early (%)
		0-14	15-24	25-34	35-45	46+
	Scenario A
0.5	PIPE	12	73	15	-	-	2.3	0.2	0.2
	TITE-PIPE-C	11	74	15	-	-	2.2	0.2	0.2
	TITE-PIPE-O	11	75	14	-	-	2.2	0.2	0.2
1	PIPE	12	73	15	-	-	2.3	0.2	0.2
	TITE-PIPE-C	12	73	15	-	-	2.2	0.4	0.4
	TITE-PIPE-O	11	75	14	-	-	2.2	0.2	0.2
2	PIPE	12	73	15	-	-	2.3	0.2	0.2
	TITE-PIPE-C	12	74	14	-	-	2.2	0.3	0.3
	TITE-PIPE-O	11	76	11	-	-	2.2	0.8	0.6
	Scenario B
0.5	PIPE	73	27	-	-	-	1.9	0	0
	TITE-PIPE-C	73	27	-	-	-	1.9	0	0
	TITE-PIPE-O	74	26	-	-	-	1.9	0	0
1	PIPE	73	27	-	-	-	1.9	0	0
	TITE-PIPE-C	74	26	-	-	-	1.9	0	0
	TITE-PIPE-O	76	24	-	-	-	1.9	0	0
2	PIPE	73	27	-	-	-	1.9	0	0
	TITE-PIPE-C	77	23	-	-	-	2.0	0	0
	TITE-PIPE-O	82	18	-	-	-	2.1	0	0
	Scenario C
0.5	PIPE	16	24	35	19	1	1.3	4.5	2.1
	TITE-PIPE-C	16	25	34	20	1	1.3	4.8	2.6
	TITE-PIPE-O	15	22	33	21	2	1.3	6.9	4.3
1	PIPE	16	24	35	19	1	1.3	4.5	2.1
	TITE-PIPE-C	14	23	35	20	2	1.3	5.6	2.8
	TITE-PIPE-O	15	22	34	20	2	1.3	7.0	4.3
2	PIPE	16	24	35	19	1	1.3	4.5	2.1
	TITE-PIPE-C	13	23	34	22	2	1.3	6.7	3.5
	TITE-PIPE-O	14	24	32	21	2	1.2	7.9	4.4
	Scenario D
0.5	PIPE	-	-	-	3	2	0	95.8	87.2
	TITE-PIPE-C	-	-	-	2	2	0	96.2	87.0
	TITE-PIPE-O	-	-	-	2	1	0	96.5	87.8
1	PIPE	-	-	-	3	2	0	95.8	87.2
	TITE-PIPE-C	-	-	-	2	2	0	96.0	86.8
	TITE-PIPE-O	-	-	-	2	1	0	97.0	87.5
2	PIPE	-	-	-	3	2	0	95.8	87.2
	TITE-PIPE-C	-	-	-	2	2	0	96.3	86.4
	TITE-PIPE-O	-	-	-	2	1	0	97.7	87.5
	Scenario E
0.5	PIPE	30	32	37	0	-	2	0.9	0.7
	TITE-PIPE-C	30	32	37	0	-	2	0.8	0.7
	TITE-PIPE-O	30	32	37	0	-	2	1.1	1.0
1	PIPE	30	32	37	0	-	2	0.9	0.7
	TITE-PIPE-C	30	31	38	0	-	2	0.8	0.6
	TITE-PIPE-O	30	33	35	0	-	2	1.1	1.1
2	PIPE	30	32	37	0	-	2	0.9	0.7
	TITE-PIPE-C	30	32	36	0-	-	2	1.2	1.1
	TITE-PIPE-O	32	33	33	0	-	2	1.8	1.4
	Scenario F
0.5	PIPE	13	70	-	11	4	1.7	2.1	1.6
	TITE-PIPE-C	12	71	-	11	4	1.7	1.9	1.5
	TITE-PIPE-O	13	71	-	10	4	1.7	2.5	2.3
1	PIPE	13	70	-	11	4	1.7	2.1	1.6
	TITE-PIPE-C	12	71	-	10	4	1.7	2.8	1.8
	TITE-PIPE-O	13	71	-	10	4	1.7	3.0	2.3
2	PIPE	13	70	-	11	4	1.7	2.1	1.6
	TITE-PIPE-C	12	70	-	11	4	1.7	3.5	2.0
	TITE-PIPE-O	13	70	-	10	3	1.6	4.6	2.6
	Scenario G
0.5	PIPE	44	38	17	1	0	2.7	0	0
	TITE-PIPE-C	45	37	17	1	0	2.8	0	0
	TITE-PIPE-O	45	36	17	1	1	2.7	0	0
1	PIPE	44	38	17	1	0	2.7	0	0
	TITE-PIPE-C	44	37	18	1	1	2.7	0	0
	TITE-PIPE-O	44	36	19	1	1	2.7	0	0
2	PIPE	44	38	17	1	0	2.7	0	0
	TITE-PIPE-C	44	36	18	1	0	2.7	0	0
	TITE-PIPE-O	45	36	18	1	1	2.7	0	0

The percentage of trials that terminate early increases as we move from PIPE to TITE-PIPE-C (largest relative increase of 1.4% (Scenario C)) to TITE-PIPE-O (largest relative increase of 2.3% (Scenario C)). This is because TITE-PIPE approaches are slightly more likely to assign patients to lower dose combinations (since partially followed-up patients contribute a partial DLT response; see Table 2), and any subsequent DLTs at lower combinations will increase the chance of terminating the trial earlier than if those DLTs were observed at higher combinations. Overall, the differences in early stopping probabilities between approaches are very small. The percentage of trials that do not recommend any MTDCs includes those trials that terminate early and trials where all 40 patients are treated, but no MTDCs can be identified (see Subsection 2.6).

When using the adaptive weighting function instead of the uniform weighting function, no major differences are observed in experimentation or recommendation results (see Supplementary Material, Table S1 and Table S2). This is not surprising; given the simulation generated uniformly distributed toxicity times, the adaptive weight function will yield similar weighted DLT outcomes to the uniform weighting function.

4.3. Trial duration and delays in treatment

Table 4 gives the mean trial durations (and percentage change from PIPE) per design and scenario, under both uniform and adaptive weight functions. Trial durations do not differ with choice of weight function when assuming uniformly distributed time-to-toxicity. Looking at the results from using the uniform weight function, trial duration is shortened under TITE-PIPE approaches by 0.4-1.2 units (λ = 0.5), 0.8-2.2 units (λ = 1), and 3.6-10.3 units (λ = 2). When the average arrival rate is two patients per time unit (λ = 2), trial duration can be shortened by 24% – 33%, without substantially compromising on experimentation and MTDC recommendation performance.

Table 4.

Mean trial durations (in time units) per design and scenario, with percentage change from PIPE (in parentheses) using uniform and adaptive weight functions (assuming uniformly distributed DLT model).

Arrival rate (λ)	Design	Scenario
		A	B	C	D	E	F	G
Uniform
0.5	PIPE	79.3 (-)	79.5 (-)	78.4 (-)	38.7 (-)	79.0 (-)	78.4 (-)	79.5 (-)
	TITE-PIPE-C	79.0 (0)	79.1 (-1)	78.0 (-1)	38.7 (0)	78.6 (0)	78.0 (0)	79.1 (-1)
	TITE-PIPE-O	78.9 (-1)	79.1 (-1)	77.2 (-1)	38.3 (-1)	78.5 (-1)	77.8 (-1)	79.1 (-1)
1	PIPE	41.8 (-)	42.2 (-)	41.1 (-)	20.0 (-)	41.6 (-)	41.3 (-)	42.0 (-)
	TITE-PIPE-C	40.0 (-4)	40.1 (-5)	39.4 (-4)	19.6 (-2)	39.8 (-4)	39.5 (-5)	40.0 (-5)
	TITE-PIPE-O	39.9 (-4)	40.0 (-5)	39.1 (-5)	19.2 (-4)	39.7 (-5)	39.4 (-5)	40.0 (-5)
2	PIPE	29.8 (-)	30.8 (-)	29.1 (-)	13.6 (-)	29.7 (-)	29.5 (-)	30.1 (-)
	TITE-PIPE-C	20.5 (-31)	20.6 (-33)	20.2 (-31)	10.3 (-24)	20.4 (-31)	20.2 (-31)	20.5 (-32)
	TITE-PIPE-O	20.4 (-31)	20.5 (-33)	20.0 (-31)	10.0 (-26)	20.3 (-32)	20.1 (-32)	20.5 (-32)
Adaptive
0.5	PIPE	79.3 (-)	79.5 (-)	78.4 (-)	38.7 (-)	79.0 (-)	78.4 (-)	79.5 (-)
	TITE-PIPE-C	79.0 (0)	79.1 (-1)	77.9 (-1)	38.7 (0)	78.6 (0)	78.0 (-1)	79.1 (-1)
	TITE-PIPE-O	78.9 (-1)	79.1 (-1)	77.1 (-2)	38.4 (-1)	78.5 (-1)	77.7 (-1)	79.1 (-1)
1	PIPE	41.8 (-)	42.2 (-)	41.1 (-)	20.0 (-)	41.6 (-)	41.3 (-)	42.0 (-)
	TITE-PIPE-C	40.0 (-4)	40.1 (-5)	39.4 (-4)	19.6 (-2)	39.8 (-4)	39.4 (-5)	40.0 (-5)
	TITE-PIPE-O	39.9 (-4)	40.0 (-5)	38.9 (-5)	19.2 (-4)	39.7 (-5)	39.3 (-5)	40.0 (-5)
2	PIPE	29.8 (-)	30.8 (-)	29.1 (-)	13.6 (-)	29.7 (-)	29.5 (-)	30.1 (-)
	TITE-PIPE-C	20.5 (-31)	20.6 (-33)	20.2 (-31)	10.2 (-25)	20.4 (-31)	20.3 (-31)	20.5 (-32)
	TITE-PIPE-O	20.4 (-32)	20.5 (-33)	19.8 (-32)	9.9 (-27)	20.3 (-32)	20.0 (-32)	20.5 (-32)

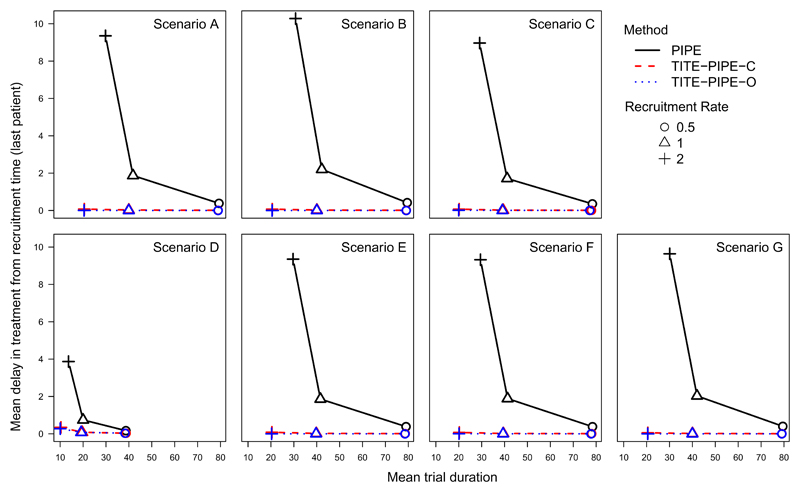
As well as reductions in trial duration, we also consider the mean delay between recruitment of the last patient onto a trial and the administration of their treatment. Figure 5 shows that under PIPE, the delay between recruitment of the last patient and treatment administration increases substantially as the recruitment rate λ increases. For λ = 0.5, this delay is approximately 0.40 time units (0.16 for scenario D, where average sample size was around 19 patients). When λ = 1, although the mean trial duration between PIPE and TITE-PIPE is very similar, there is a noticeable difference in the mean delay in treatment for the last recruited patient. When λ = 2, this delay increases dramatically to around 10 time units (3.8 time units for scenario D). Under TITE-PIPE, the delay is practically 0 (maximum of 0.35 under TITE-PIPE-C (scenario D) and 0.28 under TITE-PIPE-O (scenario D)). So as well as shortening the trial, the delay between recruitment and receiving treatment (as measured in the last patient) is almost completely removed.

Fig. 5.

Mean delay in treatment start from recruitment time for last patient in trial versus average trial duration (uniform toxicity distribution; uniform weight function).

4.4. Early-onset and late-onset toxicities

We now assume that time to toxicity is distributed as a Pareto random variable (Subsection 3.1) so that DLTs are more likely to occur earlier in a patient’s observation period than under a uniform distribution. Tables S3, and S4 show similar experimentation and MTDC recommendation results to that under the uniform time-to-toxicity distribution. Under the adaptive weight function (Tables S5 and S6), changes of 1-2% are observed when comparing the TITE-PIPE MTDC recommendations to those using uniform weightings, but otherwise very little difference is observed. For trial durations (Table S7), we again see similar time savings under different recruitment rates as observed under uniform time-to-toxicity. This is likely because we observe few toxicities on average per trial (between 4 and 12 out of 40 patients approximately), and the mean time to DLT is similar under the uniform and Pareto distributions used, even though the DLT times under the Pareto distribution are skewed towards earlier times. Essentially, the DLTs that do occur are clustered towards the start of a patient’s DLT observation window, but there are not enough of them to cause a noticeable change in model performance on the adaptive weighting function.

When time to DLT follows a Weibull distribution, so DLT times are skewed toward the end of the DLT observation period (Subsection 3.1), we again see minimal changes in each design’s operating characteristics. This applies to both the uniform weighting function (Tables S8 and S9) and the adaptive weighting function (Tables S10 and S11). Trial duration (Table S12) is reduced under the TITE-PIPE approaches regardless of which weighting function is used, and to a similar extent to that of the simulations for Uniform- and Pareto-distributed time-to-toxicity. The greatest reductions in duration are slightly more than observed under a uniform time-to-toxicity model (34-35% reduction).

5. Discussion

We have proposed an approach for incorporating censored patient toxicity outcomes into the PIPE dose-escalation design for dual-agent phase I trials. We have shown substantial reductions in trial duration can be achieved, and delays in starting treatment can be avoided even when recruitment is at a rate similar to the outcome follow-up time. These can be done without compromising on the experimentation and MTDC recommendation performance. We found that the TITE-PIPE-C approach, where two patients had to be completely followed up per combination experimented on before censored time-to-toxicity data could be used for dose escalation decisions, gave slightly better experimentation performance than TITE-PIPE-O. Furthermore, the performance of both TITE-PIPE-C and TITE-PIPE-O was generally invariant to the underlying time-to-toxicity distribution of the combination therapy and was not affected by the choice of weight function (uniform or adaptive).

We implemented a safety rule that if the probability of the lowest dose combination being above the MTC is at least 0.80, given data from patients that had completed their follow-up, then the trial is terminated. We also implemented a probabilistic rule (Bekele et al., 2008; Polley, 2011; Ivanova et al., 2016) whereby if, based on partial data, the probability of the lowest dose combination being above MTC is greater than ϵ = 0.80, then recruitment is suspended until those patients enrolled in the trial have completed their follow-up. Then we use the new set of completely observed data to assess if the trial should be terminated or not. The threshold ϵ should be carefully considered before the design is implemented in practice; we adopted a threshold of ϵ = 0.80 so the trial would be terminated if the first two patients experienced DLTs, but higher thresholds (e.g. ϵ = 0.95) have been considered (Ivanova et al., 2016) and may prove more favourable for reducing the chances of terminating a trial when there truly is at least one MTDC. Calibration of this stopping rule will need to be performed on a per trial basis, and will vary with chosen TTLs, clinical needs, and prior setups (median DLT risks and prior sample sizes).

The simulation studies conducted show that trial duration can be reduced by 5 – 6% when patients arrive at a rate of one per DLT observation window (in this study, one time unit), and reduced up to 35% when patients arrive twice as fast as expected.

We have focussed on comparing TITE-PIPE to PIPE to assess the trade-off between MTDC recommendation accuracy and trial duration. Other approaches incorporating TITE outcomes into combination therapy phase I trials have been proposed in the literature. The partial ordering TITE-CRM (Wages et al., 2013) recommends a single MTDC, rather than estimating a contour. Riviere et al. (2014) proposed a TITE extension of their Bayesian dose-finding design for combination therapies that used a four-parameter logistic model, which they compared to a non-TITE version of the same design. Our interest in comparing two versions of TITE-PIPE to the original PIPE design is motivated by the use of PIPE in practice for at least two clinical trials since its publication. Investigating an overall comparison amongst these designs is an area for further research, though ensuring appropriate simulation studies are conducted with fairly calibrated priors across different designs is a challenge that would need to be addressed.

In summary, incorporating time-to-event outcomes in the PIPE dual-agent dose-escalation design is easily achieved, and can provide worthwhile savings with respect to trial duration with comparable operating performance to the original PIPE design. We have incorporated these functions into the latest release of the R package pipe.design.