Polarization switching and electrical control of interlayer excitons in two-dimensional van der Waals heterostructures

Abstract

Long-lived interlayer excitons in van der Waals heterostructures based on transition metal dichalcogenides, together with unique spin-valley physics, make them promising for next-generation photonic and valleytronic devices. While the emission characteristics of interlayer excitons have been studied, efficient manipulation of their valley-state, a necessary requirement for information encoding, is still lacking. Here, we demonstrate comprehensive electrical control of interlayer excitons in a MoSe₂/WSe₂ heterostructure. Encapsulation of our well-aligned stack with hexagonal boron nitride (h-BN) allows us to resolve two separate narrow interlayer transitions with opposite helicities under circularly polarized excitation, either preserving or reversing the polarization of incoming light. By electrically controlling their relative intensities, we realize a polarization switch with tuneable emission intensity and wavelength. Finally, we demonstrate large Zeeman shifts of these two transitions upon application of an external magnetic field. These results are interpreted within the picture of moiré-induced brightening of forbidden optical transitions. The ability to control the polarization of interlayer excitons is a step forward towards the manipulation of the valley degree-of-freedom in realistic device applications.

Electronic devices rely on the manipulation of the charge degree of freedom to store and process information. To overcome their fundamental limitations, different degrees of freedom could be harnessed in new device concepts. Using the electron spin, for example, has been considered as an attractive alternative to charge-based devices¹. Another possibility consists of manipulating the valley degree of freedom^2,3, associated with the minima (maxima) of the conduction (valence) band a carrier is occupying. In this regard, 2D semiconductors such as transition metal dichalcogenides (TMDCs)^4–8 are particularly attractive for valley manipulation, as their band structure has inequivalent K and K´ valleys, which realize a binary pseudospin system^9–11. Neutral and charged excitons in these heterostructures are of high interest, since they can be electrically manipulated¹² and are endowed with a valley degree of freedom by their constituent electrons and holes which can be optically addressed with circularly polarized light^13–16. Previous reports have revealed that interlayer excitons¹⁷ are particularly suitable for this purpose, showing emission of polarized light with the same or the opposite handedness used for excitation^18,19. To fully exploit this property, it is however essential to find a way to manipulate at will their polarization (i.e. valley) state. The pioneering work by Rivera et al²⁰ has indeed established that the degree of preserved circular polarization can be reduced using a gate voltage.

For a full control on such manipulation, different strategies could be employed, including the creation of a moiré potential. 2D van der Waals (vdW) heterostructures possess unique physics which arises from the moiré patterns that form when different crystals with lattice mismatch are brought in contact. This opens an entirely new direction for research because the moiré can dramatically change the material properties, as experimentally demonstrated for graphene on h-BN^21,22. This approach has been also recently considered for exciton-moiré interactions. Especially the prediction of a moiré potential-induced brightening of forbidden optical transitions^23,24 and its electrostatic tuneability could enable fully switching the helicity state (i.e. realize a logic NOT), crucial for logic operations.

In this report, we demonstrate a polarization switch based on interlayer excitons in a well-aligned vdW heterostructure, whose operation is enabled by the peculiar physics of this system. This device allows manipulating the helicity of light, as well as its wavelength and intensity, by application of electric and magnetic fields.

Results

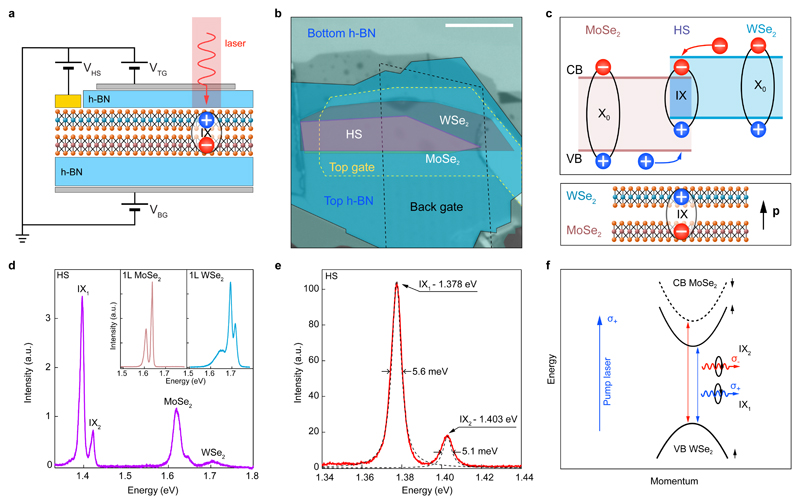
Our device consists of a contacted MoSe₂/WSe₂ heterobilayer encapsulated in h-BN, with a graphene bottom gate and a top transparent Pt gate (Figure 1a). The stack is realized using the dry-transfer technique²⁵ on a doped silicon substrate covered with 270 nm of SiO₂, and the crystals are aligned to minimize the stacking angle (δθ ≲ 1°, see Methods), thus creating a long-period moiré superlattice. This device architecture allows us to perform optical measurements on the sample while applying different voltages through the top and bottom gates, as well as the global Si back-gate and gives us the possibility to independently control the doping level and the transverse electric field. Figure 1b shows the optical microscopy image of one of our completed heterostructure devices (see methods for fabrication details). We note that all the measurements reported here were acquired at 4.2 K on the same device, unless stated otherwise.

Fig. 1. Device characterization.

a, schematic depiction of the device structure. b, optical image of the device. The pink area indicates the heterobilayer area. Scale bar is 10 µm. c, band alignment in MoSe₂/WSe₂ heterobilayer (upper panel) and artistic representation of the interlayer exciton with its dipole moment $\overrightarrow{p}$ (lower panel). d, PL spectrum from the heterostructure, showing emission from MoSe₂, WSe₂ and interlayer excitons. Insets show PL spectra from MoSe₂ and WSe₂ monolayers. e, detail of the PL spectrum from the heterobilayer B (the device is shown in S11), with numerical fits for the emission peaks. f, schematic of the spin-conserving (IX₁) and spin-flipping (IX₂) transitions in the K valley for the structure under consideration and their coupling with circularly-polarized light.

Optical characterization

The h-BN-encapsulation of the heterostructure²⁶ allows us to observe bright and sharp photoluminescence (PL) peaks from individual monolayers (Figure 1d, insets), with full-width half maxima (FWHM) between 7 and 15 meV (see Supplementary Figure S1). In the heterobilayer region, we observe an extreme quenching of the intralayer excitonic peaks, together with the appearance of low-energy emission (Figure 1d and Supplementary Figure S2) around 1.39 eV due to interlayer exciton (IX) formation. We clearly resolve two distinct emission peaks (Figure 1e), with FWHM around 5 meV and an energy separation of ~25 meV between them, which corresponds to the MoSe₂ conduction band (CB) spin-splitting²⁷. Such high resolution is achieved as a result of improved heterostructure quality, in agreement with Hanbicki et al²⁸. We will refer to these lower- and higher-energy features as IX₁ and IX₂ respectively. As we will be discussing in detail later, we attribute this doublet to a spin-conserving and a spin-flipping transition (Figure 1f). The latter is normally dark (forbidden) in monolayers, but can be brightened by the moiré pattern in our heterobilayer²⁴ due to selection rules dictated by local atomic registry.

Electrical tuning of interlayer excitons

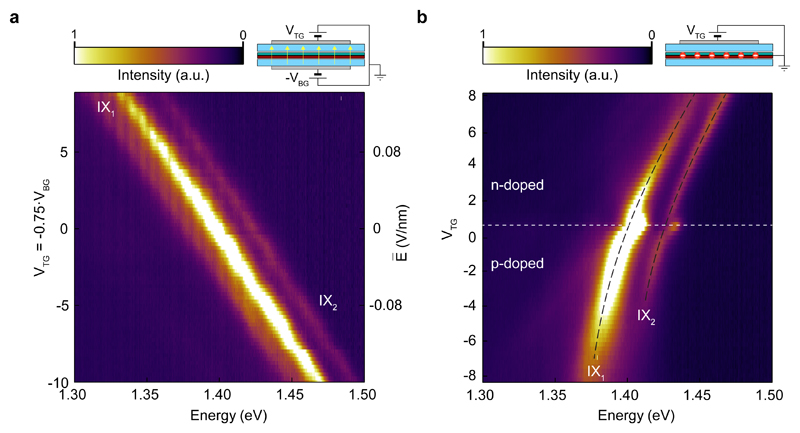
Prior to manipulating the polarization of the two transitions, we first characterize our device and demonstrate intensity and energy manipulation, which will enable the polarization switching. Stacking MoSe₂ and WSe₂ on top of each other results in the creation of a van der Waals heterostructure²⁹ with a type-II band alignment³⁰ (Fig. 1c). Since electrons and holes are confined to separate layers, interlayer excitons have a defined dipole moment $\overrightarrow{p}$ perpendicular to the heterostructure plane. This allows us to linearly tune their energy with an external electric field $\overrightarrow{E}$ along the dipole axis: $\Delta U~-\overrightarrow{p}\cdot \overrightarrow{E}.$ To this end, we apply a vertical field at constant carrier concentration. As shown in Figure 2a, a modulation of the IX emission maximum of ∆U~ 138 meV is obtained, from 1.34 to 1.47 eV. A linear fit of the energy shift yields a tuning rate of ~500 meV·nm·V^-1, from which we obtain a qualitative estimation of the dipole size d~∆U/qE ~ 0.5 nm (where q is the elementary charge), compatible with the expected interlayer spacing³¹. While this semiclassical dipole picture is oversimplified, it captures the main effects we observe. For positive electric fields, the decrease in energy of the dipole (charges are more separated) results in reduced recombination rate and a slightly larger Stark effect. On the contrary, when the exciton energy is increased, and the overlap between the electron and the hole is larger, we observe brighter PL.

Fig. 2. Electrical control of interlayer excitons.

a, map of PL emission as a function of applied gate voltages V_TG and V_BG when sweeping at constant doping. b, map of PL emission as a function of gate voltage when electrostatically doping the device.

If we ground the heterobilayer while applying voltage to the top gate, we can achieve control over the relative intensities of the two peaks by changing the charge carrier concentration. In contrast with previous reports¹⁸, our dual-gated configuration allows us to independently control exciton energy or relative peak intensity, while keeping the other property fixed. This geometry also allows for precise control over the doping of individual layers within the heterobilayer (see Supplementary Information S6 and S7). We show the results of this electrostatic doping in Figure 2b. For negative values of V_TG, the intensity of the IX₂ peak is first reduced, then suppressed around -4 V. At the same time, IX₁ becomes broader and starts to dominate the spectrum. On the contrary, at high positive voltages, we observe that IX₂ becomes the dominant emission feature, while IX₁ decreases in intensity and becomes quenched at higher electron density achieved by dual gating (see Supplementary Figure S3). This resembles closely what one would expect from a two-level system, where with increased doping more electrons are driven into the upper level: here this comes from the filling of the lower spin-split CB and population of the upper one. This interpretation is also supported by the observation of a faster increase in the intensity of IX₂ with increasing laser power in the absence of electrostatic doping (see Supplementary Figure S4 for details on power dependence). Further confirmation of this filling mechanism is the temperature dependence of the two transitions (see Supplementary Figure S5), with IX₂ becoming stronger as the upper band is thermally populated.

Polarization response

Excitonic valleytronic devices should have an optical input and output, with the information encoded in the polarization of light. Consequently, selectively addressing the valley degree of freedom of excitons with polarized light is critically important. To this end, we characterize the polarization-resolved photoluminescence from our heterostructure. As expected, the emission intensity for positive (σ⁺) and negative (σ⁻) helicity are the same in the case of linear excitation. The situation changes with circularly polarized excitation. We observe robust conservation of the incident polarization from monolayer WSe₂, but not from MoSe₂^32,33 (see Supplementary Figure S8). As shown earlier, our clean interfaces in h-BN-encapsulated heterostructures allow us to resolve the two different optical transitions, IX₁ and IX₂. Here, we observe that IX₁ and IX₂ have opposite behaviour under circularly polarized excitation, with polarization values up to 27% and -25% respectively, in agreement with recent results²⁸ (see Supplementary Figure S9). Such behaviour agrees with what is expected from a spin-conserving (-flipping) transition between the WSe₂ valence band (VB) maximum and the lower (upper) CB minimum of MoSe₂. As we discuss later in the text, in WSe₂/MoSe₂ both these transitions are allowed, with opposite polarizations and comparable intensities, for excitons localized in some energy minima of the moiré pattern.

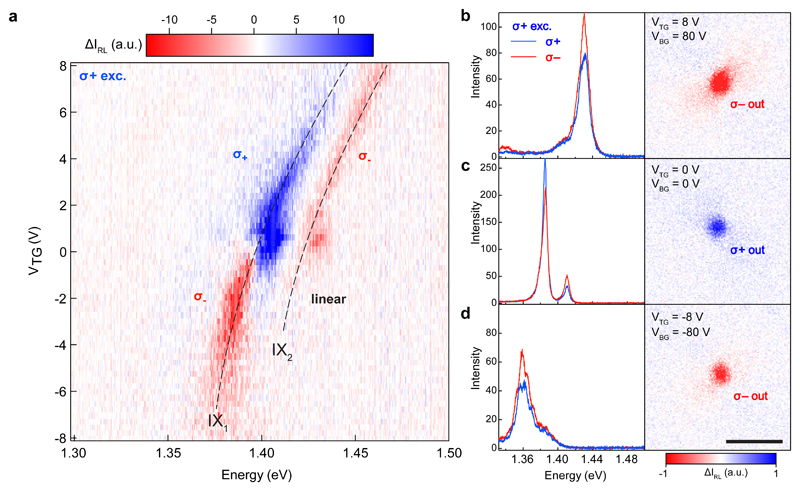
We now focus on the central point of our experiment, by combining the gate modulation of the two excitonic peaks with their unique polarization dependence. As we have seen, strong electron doping enhances IX₂, while at small or negative gate voltages IX₁ dominates. Thanks to the opposite polarization of the two peaks, this allows us to change the device operation between a polarization-inverting and polarization-preserving regime. We show the corresponding results in Figure 3 (see Supplementary Image S10 for raw left and right polarization): both excitonic peaks are clearly visible in the upper (positive) half of the map, with opposite helicity. In Figure 3c (left), the spectra corresponding to V_TG = 0 V is presented. Due to the higher intensity of IX₁ peak, the total polarization of the signal ∆I_RL (net polarization ∆I_RL = I_R−I_L integrated over the frequency spectrum) is positive (i.e., of the same sign as the excitation). This is even more clearly visible in the right panel of Figure 3c, where the spatial image of the exciton polarization acquired on the CCD is shown. For strong electron doping the situation is reversed, as seen on Figure 3b. In this configuration, IX₂ emission is stronger, resulting in an overall negative value of ∆I_RL, and our device operates here as a polarization inverter. Even more interesting is the behaviour in the p-doped region (i.e. for the application of negative gate voltage). As seen before, the higher energy IX₂ peak is suppressed at negative gate voltages, so one would expect the device to strongly preserve the helicity when electrostatically p-doped. On the contrary, IX₁ polarization behaviour is now completely reversed, while IX₂ shows a vanishing circular polarization (see lower half of Figure 3a). This results from the alteration of the moiré potential induced by electrostatic doping, which shifts the exciton localization from one to another type of local minima in the moiré pattern, with different local symmetry and thus different light coupling rules (see later). In Figure 3d we show the spectra recorded for a strong hole-doped case, demonstrating that the polarization-inverting emission is indeed coming from the lower-energy IX₁. Just as in the case of positive gate voltage, we obtain a globally negative polarization (right panel).

Fig. 3. Electrical control of polarization.

a, µ-PL map of the difference between right- and left-circularly polarized (CP) emission intensities when the device is pumped with right-CP light: δI_RL=I_R-I_L as a function of the gate voltage V_TG in single-gate configuration. The dashed lines are the same as in Figure 2b and serve as guides for the eye. b-d, details of device operation in dual-gating mode. Left panel: PL spectra for V_TG = +8 V, 0 V and -8 V. Right panel: spatial imaging of ΔI_RL in the corresponding gate configurations. The silicon back-gate is kept at V_BG = 10·V_TG to reach higher doping densities and further enhance the effect. Scale bar is 5 µm.

Based on our results, we can conclude that the contrasting reports in recent literature on the polarization dependence of PL in this system (observation of conservation²⁰, reversal¹⁹ or both²⁸ for the light helicity) could be due to different levels of natural doping occurring in the samples, over which there was previously no full control, as well as to variable amounts of disorder. Indeed, using the same device structure we could reliably reproduce our observations in successive devices (see Supplementary Figure S11), obtaining qualitatively similar results.

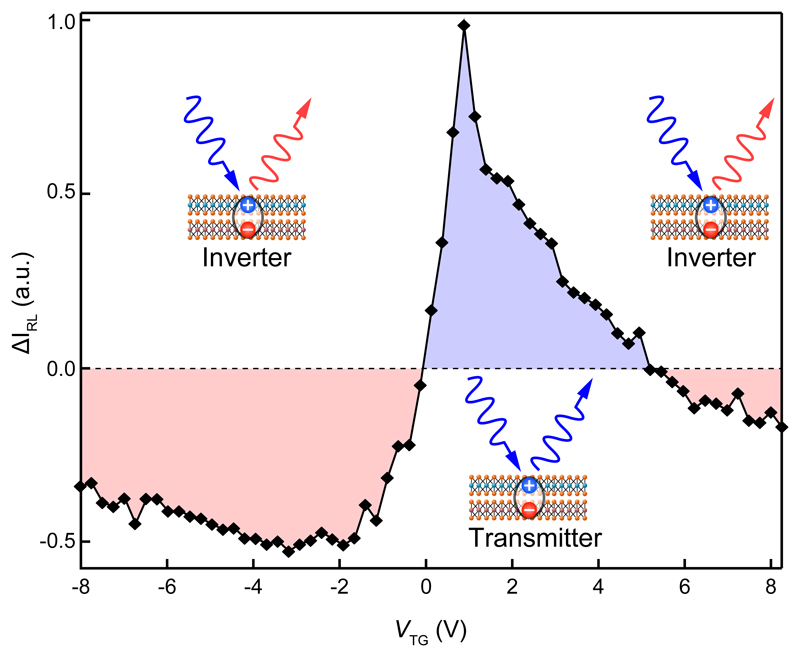
To characterize the switching operation in more detail, we study the evolution of ∆I_RL (polarization integrated over the spectrum) as a function of the applied gate voltage, as shown in Figure 4. For V_TG higher than 5 V, we have negative ∆I_RL, as a result of IX₂ being the strongest transition (as in Fig. 2b and 3a). For gate values between 5 V and 0 V, IX₁ dominates, giving positive ∆I_RL, i.e. preserving the input polarization. It is interesting to note that within this region, application of gate voltage also allows us to modulate the amplitude of the effect, with a maximum around V_TG = 1 V. We then see a sharp transition between the two logic states happening around zero gate voltage, with a small required switching voltage around ±1 V. This threshold value depends on the gate capacitance, and could thus be considerably reduced by engineering thinner dielectric layers to obtain even higher efficiency. For V_TG below 0 V, we have an inverting action, due to the polarization reversal of IX₁.

Fig. 4. Polarization switching action.

Plot of the difference between right- and left-circularly polarized (CP) emission intensities when the device is pumped with right-CP light: ΔI_RL=I_R-I_L as a function of the gate voltage V_TG. The resulting polarization is obtained by integrating over the entire measured emission spectrum.

Zeeman splitting of the doublet

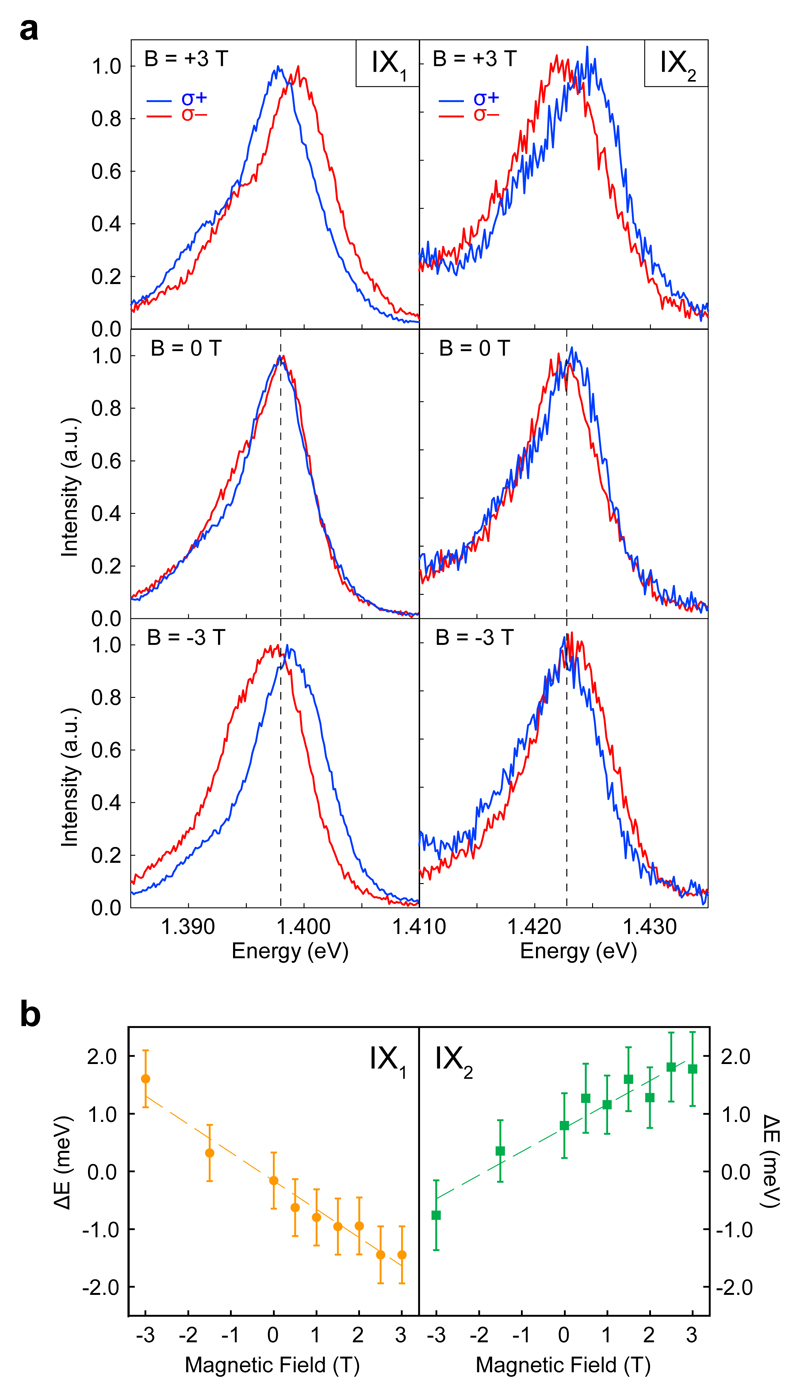
Since the valley pseudospin is associated with the magnetic moment, it is also possible to manipulate it with an external magnetic field³⁴. Indeed, to gain more insight into our double excitonic transition, the extraction of the effective g-factor could prove useful. Towards this, we perform polarization-resolved photoluminescence measurements in a magnetic field B, between -3 T and +3 T. The results are shown in Figure 5. Similarly to the monolayer case³⁵, the σ⁻ and σ⁺ components of the PL peaks experience opposite energy shifts, with a splitting $\Delta E^{\text{IX}}=E_{{\sigma }^{+}}^{\text{IX}}-E_{{\sigma }^{-}}^{\text{IX}}$ proportional to B. Interestingly, the same polarization component for each peak undergoes energy shifts slightly different in amplitude (see Figure 5). For a more quantitative analysis of the data, we extract the peak positions using a similar technique as in ref34. In Figure 5b we show the calculated shift for IX₁ and ${\text{IX}}_2:\Delta E^{\text{IX}1}=E_{{\sigma }^{+}}^{\text{IX}1}-E_{{\sigma }^{-}}^{\text{IX}1},\Delta E^{\text{IX}2}=E_{{\sigma }^{+}}^{\text{IX}2}-E_{{\sigma }^{-}}^{\text{IX}2},$ together with their linear fit. Using the Zeeman energy shift ΔE = g_effμ_BB, where μ_B, is the Bohr magneton and B is the applied field, we calculate effective g-factors $g_{\text{eff}}^{\text{IX}1}=-8.5\pm 1.5$ and $g_{\text{eff}}^{\text{IX}2}=7.1\pm 1.6$. Our result is considerably larger than previously reported effective g-factors in monolayer TMDCs (normally around -4), in line with recent results on similar heterostructures³⁶. In the latter case, larger g-factors where reported for a single interlayer transition and attributed to a large valley magnetic moment contribution caused by the AB-stacking of layers. Even within a relatively small magnetic field range, thanks to the large g-factor, we can clearly see that the two peaks show a different behaviour. The opposite sign of the g-factors comes from the fact that, for the same valley, the emission is σ⁺- or σ⁻-polarized for IX₁ and IX₂. Therefore, the measured shift $\Delta E^{\text{IX}}=E_{{\sigma }^{+}}^{\text{IX}}-E_{{\sigma }^{-}}^{\text{IX}}$ will have opposite sign for the two transitions, even if the valley shifts are in the same direction (see Figure S13). In addition to this, one would expect two different g-factors, as a transition between spin-up and spin-down bands (IX₂) will have non-zero contribution to the Zeeman shift from the spin magnetic moment: Δ_s = 2s_zμ_BB, while the spin-conserving transition (IX₁) will not, as illustrated in Supplementary Information S13.

Fig. 5. Magnetic field effect on interlayer excitons.

a, PL spectra for applied magnetic fields between +3 T and -3 T for left- and right-circularly polarized (CP) emission for IX₁ (left column) and IX₂ (right column). b, energy shift ΔE between right- and left-CP peaks for IX₁ and IX₂. Error bars are calculated from the statistical error on the fitting procedure used to determine the peak position.

Discussion

The appearance of such a double interlayer transition and its opposite polarizations have been recently captured by several theoretical studies^23,37. Here, we mostly discuss our experimental results within the picture of moiré-induced effects^23,37 while a more detailed discussion covering other mechanisms can be found in Supplementary Note S12. In this model, the potential induced by the moiré creates an array of localized emitters, with different properties determined by the local symmetry. Such a periodic pattern indeed exists in our devices, due to the good alignment and the small lattice mismatch between WSe₂ and MoSe₂. Yu et al²⁴. have calculated that the different selection rules at some of these locations can enable otherwise forbidden spin-flip transitions. We find that this mechanism could explain our experimental observations, including the existence of two optical transitions with opposite helicities separated by ~25 meV, the peculiar temperature dependence (the higher-energy IX₂ transition is enhanced at higher temperature due to the thermal excitation of excitons) and the polarization switching with electrostatic doping. Now we discuss the distinct doping dependence in detail, by again considering the effect of the moiré potential. The energy minimum for interlayer excitons is found at the R^X_h locations of the moiré for R-type (i.e. AA-stacked) WSe₂/MoSe₂ (see ref.24), where local selection rules allow both spin-conserving (IX₁) and spin-flipping transitions (IX₂), coupled with opposite polarizations of light, with comparable optical matrix elements (see also Supplementary Information S12). The different type of local energy minima R^h_h instead shows an opposite coupling with polarized light for IX₁, and a coupling with linearly polarized light for IX₂. This picture resembles remarkably well our data: when doping our structure, we alter the moiré potential landscape (by filling some minima, or by shifting their energy electrostatically), thus making a different type of symmetry location become the most favourable one for excitons. This is accompanied by a change in the coupling with light for IX₁ (sign change in ρ), and in the loss of polarization for IX₂ in the circular basis (ρ becomes zero as it is now coupled with linearly polarized light). The observation of similar Stark shifts for IX₁ and IX₂ is also consistent with this picture: these two transitions correspond to excitons localized in moiré superlattice sites with the same symmetry, and thus are expected to have similar dipole moments. Emissions from different types of moiré sites would show different dipoles (due to changing interlayer distance), and consequently exhibit significantly different slopes (and potentially crossing, as in ref.23). The magnetic field-induced splitting of IX₁ and IX₂ confirms the R-type (i.e. AA-type) stacking of the layers in our device (as for AB-staked layers g_eff ~ − 15 from ref.36). Finally, we would like to stress that other theoretical investigations including twin momentum space indirect transitions²⁸ and the presence of both a direct and indirect transition³⁸ also successfully explain some aspects of our observations.

In conclusion, we have demonstrated comprehensive electrical control over the polarization, wavelength and intensity of emission from interlayer excitons in a WSe₂/MoSe₂ vdW heterostructure. The ability to integrate all these functions in a single device to fine-tune the emitted radiation is key to practical optoelectronics and could pave the way for novel applications for valleytronic devices. Even more importantly, polarization conservation or reversal have been demonstrated to be gate-tuneable, enabling a polarization-inverting action. We also report large and opposite g-factors for both IX₁ and IX₂ transitions, which fit the exciton-moiré interaction described here. We note that while this proof of principle shows the feasibility of such a device, further optimization and engineering to increase its performance and efficiency will be needed to realize practical valley devices. These results are relevant in the context of photonic and valleytronic devices, since they enable the manipulation of the electrical manipulation of the polarization of light and deepen our fundamental understanding of interlayer excitons in these structures.

Methods

Heterostructure fabrication

Few-layer graphene flakes for the bottom gate were obtained by exfoliation from graphite (NGS) on Si/SiO₂ substrates and patterned in the desired shape by e-beam lithography and oxygen plasma etching. The heterostructure was then fabricated using polymer-assisted transfer²⁵ of mono- and few-layer flakes of h-BN, WSe₂ and MoSe₂ (HQ Graphene). Flakes were first exfoliated on a polymer double layer. Once monolayers were optically identified, the bottom layer was dissolved with a solvent and free-floating films with flakes were obtained. These were transferred using a home-built setup with micromanipulators to carefully align flakes on top of each other and minimize the stacking angle. For this, a homemade software was used to measure the angle between the flake edges, with a precision limited by the resolution of optical images (< 1°). Polymer residue was removed with a hot acetone bath. Once completed, the stack was thermally annealed under high vacuum conditions at 10^-6 mbar for 6 h. Finally, electrical contacts were fabricated using e-beam lithography and metallization (80 nm Pd for contacts, 8 nm Pt for the top-gate).

Optical measurements

All measurements presented in the work were performed in vacuum at a temperature of 4.2 K. Excitons were optically pumped by a continuous wave (CW) 647 nm laser diode focused to the diffraction limit with a beam size of about 1 µm. The incident power was ~200 µW. Spectral and spatial characteristics of the device emission were analysed simultaneously. The emitted light was acquired using a spectrometer (Andor Shamrock with Andor Newton CCD camera), and the laser line was removed with a long pass 650 nm edge filter. For spatial imaging, we used a long-pass 850 nm edge filter so that the laser light and most of the emission from monolayers were blocked. Filtered light was acquired by a CCD camera (Andor Ixon). For polarization-resolved measurements, a lambda-quarter plate on a rotator together with a linear polarizer were used to select the polarization of incident light. A similar setup was used to image the two polarizations on the CCD camera. To acquire separate spectra for left- and right-circularly polarized light, a lambda-quarter and a displacer were employed. For magnetic field-dependent photoluminescence measurements, the extraction of the peak energy shift was done with the method shown in ref34, which allows to obtain better precision without making assumptions on the peak shape. A linear fit of the resulting values was then used to extract the effective g-factor, taking the error in the determination of each point as a weighting factor. The error reported in the text is the resulting uncertainty on the fit parameter.