Abstract
Cortical pyramidal neurons receive thousands of synaptic inputs, arriving at different dendritic locations with varying degrees of temporal synchrony. It is not known if different locations along single cortical dendrites integrate excitatory inputs in different ways. Here we have used 2-photon glutamate uncaging and compartmental modelling to reveal a gradient of non-linear synaptic integration in basal and apical oblique dendrites of cortical pyramidal neurons. Excitatory inputs to the proximal dendrite sum linearly and require precise temporal coincidence for effective summation, whereas distal inputs are amplified with high gain and integrated over broader time windows. This allows distal inputs to overcome their electrotonic disadvantage, and become surprisingly more effective than proximal inputs at influencing action potential output. Thus, single dendritic branches can already exhibit non-uniform synaptic integration, with the computational strategy shifting from temporal coding to rate coding along the dendrite.
Introduction
The location of synaptic inputs on the dendritic tree can have important functional consequences (Magee, 2000; Spruston, 2008; Williams and Stuart, 2003). Dendritic filtering results in differences in the size, shape, and summation of EPSPs arriving at the soma depending on dendritic location, with distal inputs being disadvantaged compared to proximal inputs (Nevian et al., 2007; Rall, 1964; Rall, 1967; Rall et al., 1967; Stuart and Spruston, 1998; Williams and Stuart, 2002), although in some cell types the location-dependent properties of synapses and dendrites helps to mitigate these differences, making somatic synaptic integration relatively independent of dendritic location (Andersen et al., 1980; Jack et al., 1981; Magee, 1999; Magee and Cook, 2000; Stricker et al., 1996). Furthermore, the local integration of synaptic inputs also appears to depend on dendritic region. For example, synaptic inputs to the distal apical dendrites of layer 5 pyramidal cells (Schiller et al., 1997; Yuste et al., 1994) or CA1 pyramidal cells (Golding and Spruston, 1998) can trigger local dendritic spikes, and the gating (Larkum et al., 1999) and boosting (Stuart and Hausser, 2001) effects of backpropagating spikes on neighbouring synaptic input (Jarsky et al., 2005) can also be region-specific. Finally, plasticity mechanisms also appear to depend on dendritic location (Gordon et al., 2006; Letzkus et al., 2006; Sjöström and Hausser, 2006). These region-specific differences in dendritic properties may also be reflected in the preferential targeting of different types of inhibitory (Somogyi, 1977; Somogyi et al., 1998) and excitatory inputs (Markram et al., 1997; Thomson and Bannister, 1998; Petreanu et al., 2009; Richardson et al., 2009) to specific dendritic domains.
While these functional differences in macroscopic regions of the dendritic tree are now well established, it remains unclear whether the rules for synaptic integration are also heterogeneous on a smaller scale, and in particular at the level of single dendritic branches. This is especially important given the recent emphasis on the role of single dendritic branches as fundamental functional compartments for synaptic integration and plasticity (Larkum and Nevian, 2008; Losonczy and Magee, 2006; Losonczy et al., 2008; Major et al., 2008; Poirazi et al., 2003; Branco and Hausser, 2010). Do synaptic inputs along a given dendrite behave approximately equally in terms of their integrative properties, or are there systematic functional differences even along a single dendrite?
To address this question we have taken advantage of the precise spatial and temporal control of synaptic activation possible with 2-photon glutamate uncaging, and probed the thin basal and apical oblique branches of layer 2/3 and layer 5 pyramidal cells, which receive the majority of the synaptic input to these neurons (Larkman, 1991; Lubke and Feldmeyer, 2007). While strong EPSP attenuation occurs along individual branches of pyramidal cell basal dendrites (Nevian et al., 2007), it is not known if inputs at different distances along a branch are integrated similarly. We show that single cortical pyramidal cell dendrites exhibit a gradient of temporal summation and input gain that increases from proximal to distal locations. This suggests a progressive shift of computational strategies for synaptic inputs along single dendrites.
Results
The input-output function of single dendrites
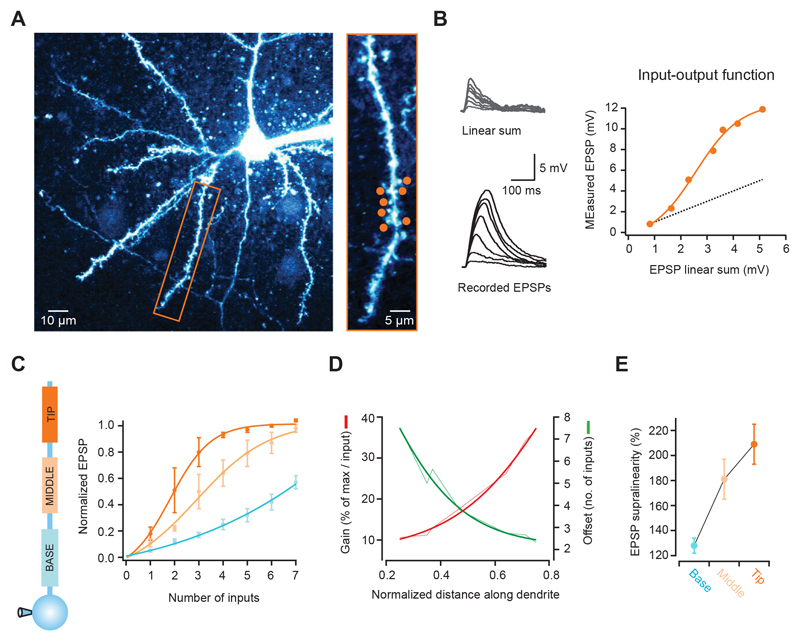
To study synaptic integration along single basal and apical oblique dendrites in cortical pyramidal cells, we first determined their subthreshold input-output function. We made whole-cell recordings from layer 2/3 pyramidal cells in the somatosensory and visual cortex to monitor somatic voltage changes, and activated an increasing number of synapses with 2-photon glutamate uncaging (Gasparini and Magee, 2006; Losonczy and Magee, 2006; Matsuzaki et al., 2001). We selected 7 spines distributed over a region of ~20-30 μm (Fig. 1A), and recorded somatic EPSPs in response to the activation of 1 to all 7 synapses (with a 1 ms interval between stimulation of each synapse). We found that the EPSP peak increased with the number of activated synapses, closely following a sigmoidal function that greatly deviated from the linear summation of each individual synapse (Fig. 1B). We then tested different regions between the tip and the branch point of single branches, and analyzed how this function varied with location. Distal synapses had a much steeper function than proximal synapses (fraction of maximum per input for tip: 0.48 ± 0.09, middle: 0.24 ± 0.06, base: 0.11 ± 0.01; n = 9, p = 0.004, ANOVA), which was also shifted to the left (number of inputs at half of the maximum for tip: 2.1 ± 0.4; middle: 3.4 ± 0.6; base: 6.1 ± 0.6, p = 0.006, ANOVA; Fig. 1C and Supplementary Fig. 1A). The gain of the input-output function increased more than 3-fold from the branch point to the dendritic tip, and was shifted by ~5 inputs (Fig. 1D). Furthermore, the EPSP supralinearity increased from 128 ± 6% to 209 ± 16% between the base and the tip of the dendrite (p = 0.015, ANOVA; Fig. 1E and Supplementary Fig. 1B). These results were also observed with small unitary gluEPSPs (~0.25 mV, see Supplementary Fig. 2 A-D) and show that there is a gradient of non-linear synaptic integration along individual dendritic branches, in which distal inputs are amplified more strongly than proximal ones.
Figure 1. The input-output function varies with distance along single pyramidal cell dendrites.
(A) Left, 2-photon image of a layer 2/3 neuron pyramidal filled with Alexa 594. Rectangular box indicates basal dendrite selected for experiment. Right, selected dendrite with 7 glutamate uncaging spots (orange circles). (B) Somatic voltage responses to increasing number of stimulated synapses (from dendrite and spots shown in a, activated at 1 ms intervals). Bottom traces show recorded responses, and top traces the linear sum expected from the individual responses to each spot. The graph on the right shows that the recorded peak EPSPs are markedly supralinear and grow as a sigmoid function (dotted line is the linear sum, orange circles the actual response; orange line is a fit to the data). (C) Differences in the input-output function according to the position along individual dendrites. Lines are sigmoid fits to the data, and values are shown normalized to the maximum of the fit. Distal synapses have a higher gain function, which is also shifted to the right (summarized in D). (E) EPSP supralinearity also increases with distance from the soma (values for activation of 3 inputs).
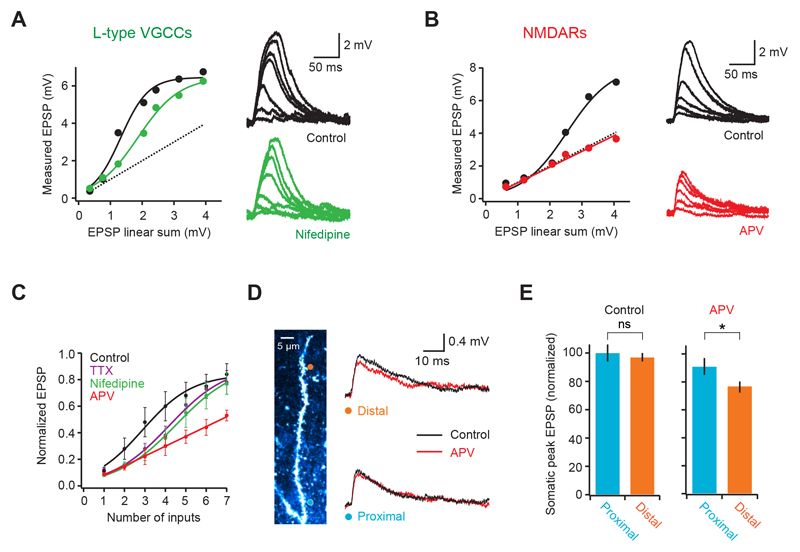
To understand the biophysical mechanism underlying supralinear integration, we used pharmacology to probe the role of specific dendritic active conductances (Johnston and Narayanan, 2008; Magee 2000; Spruston, 2008). Blocking L-type voltage-gated calcium channels (VGCCs) shifted the input-output curve to the right (Fig. 2A; number of inputs at half maximum = 215 ± 39% of control; p = 0.032; supralinearity at 3 inputs = 118 ± 10%; p = 0.0078; n = 6) without significantly affecting the gain (fraction of maximum per input: 115 ± 13% of control; p = 0.33; Fig. 2A, C). A similar effect was produced by blocking voltage-gated sodium channels (number of inputs at half maximum 159 ± 15% of control; p = 0.030; supralinearity at 3 inputs = 127 ± 15%; p = 0.024; n = 4; Fig. 2C), as well as by simultaneous VGCC and VGSC block (Supplementary Fig. 3). In contrast, block of NMDA receptors produced a linear dendritic input-output function that was consistent with linear summation of each synapse (average slope = 0.94 ± 0.1; not significantly different from 1, p = 0.54; peak EPSP at 7 synapses = 97 ± 10% of linear sum; n = 5; Fig. 2B, C). This shows that supralinear integration in L2/3 pyramidal cell dendrites crucially depends on NMDAR recruitment, which is facilitated by activation of both VGCCs and voltage-gated sodium channels (VGSCs). We next investigated how unitary EPSPs varied with distance from the branch point. Analysis of somatic EPSPs evoked by single spine uncaging revealed no significant correlation between somatic peak amplitude and distance along the dendritic branch (r = 0.13; p = 0.12; n = 139 synapses from 18 dendrites; peak of distal EPSPs = 97 ± 3% of proximal EPSPs, not significantly different; p = 0.73; laser power, plane of focus and spine size kept constant; Fig. 2D, E and Supplementary Fig. 1C). However, block of NMDARs revealed a larger NMDA component for EPSPs arising at more distal synapses (22 ± 4% for distal, 5 ± 7% for proximal; p = 0.041; n = 8), and lead to smaller somatic EPSPs for inputs at distal locations (82 ± 2% of proximal; p = 0.032), suggesting that NMDAR recruitment can partially compensate for dendritic filtering in these dendrites.
Figure 2. Biophysical mechanism of dendritic supralinear integration.
(A) Somatic voltage response to increasing number of synapses on a basal dendrite before (black) and after blocking L-type calcium channels with Nifedipine (green). Circles are datapoints, thick lines are fits to the data and dotted line is the linear sum. (B) Similar to A but comparing somatic responses before (black) and after (red) blocking NMDA receptors with APV. Note that responses become linear. (C) Summary plot (pooled data from multiple cells, n = 9 for control) showing that both Nifedipine (n = 6) and TTX (n = 4) shift the dendritic input-output curve to right, while APV (n = 5) linearizes it. (D) Activation of either a distal (orange circle) or a proximal (blue circle) single spine produces a similar size EPSP at the soma (right, black traces). Block of NMDARs reveals a larger NMDA component in the distal EPSP (right, red traces). (E) Summary data comparing EPSP size and NMDA content between proximal and distal spines (n = 8).
Temporal summation varies with input location along single dendrites
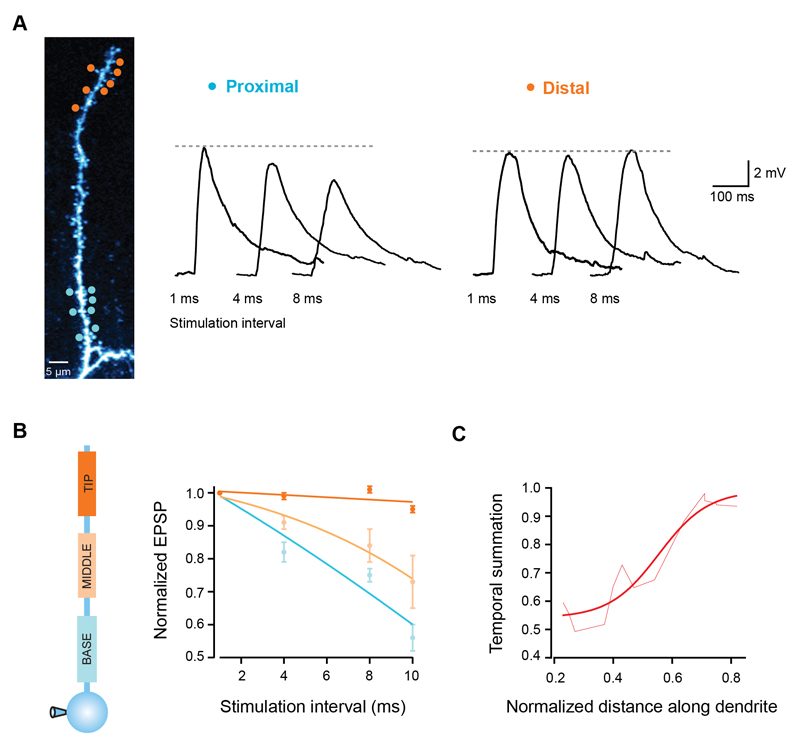
Inputs to cortical neurons can exhibit different degrees of temporal synchrony (Abeles, 1991; Konig et al., 1996; Shadlen and Newsome, 1995), and the efficacy of each particular input pattern depends on how well the individual inputs summate over time (Magee, 2000; Rall, 1964). We therefore investigated how temporal summation varies along basal and apical oblique branches. We stimulated groups of 7 synapses at different dendritic locations using different inter-stimulus intervals and monitored the somatic EPSP peak. While for proximal synapses the EPSP peak decreased as input became more asynchronous, distal synapses produced EPSPs which had remarkably similar sizes over a range of stimulation intervals (Fig. 3A). Distal EPSPs at 10 ms intervals were 95 ± 1% of the peak at 1 ms intervals, while for proximal EPSPs the peak decreased to 56 ± 4% (p < 0.0001, ANOVA, n = 19; Fig. 3B), which was also seen for small EPSPs (Supplementary Fig. 2 E-F) and for a smaller number of stimulated synapses (Supplementary Fig. 1D). Between the branch point and the tip of the dendrite, temporal summation gradually increased by almost 2-fold (Fig. 3C). This shows that in parallel with the changes in gain described above, single dendritic branches also have a gradient of efficacy for summation of asynchronous synaptic input.
Figure 3. Temporal summation gradient along pyramidal cell dendrites.
(A) Seven uncaging spots were placed either at the tip (orange circles) or close to the branchpoint of a single dendrite (blue circles), and activated with different degrees of synchrony. Traces show somatic EPSPs in response to increasing stimulation intervals for both locations. Note the invariance of the EPSP peak for distal synapses. (B) EPSP peak normalized to the response for 1 ms intervals for 3 different regions of single dendrites. Lines are fits to the data. (C) Temporal summation increases towards the dendritic tip (measured as the EPSP peak at 10 ms interval normalized to the response at 1 ms interval). Smooth line is a sigmoid fit.
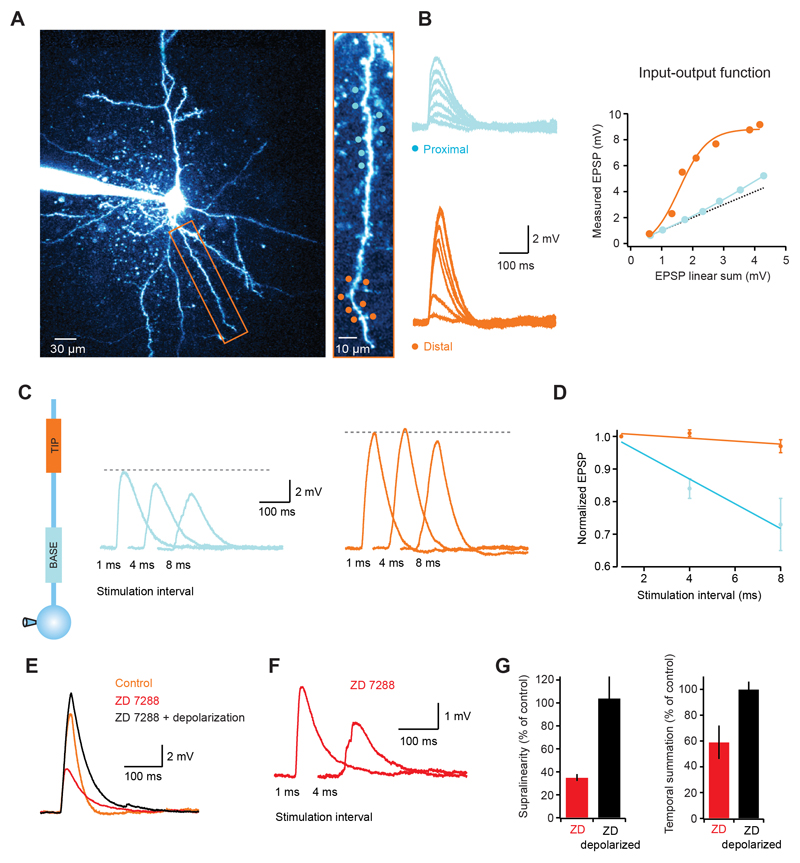
Layer 2/3 pyramidal cells lack a significant density of Ih channels (Larkum et al., 2007). In hippocampal CA1 pyramidal cells the presence of a dendritic gradient of Ih has been shown to normalize temporal summation over the dendritic tree (Magee, 2000). To test whether dendritic integration gradients are still present in cortical neurons with significant Ih, we carried out experiments in single dendrites of L5 pyramidal cells which - unlike L2/3 pyramidal dendrites - have a high density of Ih channels (Berger et al., 2001; Stuart and Spruston, 1998). We found that the dendritic input-output function in L5 pyramidal cells was supralinear and sigmoidal with a similar increase in steepness from proximal to distal locations compared to layer 2/3 pyramidal cells (Fig. 4A, B). As in layer 2/3 pyramidal cells, temporal summation in layer 5 pyramidal cells was much more effective at distal locations (peak EPSP at 8 ms intervals was 97 ± 2% of the peak at 1 ms intervals for distal synapses, while for proximal locations the peak decreased to 73 ± 8%; p = 0.019 ANOVA; n = 6; Fig. 4C, D). Blocking Ih channels caused a hyperpolarization of the somatic membrane potential by 9.1 ± 0.2 mV (cf. Berger et al., 2001; Stuart and Spruston, 1998), which was accompanied by a dramatic reduction in the degree of supralinearity (35 ± 3 % of control; p < 0.0001; n = 5; Fig. 4E, G) and efficacy of temporal summation (59 ± 13% of control for distal dendrites; p = 0.036; n = 5; Fig. 4F, G). However, somatic depolarization via current injection fully restored the supralinearity (104 ± 19% of control; p = 0.85) as well as temporal summation (100 ± 6% of control; p = 0.95), suggesting that in L5 pyramidal cells the interaction between dendritic non-linearities and the depolarizing effect of Ih can overcome the Ih–dependent speeding of the EPSP decay, and supports increased gain and temporal summation at distal sites.
Figure 4. Dendritic integration gradients in layer 5 pyramidal neurons.
(A) Left, 2-photon image of a layer 5 pyramidal cell with the dendrite targeted in experiment indicated by rectangular box. Right, targeted dendrite with distal (orange circles) and proximal (blue circles) uncaging spots. (B) Somatic EPSPs in response to increasing numbers of stimulated spines (1 ms interval) for the proximal (top, blue) and distal (bottom, orange) locations. The graph on the right shows that, like in layer 2/3 cells, distal synapses have a highly supralinear and sigmoidal input-output function, while proximal locations show a much more linear function. (C) Somatic voltage traces for stimulation at increasing intervals at proximal (blue traces) and distal (orange traces) locations. (D) Summary data showing that temporal summation is more effective at distal locations. (E) Blocking Ih channels decreases the EPSP amplitude (red trace), which is restored upon somatic depolarization (black trace). Note the difference in the EPSP decay between the black and orange (control) traces, illustrating the Ih-dependent speeding of EPSP decay. (F) Somatic EPSP for two stimulation intervals of distal synapses in Ih block. Note how the response at 4 ms is significantly smaller than at 1 ms (compare with orange traces in (C). (G) Summary data showing the effects of Ih block on dendritic supralinearity and efficiency of temporal summation.
Biophysical model of integration gradients
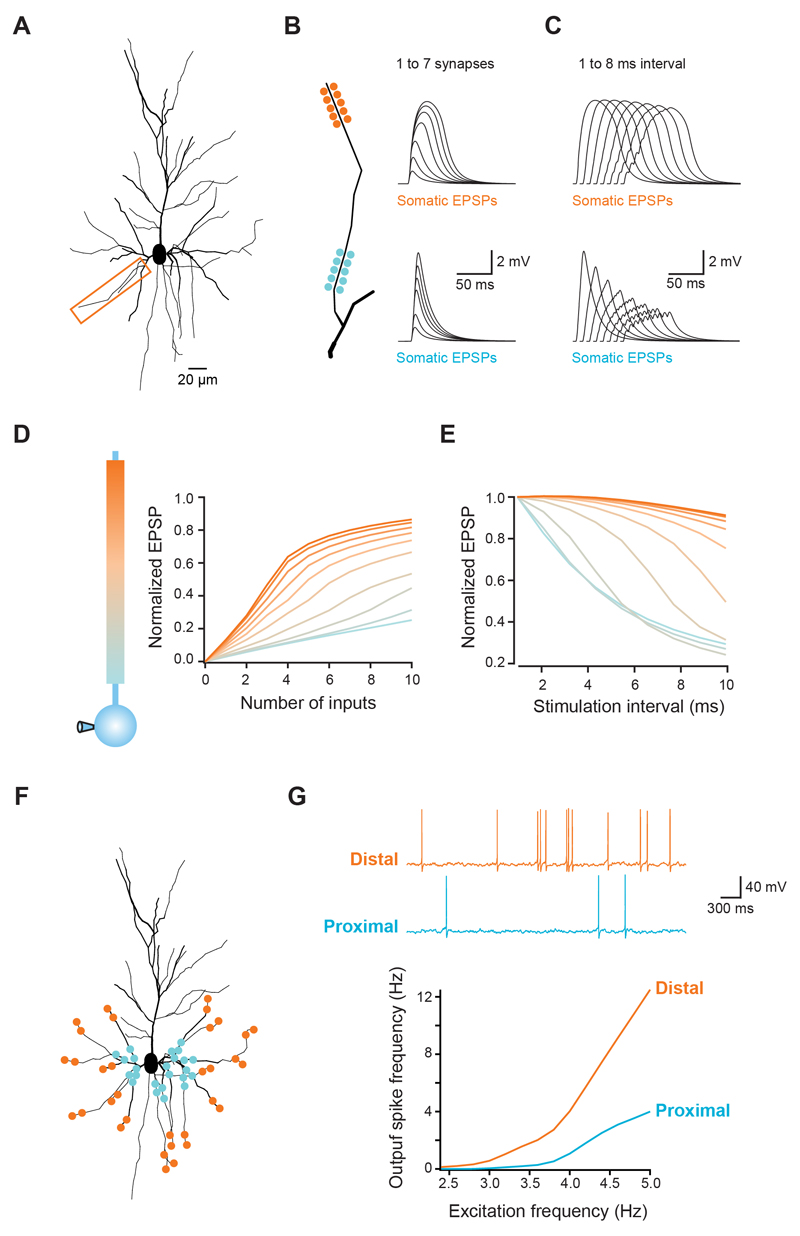
To further explore the biophysical basis of integration gradients in cortical pyramidal cell dendrites, we modeled a layer 2/3 pyramidal cell, based on a 3D reconstruction of one of our cells (Fig. 5A). Passive properties were adjusted to match our recordings, and active conductances were distributed in all compartments according to previous studies (Major et al., 2008; Nevian et al., 2007; see Experimental Procedures). Synapses containing both AMPA and NMDA receptors were placed at different locations along an individual dendrite. As in our experiments, we increased the number of activated synapses or the inter-synapse stimulation interval while recording the somatic EPSP (Fig. 5B,C). The simulation results closely matched the experimental data, showing sigmoidal input-output curves of increasing gain towards the dendritic tip, as well as increased temporal summation (Fig. 5D,E; see also Supplementary Fig. 4A-C).
Figure 5. Modelling the impact of dendritic integration gradients on neuronal output.
(A) Morphology of a reconstructed layer 2/3 pyramidal used for simulations. Box indicates dendrite used in B-E. (B,C) Clusters of synapses were placed at different locations along the dendrite (total length = 90 μm). (B) Increasing number of synapses were activated or (C) all synapses activated at different intervals. Traces show somatic voltage responses for proximal (bottom) and distal synapses (top), which reproduce the experimental data (see Figure 1A and 2A). (D,E) Summary for all tested locations in the model, showing the same gradients for the gain of the input-output function (D) and temporal summation (E) that were observed experimentally. (F) Schematic illustration of 169 synapses randomly distributed across all basal dendrites, with either a distal or a proximal bias. (G) Each synapse was activated with independent Poisson trains of increasing frequency and the somatic voltage monitored. As the excitation frequency increases, the spiking frequency increases more rapidly for distally distributed synapses. Traces show responses for distal (orange) and proximal (blue) distributions stimulated at 4 Hz.
Analysis of the simulations revealed that the synaptic integration gradients can be explained by the interaction between active conductances and the progressive increase in dendritic input impedance towards the tip of the branch. Distal synapses generate a larger local dendritic depolarization due to the high local input impedance (Jack et al., 1975; Nevian et al., 2007), which activates VGCCs and VGSCs, and relieves the magnesium block of NMDARs (Branco et al., 2010; Major et al., 2008; Mayer et al., 1984; Nowak et al., 1984; Schiller et al., 2000; Schiller et al., 1997). This generates a supralinear and highly regenerative response that is very sensitive to the addition of even a small number of synapses, thus producing a steep input-output function. Because of the slow glutamate unbinding time constant of NMDARs (on the order of ~30 ms; Cais et al., 2008), asynchronous inputs can effectively interact over a wide time window to increase the local membrane depolarization and recruit more NMDAR conductance, thereby producing a broad window for synaptic integration at distal dendrites. When synapses are placed more proximally, the lower local input impedance leads to reduced recruitment and regeneration of active conductances, leading to a smaller gain function and less efficient temporal summation. This was reproduced with a range of NMDA:AMPA ratios (Supplementary Fig. 1E), as well as with forward and reverse AMPA receptor density gradients (Katz et al. 2009; Supplementary Fig. 4F), underscoring the strength of the interaction between impedance differences and dendritic active conductances. This interaction is also sufficient to explain the increased NMDA component of single synapses at distal locations (which was present with uniform synaptic NMDA conductance density in the model), and also its compensatory effect on the somatic EPSP amplitude (Supplementary Fig. 4D), though distance-dependent differences in the density of NMDAR or other conductances cannot be ruled out as an additional contributing factor.
Finally, we used the model to explore the consequences of the integration gradients we have described on the spike output of a pyramidal neuron receiving a large number of random excitatory and inhibitory inputs. Synapses were randomly distributed across basal and apical oblique dendritic branches, and allowed to cover only the distal or the proximal 10% of each branch (Fig. 5F). Each synapse was activated with an independent Poisson train of presynaptic spikes, and the firing rate of the neuron was measured for a range of input frequencies. The suprathreshold input-output function of distal synapses was clearly steeper when compared with proximal synapses (slope of linear fit between 3.5 and 5 Hz excitation rate: distal = 7.2, proximal = 2.6), with 3.3-fold more spikes produced at an excitation rate of 5 Hz. Thus, with temporally distributed input onto basal dendrites, distal synapses are surprisingly more efficient in driving spike output in cortical pyramidal cells.
Discussion
It is now well established that different dendritic regions can exhibit different functional properties (Larkum et al., 1999; Llinas and Sugimori, 1980; Schiller et al., 1997; Yuste et al., 1994). Here we show that this functional heterogeneity also exists on a much finer spatial scale: the level of the single dendritic branch. Moreover, we show that this heterogeneity obeys a simple organizational principle: a gradient of synaptic integration along the proximal-distal axis. Distal synaptic inputs exhibit an input-output function with higher gain and a broader window for temporal summation than proximal inputs to the same dendrite. These properties can allow asynchronously activated distal synapses to overcome their relative electrotonic disadvantage compared to proximal synapses and exert a paradoxically greater influence on action potential output. Furthermore, the differential sensitivity to input timing makes proximal inputs more suited for temporal coding and distal inputs for rate coding. The fact that these differences exist along individual dendrites indicates that single dendrites are not uniform compartments, and that the computational strategy of individual synaptic inputs may depend on their precise location along the dendrite.
Mechanisms generating synaptic integration gradients along single dendrites
Using a combination of experimental and modeling approaches, we demonstrate that the synaptic integration gradients result from a combination of two basic biophysical features of single dendrites. First, dendritic non-linearities, including NMDA receptor conductances, VGCCs and VGSCs, must be recruited by increasing numbers of synaptic inputs. Previous studies have demonstrated that synchronous clustered input can recruit such dendritic non-linearities in neocortical pyramidal cells (Major et al., 2008; Nevian et al., 2007; Polsky et al., 2004; Schiller et al., 2000), which can help to enhance synaptic gain (Larkum et al., 2004) and compensate for the electrotonic filtering of distal inputs (Cook and Johnston, 1997, 1999). The second, crucial, ingredient is the gradient of input impedance that exists along single dendrites; a consequence of the impedance load as the dendritic branch meets its parent trunk (or the soma) and the end effect at the tip of the dendrite. These two factors work in concert to generate the observed gradient in integrative properties along each dendrite. Given that these two properties – dendritic nonlinearities and impedance gradients – are present in most neurons, this suggests that the observed synaptic integration gradients may be a general feature of neurons in the central nervous system.
It is important to note that the synaptic integration gradients we have observed do not require any underlying gradients in the properties of the synapses or in the dendritic distribution of voltage-gated channels. Indeed, in our model we could reproduce our experimentally observed integration gradients using entirely uniform synaptic parameters and densities of voltage-gated channels; thus the gradients arise solely from the non-uniform electronic architecture intrinsic to the fundamental asymmetry of dendritic structure. In neurons exhibiting dendritic gradients of synaptic properties (Katz et al., 2009; Magee and Cook, 2000) or voltage-gated channels (Lorincz et al., 2002; Magee, 1999; Mathews et al., 2010; Williams and Stuart, 2000), these will be superimposed on, and may modify the synaptic integration gradients that we have demonstrated.
Functional implications
How might neurons exploit the synaptic integration gradients? First, they may provide a mechanism to mitigate the unfavorable electrotonic location of distal inputs. When synapses are active individually, or during synchronous activation of multiple synapses, distally evoked events are smaller at the soma than proximally evoked events due to dendritic filtering (Major, 2008), a phenomenon also reproduced by our model (Supplementary Fig. 1A). However, in the less constrained condition of asynchronously active inputs, the increased time window for integration of distal inputs overcomes the disadvantage of filtering, making them more efficient than proximal inputs in triggering axonal output. As demonstrated in Figure 5, such a scenario is likely to be engaged in vivo, where continuous asynchronous barrages of synaptic inputs at high rates are expected (Destexhe et al., 2003; Sanchez-Vives and McCormick, 2000), particularly given that conditions of precisely synchronous activation of inputs may be achieved only rarely, or with some difficulty in vivo (London et al., 2010).
Second, the differential sensitivity to temporal information at proximal and distal locations may be used to read out different forms of information from input provided by the circuit. For example, connections placed proximally will sum almost linearly and require high temporal coincidence to effectively drive action potential firing, meaning that temporally coded information can be precisely read out (Softky and Koch, 1993). In contrast, inputs that are placed distally will be non-linearity amplified with high gain and integrated over a wide temporal window, enabling the effective readout of rate-based information (Shadlen and Newsome, 1998). Such differential readout may be particularly relevant for circuits exhibiting different functional roles for inputs to the proximal and distal regions, such as in granule cells of dentate gyrus which receive layered input from the lateral and medial entorhinal cortex along their largely unbranched dendrites (Andersen et al., 2006; Hjorth-Simonsen, 1972). Thus, the dendritic gradients we have described allow a single cell to differentially integrate and process inputs from different origins and with different temporal structure. This may help to reconcile the rate-based and timing-based views of neural coding, and the increased flexibility provided by single dendrites may also greatly increase the computational power of individual neurons.
Experimental Procedures
Slice preparation and electrophysiology
Acute sagittal brain slices were prepared from 3-6 week-old rats. Experiments were carried out at 32 - 35°C and somatic whole-cell recordings were obtained with a Multiclamp 700B amplifier (Molecular Devices). Patch pipettes were filled with a KMeSO4-based internal solution, with Alexa Fluor 594 (100 μM; Invitrogen) to visualize cell morphology. For the pharmacology experiments shown in Fig. 2 drugs were included in a second caged glutamate-puffing pipette (D-AP5, 500 μM; Nifedipine, 40 μM; TTX, 1 μM).
Two-photon imaging and uncaging
Simultaneous 2-photon imaging and uncaging was performed using a dual galvanometer-based scanning system (Prairie Technologies, Middleton, WI) using two Ti:sapphire pulsed lasers (MaiTai, Spectra-Physics). Two-photon glutamate uncaging was carried out based on previously published methods (Gasparini and Magee, 2006; Losonczy and Magee, 2006; Matsuzaki et al., 2001). MNI-caged-L-glutamate (12 mM, Tocris Cookson, UK) was puffed locally and uncaging exposure time was 100 - 500 μs with laser power adjusted to produce gluEPSPs with kinetics and amplitudes comparable to mEPSPs recorded in the same cells.
Compartmental modelling
Simulations were performed with the NEURON simulation environment (Hines and Carnevale, 1997) using a detailed 3D reconstruction (Neurolucida; Microbrightfield, Williston, VT) of a biocytin-filled L2/3 pyramidal neuron from one the experiments. Biophysical and synaptic parameters were modelled as in Branco et al. 2010. For the simulations in Fig. 5F,G, excitatory synapses were distributed over 18 dendritic branches and placed either in the proximal or distal 10% of the branch, and activated with independent Poisson trains of increasing frequencies. The same number of inhibitory synapses were placed in the same compartment of each excitatory synapse, and activated with Poisson trains at a mean frequency of 10 Hz.
Analysis
EPSP supralinearity was defined as the recorded EPSP peak over the linear sum of the individual components. Gain and offset were calculated from the derivative of the sigmoidal fit to the data points. The gain reported is the peak of the derivative and thus the maximal gain of the input-output function. Data are reported as mean ± SEM unless otherwise indicated.
Supplementary Material
Acknowledgements
We thank Mickey London, Arnd Roth and Beverley Clark for helpful discussions and comments on the manuscript. This work was supported by grants from the Wellcome Trust and the Gatsby Charitable Foundation.
References
- Abeles M. Corticonics: neural circuits of the cerebral cortex. Cambridge, UK: Cambridge University Press; 1991. [Google Scholar]
- Andersen P, Morris R, Amaral D, Bliss TV, O'Keefe J. The Hippocampus Book. New York: Oxford University Press; 2006. [Google Scholar]
- Andersen P, Silfvenius H, Sundberg SH, Sveen O. A comparison of distal and proximal dendritic synapses on CA1 pyramids in guinea-pig hippocampal slices in vitro. The Journal of Physiology. 1980;307:273–299. doi: 10.1113/jphysiol.1980.sp013435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger T, Larkum ME, Lüscher HR. High I(h) channel density in the distal apical dendrite of layer V pyramidal cells increases bidirectional attenuation of EPSPs. J Neurophysiol. 2001;85:855–68. doi: 10.1152/jn.2001.85.2.855. [DOI] [PubMed] [Google Scholar]
- Branco T, Häusser M. The single dendritic branch as a fundamental functional unit in the nervous system. Curr Opin Neurobiol. 2010;20:494–502. doi: 10.1016/j.conb.2010.07.009. [DOI] [PubMed] [Google Scholar]
- Branco T, Clark BA, Häusser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science. 2010;329:1671–5. doi: 10.1126/science.1189664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cais O, Sedlacek M, Horak M, Dittert I, Vyklicky L., Jr Temperature dependence of NR1/NR2B NMDA receptor channels. Neuroscience. 2008;151:428–438. doi: 10.1016/j.neuroscience.2007.11.002. [DOI] [PubMed] [Google Scholar]
- Cook EP, Johnston D. Active dendrites reduce location-dependent variability of synaptic input trains. Journal of Neurophysiology. 1997;78:2116–2128. doi: 10.1152/jn.1997.78.4.2116. [DOI] [PubMed] [Google Scholar]
- Cook EP, Johnston D. Voltage-dependent properties of dendrites that eliminate location-dependent variability of synaptic input. Journal of Neurophysiology. 1999;81:535–543. doi: 10.1152/jn.1999.81.2.535. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, Pare D. The high-conductance state of neocortical neurons in vivo. Nature reviews. 2003;4:739–751. doi: 10.1038/nrn1198. [DOI] [PubMed] [Google Scholar]
- Gasparini S, Magee JC. State-dependent dendritic computation in hippocampal CA1 pyramidal neurons. J Neurosci. 2006;26:2088–2100. doi: 10.1523/JNEUROSCI.4428-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding NL, Spruston N. Dendritic sodium spikes are variable triggers of axonal action potentials in hippocampal CA1 pyramidal neurons. Neuron. 1998;21:1189–1200. doi: 10.1016/s0896-6273(00)80635-2. [DOI] [PubMed] [Google Scholar]
- Gordon U, Polsky A, Schiller J. Plasticity compartments in basal dendrites of neocortical pyramidal neurons. J Neurosci. 2006;26:12717–12726. doi: 10.1523/JNEUROSCI.3502-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Hjorth-Simonsen A. Projection of the lateral part of the entorhinal area to the hippocampus and fascia dentata. J Comp Neurol. 1972;146:219–232. doi: 10.1002/cne.901460206. [DOI] [PubMed] [Google Scholar]
- Jack JJ, Redman SJ, Wong K. The components of synaptic potentials evoked in cat spinal motoneurones by impulses in single group Ia afferents. The Journal of Physiology. 1981;321:65–96. doi: 10.1113/jphysiol.1981.sp013972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack JJB, Noble D, Tsien RW. Electric Current Flow in Excitable Cells. Oxford: Oxford University Press; 1975. [Google Scholar]
- Jarsky T, Roxin A, Kath WL, Spruston N. Conditional dendritic spike propagation following distal synaptic activation of hippocampal CA1 pyramidal neurons. Nature Neuroscience. 2005;8:1667–1676. doi: 10.1038/nn1599. [DOI] [PubMed] [Google Scholar]
- Johnston D, Narayanan R. Active dendrites: colorful wings of the mysterious butterflies. Trends Neurosci. 2008;31:309–16. doi: 10.1016/j.tins.2008.03.004. [DOI] [PubMed] [Google Scholar]
- Katz Y, Menon V, Nicholson DA, Geinisman Y, Kath WL, Spruston N. Synapse distribution suggests a two-stage model of dendritic integration in CA1 pyramidal neurons. Neuron. 2009;63:171–177. doi: 10.1016/j.neuron.2009.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konig P, Engel AK, Singer W. Integrator or coincidence detector? The role of the cortical neuron revisited. Trends in Neurosciences. 1996;19:130–137. doi: 10.1016/s0166-2236(96)80019-1. [DOI] [PubMed] [Google Scholar]
- Larkman AU. Dendritic morphology of pyramidal neurones of the visual cortex of the rat: III. Spine distributions. J Comp Neurol. 1991;306:332–343. doi: 10.1002/cne.903060209. [DOI] [PubMed] [Google Scholar]
- Larkum ME, Nevian T. Synaptic clustering by dendritic signalling mechanisms. Curr Opin Neurobiol. 2008;18:321–331. doi: 10.1016/j.conb.2008.08.013. [DOI] [PubMed] [Google Scholar]
- Larkum ME, Senn W, Luscher HR. Top-down dendritic input increases the gain of layer 5 pyramidal neurons. Cereb Cortex. 2004;14:1059–1070. doi: 10.1093/cercor/bhh065. [DOI] [PubMed] [Google Scholar]
- Larkum ME, Waters J, Sakmann B, Helmchen F. Dendritic spikes in apical dendrites of neocortical layer 2/3 pyramidal neurons. J Neurosci. 2007;27:8999–9008. doi: 10.1523/JNEUROSCI.1717-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum ME, Zhu JJ, Sakmann B. A new cellular mechanism for coupling inputs arriving at different cortical layers. Nature. 1999;398:338–341. doi: 10.1038/18686. [DOI] [PubMed] [Google Scholar]
- Letzkus JJ, Kampa BM, Stuart GJ. Learning rules for spike timing-dependent plasticity depend on dendritic synapse location. J Neurosci. 2006;26:10420–10429. doi: 10.1523/JNEUROSCI.2650-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R, Sugimori M. Electrophysiological properties of in vitro Purkinje cell dendrites in mammalian cerebellar slices. The Journal of Physiology. 1980;305:197–213. doi: 10.1113/jphysiol.1980.sp013358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- London M, Roth A, Beeren L, Hausser M, Latham PE. Sensitivity to perturbations in vivo implies high noise and suggests rate coding in cortex. Nature. 2010;466:123–127. doi: 10.1038/nature09086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorincz A, Notomi T, Tamas G, Shigemoto R, Nusser Z. Polarized and compartment-dependent distribution of HCN1 in pyramidal cell dendrites. Nature Neuroscience. 2002;5:1185–1193. doi: 10.1038/nn962. [DOI] [PubMed] [Google Scholar]
- Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron. 2006;50:291–307. doi: 10.1016/j.neuron.2006.03.016. [DOI] [PubMed] [Google Scholar]
- Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452:436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]
- Lubke J, Feldmeyer D. Excitatory signal flow and connectivity in a cortical column: focus on barrel cortex. Brain Struct Funct. 2007;212:3–17. doi: 10.1007/s00429-007-0144-2. [DOI] [PubMed] [Google Scholar]
- Magee JC. Dendritic lh normalizes temporal summation in hippocampal CA1 neurons. Nature Neuroscience. 1999;2:508–514. doi: 10.1038/9158. [DOI] [PubMed] [Google Scholar]
- Magee JC. Dendritic integration of excitatory synaptic input. Nature reviews. 2000;1:181–190. doi: 10.1038/35044552. [DOI] [PubMed] [Google Scholar]
- Magee JC, Cook EP. Somatic EPSP amplitude is independent of synapse location in hippocampal pyramidal neurons. Nature Neuroscience. 2000;3:895–903. doi: 10.1038/78800. [DOI] [PubMed] [Google Scholar]
- Major G, Polsky A, Denk W, Schiller J, Tank DW. Spatiotemporally graded NMDA spike/plateau potentials in basal dendrites of neocortical pyramidal neurons. Journal of Neurophysiology. 2008;99:2584–2601. doi: 10.1152/jn.00011.2008. [DOI] [PubMed] [Google Scholar]
- Markram H, Lubke J, Frotscher M, Roth A, Sakmann B. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. The Journal of Physiology. 1997;500(Pt 2):409–440. doi: 10.1113/jphysiol.1997.sp022031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathews PJ, Jercog PE, Rinzel J, Scott LL, Golding NL. Control of submillisecond synaptic timing in binaural coincidence detectors by K(v)1 channels. Nature Neuroscience. 2010;13:601–609. doi: 10.1038/nn.2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki M, Ellis-Davies GC, Nemoto T, Miyashita Y, Iino M, Kasai H. Dendritic spine geometry is critical for AMPA receptor expression in hippocampal CA1 pyramidal neurons. Nature Neuroscience. 2001;4:1086–1092. doi: 10.1038/nn736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer ML, Westbrook GL, Guthrie PB. Voltage-dependent block by Mg2+ of NMDA responses in spinal cord neurones. Nature. 1984;309:261–263. doi: 10.1038/309261a0. [DOI] [PubMed] [Google Scholar]
- Nevian T, Larkum ME, Polsky A, Schiller J. Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nature Neuroscience. 2007;10:206–214. doi: 10.1038/nn1826. [DOI] [PubMed] [Google Scholar]
- Nowak L, Bregestovski P, Ascher P, Herbet A, Prochiantz A. Magnesium gates glutamate-activated channels in mouse central neurones. Nature. 1984;307:462–465. doi: 10.1038/307462a0. [DOI] [PubMed] [Google Scholar]
- Petreanu L, Mao T, Sternson SM, Svoboda K. The subcellular organization of neocortical excitatory connections. Nature. 2009;457:1142–1145. doi: 10.1038/nature07709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poirazi P, Brannon T, Mel BW. Pyramidal neuron as two-layer neural network. Neuron. 2003;37:989–999. doi: 10.1016/s0896-6273(03)00149-1. [DOI] [PubMed] [Google Scholar]
- Polsky A, Mel BW, Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nature Neuroscience. 2004;7:621–627. doi: 10.1038/nn1253. [DOI] [PubMed] [Google Scholar]
- Rall W. Theoretical significance of dendritic trees for neuronal input-output relations. In: Reiss R, editor. Neural Theory and Modeling. Stanford, CA: Stanford Univ. Press; 1964. pp. 73–97. [Google Scholar]
- Rall W. Distinguishing theoretical synaptic potentials computed for different soma-dendritic distributions of synaptic input. Journal of Neurophysiology. 1967;30:1138–1168. doi: 10.1152/jn.1967.30.5.1138. [DOI] [PubMed] [Google Scholar]
- Rall W, Burke RE, Smith TG, Nelson PG, Frank K. Dendritic location of synapses and possible mechanisms for the monosynaptic EPSP in motoneurons. Journal of Neurophysiology. 1967;30:1169–1193. doi: 10.1152/jn.1967.30.5.1169. [DOI] [PubMed] [Google Scholar]
- Richardson RJ, Blundon JA, Bayazitov IT, Zakharenko SS. Connectivity patterns revealed by mapping of active inputs on dendrites of thalamorecipient neurons in the auditory cortex. J Neurosci. 2009;29:6406–6417. doi: 10.1523/JNEUROSCI.0258-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Vives MV, McCormick DA. Cellular and network mechanisms of rhythmic recurrent activity in neocortex. Nature Neuroscience. 2000;3:1027–1034. doi: 10.1038/79848. [DOI] [PubMed] [Google Scholar]
- Schiller J, Major G, Koester HJ, Schiller Y. NMDA spikes in basal dendrites of cortical pyramidal neurons. Nature. 2000;404:285–289. doi: 10.1038/35005094. [DOI] [PubMed] [Google Scholar]
- Schiller J, Schiller Y, Stuart G, Sakmann B. Calcium action potentials restricted to distal apical dendrites of rat neocortical pyramidal neurons. The Journal of Physiology. 1997;505(Pt 3):605–616. doi: 10.1111/j.1469-7793.1997.605ba.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. Is there a signal in the noise? Curr Opin Neurobiol. 1995;5:248–250. doi: 10.1016/0959-4388(95)80033-6. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 1998;18:3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjöström PJ, Hausser M. A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron. 2006;51:227–238. doi: 10.1016/j.neuron.2006.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Softky WR, Koch C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J Neurosci. 1993;13:334–350. doi: 10.1523/JNEUROSCI.13-01-00334.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Somogyi P. A specific 'axo-axonal' interneuron in the visual cortex of the rat. Brain Res. 1977;136:345–350. doi: 10.1016/0006-8993(77)90808-3. [DOI] [PubMed] [Google Scholar]
- Somogyi P, Tamas G, Lujan R, Buhl EH. Salient features of synaptic organisation in the cerebral cortex. Brain Res Brain Res Rev. 1998;26:113–135. doi: 10.1016/s0165-0173(97)00061-1. [DOI] [PubMed] [Google Scholar]
- Spruston N. Pyramidal neurons: dendritic structure and synaptic integration. Nature Rev Neurosci. 2008;9:206–21. doi: 10.1038/nrn2286. [DOI] [PubMed] [Google Scholar]
- Stricker C, Field AC, Redman SJ. Statistical analysis of amplitude fluctuations in EPSCs evoked in rat CA1 pyramidal neurones in vitro. The Journal of Physiology. 1996;490:419–441. doi: 10.1113/jphysiol.1996.sp021155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart G, Spruston N. Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J Neurosci. 1998;18:3501–3510. doi: 10.1523/JNEUROSCI.18-10-03501.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart GJ, Hausser M. Dendritic coincidence detection of EPSPs and action potentials. Nature Neuroscience. 2001;4:63–71. doi: 10.1038/82910. [DOI] [PubMed] [Google Scholar]
- Thomson AM, Bannister AP. Postsynaptic pyramidal target selection by descending layer III pyramidal axons: dual intracellular recordings and biocytin filling in slices of rat neocortex. Neuroscience. 1998;84:669–683. doi: 10.1016/s0306-4522(97)00557-5. [DOI] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ. Site independence of EPSP time course is mediated by dendritic I(h) in neocortical pyramidal neurons. Journal of Neurophysiology. 2000;83:3177–3182. doi: 10.1152/jn.2000.83.5.3177. [DOI] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ. Dependence of EPSP efficacy on synapse location in neocortical pyramidal neurons. Science (New York, NY. 2002;295:1907–1910. doi: 10.1126/science.1067903. [DOI] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ. Role of dendritic synapse location in the control of action potential output. Trends in Neurosciences. 2003;26:147–154. doi: 10.1016/S0166-2236(03)00035-3. [DOI] [PubMed] [Google Scholar]
- Yuste R, Gutnick MJ, Saar D, Delaney KR, Tank DW. Ca2+ accumulations in dendrites of neocortical pyramidal neurons: an apical band and evidence for two functional compartments. Neuron. 1994;13:23–43. doi: 10.1016/0896-6273(94)90457-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.