Multi-fiber distributed thermal profiling of minimally invasive thermal ablation with scattering-level multiplexing in MgO-doped fibers

Abstract

We propose a setup for multiplexed distributed optical fiber sensors capable of resolving temperature distribution in thermo-therapies, with a spatial resolution of 2.5 mm over multiple fibers interrogated simultaneously. The setup is based on optical backscatter reflectometry (OBR) applied to optical fibers having backscattered power significantly larger than standard fibers (36.5 dB), obtained through MgO doping. The setup is based on a scattering-level multiplexing, which allows interrogating all the sensing fibers simultaneously, thanks to the fact that the backscattered power can be unambiguously associated to each fiber. The setup has been validated for the planar measurement of temperature profiles in ex vivo radiofrequency ablation, obtaining the measurement of temperature over a surface of 96 total points (4 fibers, 8 sensing points per cm²). The spatial resolution obtained for the planar measurement allows extending distributed sensing to surface, or even three-dimensional, geometries performing temperature sensing in the tissue with millimeter resolution in multiple dimensions.

1. Introduction

Minimally invasive thermotherapies are playing a significant role in cancer treatment, for the removal of solid tumors after their diagnosis [1–3]. Minimally invasive methods based on thermal ablation make use of a minimally invasive applicator, inserted in situ to deliver heat in the form of electromagnetic energy to the surrounding tissue. Tumor cells mortality is a function of temperature and exposure time [4,5], with cytotoxicity phenomena appearing over 42 °C; temperatures higher than 60 °C induce protein coagulation, resulting in a rapid cellular death [4].

Thermal ablation methods are successful in providing percutaneous treatments for solid tumors having small size in liver [3], kidney [6], thyroid [7], and brain [8] among others. Four principal methods have been implemented in clinical practice: radiofrequency ablation (RFA), which makes use of the difference of potential between an active electrode positioned on the applicator tip and a passive electrode placed in a neutral spot [1,6]; microwave ablation (MWA) uses a generator emitting around 2.4 GHz to deliver an alternate power to the tissue, which acts as an electrical load [9]; laser ablation (LA), in which a solid-state laser delivers a continuous power to the tissue through one or multiple delivery fibers [7]; high-intensity focused ultrasound (HIFU), a non-contact method, in which an arrayed element focuses an ultrasound beam scanning the target tissue [10]. Among these methods, RFA and MWA have been appreciated for their capability to treat wide portions of tissue and rapid ablation process, and recent results show that these methods can be complemented with nanoparticles to extend the ablated tissue by a significant amount [11].

One of the main challenges of thermal ablation is the measurement of temperature across the treated regions [12] because the cellular mortality is a direct function of thermal dosimetry. This task is challenging since all thermal treatments generate heat patterns in the tissue that have high spatial and temporal gradients, often overcoming 50 °C/mm and 5 °C/s [13]. Therefore [4], the possibility to measure in real-time the temperature profile resolving thermal patterns is important to estimate the ablated portion of the tissue [14]; this allows verifying that the entire tumor has been treated, making thermometry the most important control for RFA/MWA [12].

The classical method for measuring the temperature in situ makes use of thermocouples [15,16]. These sensors, however, have two major weaknesses: thermocouples, even when packaged in a miniature form factor, can affect the heating propagation due to the two metallic wires which represent their sensing part, and they measure the temperature in a single point, while they cannot measure a spatial profile of temperature. Thermocouples are mounted on the tip of modern commercial RFA devices [17]. An alternative to thermocouples is thermal imaging [18–20], which uses magnetic resonance imaging (MRI) or computed tomography (CT) to perform thermal imaging on the tissue exposed to ablation. In these techniques, the temperature change is inferred from images of temperature dependent properties of biological tissue [18,19]. MRI thermometry is based on the dependence of several MR parameters on temperature. Among others, the relaxation times and the proton resonance frequency are the most employed in these fields [18]. This technique has been already used in vivo during different thermal treatments [20]. Basically, CT thermometry is based on the influence of the temperature on the phenomenon of Compton scattering. This influence causes a decrease of the attenuation of X-ray beam with temperature which can be observed on the CT images [20]. Both these techniques have the main advantages to be non-invasive (or contactless) and to provide a three-dimensional temperature map around the tissue. Otherwise, the main concerns in the use of these techniques are the cost of MR scanner and specific sequences for obtaining good sensitivity to temperature, the need of using MR-compatible devices (for MR thermometry), the need to an X-ray dose to the patient (for CT-thermometry), and the presence of artefact due to patient respiratory movement [18,19].

Fiber optic sensors (FOS) represent the main alternative to these methods and have been recently extensively applied for temperature sensing in real time during RFA and MWA [13,14]. FOS are an excellent candidate to outperform thermocouples and MRI, because they have miniature form factor (smaller than RFA/MWA applicators), they are biocompatible in accordance to ISO 10993 standard [21] and have an instantaneous response. Most importantly, FOS have the unique property of detecting temperature patterns on a single fiber with resolutions between 0.1 mm and 10 mm [14], and the possibility of multiplexing among multiple fibers to detect the temperature pattern in one- or two-dimensional geometries [22] in a single scan. Fiber Bragg Gratings (FBGs) have been used for this task: FBG arrays make use of wavelength-division multiplexing and multiple channel interrogators to detect temperature patterns with spatial resolution included within 5 mm and 10 mm [12,14]; however, the spatial resolution is coarse compared to the thermal gradients at which the tissue is exposed in RFA [12]. An alternative is chirped FBGs [13], which can virtually reduce the resolution to the millimeter scale; however, chirped grating sensing system operate under the assumption that the temperature pattern is known a priori, such as a Gaussian function, as reported by Korganbayev et al. in 2018 [23].

Distributed sensing stands as the most modern approach for temperature sensing in thermal ablation, using methods derived from optical frequency domain reflectometry (OFDR) [14]. An OFDR system based on white-light interferometry interrogates distributed reflections occurring in the fiber [24,25]. The most important OFDR implementation for sensing is optical backscatter reflectometry (OBR), whereas the distributed reflections are the random Rayleigh backscattering components naturally occurring on any standard fiber, labeled as the “signature”. The OBR system is an OFDR with detectors sufficiently accurate to detect the fiber signature in each location and estimate the spectral shift of each signature [26–28]. After being pioneered and consolidated by Froggatt et al. [26,27], and industrialized in the OBR instrument [28], distributed sensing based on OBR has been first demonstrated in RFA by Macchi et al. [29]. OBR allows an inline measurement of temperature with resolution below the millimeter scale [14,28,29].

A major weakness of OBR is that this method is not suitable for multiplexing onto multiple fibers. It is possible to use a switch to connect multiple channels, but since each channel requires an independent triggering and the measurement is relatively slow, performing a multi-fiber measurement at a speed inferior to 1 s is not feasible. Because of this drawback, OBR measurements are inherently single-channel, resulting in a one-directional inline measurement of temperature [14]. It is possible to bend the sensing fiber around the tissue in order to obtain a multi-dimensional measurement, as reported in [29]; however, this type of layout of the fiber is suitable only in investigations performed in the laboratory and cannot mimic a percutaneous insertion of the sensor as in [13] [22,23]. The detection of a planar temperature distribution with FOS, using a setup that can be percutaneously inserted in the tissue, has been reported in [22,30] using FBG arrays, however the 1-cm spacing between each grating element limited the resolution to the centimeter level, while OBR can operate at few millimeters or below.

In this work, we propose a new method to overcome this scenario, that makes use of specialty fibers and an architecture hereby defined as “scattering-level multiplexing” (SLMux). The 2 building blocks of this concept are the use of a fiber doped with MgO-based nanoparticles that has a backscattering power of 36.5 dB larger than a standard single-mode fiber, used as sensing elements, and a matrix of fiber extenders that displaces the position of each sensor such that the scattering components do not overlap in length. For each location we observe the overlap of the scattering components of multiple fibers; however, since the sensing fibers backscatter a power orders of magnitude larger than each other fiber, it is possible to unambiguously demodulate each sensing fiber. In practice, this architecture allows detecting multiple sensing regions on a plurality of fibers, maintaining the same spatial resolution of the OBR technique. The MgO-doped fiber has a thermo-optic coefficient similar to silica fibers.

This concept allows extending OBR from one-dimensional to two-dimensional (planar) temperature measurements in thermal ablation. An experimental setup has been designed to perform a temperature detection over 4 sensing fibers, achieving a total of 96 sensing points on a surface of 900 mm². This highly resolved temperature measurement allows extending OBR to the real-time measurement of temperature spatial distribution over the inner plane of thermal ablation, providing a valuable alternative to thermal imaging at a simpler implementation.

2. Experimental setup

2.1 Experimental setup

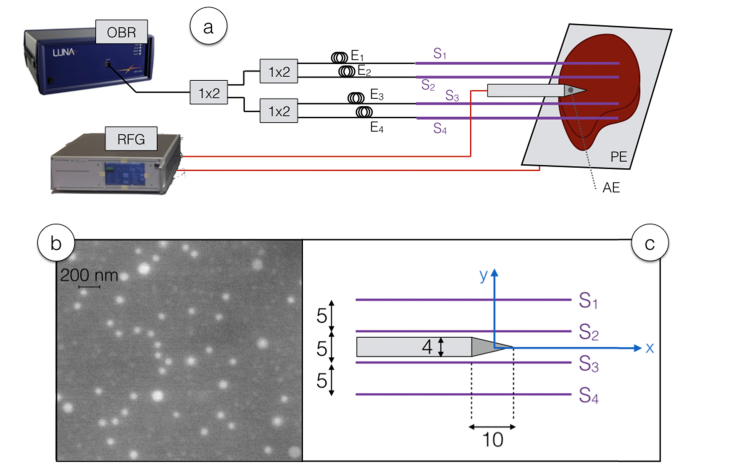
The experimental setup, embodying both the RFA setup and the distributed sensing system, is sketched in Fig. 1, while Fig. 2 shows photographic views.

Fig. 1.

Schematic of the RFA ablation and distributed sensing interrogation setup. (a) View of the whole setup, including OBR-based sensing with fibers and extenders, and the RF setup with applicator introduced into the phantom. (b) SEM (scanning electron microscope) view of a section of the core of the sensing fiber, highlighting the presence of MgO nanoparticles in the core. (c) Geometrical sketch of the position of the RF applicator and the fibers S₁-S₄, and their relative positions with respect to the xy coordinates; all sizes are in mm.

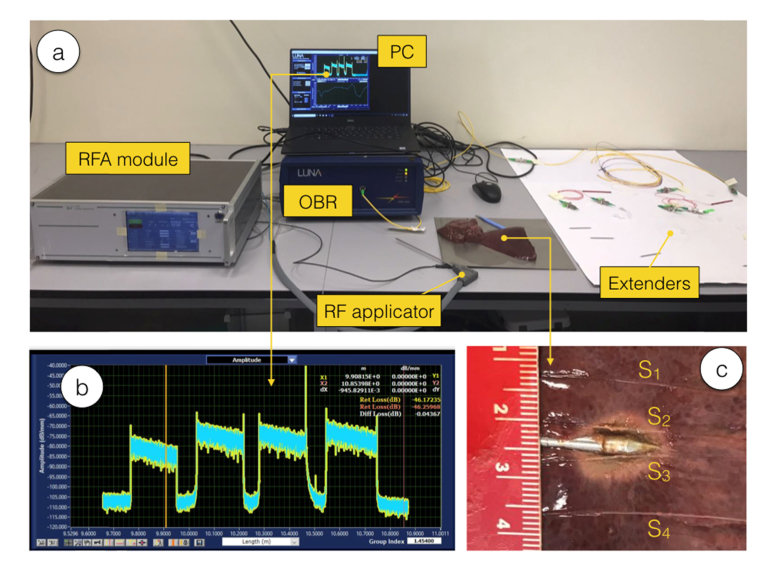
Fig. 2.

Photograph of the experimental setup. (a) View of the whole setup. (b) Inset on the scattering trace acquired on the OBR. (c) View of the ablated phantom and the sensor location after the RFA experiment; ruler scale in cm.

The RFA setup is based on a RF generator (RFG, Leanfa s.r.l., Hybrid RFA/MWA module), connected to a research-grade single-tip applicator having diameter of 3 mm and 160 mm of length. The applicator has a cylindrical shape terminated with a tip active electrode (AE) having a conic shape of 1 cm height. The passive electrode (PE) is connected to a metallic plate that is used to host the phantom. The RF power used for experiments is 40 W at 450 kHz. Measurements have been performed ex vivo on porcine liver, commercially available and refreshed until the experiment duration, following the method in [22] that is aligned with the European Union “Three Rs” principle. The impedance of the tissue is measured by the RF generator in real time through an impedance meter. The value of the tissue resistance at the start of the experiment is 120 Ω, then resistance progressively decreases until the water components of the tissue reach the boiling point, causing the impedance to abruptly rise. The RF generator has been set on “safe mode”, discontinuing the RF power as the impedance reaches the measured value of 700 Ω. A thermocouple (IKA ETS-D5) has been used to measure the reference temperature of the tissue at the start of ablation. This RFA setup, derived from [13,22], mimics the treatment of hepatic tumors such as hepatocellular carcinoma, whereas the applicator is percutaneously inserted, and the PE is positioned on the patient’s spine [1].

The measurement setup is based on a commercial OBR (Luna Inc., OBR4600), that operates as an OFDR with variable spatial resolution. The choice of the sensing parameters represents a trade-off between spatial resolution and temperature accuracy; in the experiments the spatial resolution has been set to 2.5 mm, while the overall sensing length has been set to 1200 mm taking into account all the 4 fibers in this window. The OBR output has been connected to a cascade of three 1x2 wideband splitters operating in the third optical window, i.e., the C band between 1530 an and 1565 nm. All optical connections, including lead-in fibers, splitters, and the extenders are based on standard single-mode fiber (SMF, Corning SMF-28) while the sensing fibers are based on MgO-doped fibers and have high-scattering characteristics.

The SLMux setup is based on 4 extenders (labelled E₁, E₂, E₃, E₄) each having a different length that have the role to delay the relative location of each MgO-doped sensing fiber (labeled S₁, S₂, S₃, S₄). The OBR is configured to operate in distributed sensing mode, with spot scan feature, detecting with 0.3 Hz speed the fiber signature corresponding to the Rayleigh backscattering spectrum at each location [28]. For each sensing location, the signature is acquired at the experiment start, and a mutual correlation algorithm is used to estimate the wavelength shifts in each location due to temperature variation, hence estimating the temperature distribution [26,31]. The length of each extender has been set by splicing a different fiber length that takes into account also the length of the splitters and the lead-in fibers, using a fusion splicer (Fujikura 12-S).

This setup extends over the work proposed by Parent et al. for strain sensing [31], because the high-scattering fibers are not used to improve the amount of scattered power level recorded by the OBR, but rather to create a new multiplexing domain, whereas the multiplexed variable is the scattering level that changes in each location. Within each sensor S₁-S₄, the OBR can detect a distributed temperature and by placing the fibers in a planar geometry as in Fig. 1 it is possible to obtain a two-dimensional temperature mapping maintaining a sub-centimeter scale resolution in both axes.

In the setup, the sensing fibers have been positioned in situ in the phantom tissue, in proximity of the applicator, in order to map the temperature pattern of RFA. The method reported in [22] has been used, using a catheter to insert and removing it after the insertion, in order to obtain a methodology that mimics in vivo operation [12]. The distance between each fiber has been set to 5 mm, while the length of each sensing region is approximately 180 mm, with a “useful” region of 60 mm where a temperature change occurs. With the setup arranged in this way, it is possible to obtain 96 (4 fibers × 24 useful sensing point per fiber) over an area of 900 mm² (60 mm × 15 mm).

The photographic view of the setup is shown in Fig. 2, including both the RF module and the OBR sensing system. Extenders have been laid out on a plate in order to maintain the fiber bending unaltered during measurements. The phantom after ablation is shown in Fig. 2(c), whereas the sensors are positioned on the same plane of the RFA applicator. The photo has been obtained by manually cutting the phantom, which caused fibers to slightly move from their location during the measurement; however, this figure is indicative to show the size of the ablated tissue.

2.2 Fiber characterization and interrogation

The preform was fabricated by conventional MCVD (Modified Chemical Vapor Deposition) process [32]. A Ge-doped silica porous layer of the core was immersed three times with 5 mL of the doping solution injected in the horizontally rotating tube. The composition of the ethanol-based doping solution is 0.1 mol/L of MgCl₂ and 10⁻⁴ mol/L of ErCl₃. The porous layer was dried at 1000°C under an oxygen gas flow, then sintered at 1800°C. The tube was collapsed into the preform by heating above 2000°C. The diameter of the preform was around 10 mm with a 0.8 mm core diameter. The optical fiber was drawn on a drawing tower by heating the preform at approximately 2000°C. The external diameter of the fiber was 125 µm while the core diameter is about 10 µm.

The compositions of the optical preform and fiber were measured using Energy Dispersive X-ray (EDX) analyses. The average magnesium and germanium concentrations vary along the length (axial direction) of the fiber. The highest magnesium and germanium concentrations are 1.7 and 0.4 at.%, respectively. The introduction of magnesium triggers the formation of nanoparticles through the phase separation mechanism due to high temperatures reached during the fabrication [33]. The exact composition of the nanoparticles is unknown for this fiber, but it has been reported previously for other fibers where the nanoparticles are enriched with Mg [34].

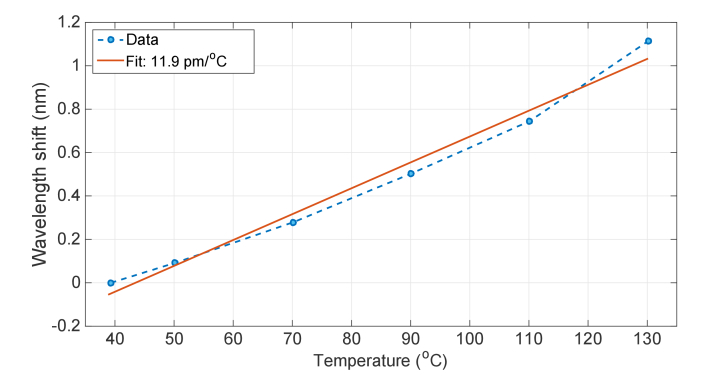
The thermal response of the fiber is shown in Fig. 3, which has been estimated by inserting a spool of MgO-doped fiber on the surface of a hot plate, recording the plate temperature with a contact thermometer and measuring the wavelength shift of the fiber scattering signature with the OBR. The result is a linear sensitivity, with coefficient 11.9 pm/°C; this value is similar to silica fibers (~10.2 pm/°C), confirming that the doping concentration does not largely modify the thermo-optic coefficient of the fiber.

Fig. 3.

Thermal response of the MgO-doped sensing fiber.

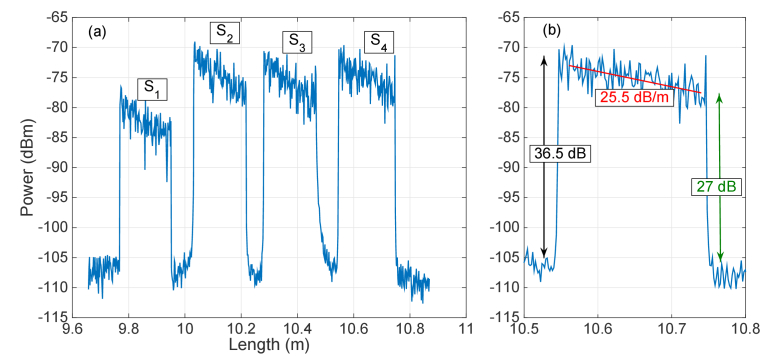
The scattering characterization of the setup is shown in Fig. 4. In the left chart, it is possible to visualize the scattering trace, corresponding to the backscattered power as a function of length in the fiber. The chart identifies the 4 sensing regions, all designed using a length of ~18 cm of MgO-doped fiber, and the effect of the extenders: since each extender has a progressive length, the 4 locations can be unambiguously separated (S₁: 9.77 – 9.95 m; S₂: 10.03 –10.21 m; S₃: 10.28 – 10.46 m; S₄: 10.55 – 10.74 m). All the sensing regions are enclosed within approximately 1 m of window on the OBR. All fibers have been cleaved prior to insertion in the tissue, and the local termination points of each fiber are not considered for the thermal map estimation.

Fig. 4.

Scattering characterization of the proposed setup. (a) Backscattered power as a function of length, as recorded on the OBR, for each fiber length. The chart identifies the 4 sensing regions S₁ – S₄, each having ~20 cm length of MgO-doped fiber. (b) Inset of the left chart, showing an individual sensing region, with estimation of scattering “gain” G, fiber attenuation 2α, and signal-to-noise ratio.

The high scattering content shows the validity of the multiplexing concept and is reported in Fig. 4(b) for the longest extender region. While the SMF fiber has a scattering level of −108.9 dBm and its attenuation is negligible over the short length of this setup, the magnitude of the MgO-doped fiber is −72.4 dBm, showing a scattering “gain” of G = 36.5 dB. In this framework, we define the gain as an additional intensity of the MgO-doped fiber that magnifies the scattering content, while there is no signal amplification [31]. The losses of the MgO-doped fiber are high and are accounted by estimating the slope of the trace in Fig. 4(b) as 2α = 25.5 dB/m cumulating the forward and backward losses that are accounted by the OBR.

The multiplexing concept works since the scattering trace of the sensing fibers is always much larger than the combination of all the scattering components of the SMF fibers. We can therefore define a signal-to-noise ratio (SNR) that relates to the only scattering component and is defined as the ratio of the scattering content of the MgO-doped fiber (signal) over the scattering of the SMF fibers that overlap to the signal at the same location (which acts as a noise that corrupts the scattering estimate). Since the MgO-doped fibers have high losses, the SNR is higher at the beginning of each sensing trace and is the lowest at the end of each sensing tract. In our setup, the worst case is observed for the sensor S₁, since it has the shortest extender and therefore it overlaps to all the other 3 SMF spans in the same location; on this specific channel, it also appears that losses are higher due to a splitter excess loss on this specific channel. In any case, even at the tail of S₁ the SNR is approximately 24 dB, while Fig. 4(b) shows that the SNR is ~27 dB at the end of S₄ region.

Empirically, we observe that a SNR of 20 dB is sufficient to ensure that the performances are limited by the trade-off between spatial resolution and accuracy of the OBR [31], without noticeable impairments due to multiple scattering components. This is also reinforced by the good noise rejection guaranteed by the mutual correlation algorithm. In comparison, FBG sensing networks operate with 20-30 dB of extinction ratio between adjacent gratings [22], confirming that the SLMux operates as a true multiplexing concept for fiber optic sensors.

Sensor interrogation has been performed by adjusting the OBR software, operating in distributed sensing, that allows continuous measurement of the scattering signatures. The mutual correlation algorithm has been used correlate the Rayleigh backscattering spectra within each gage length (i.e., the signatures), with the signatures measured at the start of the experiment. The thermo-optic coefficient previously estimated has been used to convert the wavelength shift into temperature variation for each measurement point. After the whole temperature distribution has been estimated, the thermal maps have been updated by converting each OBR location into its xy coordinates evaluated as in Fig. 1, making the conversion between the linear trace to the planar geometry. The spectral correlation output is independent upon the power level (which removes minor effects such as temperature-dependent loss of the MgO-doped fibers) and operates on an 8 pm grid, correspondent to 0.7 °C thermal resolution.

3. Results

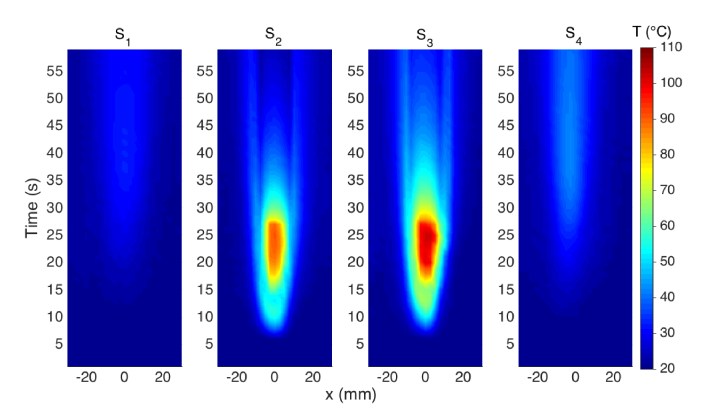
The experiments have been carried out by obtaining the reference temperature and fiber signature during the initialization, and then turning on the RFA generator in safe mode. The RF power has been delivered to the tissue until the vaporization, where the tissue impedance overcomes the threshold of 700 Ω, and then the power has been automatically discontinued. The thermal maps have been obtained on the xy plane by processing the data from each sensing fiber: temperature has been sampled with 2.5 mm resolution along the x axis parallel to the RFA applicator (corresponding to the OBR spatial resolution), with 5 mm resolution along the y axis perpendicular to the RFA applicator (corresponding to the distance between adjacent sensing fibers), and with 0.33 s time resolution (corresponding to the OBR speed in single-scan). Multiple experiments have been performed, showing similar results; in the following, we report the result for the ablation shown photographically in Fig. 2(c) as a benchmark of the distributed sensing system.

In Fig. 5 we report the thermal maps obtained in this experiment, using the notation of [22] that reports the temperature as a function of distance along the fiber (x) and time elapsed. The thermal maps show the initial temperature rising, from the ~20°C room temperature, for as the RF power is dissipated on the tissue. The heating pattern progressively enlarged, as the impedance of the tissue decreased from the initial 120 Ω to ~85 Ω. In this moment, the heat pattern was recorded by both inner sensors S₂-S₃, with the sensor placed on the right of the applicator observing a higher heating. This asymmetric pattern is confirmed by Fig. 2(c) and is largely due to the non-homogeneous properties of the tissue, including fat and capillaries that deviate the RF ablation pattern particularly for fast ablation phenomena [3]. Conversely, heat did not significantly propagate to the external fibers, that see a marginal increase of temperature. After 25 s the vaporization of the tissue occurs, causing the RF power to be discontinued; the consequence is the temperature drop, with a gradient that is steeper in the center where the RF power is discontinued and is lower in on the sides, due to the delays of heat propagation from inner parts of the tissue to the peripheral sides. The maximum temperature of 102.7°C has been observed after 25 s. The external sensors detect a heating process having a peak at 41 s and a maximum temperature of 42.4°C (S₄) and 33.2°C (S₁), 16 s after the RF power has been discontinued.

Fig. 5.

Thermal maps reporting the measured temperature as a function of distance along the fiber (direction x) and time for each of the four sensing elements, located at coordinates y = −7.5 mm (S₁), y = −2.5 mm (S₂), y = 2.5 mm (S₃), y = 7.5 mm (S₄).

This is an effect of heat propagation from the inner sides of the tissue to the peripheral parts, and agrees with both the simulative [35] and experimental [29] results of Macchi et al.

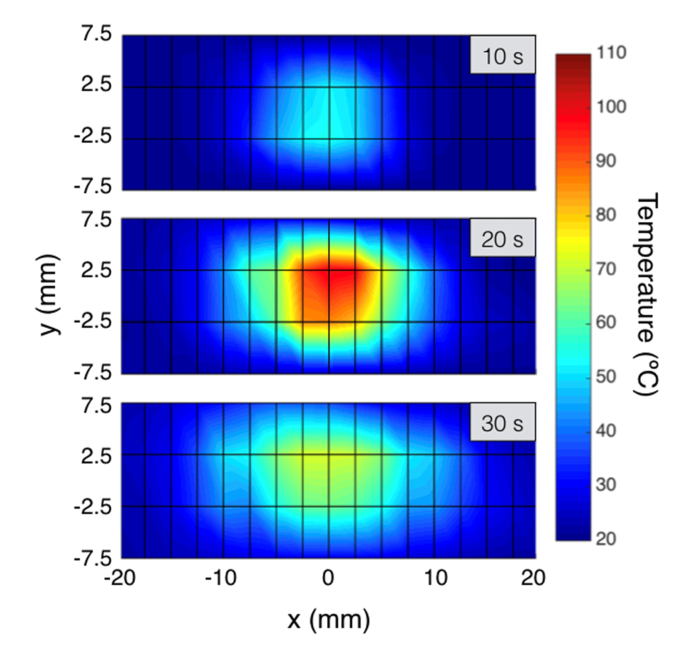
The data in Fig. 5 can be combined to generate bi-dimensional thermal maps, that report at each measurement time the temperature recorded on each xy coordinate; this arrangement allows expanding OBR measurement in two dimensions and constitutes the key of SLMux implementation. The two-dimensional maps have been reported in Fig. 6, with the color contours reporting the isothermal curves (points held at the same temperature [4]). Inter-pixel data have been interpolated as in [30]. The maps in Fig. 6 report the estimate of the ablated tissue on the xy plane: after 10 s during the heating process, heat remains confined in the inner portion of the tissue and the 60°C threshold is not achieved yet. The second chart reports the thermal maps after 20 s, close to the RF power discontinued event. The ablation is appearing slightly asymmetric with the right part of the tissue having a slightly deeper heat penetration, and the 60°C region has an extension that appears 10 mm wide on the y axis, and 15 mm wide on the x axis with a slight misalignment typical of RFA [35]. At 30 s, when the tissue is cooling, the temperature remains high in the center, and the heat propagates on the tails of the tissue, however without reaching the 60°C threshold.

Fig. 6.

Two-dimensional thermal maps, reporting temperature on the xy plane for different elapsed time (10 s, 20 s, 30 s). The plain considered is 15 × 40 mm, corresponding to a grid of 4 × 17 sensing point, spaced 5 mm on y axis and 2.5 mm on x axis. See Visualization 1 ^{(2.3MB, mp4)} .

The cinematic of the thermal maps, that contains the temperature maps for the whole heating process, are included as Visualization 1 ^{(2.3MB, mp4)} , and show the temperature maps for each measurement time (data rate has been reduced to 1 s to reduce file size).

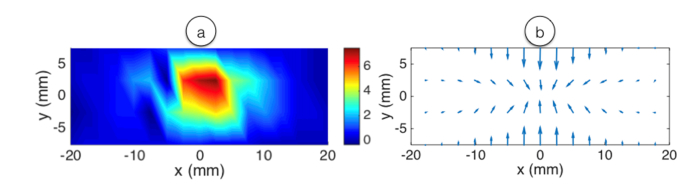
Finally, we can estimate the temperature gradients occurring both in time and in space, which is a pivotal information to predict and investigate temperature patterns [35,36]. This differential information is reported in Fig. 7. For simplicity, we report data acquired at the peak temperature event (25 s elapsed time). Temporal gradients are reported by calculating the differential of the temperature between two measurement times in the same pixels. In proximity of the centers, the gradient reaches approximately 7.5 °C/s. Spatial gradients, since they account the two-dimensional gradients of a scalar field, are reported as field lines pointing from the colder to the hotter point. The maximum gradient is accounted as approximately 5.6 °C/mm in proximity of the applicator. The measurements reported in Figs. 6-7 have a spatial resolution that is limited by the OBR along x, whereas 2.5 mm is the best fit between accuracy and absence of averaging effects, and by the number of fibers and their vicinity during the insertion along y; as concluded in [14] and [16], a 2.5-mm spatial resolution is a good value for mini-invasive thermotherapies.

Fig. 7.

Temporal and spatial temperature gradients reported after 25 s elapsed during RFA. (a) Time gradients reported in °C/s; (b) spatial gradients reported as field lines pointing from the colder to hotter points.

4. Discussion

The SLMux method proposed in this work has a different outline with respect to other spatial division multiplexing (SDM) method reported in recent works. In particular, Gasulla et al. [37] reported an SDM method on a multi-core fiber, exploiting the plurality of cores to inscribe sensors in each core element. However, the main barrier for sensing is that this method requires all sensors to be on the same fiber, negating the possibility to design arbitrarily the geometry of the sensing network, such as for the planar measurement reported in previous sections.

Compared to sensing networks based on FBG arrays, the SLMux method allows reducing the spatial resolution to the millimeter scale, while the limit of the detection of the OBR is ~0.1 mm (although this value leads to an insufficient temperature accuracy); in FBG arrays the spatial resolution is limited both by the inscription setup, particularly in phase mask methods [14], and by the need to have a grating with sufficient reflectivity. Another practical problem of FBG sensors in monitoring of RFA or other thermo-therapies is the need to strip the fiber protective jacket prior to inscribe the grating, which reduces the fiber tensile strength. This can be solved either by recoating the fiber with a polyimide buffer, but that increases the fiber thickness, or by using draw-tower gratings (DTGs), which however have typical distance between adjacent gratings of 1 cm. Distributed sensing instead does not require removing the fiber jacket.

Parent et al. [31] reported high-scattering fibers for shape sensing in OBR, having different scattering enhancement; this method, however, was not used to multiplex different sensing regions, but rather to improve the sensitivity of strain sensing.

The method described in Fig. 1 can be potentially extended by using a 1xN splitter in lieu of the 1x2 splitter cascade, and using multiple extenders E₁, …, E_N to multiplex N sensing regions S₁, …, S_N. Assuming that the length of the i-th extender is L_Ei and includes all the optical path from the splitter output to the sensor, and L_Si is the length of the i-th sensing region made with MgO-doped fiber, we can arrange the fibers such that:

$${\mathit{L}}_{\mathit{E}\mathit{i}}÷\left({\mathit{L}}_{\mathit{E}\mathit{i}}+{\mathit{L}}_{\mathit{S}\mathit{i}}\right)\mathrm{does\; not\; overlap\; with}{\mathit{L}}_{\mathit{E}\mathit{j}}÷\left({\mathit{L}}_{\mathit{E}\mathit{j}}+{\mathit{L}}_{\mathit{S}\mathit{j}}\right),\forall \mathit{i}\ne \mathit{j}$$ (1)

In this case, we can write the backscattered power P_S,i (in dBm units) from each i-th channel along the generic fiber direction z (corresponding to x in Fig. 1) as:

$${\mathit{P}}_{\mathit{S},\mathit{i}}\left(\mathit{z}\right)=\{\begin{array}{cc}{\mathit{P}}_{\mathit{S}\mathit{M}\mathit{F}}& 0\le z\le {\mathit{L}}_{\mathit{E}\mathit{i}}\\ {\mathit{P}}_{\mathit{S}\mathit{M}\mathit{F}}+G-2\alpha z& {\mathit{L}}_{\mathit{E}\mathit{i}}\le z\le \left({\mathit{L}}_{\mathit{E}\mathit{i}}+{\mathit{L}}_{\mathit{S}\mathit{i}}\right)\end{array}$$ (2)

where z = 0 is assumed to be the output of the splitter, P_SMF is the power scattered by the SMF fiber (which is assumed to be lossless over the short interrogation window of the OBR, limited to 20-70 m), G is the scattering “gain”, i.e., the amount of extra scattering provided by the MgO-doped fiber, and 2α is twice the attenuation of the MgO-doped sensing fiber, that corresponds to the forward and backward waves.

The power detected by the OBR is the combination of all backscattered waves, and from Eq. (1) it is possible to separate the location of each sensing region, as shown in Fig. 4. The worst-case scenario occurs for the shortest extender, whereas the sensing fiber overlaps to (N-1) SMF fibers, which act as a noise on the spectral signature. We can thus write the signal-to-noise ratio (SNR), in dB units, as:

$$\mathit{S}\mathit{N}\mathit{R}=\mathit{G}-2\mathit{\alpha }\mathit{z}-10{\log }_{10}\left(\mathit{N}-1\right)$$ (3)

whereas the splitter and link losses are not appearing as they apply to both the SMF fibers and the sensing fiber. By defining the target SNR and the number of fibers in the system, it is possible to obtain the maximum distance for each sensor by solving Eq. (3) for the maximum z value. Given that, from Sect. 2.2, the estimated parameters for the MgO-doped fiber are G = 36.5 dB and 2α = 25.5 dB/m, and empirically the OBR correlator appears to work without impairments for SNR ≥ 20 dB (i.e. for values of SNR higher than this threshold the performance are limited by the accuracy-resolution trade-off and not by the noise affecting the fiber signatures) for a 1x4 splitter the maximum distance is 46 cm, reducing to 19 cm for a 1x16 splitter and 6 cm for 1x32 splitter. Overall, this implies that we can transform a purely linear measurement with OBR into a multi-fiber measurement, each fiber having a length sufficient for in situ detection and maintaining a simultaneous scan even with 32 sensing fibers, considering that thermo-therapies affect the tissue by up to 3-4 cm in diameter [12].

Regarding MRI thermometry, recent findings allowed improving the performances of this technique during thermal treatments and obtaining good spatial (e.g., 1.25 × 1.25 × 3.5 mm) and temporal resolution (e.g., 1.9 s) [38]. By optimizing the SLMux method and consolidating the time-delay unit constituted by the extender array, it is possible to approach this level of resolution, but using sensors in lieu of imaging for in situ detection.

In this work, the SLMux technique has been demonstrated on a two-dimensional grid, achieving a horizontal resolution of 2.5 mm which depends on the temperature accuracy and the total sensing length on the OBR, and a vertical resolution of 5 mm that depends on the number of used fibers and how closely and precisely they can be inserted in the tissue. With these values, the estimated temperature accuracy is close to the resolution of the OBR. However, shortening the total sensing length might be beneficial to improve the accuracy or reduce the spatial resolution, as by the trade-off.

5. Conclusions

In conclusion, we report a scattering level-based multiplexing configuration that allows extending the OBR/OFDR distributed sensing to multiple fibers with a single scan. This SLMux configuration finds immediate application in the measurement of temperature patterns in cancer thermo-therapies [12–14], whereas the possibility of measuring at a fast rate with narrow spatial resolution with fibers arranged in planar configuration is needed to estimate in real time the extension of the treated tissues [16]. The SLMux configuration is enabled by fibers having superior amount of backscattering, and a set of extenders that implements a network of delayers that allows arbitrarily spacing the sensing fibers. The setup has been validated in RFA measurements, resulting in two-dimensional thermal maps with sub-centimeter resolution in both dimensions. This configuration is an excellent candidate for real-time sensing in all biomedical applications that require sensing on multiple fibers, each used as a short-length distributed sensor [14]. The spatial resolution achievable by this configuration is comparable with thermal imaging, but with the advantage of in situ measurement and the possibility of embodying the sensing elements in miniature needles.

Future work will address the expansion of the proposed method to >10 fibers arranged also in 3-dimensional way, to better identify the SNR performance limits of the SLMux concept and extending the SLMux configuration to strain/shape sensing on smart medical percutaneous catheters [14,31].

Funding

ORAU program at Nazarbayev University (LIFESTART 2017-2019, FOSTHER 2018-2020); ANR project Nice-DREAM (ANR-14-CE07-0016-03); Spanish Ministry of Economy and Competitiveness (DIMENSION TEC2017 88029-R).

Disclosures

The authors declare that there are no conflicts of interest related to this article.