Analysis of spatial resolution in phase-sensitive compression optical coherence elastography

Abstract

Optical coherence elastography (OCE) is emerging as a method to image the mechanical properties of tissue on the microscale. However, the spatial resolution, a main advantage of OCE, has not been investigated and is not trivial to evaluate. To address this, we present a framework to analyze resolution in phase-sensitive compression OCE that incorporates the three main determinants of resolution: mechanical deformation of the sample, detection of this deformation using optical coherence tomography (OCT), and signal processing to estimate local axial strain. We demonstrate for the first time, through close correspondence between experiment and simulation of structured phantoms, that resolution in compression OCE is both spatially varying and sample dependent, which we link to the discrepancies between the model of elasticity and the mechanical deformation of the sample. We demonstrate that resolution is dependent on factors such as feature size and mechanical contrast. We believe that the analysis of image formation provided by our framework can expedite the development of compression OCE.

1. Introduction

Optical coherence elastography (OCE) is emerging as a higher resolution alternative to both ultrasound elastography and magnetic resonance elastography in a range of applications including in oncology [1–3], cardiology [4,5], ophthalmology [6,7], and dermatology [8,9]. Although the higher spatial resolution of OCE has been purported to be a main advantage over the more established elastography techniques, it has yet to be clearly defined or measured. As a result, it is challenging to evaluate and compare the performance of OCE systems, and to identify the most suitable applications or, indeed, which variant to use in a given application.

In medical imaging more generally, spatial resolution is often defined as the smallest distance that two objects can be brought together and still be distinguishable as separate objects, and is an important metric to assess image quality. In optical coherence tomography (OCT) and other optical microscopy techniques, resolution is treated as a system parameter, i.e., independent of the sample, and can be estimated from the point-spread function (PSF) of the imaging system [10,11]. Following the precedent set by OCT, until now, OCE resolution has been loosely defined as a combination of system parameters, namely, the resolution of the underlying OCT system, and the signal processing used to map displacement or velocity to a mechanical property, such as elasticity [12–15]. However, in OCE, the resolution of mechanical properties is intrinsically linked to the mechanical deformation of the sample. Whilst this has been suggested in the literature, it has yet to be investigated or demonstrated.

Importantly, the mechanical properties of the sample cannot be measured directly, instead, the sample deformation induced by mechanical loading is measured. The observed deformation is then used to infer the distribution of mechanical properties in the sample using a mechanical model. A range of loading mechanisms can be used, e.g., compression and shear wave [16,17], resulting in a specific form of sample deformation and, in turn, requiring a specific mechanical model. The majority of mechanical models assume homogeneity, linearity and isotropy to readily generate elastograms. For example, in compression OCE, a quasi-static, uniaxial compression is typically applied to the entire sample surface, where stress is assumed to be uniform and uniaxial, such that the local elasticity (Young’s modulus) is inversely proportional to the experimentally measured local axial strain [12–15]. This approach provides a practical means to generate elastograms, and facilitates the rapid generation of elastograms over large tissue volumes: a requirement for clinical applications, such as breast tumor margin assessment [1,2,18]. In many instances, however, these assumptions result in deviations between the measured and true mechanical properties of the sample that degrade, in a sample-dependent manner, the spatial resolution of elastograms. An approach to reduce the need for such simplifying assumptions is to localize the mechanical loading to a single point in the sample. This is a motivation of techniques such as magneto-motive OCE [19,20], nanobomb OCE [21] and photonic-force OCE [22]. Whilst these techniques show promise, the localization of loading can be challenging to achieve in practice and to deploy in clinical applications. Current approaches provide a limited imaging field-of-view and have an elastogram acquisition rate that is considerably slower than compression and shear wave approaches, making it difficult to achieve two-dimensional (2D) and three-dimensional (3D) imaging.

This paper presents the first investigation of spatial resolution in compression OCE. We demonstrate, in both simulation and experiment, the spatially varying and sample dependent nature of resolution, and detail the relationship between the OCE system resolution (the combination of the OCT and signal processing), and the measured resolution of features in the elastogram, which we term feature resolution. To achieve this, we present a framework for assessing resolution in phase-sensitive compression OCE that combines a model of mechanical deformation using finite-element analysis (FEA) with models of the OCT system and signal processing based on linear systems theory. We measure the feature resolution at each stage of this framework to estimate the relative contribution from each of the three processes. Using this approach, we analyze spatial resolution in a number of scenarios, which are experimentally validated using tissue-mimicking silicone phantoms containing stiff inclusions, following the precedent of ultrasound elastography [23,24]. These inclusions provide a step response in elasticity in both axial and lateral directions, and we demonstrate that feature resolution in compression OCE varies along boundaries and is directly related to feature size and mechanical contrast. For instance, for a phantom containing a rectangular prism inclusion that has a 1 mm × 1 mm cross section, we show that the axial and lateral feature resolution varies from 100 μm to 200 μm and from 100 μm to 380 μm, respectively.

The results presented in this paper demonstrate that in compression OCE, mechanical deformation can impact feature resolution on length scales greater than that of the system resolution. The framework may be extended to investigate other imaging parameters, such as sensitivity and contrast, and could be adapted to other forms of OCE, such as shear wave OCE, or indeed to ultrasound elastography and magnetic resonance elastography. Importantly, our framework could be used to assess which form of mechanical loading is optimal in a given sample and can quantify the improvement in resolution brought about by using high resolution OCT systems [25–27], improved signal processing [28] and solutions to the inverse elasticity problem [29].

2. Background

OCE elastogram generation can be described in three stages; the deformation of the sample under mechanical loading, the measurement of this deformation using OCT, and the signal processing used to relate measured deformation to elasticity. In this section, we describe each of these stages in the context of phase-sensitive compression OCE.

2.1 The contribution of mechanical deformation to resolution

Typically, the goal of elastography is to recover the mechanical properties of the sample by applying mechanical loading and observing the resulting deformation. In compression OCE, the sample is placed under a static preload (referred to as the unloaded state) and a microscale compressive load is then applied (referred to as the loaded state). The change in position of each point in the sample is described by the displacement field, u. The sample in both the unloaded and loaded states is taken to be in a state of static equilibrium and, additionally, the deformation between the two states is assumed to be much smaller than the size of the sample [30]. As a result, the equations of equilibrium reduce to:

$$\nabla \cdot \mathit{\sigma }=0,$$ (1)

where σ is the infinitesimal Cauchy stress tensor field, which describes the internal stress field present in the sample [31]. The resulting deformation is described by the corresponding infinitesimal strain tensor, ε, whose components, ε_ij, are derived from the partial derivatives of u [32]:

$${\epsilon }_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial j}+\frac{\partial u_j}{\partial i}\right),\text{for}i,j\in \left\{x,y,z\right\}.$$ (2)

Commonly, the sample is assumed to be a linear elastic solid [33], whose mechanical properties are represented by a fourth-order elasticity tensor, C, that relates the stress and strain tensors:

$${\sigma }_{ij}={\displaystyle {\sum }_k{\displaystyle {\sum }_l{C}_{ijkl}{\epsilon }_{kl},\text{for}i,j,k,l\in \left\{x,y,z\right\}}}.$$ (3)

Equation (3) is termed the constitutive equation for the sample, and produces 6 independent equations with 36 material coefficients. To further simplify the analysis, the sample’s mechanical properties are typically assumed to be isotropic, which reduces Eq. (3) to:

$${\sigma }_{ij}=\lambda {\displaystyle {\sum }_k{\epsilon }_k{\delta }_{ij}+2\mu {\epsilon }_{ij}},\text{for}i,j,k\in \left\{x,y,z\right\},$$ (4)

where μ and λ are the Lamé parameters and δ_ij is the Kronecker delta, which is equivalent to 1 if i = j and 0 otherwise.

In phase-sensitive compression OCE, only the axial component of the displacement field, u_z, is measured [34]. Given an observed u_z, to solve for the mechanical properties at each point in the sample, one would need to solve for σ. However, this requires challenging numerical methods, thus, simpler models of σ are typically employed, i.e., that σ is uniaxial and uniform throughout the sample [12–15]. Under these assumptions, elasticity is specified by Young’s modulus (E), as a combination of the Lamé parameters, or the ratio of uniaxial stress, σ_zz, over uniaxial strain, ε_zz,

$$E=\frac{\mu (3\lambda +2\mu )}{\lambda +\mu }=\frac{{\sigma }_{zz}}{{\epsilon }_{zz}}.$$ (5)

That is, the elastogram of uniaxial strain is assumed to be inversely proportional to elasticity [12–15]. These assumptions have enabled elastography to be relatively easily and robustly performed with straightforward mechanical loading. However, sample characteristics such as mechanical heterogeneity, local compressible features, friction at the tissue surface, and non-uniform surface topology lead to non-uniform stress distributions which can distort the relationship between axial strain and elasticity as described by Eq. (5) [14]. It is important to note that whilst the strain resolution is determined by the system resolution, deviations from Eq. (5) result in a discrepancy between the system and feature resolution.

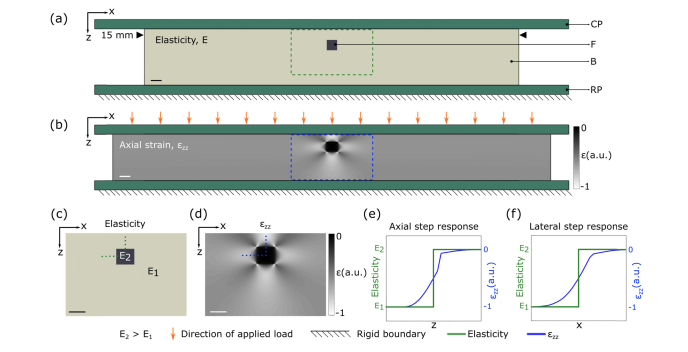
Figure 1 illustrates the degradation in feature resolution resulting from these assumptions in compression OCE. Here, we present a 2D FEA simulation of a soft bulk material featuring a stiff, square 500 μm feature (Fig. 1(a)), with the stiffness of the bulk and feature set to 21 kPa and 625 kPa, respectively. A detailed description of the FEA simulation used in this study is provided in Section 3.1. A bulk compressive strain of 15% is applied to the sample and Fig. 1(b) shows the distribution of axial strain evaluated at each node in the model mesh. Figures 1(c) and 1(d) provide close ups of the distribution of elasticity and axial strain, corresponding to the regions highlighted in the dashed boxes in Figs. 1(a) and 1(b), respectively. Figures 1(e) and 1(f) show one-dimensional (1D) plots of elasticity (a step response from soft to stiff) overlaid on the axial strain across the axial and lateral boundaries of the feature marked by the vertical and horizontal dotted lines in Figs. 1(c) and 1(d). The discrepancy between the elasticity map, and the resulting axial strain distribution in FEA is due to the three-dimensional nature of elastic deformation in incompressible materials that leads to a mechanical coupling between all parts of the sample. That is, when a load is applied, adjacent areas of the sample will deform in a dependent fashion as they are mechanically connected. This leads to a gradient in the strain distribution that effectively “blurs” the boundaries between connected components of different elasticity. We verified through simulation that this is independent of the size of the FEA mesh, assuming the mesh is fine enough to adequately sample the strain distribution. In Figs. 1(e) and 1(f), it is apparent that, considering the step response of strain to be a qualitative measure of resolution, the assumption that elasticity is inversely proportional to axial strain leads to an effective degradation in both axial and lateral resolution.

Fig. 1.

Illustration of mechanical deformation in compression OCE. (a) 2D FEA model of a stiff square feature embedded in a softer bulk material (CP: compression plate, F: feature, B: bulk, RP: rigid plate). (b) Corresponding FEA axial strain map after a 15% bulk strain is applied. Close-ups of the regions corresponding to the green rectangle in (a) and blue rectangle in (b) are shown in (c) and (d), respectively. (e) Normalized plots of elasticity (green) overlaid on axial strain (blue) across the axial boundary of the feature marked by the vertical dotted green line in (c) and blue line in (d). Similarly, (f) shows normalized plots of elasticity overlaid on axial strain across the lateral boundary of the feature marked by the horizontal dotted green line in (c) and blue line in (d). Scale bars represent 500 µm.

2.2 The contribution of OCT to resolution

In our implementation of compression OCE, axial displacement is measured using phase-sensitive OCT. OCT images of the sample are modeled as a convolution of the sample scatterers with the complex OCT PSF [10]. The OCT resolution, and hence the resolution of the displacement measurement, are defined by the width of the PSF envelope. For this study, we consider 2D elastograms presented in the x-z plane where the envelope of the OCT PSF is defined as [11]:

$${\text{PSF}}_{\text{OCT}}(x,z)=|I(x,z)|=I_0\text{exp}\left(-\frac{2x^2}{w_x^2}\right)\text{exp}\left(-\frac{2z^2}{w_z^2}\right),$$ (6)

where w_z and w_x are the 1/e² radii of the OCT intensity in z and x respectively; and I₀ is a scaling factor. By convention, OCT resolution is typically given in terms of the full-width-at-half-maximum (FWHM) of the intensity PSF where the axial and lateral resolution is$\sqrt{2\ln 2}$times w_z and w_x, respectively.

2.3 The contribution of least-squares regression to resolution

For the elastograms presented in this study, least-squares linear regression (LSR) is used to estimate the axial strain as the gradient of axial displacement with depth, over a sliding window of length Δz, typically 15 μm – 100 μm [12–14] to alleviate the impact of system noise [34]. As all measurements of axial displacement are acquired with equal spacing, ordinary least-squares linear regression is equivalent to convolution with a Savitzky-Golay (SG) kernel [35]. A 2n + 1 point, first order, SG differentiation kernel is given by [35]:

$$SG(z)=\{\begin{array}{c}\frac{\beta z}{h^2},\text{for}-nh\le z\le nh\hfill \\ 0,\text{otherwise}\hfill \end{array}$$ (7)

where β = 3/n(n + 1)(2n + 1) is the smoothing coefficient corresponding to fitting a first degree polynomial (i.e., a line) [36] and h is the spacing of the voxels in the axial dimension. Convolution of SG(z) with a unit step displacement, a(z), gives the PSF corresponding to LSR:

$${\text{PSF}}_{\text{LSR}}(z)=SG(z)\otimes a(z)=\{\begin{array}{c}\frac{\beta }{h}\left(n^2-\frac{z^2}{h^2}\right),\text{for}-nh\le z\le nh\hfill \\ 0,\text{otherwise}\hfill \end{array}$$ (8)

For a fit length given by Δz = h(2n + 1), the FWHM of the PSF for LSR is:

$${\text{FWHM}}_{{\text{PSF}}_{\text{LSR}}}=\frac{\Delta z}{\sqrt{2}}$$ (9)

In this study, the system resolution in compression OCE is modeled by the FWHM of the result of convolving PSF_OCT(x,z), Eq. (6), with PSF_LSR(z), Eq. (8). Feature resolution is modeled as the convolution of the system resolution with the effective local PSF from mechanical deformation determined from FEA, as detailed in Section 3.4.

3. Methods

3.1 Simulation

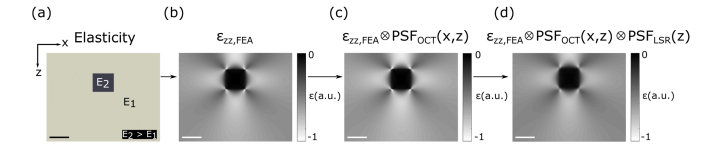
To simulate OCE, we combine a finite-element model of mechanical deformation using the Abaqus simulation software package (Dassault Systèmes, Providence, USA, v6.14), with a model of the OCT system given in Eq. (6) and a model of the method used to estimate axial strain, given in Eq. (8). This is illustrated in Fig. 2. Both the feature and bulk of each phantom, shown in Fig. 2(a), are modeled as nearly incompressible, mechanically isotropic, linear-elastic materials with a Poisson’s ratio of 0.485 for numerical stability [37]. Phantoms were fixed on the bottom surface, free on the sides and compressed from the top surface. The coefficient of static friction at the phantom-compression plate interface was varied between a lower limit of 0.05 and an upper limit of 0.3 to achieve the best match between simulation and experiment as derived in a previous study [38]. The bulk of each phantom was meshed with 50 μm quadrilateral elements and the meshing of the feature was set to one twentieth of the feature side length. Each phantom was 3 mm × 15 mm (height × width), and in all simulations, the stiff inclusion was placed 600 μm from the top surface of the phantom. A square inclusion geometry was used in all cases, and the size of the inclusion was varied by changing the height and width of the inclusion from 250 µm to 1 mm.

Fig. 2.

Illustration of the compression OCE simulation used to study resolution. (a) A heterogeneous sample represented by a phantom with a soft bulk material (with stiffness E₁) featuring a stiff square feature (with stiffness E₂, where E₂ > E₁). A compressive bulk strain of 15% applied to (a) is simulated in FEA, and the output is an axial strain elastogram (ε_{zz, FEA}) shown in (b). The elastogram in (b) is convolved with PSF_OCT(x,z) to obtain (c). The elastogram in (c) is convolved with the PSF_LSR(z) to obtain (d). Scale bars represent 500 µm.

As the phantoms are wide (15 mm) relative to the imaging field of view (5 mm), the 3D sample deformation was approximated by a 2D plane-strain model, which set the displacement and strain in the out-of-plane (y) dimension to zero [39]. Deformation in each case is simulated by applying a bulk compressive strain of 15% to the entire phantom and solving for the resulting axial strain at each point in the phantom mesh. To verify that the variation in mesh size did not affect the measured step response in axial strain across the feature, the mesh size was varied by a factor of four for each simulated phantom. In each phantom, the difference in the step response in axial strain was less than 5%, indicating that the choice of mesh size adequately sampled the strain distribution. The process used to measure the step response in axial strain is detailed in Section 3.4. The output of the FEA simulation is an elastogram of axial strain (ε_zz,FEA), shown in Fig. 2(b), representing the impact of deformation prior to measurement with OCT and least-squares regression. Shown in Fig. 2(c), the impact on resolution of sampling the deformation using OCT is simulated by convolving ε_zz,FEA with PSF_OCT(x,z) using MATLAB (v2016b, The MathWorks, USA). The FWHM of PSF_OCT(x,z) was matched to that of the OCT system used in experiment (Section 3.3). Figure 2(d) shows the impact on resolution of performing least-squares regression, simulated by convolving the axial strain elastogram in Fig. 2(c) with PSF_LSR(z) with Δz equal to 100 μm. For the results presented in Sections 4.1 – 4.3, Δz was 100 μm, and in Section 4.4, Δz was varied from 50 μm to 250 μm. Figure 2 clearly illustrates the dominant effect of deformation on feature resolution for this feature geometry.

3.2 Tissue-simulating phantoms

To validate simulation with experiment, tissue-mimicking phantoms were fabricated using silicone elastomers with controlled optical and mechanical properties. The phantoms were 3 mm thick cylinders with a diameter of 15 mm, made from Elastosil RT601, P7676, and AK50 Silicone oil (Wacker, Germany). The optical scattering properties were controlled using titanium dioxide particles (refractive index = 2.3) with a mean diameter of 1 μm, evenly mixed into the silicone (refractive index = 1.4) in concentrations of 0.5 mg/ml in the bulk and 2.5 mg/ml in the inclusions [40]. The mechanical properties were controlled by selecting different elastomers and varying the ratio of the catalyst, curing agent, and silicone oil. The stress-strain relationship of each silicone was characterized using a custom-built uniaxial compression testing apparatus. The 2D plane-strain model used in the simulations effectively assumes that the sample is infinitely long in the out-of-plane (y) dimension [39] and to best match this assumption, the inclusions were made longer (10 mm long rectangular prisms) in the y-dimension, than in the x- and z-dimensions. The inclusions were cut using a custom made silicone slicing tool, to improve the accuracy of the cross-section geometry. Each phantom was made in four steps to ensure the inclusion was placed 600 μm from the top surface. Firstly, a base layer of silicone was poured into a glass petri dish, using real-time OCT in the x-z plane to aid in achieving the correct height, which, for each inclusion size, was determined as the total phantom height (3 mm) minus the sum of 600 μm and the inclusion height. Secondly, once the base had cured, the inclusion was placed on top. Thirdly, silicone was poured over the inclusion and base, guided by real-time OCT, to a height of 600 μm above the inclusion. Finally, once cured, the phantom was removed from the petri dish using a 15 mm diameter biopsy punch. Five different phantoms were made with varying inclusion size and mechanical contrast, as shown in Table 1.

Table 1. Characterization of the silicone phantoms.

Phantom number	Inclusion dimensions height × width (μm)	Young’s modulus inclusion / bulk (kPa)	Modulus contrast
1	250 × 250	625 / 21	30
2	500 × 500	295 / 200	1.5
3	500 × 500	295 / 21	10
4	500 × 500	625 / 21	30
5	1000 × 1000	625 / 21	30

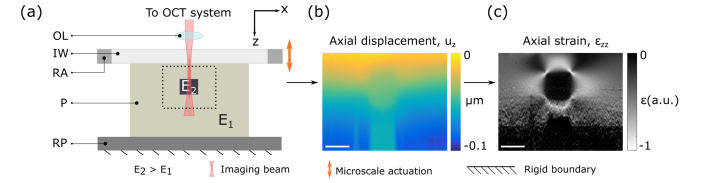
3.3 Phase-sensitive compression OCE system

OCE measurements were performed using a fiber-based spectral-domain OCT system (Telesto 320, Thorlabs Inc., USA). The light source is a superluminescent diode with a mean wavelength of 1300 nm and a spectral bandwidth of 170 nm. The measured OCT axial resolution in air is 4.8 μm (FWHM of irradiance). The objective lens (OL in Fig. 3(a)) (LSM03, Thorlabs) has a measured lateral resolution in air of 7.2 µm (FWHM of irradiance). AK50 silicone oil was applied to lubricate the phantom-imaging window interface. A preload of 15% bulk strain was applied to each phantom using a translation stage to ensure uniform contact between the rigid plate (RP in Fig. 3(a)), the phantom (P in Fig. 3(a)), and the imaging window (IW in Fig. 3(a)). The ring actuator (RA in Fig. 3(a)) (Piezomechanik GmbH, Germany) has an aperture of 65 mm and a maximum stroke of 10 µm. A 75 mm diameter imaging window (Edmund Optics Inc., USA), fixed to the ring actuator, transfers the compressive load from the actuator to the phantom. The system was operated in common-path where the imaging window itself, a partial reflector, acted as the OCT reference reflection. Scans were acquired by taking 2,000 A-scans per B-scan, and 2,000 B-scans per C-scan over a 5 mm × 5 mm region with a lateral sampling density of 2.5 μm per voxel. The ring actuator was driven in a quasi-static regime by a 12.5 Hz square wave, collinearly with the imaging beam and synchronized with the acquisition of OCT B-scans, such that alternate B-scans are acquired at different compression levels. Local axial displacement, u_z, in Fig. 3(b), is calculated from the change in phase, Δϕ(z), between B-scans acquired at the same lateral location [41]:

$$u_z=\frac{\Delta \varphi (z){\lambda }_0}{4\pi n},$$ (10)

where λ₀ is the mean wavelength of the light source, and n is the group refractive index of silicone (approximately 1.4) [40]. Local axial strain, ε_zz, is calculated from the gradient of axial displacement using weighted-least squares (WLS) linear regression over a fit length, Δz [34].

Fig. 3.

Illustration of 2D compression OCE on an inclusion phantom. (a) Sample arm of the imaging system. OL: objective lens, IW: imaging window, RA: ring actuator (the RA surrounds the IW and is shown cut-though in 2D), P: phantom (subjected to a bulk compressive strain of 15%), RP: rigid plate. (b) Axial displacement measured using phase-sensitive OCT from scans taken between different levels of microscale actuation. Least-squares regression is performed on (b) to obtain the strain elastogram of the phantom in (c). Images (b) and (c) correspond to the region denoted by the dotted black lines in (a). Scale bars represent 500 µm.

The WLS estimator is used to alleviate the impact of optical noise by assigning a greater weight to measurements of displacement acquired in regions of high OCT signal-to-noise ratio (SNR) [34]. In the case of zero optical noise, or uniform OCT SNR, WLS and ordinary least-squares (OLS) regression are equivalent [42]. Thus, although WLS is not a linear operation, in this study, its effect on resolution is modeled by OLS, as described in Section 2.3. To further reduce the effect of noise, the strain elastograms generated from experiment are averaged over a 125 μm length along the inclusion strip in the out of plane (y) dimension.

In experiment, the sample is preloaded to 15% bulk compressive strain, to achieve an even contact between the imaging window and phantom surface. A microscale actuation is then applied around this preload point, and the experimental strain elastograms were a result of this microscale actuation.

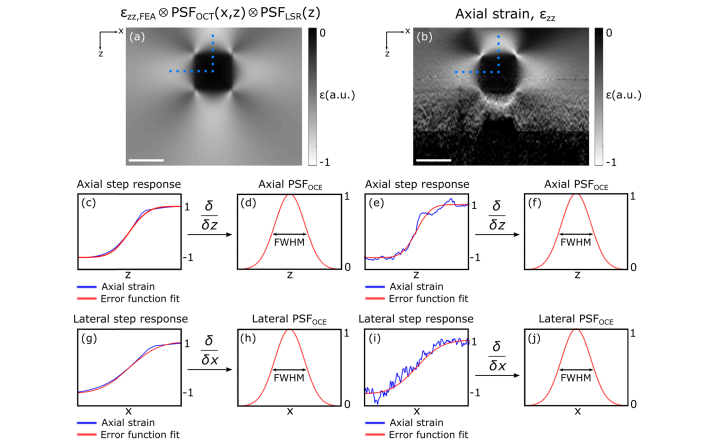
3.4 Quantifying resolution in OCE

We measure feature resolution using the step response in axial strain over the axial and lateral feature boundaries. The derivative of the step response provides an effective PSF, the width of which is defined as the resolution of elasticity at that location in the image. This process is illustrated in Fig. 4, which shows simulated (Fig. 4(a)) and experimental (Fig. 4(b)) strain elastograms of Phantom 4. The blue plots in Figs. 4(c) and 4(e) show the axial strain across the feature boundary, in the locations indicated by the vertical dotted lines in Figs. 4(a) and 4(b), respectively, normalized to between −1 and 1. The red plots in Figs. 4(c) and 4(e) show an error function,

$$\text{erf}\left(\frac{u}{a}\right)=\frac{2}{\sqrt{\pi }}{\displaystyle {\int }_0^{u/a}\text{exp}\left(-t^2\right)}dt,$$ (11)

which is fit to the normalized axial strain plots using least-squares regression to solve for the scaling factor, a. The derivative of this error function with respect to z gives the equivalent 1D Gaussian axial OCE PSF (axial PSF_OCE), shown in Figs. 4(d) and 4(f), the FWHM width of which provides a measure of axial feature resolution at that location in the image.

Fig. 4.

Illustration of the method used to measure feature resolution in phase-sensitive compression OCE. Strain elastograms of Phantom 4 in (a) simulation, and (b) experiment. In (c) and (e), the axial strain, and corresponding error function approximations, across the feature boundary at the locations denoted by the vertical dotted blue lines in (a) and (b) are presented. In (d) and (f), the axial derivatives of the error function fits, and corresponding FWHM are presented. Similarly, (g) and (i), respectively, show the axial strain and corresponding error function approximations across the lateral feature boundary denoted by the horizontal dotted blue line in (a) and (b) where (h) and (j), for simulation and experiment, respectively, show the lateral derivatives of the error function fits and corresponding FWHM. Scale bars represent 500 μm.

Similarly, Figs. 4(g) and 4(i) show the same process applied to the axial strain in the locations indicated by the horizontal dotted lines from Figs. 4(a) and 4(b), respectively. The derivative of these error function fits with respect to x gives the equivalent 1D Gaussian lateral OCE PSF (lateral PSF_OCE), shown in Figs. 4(h) and 4(j), and FWHM width of this PSF provides a measure of lateral feature resolution at that point in the image. In the following sections, we implement this technique at each point along each feature boundary, for each phantom, to investigate the spatially varying and sample dependent nature of feature resolution in OCE.

4. Results

4.1 Intra-sample resolution

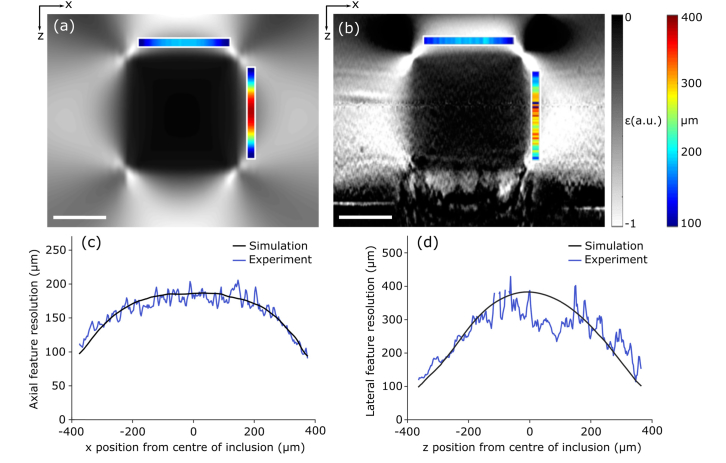
Figures 5(a) and 5(b) are strain elastograms of Phantom 5, from simulation and experiment, respectively, which show the variation in axial and lateral feature resolution as a function of position. The color maps indicate the feature resolution along the orthogonal feature boundaries. This is further illustrated in the plots in Figs. 5(c) and 5(d), which show that feature resolution varies in the axial direction from 100 μm to 200 μm, and in the lateral direction, from 100 μm to 380 μm. Figure 5 shows close correspondence between simulation and experiment, validating the linear systems approach taken to studying resolution in the simulation. These results demonstrate that feature resolution does not match the system resolution, but instead varies significantly within one elastogram.

Fig. 5.

Intrasample resolution in compression OCE. Strain elastograms of Phantom 5, with a feature cross section of 1000 μm × 1000 μm, acquired in (a) simulation and (b) experiment. The colored bars correspond to the feature resolution across the orthogonal feature boundary. (c) The measured values of axial feature resolution measured along the axial feature boundary in (a) and (b). (d) The measured values of lateral feature resolution measured along the lateral feature boundary in (a) and (b). Scale bars represent 500 μm.

As silicone, like many soft tissues, is incompressible [43], when a compression loading is applied to the entire sample, the axial deformation will be accompanied by a corresponding lateral deformation. The lateral deformation of the soft bulk is restricted by both adhesion to the stiff inclusion and friction at the imaging window surface, inducing lower strain in the bulk near these boundaries, resulting in a higher apparent Young's modulus. This leads to an axial gradient in axial strain at the axial inclusion boundaries, and a lateral gradient at the lateral inclusion boundaries. Toward the edges, and in particular, at the inclusion corners, the deformation of the bulk is less restricted. This introduces additional lateral gradients in axial strain at the axial inclusion boundaries, and axial gradients at the lateral inclusion boundaries. These gradients decrease toward the corners of the inclusion, effectively improving axial and lateral feature resolution in these locations.

4.2 Effect of feature size

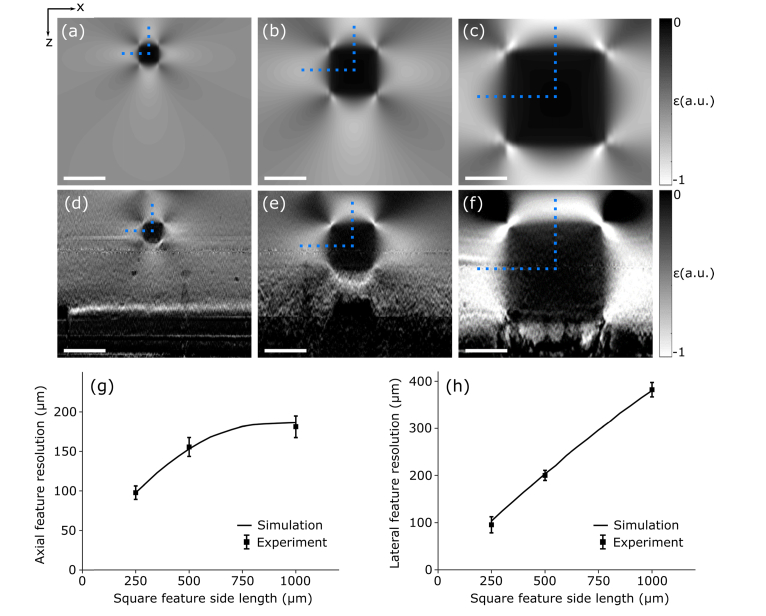
In Fig. 6, we demonstrate the impact of varying feature size on feature resolution for a fixed axial and lateral system resolution of 72 μm and 7.2 μm, respectively. Strain elastograms of phantoms with feature cross-sections in the x-z plane of 250 μm × 250 μm, 500 μm × 500 μm and 1000 μm × 1000 μm are presented in Figs. 6(a)–6(c) from simulation, and Figs. 6(d)–6(f) from experiment. The feature and bulk stiffness (at 15% strain) was maintained at 625 kPa and 21 kPa, respectively, and the axial and lateral feature resolution was measured in line with the central axis of the feature as denoted by the vertical and horizontal dotted blue lines, respectively.

Fig. 6.

The impact of feature size on axial and lateral resolution. Strain elastograms of phantoms with feature cross-sections of 250 μm × 250 μm, 500 μm × 500 μm and 1000 μm × 1000 μm are presented for (a)–(c) simulation and (d)–(f) experiment. In (g) and (h), the axial and lateral feature resolution (mean ± standard deviation) measured through the center of each feature, denoted by the vertical and horizontal dotted blue lines, respectively, is overlaid on curves obtained from simulation. Scale bars represent 500 μm.

In simulation, the feature cross-sectional size was varied from 250 μm × 250 μm to 1000 μm × 1000 μm in increments of 1 μm × 1 μm, and the measured values of axial and lateral feature resolution are shown as the solid black curves in Figs. 6(g) and 6(h), respectively. In experiment, six strain elastograms were generated for each feature size, obtained from six independent regions along the inclusion strip in the out-of-plane (y) dimension, and the axial and lateral feature resolution (mean ± standard deviation) are presented in Figs. 6(g) and 6(h) respectively, showing close agreement with the simulation. Figures 6(g) and 6(h) show that degradation in both axial and lateral feature resolution is proportional to feature size, where the axial and lateral feature resolution varies from 100 μm to 180 μm, and 100 μm to 400 μm, respectively.

As the feature size increases, a greater proportion of the soft bulk is adhered to the stiff feature, restricting deformation to a greater degree. This increases the gradient in axial strain at the feature boundaries, degrading axial and lateral feature resolution. This is consistent with the scale invariant nature of deformation [44], where we can expect the gradient in axial strain to be linear with feature size. The exception is the axial direction, where the proximity of the feature to the imaging window is not changing. The lateral deformation of the bulk above the feature is restricted by friction at the imaging window. As the feature size is increased, the lateral deformation of the bulk between the feature and the imaging window will become increasingly restricted. This increases the apparent stiffness in the bulk in that region, limiting deformation and, in turn, limiting the gradient in axial strain. This effect can be seen by the bend in the axial feature resolution curve in Fig. 6(g). Unlike in the axial case, the lateral edges of the feature are far from the imaging window and lateral boundaries of the phantom, resulting in lateral feature resolution degrading in a linear fashion, shown in Fig. 6(h).

4.3 Effect of feature mechanical contrast

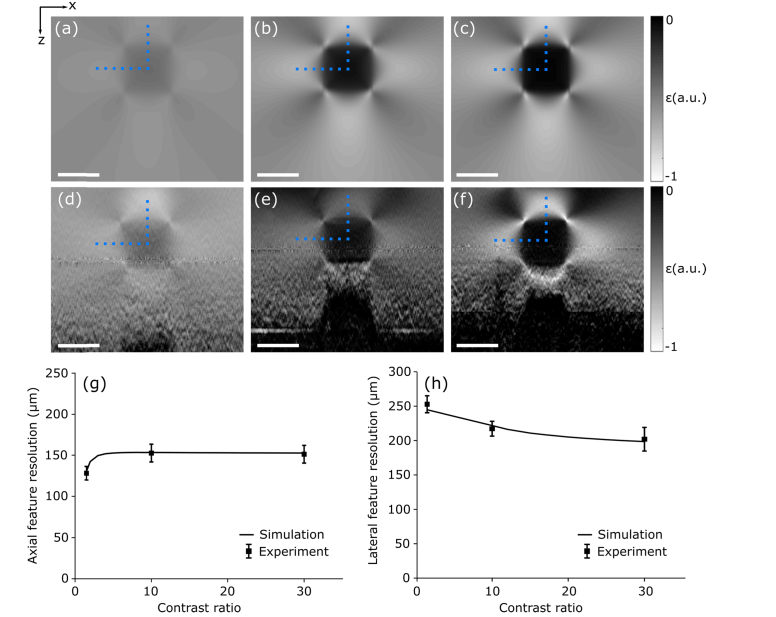
In Fig. 7, we demonstrate the impact of varying the mechanical contrast on feature resolution. Strain elastograms of phantoms with feature-to-background mechanical contrast ratios of 1.5, 10 and 30 are presented in Figs. 7(a)–7(c) from simulation, and Figs. 7(d)–7(f) from experiment. The feature cross-section was maintained at 500 μm × 500 μm and the axial and lateral feature resolution was measured in line with the central axes of the inclusion as denoted by the vertical and horizontal dotted blue lines, respectively. In simulation, the contrast ratio was varied in increments of 1, and the corresponding values of axial and lateral feature resolution are shown as the solid black curves in Figs. 7(g) and 7(h), respectively. In experiment, six strain elastograms were generated for each feature size, obtained from six independent regions along the inclusion strip in the out-of-plane (y) dimension. The axial and lateral feature resolution (mean ± standard deviation) are presented in Figs. 7(g) and 7(h) respectively, overlaid on the curves obtained from simulation.

Fig. 7.

The impact of mechanical contrast on axial and lateral feature resolution. Strain elastograms of phantoms with feature-to-background mechanical contrast ratios of 1.5, 10 and 30 are presented for (a)–(c) simulation and (d)–(f) experiment. In (g) and (h), the axial and lateral feature resolution (mean ± standard deviation) measured through the center of each feature, denoted by the vertical and horizontal dotted blue lines, respectively, is overlaid on curves obtained from simulation. Scale bars represent 500 μm.

The values of feature resolution between simulation and experiment are in close agreement. Figure 7 shows that, for this feature geometry, relative to the impact of varying size, varying mechanical contrast has a relatively minor impact on feature resolution, with the axial and lateral feature resolution varying from 130 μm to 150 μm and from to 250 μm to 210 μm, respectively.

As the stiffness of the feature increases, the deformation of the soft bulk is restricted to a greater extent. This increases the gradient in axial strain in the bulk at the axial feature boundaries and degrades axial feature resolution. Similar to the impact of increasing feature size, as the feature stiffness is increased in close proximity to the imaging window, the lateral deformation of the bulk between the inclusion and the imaging window will become increasingly restricted. As described in Section 4.2, this will limit the gradient in axial strain. However, for contrast ratios between 10 and 30, the extent of the axial deformation does not appear to vary significantly. These effects can be observed in the shape of the axial feature resolution curve in Fig. 7(g). There are two main factors affecting lateral feature resolution as the feature stiffness increases. First, the axial deformation of the bulk will become restricted to a greater extent, increasing the gradient in axial strain in the bulk near the lateral boundaries of the inclusion, degrading lateral feature resolution. Second, as the stiffness of the inclusion increases, the deformation of the feature itself will decrease. This will decrease the lateral gradient in axial strain occurring within the feature, improving lateral feature resolution. The latter effect appears to be the dominant contribution to lateral feature resolution for this feature geometry, shown by the improvement in lateral feature resolution with increasing mechanical contrast in Fig. 7(h).

4.4 Effect of system resolution

In Fig. 8, we illustrate the relationship between system and feature resolution for the case of axial resolution. We analyze Phantoms 1, 4 and 5, where for each feature size, we vary the axial system resolution and measure the corresponding change in axial feature resolution. The OCT axial and lateral resolutions were held constant at 4.8 µm and 7.2 µm, respectively. The axial system resolution was varied from 5 μm to 142 μm for Phantom 1, and from 5 μm to 178 μm for Phantoms 4 and 5, by changing the value of Δz used in least-squares regression from 50 µm to 250 µm. It is important to note that if Δz is larger than the feature size, least-squares regression will smooth the feature and background to an extent that reduces the accuracy of the approach used to measure feature resolution described in Section 3.4. Accordingly, for Phantom 1, with a feature cross-section of 250 μm × 250 μm, Δz was only varied from 50 μm to 200 μm. For the larger feature sizes in Phantoms 4 and 5, Δz was varied from 50 μm to 250 μm. For each phantom, and for each system resolution, six strain elastograms were generated, obtained from six independent regions along the inclusion strip in the out of plane (y) dimension. The values of axial feature resolution measured in line with the central axis of the feature are shown in Figs. 8(a)–8(c). The axial feature resolution (mean ± standard deviation) obtained for each experiment is overlaid on the curves obtained from simulation. In addition, the axial feature resolution for each feature size calculated from FEA alone is plotted as the dashed horizontal lines in Figs. 8(a)–8(c) which represent the limit to feature resolution imposed by deformation: 84 μm, 148 μm and 180 μm for Phantoms 1, 4 and 5, respectively.

Fig. 8.

Resulting axial feature resolution with varying axial system resolution for (a) 250 μm × 250 μm, (b) 500 μm × 500 μm and (c) 1000 μm × 1000 μm feature cross-sections. In (a), the axial system resolution was varied from 5 μm to 142 μm in simulation, and measurements were taken in experiment with system resolutions of 36 μm, 71 μm, 107 μm and 142 μm. In (b) and (c), the axial system resolution was varied from 5 μm to 178 μm in simulation, and measurements were taken in experiment with system resolutions of 36 μm, 71 μm, 107 μm, 142 μm and 178 μm. The solid black curve in each figure is obtained from simulation, and experimental measurements (mean ± standard deviation) are overlaid for each of system resolution used in experiment. The dashed lines show the respective values of axial feature resolution measured from FEA alone.

In Fig. 8, as the axial system resolution is improved, the feature resolution approaches the limit imposed by mechanical deformation. For Phantom 1, the feature resolution was reached to within 10% of the deformation limit with a system resolution of 36 μm (Δz = 50 μm). For Phantoms 4 and 5, the feature resolution was reached to within 10% of the deformation limit with a system resolution of 107 μm (Δz = 150 μm). This result demonstrates that prior knowledge, or reasonable assumptions about the sample geometry, can enable the optimal system resolution to be designed for a given application.

5. Discussion

We have presented the first study of resolution in OCE, by combining a finite-element model of mechanical deformation, with a model of the OCT system and a model of the signal processing, both based on linear systems theory, validated by close correspondence with experiment. This study illustrates the limitations imposed on resolution by sample mechanics and the elastogram formation process. Previously, Kennedy et al. analyzed the impact of mechanical deformation on contrast in OCE, and showed that sample-specific factors such as geometry and mechanical contrast limit elastogram accuracy and sensitivity [45]. Their study employed FEA to model deformation of elastic features in the absence of system noise to investigate the theoretical limits of elastogram contrast. Separately, Chin et al. combined FEA with a linear systems model of OCT to demonstrate that, in addition to the commonly considered effects of optical noise, the coupling between mechanical deformation and its optical detection impacts the precision of phase-sensitive compression OCE [46]. A promising avenue for future work is to integrate these previous studies into a similar framework presented in this study to develop a more complete model of image formation in OCE.

The results presented in Section 4 demonstrate that due to the limit imposed by mechanical deformation, feature resolution in compression OCE varies along feature boundaries and is dependent on feature size and mechanical contrast. Improving the OCT and signal processing resolution beyond this deformation limited state will not improve the feature resolution, but will instead unnecessarily trade off other image quality metrics such as contrast, sensitivity, imaging depth and field-of-view. The proportionality between feature resolution and size is predominately due to the scale invariant nature of deformation [44] and the incompressibility of the sample, leading to non-uniform stress that is not accounted for in the mechanical model. Similarly, the dependence of feature resolution on mechanical contrast is also attributed to incompressibility. Due to the assumption of uniform stress and the incompressibility of many soft tissues [43], similar results could be expected in tissue.

A square inclusion geometry was used in this study to readily measure a step response in both axial and lateral directions. From the theory presented in Section 2 and the results presented in Section 4, a different feature shape, e.g., a cylindrical or spherical inclusion, will likely exhibit a different intra-sample resolution distribution. As shown in Section 4.1, the incompressibility of the sample and adhesion of the soft bulk to the stiff inclusion leads to gradients in axial strain at the inclusion boundaries, degrading feature resolution. At the corners of the rectangular inclusions, the deformation of the bulk is less restricted, effectively improving axial and lateral resolution in these locations. In the case of cylindrical or spherical inclusions, which effectively have a circular cross-sectional geometry, the axial deformation of the bulk at the inclusion boundaries will be restricted in a different way, likely resulting in a different distribution of feature resolution. The focus of this study was to demonstrate that the sample has a pronounced effect on the resolution of OCE, and to establish a framework that incorporates the deformation of the sample with that of the OCT and signal processing to analyze resolution in compression OCE; however, an analysis of the effect of feature shape on resolution represents an avenue for future research.

The assumptions in the mechanical model used to relate deformation to elasticity in OCE can directly affect feature resolution, and importantly, suggests that a more complex mechanical model that makes fewer assumptions about sample deformation can improve feature resolution. This can be achieved by using numerical solutions to the inverse elasticity problem as demonstrated by Dong et al. [29]. Their work employs an iterative approach to solving Eqs. (1) and (4) for the mechanical properties of the sample and, importantly, removes the assumption of uniform and uniaxial stress. Preliminary results from elastograms presented in their study demonstrate a homogenization of resolution across the field-of-view that is achieved by reducing the link between feature properties and resolution. However, the improvement to feature resolution through this approach is yet to be quantified. Further removing assumptions of sample homogeneity, linearity and isotropy can likely lead to improved feature resolution in OCE, where our framework could be used to quantify these improvements.

A potential application of OCE is in tissue engineering and cell mechanics [47]. Contemporary developments in this area seek to mimic the mechanical complexity of the extracellular environment, moving towards complex, multi-parameter, 3D biomaterials [48]. OCE is well-poised to provide a non-invasive technique that can characterize biomaterials in 3D. Previous studies have used compression OCE systems with an OCT axial and lateral resolution of below 2 μm to study cellular scale structures in animal models and excised tissue [25–27]. For example, features with a lateral length of 20 μm in excised mouse aorta were observed with a measured equivalent Gaussian FWHM lateral feature resolution of approximately 10 μm to 15 μm [27], which is consistent with our framework. However, the diameter of many animal cells lies below 10 μm [49], and to study cells with a feature resolution below this limit will likely require solving more complex mechanical models, or indeed employing techniques that localize deformation [19–22]. The limit on achievable resolution may result in compression OCE being most useful in studying the mechanical properties over the entirety of the cell and the interactions between the cell and its environment over relatively large fields-of-view. Our framework can help to address this question.

In the simulations presented in this study, we consider the OCT and least-squares regression resolution independently, however, in experiment, the resolution of the OCT system determines speckle size [50]. Due to the impact of speckle on the accuracy of displacement measurements [30] and therefore strain accuracy [34], the fit length of axial displacement used in least-squares regression is effectively dependent on the OCT resolution. This dependence between OCT and least-squares regression resolution was not considered in our study, but could be incorporated into our framework by combining previous work by Chin et al. [46]. From the results in this study, the degradation to feature resolution from least-squares regression was typically much greater than OCT. Our framework suggests that improving displacement accuracy in phase-sensitive OCE can lead to significant improvements in feature resolution by removing the need for larger fit lengths in least-squares regression.

This study has focused on phase-sensitive compression OCE, however, our framework could be extended to other elastography techniques. For example, quantitative micro-elastography (QME), an extension of compression OCE, uses a compliant silicone layer placed between the sample and the imaging window to map the 2D uniaxial stress applied at the sample surface [51]. The stress is assumed to be uniform with depth, which, along with the volume of local axial strain, provides an estimate of Young’s modulus throughout the sample. However, as QME uses the distribution of local axial strain to determine the distribution of Young’s modulus, the spatial resolution of QME is tethered to the resolution of compression OCE. Consequently, feature resolution in QME will also likely be spatially varying and sample dependent where our framework could be applied to assess feature resolution. Further, alternative OCE loading methods, such as shear wave and surface acoustic wave OCE [6,17,52], typically rely on the same assumption of homogeneity to access sample mechanical properties. It is likely that mechanical heterogeneity will lead to similar discrepancies between feature and system resolution. A study comparing all such methods with our framework would be informative and the feature resolution could help determine the most efficient approach for various applications. Similarly, our framework can be extended to quantify improvements in feature resolution brought about by high resolution OCT systems [25–27], improved signal processing [28,29] and extended to shear wave OCE and surface acoustic wave OCE or indeed to ultrasound elastography [53] and magnetic resonance elastography [54].

6. Conclusion

We have presented the first framework to study resolution in phase-sensitive compression OCE that incorporates the mechanical deformation of the sample in response to a load, the measurement of the resulting displacement in the sample using OCT, and the signal processing used to estimate local strain. This framework enables us to analyze the impact of these factors on both system and feature resolution. We have demonstrated, through simulation and experiment, that mechanical deformation is typically the dominant determinant of resolution in compression OCE, and imposes a limit to resolution. Due to this limit imposed by mechanical deformation, the ability to resolve features in an underlying distribution of mechanical properties varies along feature boundaries and is dependent on feature size, mechanical contrast and location.

Funding

Australian Research Council; the Cancer Council Western Australia; OncoRes Medical; William and Marlene Schrader Trust of the University of Western Australia scholarship.

Disclosures

BFK: OncoRes Medical (F, I) and LC: OncoRes Medical (I). The other authors declare that there are no conflicts of interest related to this article.