Single etalon design for two-stage cross-axis VIPA spectroscopy

Abstract

Two-stage cross axis VIPA spectrometers have been widely used in Brillouin microscopy since they provide single shot spectral measurements at high throughput and extinction. However, this spectrometer configuration presents challenges such as size, cost and alignment difficulties between the two cascaded etalons. Here, we present a cross-axis VIPA spectrometer that implements a single etalon, using a light recirculation architecture to achieve the multistage configuration.

1. Introduction

Brillouin scattering is an inelastic light-matter interaction [1,2] that can be used to investigate several physical properties of the sample [3–6]. Traditionally, Brillouin spectra are acquired using a scanning multipass tandem Fabry-Perot interferometer, developed in 1970 by J.R. Sandercock [7,8]. The idea of a single shot spectral measurement was introduced in the 1990s [9–11], but became widespread with the development of multi-stage cross axis VIPA spectroscopy [12–14]. This technique allowed single shot spectral measurement with sufficiently low illumination power and high spectral extinction for Brillouin spectroscopy in biological samples; at the same time, the rapid acquisition time of single spectra enabled combining Brillouin spectrometers with confocal microscopes to provide high, three-dimensional resolution mapping of mechanical properties [15–17]. Since then, fast Brillouin microscopy quickly emerged as a non-invasive, high-resolution imaging modality to map mechanical properties of biological samples [18], being used to investigate biomechanics of eye [19–24], cells [25–32], cerebrospinal fluid [33], embryo development [34–36], spinal cord injury [37], fibroatheroma plaques [38], bacterial biofilms [39].

In the last decade, a powerful configuration used has been the one featuring two VIPA etalons in cross-axis configuration since it offers an optimal compromise between insertion loss and spectral extinction: a standard two-stage VIPA spectrometer typically provides overall throughput of ~40%, finesse greater than 35 and extinction ratio of ~60 dB [14]. Two stage cross axis VIPA spectrometers have witnessed constant development that greatly improved their performances, such as the addition of a third VIPA stage [14], apodization filters [27], etalon notch/bandpass filters [40,41], interferometric filters [39,42], spectral coronography [43,44], gas cells [45], etc. However, the two-etalon configuration carries unresolved drawbacks such as the size, that can reach 1.8 m in length by 0.3 m in width when using typical 200 mm optics [46], as well as the need to have and align two VIPA etalons on different spatial axis. As a result, several attempts have been made to avoid a second etalon, maintaining the same level of performance [24–26,47–51]. In this paper we present a novel approach to the construction of a two stage VIPA spectrometer featuring only one VIPA etalon; thanks to a beam folding design that relies on two polarized beam splitters and a beam steering element, light is dispersed on two orthogonal axes within the same etalon. We thus obtained a compact, single etalon spectrometer (0.5 by 0.4 meters) with performance equivalent to the standard implementation, and a footprint of about three-fold reduced in length and area.

2. Principle

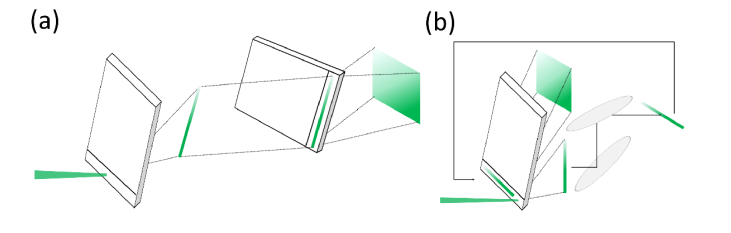
A traditional two stage cross axis VIPA spectrometer (Fig. 1(a)) is designed so the light is independently dispersed on two spatial axes: the light is focused in the first etalon and the output pattern is then focused on the orthogonal axis into a second etalon mounted perpendicularly to the first one. The resulting pattern is then imaged onto a CCD camera. Our goal was to recreate the same dispersions steps, while using and aligning a single VIPA etalon. In order to achieve this result, we designed a light folding architecture that allows the light to be dispersed twice by the same VIPA on two different spatial axes (Fig. 1(b)). The dispersion on the second dimension is accomplished by rotating the VIPA pattern at 90° and focusing it into the entrance of the VIPA a second time. Thus, the system results to be equivalent to a second VIPA oriented along the orthogonal axis with respect to the first one. Figure 1 shows how the classic and the single etalon folded implementation lead the input beam through the same dispersive steps; thus, the two system are expected to have same spectral performance, with the latter configuration to be preferred in terms of compactness, cost and ease of alignment.

Fig. 1.

(a) 2-stage cross axis VIPA spectrometer in which light is dispersed on two spatial axis with two different etalons in cross axis configuration. (b) Single etalon cross axis VIPA spectroscopy principle; the output pattern from the first pass is rotated and recirculated through the same etalon.

3. Experimental setup

In our experiment we used a 532nm CW laser (Laser Quantum, Torus-532) coupled into a single mode fiber as light source, and a VIPA etalon with free spectral range of 20 GHz (Light Machinery) as dispersive element. In practice, the described system has been implemented as shown in Fig. 2: a half-wave plate (HWP1) at the output of a single mode fiber (SMF) orients the polarization of the beam on the parallel plane (S-state). The beam is then focused by a cylindrical lens (C1), transmitted by the first polarized beam splitter (PBS1) and dispersed by the VIPA etalon; at this stage a second half-wave plate (HWP2) oriented perpendicularly to the first one changes the polarization to P-state, allowing the beam to be reflected by the second polarized beam splitter (PBS2). The VIPA pattern is focused by a cylindrical lens (C2) in a 1-dimensional spatial filter (SLIT1). A spherical lens (S1) focuses the light into the VIPA for the second time, after being rotated by a beam steering system (BSS) and reflected by PBS1 thanks to its opposite polarization. Like in the first pass, the polarization is inverted back to P-state by the HWP2 so that the pattern can now pass through PBS2, be focused by a second spherical lens (S2) through the second slit (SLIT2), and imaged onto the CCD camera.

Fig. 2.

Experimental setup of a single etalon cross axis VIPA spectrometer. SMF: single mode fiber, HWP: half wave plate, C: cylindrical lens, f = 200mm, S: spherical lens, f = 200 mm, PBS: polarized beam splitter

Unlike a standard cross axis two-stage VIPA spectrometer, in this novel approach there is a single etalon that needs to be aligned with the first passing beam. The second pass beam is aligned to be perfectly parallel to the former, resulting in minimal VIPA adjustment required at the second stage. In order to align the two beams parallel to each other, we used the residual light reflected by PBS1 at first passage, and transmitted at the second. The two weak beams have been aligned to be parallel at long distance, resulting in their stronger counterparts to be aligned as well. In case brighter beams are required, it is possible to adjust HWP1 so the alignment beams gradually gain intensity. In conclusion. we found the additional optics elements such as PBS, HWP and BSS to be quicker to align and optimize than a second stage VIPA. Perhaps, among the additional elements introduced in this configuration, BSS is the most sensitive; there are several ways to realize the pattern rotation, such as a two-mirrors beam steerer or a Dove prism oriented at 45°. In our demonstration, we opted for the former since it is simpler to implement. It should be noticed how, to minimize cross talk between the two passes, the two light paths are not overlapped but rather parallel to each other. However, even though the beams are separated, for the sake of optimal performance, it is crucial that the incident angle in the VIPA of both beams is the same. As a result, not only the same interference order will be optimized on both dispersion axis, but it is also possible to tune both VIPA stages adjusting the tilt of the single etalon. In other words, the same entrance angle in the etalon ensures equal dispersive performance on both axes and allows one-touch fine tuning capability.

4. Results

In order to characterize our instrument, we measured the effective throughput and finesse as a function of the angle between the incoming beam and the VIPA etalon. Varying this angle changes the path of the light inside the etalon, modifying resulting interference pattern. Specifically, it is possible to adjust and optimize the entrance angle so that a specific interference order is preferred to the others in terms of throughput. As previously mentioned, if the two incident beams enter the VIPA with the same angle, the peak order will be the same on both axes. Thus, tuning the tilt of the VIPA will adjust both stages of the spectrometer. The results of this measurement are reported in Fig. 3(a), showing an optimal compromise between the third and the fourth order, with effective throughput around 18% and finesse of ~40. It is important to remark that the effective throughput is defined as total input power over power output of a single VIPA interference order, while the overall throughput expressed as total output power over total input power was 23% at peak performance. Experimentally, the measurement is performed by physically blocking all other orders with a slit, and placing a power meter right after the slit. This reflects the conditions in which Brillouin spectral measurements are usually configured, and therefore more descriptive of our instrument performance.

Fig. 3.

(a) Effective throughput and finesse performance as a function of the VIPA order. Effective throughput is measured as ratio between total power output at given order after two VIPA stages and the overall input power. Finesse is measured as spectral linewidth over free spectral range (FSR). (b) Step-by-step throughput characterization. Blue bars report the transmission efficiency of every element, the red line shows the overall throughput at every location. In parenthesis is expressed the iteration through a certain optical element.

In order to better characterize the losses, we performed a step by step analysis of the efficiency of all optical components, which is reported in Fig. 3(b). From this analysis, we concluded that our polarization switch system (PBS-HWP) has a relatively low efficiency (~95% per pass) which leads to an overall 20% loss over the required four passes. More efficient components or a mirror based recirculating system can greatly improve the throughput. Moreover, our beam steering also shows low efficiency performance (~80%) which we linked to the large size of the VIPA pattern compared to the mirror size. As a result, in ideal experimental conditions, we expect losses only due to the VIPA etalon, which in our case would mean an overall throughput of ~35%.

To evaluate the spectral performance of our instrument, we characterized the spectral linewidth and extinction ratio. Fitting the two-peak profile obtained on the CCD camera (Fig. 4(a)) with a double Lorentzian function, we measured a linewidth of 0.48 GHz. Subsequently we measured the spectral contrast after the first and second stage. In order to quantify the performance at the first stage we simply changed orientation of HWP2, letting the beam to be imaged on the CCD sensor without recirculation. In contrast, the second stage measurement has been performed with the recirculation enabled. The ability to visualize either one or two stage on the camera becomes crucial during the first alignment and characterization, thus it is worth mention it. As shown in Fig. 4(b) our instrument reaches an extinction of ~58dB, comparable with a standard two stage cross axis spectrometer. It is important to remark that, while the bare architecture of two cascaded VIPA stages offer a spectral extinction of ~60dB, in practice other optical elements are used to improve the extinction ratio such as VIPA apodization, etalons, interferometric filters and spectral coronography, so that a contrast of 75-80 dB is easily achieved. The design proposed here remains compatible with most of the mentioned solutions; for instance, apodization filters can be placed after the two exit sides of the PBS2, while a coronography can be implemented before the CCD camera.

Fig. 4.

(a) Camera frame and line plot of laser profile on the CCD camera. (b) Extinction ratio measurement of single stage and two stage VIPA spectrometer.

5. Conclusions

We have demonstrated a new implementation of a cross axis VIPA spectrometer in which the light is recirculated through the same etalon, obtaining overall throughput of ~23%, finesse greater of ~40 and extinction ratio of ~58 dB. The throughput of the two VIPA stages is about 35%, a value compatible with standard two stage implementation; thus, the overall transmission efficiency performance can be greatly improved with high quality polarization management elements and larger beam steering mirrors; similarly, the spectral extinction can be improved with apodization and coronography filters. The footprint of our instrument is roughly three-fold smaller than previously reported instruments, with same focal length optics; this can be considered the main achievement of this optical design. In conclusions, our results show an equivalent performance to previous two-VIPA spectrometers, with advantages in terms of size, cost effectiveness and ease of alignment.

Funding

National Institutes of Health (R33CA204582, R01EY028666, R01HD095520 and U01CA202177); National Science Foundation (CMMI-1537027), and TEDCO Maryland Innovation Initiative.

Disclosures

The authors declare that there are no conflicts of interest related to this article.