Parallel deep neural networks for endoscopic OCT image segmentation

Abstract

We report parallel-trained deep neural networks for automated endoscopic OCT image segmentation feasible even with a limited training data set. These U-Net-based deep neural networks were trained using a modified dice loss function and manual segmentations of ultrahigh-resolution cross-sectional images collected by an 800 nm OCT endoscopic system. The method was tested on in vivo guinea pig esophagus images. Results showed its robust layer segmentation capability with a boundary error of 1.4 µm insensitive to lay topology disorders. To further illustrate its clinical potential, the method was applied to differentiating in vivo OCT esophagus images from an eosinophilic esophagitis (EOE) model and its control group, and the results clearly demonstrated quantitative changes in the top esophageal layers’ thickness in the EOE model.

1. Introduction

Image-based medical diagnosis and prognosis rely on accurate interpretation of a large number of images. The task is laborious and prone to error. It would be highly beneficial to have a computer assisted system that can automatically detect and analyze abnormalities in the images and generate a more objective and quantitative analysis [1]. A crucial step toward such a system is to obtain accurate segmentation of features of interest in the images and to compute tissue characteristics such as shape, area, volume, thickness, and eccentricity [2].

Endoscopic OCT is an optical imaging modality capable of high-resolution, real-time, and three-dimensional (3D) imaging of internal luminal organs. It can be used in various clinical applications such as detection of subepithelial esophageal lesions [3] and coronary vulnerable plaques [4], where micro-structures yield important diagnostic information [5,6]. Automated segmentation of OCT images is a difficult task as segmentation algorithms are generally sensitive to speckle noise, intensity inhomogeneity, low image contrast, and other artifacts. So far, most efforts on endoscopic OCT image segmentation have focused on simple layer segmentation, such as stent strut detection and fibrous cap quantification of intravascular OCT images [7–10] and classification of esophagus OCT images [11]. Automated segmentation of OCT images with multiple layers has mainly targeted retinal and coronary images [12–15], again primarily using graph-based methods [14–18] or more recently deep learning techniques [19–27]. Endoscopic OCT images with multiple layers, however, often face elevated challenges such as complex layer boundary slopes due to tissue folding, blockage by mucus or some debris, and in-layer image intensity nonuniformity [28]. Recently, a graph-based method has been demonstrated for segmentation of multilayered endoscopic OCT esophagus images [29]. Compared to traditional image processing methods, deep learning techniques have higher tolerance to structure variability and require less prior knowledge of the structures in the input images [30,31]. These advantages make them more attractive for developing automated segmentation methods [32].

In this paper, we proposed a robust segmentation method based on deep neural networks. To achieve robust layer segmentation, particularly with a limited training data set, U-Nets [19] were trained in parallel and then used to segment in vivo endoscopic OCT images. The paper first introduces the image collection process, describes the parallel training scheme in detail, and then demonstrates the performance of this method, including its robust segmentation ability, segmentation accuracy, and clinical potential. Robustness and accuracy were demonstrated with in vivo cross-sectional endoscopic OCT images of guinea pig esophagus; Clinical potential was demonstrated by quantitatively comparing the layers’ thickness of in vivo OCT esophagus images between an eosinophilic esophagitis (EOE) model and a control group.

2. Data collection, preparation and control group

Endoscopic OCT esophagus images from five guinea pigs (male, Hilltop, Scottsdale, PA) were collected in vivo using an 800 nm endoscopic OCT system (with an OCT endoscope of a 1.3-mm outer diameter). The endoscope was disinfected before deployment into the esophagus. The animals were handled under protocols approved by the Animal Care and Use Committee (ACUC) of the Johns Hopkins University.

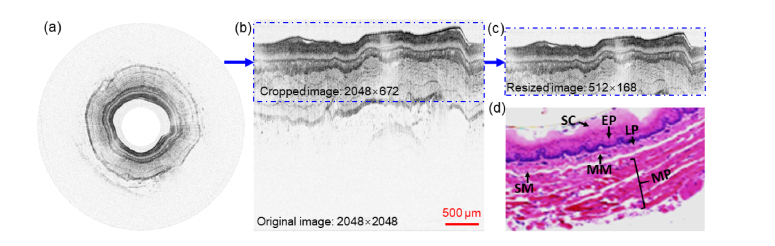
Along with a home-built spectral-domain (SD) OCT system [28], the OCT endoscope offered a measured axial resolution of about 2.1 μm in tissue (using a Ti:Sa laser as the low coherence light source with a center wavelength ${\lambda }_0=835nm$ and a spectral bandwidth$\Delta \lambda =150nm$). With the guinea pig under anesthesia, the OCT endoscope was inserted into the esophagus until reaching the gastro-esophageal junction. 3D imaging was performed by scanning the imaging beam circumferentially during endoscope pullback. Among the five guinea pigs, three were inducted with EOE [33] and the other two served as control. Two hundred cross-sectional images were collected from each guinea pig along the pullback direction. The guinea pigs used in the experiment were at the same age with roughly the same weight. The images used in this manuscript partially overlapped with the ones we previously used to demonstrate our graph-based image processing algorithms [29,34]. Figure 1(a) illustrates a representative cross-sectional OCT image, where the layered structures can be clearly identified by eye (Fig. 1(b)) and correlated well with histology (Fig. 1(d)).

Fig. 1.

(a) Representative in vivo ultrahigh-resolution circumferential OCT image of guinea pig esophagus. (b) Cut-open (rectangular) OCT image and cropped part. (c) Resized image. (d) Corresponding histology micrograph. SC: stratum corneum, EP: epithelium, LP: lamina propria, MM: muscularis mucosae, SM: submucosa, MP: muscularis propria.

2.1 Data preparation

To facilitate image processing, the circumferential OCT images were converted into a rectangular format, as shown in Fig. 1(b). The rectangular OCT images were then manually segmented based on the normal 6-layer esophagus structure of guinea pig and used to train and test the deep neural networks. To run the image processing efficiently and avoid potential memory overflow, each rectangular image (2048 × 2048 pixels, lateral × axial) was cropped along depth to keep only the regions of tissues, resulting in a final image size of 2048 × 672 pixels (lateral × axial). The cropped images were further resized down to 512 × 168 pixels by binning every 4 pixels along both the lateral and axial directions (see Fig. 1(c)). The resized images were then augmented by horizontal flipping, spatial translations, and cropping [22]. We trained the networks with 235 OCT images from two guinea pigs with EOE, one control, and their corresponding manual segmentation layer maps (ground truth), among which 215 images served as training data set and the rest 20 images for validation. We tested the trained networks with 40 images and their corresponding ground truth, among which 20 images were from the third EOE guinea pig and 20 images from the second control. It should be mentioned that there was no overlap between the training and testing data sets.

3. Methods

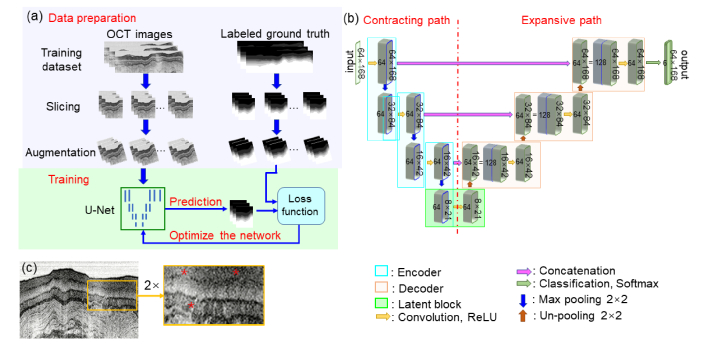
General description: Our parallel-trained deep neural networks contained three U-Nets [19]. Figure 2(a) shows the training procedure of one representative U-Net. The images and corresponding ground truth in the training data set were first divided along the lateral direction into eight non-overlapping sets of smaller images (termed slices) and then spatial-augmented as the input for the U-Net. The net parameters were initialized randomly, following a normal distribution [39]. The output of the U-Net was the prediction of the esophageal layers. The prediction was compared with the corresponding manual segmentation with a selected loss function. The output of the loss function was used to update the U-Net parameters. The training process was repeated until the loss function reached its minimum. The trained net was then used for automated image segmentation.

Fig. 2.

(a) Schematic of the Net training process. (b) Schematic of a single U-net, which contains 64 kernels for preserving the image features [35]. Rectified Linear Unit (ReLU) induces nonlinearity for efficient training [36]. Max pooling reduces feature maps by a factor of 2 along each dimension [37]. Concatenation helps increase spatial resolution and training stability [38]. (c) Original OCT image with a low image contrast region (see the zoomed-in region indicated by “*”).

3.1 U-net structure

U-Net is fast and precise for medical image segmentation [19,40]. The schematic of our U-net is shown in Fig. 2(b). The network consisted of a contracting path (on the left side of the net), an expansion path (on the right), and a classification layer. There were three encoder blocks (indicated by the cyan color boxes) in the contracting path and three decoder blocks (indicated by the brown color boxes) in the expansion path. The encoder blocks were used for learning the contextual feature hierarchy and the decoder blocks for semantic segmentation. The decoder blocks were concatenated with the corresponding encoder blocks. The classification block used a convolutional layer with 1 × 1 kernels to narrow down the feature maps to seven classes, and in our case, the seven classes represent the six esophageal layers and the background. Finally a softmax layer was used to estimate the probability of each pixel belonging to any of the seven classes [41].

Each resized OCT image (512 × 168 pixels) was laterally divided into eight slices (each of 64 × 168 pixels) and then spatial augmented. The augmented images were fed into the encoder blocks. In the first encoder block, the input was convolved with 64 kernels to generate (64 × 168) × 64 feature maps. The feature maps were normalized, activated with ReLU, and sent through a max pooling step for down-sampling by a factor of 2 along both the lateral and depth directions; this process yielded (32 × 84) × 64 feature maps. The encoding process repeated three times. At the bottom of the U-Net, a latent block served as a transition from the encoder blocks to the decoder blocks, where the (8 × 21) × 64 feature maps were not down-sampled but instead went through an un-pooling process for up-sampling by a factor of 2 along each dimension, which yielded (16 × 42) × 64 feature maps. The (16 × 42) × 64 feature maps were then concatenated with the output from the third encoder block. This concatenated map was convolved, normalized, and activated by ReLU in the remainder of the decoding process. The decoding process repeated twice, and the output of the final decoder block was then sent to the classification block.

3.2 Net parameters update

During the training process, the randomly initialized net parameters were updated for layer prediction by minimizing a loss function. We selected weighted multi-class dice loss function to evaluate the difference between the prediction and manual segmentation [42]. The weighted multi-class dice loss function performed well to compensate for class-imbalance and encouraged kernels that were discriminative towards layer transitions [22,43]. During the training process, we optimized the loss function with an additional Frobenius norm term for regularization [44]. The final loss function is shown below:

$$J=1-\frac{2{\displaystyle \sum _x{p}_l(x)g_l(x)}}{{\displaystyle \sum _x{p}_l^2(x)+{\displaystyle \sum _x{g}_l^2(x)}}}+{\Vert W\Vert }^2$$ (1)

where $x$ is the pixel index, $g_l(x)$ is the true label at pixel x, $p_l(x)$ is the estimated probability for pixel $x$ to belong to class l (there were seven classes in our case), W is the weight for the kernels, and ${\Vert W\Vert }^2$ is the Frobenius norm term. The output of the loss function layer was used to update the U-Net parameters by trying to reach its minimum. The loss function was minimized by stochastic gradient decent (SGD) with a momentum of 0.9 and an adaptive learning rate during the optimization process [35,45]. The final U-Net parameters were then used for automated image segmentation.

3.3 Parallel training

It has been shown that U-Net can predict retinal layers after being trained by hundreds (at least) of labeled OCT images [23]. The labeled images were either taken from public repositories [22,23,46] or labeled with a well-established software [47]. Labelling endoscopic OCT images is more difficult because of the following factors: (1) any dramatic variation of fine structures on the endoscopic images, (2) geometric complexity induced by tissue folding, or (3) low contrast regions due to sublayers and in-layer fine structures. Due to the first factor, a universally labeled data set or a well-established labeling software don’t exist. The last two factors increase labeling difficulty and inaccuracy. Furthermore, the network also requires a larger training data set to deal with geometric complexity and low image contrast. All these factors result in an elevated cost in data set preparation. Therefore, an effective neural network feasible with a limited training data set is highly desirable.

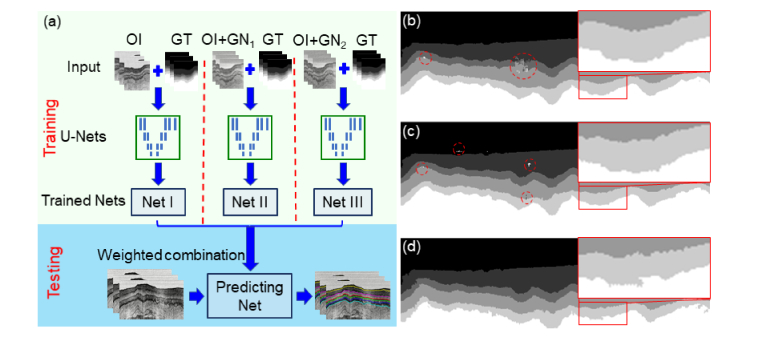
Spatial augmentation such as horizontal flipping, translating, and cropping can enlarge the training data set and has served as a standard step in our training stage [48]. However, when we trained a single U-Net (i.e., Net I in Fig. 3(a)) with our limited original training data set, which contained 215 labeled endoscopic OCT images, the prediction of the trained U-Net exhibited layer topology disorders (see the red circle regions in Fig. 3(b)). We also trained two more networks separately by the original training data set added with different levels of zero-mean Gaussian noises (Net II and Net III). Each network was forced to learn topologically correct feature maps within a given noise regime. We noticed that topology disorder decreased when the noise distribution broadened (as shown in the red circle regions in Figs. 3(b-d)), while the predicted boundaries became noisier (as shown in the zoomed-in regions in Figs. 3(b-d)). The trade-off between topology disorder and predicted layer boundary accuracy suggested that a combination of those U-Nets might help achieve a good pixel accuracy and at the same time maintain good shape priors. We then tried different combinations of the U-Nets and compared the outcomes. When any two of the above three networks (Net I, II, and III) were combined, we found topology disorders still existed. When all three networks were combined, topology disorders disappeared. We also noticed that the performance didn’t exhibit obvious improvement when more than three networks were combined (i.e., the above three networks plus additional networks trained by the original data set added with broader zero-mean Gaussian noises). Considering the computational time increased almost linearly with the number of networks involved, we adopted the combination of three parallel-trained networks (Net I, II, and III). The combining weights, [0.5, 0.3, 0,2], were selected by minimizing the total layer boundary prediction error for the validation data set (see detailed description of prediction error in Section 4.1).

Fig. 3.

(a) Flow chart of our parallel training scheme. Three U-Nets (Net I, II, and III) were trained seperately and then combined for layer prediction. Net I was trained by the original images (OI) and the corresponding ground truth (GT); Net II was trained by the original images added with zero-mean Gaussian noise (σ = 1, GN₁) and the corresponding ground truth; Net III was trained by the original images added with zero-mean Gaussian noise (σ = 2, GN₂) and the corresponding ground truth. (b) Feature map predicted by the trained Net I. (c) Feature map predicted by the trained Net II. (d) Feature map predicted by the trained Net III. Dashed circles show the regions with layer topology disorders, which decrease from (b) to (d). Zoomed-in boxes show the predictions of layer boundaries, which become noisier from (b) to (d).

4. Results

4.1 Evaluation of the parallel training scheme

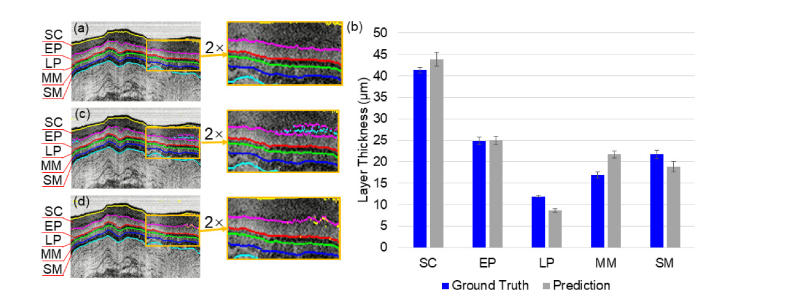
Figure 4(a) shows representative layer segmentation by the parallel-trained three U-Nets on the testing data set. The result is free from layer topology disorder and the predicted boundaries are smooth as shown in the zoomed-in region of Fig. 4(a). Figure 4(b) illustrates the prediction accuracy in terms of the difference of layers’ thickness between prediction and the ground truth. The averaged relative error of prediction (normalized by the ground truth layer thickness) is about 6.0% for all layers. This error might be influenced by non-ideal ground truth. The origin of non-ideal ground truth can be multifaceted. For example, OCT signal saturation at the tissue surface would make it challenging to accurately determine the top boundary of the SC layer, which could result in the large difference between the predicted and ground truth SC layer thickness as seen in Fig. 4(b). In addition, any weak contrast between layers might generate a bias in determining the boundaries of the LP and MM layers, which could lead to the large difference in the predicted and ground truth thickness for the LP and MM layers shown in Fig. 4(b). Error bars in Fig. 4(b) represent the layer thickness variance for each layer for all the images in the testing data set. The absolute boundary error was calculated as the maximum difference of each boundary between the prediction and ground truth. The boundary error averaged over all the boundaries was about 1.4 µm.

Fig. 4.

(a) Representative layer segmentation by the parallel-trained U-Nets (Net I, Net II and Net III) The empirical combination weights are [0.5, 0.3, 0.2]. (b) Layer thickness comparison between the ground truth and the prediction of the parallel-trained U-Nets. Error bars represent the standard deviation of layer thickness for all the images in the testing data set. SC: stratum corneum, EP: epithelium, LP: lamina propria, MM: muscularis mucosae, SM: submucosa. (c) Representative layer segmentation by a single U-Net trained by the original training data set. (d) Representative layer segmentation by a single U-Net trained by a noise-augmented data set which was the combination of the original training data set, the original training data set added with the first Gaussian noises (σ = 1), and the original training data set added with the second Gaussian noises (σ = 2).

In comparison, we also trained a single U-Net with (1) only the original training data set and (2) the noise-augmented data set which was the combination of the original training data set, the original training data set added with the first Gaussian noises (σ = 1), and the original training data set added with the second Gaussian noises (σ = 2). Figure 4(c) shows representative layer segmentation by a signal U-Net trained by original data set. Pronounced layer topology disorders (see the boxed region and its zoomed-in view in Fig. 4(c)) occurred in the low contrast area. The averaged error rate of prediction was about 7.0%. Figure 4(d) shows representative layer segmentation by a single U-Net trained by the noise-augmented data set. Layer topology disorders became less pronounced but still visible. The averaged error rate of prediction was about 6.5%. In comparison with Fig. 4(a), the parallel-trained U-Nets not only reduced layer topology disorders, but also improved segmentation accuracy.

4.2 Differentiation of esophageal layers thickness between the EOE and normal guinea pig models

It has been shown that EOE severity level positively correlated with the thickness of the superficial layers (i.e., the stratum corneum and the epithelium) [49]. To further explore the potential clinical utility of the above parallel-trained U-Nets method, we applied it to differentiating layer thickness of the EOE model and the control using the testing data set.

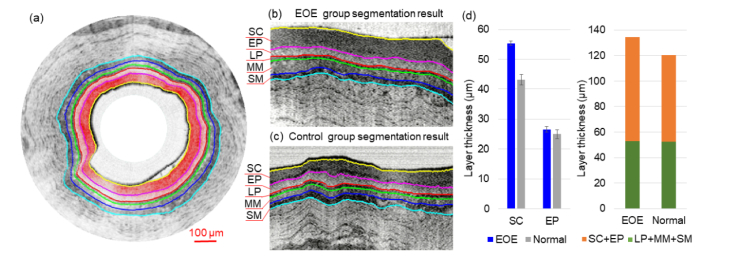
Figure 5(a) shows a representative OCT image overlaid with the segmented boundaries where the top-two layers (SC and EP) are color coded. We found that the parallel-trained U-Nets were able to clearly identify and segment the top five layers, as further shown in the zoomed-in regions for the EOE model (Fig. 5(b)) and the control (Fig. 5(c)). One unique value of segmentation is layer thickness quantification. Figure 5(d) shows the layers’ thicknesses and comparison between the EOE model and the control. The sum thickness of the top-five layers (averaged over the testing data set) was about 134 µm for the EOE group and 122 µm for the control group. When looking into individual layer, we noticed that (1) the sum thickness of the LP, SM and MM layers remained nearly unchanged, and (2) the SC and EP layers, particularly the SC layer, thickened in the EOE model, with a two-layer sum thickness of 82 µm, which was about 17% thicker than the two-layer sum thickness (70 µm) of the control group. This overall trend was clear and consistent across all images from the testing data set.

Fig. 5.

Layer segmentation and statistics analysis of EOE esophagus model and normal control. (a) Layer segmentations with color-coded SC and EP layers. (b) EOE group layer segmentation result in detail (c) Control group layer segmentation result in detail. (d) Layer thickness comparison between the EOE model and the control group. SC: stratum corneum, EP: epithelium, LP: lamina propria, MM: muscularis mucosae, SM: submucosa, MP: muscularis propria.

5. Discussion

In this paper, we demonstrated that parallel-trained U-Nets can robustly segment the layers in endoscopic OCT images with reduced layer topology disorders. The topology disorders appeared due to the limited training data set, geometric complexity, and low contrast. By combining the U-Nets trained separately with varying levels of Gaussian noise, the layer topology disorders in the prediction were reduced. The proposed scheme demonstrated superb performance mainly due to two reasons: (1) added Gaussian noises prevent overfitting when the original training data set is limited [50]; and (2) separate training of different networks effectively enforces each U-Net to learn shape priors for a given noise regime [51]. In this paper, two zero-mean Gaussian noises of different variances were used for training data set augmentation. This noise model might not be ideal, as the exact noise model for OCT images of biological tissue is very complex [56]. Nonetheless, this two-variance Gaussian model worked well and was computationally efficient for the parallel-trained deep neural networks scheme. The results show that our prediction accuracy is comparable to the latest published OCT segmentation methods based on deep learning, in which the networks were trained by much larger training data sets with less geometric complexity in the images [52–55]. In the current work, our training and testing data sets focused on OCT images with layered esophageal structures from guinea pig. For endoscopic OCT images collected from other disease models or human subjects with disrupted layer structures such as Barrett’s esophagus, the networks need to be re-trained and tested with relevant images.

We also investigated the computational cost for our new method. The computational time for analyzing one image of 2048 × 672 pixels was about 0.6 s on a Windows computer with a 4-core, 4.2-GHz CPU and a GPU with 4 GB memory with the codes implemented in MATLAB. The speed was about ten times faster than our previously reported graph-based methods [29]. The speed is expected to improve dramatically with a hardware upgrade and implementation in C + + , which would be very attractive for future real-time layer segmentation and tracking in various clinical applications.

Funding

National Institutes of Health (R01HL121788, R01CA200399, R01EY024655); the Wallace H. Coulter Foundation.

Disclosures

The authors declare that there are no conflicts of interest related to this article. The code will be available by emailing request to jhu.bme.bit@gmail.com.