Imaging mechanical properties of sub-micron ECM in live zebrafish using Brillouin microscopy

Abstract

In this work, we quantify the mechanical properties of the extra-cellular matrix (ECM) in live zebrafish using Brillouin microscopy. Optimization of the imaging conditions and parameters, combined with careful spectral analysis, allows us to resolve the thin ECM and distinguish its Brillouin frequency shift, a proxy for mechanical properties, from the surrounding tissue. High-resolution mechanical mapping further enables the direct measurement of the thickness of the ECM label-free and in-vivo. We find the ECM to be ~500 nm thick, and in very good agreement with electron microscopy quantification. Our results open the door for future studies that aim to investigate the role of ECM mechanics for zebrafish morphogenesis and axis elongation.

1. Introduction

At the heart of tissue morphogenesis lies a tight coordination between patterns in mechanical properties and signaling molecules that together determine cell fate and shape. Mechanical properties in cells and tissues are determined by the cytoskeleton and the extracellular matrix (ECM). Differences in ECM stiffness have been shown to be sufficient to determine cell fates [1]. Furthermore, in textbook examples of organ elongation, such as germband extension in Drosophila or neural plate extension in vertebrates, the mechanical anisotropies that instruct shape are known to be generated within the cell’s cytoskeleton. In comparison, how the mechanical properties of the ECM influence organ elongation is less well understood. Specifically challenging has been the study of the formation, elongation and branching morphogenesis of tubes. These morphological events are crucial for the development and function of organs such as the mammary ducts, the kidney tubules or lung alveoli [2]. Moreover, Crest et al. recently showed how patterning anisotropic resistance within the ECM can drive Drosophila follicle elongation [3]. Determining to what extent these mechanics are conserved in vertebrates would require ECM stiffness measurements in 3D.

Measuring these mechanical properties at high spatial resolution in live, three-dimensional tissues is challenging [4,5]. Among the approaches to measure mechanical properties, such as elasticity or viscosity, of live cells and tissues in the micrometer regime, Atomic Force Microscopy [6] (AFM) and micropipette aspiration [7] are most often used. However, both together with magnetic twisting cytometry [8], require the transmittance of contact forces which could perturb the sample, are restricted to cell surfaces only, and rely on mechanical models to extract local elasticity parameters. Optical approaches based on optical tweezers [9] measure viscoelastic properties from cellular deformations induced by potentially high power (up to 1 Watt) laser beams, which also limit their application to live tissues. Recently, methods have been put forward that involve the injection of micro-beads or droplets into 3D tissues or large cells to actively apply forces to them with optical tweezers or magnetic fields [10–12]. While such approaches provide elasticity information in an in situ context, the invasive introduction of foreign matter into live biological samples is likely to interfere with sensitive biological processes such as those encountered during embryo development and only provide limited spatial information.

Brillouin microscopy has recently emerged [13] as a new technique in the field of mechanobiology to explore the mechanics of living cells and tissues. Brillouin microscopy is an all-optical method that probes the visco-elastic properties of a material via light scattering. Thus, it achieves high spatial, i.e. near diffraction-limited resolution in 3D. Furthermore, it does not require artificial labelling nor external loading of the sample, thus making it a promising label-free and non-contact method to study mechanical properties of living tissues. Typically, the spontaneous Brillouin scattering signal is weak, which has in the past required the use of high laser powers and long acquisition times [14], which however are often incompatible with meaningful applications in live cell biology. In the last decade, the development of alternative spectrometer designs [13] based on the virtually-imaged phased array (VIPA) has greatly increased the spectral detection efficiency thus enabling mechanical characterization of biological tissue at safe power levels and opening up new avenues for in-vitro and in-vivo studies.

In recent years, Brillouin microscopy has enabled applications in cell biology [15–17], ophthalmology [18,19], as well as disease detection [20]. Among others, previous works have established that it is in principle feasible to measure cell mechanical properties with subcellular resolution [15,16]. Furthermore, Schlüßler et al. have used Brillouin microscopy in living zebrafish to show that the longitudinal modulus decreases during the process of spinal cord regeneration. Also, they have highlighted the importance of in-vivo measurements, as the mechanical properties are not conserved in excised tissues [21]. Palombo et al. have studied the contribution of different ECM from various fibrous connective tissue ex-vivo as well as the dependence of the Brillouin shift on the relative fiber alignment [22]. Lastly, Elsayad et al. showed how Brillouin microscopy could be used to map the viscoelastic signature of the ECM of Arabidopsis thaliana and their relation to the hydrostatic pressure of the cells within [23].

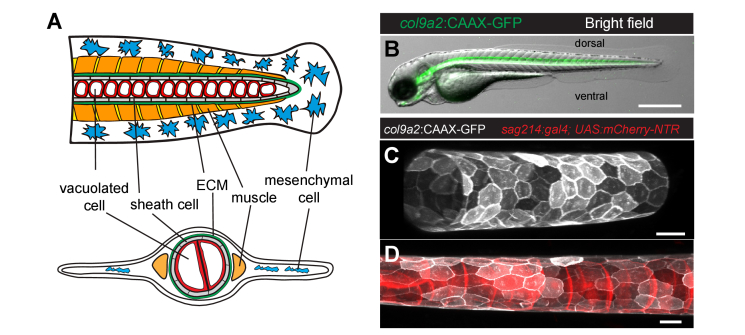
Here, we aim to quantify the stiffness of thin ECM layers in-vivo, thereby overcoming some of the limitations present in those previous studies. Specifically, we focus on a vertebrate tissue that undergoes elongation, the zebrafish notochord (Fig. 1(A,B)). The notochord is an embryonic midline structure common to all members of the phylum Chordata that serves as the axial skeleton of the embryo and contributes to the center of the intervertebral discs [24]. It provides structural support to the developing embryo and secretes inducible signals to several tissues. In zebrafish, the notochord is an almost perfect cylinder (Fig. 1(C)) formed by two cell types: sheath and vacuolated cells (Fig. 1(D)). Sheath cells are epithelial cells that form a tube-like structure and basally secrete ECM, while vacuolated cells are located apically in the lumen and provide hydrostatic pressure to straighten the antero-posterior body axis of the embryo [25,26]. The ECM is formed by three layers: a thin inner laminin-rich basement membrane layer [27], a middle layer of densely packed collagen fibers (especially rich in collagen type-II which is also a major constituent of cartilage [24]), and an outer layer in which extracellular fibers run perpendicularly to the middle layer [28]. The notochord’s cylindrical shape depends on an adequate balance of forces between the pressure generated by the vacuolated cells and the ECM withstanding it. In fact, if too many vacuolated cells die in the same embryo, for example in cavin1-knockout embryos, the resulting fish is unable to produce the necessary intra notochord pressure and will have a shorter antero-posterior axis [29]. On the other hand, a loss in ECM integrity (by for example inhibiting cross-linkers of collagen [30]) also leads to a shorter and kinked axis. Being able to measure the mechanical properties of ECM in-vivo during development could open the door to study its role in morphogenesis.

Fig. 1.

Characterization of the zebrafish notochord at 3 days post fertilization (dpf). (A) Schematic of the zebrafish tail at 3 dpf. Lateral (top) and transverse (bottom) views. (B) Bright field with overlapping fluorescence of a Tg(col9a2:GFPCaaX) zebrafish embryo at 3 dpf with GFP fluorescence from sheath cells. (C-D) Maximum intensity projection of the notochord in triple transgenic Tg(col9a2:GFPCaaX); SAGFF214A; Tg(UAS-E1b:NfsB-mCherry) zebrafish embryo at 3 dpf. Sheath cells (C) or simultaneously sheath and vacuolated cells (D) can be observed. Scale bars, 500 μm in (B), 20 μm in (C and D). ECM, extracellular matrix.

2. Experimental methods

Brillouin scattering

Brillouin microscopy uses visible or infrared monochromatic (laser) light to probe the mechanics of a material through light scattering from thermally induced, gigahertz-frequency acoustic modes, i.e. ‘phonons’. A typical spectrum from Brillouin scattering will consist of a symmetric pair of peaks – the Brillouin Stokes and anti-Stokes peaks – on each side of the elastically scattered (Rayleigh) input light, which can be many orders of magnitude more intense for non-transparent biological samples. This spectrum provides information about the local mechanical properties of the sample. Specifically, the change in frequency (GHz) of the Brillouin scattered light due to photon-phonon interactions is given by:

$${\upsilon }_B=\frac{2n}{{\lambda }_0}V\text{sin}\left(\raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right),$$ (1)

where n is the material refractive index within the scattering volume, λ₀ is the incident wavelength, θ is the angle between the incident and scattered light, and V is the medium’s sound velocity. The acoustic velocity V is then related to the complex longitudinal modulus, M, of which the real part, defined as the ratio of stress to strain in a uniaxial strain state, is given by M’ = ρV², where ρ is the density. The linewidth Δ (full-width at half-maximum, FWHM) of the Brillouin spectrum is related to the imaginary component of M, i.e. the loss modulus, which is a measure for viscosity, by M” = ρV²Δ/υ_B. Mapping frequency shifts and linewidth in space across a specimen will thus lead to a 3D resolved mechanical image.

While Eq. (1) requires knowledge of ρ and n, i.e. the density and refractive index to compute an absolute elastic modulus, previous studies have shown that the variation of the ratio ρ ∕ n² is fairly small for various biological samples [15,31], and can in fact be neglected in zebrafish larvae [21]. Therefore, the Brillouin shift itself is a good approximation for the longitudinal modulus. In general, the longitudinal modulus in biological material (e.g. tissues, cells, biopolymers) is several orders of magnitude higher than the traditional quasi-static Young’s modulus, due to the incompressibility of the material and the frequency dependence of the modulus. The relationship between the high-frequency longitudinal modulus probed by Brillouin scattering and the traditional quasi-static Young’s modulus which is often used in the field of mechanobiology has yet to be fully understood for biological tissues. In our study, we report the Brillouin shift as a metric of mechanical properties of the zebrafish embryos as it is the direct parameter measured in the experiment.

Imaging setup

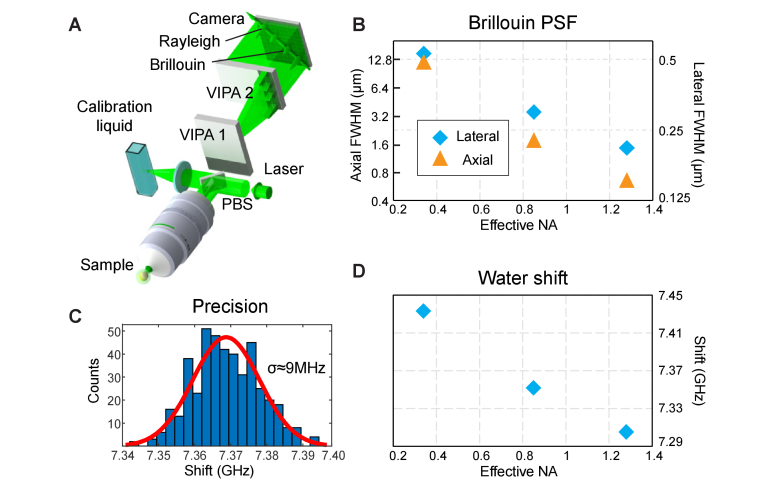
Our confocal Brillouin microscope (Fig. 2(A)) is conceptually based on a two-stage VIPA spectrometer design adapted from Scarcelli et. al. [32]. The laser source is a single-frequency mode, 532-nm continuous-wave (CW) laser (Torus, Laser Quantum), that is single-mode coupled to ensure a Gaussian beam profile. After collimation, the illumination light passes a half-wave plate (HWP) and polarized beam splitter (PBS), which serves to control the intensity of the light being sent to the microscope and calibration arm, respectively. Afterwards, the beam enters the microscope body (Zeiss Axiovert 200M) through a sideport and is then focused into the sample by an objective lens (either Zeiss Plan-Apochromat 40x, 1.0 NA with adjustable numerical aperture (NA) or Zeiss Plan-Apochromat 63x 1.4 NA). This allows us to vary the extent of the optical point-spread function (PSF) and therefore the volume over which the Brillouin scattered light is captured (Fig. 2(B)). The PSF was measured by scanning the focal volume across an oil/glass interface and fitting an Erf-function to the obtained edge response of the amplitude of the Brillouin spectrum of oil. This also determined the effective NA. The microscope is further equipped with a Piezo translation stage (P-545.3R8H, Physik Instrumente) that allows positioning of the sample with nanometer precision.

Fig. 2.

Brillouin microscope setup and characterization. (A) Schematic of the dual-stage VIPA based imaging setup. PBS – polarizing beamsplitter. (B) Experimentally recorded PSF width as a function of effective objective NA (linear-log scale). (C) Brillouin shift precision, obtained from 440 individual measurement of water under the same conditions used for in-vivo imaging (8.3 mW, 180 ms camera integration time). (D) Recorded Brillouin shift of water as a function of effective objective NA.

The Brillouin scattered light is collected in backscattering direction by the same objective and sent to the Brillouin spectrometer by coupling into a single-mode fiber, which also ensures confocality of the light detection. A quarter-wave plate (QWP) before the PBS ascertained that most of the backscattered light collected by the objective lens is delivered to the spectrometer. The Brillouin spectrometer consists of a two-stage virtually imaged phased array in cross-axis configuration, similar to a previous report [32], but with the addition of a Lyot stop [33] before the camera (iXon DU897, EMCCD camera; Andor Technology). The spectrometer features a free spectral range of 30 GHz, with a nominal spectral resolution of 460 MHz (finesse ~65). The VIPA cross-axis and Lyot stop configuration yield a high, ~65 dB elastic background suppression, sufficient for in-vivo imaging of the zebrafish embryo.

Our confocal Brillouin microscope furthermore offers the ability to perform simultaneous or sequential confocal fluorescence imaging, by employing the Brillouin or a separate CW 488nm laser, respectively. The fluorescence light is separated from the Brillouin light by a narrowband bandpass filter (Semrock LL01-532), and detected by a proper combination of focusing lens (f = 75 mm), pinhole (40 µm) and photomultiplier tube (Thorlabs PMT1001).

The acquired scattering spectra are analyzed in real time with a custom-written Labview program by fitting Lorentzian functions to obtain the position, width and intensity of the Brillouin peaks. In order to calibrate the frequency axis, a reference measurement of a water sample is acquired after every 50 measurements (~10s). The conversion between camera pixels and GHz is performed assuming a linear relationship between the distance of the Brillouin peaks on the camera ($d_p$) and the corresponding Brillouin shift ($s$): 𝑠 = (𝐹𝑆𝑅-𝛼∙d_p)/2, where the coefficient $\alpha$ (GHz/pixel) is measured from the calibration spectrum of water (shift of 7.46 GHz at room temperature). While such a calibration does not fully capture the non-linearity of the VIPA dispersion [34], we note that the systematic error remains small (<0.7%), as calculated by comparing the previously measured value of water to our measurement using methanol as a calibration material [13]. In the experiment, the water sample is placed in the transmitted beam path of the PBS (c.f. Figure 2(A)) that acts as a separate calibration arm, and mechanical shutters switch between the light-paths. A linearly interpolated value of the coefficient $\alpha$ is used for each of the 50 points in-between calibrations. This recalibration compensates for omnipresent frequency drifts in the sub-GHz regime of the laser, and allows to correct the drift of the spectral axis on the camera and to update the conversion coefficient $\alpha$ during the experiment. Altogether this ensures a high, ~9 MHz, precision in our frequency shift measurements under in-vivo experimental conditions (Fig. 2(C)). As the measured Brillouin frequency shift is slightly dependent on the NA, as previously shown [35], we performed a shift vs. NA calibration (Fig. 2(D)) to correct the raw Brillouin frequency shift measurements in our experiment.

Zebrafish experiments

For illustration purposes in Fig. 1, a triple transgenic Tg(col9a2:GFPCaaX)^pd1151; SAGFF214A [36]; Tg(UAS-E1b:NfsB-mCherry)^c264 [37] labelling sheath and vacuolated cells was used. To avoid potential toxicity of proteins absorbing at 532 nm, however, for all Brillouin and electron microscopy (EM) images we used a Tg(col9a2:GFPCaaX)^pd1151 zebrafish line [29] that labels sheath cells. In all experiments, 1-phenyl 2-thiourea (PTU) was added at 0.003% concentration at 10 hours post fertilization to avoid pigmentation. For Brillouin imaging, fish were immobilized and mounted with the right side of the fish next to the objective in 1% agarose with 0.003% PTU and 0.016% tricaine. After the Brillouin imaging experiments, the larvae were released from the agarose and behaved normally after cessation of sedation.

For EM imaging, samples were chemically fixed by immersing them in 2.5% glutaraldehyde and 4% paraformaldehyde in 0.1M PHEM buffer. Sections were post-stained with uranyl acetate for 5 minutes and with lead citrate for 2 minutes. The overall EM protocol is similar to Ref [38,39].

3. Results

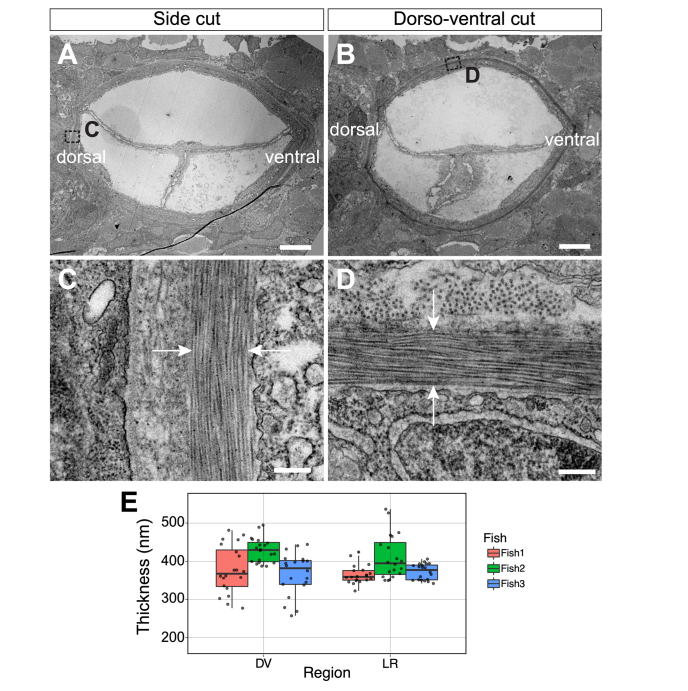
In order to assess the ultrastructure of the zebrafish ECM, we performed transmission electron microscopy (TEM) (JEOL 2100 at 120 kV) on 70 nm thick cross-sections collected from 200 to 250 µm before the end of the notochord (Fig. 3). We performed both side and dorso-ventral cuts to avoid compression artefacts due to the pressure of the diamond knife on the sample and measured the ECM thickness across 20 locations in each fish in the region of the notochord perpendicular to the cut (Fig. 3(A-D)). We observed that even with embryo-to-embryo variability the thickness of the medial ECM layer is consistent around the notochord in all the samples measured, with a dorso-ventral average of 390 ± 58 nm and a left-right average of 383 ± 43 nm (mean ± S.D.) (Fig. 3(E)).

Fig. 3.

(A-B) Low magnification TEM of transverse notochord after side (A) and dorso-ventral (B) cuts of a Tg(col9a2:GFPCaaX) zebrafish embryo at 3 dpf and ~200-250 µm anterior from the posterior end of the notochord. (C-D) High magnification TEM of transverse view ECM (between white arrows) after side (C) and dorso-ventral (D) cuts. (E) Quantification of ECM thickness in left-right (LR) and dorso-ventral (DV) regions of 3 embryos. Scale bars, 5 μm in (A and B) and 250 nm in (C and D).

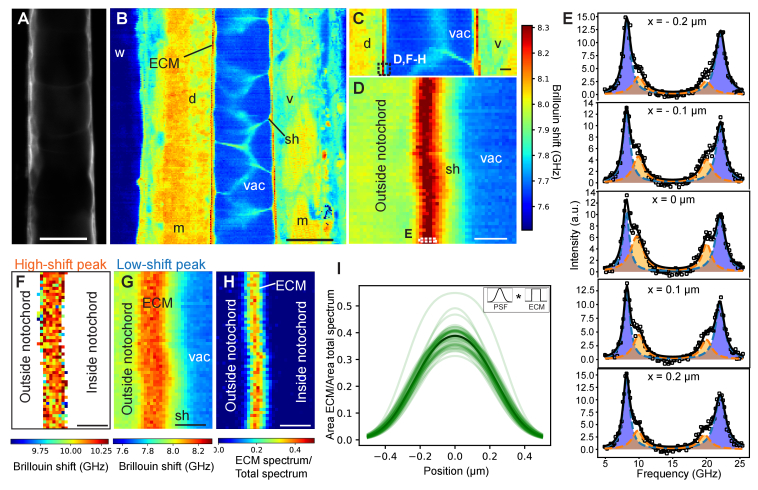
Next, we imaged the ECM in-vivo using Brillouin microscopy (Fig. 4). To do so, we first acquired an overview image with a 0.85 NA objective over a ~200x200 µm field-of-view (FOV). Plotting the Brillouin frequency shift, several tissue types including the notochord and the surrounding muscle segments can be identified, in agreement with previously reported work in the zebrafish larvae [21] (Fig. 4(B)). Moreover, here we are also able to differentiate the thin structure of the ECM that becomes indeed visible due to the expected high Brillouin shift of the ECM’s collagen fibers [22], even when spatially undersampling the image acquisition (1 µm step size compared to ~400 nm ECM thickness). We further confirmed that the ECM was indeed the source of the high Brillouin shift by comparing the Brillouin image with a subsequently recorded confocal fluorescence image at the same focal position, as the ECM secreting sheath cells where labelled with GFP (Fig. 4(A)). Based on these recordings, we performed further Brillouin imaging at high spatial sampling (100 nm step size) over a ~5x5 µm region (Fig. 4(C,D)) centred 250 µm anterior to the posterior end of the notochord, which indeed identified the ECM as a 400-500 nm thick region with relatively high Brillouin shift. We further observed that the Brillouin spectrum in the central region displayed a strong asymmetry towards higher Brillouin shift, indicative of a second spectral peak. By fitting the spectrum with the sum of two independent Lorentzian functions, we can indeed separate the ECM and other tissue components and their respective contribution to the overall Brillouin spectrum (Fig. 4(E)). Compared to previous work [40] which performed similar analysis by subtraction the cell’s buffer medium from the overall spectrum, our direct fitting approach also works in heterogeneous tissues and is less susceptible to (laser drift induced) artefacts. Thus, we find that careful spectral analysis allows distinguishing mechanical properties of different mechanical components even in a regime where the structure size approaches the optical resolution of the Brillouin microscope. In particular, we find the ECM to display a significantly higher shift of 10.08 ± 0.12 GHz (n = 4 fish, Fig. 4(F)) when averaged along the ECM and across individual fish, significantly higher than the surrounding cells (7.89 ± 0.03 GHz, n = 4 fish). Also, we note that inside the ECM the “low-shift” peak displayed a slight, ~270 MHz increase (8.16 ± 0.02 GHz, n = 4 fish) compared to regions outside the ECM (Fig. 4(G)). Since in this condition we don’t expect any major contribution to the spectrum from the surrounding cells, we attribute this to the observation of two acoustic modes (bulk and parallel-to-surface) within the ECM, consistent with recent experiments by Palombo et al. [22].

Fig. 4.

High-resolution mechanical imaging of zebrafish notochord ECM in-vivo. Brillouin shift maps were acquired in the middle between the left-right animal’s side (posterior, top; anterior, bottom). (A) Confocal image of sheath cells (GFP) as well as corresponding coarse-grained overview Brillouin image in (B) recorded with 1 µm step size at 3 days post fertilization (dpf) centred ~500 µm anterior from the posterior end of the notochord. (C) Brillouin shift map at 3 dpf centred ~250 µm from the posterior end (1 µm step size). (D) High-resolution Brillouin map of boxed area denoted in (C) with a step size of 0.1 µm. (E) Brillouin spectra recorded at discrete positions across the ECM (boxed area in (D)). Double-peak fitting distinguishes two Brillouin shifts of the ECM (orange and blue). Here, the fitting parameters were seeded from the parameters obtained from the fit to the pixel with highest ECM peak contribution and then subsequently constraining the ECM peak around ± 0.7 GHz when analyzing the surrounding pixels in order to prevent artefacts. We note that the observed variability in ECM peak shift is much lower than this fitting constraint. Brillouin shift map for the “high-shift” peak (F) and for the “low-shift” peak (G) – here pixels without a second peak are removed. A spatial map of the ratio of the spectral contributions is plotted in (H). (I) Line plots of ECM contribution to total spectrum across the ECM in (H), centred by their respective maximum. The represented curves are the result of the fitting with the convolution of the measured PSF (Gaussian) and ECM (box function - as shown in the inset). Black line denotes average of individual line plots. Brillouin images were obtained with a 0.85 NA objective and using 8.3 mW of laser power and 0.25 s of exposure time per pixel. w, water; m, muscle; sh, sheath cell; vac, vacuole; ECM, extracellular matrix; d, dorsal; v, ventral. Scale bars, 20 μm in (A,B), 5 μm in (C), 1 μm in (D,F,G,H).

In principle, it would be informative to calculate the longitudinal modulus or sound velocity of the ECM from the measured frequency shifts. This, however, would require in-situ measurements of refractive index n and/or density ρ, both of which are experimentally challenging in thick biological samples. Palombo et al. [22] have measured these properties in cartilage, which in terms of fiber composition is similar to the notochord ECM. However, both the fiber arrangement as well as hydration levels [24] are different, both of which could contribute to differences in ρ and n, which thus prevent rigorous quantitative conversions to elastic properties.

Furthermore, analyzing the Brillouin spectrum across the ECM allows us to characterize the ECM thickness in-vivo and in a label-free manner by plotting the ratio of the respective amplitudes of the Brillouin peaks (Fig. 4(H,I)). The amplitude of the ECM contribution to the overall spectrum is a convolution of the optical PSF and the physical size of the ECM (approximated by a box-like function). Since we have characterized the Brillouin PSF of our microscope (Fig. 2(B)), we can thus estimate the physical thickness of the ECM by deconvolution of the measured line response. This yielded an average ECM thickness of 488 ± 72 nm (n = 5 fish), in very good agreement with the EM image analysis (Fig. 3(E)). This shows that with diligent spectral analysis it is indeed possible to characterize the mechanical properties of thin ECM in living organisms.

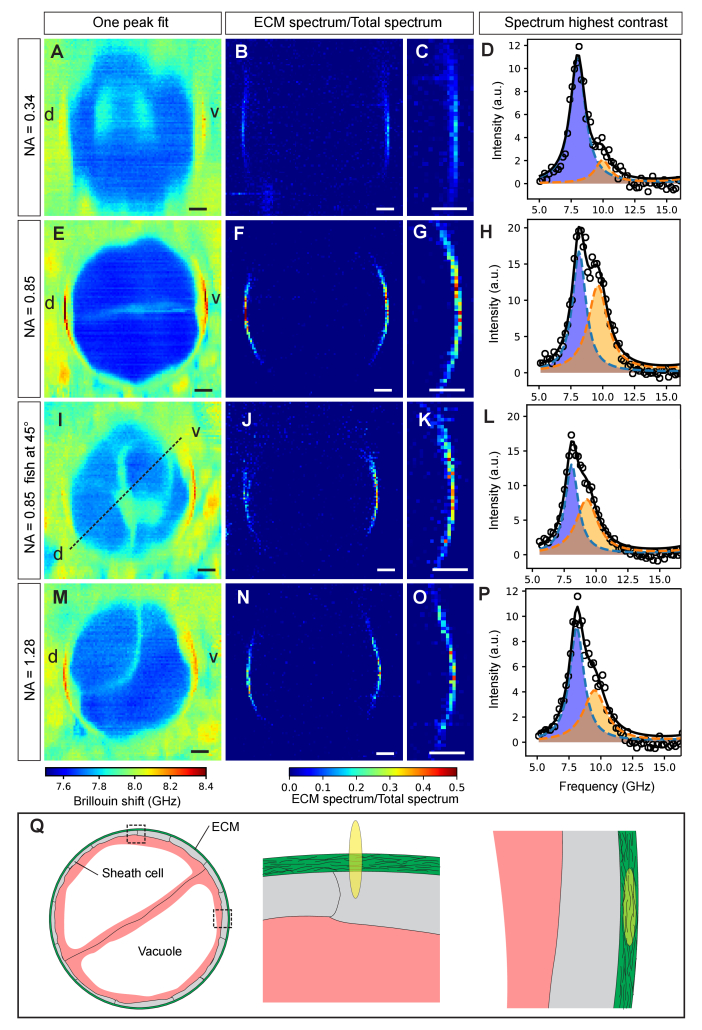
In order to assess the ECM also in a perpendicular, i.e. transverse plane, we also performed axial imaging of the zebrafish (Fig. 5). Here, we again observed that the Brillouin shift map obtained from a single-Lorentzian peak fit hardly revealed the ECM, and that the contribution of the ECM was only visible in a narrow, 10-20 µm region surrounding the dorso-ventral midline (Fig. 5). Also, the area of high shift (> 8.2 GHz) showed a strong dependence on the effective NA used for the Brillouin imaging (Fig. 5(A,E,I,M)). In particular, we found that a relatively medium NA of 0.85 yielded the best contrast. Overall, a double-peak fit analysis again led to a higher contrast of ECM when compared to the surrounding tissue (Fig. 5(B-D,F-H,J-L,N-P)). While the ECM is not visible on the lateral sides of the notochord, we note that this is not caused by differences of the ECM structure or composition in these areas (Fig. 3(C-E)). To further confirm the rotational symmetry of the ECM we also imaged a fish rotated by ~45 degrees around the anterior-posterior axis, and found similar contrast and Brillouin shift (Fig. 5(I-L)).

Fig. 5.

Axial cross-section of zebrafish notochord mechanics. The effect of objective NA on the Brillouin map and contrast of the ECM is shown for low (0.34), medium (0.85), medium (0.85) of 45-degree rotated sample and high (1.28) effective NA in A-D, E-H, I-L and M-P respectively. In traditional single-peak fit Brillouin shift maps the ECM displays poor visibility (A,E,I,M). Dual-peak analysis and plotting the spectral ratios does improve contrast (B,F,J,N). (C,G,K,O) Zoom-ins. (D,H,L,P) Spectra of pixels with the highest contrast in (C,G,K,O), respectively. (Q) Illustration showing the cross-section of the notochord (left) as well as the overlap of the PSF with the ECM when measuring on the lateral (middle) and dorso-ventral (right) side, respectively. Brillouin images were obtained using 8.3 mW of laser power and 0.25 s of exposure time per pixel. Step size: 0.5 µm. d, dorsal; v, ventral. Scale bars, 10 µm.

4. Discussion and outlook

In this work, we showed for the first time that Brillouin microscopy is capable of measuring the mechanical properties of the ECM in-vivo and with high spatial resolution inside a vertebrate organism. This was achieved by optimization of the imaging system and careful spectral analysis. In particular, diligent multi-peak spectral fitting allowed to clearly separate the mechanical properties of the ECM from the surrounding tissue, which so far was only demonstrated with Fabry-Perot based Brillouin spectrometers that typically feature much higher spectral resolution (at the expense of lower efficiency and imaging speed typically prohibitive of in-vivo measurements). Furthermore, our high-resolution mechanical measurements were able to determine the physical size of the ECM, in very good agreement with ultrastructural analysis based on EM images.

The fact that we have achieved the optimal ECM Brillouin signal contrast with the use of a medium NA objective is indeed interesting and warrants further discussion. There are likely different factors contributing to this effect: First, one has to consider the spatial overlap of the axially elongated PSF with the structure of the ECM (Fig. 5(Q)). Given the ECM thickness, geometry and radius, a slightly elongated PSF (~0.3 and 1.8 µm in x,y and z-direction, respectively for our 0.85 NA objective) has the optimal volumetric overlap and thus expected to yield the highest signal, i.e. backscattered Brillouin photons compared to high NA, low PSF volume, and therefore also highest signal-to-noise. Second, at higher NA, the higher variation in scattering angles could probe the two acoustic modes (bulk and parallel-to-surface) within the ECM differently, and thus lead to a different contrast in Fig. 5(B,F,N).

Another point worth discussing is the observation that in Fig. 5 the ECM is not visible on the lateral sides of the fish. We attribute this largely to the small PSF-ECM overlap in combination with the dependence of the Brillouin shift on the ECM collagen fibers’ orientation, as previously characterized [22]. In particular, when probing the fibers in an orthogonal (isostress) direction, as is the case on the lateral sides of the animal given our microscope arrangement, the spectral shift is expected to decrease by 10-15% [22].

Finally, one has also to consider the fact that if the axial extent of the PSF becomes smaller than the attenuation length of the acoustic modes, only an average mechanical property will be probed, i.e. one would not expect a double-peak in the Brillouin spectrum, and thus one could not distinguish and measure the properties of individual components in the probed focal volume [40]. Our results thus encourage a careful consideration of the spatial scales in Brillouin microscopy with respect to the biological structures of interest, especially when optimizing the relevant optical imaging parameters as well as the sample’s relative orientation.

Altogether, our results provide interesting avenues for future research, such as a more detailed and comprehensive mechanical characterization of the ECM in-vivo, in terms of the elasticity tensor. From a biological viewpoint, the ability to image mechanical differences inside tissues allows deciphering how tissue elasticity and viscosity contribute to development and organogenesis, where the interplay between mechanical properties, forces and signaling determines size and shape. Specifically, for the zebrafish notochord, a characterization of how ECM mechanics evolve in space and time could help understand how the balance of sheath and vacuolated cell activity contribute to its perfect cylindrical shape. Of particular interest would be to combine Brillouin microscopy with reported perturbations of sheath and vacuolar activity [41,42] to shed light on how axis elongation depends on the balance of forces between ECM mechanics and intratubular pressure. For pattern formation during tube morphogenesis in general, several major open questions could now be addressed in future experiments: Does the ECM have a universal role for tube elongation? If so, what are the necessary mechanical anisotropies to drive elongation? Our results are encouraging for future work which aims to answer these questions and validate how conserved the identified mechanism are across size scales and among different tubular structures. Thus, our work opens the door to performing such delicate mechanical measurements in space and time and might shed new light on the role of ECM stiffness for tube elongation in vertebrates.

Funding

European Molecular Biology Laboratory; Deutsche Forschungsgemeinschaft (DFG) (DI 2205/2-1); EMBO fellowship (ALTF 306-2018); COST Action CA16124 ‘BioBrillouin’.

Disclosures

The authors declare that there are no conflicts of interest related to this article.