Denoising of Joint Tracking Data by Kinect Sensors Using Clustered Gaussian Process Regression

Abstract

Using Kinect sensors to monitor and provide feedback to patients performing intervention or rehabilitation exercises is an upcoming trend in healthcare. However, the joint positions measured by the Kinect sensor are often unreliable, especially for joints that are occluded by other parts of the body. Motion capture (MOCAP) systems using multiple cameras from different view angles can accurately track marker positions on the patient. But such systems are costly and inconvenient to patients. In this work, we simultaneously capture the joint positions using both a Kinect sensor and a MOCAP system during a training stage and train a Gaussian Process regression model to map the noisy Kinect measurements to the more accurate MOCAP measurements. To deal with the inherent variations in limb lengths and body postures among different people, we further propose a joint standardization method, which translates the raw joint positions of different people into a standard coordinate, where the distance between each pair of adjacent joints is kept at a reference distance. Our experiments show that the denoised Kinect measurements by the proposed method are more accurate than several benchmark methods.

1 INTRODUCTION

Having patients performing prescribed exercises is an important clinical intervention for many health conditions such as chronic pain management, post-surgery rehab, and physical therapy after a sports injury. Using sensor-based systems to automatically track patients’ movements during their exercises and to provide instant feedback to the patients regarding the “correctness” of their movements holds great promise in reducing the cost for such interventions and increasing their effectiveness.

Generally, a gold standard for motion sensing is the so-called Motion Capture (MOCAP) system. It consists of multiple cameras positioned in a specially designed room to capture the 3D positions of reflective markers put on an actor’s clothing. Such system can track human action accurately but it is not a practical solution for clinical use since users have to wear tight suits with markers and such systems are very expensive [1]. Compared with the expensive motion capture system, the Kinect sensor by Microsoft (or similar sensors such as Realsense by Intel) is more affordable and convenient to most of the clinics or even in patients’ home. Kinect contains an RGB camera, an infrared sensor and infrared emitters which can be used to track joint positions in the 3D domain and perform motion analysis. However, because Kinect derives the 3D position from a single view point, the estimated positions of some joints are not accurate, when these joints are occluded or partially occluded. A number of works have been reported for stabilizing the joint tracking and improving pose reconstruction. Shum et al. proposed an optimized data driven method to solve posture reconstruction problem. Instead of using the MOCAP postures as ground truth to reconstruct movement directly, the authors first remove the similar postures by thresholding the sum of squared differences of body parts positions. Then they use Principle Component Analysis (PCA) to reduce dimensions of postures. Once Kinect captures a noisy posture, the system does back projection PCA basis to reconstruct postures. The reconstruction results heavily depend on the database [2]. Wei et al. formulated this problem into a Maximum A Posteriori (MAP) based on Kinect depth image. Although the proposed algorithm is multithreading and can be implemented on GPU to accelerate the speed, it needs to initialize the starting pose manually and it sometimes will be stuck at the local minimum which makes reconstruction fail [3]. Tripathy et al. use Kalman filter with a bone length constraint for the body segment between every two connected joints. This algorithm can make the joints trajectories smoother and preserve the joints’ kinematic characteristics. However, because the algorithm considers one segment at a time, it does not effectively exploit the relationship among multiple joints during a human action [4].

In our work, we first capture the joint movement traces of different people performing the same exercise by using a motion capture system and a Kinect V2 sensor simultaneously. Second, we convert each captured trace to a standardized domain which can eliminate the bias due to the different body sizes of the users. Then, we train a Gaussian process regression model that can predict the MOCAP measurement (consisting of 3D positions of all joints of interests) from the Kinect measurement at each sampling time. To reduce the computation time for prediction we cluster all the MOCAP samples and correspondingly the Kinect samples in the training set into a smaller number of groups, and form a reduced training dataset using the group centroids.

The rest of this paper is organized as follows. In Section 2, we describe the data acquisition and preprocessing. Then in section 3, we present our proposed clustered Gaussian process regression method. Experimental results to demonstrate the effectiveness of the proposed algorithm is shown in Section 4. We conclude this paper in Section 5

2 DATA CAPTURE and STANDARDIZATION

For the data recording, we used a motion capture system consisting of 14 cameras in NYU-X lab called “Motive” [5] to record the marker positions of a human actor. The markers are put at 25 positions in the upper body part as shown in Fig. 2. We also place a Kinect V2 sensor in front of the actor to record an RGB image and depth map of the actor, from which the joint positions are derived using the Kinect SDK 2.0. The MOCAP joint trace and the Kinect joint trace are captured simultaneously while the actor is performing a certain exercise. Both systems capture the joint positions at 30 frames/sec. Fig. 1 illustrates the data capture system set up.

Figure 2.

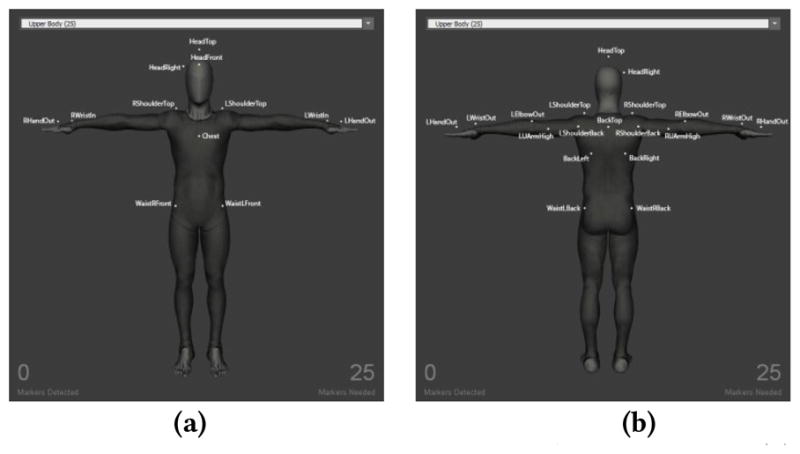
Motion capture system marker positions: (a) front upper body, (b) back upper body [5].

Figure 1.

Data capture system set up

2.1 Convert MOCAP Data to Kinect-Like Data

For capturing human motion by using the motion capture system, we need to put several reflective markers on the user body in the positions shown in Fig. 2. These positions differ from the joints captured by Kinect shown in Fig. 3. To deal with this problem, we map the joint positions captured by the MOCAP system into the Kinect-like joint positions by considering the human Anthropometry feature [6].

Figure 3.

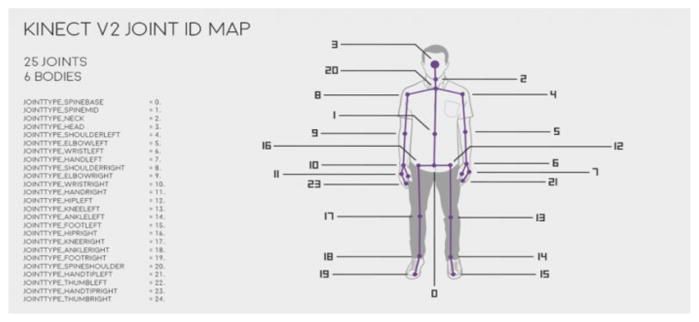
Kinect V2 Joint position [7].

2.2 Mapping the MOCAP and Kinect Data into a Standardized Domain

Since different users have different body sizes, it is hard to train a single regression model applicable for all people using raw training data. To deal with this problem, we mapped all the Kinect and MOCAP data into a standardized domain so that the distance between every two connected joints is fixed at some reference length. For time sample t, for joint i with position P_i(t) and its neighborhood joint j with position P_i(t), the standardized vector between joint i and joint j is

$${\mathit{Vec}}_{ij}(t)=\frac{P_i(t)-P_j(t)}{{\Vert P_i(t)-P_j(t)\Vert }_2}$$ (1)

If we set position of joint j as the reference position, then the mapped position of joint i will be

$$P_i^{\prime }(t)=P_j(t)+{\mathit{Vec}}_{ij}(t)\times L_{ij}$$ (2)

where L_ij is the reference length between joints i and j. In this paper, we set the spine base position captured by Kinect as a reference position first; then apply (1) to generate the standardized vector between spine base and spine middle, and then use (2) with the assigned segment length between spine base and spine middle to generate the standardized spine middle position. We then use this position as a new reference position to generate the spine shoulder position, and so on, until we reach the left wrist and right wrist, respectively. Fig. 4 shows the raw joint positions and the standardized ones for a sample pair of Kinect and MOCAP measurements. We argue that training the denoising algorithm in the standardized domain is more effective, as it will not be affected by the variations in the limb lengths of different people. It also aligns the MOCAP and Kinect data, although there is still a certain bias between the MOCAP and Kinect captured positions for the same joint. The bias for the same joint varies depending on the action pose. Because the bias is relatively small, compared to the limb length, we ignore such biases and consider the standardized MOCAP positions as the target denoised positions for the Kinect measurements in the standardized domain.

Figure 4.

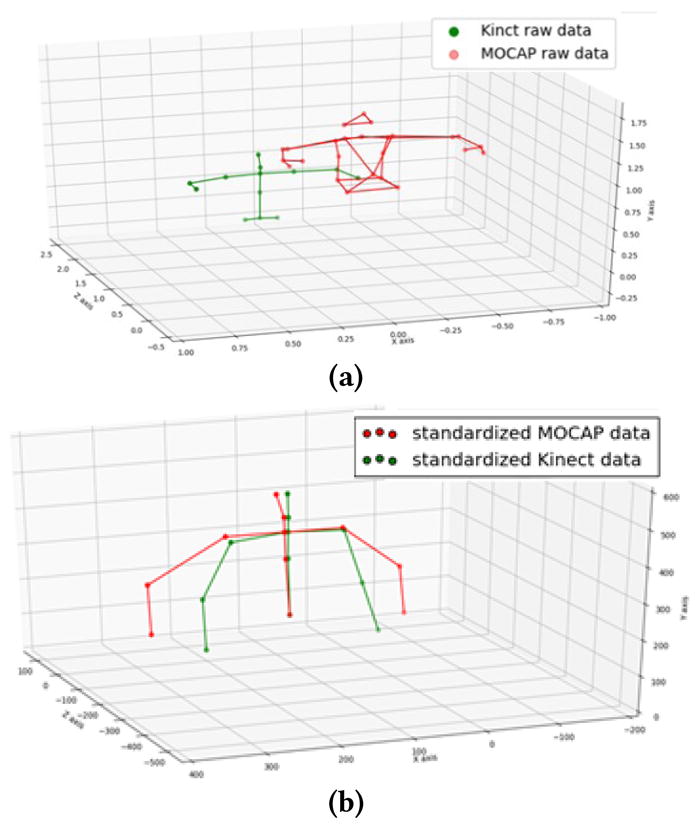
Sample upper body skeletons. (a) raw Kinect data and raw MOCAP data. (b) standardized Kinect data and MOCAP data.

Once the denoised positions are determined in the standardized domain, we can bring them back to the raw data domain for each person, by reversing the process using the length between every two connected joints for this person, which can be captured during a short training process in the beginning of an exercise. This inverse standardization process is necessary since we want to overlay the denoised joint positions on the RGB pictures of the user performing the exercise. Note that the joint position denoising and pose recognition (not considered in this paper) only need to be accomplished in the standardized domain.

3 PROPOSED METHOD

3.1 Denoising Using Gaussian Process Regression Model

As described in section 2, during the training stage, we capture joint traces of multiple volunteer actors performing different exercises with both a motion capture system and a Kinect sensor simultaneously. Let x_i = [x_i,1, x_i,2,....x_i,N]^T represent the vector that contains the i-th Kinect measurement sample, where x_i,n = [x_i,n,x, x_i,n,y, x_i,n,z]^T is the 3D position of the n-th joint being tracked, and N is the total number of joints. Similarly, let y_i = [y_i,1, y_i,2,....y_i,N]^T represent the vector that contains the i-th MOCAP measurement sample. We will regard y_i as the output corresponding to the input x_i. Note that each sample for an exercise contains the measured positions of all joints of an actor at a single sampling time. We model all possible output values y_t (in each joint and each of the x, y, z coordinate) corresponding to all possible input variables x_t (consisting of all joint positions at the same time) as a Gaussian Process [8]. Let X = [x₁, x₂, …, x_I]^T be the input data matrix (I by N) consisting all Kinect measurement samples, where I is the total number of the training samples and Y = [y₁, y₂, …, y_n]^T be the output data matrix (I by N). We train a Gaussian regression model using the training data and Y. Inspired by the example given in [8], we define the covariance between the i-th and j-th samples as:

$$K\left({\mathit{x}}_{\mathrm{i}},{\mathit{x}}_{\mathrm{j}}\right)={\theta }_1\text{exp}(-\frac{{\Vert {\mathit{x}}_{\mathit{i}}-{\mathit{x}}_{\mathit{j}}\Vert }_2^2}{2l_1^2})+{\theta }_2\text{exp}(-\frac{{\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert }_2^2}{2l_2^2})+{\sigma }_n^2{\delta }_{ij}$$ (3)

The first term is intended to model the general behavior of the input and output relationship, and the second term is used to describe the output variation among similar input samples. Note that l₁ and l₂ are length-scale, θ₁ and θ₂ are signal variance and the ${\mathrm{\sigma }}_{\mathrm{n}}^2$ is the output noise variance. The covariance matrix is defined as k(X, X) = [k(x_i, x_j)]. We learn the hyper-parameter (θ₁, θ₂, l₁, l₂, ${\sigma }_n^2$) in (3) by maximizing the log marginal likelihood [8]:

$$log(p(\mathit{Y}\mid \mathit{X}))=-\frac{1}{2}{\mathit{Y}}^T{\mathit{K}}^{-1}\mathit{Y}-\frac{1}{2}\mathit{log}\mid \mathit{K}\mid -\frac{n}{2}log(2\pi )$$ (4)

After obtaining the hyper-parameters from the training process, we can apply this model to predict the output y_* (unavailable MOCAP measurement) corresponding to any input (Kinect measurement) x_*, based on the conditional probability distribution

$$p({\mathit{y}}_{\ast }\mid {\mathit{x}}_{\ast },\mathit{X},\mathit{Y})~N({\mathit{\mu }}_{\ast },{\mathrm{\sigma }}_{\ast }^2)$$ (5)

where μ_* = K(x_*, X)K(X, X)⁻¹Y and ${\mathrm{\sigma }}_{\ast }^2=K({\mathit{x}}_{\ast },{\mathit{x}}_{\ast })-\mathit{K}(x_{\ast },\mathit{X})\mathit{K}{(\mathit{X},\mathit{X})}^{-1}\mathit{K}(\mathit{X},{\mathit{x}}_{\ast })$. In our denoising algorithm, we take the mean μ_* as the denoised joint positions corresponding to the Kinect measurement at any particular time x_*. Note that M = K(X, X)⁻¹Y is an I by N matrix, and can be pre-computed during the training process. At the denoising stage, we only need to compute K(x_*, X), which is a 1 by I vector, and the multiplication of K(x_*, X) and M.

3.2 Incorporating the Limb Length Constraint

The denoising algorithm described in Sec. 3.1 will be applied to standardized Kinect measurements, using the model parameters trained using the standardized Kinect and MOCAP data. Because the regression model does not consider the segment length explicitly, the resulting joint positions may still violate the predefined reference lengths for some segments. To enforce such length constrain, we apply the standardization method, described in Sec. 2.2, to the resulting joint positions, so that the distance between every two connected joints follows the reference length. Note that even though we standardize the joint positions sequentially, from spine base to wrist, because large measurement error usually only occurs in the elbow joints and wrist joints, the sequential standardized process does not suffer from serious error propagation issue.

3.3 Clustered Gaussian Processing

Once the GPR model is trained, the matrix M = K(X, X)⁻¹Y can be precomputed. During the denoising time, given each Kinect sample x_*, we only need to compute K(x_*, X) and the matrix multiplication of K(x_*, X) and M Therefore, the computsation time for denoising is linearly increasing with the number of the training samples. Our training data consists of around 22000 samples for each exercise, making the denoising process very slow. If we want to build a real-time intervention system, then we need to find some way to reduce the size of the training set. In sparse Gaussian Process model, a subset of training samples are chosen following some optimization criterion [9], or a set of pseudo input samples are derived along with other model parameters [10]. In our work, we apply the classical K-means method to separate the original motion capture data samples into Q different clusters. Based on the correspondence between the Kinect and MOCAP data, the Kinect data will also be separated into different clusters. Instead of utilizing all Kinect and motion capture training data in the training process, we use the centroids of all clusters ${\mathbf{X}}_{\text{center}}=[{\mathit{x}}_{\mathit{center}}^1,{\mathit{x}}_{\mathit{center}}^2,\dots ,{\mathit{x}}_{\mathit{center}}^Q]$ and ${\mathbf{Y}}_{\text{center}}=[{\mathit{y}}_{\mathit{center}}^1,{\mathit{y}}_{\mathit{center}}^2,\dots ,{\mathit{y}}_{\mathit{center}}^Q]$ to train the Gaussian process regression model. The performance using this approach under different cluster numbers is shown in Fig. 5. As expected, the regression error (for exercise 4 in Table 2) decreases as the cluster number increase. But we found that Q = 800 is a sweet spot, obtaining a local minimum in the regression error, and yet having a relatively short computation time. The computation time here is measured when the algorithm runs on a Windows 7 computer with Intel i5-4570 CPU and 16GB RAM.

Figure 5.

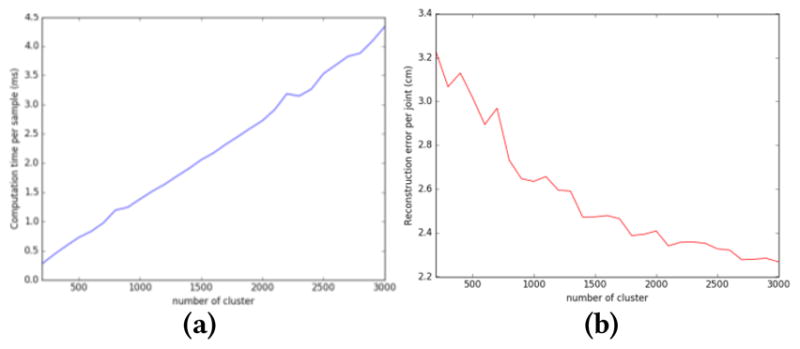
(a) Average computation time per time sample with different cluster number, (b) error per joint with different cluster number.

Table 2.

Average reconstruction error per joint by different methods (in unit of cm)

Name of dataset		Number of samples	Kinect data	Method of [12]	Proposed method
muscle-tightening deep breathing (Exercise 1)	All testing data	9018	10.22	4.91	1.46
	Unreliable testing data	3514	13.82	6.49	3.10
clasp and spread (Exercise 2)	All testing data	8043	9.21	8.18	1.76
	Unreliable testing data	2436	13.12	11.89	6.23
over-the-head-pumping (Exercise 3)	All testing data	8638	8.94	7.36	3.38
	Unreliable testing data	3222	13.57	11.54	7.45
push-down-pumping (Exercise 4)	All testing data	10051	8.38	6.27	2.70
	Unreliable testing data	4400	13.79	10.13	6.76

4 EXPERIMENTAL RESULTS

4.1 Training and Testing Data Sets

We have a total of 14 volunteers participating in training data collection. Each person performs a subset of the lymphatic exercise in a room set up with simultaneous recording by a Kinect sensor and the “Motive” MOCAP system described earlier. Each person records each exercise 3~7 time. The motion capture is done at 30 frames/sec. After deleting some damaged recordings, we have around 70 Kinect and MOCAP pairs of motion traces for each exercise. Each trace includes 400~900 samples. For detail, please check Table 1.

Table 1.

Training and testing data set

Name of the data set	Number of training samples	Number of testing samples
		Reliable data	unreliable data
muscle-tightening deep breathing (Exercise 1)	22252	5564	3514
clasp and spread (Exercise 2)	22425	5607	2436
over-the-head-pumping(Exercise 3)	21664	5416	3222
push-down-pumping(Exercise 4)	22600	5651	4400

The lymphatic exercise is developed by Co-Author Fu known as The Optimal Lymph Flow (TOLF) exercise. It contains a set of exercises that have been shown to improve lymph flow, lessen symptom severity, and reduce the risk for chronic breast-cancer-related lymphedema [11]. Currently, we only focused on a subset of the TOLF exercises that require the tracking of the upper body joints, specifically left/right shoulder, left/right elbow, left/right wrist and spine shoulder.

Given the measured joint positions at any time, we first convert them to the standardized positions following the description of Sec. 2.2. This is done for both the Kinect and MOCAP measurements. Because the joint movements are coordinated during an exercise, it is important to consider them together as a multi-variable input and multi-variable output. So our input sample and output sample are both 21 dimensional, consisting of the x-y-z coordinate of 7 joints (left shoulder, right shoulder, Left elbow, right elbow, left wrist, right wrist and spine shoulder). When training the Gaussian Process regression model, we only use the reliable samples (i.e. those samples where the Kinect measurements for all 7 joints are considered reliable). A joint measurement is considered reliable if its reliability score (see Sec. 4.2) is larger than a certain threshold; in this paper, we set the threshold as 0.7. Table 1 provides the details about the training and testing data for four different exercises.

4.2 Reliability

In order to train the GPR using only reliable data samples, we define the reliability for each joint position reported by the Kinect. Three factors are considered and are combined to set the overall reliability.

4.2.1 Kinematic Reliability

For the kinematic part, we consider the length between every joint and its neighboring joints. For example, spine shoulder connects with spine middle, neck, left shoulder and right shoulder. For each recording, we ask each user first pose in the “T-pose” as shown in Fig. 1(b). Then we capture the joint positions and calculate each connected joint pair’s length as a reference segment length for this person. We define the kinematic reliability of joint i in frame t as follows:

$$\mathrm{\Delta }{L}_{ij}(t)=\frac{\mathit{abs}({\Vert x_i(t)-x_j(t)\Vert }_2-\mathit{ref}\_{\mathit{len}}_{ij})}{\mathit{ref}\_{\mathit{len}}_{ij}}$$ (6)

$${\mathit{Rel}}_i^k(t)=1-\frac{{\sum }_{j\in N_i}\mathrm{\Delta }{L}_{ij}(t)}{\mathit{size}of{N}_i}$$ (7)

where x_i(t) denotes the positions of joint i in frame t, and N_i denotes the set of all neighboring joints for joint i.

4.2.2 Temporal Reliability

Through our experiment, we have found that Kinect only makes large measurement error when a joint is occluded, which usually happens over a short time period. When sampling at 30 frames/sec, the large error in a joint usually only appears in one frame and goes back to the relatively correct position in the next frame. Let x_i(t) denote the measured position of joint i at time t, we can define two distances:

$${\mathrm{d}}_1={\Vert {\mathrm{x}}_{\mathrm{i}}(\mathrm{t})-{\mathrm{x}}_{\mathrm{i}}(\mathrm{t}-2)\Vert }_2$$ (8)

$$d_2={\Vert {\mathit{x}}_i(t)-{\mathit{x}}_i(t-1)\Vert }_2$$ (9)

When x_i(t − 1) is erroneous, usually d₂ is large, but d₁ is small. Based on this observation, we define the temporal reliability as follows:

$${\mathit{Rel}}_i^{\mathit{tmp}}(t)=\{\begin{array}{rr}\hfill 1,& if(d_1<T)\hfill \\ \hfill max\left(\frac{1-4\ast (d_2-T)}{T},0\right),& if(d_1>T)\mathit{and}(d_2>T)\hfill \\ \hfill 1,& if(d_1>T)\mathit{and}(d_2<T)\hfill \end{array}$$ (10)

where T is a threshold, set to 0.03 in our experiment.

4.2.3 Reliability of Kinect tracking

Kinect provides the tracking state information for all the body joints to indicate whether a joint is tracked, not tracked, or inferred from other joints. We define the reliability of Kinect tracking as follows:

$${\mathit{Rel}}_i^{\mathit{trk}}(t)=\{\begin{array}{ll}\hfill 1,\hfill & if\mathit{tracked}\hfill \\ \hfill 0,\hfill & if\mathit{not}\mathit{tracked}\hfill \\ \hfill N/A,\hfill & if\mathit{inferred}\hfill \end{array}$$ (11)

4.2.4 Overall Reliability Score

We combine the previously defined three reliability terms to generate the overall reliability score as follows.

$$R_i(t)=\sum _{t-1}^{t}w(\tau )\ast min({\mathit{Rel}}_i^k(\tau ),{\mathit{Rel}}_i^{\mathit{tmp}}(\tau ),{\mathit{Rel}}_i^{\mathit{trk}}(\tau ))$$ (12)

The overall reliability score is a weighted average of the reliability for both current frame t and previous frame t − 1 We use weighting factors w(t) =0.7, and w(t − 1) =0.3.

4.3 Results and Discussion

In Fig. 6, we show the skeleton captured by Kinect originally and the denoised skeleton using the proposed method (consisting of four steps: standardization, clustered Gaussian Process regression, projection based on segment length constraint, inverse standardization). It is very clear to see that when the hands are close to the chest (Fig. 6(a)), the Kinect tracking result for the wrists can be very unreliable, even outside the human body. In Fig. 6(b), Kinect failed to accurately detect the positions of both elbows and wrists. The proposed method is able to correct these errors successfully.

Figure 6.

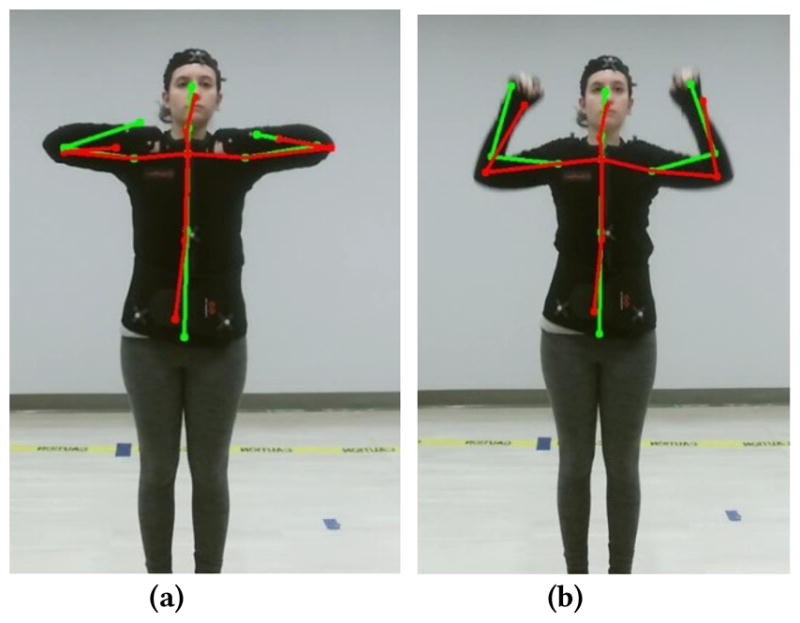
The raw captured skeleton by Kinect (green) and the denoised skeleton by the proposed method (red) overlaid on the RGB image. (a) push-down-pumping exercise; (b) over-the-head-pumping exercise.

As a benchmark for evaluation, we have implemented the method described in [12] and applied it to our standardized data. Table 2 compares the reconstruction error of the proposed method and the method of [12]. The reconstruction error is defined as the average Euclidean distance per joint between the converted MOCAP measured position (which we consider as the ground truth) and the denoised position from the Kinect data. We report the average error both over all test samples as well as the unreliable test samples. We can see that the proposed method provided more accurate joint position estimation than [12] method. Table 3 shows the reconstruction error in each joint. For the left and right shoulder, because they are never occluded and do not move much in the TOLF exercises, the reconstruction error is extremely small. On the other hand, the wrist joints have the largest error because when they are too close to the chest, Kinect has trouble separating it from the chest when observed from the front.

Table 3.

Reconstruction error (in unit of cm) for each joint: (a) Method present in [12]. (b) Proposed method

(a)
Name of the data set With [12]		Left shoulder	Right shoulder	Left elbow	Right elbow	Left wrist	Right wrist
muscle-tightening deep breathing (Exercise 1)	All testing data	1.98	2.40	5.42	6.10	5.94	7.63
	Unreliable testing data	2.60	2.53	6.54	6.48	6.15	7.79
clasp and spread (Exercise 2)	All testing data	4.62	6.75	7.64	9.13	9.77	11.15
	Unreliable testing data	6.50	8.08	8.59	9.82	13.65	13.41
over-the-head-pumping (Exercise 3)	All testing data	3.22	3.47	8.56	8.78	9.86	10.26
	Unreliable testing data	5.89	6.46	10.84	10.65	11.93	12.68
push-down-pumping (Exercise 4)	All testing data	1.92	1.84	6.32	8.38	11.38	8.74
	Unreliable testing data	2.49	3.01	5.74	8.49	12.76	9.78

(b)
Name of the data set With proposed method		Left shoulder	Right shoulder	Left elbow	Right elbow	Left wrist	Right wrist
muscle-tightening deep breathing (Exercise 1)	All testing data	0.14	0.14	1.57	2.01	2.14	2.78
	Unreliable testing data	0.21	0.21	3.77	3.19	2.41	3.40
clasp and spread (Exercise 2)	All testing data	0.13	0.13	1.95	1.94	3.08	3.33
	Unreliable testing data	0.17	0.17	4.38	4.14	7.40	7.75
over-the-head-pumping (Exercise 3)	All testing data	0.21	0.21	4.19	4.48	5.25	5.91
	Unreliable testing data	0.23	0.25	7.18	7.01	7.59	8.37
push-down-pumping (Exercise 4)	All testing data	0.18	0.18	2.68	2.76	5.08	5.33
	Unreliable testing data	0.25	0.44	3.81	4.21	7.77	7.59

In Fig. 7(a), we show the trace of the left wrist when an actor is doing the push-down-pumping exercise. In the middle of this exercise, the actor closes his hands in front of the chest. In this pose, the wrists are very close to the chest and the Kinect sensor has difficulty in telling the difference in the depth of the wrists and the chest. The estimated position of the wrists by the Kinect sensor is wrong as shown on the blue line. This self-occlusion causes the joint vibration in the Kinect detection result. In Fig. 7(b) we show the trace of the left elbow when an actor is doing the over-head-pumping exercise. In this exercise the elbow is not blocked by other body part, so the trajectory is relatively smooth, but the measured position by Kinect has a consistent bias from the “true” position. Compared with the raw Kinect data and denoising result of method [12], our proposed method can eliminate most of the errors in the Kinect measurement and make the trajectory smooth and close to the ground truth (the MOCAP data).

Figure 7.

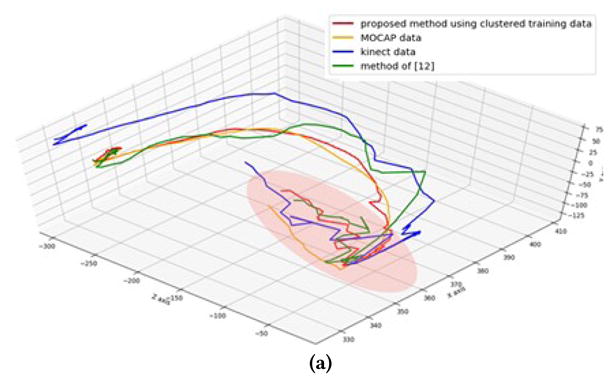
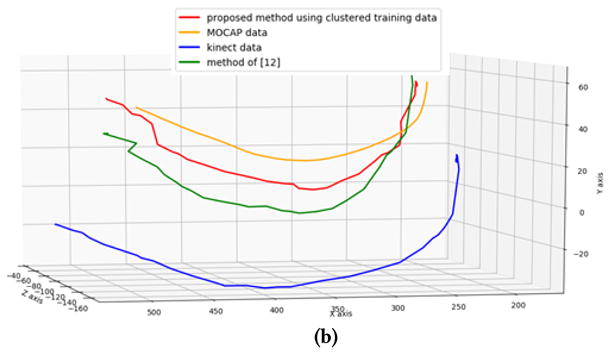
Trajectory of the joint during the exercise. (a) Trajectory of left wrist when doing the push-down-pumping exercise. (The red region is when the wrist close to the chest) (b) Trajectory of left elbow when doing the over-head-pumping exercise.

5 CONCLUSION

In this paper, we propose a novel approach for denoising the joint traces captured by a Kinect sensor. The core of our algorithm is the Gaussian Process regression model that can predict the MOCAP measurements (the target denoised data) from the Kinect measurements, learned from training data consisting of joint traces captured by both a Kinect sensor and a MOCAP system. To circumvent the difficulty caused by the high variance of the joint positions due to the variety of human body sizes, we map the measured joint positions into a standardized domain and learn the regression model in this domain. We further modify the denoised results by Gaussian process regression so that the length of each segment between connected joints is preserved. To reduce the computation with the regression model, we cluster all the training samples into a small number of groups and use the cluster centroids as the reduced training set. Our experiments show that the proposed method can effectively correct the errors in Kinect measurements due to self-occlusion, and performs better than a benchmark system, which also makes use of the correspondence between the MOCAP and Kinect measurements.