Using diffusion anisotropy to study cerebral cortical gray matter development

Abstract

Diffusion-weighted magnetic resonance imaging (diffusion MRI) is being used to characterize morphological development of cells within developing cerebral cortical gray matter. Abnormal morphology is a shared characteristic of cerebral cortical neurons for many neurodevelopmental disorders, and therefore diffusion MRI is potentially of high value for monitoring growth-related anatomical changes of relevance to brain function. Here, the theoretical framework for analyzing diffusion MRI data is summarized. An overview of quantitative methods for validating the interpretations of diffusion MRI data using light microscopy is then presented. These theoretical modeling and validation methods have been used to precisely characterize changes in water diffusion anisotropy with development in the context of several animal model systems. Further, in diffusion MRI studies of several preclinical models of neurodevelopmental disorders, the ability is demonstrated of diffusion MRI to detect abnormal morphological neural development. These animal model studies are reviewed along with recent initial efforts to translate the findings into an approach for studies of human subjects. This body of data indicates that diffusion MRI has the requisite sensitivity to detect abnormal cellular development in the context of several models of neurodevelopmental disorders, and therefore may provide a new strategy for detecting abnormalities in early stages of brain development in humans.

Graphical abstract

Introduction

Joe Ackerman’s drive to understand the biophysical mechanisms that influence magnetic resonance signals measured in biological tissue profoundly shaped the body of data reviewed here. Joe designed many influential experiments that revealed how water diffusion, as encoded in diffusion-weighted magnetic resonance imaging (diffusion MRI) can be used to monitor brain physiology and anatomy on the cellular level. Many of these experiments were performed under his direction at the Biomedical MR Laboratory (BMRL) at Washington University. In the period from 2000-2005, I was fortunate to be a member of the BMRL and join the efforts of several researchers who were contributing to the efforts to develop a new way to non-invasively characterize anatomical development of cells within the cerebral cortex. This method utilized diffusion MRI in novel way. Rather than focusing on brain white matter structures, which at the time were known to induce anisotropy in water diffusion in ways that reflect their coherent organization as well as their pathophysiological characteristics in neurological disorders [1-3], the phenomenon being studied was water diffusion anisotropy within early developing cerebral cortical gray matter. Already by 1997, water diffusion anisotropy within the immature cerebral cortex had been reported in studies of cats [4] and pigs [5], and shortly thereafter Mori and co-workers characterized this phenomenon in the developing mouse brain [6]. Within the BMRL at this time, Jeff Neil was spearheading an effort to systematically study within neonatal humans brain development using diffusion MRI [7-9], with the objective to establish relationships between cellular-morphological development abnormalities revealed by this technique and the risk for subsequent cognitive and behavioral disorders in prematurely delivered human infants. Joe Ackerman integrated with this focused clinical objective a team of talented scientists in statistical physics, data analysis, biomechanics, cell biology neuroscience, neurophysiology, and small-animal MRI. Several of these individuals also share perspectives in this special issue of JMR.

This review summarizes contributions made in preclinical studies of the analysis of water diffusion anisotropy within developing cerebral cortical gray matter. Studies of animal model systems have facilitated the development of theoretical modeling strategies for analyzing the diffusion-attenuated MRI signal in gray matter as well as independent experimental methods for validating the interpretations of biophysical models. Further, they have enabled precise characterization of the normal trajectory of diffusion anisotropy changes with cortical maturation, and they have led to the generation of a series of animal model systems for assessing the value of diffusion MRI in identifying abnormal development. Joe Ackerman has facilitated this work through his mentorship individuals who subsequently positively affected the growth of this field and through direct contributions.

Diffusion within cerebral cortical gray matter: Dispersion in the orientation distribution of axons and dendrites.

The cerebral cortex is the 1-5 mm-thick outer-most sheet of tissue in the mammalian brain. This is where synaptic connections reside that integrate sensory input, facilitate planning of responses, and instigate motor activities. A major focus for most diffusion MRI studies is the development, pathology, or anatomical organization of brain white matter. There are fundamental differences in the biological processes that influence water diffusion anisotropy in cerebral white matter compared to other brain structures. In white matter, axon fiber bundles that are comparable in size (length as well as cross-sectional area) to an MRI voxel restrict water diffusion perpendicular to the bundle more than in the direction parallel to the bundle. Degradation of the fiber bundle structure secondary to myelin or axonal injury, or disease, can result in reduced anisotropy in water diffusion [10, 11]. Maturation of fiber bundles involves axonal organization and myelination, which are process associated with increases in water diffusion anisotropy [6, 8, 12]. Under each of these conditions, white matter exhibiting highly anisotropic water diffusion is associated with mature, healthy, often myelinated axons consisting primarily of parallel structures.

In addition to cerebral white matter, anisotropy in water diffusion can also be observed in gray matter. In particular, properties of water diffusion reflect cellular morphology in gray matter structures with laminar organization, such as the cerebral cortex and hippocampus (see [13] for a recent review). In the mature cerebral cortex, the majority of tissue volume consists of cylindrical cell processes such as axons and dendrites. Bourgeois and Rakic have estimated that approximately 60% of the cerebral cortex to be occupied by the “neuropil” at maturity [14]. Thus, on a microscopic cellular size scale, water diffusion is expected to be anisotropic. However, as a consequence of the broad distribution of cellular process orientations, water diffusion averaged over a volume of a standard diffusion MRI voxel in most gray matter stuctures exhibits very little directional dependence compared to most white matter structures. Water diffusion in the mature cerebral cortex is locally anisotropic but macroscopically nearly (but not completely [15, 16]) isotropic. The immature cerebral cortex differs from the mature cortex in this regard. Immediately following migration of pyramidal neurons from ventricular and subventricular zones to the cortical plate, such as half way through gestation in humans or non-human primates, or the first days of life in mice and rats, most synaptic connections have not yet formed, and the morphology of neurons is simple (Figure 1). Cellular processes within the cortical plate are nearly uniformly radially oriented, and correspondingly, water diffusion is as anisotropic as it is in mature white matter fiber bundles (e.g., see Figure 4). In 2002, McKinstry and co-workers posited that water diffusion anisotropy changes associated with maturation reflect morphological changes in neurons and radial glia [9]. Healthy development is associated with reductions in water diffusion anisotropy, and as has been more explicitly refined since then, water diffusion anisotropy decreases with increasing dispersion in axonal and dendritic cellular process orientations (Figure 1) [17]. It is important to precisely characterize the relationship between biological structures and cortical diffusion anisotropy because morphological development of neurons is reported to be abnormal in several neurodevelopmental disorders. If this abnormal morphology affects the trajectory of cortical FA changes with development, then the analysis of cortical FA could be of value for identifying individuals affected by neurodevelopmental disorders. This review summarizes work performed with several animal models of disease, in addition to studies of human subjects, that characterize the link between abnormal neural morphology and diffusion MRI studies focused on the developing cerebral cortex.

Figure 1.

Morphological development of cerebral cortical pyramidal neurons with development. Traces of dendritic arbors for neonatal rat neocortical pyramidal neurons were generated by Furtak and co-workers [80] and made available through the NeuroMorpho database [81] (http://www.neuromorpho.org). Neurons from rats of ages ranging from postnatal day 1 (P1) through P14 are shown. Apical dendrites are red, basal dendrites are blue, and cell bodies are represented as black spheres. The orientation distribution of dendritic processes, schematized at right, broaden with age as dendritic arbors gain complexity.

Figure 4.

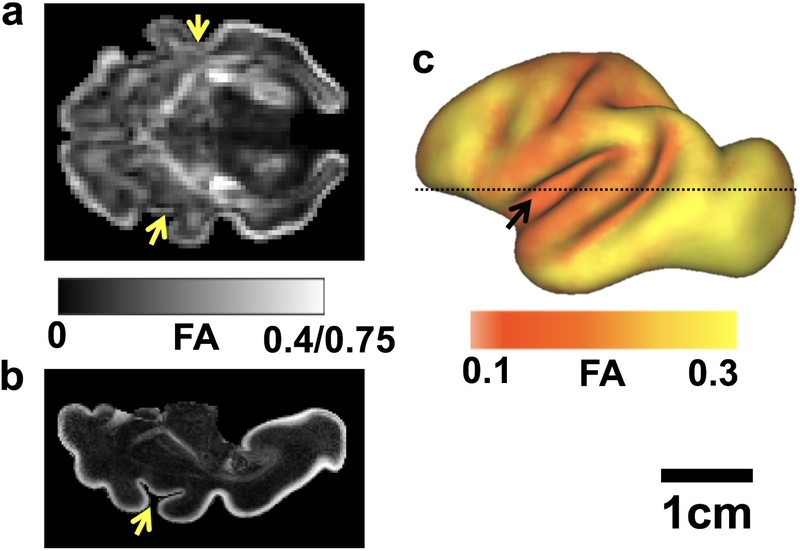
Regional patterns of cerebral cortical diffusion anisotropy in the fetal rhesus macaque brain. (a-b) Axial views of FA maps are shown for G110 brains (a) in utero and (b) post mortem. The FA scale ranges from 0 to 0.4 for the in utero parameter map, and from 0 to 0.75 in the post mortem parameter map. Yellow arrowheads indicate the location of the insular cortex, near the source of the transverse neurogenic gradient, which is characterized by relatively low diffusion anisotropy, for orientation relative to the surface map in (c). FA values were projected onto models of the G110 cerebral cortical surface from multiple brains, and averaged onto a common surface [41]. (c) Lateral view of the G110 average surface. Black arrowhead indicates the location of the insula, and the dashed line is the approximate location of the axial planes shown in (a-b).

Biophysical Modeling of Water Diffusion in the Developing Cerebral Cortex

A common approach has been adopted for quantitative modeling of the influence of dispersion in the orientations of axon, dendrites, and other cylindrical cellular processes within a voxel [18-21]. This framework relies on three fundamental assumptions:

1. Water molecules reside within one of two environments. The “cylindrical” environment consists of cellular processes such as axons and dendrites and is characterized by the volume fraction v. The “extra-cylindrical” environment consists of non-cylindrical structures such as cell bodies, and occupies the remaining 1- v volume fraction of the voxel.

2. Water exchange between the two environments during the diffusion inter-pulse delay, Δ, is negligible.

3. The Gaussian phase approximation is made within each environment.

The consequences of the first two assumptions are that the dependence of the signal intensity S(b) on diffusion weighting b, relative to the reference intensity S(0) can be written as the sum of two terms

$$\mathit{S}(\mathit{b})∕\mathit{S}(0)=\mathit{v}{\mathit{S}}_{\mathit{c}}(\mathit{b})+(1-\mathit{v}){\mathit{S}}_{\mathit{e}}(\mathit{b})$$ (1)

in which S_c(b) and S_e(b) correspond to the signal intensity components arising from the cylindrical and extracylindrical compartments, respectively, and b is the standard diffusion weighting term defined in diffusion measurements using pulsed-field gradient magnetic resonance techniques [22]. If water diffusion is assumed to be isotropic within the extracylindrical compartment, diffusion is characterized by the extracylindrical apparent diffusion coefficient (ADC_e) according to the expression

$${\mathit{S}}_{\mathit{e}}(\mathit{b})=\text{exp}\left(-\mathit{b}\cdot {\mathit{ADC}}_{\mathit{e}}\right).$$ (2)

To account for anisotropic diffusion within the extracylindrical environment, the scalar-valued ADC_e can be replaced with a diffusion tensor D [23, 24], as in [25].

Mathematical expressions for the cylindrical term S_c(b) as a function of diffusion weighting oriented along an arbitrary diffusion sensitization direction, are first provided for the two limiting cases of extreme anisotropy of cellular process orientation, and perfectly isotropic orientation distribution of cellular processes. Under conditions of extreme anisotropy, all cylindrical cellular process are oriented parallel to each other, and α is the angle between this common orientation and the direction of the applied diffusion-sensitizing magnetic field gradients. Local diffusion anisotropy within the cylindrical structures is represented as a difference between the (larger) diffusion coefficient characterizing displacements parallel to the cellular process axis (D_ax) and the (smaller) diffusion coefficient characterizing displacements perpendicular to the cellular process axis, oriented radially in the local frame (D_rad). As a consequence of the Gaussian phase approximation

$${\mathit{S}}_{\mathit{c}}(\mathit{b})=\text{exp}(-\mathit{b}\cdot ({\mathit{D}}_{\mathit{ax}}{\mathit{cos}}^2\alpha +{\mathit{D}}_{\mathit{rad}}{\mathit{sin}}^2\alpha )).$$ (3)

In order to account for heterogeneity in the orientations of different axon, dendrite, or other cellular processes, the contributions of all cylinder orientations are integrated over the orientation distribution. For the extreme case of a uniform cylinder orientation distribution, in which all cylinder orientations are equally probable, the distribution of angles α, f(α), equals sin(α)/2. As detailed in [26, 27],

$$\begin{gathered} {\mathit{S}}_{\mathit{c}}(\mathit{b})={\int }_0^{\pi }\mathit{sin}(\alpha )∕2\text{exp}\left(-\mathit{b}\cdot ({\mathit{D}}_{\mathit{ax}}{\mathit{cos}}^2\alpha +{\mathit{D}}_{\mathit{rad}}{\mathit{sin}}^2\alpha )\right)\mathit{d}\alpha \\ =\text{exp}(-\mathit{b}\cdot {\mathit{D}}_{\mathit{rad}})\sqrt{\frac{\pi }{4\mathit{b}\cdot ({\mathit{D}}_{\mathit{ax}}-{\mathit{D}}_{\mathit{rad}})}}\Phi \left(\sqrt{({\mathit{D}}_{\mathit{ax}}-{\mathit{D}}_{\mathit{rad}})}\right) \end{gathered}$$ (4)

in which Φ(χ) is the error function of χ. In a diffusion-weighted magnetic resonance spectroscopy study of the adult rat brain, expression [4] was used to analyze diffusion of N-acetylaspartate (NAA) [28]. This endogenous molecule is present in high concentrations in neurons, and therefore provides an opportunity to examine a situation in which v ≈ 1, and under these conditions, remarkable agreement between Eq. [4] was observed with the experimental data.

To more generally account for cylinder orientation distributions that span the range from extreme anisotropy to isotropic, it is useful to consider the orientation distribution function (ODF) expressed as a function of the polar angles θ and ϕ, f(θ, ϕ). The expression analogous to Eq. [4], but for a general ODF is [29]

$${\mathit{S}}_{\mathit{c}}(\mathit{b})={\int }_0^{2\pi }{\int }_0^{\pi }f(\theta ,\varphi )\text{exp}\left(-\mathit{b}\cdot ({\mathit{D}}_{\mathit{ax}}{\mathit{cos}}^2\alpha +{\mathit{D}}_{\mathit{rad}}{\mathit{sin}}^2\alpha )\right)\mathit{sin}\theta \mathit{d}\theta \mathit{d}\varphi .$$ (5)

Thus, the analysis of dispersion in axon and dendrite orientations involves characterizing the function f(θ, ϕ). One approach is to approximate f(θ, ϕ) as a truncated spherical harmonic expansion [20, 25, 29]. A challenge encountered with numerical estimation of f(θ, ϕ) using a spherical harmonic expansion is that a high-order expansion is needed to precisely approximate a narrow distribution of orientations, such as in white matter fibers, or the early-developing cerebral cortex. As a result, a large number of adjustable parameters are needed, which has the disadvantage of introducing instability in model parameter estimation. To overcome this issue, one approach has been to model f(θ, ϕ) as a Watson [21, 30] (or Bingham [31]) distribution, a strategy adopted in the popular neurite orientation dispersion and density imaging (NODDI) method of data analysis. In these cases, the width of the fiber orientation distribution is reflected as model distribution parameters, such as the Watson distribution concentration parameter κ [32] which is high for a narrow distribution of fibers (e.g. immature cerebral cortex) and low for a broad distribution (mature cortex). Drawbacks to this approach, however, are that the minimum number of diffusion encodings necessary for its use have not been characterized, and nonlinear optimization, or other specialized computational methods, are necessary for its implementation. In the context of the model assumptions, the issue of parameter estimation has specific challenges associated with it [33].

Another approach that facilitates interpretation of water diffusion anisotropy in terms of the axon and dendrite ODF, that avoids the difficulties posed by analytical modeling and closely parallels the standard diffusion tensor analysis [23, 24], results from expanding Eq. [5] as a Taylor series with respect to b [34]. The term that is linear in b contains the diffusion tensor, D, and the second moment of f(θ, ϕ), which is the scatter matrix T. The standard way to quantify anisotropy in D is to express variation in its eigenvalues through the fractional anisotropy (FA) [35], which ranges from 0 (isotropic diffusion) to 1 (extreme anisotropy). In a similar manner, it is possible to compute eigenvalues of T and to express anisotropy in the ODF’s scatter matrix as FA_T. This analysis leads to a monotonic relationship between FA and FA_T, which is a result that facilitates an interpretation of FA in terms of anatomical properties of the cerebral cortex; namely, the neuropil volume fraction, the local diffusion coefficient magnitudes, and anisotropy in the axon/dendrite orientation distribution. In the following sections, it is assumed that v, D_ax, and D_rad do not change with age, and that changes in cortical FA with development are caused by changes in FA_T. Experimental support of this interpretation can be gleaned from the data to be reviewed, however further direct experimental investigation of these assumptions would clearly be of value.

Validation of the Interpretation of FA Changes in Terms of Neuron Morphological Development Using Independent Experimental Methods

In order to validate interpretations of cortical FA based on the intricate biophysical modeling reviewed in the previous section, quantitative comparisons to results from independent experimental methods are needed. A typical voxel volume in a diffusion MRI experiment conducted on a human brain is on the order of 8 microliters (2×2×2 mm³). Therefore, MRI measurement of water diffusion anisotropy provides a quantitative aggregate measure of cellular complexity that reflects the structural characteristics of thousands of neurons. Morphological complexity of large populations of cells can be difficult to quantify using traditional light microscopy, because standard methods involve manually tracing neuronal processes, which presents challenges for use as a practical validation strategy. Microscopy-based validation studies have thus incorporated novel methods for tracing, as well as statistical methods for analyzing images that circumvent the need to perform extensive tracing operations.

Explicit orientation distribution determinations using cell tracing data

One early study in which the orientation distribution of myelinated axons was directly measured in gray matter of the superior colliculus, as well as the white matter of the corpus callosum, was performed by Leergaard and co-workers [36]. Diffusion MRI measurements were performed on post mortem rat brain tissue, and subsequently, using the same tissue, a stereological approach was taken to estimate the orientation distribution of myelinated axons. Within regions that matched the in-plane resolution of the MRI data set, myelinated axons were manually traced, and the orientation distribution of fibers was compared to the fiber orientation distribution calculated from the diffusion MRI data. The magnitude and direction of anisotropy in the orientation distribution closely matched the orientation distribution predicted from the diffusion MRI data. An automated approach for analyzing cell tracings in terms of cell process orientation distribution functions is illustrated in Figure 2a-c. Each segment of 10 μm in length (the distance that approximately matches the root-mean-squared displacement in a diffusion MRI experiment) is fitted to a line, and the orientation distribution of resulting lines can be estimated. Such an analysis has been performed for neuron traces that have been deposited in the NeuroMorpho database [37].

Figure 2.

Light microscopy methods for validating cellular process orientation distributions inferred through diffusion MRI measurements of diffusion anisotropy. (a-c) Cell tracing methods enable explicit determination of cell process orientation distributions. (a) Tracings of a P4 (upper) and P14 (lower) rat pyramidal neuron are illustrated as in Figure 1. (b) Each dendrite branch is separated into 25 μm sections, and approximated as a cylinder. Cylinders are translated to a common origin in (c) to illustrate the difference in dendrite orientation distribution width between the two different neurons. (d) 3D structure tensor calculations reveal anisotropy in cell process orientation along three orthogonal axes. (e) A 3D montage of hippocampal gray matter (CA1) and neighboring white matter (alveus, inferior longitudinal fasciculus (ILF)), stained with DiI, is shown in the lower panel, as described in [39]. The primary orientations of cell processes are indicated with arrows that are color-coded according to direction following the color scale used for (d). In (d), 3D structure tensors are overlaid on the 3D histological images, indicating the direction and magnitude of diffusion anisotopy expected for each of the tissue sub-regions.

A subsequent post mortem diffusion MRI and light microscopy study extended the tracing approach to a 3D strategy that focused on early developing cerebral cortical gray matter [34]. Following diffusion MRI procedures, cerebral cortical tissue from postnatal day 13 (P13) and P31 ferret brains was stained using the rapid Golgi method, and examined with confocal microscopy. The through-plane resolution of the confocal images was sufficiently high to generate 3D traces of the Golgi-stained neurons. An automated tracing method was used to analyze 3D image stacks, and obtain traces of multiple stained neurons throughout tissue volumes comparable to a diffusion MRI voxel size. Similarity in fractional anisotropy of the axon/dendrite orientation distribution scatter matrix (FA_T) and water diffusion FA confirmed the theoretical predictions relating these two parameters.

Other image analysis methods to corroborate diffusion MRI findings

Although cell tracing-based methods facilitate explicit estimations of the axon/dendrite orientation distribution, there are disadvantages associated with relying on their calculation for validating interpretations of diffusion MRI data. First, it is difficult to trace neural processes accurately, but with sufficiently high throughput to provide an estimate of the average morphological characteristics that affect water diffusion. Second, many histological procedures are not appropriate for cell tracing. For example, some procedures stain tissue too densely to trace individual cells or cell processes. Image analysis procedures that to not require tracing can provide straightforward strategies for quantifying cell morphology, and can be applied to a broader set of staining techniques.

In 2012, Budde and Frank [38] introduced using structure tensor analyses for validating diffusion MRI data. The structure tensor of an image quantifies the direction dependence of image variation in intensity. For most staining methods, image intensity is homogeneous within a given cell process, and therefore in directions parallel to the principal axis if a diffusion tensor, image intensity variation is expected to be minimal. In directions perpendicular to the primary orientation of cell processes, image intensity varies. Thus, the orientation, and magnitude of anisotropy within a structure tensor is expected to correspond to the orientation and magnitude of anisotropy of the diffusion tensor for the same region of tissue. The first implementation of structure tensor calculations for guiding the interpretation of diffusion MRI [38], demonstrated striking correlations between diffusion tensor and structure tensor orientation and magnitude of anisotropy. These authors similarly demonstrated that structure tensor analysis is a simple yet robust analysis that can be applied to tissue stained using a variety of immunohistochemical, as well as other staining methods. Subsequent work [39, 40] generalized the structure tensor analysis to 3D (Figure 2d-e), which is beneficial for studying complex structures that are oblique to any given sectioning plane, such as is commonly encountered in studies of the convoluted cerebral cortex of gyrencephalic species. Recent comparisons between 3D structure tensors and diffusion MRI results in the fetal rhesus macaque brain have shown that the morphology of dendritic processes closely corresponds to anisotropy of water diffusion in the developing cerebral cortex [41], which supports the role of development of dendritic arbors in maturation-related changes in cerebral cortical diffusion anisotropy.

Although structure tensor analysis has the advantage of being highly flexible for performing validation studies of diffusion MRI data, a drawback is that the relationship between the structure tensor and the axon/dendrite orientation distribution is in most cases not well understood. Thus, although quantitative, structure tensor analyses are of limited value for more detailed biophysical modeling. Other statistical analyses of histological images have also been proposed. As one example, Novikov and co-workers have proposed a classification scheme based on the diffusion time dependence of the diffusion MRI signal, which has implications in terms of the spatial autocorrelation function of the underlying tissue [42]. This approach has yet to be incorporated into a validation analysis of developing cerebral cortical tissue.

Empirical Model of the Loss of Water Diffusion Anisotropy with Maturation of the Cerebral Cortical Gray Matter

Precise knowledge of the developmental trajectory of cerebral cortical diffusion anisotropy in the normally-developing brain is important for optimizing the sensitivity with which diffusion MRI can be used to detect abnormal development. Cortical FA values have been determined as a function of age in several species across multiple laboratories. Remarkable consistency in the dependence of FA on age, laminar position, and cortical region has been observed in comparisons between these studies.

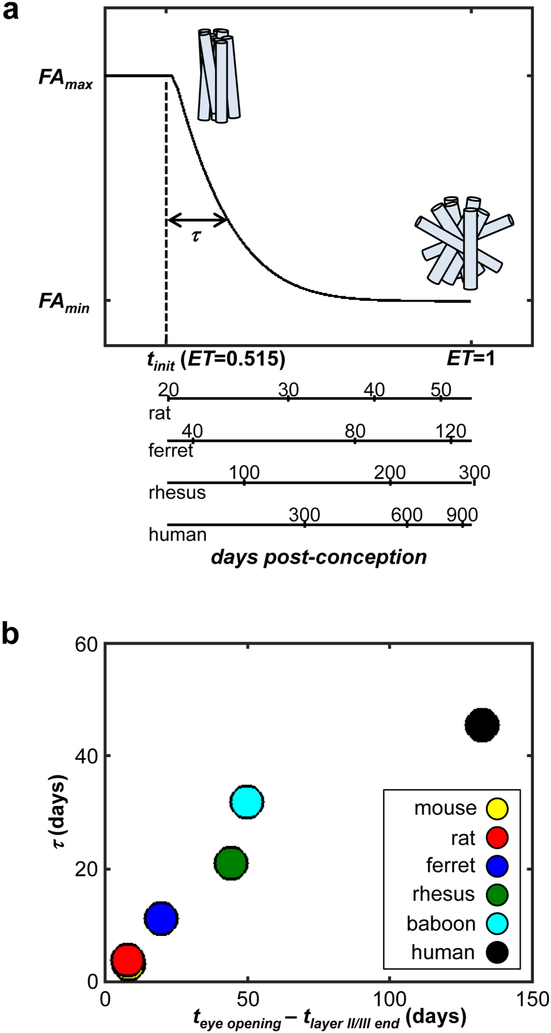
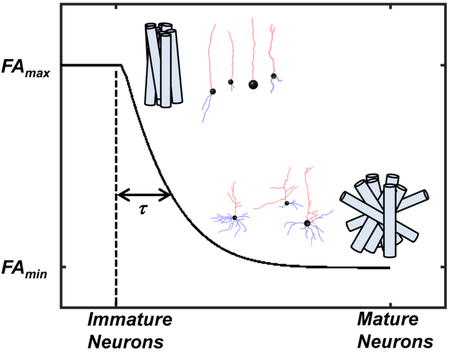
One way to compare results reported by different researchers is through reference to an analytical model of FA changes with development (Figure 3a). Cortical FA ranges between extreme cases of a maximal FA value observed in the immature cortex, FA_max, and a minimal (but non-zero [43]) value at maturity, FA_min. At the conclusion of neural migration to the cortical plate, the addition of new morphologically simple neurons to the cortical plate ceases, neurons initiate morphological differentiation, and cortical FA begins to decrease from FA_max toward FA_min. The time in which the reduction in FA is initiated is termed t_init. Reduction in FA with development has been empirically approximated as an exponential decay, characterized by the species-dependent decay time constant τ [17] (Figure 3a). The resulting expression for cortical changes in FA as a function of time, t, is

$$\mathit{FA}(\mathit{t})=\{\begin{array}{c}\begin{array}{c}\hfill {\mathit{FA}}_{\mathit{max}}\text{if}\mathit{t}<{\mathit{t}}_{\mathit{init}}\hfill \\ \hfill ({\mathit{FA}}_{\mathit{max}}-{\mathit{FA}}_{\mathit{min}})\mathit{exp}(-(\mathit{t}-{\mathit{t}}_{\mathit{init}})∕\tau )+{\mathit{FA}}_{\mathit{min}}\text{if}\mathit{t}\ge {\mathit{t}}_{\mathit{init}}\hfill \end{array}.\hfill \end{array}\phantom{\}}$$ (6)

Figure 3.

Comparison of the rate of age-dependent FA reduction between species. (a) For a given species, beginning at the time t_init, FA decreases exponentially with a decay time constant τ. Over this period, neural morphological development occurs, as represented by the cylinders with increasing orientation dispersion, as shown in Figure 1. To compare changes in FA between species, the post-conception age can be converted to a species-independent event time (ET). The FA changes for rhesus macaques is plotted as a function of ET, and the approximate value of τ is illustrated on the plot. For reference, corresponding ages for rats, ferrets, and humans are shown alongside the rhesus time line. (b) Comparisons between τ and the interval length between the conclusion of layer II/III neurogenesis and eye opening are shown for six species, following procedures described in [56]. The approximately linear relationship indicates consistency in the rates of development measured by FA changes and by the meta-analysis performed by Workman and colleagues [57].

Thus, the time constant τ reflects the pace of cerebral cortical development for a given species. For example, τ is expected to be longer in humans than in more rapidly developing species such as mice, because human cortical development occurs over a more protracted period of time. Within this framework, it is noted that the cerebral cortical thickness is comparable to, or even smaller than the voxel dimensions typically used in diffusion MRI studies. The observed FA value is a volume-fraction-weighted average of FA within the cortex, as well as within neighboring cerebrospinal fluid (CSF) and subplate tissue [44]. Water diffusion is isotropic in the CSF and subplate, and therefore the parameters FA_max and FA_min, as well as FA(t) in general, will be reduced by partial volume averaging of the cortex with neighboring tissue or CSF. The extent of this reduction will depend on the image resolution. However to a first approximation, the relative sizes of FA_max, FA_min, and FA(t) are expected to be consistent for a given image resolution. Due to the fact that parameters t_init and τ are sensitive to relative values of FA at varying values of t rather than absolute values, t_init and τ are expected to be (approximately) comparable between studies, in spite of different degrees of partial volume averaging between studies.

Changes in cortical FA with development have also been expressed using other analytical models. In studies of human subjects, changes in FA have been modeled as a linear reduction with time [45-47]. One drawback to such an approximation is that it is inaccurate for limiting cases. Physically impossible FA values larger than unity, or smaller than 0 are predicted for young or old ages, respectively. Further, inter-study comparisons are only possible if subjects are analyzed over similar developmental age ranges, because changes in FA per unit time decrease as the value at maturity, FA_min, is approached. There have also been studies focused on very early stages of cerebral cortical development that have documented FA increases with age [48-50]. In these cases, the thickness of the cortical plate changes dramatically compared to the image resolution, and this leads to an increase in FA with age. Such observations reflect changes in partial volume averaging between cell types, rather than changes in cellular morphology. Under such conditions, Eq. [6] is not appropriate for analyzing FA(t) due to its dependence on partial volume averaging noted above. The objective of this review is to focus on subsequent stages of development, in which cortical thickness does not change as dramatically.

Published cortical FA values for mouse [51], rat [52, 53], ferret [17, 54], baboon [55], and human [9, 50], have been analyzed using Eq. [6], and the fitted values of τ are comparable to independently estimated species-dependent rates of central nervous system development (Figure 3b) [56]. The independent estimate of the rate of CNS development is provided by Workman and co-workers [57], (http://www.translatingtime.net) who have compiled developmental data published for multiple species, and built a regression model that can convert the age of an individual, in terms of days post-conception, into a species-independent event time (ET) which ranges between values of 0 and 1. It was found that the exponential time constant for cortical FA changes was proportional to the predicted time elapsed between two well-conserved developmental events (the conclusion of neurogenesis for cortical layers II/III, and eye opening, Figure 3b) [56]. This proportionality implies that the rate of change of cortical FA follows that predicted by the rate of CNS development for a given species. Therefore, FA changes observed in an animal model of a developmental process or a neurodevelopmental disorder are expected to relate to FA changes observed in humans in a comparable way. Indeed, the onset of the reduction in FA, t_init, is now included in the translating time regression model (http://www.translatingtime.net), and the units for the abscissa in Figures 3a and 3b are species-independent ET values defined by Workman and colleagues [57].

Data collected from in vivo, as well as aldehyde-fixed post mortem tissue are included in the Figure 3b plot. Several studies have directly investigated the comparability of diffusion measurements performed before and after death and fixation in brain tissue, and while the directionally-averaged water diffusivity is markedly reduced in post mortem tissue compared to in vivo conditions, the extent of diffusion anisotropy is preserved [58]. Figure 4a shows an FA parameter map measured from a G110 rhesus macaque in utero, compared to an FA map derived from a G110 hemisphere from a different animal, determined post mortem in Figure 4b. As discussed above, cortical FA is higher in the post mortem data as a consequence of higher image resolution and reduced partial volume averaging. However, the relative variation in FA values, apparent in the regional patterns of FA, are preserved between the two tissue conditions. Systematic differences between living and ex vivo tissue are not observed the data used to produce Figure 3b, though the differences in physiological state of the tissue for these measurements should be recognized, as discussed in greater detail in [56], and references cited therein.

The developmental reduction in FA with time, averaged over the entire cerebral cortex, suggests a relationship between water diffusion anisotropy and the age of cortical neurons within the tissue being studied. The association between reductions in diffusion anisotropy with neuron age is also apparent on the finer scales of cerebral cortex anatomy such as the laminar and regional position. There is a gradient in neuron age across the layers of the cerebral cortex due to its “inside-out” development. Neurons that form the inner cortical layers (layers V/VI) are born at an earlier age than the neurons present in the outer layers (layers II/III), and as a consequence, neurons of inner cortical layers exhibit more mature and complex morphology than neurons of the outer layers at early stages of development [59, 60]. Expressed in terms of concepts relevant to water diffusion anisotropy, the orientation distributions of axons and dendrites of inner cortical layers at a given stage of development are broader than those of the outer layers due to the difference in neuron age. Therefore, water diffusion anisotropy is expected to be lower within the deeper layers. This layer dependence has been explicitly demonstrated in baboons [55, 61], rhesus macaques [44], and ferrets [17], and is apparent in images of other diffusion MRI studies that generated high-resolution parametric maps of diffusion anisotropy (for example, [48, 53]). In addition to the laminar gradient in neuron age, a regional gradient termed the translational neurogenic gradient (TNG), also exists [62, 63]. The TNG is structured such that neurons of a given lamina are oldest near the insular cortex, which is located on the ventral and lateral cortex bordering the frontal lobe, and neurons are progressively younger for regions more distant to the insular TNG source. A regional gradient in FA has been quantified in ferrets [17], rhesus macaques [41], and baboons [55], that is parallel to that expected from the TNG (Figure 4c). Specifically, FA is lowest near the insula and it increases as a function of distance from the presumed TNG source. Efforts to quantify the TNG magnitude (e.g. the difference in age of neurons at the TNG source vs. the frontal and occipital poles) indicate quantitative agreement with values estimated based on histological and cell birthdating studies [17]. The close associations observed between cerebral cortical diffusion anisotropy and neuronal age strongly support that morphological development of neurons critically influence FA changes in the developing cerebral cortex.

A final consideration is whether cytoarchitectural differences lead to distinct developmental trajectories for different areas of the cerebral cortex. Cortical areas involved in different functions have different cytoarchitectural characteristics. Recent advances in neuroimaging approaches for studying the mature human brain have created the possibility of generating fine-scale parcellations of the cerebral cortex within individuals [64], which would be an exceptionally valuable capability for neuroscience and neurological research. Further, although cortical diffusion anisotropy is not currently used for cytoarchitectural parcellation of the cerebral cortex, high-resolution diffusion MRI studies of post mortem human brain sections have demonstrated rich differences in cortical diffusion anisotropy between areas with different cytoarchitecture [16]. The need for high spatial resolution is well-recognized, to avoid confounds associated with neighboring white matter structures [65]. Nevertheless, an intriguing finding is that it has been possible to detect differences in the orientation of the least restricted direction of diffusion, relative to the radial orientation of pyramidal neuron apical dendrites, in high-resolution diffusion MRI studies of adult human subjects [15]. It is therefore of high interest to determine whether diffusion MRI can be used to monitor the transition of the developing cerebral cortex from the cortical plate to a cytoarchitecturally mature, functionally distinct region of cortex. Two reproducible patterns observed in multiple species are a highly conspicuous transition from high to low FA that marks the boundary between isocortex (high FA) and allocortex (low FA), and the observation that primary motor and sensory cortical areas experience an earlier t_init than their neighboring cortical areas, resulting in relatively low FA [17, 55]. Based on the findings reported in studies of mature brains, it is anticipated that improvements in the precision of cytoarchitectural development will be facilitated as diffusion MRI measurements with increasing image resolution become feasible.

Abnormal Developmental Trajectories of FA Changes Observed in Preclinical and Clinical Studies

Abnormal morphology of dendritic arbors of neurons in the cerebral cortex is consistently reported in animal models of several neurodevelopmental disorders. The influence of environmental factors on cerebral cortical neuron morphology was famously demonstrated in studies showing that environmental enrichment can cause increased dendritic arbor complexity [66]. Inversely, poorly enriched environments, such as social isolation results in the appearance of abnormally simplified cortical dendritic arbors [67]. Linkages between more specific sensory input have been observed for corresponding regions of the cortex. As an example, perturbed visual experience [68] has been shown to result in disturbances in dendritic arbor complexity in visual cortex. Thus, it is perhaps unsurprising that environmental exposures known to cause neurodevelopmental disorders, such as fetal alcohol exposure [69] or perinatal hypoxia/ischemia [70], are also associated with markedly reduced cerebral cortical dendritic arbor complexity. In addition to environmental influences, neurodevelopmental disorders of genetic origin, such as Rett syndrome [71], are additional example cases in which abnormal dendritic morphology is implicated disease. The common finding of abnormal neural morphological development in neurodevelopmental disorders with diverse etiologies suggest this effect is central to their pathophysiology, and therefore a non-invasive method to detect abnormal anatomical development could be of value for early detection, or prediction of risk for future functional impairment.

Mounting evidence from preclinical studies of animal model systems indicates that abnormalities in dendritic arbor complexity secondary to insults associated with neurodevelopmental disorders in humans can lead to increased anisotropy in cortical water diffusion compared to age-matched controls. In a study of fetal exposure to alcohol, diffusion MRI measurements performed on post mortem neonatal rat brain tissue revealed increased cortical FA in offspring to rats that were fed alcohol throughout pregnancy compared to animals fed an isocaloric control solution [72]. Two dimensional structure tensor calculations performed on the same tissue following DiI staining [38] served to validate that abnormal dendritic arborization was associated with the observed abnormally high FA. In a post mortem diffusion MRI study of perinatal sheep following experimentally induced hypoxia/ischemia, cortical FA was observed to be higher than in control animals, and corroborative analyses of the same tissue following Golgi staining indicated basal dendrites exhibited simpler morphology in affected animal brains [70]. Visual deprivation has similarly been shown to produce abnormally high FA in the visual cortex of early postnatal ferrets, and these findings were supported by 2D dendrite orientation distribution analyses [73]. Lastly, in utero diffusion anisotropy measurements have been shown to result in increased cortical FA in the context of a rhesus macaque fetus as a result of a functional deficit in the placenta [74]. These results are summarized with respect to overall changes in cortical FA in Figure 5. Although it is currently not possible to quantitatively interpret differences in FA of control vs. experimentally-perturbed cases in terms of specific anatomical differences, together, these findings indicate in a qualitative sense that diffusion MRI directed at the developing cerebral cortex potentially has the sensitivity needed to detect abnormal morphological development of neurons in the context of neurodevelopmental disorders. It should also be noted that not all perinatal insults lead to increased cortical FA. For example, in rat pups subjected to hypoxic/ischemic injury on the third day of life, cerebral cortical FA was reduced, compared to controls, when assessed three days later [75]. Subsequent histological examination of the brains of these animals indicated that disrupted organization of nestin-positive radial glial cells was the cause of the relatively low FA. Given this expected heterogeneity in biological processes associated with abnormal development, continued use of animal models will be of value to validate the histological underpinnings of diffusion MRI measurements.

Figure 5.

Experimental models of neurodevelopmental disorders that have been demonstrated to produce an increase in cerebral cortical FA relative to age-matched controls. The species-averaged FA value for control animals (black trace) was determined by converting curves for each species (such as shown for rhesus macaques in Figure 4a) to species independent ET, and averaging the result. The ages of animals for individual experimental perturbations were translated to the ET scale using species-dependent parameters given in [57].

Recent human subject studies support the interpretations of cortical diffusion MRI based on preclinical work. Comparisons of cortical FA between prematurely born and termborn infants show that early exposure to the extra-uterine environment hampers the loss of diffusion anisotropy [47]. Further, in prematurely-delivered human infants, the extent of reduction in cerebral cortical FA has been shown to correlate with measures of infant growth [76]. Regional patterns in the loss of cortical FA in human infants have been reported [77], and comparisons to measures of white matter development indicate that cortical maturation, as reflected in the reduction in diffusion anisotropy, is coupled to white matter development [46]. This integration with other aspects of brain development suggest that abnormalities in cortical diffusion anisotropy may be of functional relevance. A critical next step for this imaging modality will be to establish linkages between diffusion MRI findings during the perinatal period and subsequent cognitive and behavioral outcomes.

Conclusion

Diffusion MRI provides a unique opportunity to non-invasively characterize cellular morphological development of neurons in the early developing cerebral cortex. This aspect of brain development is critical to support the formation of synaptic connections and hence functional circuits. Invasive studies using microscopy have identified that abnormal morphology of developing cortical neurons is associated with various neurodevelopmental disorders. Preclinical, as well as initial human subject studies indicate that measurements of cerebral cortical diffusion anisotropy possess the requisite sensitivity to detect abnormal development of neurons. However, due to the lack of specificity of the characteristics of water diffusion averaged over an MRI voxel, it has been necessary to design specialized analyses of microscopy data to quantitatively validate the interpretations of diffusion MRI findings. Yet from another perspective, the averaging of water diffusion over thousands of cellular processes, that is intrinsic to diffusion MRI measurements, presents an advantage of efficiently measuring the average structural characteristics of large ensembles of cells. Such averaging enables the detection of subtle structural effects, provided they are sufficiently widespread to affect a large number of cells. This could be considered a valuable capability, relative to other experimental approaches, for research focused on neurodevelopmental disorders.

The developmental period associated with the loss of cerebral cortical water diffusion anisotropy is a critical time for CNS development, but is difficult to access using other techniques. Ideally, non-invasive modalities would be of use for detecting abnormalities at early stages of development, prior to the emergence of cognitive and behavioral deficits. Diffusion MRI directed at the immature brain meets this need. In addition, the endogenous image contrast obtained in diffusion MRI is possible to use in the study of vulnerable populations, such as prematurely delivered human infants (see Neil and Smyser, this issue). Improvements in retrospective motion correction techniques will further bolster the value of diffusion MRI by extending the ability to apply this approach to the study of developing fetuses [78, 79]. In summary, it is hoped that this versatile technique for characterizing cerebral cortical maturation throughout the entire brain will provide new strategies for early detection of anatomical abnormalities associated with neurodevelopmental disorders, and as a potential way to monitor responses to proposed therapeutic interventions.