Abstract
Feature selection in Liquid Chromatography-Mass Spectrometry (LC-MS)-based metabolomics data (biomarker discovery) have become an important topic for machine learning researchers. High dimensionality and small sample size of LC-MS data make feature selection a challenging task. The goal of biomarker discovery is to select the few most discriminative features among a large number of irreverent ones. To improve the reliability of the discovered biomarkers, we use an ensemble-based approach. Ensemble learning can improve the accuracy of feature selection by combining multiple algorithms that have complementary information. In this paper, we propose an ensemble approach to combine the results of filter-based feature selection methods. To evaluate the proposed approach, we compared it to two commonly used methods, t-test and PLS-DA, using a real data set.
Index Terms–: biomarker discovery, ensemble learning, ensemble feature selection, filter methods, scoring functions
I. INTRODUCTION
The National Institutes of Health (NIH) of USA defined biomarker as “A characteristic that is objectively measured and evaluated as an indicator of normal biological processes, pathogenic processes, or pharmacologic responses to therapeutic intervention” [1]. Biomarker play an important role in early diagnosis of diseases. The accuracy of selecting biomarkers is important due to its effect on specificity and sensitivity of developing diagnostic and prognostic assays [2]. In biomarker discovery, the goal is to find the biomarkers that can discriminate between disease samples and normal samples.
Biomarker discovery is analogous to feature selection (variable estimation) methods in machine learning. A Feature selection algorithm aims to reduce the feature space by eliminating irrelevant and redundant features and keeping the more informative features. In contrast to other dimensionality reduction algorithms such as principal component analysis (PCA), feature selection methods do not combine the features to make new features. They keep the original features and select a subset of them [3].
Two significant problems arise when dealing with biomarker discovery; high dimensionality (large number of noisy features); and low sample size. These problems lead to instability in most feature selection algorithms [4]. To overcome this problem, we propose an ensemble-based feature selection method for biomarker discovery. Ensemble-based approaches are mostly heuristic and based on the idea that individual algorithms can have complementary information. Thus, if these methods cooperate, group decisions can take advantage of the strengths of individual algorithms, overcome their weaknesses, and achieve more robust results. Our approach is general and can integrate any filter-based feature selection algorithm that can rank the features based on their discriminative power. It aggregates the rankings of different methods to create the ensemble result which will be shown to be more stable than using any of the individual methods.
To validate our approach, we use spiked-in dataset generated by metabolites that were extracted from a pooled mouse liver sample.
The organization of the rest of this paper is as follows. In section II, we provide an overview of the feature selection methods that will be combined. Section III describes our proposed ensemble feature selection method. Finally, we give the results of our proposed method and compare them with the state of the art methods that are based on t-test and PLS-DA on a spiked-in dataset in section IV.
II. RELATED WORK
Feature selection methods reduce the feature space by selecting the most discriminative features in the dataset. It can lead to a better understanding of the data, reducing computational complexity and the effect of the curse of dimensionality as well as improving the predictor performance. The ideal feature selection method in biomarker discovery should select most of the discriminative features while minimizing the number of irrelevant ones [2].
Feature selection methods can be classified into four different categories, filter, wrapper, embedded and ensemble methods [5]. Filter methods strive to find the most discriminating features by filtering out non-discriminating features. First, they assign a score to each feature using a statistical measure. Then, they select a subset of features with scores above a threshold. Filter methods are independent of the classifiers. Wrapper methods, on the other hand, select a subset of features based on the accuracy of a predictive model. These methods consider feature selection as a search problem. They generate different subsets of features, evaluate each subset using a classifier and find the subset that maximizes the classifier’s accuracy. Embedded methods are a variation of the wrapper approach that were proposed to reduce the computational complexity. The main idea behind this approach is to integrate the feature selection in the training phase of the classifier [6]. Thus, embedded methods search the feature selection space and the learning algorithm parameter space simultaneously [7]. The forth category of feature selection methods, ensemble methods, assume that combining the results of multiple algorithms is better than the result of one single algorithm [8]. They have been proposed to cope with the instability issues of many feature selection methods [5].
Feature selection methods have been applied successfully to the problem of biomarker discovery [3], [5], [6], [8], [9]. In particular, Christin et al. [2] evaluated the performance of six widely used feature selection methods for LC-MS-based proteomics and metabolomics biomarker discovery. Grissa et al. [10] performed a comparative study of feature selection methods and evaluated them to select a subset of predictive features. Researchers tend to use filter-based methods, since they are based on ranking, to select the top biomarkers. Lazer et al. [5] proposed a taxonomy for scoring functions which are at the core of filter methods. According to their study, scoring functions can be grouped into few categories: rank score [11], fold-change [12], t-test [13], [14], Bayesian [15], pdf based [16], information theory based [17], correlation based [18] and other scoring functions [19].
Recently, to make the feature selection algorithms more robust and stable, researchers have shifted to using combinations of feature selection methods as hybrid or ensemble method [8]. For instance, Abeel et al. [20] presented an ensemble feature selection method using linear SVMs and recursive feature elimination known as RFE [21]. Moon and Nakai [22] presented an ensemble feature selection method based on L1-norm support vector machine. Bolon-Canedo [23] investigated combining the feature subsets selected by multiple filter methods (i.e. union of subsets).
In this paper, we propose an ensemble approach based on fusion of five feature selection methods; rank product [11], fold change ratio [12], ABCR [19], t-test [14] and PLSDA [24]. We combine the results of these algorithms using Borda count [25]. One of the main advantages of using Borda fusion is that it is based on relative ranking of the features and does not require the scores of the different algorithms to be normalized within the same dynamic range. The details of these individual methods are described in the following sections.
As described in section IV the spiked-in dataset contains six different sample groups: group0 which indicates control sample group and five sample groups groupg, g = 1, …, 5 with increasing level of spiked-in compound standards. For our experiments, we consider only two groups at a time, group0 and groupg g = 1, …, 5. Thus, at any time, the dataset will be an M × N matrix, where M is the number of compounds(features) and N is the number of samples in the two considered groups. Let ng, for g = 0, …, 5 denote the number of samples in groupg. Thus, N = n0 + ng. We denote feature i, i = 1, …, M by fi and we use x0,i to refer to values of feature i in group0 and xg,i to refer to values of feature i in groupg. The spiked-in standards represent the discriminative features or biomarkers. This information is not used in our algorithm. It is only used in the evaluation phase. Let NB be the number of biomarkers in dataset.
A. Rank Product
Rank product is a straightforward and statistically stringent method to quantify the significance of each feature. It is similar to Wilcoxon rank sum method [26]. First, for each feature, we sort the values of all samples in ascending order. Then, a rank is assigned to each sample. Let Rsn,i denote the rank of feature i of sample sn. After calculating the rank, the score for each feature is calculated using:
| (1) |
Feature ranks of samples in groupg is used to calculate the score of feature i. Rank Product provides flexible control of the false-positive rate and family wise error rate (FWER). Also, it is reliable in highly noisy datasets [11]. One factor that contributes to the success of this method is that it makes only weak assumption about the data distribution (it expects nearly equal variance for all features) [11].
B. Fold Change Ratio
Fold change ratio assigns scores to each feature based only on estimates of the mean [12]. Let and denote mean of feature i of group0 and groupg, respectively. The score for this method is computed by taking the log of the ratio of means.
| (2) |
C. ABCR
Parodi et al. [19] developed a feature selection method based on the area under the curve (AUC) and the area between the curve and the rising diagonal (ABCR). ABCR is measure of distance between two distributions generated by group0 and groupg samples. This method calculates the empirical Receiver Operating Characteristic curve (ROC curve) by considering different threshold values hk, where hk, k = 1, …, ui , is the kth unique value of fi in decreasing order.
In our work, we use a variation of ABCR that proved to be more efficient and robust. Instead of considering every unique value of fi as a threshold, we discretize each fi into a fixed number of bins, Bi, (typically 10) and consider only the bins centers as thresholds hk, k = 1, …, Bi.
For each considered threshold value hk, true and false positive fractions, denoted by TPF (hk) and FPF (hk), are computed. Let AUCk be the partial area under an ROC cuve between FPF (hk−1) and FPF (hk).
When TPF (hk) = FPF (hk) = k/ui for k = 1, …, ui, every hk cannot provide a valid classification and the class is assigned by chance. In this case, the resulting ROC curve is called chance line [19]. Let the partial area of this rising diagonal be denoted by Ak and computed using:
| (3) |
Each feature score can be computed using:
| (4) |
In (4), AUCk is computed using:
| (5) |
Where
| (6) |
and
| (7) |
Similarly,
| (8) |
and
| (9) |
In (6)-(9),
| (10) |
D. t-test
The t-test is a hypothesis test to compare whether two populations have different means. One of the outputs of t-test is the statistical significance (i.e. p-value), which indicates whether the difference between sample averages is likely to represent an actual difference between populations. The t statistic of fi is calculated as follows:
| (11) |
where and are variances of feature i using samples in group0 and group5. The output p-value (S(fi)) is then calculated by placing the test statistic in an ordinary t-distribution with the degrees of freedom df, which is calculated as:
| (12) |
E. PLS-DA
The partial least squares discriminant analysis (PLS-DA) is a supervised analysis method to sharpen the separation between groups of observations to obtain a maximum separation among the classes, and to understand which variables carry the class separating information. The Variable Importance in Projection (VIP) in a PLS-DA is used to calculate the importance of individual metabolite feature among groups. The VIP score for the feature i is defined as:
| (13) |
where L is the number of latent variables, M is the number of features, wmi is the PLS weight of the i-th variable for the m-th latent variable, and SS(bn.tn) is the percentage of y explained by the m-th latent variable.
III. PROPOSED ENSEMBLE-BASED FEATURE SELECTION
In this paper, we propose an ensemble method to combine the results obtained by multiple feature selection algorithms and vote for the most discriminative features in the dataset. Any of the feature selection methods described in section II can be used to provide a score indicating the feature’s importance. Due to the small size of the data, a simple ranking may be very sensitive to the distribution of the data. To take this into consideration, we use a random sampling approach, called permutation test [27], to make sure that ranks are not acquired by chance.
For each algorithm j, using its scoring function Sj(), we apply the following procedure on the selected set of dataset generated by samples from group0 and groupg.
First, we calculate score of all the features using samples from their correct groups. We call these scores, actual scores. Let indicate the actual score of feature i calculated by algorithm j. Then, we run the scoring function multiple times on the same dataset, except that samples from the two groups are permuted randomly each time. Considering the two groups (group0 and groupg), there are possible splits of samples into two groups. In practice, due to the large number of possible permutations, evaluating all possible splits cannot be performed. In these cases, we use a fixed number of permutations denoted by P. We call the sample distribution of scores obtained by permuting group labels, permuted scores. Let tj,i denote the permuted scores of feature i calculated by algorithm j.
After the first step, for each feature fi, we have one actual score , and a distribution of permuted scores, tj,i, for all considered permutations. To achieve the significance level of fi (estimated p-value), we compare its actual score to its permuted scores. The estimated p-value will be the probability that permuted scores are larger than or equal to the actual score. That is,
| (14) |
where I() is an indicator function as defines in (10).
Our assumption is that if a feature is not discriminative, its score will not differ much when using actual group labels or using permuted labels. Therefore, samples from both groups would appear to belong to the same sample distribution. On the other hand, if the feature is discriminative, the score should change significantly using permuted group samples.
Next, we rank all features in ascending order based on their p-values. Let pj,i and rj,i be the p-value and rank associated with fi by algorithm j, respectively.
After running all the feature selection algorithms (αj, j =1, …, NumAlg), for each algorithm j, we have the features’ rank rj,i. The objective of our ensemble method is to combine the ranks of the different algorithms and take advantage of their strengths. A relevant feature (i.e. biomarker) might get a high rank in one method and a low rank in another method. The fusion of multiple algorithms can increase the accuracy of the selected features. In this paper, we use a variation of Borda count [25] to combine the individual ranks.
In particular, we compute the fusion rank of each feature as a weighted sum of the ranks assigned by the individual algorithms. Formally,
| (15) |
In (15), wj is a weight assigned to each algorithms. It can be assigned using prior knowledge or computed based on the relative performance of algorithm j. If no information is available, wj can be set to 1 for all algorithms. The top features ( with lowest Sens(fi) ) will be detected as the most relevant features and identified as biomarkers.
To summarize, our ensemble feature selection approach has two main steps:
Assign ranks to features using different types of feature selection algorithms based on p-values as in (14)
Calculate the fusion rank for each feature using cumulative ranks of all algorithms using (15)
IV. EXPERIMENTS AND RESULTS
To validate our approach, we use spiked-in dataset generated by metabolites that were extracted from a pooled mouse liver sample using a solvent mixture water:methabol (v:v=8:2). The metabolite extract was then equally split into 60 aliquots to form 6 sample groups (group0, group1, …, group5) with (n = 10 in each group). Different volumes of a mixture of 48 metabolite standards were spiked in each sample. The concentrations of each metabolite standard spiked in the 6 sample groups were 0 μM, 0.625 μM, 1.25 μM, 2.5 μM, 5 μM and 10 μM, respectively. All samples were analyzed on a Q Exactive HF Hybrid Quadrupole-Orbitrap Mass Spectrometer equipped with a reversed phase column and a hydrophobic interaction liquid chromatography column. The MS was operated in both positive and negative modes to acquire the full MS and MS2 spectra for each metabolite. LC-MS data were initially analyzed using MetSign software for spectrum deconvolution, metabolite assignment and cross sample peak list alignment.
First, we ran the 5 individual feature selection algorithms described in section II, considering 2 groups at a time: group0 and groupg for g = 1, …, 5. For each αj, we use the assigned score to each feature, S(fi), and the ground truth to generate an ROC curve. In fig 1, we display the ROC’s when groups 0 and 5 are considered and in fig 2, we display the results when groups 0 and 1 are considered. Since group 5 samples were spiked with the highest concentration of each metabolite standard, the biomarkers of this group can be identified with much fewer false positives than biomarkers of group 1. The results for the remaining groups follow the same pattern and are not shown here due to the paper limit.
Fig. 1:
performance of the 5 individual feature selection algorithms when samples from groups 0 and 5 are considered.
Fig. 2:
performance of the 5 individual feature selection algorithms when samples from groups 0 and 1 are considered.
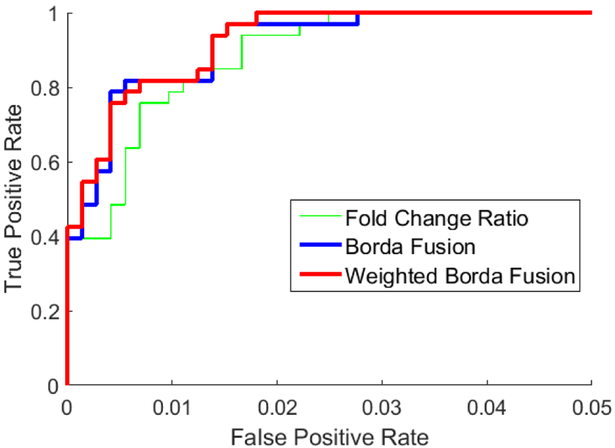
Next, we combine the results of the 5 algorithms using the proposed ensemble approach (eq (15)). For the weights, wj : j = 1, …, 5, we consider two options. The first one assigns equal weights (wj = 1) to each algorithm. We refer to this as Borda fusion. For the second option, we assign weights proportional to the relative performance of the algorithms, where performance is measured by area under the curve. We refer to this option as weighted Borda fusion. The results are shown in fig 3 for groups 0 and 5 and in fig 4 for groups 0 and 1. As a reference, in these figures we also show the ROC of the best performing individual algorithm (fold change ratio). First, we note that for both cases, the fusion results outperform the best individual algorithm. The results of the easiest case (groups 0 and 5), which are illustrated in fig 3, show that fusion methods clearly outperform the best individual algorithm. Also, for the second case (the hardest one), as it is shown in fig 4, fusion methods perform better than the best single algorithm. Second, for the easy case of groups 0 and 5, Borda and weighted Borda methods have comparable accuracy. However, for the harder case of groups 0 and 1, the non-equal weights (weighted Borda fusion) have improved the accuracy slightly.
Fig. 3:
performance of the proposed ensemble approach when groups 0 and 5 are considered.
Fig. 4:
performance of the proposed ensemble approach when groups 0 and 1 are considered.
V. CONCLUSIONS
In this paper, we introduced an ensemble feature selection algorithm to improve the accuracy of biomarker discovery. Our proposed method consists of combining five feature selection algorithms using a simple approach that is based on ranking. Thus, avoiding the normalization of the individual scores to fit within the same range.
To evaluate our proposed method, we have generated a spiked-in dataset using metabolites that were extracted from a pooled mouse liver sample with varied concentration levels. Our results have indicated that, for all concentration levels, fusion outperforms the best individual algorithm. We have also shown that we can use a simple aggregation where all weights are set to 1 or we can use weighted fusion where weights reflect the relative performance of the individual algorithm. For groups with lower concentration (harder case), assigning higher weights to the better individual algorithm can improve the fusion results. However, this is not the case for groups with higher concentration (easier case).
ACKNOWLEDGMENTS
This work was supported by NIH of USA grant nos. 1S10OD020106, 1P20GM113226, and 1P50AA024337, 1U01AA021893, 1U01AA021901–01, 1U01AA022489–01A1 and 1R01AA023681. This work was also supported in part by U.S. Army Research Office Grants Number W911NF-13–1-0066 and W911NF-14–1-0589. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the National Institute of Health, the Army Research Office, or the U.S. Government.
REFERENCES
- [1].Colburn W, DeGruttola VG, DeMets DL, Downing GJ, Hoth DF, Oates JA, Peck CC, Schooley RT, Spilker BA, Woodcock J, et al. , “Biomarkers and surrogate endpoints: Preferred definitions and conceptual framework. biomarkers definitions working group,” Clinical Pharmacol & Therapeutics, vol. 69, pp. 89–95, 2001. [DOI] [PubMed] [Google Scholar]
- [2].Christin C, Hoefsloot HC, Smilde AK, Hoekman B, Suits F, Bischoff R, and Horvatovich P, “A critical assessment of feature selection methods for biomarker discovery in clinical proteomics,” Molecular & Cellular Proteomics, vol. 12, no. 1, pp. 263–276, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Saeys Y, Inza I, and Larrañaga P, “A review of feature selection techniques in bioinformatics,” bioinformatics, vol. 23, no. 19, pp. 2507–2517, 2007. [DOI] [PubMed] [Google Scholar]
- [4].Awada W, Khoshgoftaar TM, Dittman D, Wald R, and Napolitano A, “A review of the stability of feature selection techniques for bioinformatics data,” in Information Reuse and Integration (IRI), 2012 IEEE 13th International Conference on, pp. 356–363, IEEE, 2012. [Google Scholar]
- [5].Lazar C, Taminau J, Meganck S, Steenhoff D, Coletta A, Molter C, de Schaetzen V, Duque R, Bersini H, and Nowe A, “A survey on filter techniques for feature selection in gene expression microarray analysis,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 9, no. 4, pp. 1106–1119, 2012. [DOI] [PubMed] [Google Scholar]
- [6].Chandrashekar G and Sahin F, “A survey on feature selection methods,” Computers & Electrical Engineering, vol. 40, no. 1, pp. 16–28, 2014. [Google Scholar]
- [7].Liu H and Motoda H, Computational methods of feature selection. CRC Press, 2007. [Google Scholar]
- [8].Bolón-Canedo V, Sánchez-Marono N, Alonso-Betanzos A, Benítez JM, and Herrera F, “A review of microarray datasets and applied feature selection methods,” Information Sciences, vol. 282, pp. 111–135, 2014. [Google Scholar]
- [9].Hira ZM and Gillies DF, “A review of feature selection and feature extraction methods applied on microarray data,” Advances in bioinformatics, vol. 2015, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Grissa D, Pétéra M, Brandolini M, Napoli A, Comte B, and Pujos-Guillot E, “Feature selection methods for early predictive biomarker discovery using untargeted metabolomic data,” Frontiers in molecular biosciences, vol. 3, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Breitling R, Armengaud P, Amtmann A, and Herzyk P, “Rank products: a simple, yet powerful, new method to detect differentially regulated genes in replicated microarray experiments,” FEBS letters, vol. 573, no. 1–3, pp. 83–92, 2004. [DOI] [PubMed] [Google Scholar]
- [12].Witten D and Tibshirani R, “A comparison of fold-change and the t-statistic for microarray data analysis,” Analysis, vol. 1776, pp. nbsp58–85, 2007. [Google Scholar]
- [13].Welch BL, “The significance of the difference between two means when the population variances are unequal,” Biometrika, vol. 29, no. 3/4, pp. 350–362, 1938. [Google Scholar]
- [14].Xi B, Gu H, Baniasadi H, and Raftery D, “Statistical analysis and modeling of mass spectrometry-based metabolomics data,” Mass spectrometry in metabolomics: methods and protocols, pp. 333–353, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Long AD, Mangalam HJ, Chan BY, Tolleri L, Hatfield GW, and Baldi P, “Improved statistical inference from dna microarray data using analysis of variance and a bayesian statistical framework analysis of global gene expression in escherichia colik12,” Journal of Biological Chemistry, vol. 276, no. 23, pp. 19937–19944, 2001. [DOI] [PubMed] [Google Scholar]
- [16].Wilinski A, Osowski S, and Siwek K, “Gene selection for cancer classification through ensemble of methods,” in International Conference on Adaptive and Natural Computing Algorithms, pp. 507–516, Springer, 2009. [Google Scholar]
- [17].Chuang L-Y, Ke C-H, Chang H-W, and Yang C-H, “A two-stage feature selection method for gene expression data,” OMICS A journal of Integrative Biology, vol. 13, no. 2, pp. 127–137, 2009. [DOI] [PubMed] [Google Scholar]
- [18].Park PJ, Pagano M, and Bonetti M, “A nonparametric scoring algorithm for identifying informative genes from microarray data.,” in Pacific Symposium on Biocomputing. Pacific Symposium on Bio-computing, pp. 52–63, 2000. [DOI] [PubMed] [Google Scholar]
- [19].Parodi S, Pistoia V, and Muselli M, “Not proper roc curves as new tool for the analysis of differentially expressed genes in microarray experiments,” BMC bioinformatics, vol. 9, no. 1, p. 410, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Abeel T, Helleputte T, Van de Peer Y, Dupont P, and Saeys Y, “Robust biomarker identification for cancer diagnosis with ensemble feature selection methods,” Bioinformatics, vol. 26, no. 3, pp. 392–398, 2010. [DOI] [PubMed] [Google Scholar]
- [21].Guyon I, Weston J, Barnhill S, and Vapnik V, “Gene selection for cancer classification using support vector machines,” Machine learning, vol. 46, no. 1, pp. 389–422, 2002. [Google Scholar]
- [22].Moon M and Nakai K, “Stable feature selection based on the ensemble l 1-norm support vector machine for biomarker discovery,” BMC genomics, vol. 17, no. 13, p. 1026, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Bolón-Canedo V, Sánchez-Maroño N, and Alonso-Betanzos A, “An ensemble of filters and classifiers for microarray data classification,” Pattern Recognition, vol. 45, no. 1, pp. 531–539, 2012. [Google Scholar]
- [24].Pérez-Enciso M and Tenenhaus M, “Prediction of clinical outcome with microarray data: a partial least squares discriminant analysis (pls-da) approach,” Human genetics, vol. 112, no. 5–6, pp. 581–592, 2003. [DOI] [PubMed] [Google Scholar]
- [25].de Borda J-C, “Memoire sur les elections au scrutin,” Histoire de lAcadTmie Royale des Sciences. [Google Scholar]
- [26].Wilcoxon F, “Individual comparisons by ranking methods,” Biometrics bulletin, vol. 1, no. 6, pp. 80–83, 1945. [Google Scholar]
- [27].Radivojac P, Obradovic Z, Dunker AK, and Vucetic S, “Feature selection filters based on the permutation test,” in ECML, pp. 334–346, Springer, 2004. [Google Scholar]