Keys to the Gate? Equal Sign Knowledge at Second Grade Predicts Fourth-Grade Algebra Competence

Abstract

Algebraic competence is a major determinant of college access and career prospects, and equal sign knowledge is taken to be foundational to algebra knowledge. However, few studies have documented a causal effect of early equal sign knowledge on later algebra skill. This study assessed whether second-grade students’ equal sign knowledge prospectively predicts their fourth-grade algebra knowledge, when controlling for demographic and individual difference factors. Children (N = 177; M_age = 7.61) were assessed on a battery of tests in grade 2 and on algebraic knowledge in grade 4. Second-grade equal sign knowledge was a powerful predictor of these algebraic skills. Findings are discussed in terms of the importance of foregrounding equal sign knowledge to promote effective pedagogy and educational equity.

Having access to algebra is having access to an important form of power (Moses & Cobb, 2001). This is true in at least two important senses: On the one hand, algebra represents an important pathway into the higher mathematics and science that provide foundational knowledge for STEM fields (Chen, 2013; National Mathematics Advisory Panel, 2008). In this sense, the power of algebra is the power to unlock ever more knowledge, be it simply for knowledge’s sake or for the productive potential that math and science holds for moving modern society forward.

On the other hand, access to algebra is deeply tied up in issues of social equity (Faulkner, Stiff, Marshall, Nietfeld, & Crossland, 2014; Gamoran & Hannigan, 2000). Placement in middle school algebra is an important determinant of high school math placement (Burris, Heubert, & Levin, 2004; Dauber, Alexander, & Entwisle, 1996; Gamoran & Mare, 1989), and success in higher math courses is the strongest high school curricular predictor of college graduation, regardless of a student’s eventual field of study (Adelman, 2006; Trusty & Niles, 2003).

Unfortunately, many children are tracked into lower-level math classes that constrain their eventual access to higher education (Faulkner et al., 2014; Gamoran & Hannigan, 2000). Thus, algebra is a gatekeeper not only for STEM fields, but also for higher education more generally. This two-fold picture of the power of algebra underscores the critical role access to algebra plays in education. As a result, it is vitally important to identify factors that increase students’ access to algebra.

Against this backdrop, efforts have been made to introduce strands of algebraic and pre-algebraic thinking much earlier in the curriculum (e.g., Carpenter, Franke, & Levi, 2003; Kaput, Blanton, & Moreno-Armella, 2008; National Council of Teachers of Mathematics, 2000). Indeed, the Common Core now includes algebraic thinking standards that extend down to kindergarten. In contrast to focusing on full-fledged formal algebra, these standards focus on basic concepts, properties, and representations that extend to algebra (McCallum, Zimba, & Daro, 2011). If algebra is the gatekeeper, then the knowledge and skills covered by these early standards are thought to be the keys to the gate.

Knowledge of the equal sign is taken to be one particularly important element of early algebraic thinking (Carpenter et al., 2003; Kieran, 1981). However, little is known empirically about the extent to which early developing equal sign knowledge actually predicts later algebraic thinking. The purpose of the present analysis was to investigate the prospective power of equal sign knowledge at second grade for predicting later algebraic competence in fourth grade.

The Role of the Equal Sign in Algebraic Thinking

The equality relation symbolized by the equal sign is a “big idea” in mathematics that has long been viewed as critical for developing algebraic competence (Baroody & Ginsburg, 1983; Carpenter et al., 2003; Falkner, Levi, & Carpenter, 1999; Filloy & Rojano, 1989; Kieran, 1981; MacGregor & Stacey, 1997; National Council of Teachers of Mathematics, 2000). The equal sign is a relational symbol that indicates the sameness or interchangeability of two sides of an equation, and as such, it is inherently propositional. Indeed, the equal sign is one of the earliest instances in which children are introduced to the idea that math should be about sense making: In order for 3 + 4 = 6 + 1 to be true, both sides must add to the same amount. This relational aspect of a robust understanding of the equal sign makes it a critical link between arithmetic and algebra (Carpenter et al., 2003; Kieran, 1981; MacGregor & Stacey, 1997).

Unfortunately, decades of research have detailed the difficulties American school children have understanding the equal sign (e.g., Behr, Erlwanger, & Nichols, 1980; Falkner et al., 1999; Li, Ding, Capraro, & Capraro, 2008; Matthews, Rittle-Johnson, McEldoon, & Taylor, 2012; McNeil & Alibali, 2005; Perry, 1991; Renwick, 1932). Instead of developing a relational view of the equal sign, children often interpret it as an operator that means “get the answer” or “the total” (Behr et al., 1980; McNeil & Alibali, 2005; Seo & Ginsburg, 2003). As a result, most elementary school aged children solve problems such as 8 + 4 = _ + 5 incorrectly, writing 12 or 17 on the blank (e.g., Falkner et al., 1999). Additionally, students with an operational view of the equal sign often reject problems that are not in standard a + b = c format (e.g., 4 + 1 = 2 + 3, or 8 = 3 + 5) as incorrect or nonsensical (Behr et al., 1980). Such operational understandings of the equal sign are pervasive and difficult to overcome. Importantly, these operational understandings are correlated negatively with understanding of algebra (Byrd, McNeil, Chesney, & Matthews, 2015; Knuth, Stephens, McNeil, & Alibali, 2006; Steinberg, Sleeman, & Ktorza, 1991).

In contrast, cultivating a relational view of the equal sign is thought to be critical for the development of algebraic skills. A relational view of the equal sign takes it to mean “the same as” or to indicate that two amounts or expressions can be interchanged (Kieran, 1981). Because algebra is at root about the study of functions, relations, and systems as opposed to computation, theorists and empirical researchers using qualitative methods and teaching experiments have taken a relational understanding of the equal sign to indicate algebraic reasoning (e.g., Carpenter et al., 2003; Filloy & Rojano, 1989; Kaput et al., 2008; Kieran, 1981; NCTM, 2000; Seo & Ginsburg, 2003; Sfard & Linchevski, 1994).

The empirical evidence supports these conclusions. A sizeable body of research indicates that holding a relational view of the equal sign is positively related to students’ concurrent abilities to solve algebraic equations (Alibali, Knuth, Hattikudur, McNeil, & Stephens, 2007; Booth & Davenport, 2013; Fyfe, Matthews, Amsel, McEldoon, & McNeil, 2018; Knuth et al., 2006; Matthews et al., 2012; Steinberg et al., 1991). Moreover, research shows that equal sign instruction improves student abilities to solve nonstandard open equations, which are precursors to the sorts of equations students encounter in formal algebra courses (e.g., Matthews & Rittle-Johnson, 2009; Perry, 1991; Powell & Fuchs, 2010). Yet, most attempts to investigate the relations between equal sign knowledge and algebraic competence have involved measuring both at either the same time point or at two points close in time, a design feature that renders them inappropriate for determining the role of equal sign knowledge in the development of algebraic knowledge over time. To answer this causal developmental question, more longitudinal data are needed.

We identified only two published studies documenting that early knowledge of the equal sign prospectively predicts later algebra knowledge. Alibali et al. (2007) found that sixth graders who offered more sophisticated operational definitions of the equal sign were better at solving equivalent equations at eighth grade. Similarly, Byrd, McNeil, Chesney, Matthews et al. (2015) found that sophistication of equal sign definitions at the beginning-of-the-year predicted end-of-year performance on an early algebra assessment for third- and fifth-grade students.

These studies, however, were limited in four important ways. First, Alibali et al. (2007) only used two items to assess algebraic reasoning, whereas Byrd et al. used only a single item. As a result, the primary predictors were granular and of limited variability. See Matthews et al. (2012) for an extended discussion of how the binary nature of a single item necessarily limits the variance that can be explained by those studies. By contrast, continuous measures of equal sign knowledge constructed using more items of various difficulties have explicitly been shown to unpack more variance in the data (Matthews et al., 2012; Rittle-Johnson, Matthews, Taylor, & McEldoon, 2011).

A second limitation is that both previous prospective studies used measures that focused heavily on students’ explicitly offered definitions of the equal sign. Yet, Rittle-Johnson et al.’s (2011) item response theory-based model showed that the difficulty of these items tends to be higher than the average ability levels of second-grade students. Therefore, such items provide low test information for young participants compared to items with more appropriate difficulty. Third, neither previous study controlled for covariates of cognitive abilities that previous studies have found to be predictive of developing algebraic competence, such as IQ, attentive behavior, arithmetic calculation skill, or number line estimation ability (Fuchs et al., 2014, Fuchs et al., 2016).

Finally, we note that the elementary school aged children in Byrd et al. (2015) received explicit supplemental instruction on how to solve mathematical equivalence problems as well as on how to solve unknown values represented by literal variables. Thus, the sole existing longitudinal study linking early elementary students’ equal sign knowledge to later algebra outcomes did not pertain to children who received business-as-usual instruction. Indeed, the effect observed by Byrd et al. (2015) is best characterized as that of an interaction between prior equal sign knowledge and explicit instruction on the sorts of problems assessed at posttest. The present analysis extends this work by observing these relations among even younger children who do not receive such instruction.

The Present Analysis

The purpose of the present analysis was to investigate whether students’ equal sign knowledge at end of second grade predicts their later algebraic knowledge in fourth grade while controlling for demographic variables and several measures of individual differences in cognitive processing and prior knowledge. Specifically, we included the following domain-general cognitive resources and math-specific skills previously shown to be related to algebraic knowledge by Fuchs et al. (2012) and Fuchs et al. (2016). IQ was included because theory suggests that algebra requires more complexity and overall cognitive demand than arithmetic does (e.g., Kieran, 1990). Attentive behavior was included because it has been shown to play a role in learning mathematics in general (Fuchs et al., 2006), as focusing attention is an important requisite step in learning. Arithmetic calculation skill was included because according to Pillay, Wilss, and Boultin-Lewis’s (1998) model, arithmetic competence provides the foundation for algebraic competence. Number line estimation was included because it has emerged in recent years as a general predictor of young children’s mathematical understanding (e.g., Booth & Siegler, 2008; Sasanguie, De Smedt, Defever, & Reynvoet, 2012).

We included students’ sex, due to ongoing interest in the role that sex differences may play in mathematics interest and achievement (e.g., Reilly, Neumann, & Andrews, 2015), as well as children’s eligibility for free and reduced lunch, as poverty is frequently viewed as a powerful factor limiting children’s academic potential (e.g., Duncan, Yeung, Brooks-Gunn, & Smith, 1998). Each of these demographic variables has also previously been found to affect children’s algebraic reasoning skills (Fuchs et al., 2014). Finally, we included a variable indicating whether children qualified for tutoring as assessed by calculation and word-problem screening measures in the parent study. The screener, which was designed to identify students who were at risk for poor math learning outcomes, was previously shown to be predictive of some measures of algebraic reasoning (Fuchs et al., 2014).

To index equal sign knowledge, we used open equations, which are frequently referred to as “math equivalence problems” in the literature (McNeil & Alibali, 2005; Perry, Church, & Goldin-Meadow, 1988; Bethany Rittle-Johnson, 2006; Sherman & Bisanz, 2009). Importantly, multiple open equations of various formats ensure that the assessment measures a range of equal sign knowledge levels that cover the typical skill set of second-grade students (see Rittle-Johnson et al, 2011; Matthews et al., 2012). The chief outcome was a two-part assessment of algebraic reasoning and skill administered to the same students two years later.

The goal of the analysis was to extend knowledge regarding the causal effects of early equal sign knowledge on later algebra skills. Finding evidence of a predictive relation between second-grade equal sign knowledge and later algebra skill would represent the first finding of this link among children this early in development. Additionally, finding such a link would provide important empirical corroboration of a causal connection that has been widely postulated but rarely investigated with longitudinal designs. The existence of such a link would underscore the importance of identifying validated early pedagogical approaches for promoting understanding of the equal sign. Moreover, the simplicity of administration of the chief measure of equal sign knowledge makes it a candidate for potential curriculum-based formative assessment measures that can be aligned with standards focused on the cultivation of equal sign knowledge. If findings indicate that equal sign knowledge is a unique predictor over and above other cognitive and demographic covariates, results will bolster arguments about the critical role of educational access in promoting such knowledge in the primary grades.

Method

Participants

Children were control group participants from a parent study conducted in a southeast metropolitan school district in the southeastern United States. The parent study investigated whether symbolic calculation or word-problem instruction better supports algebraic thinking (Fuchs et al., 2014). In the parent study, second-grade classrooms were randomly assigned to a control condition or to one of two instructionally enriched conditions, focused on word problems or calculations. Classroom teachers relied primarily on the basal program Houghton Mifflin Math (Greenes et al., 2005) to guide mathematics instruction.

Screening for study entry occurred with an initial sample of 1,917 students who had parental consent and assent (screening measures are described below in the Measures section). The 2-subtest Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999) was administered to exclude children scoring <9^th percentile on both subtests (because the study was not about intellectual disability). We excluded students in the instructionally enriched conditions because the enriched conditions were each designed to alter the course of typical development, and the present analysis aimed to investigate how prospective equal sign knowledge predicts algebra score in a business-as-usual instructional setting. As a result, the final sample for the current study was comprised of 191 students who scored above the criterion on the WASI, who did not receive instruction, and who were tested for equal sign knowledge. More complete information on the sampling procedure is available in the supplemental file.

In the final sample, 55.5% were female; 83.8% received subsidized lunch; 17.8% were English Language learners (EL); 35.6% were African American, 29.3% were white non-Hispanic, 26.2% were Hispanic, and 5.8% were other. 8.4% received special education services. Students’ mean age at the start of the study was 7.61 years (SD = 0.43). Table 1 includes summary demographics from the analytic sample.

Table 1.

Demographic Variables

Variable	N (%)		Variable	N (%)
Gender			Non-Native English Speaker
Female	106 (55.5%)		Yes	34 (17.8%)
Male	85 (44.5%)		No	157 (82.2%)
Race/Ethnicity			Eligible for Free/Reduced Lunch
African-American	68 (35.6%)		Yes	160 (83.8%)
White Hispanic	50 (26.2%)		No	31 (16.2%)
Kurdish	6 (3.1%)		Received Special Education Services
White Non-Hispanic	56 (29.3%)		Yes	16 (8.4%)
Other	11 (5.8%)		No	175 (91.6%)
Age at Start of Study			Eligible for Tutoring
6	7 (3.7%)		Yes	63 (33.0%)
7	153 (80.1%)		No	128 (67.0%)
8	31 (16.2%)

Measures

Screening measures.

The 2-subtest WASI comprises Matrix Reasoning and Vocabulary. With Matrix Reasoning, the child completes matrices; from each, a section is missing, and the child restores the matrix by selecting from 5 options. With Vocabulary, the tester presents pictures or says words, and the child constructs a definition for each. The subtests combined to yield a composite IQ score (α = .92). Four subtests of the Second-Grade Calculations Battery (Fuchs, Hamlett, & Powell, 2003) were also administered: Sums to 12, Sums to 18, Minuends to 12, and Minuends to 18. For each, students have 1 min to complete 25 problems (in the parent study, α = .85–.93). The screener was Sums to 12. Finally, a Story Problems assessment (Jordan & Hanich, 2000) was administered, which comprised 14 combine, compare, and change word problems, requiring single-digit addition or subtraction (α = .87).

The WASI was used as a screener for study inclusion, as described above. Calculation and word problem screeners were used to determine whether participants in the parent study’s treatment groups were eligible for small-group tutoring. Because students in the present analysis were in the control group, none received tutoring, but we did use second-grade eligibility for tutoring as a predictor of fourth-grade outcomes.

Second-Grade Predictor Measures

Attentive behavior was measured with the Strength and Weaknesses of ADHD Symptoms and Normal Behavior scale (SWAN; Swanson et al., 2004). The SWAN is an 18-item teacher rating scale (Swanson et al., 2012) that samples items from the Diagnostic and Statistical Manual of Mental Disorders-IV (APA, l994) criteria for Attention-Deficit/Hyperactivity Disorder for inattention (items 1–9) and hyperactivity/impulsivity (items 10–18). Validity is supported in the literature (Lakes, Swanson, & Riggs, 2012; Swanson et al., 2012). Items are rated as 1 = Far Below, 2 = Below, 3 = Slightly Below; 4 = Average, 5 = Slightly Above, 6 = Above, 7 = Far Above. We report data for the attentive behavior subscale as the average rating across the nine relevant items. We selected this subscale to index attentive behavior, or the ability to maintain focus of attention. The SWAN correlates well with other dimensional assessments of behavior related to attention. In the parent study, α = .99.

Equal sign knowledge was measured with The Open Equations Test (Powell, 2007), on which children solve 30 open equations, each featuring a blank representing a missing number. The equations are classified in terms of difficulty according to Rittle-Johnson et al.’s (2012) 4-level construct map for equal sign knowledge, with difficulty increasing as the knowledge level increases (Table 2). This construct map predicts the difficulty of items a priori based on features such as the sides on which items feature operators and the side on which the unknown is located (also see Powell, Kearns, & Driver, 2016). A list of the open equation items used, their a priori assigned levels on the construct map, and observed accuracies is shown below in Table 3 of the results section. Although the construct map is presented as having four levels for purposes of conceptual clarity, the underlying theoretical model of the construct is continuous and not discrete (Rittle-Johnson et al., 2011). For this sample, α = .87.

Table 2.

Construct Map for Math Equivalence Knowledge

Level	Description	Equation Structure	Sample Items
4 Comparative Relational	Successful with a variety of equation structures by comparing expressions on the two sides of the equal sign. Generate a relational definition of the equal sign.	Operations on both sides with multi-digit numbers or with multiple instances of a variable.	ST	67 + 86 = 68 + 85 (true or false? explain why)
			EQ	What does the equal sign mean?
			OE	__ + 55 = 37 + 54
3 Basic Relational	Successful with equation structures with operations on both sides of the equal sign. Recognize a relational definition of the equal sign as correct.	Operations on both sides: a + b = c + d a + b – c = d + e	ST	31 + 16 = 16 + 31 (true or false?)
			EQ	Is “the same as” a good definition of equal sign?
			OE	5 + __ = 6 + 2
2 Flexible Operational	Successful with equation structures that are compatible with an operational view of the equal sign.	Operations on the right side: c = a + b No operations: a = a	ST	4 = 4 + 0 (true or false?)
			EQ	10 cents __ one dime (select correct symbol)
			OE	7 = __ + 3
1 Rigid Operational	Successful with an operations-equals-answer equation structure. Generate an operational definition of the equal sign.	Operations on the left side: a + b = c	ST	5 + 2 = 7 (true or false?)
			EQ	Identify a pair equal to 3 + 6
			OE	__ + 5 = 9

Note. Table adapted from Rittle-Johnson et al. (2011, p. 87). Success includes the ability to solve, evaluate, and encode equations of a particular structure. ST = Equation-Structure Items, EQ = Equal-Sign Items, OE = Open Equation-Solving Items.

Table 3.

Open Equation Items with their a priori Levels on the Construct Map, and Accuracies

Item Number	Item	Construct Map Level	Mean Accuracy	SD
1	2 + __ = 8	1	0.77	0.42
2	__ − 4 = 3	1	0.44	0.50
7	9 −__ = 6	1	0.62	0.49
8	5 + __ = 11	1	0.74	0.44
12	14 − __ = 6	1	0.47	0.50
13	__ + 6 = 13	1	0.55	0.50
16	__ + 3 = 7	1	0.60	0.49
19	4 + 5 = __	1	0.76	0.43
23	__ − 6 = 4	1	0.18	0.38
30	8 − 3 = __	1	0.52	0.50
	Mean Accuracy Level 1		.57	.28
3	__ = 4	2	0.23	0.42
4	6 = 2 + __	2	0.50	0.50
5	9 = 14 − __	2	0.34	0.47
6	15 = __ + 7	2	0.47	0.50
10	5 = 9 − __	2	0.39	0.49
15	12 = 7 + __	2	0.38	0.49
18	__ = 6 + 5	2	0.43	0.50
21	6 = __ − 8	2	0.05	0.21
22	7 = __ − 2	2	0.15	0.36
25	__ = 7 − 4	2	0.35	0.48
26	7 = __	2	0.20	0.40
27	8 − 3 = __	2	0.36	0.48
	Mean Accuracy Level 2		.32	.25
9	11 − __ = 9 − 5	3	0.03	0.16
11	12 − 5 = __ − 3	3	0.05	0.21
14	7 + 4 = __ + 6	3	0.04	0.19
17	6 + __ = 2 + 8	3	0.10	0.31
20	__ + 4 = 5 + 2	3	0.08	0.27
24	3 + 5 = 4 + __	3	0.07	0.26
28	__ − 3 = 7 − 2	3	0.04	0.20
29	9 − 6 = 7 − __	3	0.07	0.25
	Mean Accuracy Level 3		.06	.15

Note: Items in gray yielded accuracies that were significantly lower than others in the same hypothesized level of the construct map. Each of these three took the form X = _ − Y

Arithmetic calculation skill was measured with the Wide Range Achievement Test 3–Arithmetic (WRAT- 3; Wilkinson, 1993), which includes an oral and a written component. The oral portion focuses on early numerical competencies. In the written section, students have 10 min to answer written calculation problems that progress from one-digit addition and subtraction to two-digit addition and subtraction to whole-number multiplication and division to problems involving fractions, decimals, and more complex calculation skills. Because we wanted to estimate start-of-second-grade calculation skill, we relied on the written component. In the parent study, α = .93.

Number line estimation skill was measured with a 0–100 Number line estimation task. Children indicated where a target number was located on a number line marked with 0 and 100 as endpoints. Target numbers were 3, 4, 6, 8, 12, 17, 21, 23, 25, 29, 33, 39, 43, 48, 52, 57, 61, 64, 72, 79, 81, 84, 90, and 96. Items were presented in random order and administered at a self-paced rate, without a time limit. Performance was defined as each participant’s mean percentage of absolute error (PAE), where PAE was generated by (|answer – correct answer|/numerical range) and the numerical range was 100, corresponding to the total range presented on the number line. A smaller PAE indicates more accurate responding. Test–retest reliability conducted on 87 children in the parent study was .85 (Fuchs et al., 2016).

Fourth-Grade Outcome Measures

Algebraic knowledge was measured with an adapted version of The Test of Basic Algebra and Procedures based on items developed by Fuchs, Seethaler, and Powell (2009). The assessment includes two subtests, each featuring a different type of item: solving equations with variables and function tables (see Figure 1 for example items). The solving equations subtest comprises 20-items on which children solved simple algebraic problems featuring letters standing for missing quantities (α = .91).

Figure 1.

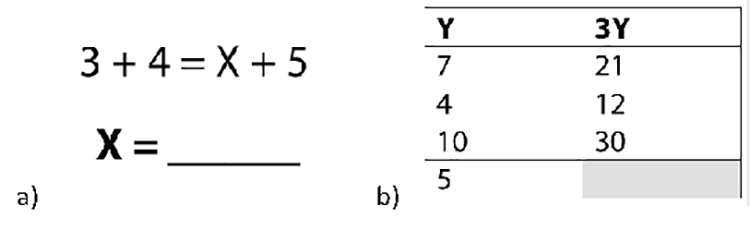
Sample items from (a) equation solving and (b) functions subtests.

The function tables subtest features six items. Each shows a 2-column table in which the header row indicates that the left column represents different values a variable can take and that the second column represents a linear function transforming that variable. All but the target row indicates a value the variable can take and the corresponding value for the function. In the target row, the value of the function is empty, and children are directed to “write the answer in the empty gray box.” Unlike the open equation predictor items, some function table items involve formalisms for variables multiplied by coefficients (e.g., 2x+1). For this subtest α = .81

Procedure

Testing occurred in classrooms for measures administered in groups. All other measures were administered individually in other, quiet school locations. Students were assessed on math screening measures in large groups and on WASI individually in September of second grade. In September-October of second grade, students were tested on the WRAT-Arithmetic in large groups and on number line estimation individually, and teachers completed the SWAN. In March and April of second grade, students were assessed in large groups on open equations. In March and April of fourth grade, they were assessed on algebraic reasoning. Testers were trained to criterion on each measure, and all individual test sessions were audiotaped, 20% of which were independently rescored to administration fidelity (agreement = 98%). Fidelity exceeded 99%. All data were double entered and verified.

Results

Distribution and Difficulty of the Equal Sign Predictor Measure

We began by examining the difficulties of the equal sign knowledge predictor items as a validity check on the chief predictor of interest. First, we assessed whether empirically observed difficulty for each of the 30 open equation items, as assessed by mean accuracy, aligned with hypothesized difficulties based on Rittle-Johnson et al.’s (2011) construct map. A priori hypothesized item difficulty was highly correlated with observed mean accuracy, r (28) = −.83, p < .001 (see Table 3).

Second, we checked the distribution of the equal sign knowledge predictor variable. Performance was normally distributed (skewness = .23, kurtosis = −.42). Items were sufficiently difficult that mean accuracy for the 10 Level 1 items was only 57%. Level 3 items were difficult enough that 147 of the 191 participants (77.0%) failed to solve a single item (of 8) correctly, and overall accuracy was only 6%. Still, performance spanned nearly the entire range of possible values (M =9.99, SD = 5.71, range = 0 – 28 of 30). There was an absence of ceiling and floor effects.

A Direct Model: Predicting Fourth-Grade Algebra from Second-Grade Equal Sign Knowledge

We next investigated the extent to which second-grade equal sign knowledge prospectively predicted algebra competence in fourth grade. Zero order correlations are shown in Table 4. Initially, we directly regressed each of the two fourth-grade algebra subtests against our set of predictor variables using Ordinary Least Squares (OLS). Fall of second-grade predictors were sex, eligibility for free or reduced lunch, eligibility for math tutoring, IQ, attentive behavior, arithmetic skill, and number line estimation performance. Equal sign knowledge was entered as a spring of second-grade predictor. We report standardized coefficients for this analysis (see Table 5), because they facilitate interpretation of effects in terms of a common scale.

Table 4.

Means, Standard Deviations, and Correlations (n = 191)

			Correlations
Variable type/Variable	Mean	SD	1	2	3	4	5	6	7	8	9	10
Fall of Second Grade
1. Sex (female = 1)	.55		−
2. Eligible Free/Reduced Lunch (yes = 1)	.84		.15*	−
3. Eligible for tutoring (yes = 1)	.33		.05	.19**	−
4. IQ	92.60	12.18	−.07	−.22**	−.31**	−
5. Attentive Behavior	39.39	13.88	.10	−.18*	−.42**	.39**	−
6. Arithmetic Skill	93.69	13.64	−.01	−.01	−.41**	.43**	.38**	−
7. Number Line estimation	15.50	7.53	.32**	.23**	.32**	−.33**	−.34**	−.28**	−
Spring of Second Grade
8. Equal Sign Knowledge	9.99	5.70	−.08	−.24**	−.41**	.42**	.51**	.44**	−.46**	−
Fourth Grade
9. Solving Equations	12.35	5.07	−.16*	−.15*	−.41**	.54**	.54**	.49**	−.46**	.66**	−
10. Functions	3.68	1.94	−.03	−.07	−.34**	.45**	.44**	.45**	−.32**	.55**	.61**	−

Note: IQ is a composite of Verbal and Matrix Reasoning subtests from the Wechsler Abbreviated Scale of Intelligence. Arithmetic skill is Wide Range Achievement Test–Arithmetic. Number Line Estimation is percent absolute error (PAE); a lower number line PAE indicates higher performance, so a negative correlation with PAE indicates a positive relation with number line estimation skill. Attentive behavior is Strengths and Weaknesses of ADHD Symptoms and Normal Behavior Rating Scales. Equal Sign Knowledge is summed accuracy for open equations. Solving Equations is the solving equations subtest of The Test of Basic Algebra and Procedures. Functions is the solving functions subtest of The Test of Basic Algebra and Procedures.

^*p < .05

^**p < .01

Table 5.

OLS Regressions of Fourth Grade Outcomes Against Second Grade Predictors (n = 191)

	DV: Solving Equations R2=.60			DV: Functions R2=.40
Variable type/Variable	β	p	sr2	β	p	sr2
Fall of Second Grade
Sex (female = 1, male = 0)	.10	.057	.01	−.02	.742	.00
Eligible Free/Reduced Lunch (yes = 1, not= 0)	.07	.180	.00	.08	.214	.01
Eligible for tutoring (yes = 1, no = 0)	−.05	.435	.00	−.02	.763	.00
IQ	.19	.002	.02	.16	.033	.02
Attentive Behavior	.19	.003	.02	.14	.058	.01
Arithmetic Skill	.12	.053	.01	.19	.014	.02
Number Line Estimation PAE	−.10	.095	.01	−.03	.720	.00
Spring of Second Grade
Equal Sign Knowledge	.39	<.001	.09	.32	<.001	.06

Note: All coefficients are standardized. A lower number line PAE indicates higher performance, so a negative correlation with PAE indicates a positive relation with number line estimation skill.

In this model, the single largest predictor of fourth-grade equation solving skill was equal sign knowledge in spring of second grade (β = 0.39, p < .001), with a one standard deviation increase in equal sign knowledge corresponding to a 0.39 standard deviation increase on the equation solving subtest. Fall of second-grade predictors IQ (β = 0.19, p = .002) and attentive behavior (β = 0.19, p < .003) were also uniquely predictive. We analyzed squared semi-partial correlation coefficients (sr²) to quantify the explanatory power of equal sign knowledge relative to other predictors in this model: the unique variance explained by each variable in the final model over and above shared variance among items, which corresponds to change in R² if the variable were to be subtracted from the model. We calculated a ratio of the sr² for equal sign knowledge to the summed sr² for all other variables in the model. This ratio indicated that equal sign knowledge alone explained 1.11 times as much unique variance than all other predictors combined.

Similarly, spring-of-second-grade equal sign knowledge was also the largest predictor of fourth-grade functions performance (β = 0.32, p < .001), with a one standard deviation increase in equal sign knowledge corresponding to a 0.32 standard deviation increase in functions performance. Fall-of-second-grade IQ (β = 0.16, p = .033) and arithmetic calculation skill (β = 0.19, p = .014) were also significant predictors. The ratio of the sr² for equal sign knowledge to that of other variables was .99, indicating that equal sign knowledge alone explained as much unique variance as all other predictors combined.

Equal Sign Knowledge as Mediator

Use of the direct regression model examined above reflected our hypothesis that all independent variables affected algebra outcomes directly. However, we note two features of our data that may indicate an alternative model for analysis. First, the spring-of-second-grade measure of equal sign knowledge was collected at a later time point than other second-grade measures. Second, given that ability measures like IQ and prior math knowledge measures (e.g., number line estimation) are generally hypothesized to facilitate or constrain learning, it may be the fall measures affect equal sign learning between fall and spring time points. Thus, fall individual difference measures may plausibly be causally related to differences in spring equal sign knowledge, which in turn lead to differences in fourth-grade algebra outcomes. For these reasons, we also modeled spring-of-second-grade equal sign knowledge as a mediator of fall predictors on the fourth-grade algebra outcomes.

We tested for mediation following an OLS-based path analytic framework using Hayes’ (2013) MEDIATE macro for SPSS. This analysis calculated decomposed effects, with estimates of the direct paths as well estimates of indirect effects via equal sign knowledge and total effects of both direct and indirect paths. The macro used bootstrapping estimation with 10,000 draws to estimate standard errors and 95% confidence intervals (CIs) for indirect and total effects. We converted all variables to standard scores prior to running the model. Analyses were run for each subtest, and parameter estimates are detailed in Table 6. CIs that do not cover zero are statistically significant. Because direct effects of fall variables correspond to the OLS regression discussed above, we focus presentation of results on indirect and total effects of the fall predictors.

Table 6.

Indirect and Total Effects of Second Grade Fall Predictors on Second Grade Equal Sign Knowledge and on Fourth Grade Outcomes Mediated via Equal Sign knowledge (n = 191)

	Fall of Second Grade Predictors
	Sex Female = 1	Eligibility for Free/Reduced Lunch	Eligibility for tutoring	IQ	Attentive Behavior	Arithmetic Skill	Number Line Estimation
Effects on Second Grade Equal Sign Knowledge (mediator) R2 = .43	0.023 [−0.101,0.146]	−0.129* [−0.243,−0.007]	−0.109 [−0.243,0.024]	0.115 [−0.024,0.254]	0.272* [0.134,0.409]	0.165* [0.026,0.305]	−0.205* [−0.340,−0.071]
Effects on 4th Grade Solving equations
Indirect effect (CI)	0.009 [−0.040,0.061]	−0.050 [−0.105,0.002]	−0.043 [−0.102,0.010]	0.045 [−0.009,0.104]	0.106* [0.047,0.178]	0.065* [0.009,0.129]	−0.080* [−0.145,−0.026]
Total Effect (CI) R2 = .51	0.112 [−0.004,0.223]	0.022 [−0.092,0.133]	−0.088 [−0.213,0.033]	0.238* [0.108,0.364]	0.295* [0.166,0.419]	0.184* [0.054,0.310]	−0.181* [−0.306,−0.059]
Effects on 4th Grade Functions
Indirect effect (CI)	0.007 [−0.034,0.051]	−0.041 [−0.093,0.003]	−0.035 [−0.089,0.006]	0.037 [−0.008,0.092]	0.087* [0.034,0.157]	0.053* [0.007,0.113]	−0.066* [−0.129,−0.020]
Total Effect (CI) R2 = .34	0.029 [−0.105,0.163]	0.041 [−0.092,0.173]	−0.057 [−0.201,0.088]	0.197* [0.046,0.348]	0.233* [0.083,0.382]	0.239* [0.088,0.390]	−0.092 [−0.238,0.054]

Note: All coefficients are standardized. A lower number line PAE indicates higher performance, so a negative correlation with PAE indicates a positive relation with number line estimation skill.

^*p < .05 level.

Fall of second-grade predictors explained 43% of the variance in equal sign knowledge. Free or reduced lunch, attentive behavior, arithmetic skill, and number line estimation were directly related to spring-of-second-grade equal sign knowledge (note that number line estimation is scored such that a negative coefficient reflects a positive relation). The observed relations between arithmetic skill, number line estimation, and equal sign knowledge are consistent with the conclusion that baseline level of numerical competence serves as a limiting factor for correct processing of open equation items.

Three indirect paths also emerged as significant for predicting equation solving in fourth grade (Figure 2). Higher attentive behavior, stronger arithmetic skill and better number line estimation each showed significant positive indirect effects via equal sign knowledge. The combinations of indirect effects via mediation and direct effects revealed significant total effects for multiple variables that were somewhat larger than those shown in our initial direct regression analysis: IQ (β = 0.24 vs. 0.19) and attentive behavior (β = 0.30 vs. 0.19) bore larger effects compared to the OLS analysis. Moreover, arithmetic skill (β = 0.18 vs. 0.12) and number line estimation (β = −0.18 vs. −0.10) had positive total effects in this mediation model as opposed to the direct OLS model.

Figure 2.

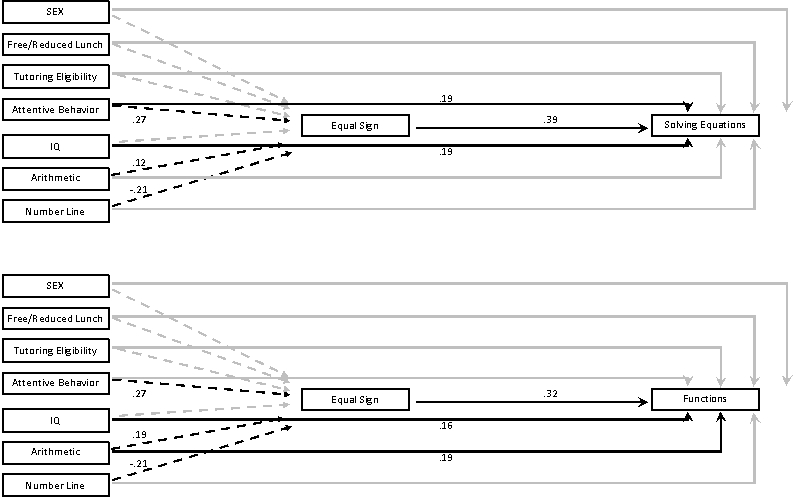
Models showing direct (solid lines) and indirect (broken lines) paths to solving equations (top) and functions (bottom) subtest performance. Black lines indicate significant paths, and gray lines nonsignificant paths. Factors in in the first column were measured in fall of second grade, equal sign knowledge was measured in spring of second grade, and solving equations performance was measured in fall of fourth grade. Note: These figures depict path diagrams for which coefficients are listed in Tables 5 and 6.

There were also significant positive indirect effects for attentive behavior, arithmetic skill, and number line estimation for predicting fourth-grade performance on fourth-grade algebraic functions outcome (see Figure 2). The combinations of indirect via mediation and direct effects revealed significant total effects for multiple variables, which were somewhat larger than those shown in our initial direct regression analysis: IQ (β = 0.20 vs. 0.16), attentive behavior (β = 0.23 vs. 0.14) and arithmetic calculation skill (β = 0.24 vs. 0.19). Indeed, attentive behavior was nonsignificant in the direct analysis but was positively related to functions subtest performance according to the mediation model. Even so, the mediation model explained somewhat less variance in equation-solving performance compared to the direct model (R²_Mediation/R²_Direct = .86). This was also the case for functions performance (R²_Mediation/R²_Direct = .85).

Discussion

We found that second-grade equal sign knowledge prospectively predicted fourth-grade algebraic thinking skills using two different models: a direct regression model and a model in which equal sign knowledge served as a mediator. According to the direct regression model, equal sign knowledge was a significant predictor of performance on both algebraic reasoning subtests administered two years later. Across the two reasoning tasks, IQ, attentive behavior, and arithmetic calculation skill also emerged as significant predictors of algebraic reasoning according to the direct model. Still, equal sign knowledge explained as much unique variance as all other predictors combined.

The alternative mediation yielded somewhat larger total effects for IQ and attentive behavior. This model also yielded significant total effects for start-of-second-grade arithmetic calculation skill and number line estimation on fourth-grade equation solving as well as total effects for second-grade arithmetic calculation on fourth-grade functions performance. However, results indicated that more than half the variance in equal sign knowledge (the hypothetical mediator) was left unexplained by the other fall of second-grade factors. This means that other exogenous factors inherent in equal sign knowledge were responsible for a large portion of the direct path to solving equations and functions. Moreover, the direct model explained more variance on the outcomes than the mediator model for both algebraic subtests. These findings combined with our theoretical priors lead us to prefer the direct model over the mediation model, but both converge to make one thing clear: Knowledge of the equal sign is important for the development of algebraic thinking.

These longitudinal results strengthen empirical evidence for a causal link between knowledge of the equal sign and algebraic reasoning. Despite a wealth of theory suggesting such a causal connection (e.g., Carpenter et al., 2003; Filloy & Rojano, 1989; Kaput et al., 2008; Kieran, 1981; National Council of Teachers of Mathematics, 2000; Seo & Ginsburg, 2003; Sfard & Linchevski, 1994; Steinberg et al., 1991), the present analysis is only the third published study empirically showing that equal sign knowledge predicts later algebra knowledge (Alibali et al., 2007; Byrd et al., 2015). This study is the first to do so with students as young as second grade.

The True Nature of Risk?

Knowledge of the equal sign was by far the strongest predictor of performance on both subtests of algebra according to our preferred direct model. In fact, the effect of equal sign knowledge was larger than the combined effects of individual differences in IQ and attentive behavior combined. Moreover, both eligibility for subsidized lunch and eligibility for tutoring (based on low second-grade math screening scores) failed to emerge as significant predictors for either algebra outcome subtest. Although typically considered to be risk factors, these provided little value in predicting algebraic thinking in our analysis that controlled for a variety of cognitive, mathematical, and socioeconomic variables. All told, findings provide persuasive evidence that equal sign knowledge accrues benefits for future algebraic reasoning beyond the cognitive and demographic factors sometimes viewed as constraining potential for educational achievement.

Our findings are consistent with decades of research demonstrating that children across a wide age span typically have limited understanding of the equal sign (e.g., Baroody & Ginsburg, 1983; Behr et al., 1980; Falkner et al., 1999; Jacobs, Franke, Carpenter, Levi, & Battey, 2007; Li et al., 2008; McNeil, 2008; Perry, 1991; Powell & Fuchs, 2010). Children in the present study were only 50% accurate on open equation items, despite the fact that no numbers were greater than 14. For example, children in the present analysis solved 4 + 5 = __ with 76% accuracy and 5 + _ = 11 with 74% accuracy, but only solved __ = 6 + 5 with 43% accuracy. Thus, the primary factor for low open equation performance appears to be conceptual misunderstanding, which is consistent with Rittle-Johnson et al.’s (2011) equal sign knowledge construct map.

To be clear, this is not just a second-grade issue. Falkner et al (1999) found that when presented with the problem 8 + 4 = __ + 5, all 145 sixth graders in their sample answered either 12 or 17. Similarly, Fyfe et al. (2018) found that a full 10% of Grade 7–12 students in their sample failed to properly solve 7 + 6 + 4 = 7 + __. Thus, without intervention, such conceptual difficulty found among second graders can persist until middle and high school, and such misconceptions are related to difficulties in algebraic reasoning in later grades (e.g., Byrd et al., 2015; Fyfe et al., 2018; Knuth et al., 2006). This early conceptual difficulty is important enough that it can impede students’ eventual access to algebra and alter future educational and employment prospects.

The persistence of these deficits is particularly troublesome given that multiple studies have shown that brief conceptual intervention can lead to improvements in children’s equal sign knowledge (e.g., Fyfe et al., 2014; Matthews & Rittle-Johnson, 2009; Perry, 1991; Powell & Fuchs, 2010; Rittle-Johnson & Alibali, 1999). Unfortunately, it remains the case that the majority of available resources available to educational practitioners fail to provide adequate attention to teaching children about the equal sign. Indeed, most textbooks neither explicitly define the equal sign nor expose students to nonstandard equations that can help promote equal sign knowledge (Capraro, Capraro, Ding, & Li, 2007; McNeil et al., 2006; Powell, 2012; Rittle-Johnson et al., 2011). In a similar vein, although the Common Core State Standards currently include understanding the equal sign in the first-grade standards for Operations and Algebraic Thinking, explicit focus disappears from the standards by second grade. This is the case even though, as shown in the present analysis, the deficit is clearly present at second grade. If the education system is committed to ensuring equitable access to algebra and the power it confers, then a commitment is needed to influence the malleable factors that promote its acquisition. Equal sign understanding is clearly one critical malleable factor.

Limitations and Future Directions

Before closing, we note some important study limitations. First, the present analysis was limited by the measures used and by the age ranges tested. Our measure of equal sign knowledge was limited to performance on open equations, and adding more comprehensive measures that span the entire range of difficulty on the math equivalence construct map can broaden understanding of effects (see for example Matthews et al., 2012). Covering a larger range of item types and difficulties would allow for integration of powerful items such as assessing students’ explicit definitions and permit the development of a vertically scaled measure of equal sign knowledge, which might be used effectively across grade ranges to explore its relations to algebraic thinking. Use of such a vertically scaled assessment may extend similar studies to include children beyond second through fourth grades and perhaps into adulthood (cf. Fyfe et al., 2018). Future studies using more comprehensive measures with a broader age range are thus necessary to create a fuller picture of the role of equal sign knowledge.

More generally, even though the assessment of algebraic thinking we used covered key aspects of algebra, it still only covered a subset of the domain. To the extent that the goal is to understand how knowledge of equality relates to algebra, these relations should be tested with additional facets of the domain, including topics like understanding linear equations in two or more variables, understanding quadratics, solving word problems, and interpreting variable expressions. Assessments could also be developed to test more nuanced aspects of algebraic thought such as the transition from viewing an expression like 3(x + 5) + 1 as a computational process to seeing it as a function that transforms every number x into another (Sfard & Linchevski, 1994) or other cognitive gaps between algebraic and arithmetic thinking (Herscovics & Linchevski, 1994). Some of these topics require longer-term predictions. Using more varied and nuanced assessments that span initial stages of formal algebra instruction may extend our understanding of the extent to which the equality concept promotes general algebraic competence.

Finally, there is a need to conduct studies with strong interventions that continue to track development over the long term. The present analysis focused on the predictive power of existing equal sign knowledge, but included no intervention, and existing intervention studies tend to focus on short-term effects of single-dose instruction (but see Byrd et al, 2015). Additionally, no studies have sought to teach children to a criterion regarding equal sign knowledge and followed their subsequent development over time. Moreover, no studies have taken laboratory methods for increasing equal sign knowledge and employed them in a spaced pattern that a century of research has shown leads to long-term retention of the concept (Ebbinghaus, 1885/1964; Vlach, 2014). Such studies, seeking to optimize the dosage and spacing of instruction on the equal sign, are essential for determining the upper bounds on the effectiveness of equal sign knowledge in promoting algebraic competence

Conclusion

This research shows that early understanding of the equal sign is a powerful predictor of later algebraic competence. The effects of this knowledge outstripped all other predictors we investigated, including IQ and attentive behavior as well as arithmetic skill and eligibility for subsidized lunch. Thus, if algebra serves as a gatekeeper for students’ future academic and economic success, then it appears that knowledge of the equal sign serves as a key to the gate. One important implication of this finding is that efforts to improve algebra access should focus on promoting knowledge of the equal sign and disseminating information about its importance.