Simultaneous Bayesian inference of phylogeny and molecular coevolution

Significance

Phylogenetic methods inferring molecular coevolution have recently gained traction for their capacity to predict protein surface interactions and to clarify their function within metabolic pathways. These methods rely on phylogenies inferred under the assumption that coevolution does not exist (i.e., sites evolve independently). However, violations of this assumption lead to considerable inaccuracies in the inferred phylogeny, which in turn can negatively affect the estimation of coevolution. We tackle this problem by developing a Bayesian method to simultaneously infer phylogenetic relationships and predict coevolution from nucleotide sequences. The main novelty of our method is its ability to account for the interdependencies between molecular coevolution and phylogeny, thus relaxing a long-standing assumption in the study of molecular evolution.

Abstract

Patterns of molecular coevolution can reveal structural and functional constraints within or among organic molecules. These patterns are better understood when considering the underlying evolutionary process, which enables us to disentangle the signal of the dependent evolution of sites (coevolution) from the effects of shared ancestry of genes. Conversely, disregarding the dependent evolution of sites when studying the history of genes negatively impacts the accuracy of the inferred phylogenetic trees. Although molecular coevolution and phylogenetic history are interdependent, analyses of the two processes are conducted separately, a choice dictated by computational convenience, but at the expense of accuracy. We present a Bayesian method and associated software to infer how many and which sites of an alignment evolve according to an independent or a pairwise dependent evolutionary process, and to simultaneously estimate the phylogenetic relationships among sequences. We validate our method on synthetic datasets and challenge our predictions of coevolution on the 16S rRNA molecule by comparing them with its known molecular structure. Finally, we assess the accuracy of phylogenetic trees inferred under the assumption of independence among sites using synthetic datasets, the 16S rRNA molecule and 10 additional alignments of protein-coding genes of eukaryotes. Our results demonstrate that inferring phylogenetic trees while accounting for dependent site evolution significantly impacts the estimates of the phylogeny and the evolutionary process.

Molecular coevolution is the evolutionary process by which interactions between distant sites of a molecule, or sites of different molecules, are maintained such as to preserve advantageous functional or structural properties. For instance, coevolving fragments within protein sequences are involved in folding constraints and informative of folding intermediates, peptide assembly, or key mutations with known roles in genetic diseases (1, 2). The ever-growing availability of molecular sequences (nucleotides and amino acids) provides us with an unprecedented amount of data that hold a strong potential to reveal genes and gene regions evolving under a constrained process (3, 4).

There exist several methods to infer coevolution from sequence data alone (based on matching patterns between sites, as reviewed in refs. 5 and 6). However, these methods do not exploit a key component in modeling the underlying evolutionary processes: the phylogenetic tree describing the relationships between molecular sequences. Incorporating the phylogenetic signal in the analysis of coevolution is crucial because it enables us to distinguish between truly coevolving patterns and similar patterns induced by the shared history of sequences (5, 7). To this end, several methods have been developed to infer coevolution while accounting for phylogenetic relationships (7), but only a few of these explicitly model the process of coevolution along a given phylogenetic tree (8–11).

All phylogeny-aware methods to detect coevolution rely on the assumption that the phylogenetic relationships between sequences are known and can be treated as “observed data.” Typically, phylogenetic trees are themselves inferred from molecular data (12), but their inference is based on a fundamental assumption that each site evolves independently of all of the others (13). This assumption, which is evidently violated in the presence of coevolution, has benefits in terms of computational tractability, because the likelihood of an alignment given a phylogenetic tree is the product of the individual likelihood of each site. This simplification of the evolutionary mechanism in the presence of nonindependent sites has been shown to decrease the accuracy of the inferred phylogenetic trees (14, 15). However, datasets with strong functional or structural constraints are often analyzed within phylogenetic frameworks that assume independence among sites. For instance, the small ribosomal subunit (16S) is frequently used to estimate the earliest evolutionary relationships between the major lineages of the tree of life (16, 17), neglecting its numerous structural constraints and evidence of coevolution (18).

The presence of coevolutionary patterns across many nucleotide and amino acid sequences extends far beyond the 16S gene and is supported by a large body of evidence (9, 19). Ignoring the interdependencies between the phylogenetic history of the sequences and the constrained processes governing the evolution of nucleotides or amino acids can severely hamper our ability to infer correct phylogenetic trees (14, 15) and accurately detect coevolution (5, 7). However, the inference of these interdependent processes is still conducted separately for mathematical convenience, at the expense of assuming independence among sites which was originally described as “not necessarily biologically valid” by Felsenstein in 1983, at the dawn of likelihood-based molecular phylogenetics (13). To address this issue, we present a Bayesian framework to analyze a nucleotide alignment and jointly estimate (i) the number of pairs of sites that coevolve and their position in the sequence, thus differentiating from a background model of independent evolution, (ii) the parameters of the independent and dependent models of substitution, and (iii) the phylogenetic tree describing the relationships between sequences. Our method is called CoevRJ and the software implementing it is available at https://bitbucket.org/XavMeyer/coevrj.

We evaluate the performance of CoevRJ in reconstructing phylogenetic trees and inferring coevolution based on an extensive range of simulated datasets, an alignment of the highly coevolving 16S rRNA and 10 empirical eukaryote datasets of protein-coding genes. We show that CoevRJ provides an accurate identification of the coevolving sites, as validated by simulated and empirical data. We assess the effects of coevolution on phylogenetic estimates by comparing our results with those obtained under the assumption of independent evolution and demonstrate the importance of accounting for dependence among sites when inferring phylogenetic trees on datasets subject to coevolution.

Results

CoevRJ: A Bayesian Framework to Jointly Estimate Phylogeny and Molecular (Co)evolution.

The CoevRJ method simultaneously infers the phylogenetic relationships between molecular sequences as well as the number and position along the sequence of the sites (if any) that evolved in a dependent fashion. The method estimates the posterior probability of the many scenarios of evolution considered, as well as their parameters values using the reversible jump Markov chain Monte Carlo (RJMCMC) algorithm (20) (Fig. 1).

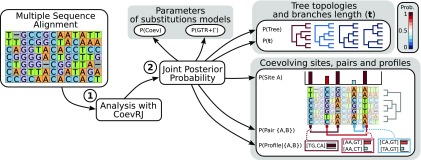
Fig. 1.

CoevRJ analysis flow. (1) A multiple sequence alignment containing nucleotides must be provided as input for CoevRJ. (2) After the analysis of the dataset, CoevRJ produces log files containing samples from the joint posterior distribution. These samples enable the estimation of the posterior probability of (i) the parameters of the evolutionary processes (GTR+$\mathrm{\Gamma }$ and Coev), (ii) the tree topologies and the branch lengths, and (iii) the pairs of sites and their profile. Further postanalyses with CoevRJ define the significance threshold for the coevolving pairs and provide easily readable summary statistics.

Our approach, further described in Materials and Methods, includes a mixture of two evolutionary models that can accommodate many possible scenarios of dependent and independent evolution among sites within a gene. Sites are not a priori assigned to either category; rather, their mode of evolution is estimated from the data. Independent sites are considered to evolve under a general time-reversible substitution model with rate heterogeneity among sites modeled by a Gamma distribution [GTR+$\mathrm{\Gamma }$ model (21)]. The mean rate of substitution is set to 1 and the shape of the Gamma distribution is modeled by a single parameter $\alpha$ and discretized into a finite set of rate multipliers to incorporate varying substitution rates across all sites of the alignment.

Dependent sites are modeled with an adapted version of the Coev model (11), under which coevolving pairs of sites evolve in a dependent fashion, such that the nucleotides at both sites remain within a predefined set of nucleotide pairs, defined as the “coevolving profile.” A substitution in one site of a coevolving pair is expected to trigger a subsequent substitution at the other site such that the nucleotides combination remains in the profile. A coevolving profile contains between two and four nucleotide pairs encompassing the possible cosubstitutions. For instance, pairs (AA, CC, TT, GG) or the Watson–Crick base pairs (AT, CG) may form a coevolving profile. However, the Watson–Crick base pairs augmented with the wobbling pair GT cannot form a profile since the wobbling pair differs by a single substitution from the two other pairs (11). The coevolution process is modeled as a reversible continuous-time Markov chain with rate parameters distinguishing among single site substitutions (i) leading to the profile (rate $d$), (ii) breaking the profile (rate $s$), and (iii) allowing the pairs of sites to evolve within out-of-profile pairs (rate $r$).

The combination of GTR+$\mathrm{\Gamma }$ and Coev forms a mixture of models parameterized by the number of coevolving pairs of sites and their position within the molecular alignment. This mixture of models ranges from sites being fully independent and evolving under a pure GTR+$\mathrm{\Gamma }$ model to all sites being involved in nonoverlapping coevolving pairs. Independent and coevolving sites, regardless of the configuration of the mixture, are assumed to evolve on the same phylogeny (including topology and branch lengths), and therefore both contribute to its estimation. The branch lengths are, however, decoupled between models by scaling their respective rate matrices to yield an expected value of one substitution per branch length unit and by applying a unique branch length (or rate) multiplier $\nu$ for sites under coevolution.

Estimating all these parameters represents a significant computational challenge that we overcome by making some simplifying assumptions. We assume the coevolving pairs to follow a homogeneous (co)evolutionary process and share the same substitution rates ($d,s,r$). This (co)evolutionary process is mainly characterized by parameters $d$ and $s$ that define the attraction of a pair of sites to their coevolving profile. As these two rate parameters are not expressed in the GTR+$\mathrm{\Gamma }$ model, we considered the rate parameters of coevolving and independent sites as independent. Finally, we infer the profile of each coevolving pair from a reduced set of profiles limited to the nucleotide pairs observed at the corresponding sites in the alignment. Under these assumptions, Bayesian inference of the GTR+$\mathrm{\Gamma }$ and Coev mixture of models is tractable with the CoevRJ method, as we demonstrate in the following sections using synthetic and empirical datasets.

CoevRJ Accurately Estimates Pairs of Sites and the Phylogeny.

To assess the performance of CoevRJ, we generated a total of 250 alignments of nucleotides each with 1,000 sites and 50 taxa, with a proportion of coevolving sites ranging from 0% (independent evolution) to 50% of the sites. CoevRJ correctly recovered the number of pairs of coevolving sites and their position (if any) under each scenario, with accuracy equal to 0.99 or higher (SI Appendix, Table S1). For datasets simulated under independent evolution, CoevRJ identified at most one pair over the 1,000 simulated sites. For datasets simulated with coevolving pairs, CoevRJ accurately identified most of the coevolving pairs of sites with a sensitivity of 98%. Overall, the models inferred with CoevRJ were consistent with the amount of coevolution simulated: Both the number of coevolving sites and their position were accurately identified as well as the sites that were not coevolving.

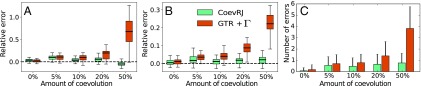
We then measured the ability of CoevRJ to recover the simulated amount of rate heterogeneity (i.e., the $\alpha$ parameter of the GTR+$\mathrm{\Gamma }$ model) and the total number of substitutions, measured as the total branch length of the reconstructed phylogenetic tree. To estimate the effects of ignoring coevolution between sites, we reanalyzed the datasets under a standard GTR+$\mathrm{\Gamma }$ model where all sites are considered to evolve independently [as implemented in MrBayes (23)]. The performances of CoevRJ and GTR+$\mathrm{\Gamma }$, assessed by the relative errors with respect to the simulated parameters, were equivalent in the absence of coevolution, reflecting the fact that CoevRJ correctly reduced to a model where all sites are independent (Fig. 2 A and B). However, as the proportions of coevolving sites in the alignment increased, the accuracy of the estimated rate heterogeneity and branch lengths decreased substantially under the GTR+$\mathrm{\Gamma }$ model, while it remained essentially unchanged under CoevRJ (Fig. 2 A and B).

Fig. 2.

Validation of CoevRJ and comparison with a model assuming independence among sites (GTR+$\mathrm{\Gamma }$) on synthetic datasets. Relative errors on (A) the rate heterogeneity and (B) the total branch length when inferred by CoevRJ and the GTR+$\mathrm{\Gamma }$ model in proportion to the amount of coevolution simulated. Box-plot whiskers extend to 1.5× the interquartile range; outliers are not shown. (C) Number of bipartitions, or internal nodes, exclusively misidentified by CoevRJ or GTR+$\mathrm{\Gamma }$ (bipartitions misidentified with both models are not reported). Misidentified bipartitions can be either bipartitions not present in the simulated phylogeny but inferred with $P>0.95$ or bipartitions present in the simulated phylogeny but inferred with $P<0.5$. Errors bars represent the SD.

Finally, the accuracy of the inferred phylogenetic tree with increasing levels of coevolution was consistently improved when using CoevRJ rather than the standard GTR+$\mathrm{\Gamma }$ model. In presence of coevolution, the tree topologies inferred with CoevRJ were more accurate than those inferred under the GTR+$\mathrm{\Gamma }$ model (SI Appendix, Fig. S1). The divergence between the trees estimated by the GTR+$\mathrm{\Gamma }$ model and CoevRJ increased significantly with the proportion of coevolution (SI Appendix, Fig. S1) as a small but significant increase in misidentified bipartitions (internal nodes) affected the phylogenetic trees inferred under the independent sites model (Fig. 2C).

CoevRJ Identifies Alternative Hypotheses for the “Tree of Life.”

To gain insight on the effect of accounting for coevolution on an empirical dataset, we analyzed an alignment of the 16S rRNA that includes sequences for 146 taxa spanning the three domains of life, Bacteria, Archea, and Eukaryotes (18). The 16S rRNA is subject to many structural constraints and is therefore used as a benchmark for the method’s ability to predict coevolution. Using this dataset, pairs of sites predicted as coevolving can be assessed by comparing them to the known 3D structure of the small ribosomal subunit for several species [E. coli (24), Drosophila melanogaster (25) and Homo sapiens (26)]. Coincidentally, since 16S is shared by all prokaryotes and eukaryotes and is a slow-evolving gene, it is also often used to infer phylogenetic relationships, especially focusing on the earliest nodes in the tree of life (16, 17).

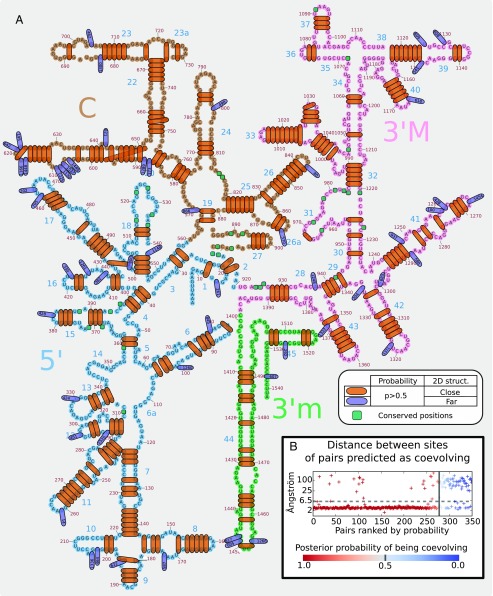
CoevRJ predicted 256 pairs of nucleotides (19.5% of the alignment positions) as coevolving with a posterior probability greater than 0.95. Of these, 94% of the pairs of sites were located very closely on the 3D structure, for example less than 6.5 Å for E. coli (Fig. 3 and Materials and Methods). The majority of these pairs (71%) were inferred as having a profile consistent with Watson–Crick base pairs (AT, GC). Among the 16 pairs having probability greater than 0.95 and not supported by the structure of E. coli, 14 were inferred with profiles diverging from a pure Watson–Crick profile, suggesting that they could be involved in functional constraints (SI Appendix, Table S2). Additionally, 12 of them are known to bind with other small ribosomal subunits not represented in our dataset (summarized in SI Appendix, Table S2 from ref. 28). Sites involved in such bonds could be coevolving with residues on other sequences and may thus present evolutionary patterns departing strongly from the one of independent evolution, which may lead CoevRJ to infer them as coevolving within the 16S rRNA. Finally, 108 pairs were predicted as significantly coevolving but with probability lower than 0.95 (27% with sites closely located on the structure of E. coli). Empirically validating these predictions is difficult as they could result from coevolution affecting only a portion of the phylogeny and would require the 3D structures for many species. However, the interpretation of the coevolving pairs based on the 3D structure of E. coli was confirmed when using the D. melanogaster and H. sapiens structures for validation (SI Appendix, Fig. S2).

Fig. 3.

(A) Mapping of CoevRJ predictions of coevolving pairs on the structure of Escherichia coli 16S rRNA. All predicted coevolving pairs with $P>0.5$ are reported on the 2D structure of E. coli (22). Pairs highlighted in red are at most 6.5 Å distant on the 3D structure (Materials and Methods). Pairs in blue are more distantly located than this threshold; for that reason, the second position of the pair is indicated within the pair highlight. (B) Distance between positions of pairs ranked by their posterior probability of being coevolving. Only pairs with $P>0.05$, corresponding to strongly significant pairs compared with the prior expectation (Materials and Methods), are reported in this figure.

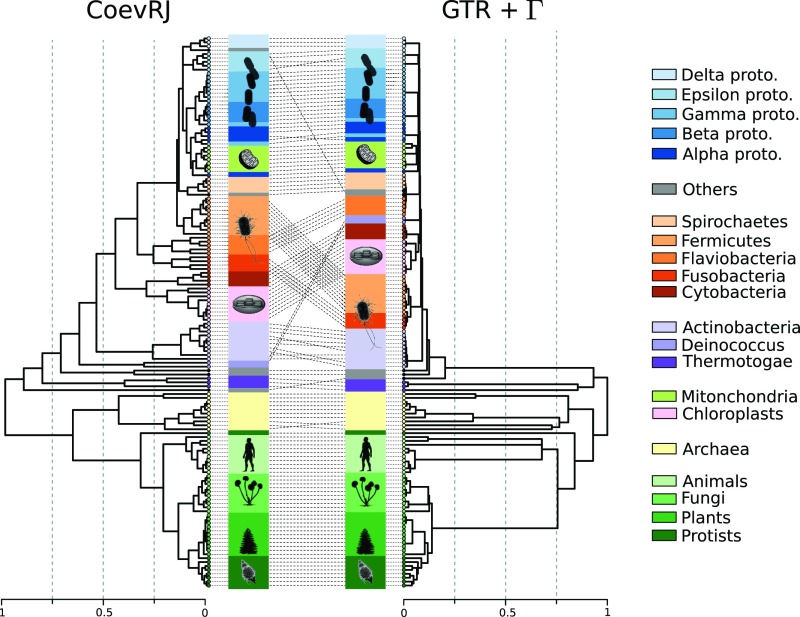
The phylogenetic tree inferred by CoevRJ from the 16S RNA dataset significantly differed from the one obtained under the assumption of independence among sites. Our analyses identified 51 internal nodes not shared between the two topologies (normalized Robinson–Foulds distance (29) of 0.18; Fig. 4 and SI Appendix, Figs. S3–S9). In addition to topological differences, the two models inferred substantially different branch lengths. For instance, the branch separating the Archaea from the Eukaryotes had an estimated branch length that was 25% longer with CoevRJ than with the GTR+$\mathrm{\Gamma }$ model, while branches deep in the bacterial clades were generally inferred as shorter with CoevRJ (SI Appendix, Figs. S10–S12). These discrepancies have a strong impact on the estimates of divergence times based on these phylogenies. Indeed, we found strongly differing ultrametric trees when using the phylogeny estimated under the CoevRJ or the GTR+$\mathrm{\Gamma }$ model (Fig. 4), and conflicting estimates of the divergence times were observed for varying settings of the underlying molecular clock (SI Appendix, Fig. S13).

Fig. 4.

Impact of accounting for dependent sites on the dating of the tree of life. Ultrametric trees resulting from an analysis with the penalized likelihood method (27) configured to accommodate for large rate variation ($\lambda =0$) of the majority rule consensus trees inferred by CoevRJ (left) and a purely independent sites model (GTR+$\mathrm{\Gamma }$, right). The root age is arbitrarily placed at 1.

A Wider Perspective on the Failure to Account for Dependence Among Sites.

We tested the CoevRJ approach on a diverse range of 10 protein-coding genes of eukaryotes from the Selectome database (30) having significantly different alignment size and gene annotation (SI Appendix, Table S3). These alignments were specifically selected out of 8,000 protein-coding genes for their significant signals of coevolution as predicted by the Coev method (11). For each dataset, we inferred the parameters with both CoevRJ and GTR+$\mathrm{\Gamma }$ and computed the discrepancies measured between the methods for the inferred rate heterogeneity, branch lengths, and tree topology.

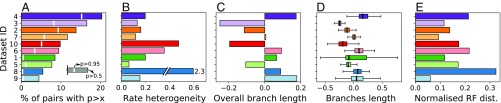
While the proportion and intensity of coevolution detected within these datasets varied (Fig. 5A and SI Appendix, Fig. S14), not accounting for dependence among sites led to decrease in the estimate of the rate heterogeneity between sites (Fig. 5B). Additionally, the estimates of branch lengths differed substantially between CoevRJ and GTR+$\mathrm{\Gamma }$. The total branch length inferred on these datasets was inconsistent between both methods without showing a bias (Fig. 5C). Notably, the difference in total branch length did not come from a global factor equally affecting all branches but from many changes of varying amplitude on different branches (Fig. 5D).

Fig. 5.

Differences between analyses conducted with CoevRJ and a model assuming independence among sites (GTR+$\mathrm{\Gamma }$). Datasets are ranked by the percentage of coevolving pairs predicted with $P>0.5$. The percentage is defined with respect to the maximum number of coevolving pairs observable at once (defined as the alignment length divided by 2). (A) Percentage of predicted coevolving pairs with $P>0.5$ (bar length) and $P>0.95$ (white stripe). (B–D) Divergences between parameters inferred with the purely independent sites model (GTR+$\mathrm{\Gamma }$) and CoevRJ. The relative differences using CoevRJ as reference are reported for (B) the rate heterogeneity, (C) the overall branch length, and (D) the branch lengths shared in both consensus trees. Box-plot whiskers extend to 1.5× the interquartile range; outliers are not shown. (E) Percentage of inconsistently placed internal nodes between both consensus trees as defined by the normalized Robinson–Foulds distance (29).

The tree topologies inferred under CoevRJ and GTR+$\mathrm{\Gamma }$ differed for all genes (Fig. 5E). The amount of differences among topologies obtained under the different methods ranged from 0.06 to more than 0.3 (normalized Robinson–Foulds distance). The differences measured on the substitution rates, branch lengths, and tree topologies suggested that accounting for dependence among sites significantly impacted the parameter estimates without presenting a consistent bias. The diversity of these discrepancies suggests that failing to account for the dependencies between sites led to unpredictable effects on the inferred evolutionary histories.

Discussion

We presented a method to analyze an alignment, while moving beyond the unrealistic assumption that all sites evolve as independent units. CoevRJ jointly infers the posterior probability of the phylogenetic tree, the pairs of coevolving sites, and the underlying parameters of the evolutionary models. CoevRJ therefore enables us to capture the reciprocal effects of the shared evolutionary history of molecular sequences and the pairs of sites that coevolve. The joint analysis of these two processes has remained an unsolved challenge in previous approaches (6, 31). Our results show that CoevRJ can accurately estimate both the phylogenetic tree and the parameters of the underlying (co)evolutionary process.

Modeling the evolutionary process enables CoevRJ to extract more information from the data than just the position of the pairs of coevolving sites. The posterior probability of each coevolving pair is informative of the strength of the nucleotide pairing along with the inferred distribution of profiles that determine the nature of the pairings. Estimating these parameters within a Bayesian framework results in intuitive posterior probabilities and enables us to use Bayes factors to properly define thresholds for the significance of predicted coevolving pairs (Materials and Methods). Given these advantages, the power of CoevRJ to predict coevolution compared favorably to existing methods on the 16S rRNA dataset (SI Appendix, Fig. S15).

Our findings join previous studies showing that the accuracy of standard phylogenetic inference is negatively impacted when dependence among sites is present in the data (14, 15). Phylogenetic trees inferred from synthetic datasets with CoevRJ show that our method can correct these inaccuracies. Similarly, phylogenetic trees inferred on the eukaryote datasets strongly differed from the ones inferred with a model assuming that sites evolve independently. The extent of the divergences were not predictable with respect to the nature and magnitude of the coevolutionary predictions. Such inaccuracies in the phylogeny could impact analyses using these phylogenetic trees. For instance, phylogenies inferred on the 16S rRNA datasets suggested that conflicting conclusions would be reached when aiming to date the tree of life (Fig. 4).

The machinery developed for CoevRJ can be extended to other mixtures of models for RNA, DNA, or amino acid sequences. For instance, a targeted study of the secondary structure of RNA could be conducted by replacing the Coev model by models accounting for substitution between Watson–Crick pairs and wobbling pairs (e.g., refs. 8 and 32). However, further improvements to the performance of this machinery are required to relax the most limiting assumptions on the current mixture of models to better integrate the richness and complexity of molecular evolution. For instance, the assumption of rate homogeneity of the coevolving pairs could be relaxed by adding a Gamma model of rate heterogeneity, as for the independent sites, or by considering a mixture of coevolutionary processes with different substitution rates ($d,s,r$). Additionally, extending the model to consider coevolution at more than two sites at a time (e.g., triplet, quadruplet, or n-tuple) could better capture the potential underlying molecular structures. Finally, the study of coevolution in protein-coding genes would deeply benefit from the integration of codons or amino acid models, which is currently computationally prohibitive.

Extending CoevRJ to amino acid models would enable further investigation of the effect of dependent sites on dating of the tree of life, which is frequently achieved by analyzing the RNA and the proteins in the small ribosomal subunit (16, 17). Solving this computational challenge would also facilitate the study of protein–protein interactions (4) jointly with the underlying evolutionary process. While several methodological challenges remain, our approach paves the way to a new generation of more realistic models of molecular evolution. Improving our understanding of the shared history of genes and species requires that we integrate more complexity in evolutionary models (33), and our method demonstrates that such additional complexity is counterbalanced by a significant improvement of the inferred phylogenetic relationships and (co)evolutionary processes.

Materials and Methods

Evolutionary Models.

We designed a set of models in which nucleotides can either evolve independently of the others or according to a coevolutionary process whereby pairs of sites evolve in a mutually dependent fashion. The proportions of both types of sites in an alignment, as well as the specific assignment of each site to either model, is assumed to be unknown and estimated from the data.

Our Bayesian model allows us to jointly infer the following parameters (which are described in detail in the paragraphs below):

• i)the phylogenetic tree (topology and branch lengths) describing the relationships between genes;
• ii)the number of pairs of coevolving sites in the alignment;
• iii)the assignment of each individual site to either a coevolving pair or to the set of independently evolving sites;
• iv)the parameters of the substitution model describing independent site evolution; and
• v)the parameters of the substitution model for coevolving pairs of sites.

Independent substitution model.

Independent sites are modeled as evolving under the GTR+$\mathrm{\Gamma }$ model (21). This model accounts for rate heterogeneity using a discrete Gamma distribution model with four different rate multipliers known as the GTR+$\mathrm{\Gamma }$. We identify the instantaneous rates quantifying the rate of change from one nucleotide to another $\left(a,b,c,d,e,f\right)$, as well as the parameter $\alpha$ defining the shape of the Gamma distribution with ${\theta }_{GTR}$. We scale the instantaneous rate matrix $Q_{GTR}$ by the sum of its off-diagonal elements to disentangle the effect of the branch lengths $\mathbf{t}$ and the rate parameters $\left(a,b,c,d,e,f\right)$.

The likelihood of each independent site contained in the set $S_{indep}$ is computed separately using the Felsenstein pruning algorithm (13) on the phylogenetic tree $\tau$. The joint likelihood, under the assumption of independence among sites, is then computed as

$$f\left(X_{S_{indep}}|\tau ,\mathbf{t},{\theta }_{GTR}\right)={\prod }_{i\in S_{indep}}f\left(X_i|\tau ,\mathbf{t},{\theta }_{GTR}\right)$$

with $\tau$ identifying the tree topology.

Dependent substitution model.

Dependent sites are assumed to follow a pairwise coevolution model adapted from ref. 11. Under this model, a pair of sites defined by two positions $\left(i,j\right)$ in the alignment are assumed to evolve within a profile of coevolution identified as $\varphi$. Following ref. 11, we define as “coevolving profile” the set of coevolving nucleotides for two sites (e.g., AT and CG). For any pair of nucleotides, there exist up to 192 possible profiles representing all of the possible combinations of pairs of nucleotides (34).

Since the Coev model does not allow double substitutions, evolutionary changes within the coevolving profile require at least two substitutions, for instance AT $\to$ GT $\to$ CG. We model this process with two parameters describing (i) the rate at which a coevolving pair is replaced by a noncoevolving one (e.g., GT), thus exiting the coevolving profile, and (ii) the rate at which the pair of sites return to the coevolving profile (e.g., CG). We indicate the two rates with $s$ and $d$, respectively. In a coevolving pair, we expect the rate $d$ to be much larger than the rate $s$, that is, it should be rare to leave a coevolving profile (low $s$) and it should be highly probable to regain a coevolving pair (high $d$). Therefore, the ratio $d/s$ expresses the attraction of pairs of positions to stay within the coevolving profile. Additionally, substitutions maintaining the pair of positions out of the profile occur at rate $r$ for each position.

The matrix of instantaneous substitution rates $Q_{Coev}$ is then composed of the rates $q_{ij}$ quantifying the rate of going from a pair of nucleotides $i$ to the pair $j$ and defined by

$$q_{ij}=\left\{\begin{array}{cc}0,\hfill & \text{if}\hspace{0.17em}i\hspace{0.17em}\text{and}\hspace{0.17em}j\hspace{0.17em}\text{differ at more than one nucleotide,}\hfill \\ r,\hfill & \text{if}\hspace{0.17em}i\notin \varphi \hspace{0.17em}\text{and}j\notin \varphi ,\hfill \\ s,\hfill & \text{if}\hspace{0.17em}i\hspace{0.17em}\in \varphi \hspace{0.17em}\text{and}\hspace{0.17em}j\notin \varphi ,\hfill \\ d,\hfill & \text{if}i\notin \varphi \text{and}j\in \varphi .\hfill \end{array}\right.$$

Branch lengths were not inferred by the original Coev method. Therefore, substitution rates were assumed to be consistent under the site-independent and site-dependent hypotheses. In other words, a substitution on two independent sites was equivalent to two substitutions on a pair of sites such that the total number of substitutions was preserved. This was achieved by doubling the length of branches under the Coev model.

Here we relax that assumption by inferring from the data the factor describing the difference in units of branch length between independent and coevolving substitutions. Branch lengths are therefore decoupled for sites under dependent and independent evolution by a rate modifier $\nu$. This modification leads the probability transition matrix for coevolving pairs to be computed as

$$P_{Coev}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\nu \times t_i\times Q_{Coev}\right)$$

for the $i$th branch. As for the $Q_{GTR}$, we normalize the matrix $Q_{Coev}$ to disentangle the effects of the branch length $\mathbf{t}$ and the rate scaling $\nu$. Furthermore, we assume that all coevolving pairs share the same parameters $r,d,s$ of the matrix $Q_{Coev}$, whereas an individual coevolving profile $\varphi$ is estimated for each pair.

In summary, a set of dependent sites $S_{dep}$ is formed of $k$ pairs. Each pair is characterized by its positions and profile ${\rho }_k=\left\{i_l,j_l,{\varphi }_l:\forall l\in [1\dots k\right])$ and its evolution is characterized by the modified Coev substitution model with parameters ${\theta }_{Coev}=\left(r,s,d,\nu \right)$. The likelihood of each coevolving pair is computed using the Felsenstein pruning algorithm (13) on the phylogenetic tree $\tau$. The joint likelihood of dependent sites is then given as

$$f\left(X_{S_{dep}}|\tau ,\mathbf{t},{\theta }_{Coev},{\rho }_k\right)={\prod }_{\left(i,j,\varphi \right)\in {\rho }_k}f\left(X_i,X_j|\tau ,\mathbf{t},{\theta }_{Coev},\varphi \right).$$

This model therefore assumes independence between coevolving pairs and thus does not directly account for dependence between three or more sites.

The set of models.

Given sequences of $N$ sites, we consider the set of models defined by the number of coevolving pairs $k$ such that $k\in \left[0,\dots ,\lfloor N/2\rfloor \right]$. These $N$ sites are split in a subset of independent sites $S_{indep}$ and a subset of coevolving pairs (dependent sites),

$$S_{dep}={\bigcup }_{\left(i,j,\varphi \right)\in {\rho }_k}\left(i\cup j\right).$$

Although site assignment to either category can change during the Bayesian sampling algorithm, each site is exclusively dependent or independent in a given sample ($S_{indep}\cap S_{dep}=\varnothing$) and, if dependent, a site can only be present in one pair at a time. Finally, the joint likelihood of both types of sites is given as

$$\begin{array}{ll}\hfill f\left(X|\tau ,\mathbf{t},{\theta }_{GTR},{\theta }_{Coev},{\rho }_k\right)=& f\left(X_{S_{indep}}|\tau ,\mathbf{t},{\theta }_{GTR}\right)\hfill \\ \hfill & \times f\left(X_{S_{dep}}|\tau ,\mathbf{t},{\theta }_{Coev},{\rho }_k\right).\hfill \end{array}$$

Bayesian Framework.

We implemented the models in a Bayesian framework named CoevRJ that estimates all of the free parameters $\theta =\left(\tau ,\mathbf{t},{\theta }_{GTR},{\theta }_{Coev},{\rho }_k\right)$ as well as the number of pairs $k$. We used the RJMCMC algorithm (20) to estimate the joint posterior distribution of the parameters and models space:

$$\pi \left(\theta ,k|X\right)\sim p\left(k\right)p\left(\theta |k\right)\times f\left(X|\theta ,k\right),$$

which contains the probability for how many and which sites evolve independently or in coevolving pairs. The analysis starts from a model where all sites are independent ($k=0$) and proposes alternative configurations where pairs of sites are coevolving.

Proposals.

To explore this complex parameter and model space, we designed several proposals. Two types of parameters were differentiated: those that do or do not depend on $k$.

Proposals for the phylogenetic tree and GTR+$\mathrm{\Gamma }$ model parameters.

These proposals aim to update the branch lengths $\mathbf{t}$, the tree topology $\tau$, and the parameters ${\theta }_{GTR}$. The space of phylogenetic tree topologies $\tau$ is sampled by using the stochastic nearest-neighbor interchange as well as the extended subtree pruning and regrafting proposals, while the continuous parameters of this category are sampled using adaptive multivariate normal proposals as described in ref. 35.

Proposals for the Coev model parameters ($\mathrm{k}>0$).

The parameters ${\theta }_{Coev}$ are sampled whenever $k>0$. The branch-length scaling factor $\nu$ is updated using two different proposals. The first one is a simple multiplier proposal. The second proposal accounts for a potential negative correlation between $\nu$ and $\mathbf{t}$ enabling both sets of parameters to change without impacting the overall number of substitutions in the phylogenetic tree.

Negative correlation between these parameters may happen when the model transitions from a purely independent sites model ($k=0$) to a model with many coevolving pairs ($k\gg 0$) evolving faster than the independent sites ($\nu \gg 2$). Under these circumstances, many independent proposals would be required to reduce the branch lengths $\mathbf{t}$ while increasing $\nu$, and therefore would strongly impact the mixing and the convergence of the sampling process.

Therefore, we account for this negative correlation by proposing a move with a multivariate normal distribution $\mathcal{N}\left(0,\mathrm{\Sigma }\right)$ having covariance matrix $\mathrm{\Sigma }\in {\mathcal{R}}^{\left|\mathbf{t}\right|+1}\times {\mathcal{R}}^{\left|\mathbf{t}\right|+1}$, where the $i$th row corresponds to the branch length $t_i$ and the last row corresponds to the parameter $\nu$. This covariance matrix is built such that

$${\mathrm{\Sigma }}_{i,j}=\left\{\begin{array}{cc}{\sigma }_t^2,\hfill & \text{if}\hspace{0.17em}i=j\hspace{0.17em}\text{and}\hspace{0.17em}i<\left|\mathbf{t}\right|+1\hfill \\ {\sigma }_{\nu }^2,\hfill & \text{if}\hspace{0.17em}i=j\hspace{0.17em}\text{and}\hspace{0.17em}i=\left|\mathbf{t}\right|+1\hfill \\ -\delta {\sigma }_t{\sigma }_{\nu },\hfill & \text{if}\hspace{0.17em}i\ne j\hspace{0.17em}\text{and}\hspace{0.17em}i=\left|\mathbf{t}\right|+1\text{or}j=\left|\mathbf{t}\right|+1\hfill \\ \delta {\sigma }_t^2,\hfill & \text{otherwise}\hfill \end{array}\right.$$

with $\delta =0.95$ and variances arbitrarily fixed (e.g., ${\sigma }_t=10^{-2}/\sqrt{\left|\mathbf{t}\right|}$ and ${\sigma }_{\nu }=5\cdot 10^{-3}$). The choice of these parameters results from empirical observations on the mean (Monte Carlo) sampling variance of branch length $\mathbf{t}$ and the multiplier $\nu$. The value of the $\delta$ parameter enforces that we expect significant correlations between the branch lengths and a negative correlation with the rate multiplier.

Furthermore, given that the $Q_{Coev}$ matrix is normalized, the parameters $r,s,d$ are defined on the $\left[\mathrm{0,1}\right]$ interval and have their sum constrained to one. To obtain an efficient sampling of such parameters, we use the reparameterization described in ref. 36. We replace the parameters $r,d,s$ by the parameters ${\psi }_1,{\psi }_2,{\psi }_3$. The values of $r$ and $d$ are then given as

$$r\hspace{0.17em}=\hspace{0.17em}\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\psi }_1\right)}{{\sum }_j\mathrm{e}\mathrm{x}\mathrm{p}\left({\psi }_j\right)}\hspace{0.17em}\text{and}\hspace{0.17em}d\hspace{0.17em}=\hspace{0.17em}\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\psi }_2\right)}{{\sum }_j\mathrm{e}\mathrm{x}\mathrm{p}\left({\psi }_j\right)}.$$

We then fix the parameter ${\psi }_3=0$. One of the advantages of this reparameterization is that the new parameters ${\psi }_i$ are lying in $\mathbb{R}$ and can thus be sampled with standard proposal kernels. We therefore sample parameters ${\psi }_1$ and ${\psi }_2$ using normal distributions with variances empirically calibrated to provide proper mixing on simulated datasets.

Proposals affecting k and the positions of pairs.

We have three different types of proposals that operate on the parameters $k$ and ${\varphi }_k$; specifically, the proposals (i) add and remove pairs, (ii) change sites included in a pair, and (iii) change the coevolving profile in a pair.

Proposals moving through the model space.

The first two proposals are transdimensional moves because they change the number of parameters in the model and their acceptance probabilities are given by the RJMCMC algorithm (20). Our set of models defines a sequence of models $M_k$ with $k\in \left[0,\dots ,\lfloor N/2\rfloor \right]$ being the number of pairs and with each model having $n_k$ parameters identified by $\theta$. The sequence $M_k$ increases the model complexity such that $n_k<n_{k+1}$.

The probability of making a jump from a model $M=M_k$ with parameters $\theta$ to a more complex model $M\prime =M_{k+1}$ with parameters $\theta \prime$ is given as

$$min\left\{1,A\left(\theta ,\theta \prime \right)\right\},$$ [1]

where A is defined as

$$A\left(\theta ,\theta \prime \right)=\underset{\text{Posterior ratio}}{\underbrace{\frac{\pi \left(\theta \prime \right)}{\pi \left(\theta \right)}}}\times \underset{\text{Hastings ratio}}{\underbrace{\frac{p\left(M\prime \right)}{p\left(M\right)}\times \frac{p\left(\mathbf{u}\prime \right)}{p\left(\mathbf{u}\right)}}}\times \underset{\text{Jacobian}}{\underbrace{\left|\frac{\partial \left(\theta \prime ,\mathbf{u}\prime \right)}{\partial \left(\theta ,\mathbf{u}\right)}\right|}}.$$ [2]

The first ratio represents the ratio of posterior probabilities. The second is the ratio of the proposal probabilities and the third is the ratio between the probability of drawing the random values required for the moves. The last term is the Jacobian of the mapping function that defines the relation between the parameters and the auxiliary variables in both models.

When proposing a move to a model having a different number of parameters, vectors of random numbers $\mathbf{u}\sim p\left(\mathbf{u}\right)$ and $\mathbf{u}\prime \sim p\left(\mathbf{u}\prime \right)$ are drawn such as to complete the parameters spaces of $M_k$ and $M_{k+1}$ such that $n_k+m_k=n_{k+1}+m_{k+1}$ with $\mathbf{u}\in {\mathbb{R}}^{m_k}$ and $\mathbf{u}\prime \in {\mathbb{R}}^{m_{k+1}}$. Assuming independent random numbers $u_i\in \mathbf{u}$, the probability of drawing $\mathbf{u}$ is defined as

$$p\left(\mathbf{u}\right)={\prod }_{i=1}^{m_k}p\left(u_i\right).$$

To move from model $M_k$ to $M_{k+1}$, we first draw a pair of independent sites. For the sake of simplicity, we consider hereafter that sites and profiles are drawn from uniform distributions. The notation used, however, accommodates more sensible approaches (see SI Appendix for details of the CoevRJ implementation).

In this proposal, a pair of positions is drawn by first selecting a position $i\sim p\left(i|S_{indep}\right)$ and then a second position $j\sim p\left(\left(i,j\right)|S_{indep},i\right)$. The probability $p\left(M\right)$ of making this move is given as

$$\begin{array}{ll}\hfill p\left(M\right)=& p\left(i|S_{indep}\right)p\left(\left(i,j\right)|S_{indep},i\right)\hfill \\ \hfill & +p\left(\hspace{0.17em}j|S_{indep}\right)p\left(\left(i,j\right)|S_{indep},j\right).\hfill \end{array}$$

A new profile must then be assigned to this new pair by drawing it directly from the distribution $\varphi \sim p\left(\varphi |i,j\right)$.

The opposite move going from $M_{k+1}$ to $M_k$ removes a pair arbitrarily chosen among the $k+1$ existing pairs with probability $p\left(M\prime \right)=1/\left(k+1\right)$. Since this move only removes parameters, no random numbers $\mathbf{u}\prime$ are drawn. Therefore, Eq. 2 defining the acceptance probability of both moves simplifies to

$$A\left(\theta ,\theta \prime \right)=\frac{\pi \left(\theta \prime \right)}{\pi \left(\theta \right)}\times \frac{p\left(M\prime \right)}{p\left(M\right)}\times \frac{1}{p\left(\mathbf{u}\right)}\times \left|\frac{\partial \left(\theta \prime \right)}{\partial \left(\theta ,\mathbf{u}\right)}\right|.$$ [3]

Additionally, given that the random parameters $\mathbf{u}$ are drawn independently from the current parameter value $\theta$, the last term of Eq. 3, the determinant of the Jacobian, is equal to 1.

For the general case where $k>1$, the probability of making the move ($M_k\to M_{k+1}$) is then given by Eq. 3. The probability of a backward move ($M_{k+1}\to M_k$) is given as $A{\left(\theta ,\theta \prime \right)}^{-1}$. In the special case identified by the proposals $M_0\leftrightarrow M_1$, that moves from a model having only independent sites ($k=0$) to a model having one coevolving pair ($k=1$), parameters ${\theta }_{Coev}$ as well as $\nu$ must be proposed. Coev parameters ${\psi }_1$ and ${\psi }_2$ are drawn from independent normal distributions with parameters $\left({\mu }_1,{\sigma }_1^2\right)$ and $\left({\mu }_2,{\sigma }_2^2\right)$, respectively, while the branch-length scaling factor $\nu$ is drawn from a Gamma distribution with parameters (${\alpha }_{\nu },{\beta }_{\nu }$). In CoevRJ, these distributions have been tuned to result in more efficient proposals. For this special move, the probability $p\left(\mathbf{u}\right)$ is therefore altered and is given by

$$p\left(\mathbf{u}\right)=p\left(\varphi |i,j\right)p\left(\nu |{\alpha }_{\nu },{\beta }_{\nu }\right)p\left({\psi }_1|{\mu }_1,{\sigma }_1^2\right)p\left({\psi }_2|{\mu }_2,{\sigma }_2^2\right).$$

Proposals sampling the pair space ($\mathrm{k}>0$).

Two proposals aim to provide a proper mixing of the pairs of positions under coevolution without affecting the number of pairs $k$ and are subject to the standard Metropolis–Hastings acceptance ratio (37). The first proposal breaks an existing pair and exchanges one of its positions with a site considered as independent. A pair $\left(i,j\right)$ is selected arbitrarily among the existing $k$ pairs. The position kept $y$ is equal to $i$ with probability $p\left(y=i\right)=S\left(i\right)/\left(S\left(i\right)+S\left(j\right)\right)$, otherwise the position $y=j$ with probability $p\left(y=j\right)=1-p\left(y=i\right)$. The position $y\prime =\left(i\cup j\right)\backslash y$ is then removed from the pair.

The independent site $z$ is drawn from the probability distribution $p\left(\left(y,z\right)|S_{indep},y\right)$ and a new profile $\varphi$ is drawn according to the profile probability distribution $p\left(\varphi |y,z\right)$. The Hastings ratio for this move is thus given by

$$\frac{\left(1/k\right)\times p\left(y|y,z\right)\times p\left(\left(y,y\prime \right)|S_{indep},y\right)\times p\left(\varphi |i,j\right)}{\left(1/k\right)\times p\left(y|i,j\right)\times p\left(\left(y,z\right)|S_{indep},y\right)\times p\left(\varphi |y,z\right)}.$$

The second proposal chooses two pairs $P_1,P_2$ arbitrarily among the existing $k$ and mixes their positions randomly. Once the new pairs $P_1^{\prime },P_2^{\prime }$ are created, new profiles ${\varphi }_1^{\prime }$ and ${\varphi }_2^{\prime }$ have to be drawn. This proposal is symmetrical with the exception of the proposals on the profiles. The Hastings ratio is then given by

$$\frac{p\left({\varphi }_1|P_1\right)\times p\left({\varphi }_2|P_2\right)}{p\left({\varphi }_1^{\prime }|P_1^{\prime }\right)\times p\left({\varphi }_2^{\prime }|P_2^{\prime }\right)}.$$

Proposals exploring the profile space $\mathrm{\theta }$ (when k $>\mathit{0}$).

The last proposal samples the possible profiles for any given coevolving pairs by drawing a new profile $\varphi$ for a pair $\left(i,j\right)$ according to the probability $p\left(\varphi |\left(i,j\right)\right)$. Its Hastings ratio is equal to 1 given that such moves are symmetric.

Priors on standard parameters.

We assume a uniform prior on the tree topology $\tau$ and an exponential prior on each branch length with rate $\lambda =10$. The Gamma rate distribution modeling the rate heterogeneity of independent sites is defined by its shape parameter $\alpha$ for which we assume an exponential distribution with rate $\lambda =0.005$. Finally, to maintain consistency with the GTR model implemented in MrBayes (23), the exchangeability rates of this model are assigned a flat Dirichlet prior distribution.

Priors on Coev model parameters.

The branch-length scaling parameter $\nu$ for the coevolving pairs has a Gamma prior distribution with shape and scale parameters equal to 2. This distribution has its mode located at 2, which expresses our prior belief that two dependent sites should evolve at the same pace as two independent sites. Parameters ${\psi }_1,{\psi }_2$ that are used to reparameterize the parameters ($r,s,d$) have a normal prior distribution $\mathcal{N}\left({\mu }_{{\psi }_i},{\sigma }_{{\psi }_i}^2\right)$. These normal distributions are defined such as to favor a substitution rate $d$ greater than the others (SI Appendix, Table S4). This parameterization reflects our belief that pairs of sites under coevolution should differ from an independent evolutionary process (i.e., $r=d=s$) and be constrained to stay within the profile (i.e., high $d/s$ ratio), which is also supported by empirical findings and simulations (11).

For the 16S rRNA dataset, we used results from the Coev model (11) to estimate informed prior distributions on parameters ($r,s,d$), which we derived following the methodology described in refs. 36 and 38. We computed the mean and SD of parameters ($r,s,d$) from pairs of positions with significant support for the Coev model ($\mathrm{\Delta }AIC>6$). Using these values, we estimated the moments of the prior distributions for the ${\psi }_1,{\psi }_2$ parameters. The resulting parameterization (SI Appendix, Table S4) is close to the one defined for the default prior that results in a stationary frequency for nucleotide pairs in the profile to be close to $80\%$.

Finally, we defined a uniform prior distribution on the profile $\varphi$ based on the set of profiles observed in the alignment for a given pair of positions. This empirical prior reduces the space of parameters to explore and plays a key role in making analysis tractable with CoevRJ. However, this simplification implies that pairs of sites cannot (co)evolve under an unobserved profile (e.g., invariant sites are evolving under an independent process by default).

While more informative priors on the distribution of profiles could be used for specific type of molecular data (e.g., favoring Watson–Crick profiles for RNA sequences), we chose to use this conservative and vague prior since it accommodates the wide range of scenarios we considered including coevolution within DNA sequences. Under this prior, the marginal probability of the profiles inferred on the 16S rRNA dataset showed that the method had the power to infer the profile even without more informative priors. Indeed, 71% of the estimated coevolving pairs followed a pure Watson–Crick profile (AT, CG) and 17% of the pairs evolved under a profile containing canonical pairs coupled with other ones (AT, XX or CG, XX or AT, CG, XX). These results suggest that our priors do not prevent us from inferring common coevolving profiles.

Priors on the number of pairs.

We used a hierarchical prior on the number of pairs $k$ by assigning a Poisson distribution with rate $\lambda$ on the number of pairs and by an exponential distribution with parameter ${\alpha }_{\lambda }$ as a hyperprior on $\lambda$. This scheme enables the parameter $\lambda$ to be estimated using Gibbs sampling. We fixed the value of ${\alpha }_{\lambda }$ to 10. This hyperprior results in an expected value for $\lambda$ of 0.1 (i.e., a Poisson distribution with mode at $k=0$), which expresses our prior belief that coevolution should be a rare evolutionary event. Furthermore, the choice of parameter ${\alpha }_{\lambda }$ was validated by analyses conducted on the simulated datasets (SI Appendix, Fig. S16). The parameter values used for the hyperprior maintained $k$ close to the true number of simulated coevolving pairs.

Priors on the configuration of pairs.

The last prior defines the probability of observing a given set of coevolving pairs of positions. We assumed a uniform prior reflecting that pairs of sites are considered a priori to be equally likely to be under coevolution. Under this assumption, the prior is given by the number of possible configurations of $k$ pairs for a sequence of $N$ positions. Considering that we do not differentiate the order of positions in a pair, the total number of configurations for a given $k$ is defined as

$${\prod }_{i=0}^{k-1}\frac{\left(N-2i\right)\left(N-\left(2i+1\right)\right)}{2}=\frac{N!}{2^k\left(N-2k\right)!}.$$

Furthermore, we do not differentiate the ordering of the $k$ pairs. There are $k!$ permutations for a set of $k$ pairs and thus the total number of ordered configurations is given by

$$M\left(k,N\right)=\frac{N!}{2^k\left(N-2k\right)!}\frac{1}{k!}.$$

The probability of observing a given configuration is then given as $p\left(\cdot |k,N\right)={\left(M\left(k,N\right)\right)}^{-1}.$

Significance of Pairs Inferred as Coevolving.

To confidently consider pairs to be coevolving, we designed a method defining a threshold $T_{sig}$ on the probability at which a pair is considered as strongly significant. This threshold ensures that we only report pairs predicted with a marginal posterior probability significantly higher from the one we expect from the random sampling of pairs under a uniform prior on their positions integrated over the prior probability of seeing any given number of pairs.

We define this threshold after an MCMC run with CoevRJ by using the inferred posterior probability ${\pi }_{ij}$ of a given pair $\left(i,j\right)$ to compute the Bayes factor

$$BF\hspace{0.17em}=\hspace{0.17em}\frac{{\pi }_{ij}}{1-{\pi }_{ij}}/\frac{p_{ij}}{1-p_{ij}},$$ [4]

where $p_{ij}$ is the prior probability of pair $\left(i,j\right)$ to be coevolving.

This prior probability $p_{ij}$ explains the uniform probability of observing pair $\left(i,j\right)$ assuming that every pair is equally likely to be sampled. This probability is conditioned on the number of pairs $k$, such that $p_{ij}=p\left(k\right)p\left(i,j|k\right)$. Here we adopt a conservative approach and use the inferred posterior probability of $k$ as the probability $p\left(k\right)$. The prior probability of sampling a pair given $k$ is defined as

$$\begin{array}{ll}\hfill p\left(i,j|k\right)& =p\left(i,j|q=1\right)\hfill \\ \hfill & +\sum _{v=2}^k\left[p\left(i,j|q=v\right)\cdot \prod _{w=1}^{v-1}\left[\overline{p}\left(i,j|q=w\right)\right]\right]\hfill \\ \hfill p\left(i,j|k\right)& =\frac{2k}{N\left(N-1\right)},\hfill \end{array}$$

where $N$ defines the number of nucleotides in the sequence. The probability of drawing pair $\left(i,j\right)$ at step $l-1$ is given as

$$p\left(i,j|q=\left(v-1\right)\right)=\frac{2}{\left(N-2v\right)\left(N-2v-1\right)},$$

while the probability of not drawing $i$ or $j$ is defined as

$$\overline{p}\left(i,j|q=\left(w-1\right)\right)\hspace{0.17em}=\hspace{0.17em}\left(1-\frac{2}{N-2w}\right)\left(1-\frac{2}{N-2w-1}\right).$$

The significance threshold $T_{sig}$ for a pair is then derived from Eq. 4 by using the threshold for strong significance $2ln\left(BF\right)>10$ suggested by Kass and Raftery (39). When applied on the posterior distribution inferred with CoevRJ on the 16S rRNA dataset, this approach resulted in a threshold of $\approx 0.05$. Pairs inferred with a posterior probability smaller than this value were therefore treated as insignificant.

Experimental Setting.

Experiments on all of the datasets consisted of a comparison of results obtained with CoevRJ to the ones obtained with the GTR+$\mathrm{\Gamma }$ model assuming site independence as implemented in MrBayes (23). Prior distributions in MrBayes were set as the ones for CoevRJ with $k=0$. Both implementations were run under similar settings with four processors dedicated for ${\mathrm{M}\mathrm{C}}^3$ (40).

Runs were considered as having converged when the distribution of tree topologies stabilized [i.e., when the average SD of the splits frequencies (41) was measured to reach 0.05 using three independent runs for each dataset]. In addition, the parameter traces were examined to ensure proper convergence. The burn-in phase of each run was discarded and the remaining samples were used to estimate the posterior distribution. Comparisons between tree distributions were conducted by (i) computing the majority-rule consensus tree from the tree distributions obtained under each model and (ii) computing the normalized Robinson–Foulds distance (29) between the consensus trees.

Simulation of datasets.

We simulated five categories of nucleotides sequences with varying amount of coevolving sites (0, 5, 10, 20, and 50%). We simulated 50 replicates for each of these categories. For each replicate, we simulated a random phylogenetic tree with 50 tips using the R package APE (42) with branch length drawn from an exponential distribution ($\lambda =15$). This tree was used to generate an alignment composed of 1,000 nucleotides.

Sites evolving independently were simulated with the Evolver simulator (43) using a GTR+$\mathrm{\Gamma }$ model with arbitrary rates. The shape parameter $\alpha$ of the Gamma distribution was drawn from a distribution Gamma$\left(\mathrm{4,2}\right)$.

Pairs of coevolving sites were simulated using the Coev simulator (34). Each pair was attributed a random profile composed of two nucleotide pairs (e.g., AA, CC). The parameters for the Coev simulator were set to $r_1=r_2=0.5,d=100$ and $s=1.$ such as to generate strongly coevolving pairs of sites ($d/s=100$). For both the site-independent and site-dependent models, we assumed equal base frequencies for each state (i.e., 25% for each state in the GTR model and 6.25% for each state in the Coev model).

Proximity of nucleotides on the 3D structure of the 16S rRNA dataset.

To validate CoevRJ predictions of coevolution on the 16S rRNA dataset, we compared these results with pairs of nucleotides located closely on the 3D structure of the molecule (and thus potentially bonding). These pairs were identified as nucleotides having their two closest atoms at a distance of less than 6.5 Å. This threshold is consistent with the one used in ref. 18 (8 Å) and is representative of the average resolution of the Protein Data Bank (PDB) structure considered (24–26). The results obtained with this threshold are robust when considering other possible values in the range of 4 Å to 8 Å (SI Appendix, Fig. S3).

Molecular dating of the 16S rRNA dataset.

We analyzed the consensus trees obtained with both CoevRJ and the pure GTR+$\mathrm{\Gamma }$ model using the penalized likelihood framework (27) as implemented in the R package APE (42). We used multiple relaxed molecular clock models (i.e., correlated and relaxed) to ensure that our observations were not due to the use of a specific model. Furthermore, each model was used under four different $\lambda$ values, changing the strength with which the rate is constrained along branches. This parameter took the value $\left\{\mathrm{0,0.1},\mathrm{1,10}\right\}$ ranging from rates along the branch being totally independent to strongly related.

Data Availability.

The simulated and empirical molecular sequences used for the analyses can be found on the CoevRJ git repository (https://bitbucket.org/XavMeyer/coevrj). The PDB structures used to validate the findings can be accessed on the RSCB PDB (https://www.rcsb.org) with the identifiers 4GD2 (E. coli, ref. 24), 5VYC (H. sapiens, ref. 25), and 4V6W (D. melanogaster, ref. 26).