Abstract
Craniosynostosis is a medical condition caused by the early fusion of the cranial joint. The finite element method (FEM) is a computational technique that can answer a variety of “what if” questions in relation to the biomechanics of this condition. The aim of this study was to review the current literature that has used FEM to investigate the biomechanics of any aspect of craniosynostosis, being its development or its reconstruction. This review highlights that a relatively small number of studies (n = 10) has used FEM to investigate the biomechanics of craniosynostosis. Current studies set a good foundation for the future to take advantage of this method and optimize reconstruction of various forms of craniosynostosis.
Key Words: Biomechanics, Finite element, Model validation, Skull growth
During the early years of life, human brain volume increases rapidly, and the cranium undergoes rapid morphological changes in both size and shape [Dekaban, 1977; Abbott et al., 2000; Scheuer and Black, 2004]. The neurocranium in particular is required to expand to provide protection for the brain [Morriss-Kay and Wilkie, 2005; Richtsmeier and Flaherty, 2013]. This is accommodated by the cranial joints, i.e., sutures [Opperman, 2000; Herring, 2008]. Premature closure of the sutures, or craniosynostosis, is a medical condition that occurs in about 1 in 2,000 births with several reports of increase in its occurrence [van der Meulen et al., 2009; Johnson and Wilkie, 2011; Cornelissen et al., 2016; Al-Rekabi et al., 2017]. The majority of cases (70%) are non-syndromic, i.e., single suture synostosis, with the remaining instances being syndromic (e.g., Crouzon and Apert syndrome), in which more than one suture fuses and where additional features are present such as midfacial hypoplasia [Morriss-Kay and Wilkie, 2005; Wilkie et al., 2017].
Current treatments of this condition in the majority of cases involve invasive surgery, where a multidisciplinary working group of plastic and reconstructive surgeons, neurosurgeons, anaesthestist, maxillofacial surgeons, and orthodontists correct this craniofacial deformity. This group is also supported by a larger team of experts in psychology, speech and language therapy as well as genetics [Mathijssen, 2015]. The underlying aim of the surgery is to release the pressure on the brain and provide the required space for it to grow while the overlying complex of bones and sutures form a protective shell. At the same time, there are a large number of patient-specific factors that need to be considered during the course of craniosynostosis treatment such as age and intracranial pressure. There are a number of reconstruction techniques for different forms of craniosynostosis. These techniques have generally evolved over years in each craniofacial centre due to their experience, while ensuring the best surgical outcome for the child [e.g., McCarthy et al., 1995; Clayman et al., 2007; Thomas et al., 2015]. Nonetheless, when comparing different centres' techniques for treatment of a single form of craniosynotosis, there could be huge variations between them [e.g., Hopper et al., 2002; Taylor and Maugans, 2011; Simpson et al., 2017]. For example, in the case of sagittal synostosis which is the most common form of craniosynostosis [Wilkie et al., 2017], there are a number of different techniques used. These range from newer methods such as: minimally invasive endoscopic strip craniotomy with helmeting or spring-mediated cranioplasty, to other invasive calvarial reconstruction techniques such as Pi and modified Pi techniques, H technique, or total cranial vault remodelling [e.g., Jimenez and Barone, 2013; Gerety et al., 2015; Simpson et al., 2017].
Calvarial reconstruction in craniosynostosis can be optimized using various computational tools. The finite element method (FEM) is a well-established tool that has been widely used to design, develop, and optimize various mechanical structures such as aeroplanes and bridges [e.g., Fagan, 1992]. In brief, FEM works by dividing the geometry of the problem under investigation into a finite number of sub-regions, called elements. The elements are connected together at their corners and sometimes along their mid-side points, called nodes. For mechanical stress analysis, a variation in displacement (e.g., linear or quadratic) is then assumed through each element, and equations describing the behaviour of each element are derived in terms of the (initially unknown) nodal displacements. These element equations are then combined to generate a set of system equations that describe the behaviour of the whole problem. After modifying the equations to account for the boundary conditions applied to the problem, these system equations are solved. The output is a list of all the nodal displacements. The element strains can then be calculated from the displacements and the stresses from the strains. This method can be then performed iteratively to optimize a particular design to achieve a certain displacement or level of strain and stress considering the loading applied to the system and its requirements.
FEM was introduced to the field of orthopaedic trauma in the 1950s [Huiskes and Chao, 1983] and is nowadays widely used in design and development of various implantable devices. Perhaps the earliest finite element (FE) analysis of the craniofacial system dates back to the 1970s [e.g., Hardy and Marcal, 1973; Tanne et al., 1988; Lestrel, 1989]. For example, Hardy and Marcal [1973] developed a simplified model of the skull and concluded that it is well designed for resistance to anterior loads. There are a large number of studies that have used FEM in a wide range of application on the craniofacial system. Many studies have used FEM for example in the field of craniofacial injury and trauma with a number of studies focusing on adult as well as infant-related trauma [e.g., Horgan and Gilchrist, 2003; Roth et al., 2010; Wang et al., 2016; Dixit and Liu, 2017; Ghajari et al., 2017]. At the same time in the past 20 years, evolutionary biologists and functional morphologists have widely used this technique to understand the form and function of craniofacial systems in an evolutionary context [e.g., Rayfield, 2007; Moazen et al., 2009; Wang et al., 2010; O'Higgins et al., 2011; Prado et al., 2016]. More recently, this technique has been used to understand the biomechanics of craniofacial development and its associated congenital diseases such as cleft lip/palate and craniosynostosis [e.g., Remmler et al., 1998; Pan et al., 2007; Khonsari et al., 2013; Jin et al., 2014; Lee et al., 2017; Marghoub et al., 2018].
The aim of this study was to review the current literature that has used FEM to investigate the biomechanics of craniosynostosis in its development or its reconstruction. This review was organized to analyze these studies with respect to the steps involved in development of such models and to briefly describe their results. Recommendations for future research and areas which require further scientific investigation are also discussed.
Materials and Methods
A detailed survey of literature was carried out to identify the studies that used FEM to investigate the biomechanics of craniosynostosis. A number of databases: Web of Science, SCOPUS, PubMed, and Google Scholar were searched with the following keywords: craniosynostosis AND finite AND element. We identified 10 published articles that met the inclusion criteria of this review. The overall aims of these studies and type of synostosis are summarized in Table 1.
Table 1.
A summary of previous studies objectives, details of patient population considered
| Authors | Aims/objectives | Type of synostosis/groups | Patient(s)/specimens | Source of geometry |
|---|---|---|---|---|
| Nagasao et al., 2010 | To compare the difference in orbital deformation in patients with unicoronal synostosis between those whom only show unicoronal synostosis and those whom also show sphenoidal fusion | Unicoronal Unicoronal, lambdoid |
4.2 ± 1.4 mo (8 unicoronal) 4.6 ± 2.2 mo (7 unicoronal and lambdoid) Untreated, normal expansion |
CT |
| You et al., 2010; Jiang et al., 2010 | To analyze the relationship between different craniotomies and the overall skull rigidity in Pi-shape reconstruction | Not specified | Not specified Untreated, virtual surgery |
CT |
| Nagasao et al., 2011 | To investigate how normal, preoperative metopic and postoperative metopic craniosynostosis orbital morphology are affected by the loading from intracranial pressure | Metopic, untreated Metopic, treated HS |
8.2 ± 4.5 mo (10 metopic patients) 8.6 ± 4.3 mo (10 HS patients) Untreated and treated, normal expansion |
CT |
| Larysz et al., 2012 | To propose a method of preoperative planning for craniosynostosis based on 3D modelling and biomechanical analysis using finite element method | Sagittal Metopic |
1 y, male 3 mo, male Untreated, virtual surgery |
CT MRI |
| Wolański et al., 2013 | To highlight the potentials of finite element method for preoperative planning and postoperative evaluation of patients with craniosynostosis | Sagittal Metopic |
5 mo, male (2 scenarios) 3 mo, male (2 scenarios) Untreated, virtual surgery |
CT |
| Zhang et al., 2016 | To present and validate a system which accurately can predict the optimal spring force for sagittal craniosynostosis reconstruction | Sagittal, spring-assisted surgery | 3–6 mo, unknown sex (15 patients) >6 mo, unknown sex (8 patients) Virtual surgery |
CT Laser |
| Weickenmeier et al., 2017 | To predict typical skull morphologies in most common forms of craniosynostosis | Unicoronal, untreated Bicoronal, untreated Lambdoid, untreated Metopic, untreated Sagittal, untreated HS, untreated | 2D study: cross-sectional area of newborn scaled to healthy CI value of 78 (first 4 scenarios above) 3D study: approximated as ellipsoid with CI of 78 (all 6 scenarios above) |
MRI (2D) CAD (3D) |
| Li et al., 2017 | To quantify the positive outcome of using computer assisted preoperative planning such as biomechanical analysis and 3D printing | Sagittal, calvarial vault remodelling | 8–13 mo, 7 male, 3 female (10 patients, traditional treatment) 8–13 mo, 4 male, 4 female (8 patients, computer-assisted preoperative planning) |
CT MRI Cephalograms |
| Borghi et al., 2018 | To develop a patient-specific computational model of spring-assisted cranioplasty to predict the individual overall head shape | Sagittal | Preoperative CT data at 4.4 mo 1 male and postoperative 3D surface data at 5.5 mo of the same patient | CT |
CAD, computer-aided design; CI, cephalic index; HS, healthy skull; mo, months; y, year; CT, computed tomography; MRI, magnetic resonance imaging.
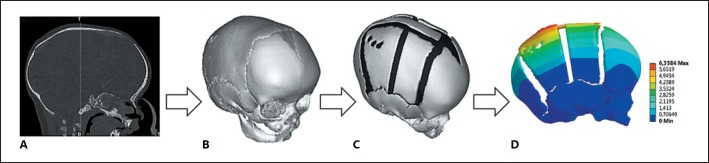
Four key steps were highlighted in the identified studies (as per any FE study): representation of the skull, sutures, and craniotomies; representation of the material properties of bones and sutures; representation of the loads, and simulation predictions. Figure 1 shows how one of these studies transformed CT data of a patient with sagittal synostosis to model a reconstruction technique for treatment of this condition using FEM [Wolański et al., 2013]. The following sections review these steps in the identified studies. These details are also summarized in Tables 1, 2.
Fig. 1.
A summary of model development from computed tomography (A) to a 3D reconstructed model of the skull preoperatively (B), to a 3D virtual reconstruction postoperatively (C), and then to finite element predictions (D), here due to constant pressure applied to the inner surface of the skull (modified with permission from Wolański et al., 2013).
Table 2.
A summary of the material properties and boundary conditions considered in the previous studies
| Authors | Material properties | Constraints | Loading |
|---|---|---|---|
| Nagasao et al., 2010 | Cortical bone: E = 134,000 MPa, v = 0.3 Cancellous bone: E = 7,700 MPa, v = 0.3 Cranial sutures: E = 3.78 MPa, v = 0.45 Remained constant |
Foramen magnum: fixed in all DOF | Intracranial pressure of 15 mm Hg applied normal to all elements of the inner surface of the skull |
| You et al., 2010; Jiang et al., 2010 | Bone: E = 2,500 MPa, v = 0.22, density = 2.15 kg/cm3 Dura mater: E = 34.5 MPa, v = 0.45, Density = 1.14 kg/cm3 remained constant |
Posterior distal edge of parietal bone: fixed in all DOF | Intracranial pressure of 2 kPa (15 mm Hg) applied normal to all elements of the inner surface of the skull |
| Nagasao et al., 2011 | Cortical bone: E = 134,000 MPa, v = 0.3 Cancellous bone: E = 7,700 MPa, v = 0.3 Cranial suture: E = 3.78 MPa, v = 0.45 Remained constant |
Foramen magnum: fixed in all DOF | Intracranial pressure of 15 mm Hg applied normal to all elements of the inner surface of the skull |
| Larysz et al., 2012 | Bone: E = 380 MPa Based on radiological density in Hounsfield Units remained constant |
Not specified | Not clear to us |
| Wolański et al., 2013 | Bone: E = 380 MPa, v = 0.22 Remained constant |
Fixed: base of skull | Intracranial pressure of 2.66 kPa (19.95 mm Hg) applied normal to all elements of the inner surface of the skull, applied deformation based on re-modelling of skull |
| Zhang et al., 2016 | Bone: E = 1,300 MPa, v = 0.28 (group A) Bone: E = 6,500 MPa, v = 0.22 (group B) Remained constant |
Opposite edge of spring fixed | Point loading force at spring contact region (initial value of 6.9 N) |
| Weickenmeier et al., 2017 | Not specified | 2D: fixed at the center and kinematic constraint on sutures 3D: center fixed and corresponding suture region depending on scenario |
2D: unidirectional homogeneous expansion 3D: orthotropic in-plane growth: length, width and bidirectional loading (simulates 12 months growth, 30% increase in circumference) |
| Li et al., 2017 | Bone: details are not specified Fixation device: details are not specified |
Not specified | Not specified |
| Borghi et al., 2018 | Bone: E = 421 MPa, v = 0.22 Sutures: E = 16 MPa, v = 0.49 Viscoelasticity of both bone and sutures modelled through Prony shear and bulk relaxation relationship |
Model constrain at the distal end of three quarters of the skull (in the transverse plane), avoiding free expansion of the head base in this plane | Spring expansion simulated |
DOF; degrees of freedom; E, elastic modulus.
Representation of the Skull, Sutures, and Craniotomies
Computer-aided design tools have been used to simplify the morphology of the human head to geometries such as spherical, spheroidal, or ellipsoidal shells. A study by Weickenmeier et al. [2017] used such an approach to model several types of craniosynostosis, i.e., predicting the preoperative calvarial morphology. On the other hand, CT and MRI have also been used to develop a more detailed representation of the skull [e.g., Nagasao et al., 2010; Wolański et al., 2013; Li et al., 2017; Borghi et al., 2018]. The images are generally reconstructed using an image processing software. Some studies have only modelled craniofacial bones and craniotomies [e.g., You et al., 2010; Larysz et al., 2012; Wolański et al., 2013; Zhang et al., 2016; Li et al., 2017], while others have also included the cranial sutures [e.g., Nagasao et al., 2011].
Representation of the Material Properties of Bones and Sutures
Bone and sutures have been generally modelled as linear elastic materials with most of the studies using a constant value across the skull [You et al., 2010; Larysz et al., 2012; Wolański et al., 2013; Zhang et al., 2016]. Nonetheless, a wide range of elastic moduli have been used to model the calvarial bones. For example, studies of Larysz et al. [2012] and Wolański et al. [2013] used an elastic modulus of 380 MPa for bones in children aged 3-5 months and 1 year of age. Zhang et al. [2016] used an elastic modulus of 1,300 MPa for infants aged 3-6 months and 6,500 MPa for infants older than 6 months (see Tables 1, 2). For suture material properties, however, only one value of 3.8 MPa was reported by Nagasao et al. [2010, 2011]. Borghi et al. [2018] recently used a value of 16 MPa to model coronal and lambdoid sutures in a patient-specific model of sagittal synostosis spring-assisted reconstruction.
Representation of the Loads
Most of the studies considered the foramen magnum as a stationary point on the human skull during growth [e.g., Nagasao et al., 2010, 2011]. This anatomical point has, therefore, been used as the main area of constraint for most of the FE studies. Most of the research modelled immediate postoperative reconstruction and only loaded their models with a constant intracranial pressure [Jiang et al., 2010; Nagasao et al., 2010, 2011; You et al., 2010; Larysz et al., 2012; Wolański et al., 2013; Zhang et al., 2016; Li et al., 2017]. The only study that modelled calvarial growth during development is Weickenmeier et al. [2017].
Simulation Predictions and Accuracy
Generally, 2 parameters have been extracted from the results of the FE models: (1) deformation of the skull, which has also been used to calculate the cephalic index (the maximum width to maximum length ratio multiplied by 100) and (2) mechanical strain and stress within the calvarial bone.
The accuracy of the FE models depends on the choice of input parameters as well as the number of computations used to derive the solution. The number of computations is related to the number and type of elements in the model, i.e., mesh convergence. Most of the studies have used the input parameters related to material properties of their models based on previous experimental studies [Nagasao et al., 2010, 2011; You et al., 2010; Zhang et al., 2016; Li et al., 2017; Weickenmeier et al., 2017]. However, they generally have not reported details of mesh convergence.
Results
The cases studied and their key outcomes are summarized in Table 3. In brief, studies of Nagasao et al. [2010, 2011] mainly focused on the deformation of the orbits either preoperatively investigating the effect of different types of craniosynostosis or postoperatively investigating the effect of forehead remodelling. Studies of You et al. [2010], Jiang et al. [2010], Larysz et al. [2012], Wolański et al. [2013], and Li et al. [2017] compared different methods of reconstruction for sagittal and metopic synostosis. Authors virtually reconstructed the skull based on different craniotomies and commented on the skull shape immediately postoperatively and the pattern of stress and strain distribution in different reconstructions (see example from Wolański et al. [2013] in Fig.1). Zhang et al. [2016] used FEM to quantify the spring force in spring-assisted cranioplasty for sagittal synostosis. They measure spring forces in the range of 5-8 N. A study by Weickenmeier et al. [2017] predicted calvarial growth for different types of craniosynostosis.
Table 3.
A summary of results of current finite element analysis of craniosynostosis
| Authors | Presented data | Validation | Outcome |
|---|---|---|---|
| Nagasao et al., 2010 | Orbital deformation around the eye socket | Quantitative analysis of clinical data | Results showed that only frontoparietal synostosis caused more deformation around the orbit compared to combined frontoparietal and frontosphenoidal synostosis Degree of fusion presented by frontosphenoidal synostosis should be evaluated in detail |
| You et al., 2010; Jiang et al., 2010 | FE stress and displacement on different craniotomies for Pi-shaped operation | NA | Results indicated that cranial bone rigidity is a key factor with profound influence on postoperative outcomes, and lower bone rigidity leads to better results (schemes 4–5) No validation of the research was provided to support these results/claims |
| Nagasao et al., 2011 | Orbital deformation around eye socket for normal skulls, untreated and treated metopic synostosis skulls | Quantitative analysis of clinical data | Results showed that expansion of interorbital distances due to intracranial pressure is constrained structurally in metopic synostosis The remodelling of the frontals during metopic synostosis treatment allows the expansion of the frontals, and this then increases the interorbital distance and improves the facial morphology |
| Larysz et al., 2012 | FE stress and deformation on critical sections of the skull following endoscopic surgical cuts | NA | Pattern of skull deformation following patient-specific metopic and sagittal synostosis calvarial reconstruction were shown Authors also presented bone thickness and the loading levels required to cut the calvarial bones |
| Wolanski et al., 2013 | FE stress and displacement of cranium following virtual surgery | Qualitative analysis of clinical data | Results showed that in metopic reconstruction, remodelling of the forehead by 1 incision along the metopic and 2 incisions along the coronal sutures showed higher maximum displacement compared to the same craniotomies with additional 2 incisions in the middle of each half of the frontal bones Results showed that in sagittal reconstruction, inverted modified Pi procedure with half-incisions in the middle of the parietal bone showed lower maximum displacement compared to the same craniotomy with full incision in the parietal bone; note, skulls were loaded with intracranial pressure |
| Zhang et al., 2016 | Optimal spring force based on preoperative patient-specific properties | Quantitative analysis of clinical data | Development of a computer platform capable of predicting optimal spring force in SAS for sagittal sysnotosis was achieved In vivo and clinical data results indicated that bone thickness and spring force play a crucial role in surgical outcome |
| Weickenmeier et al., 2017 | CI values for various simulated craniosynostosis models in 2D and 3D | Quantitative analysis of clinical data | Typical craniosynostotic skull shapes were predicted using simplified 2D and 3D elliptical models. The CI predictions based on the 2D model showed 0.5–12% difference with clinical data across sagittal, lambdoid, metopic, and uni/bi coronal synostosis The 3D model showed 0.5–3.5% difference between the predicted and clinical CIs |
| Li et al., 2017 | Surgical data such as time, blood loss, cost, and CI values measured and compared | Qualitative analysis of clinical data | Stress and strain analysis of a single case for sagittal synosotsis reconstruction was presented Quantitative data, i.e., operative duration, blood loss, hospital cost, pre- and postoperative CIs were also presented comparing a preoperative planning cohort versus a non-preoperative planning cohort |
| Borghi et al., 2018 | Spring opening over time and predicted calvarial shape following surgery | Quantitative comparison versus 3D surface data obtained from a handheld scanner | A validated patient-specific model of spring-assisted sagittal synostosis was developed The potentials of FEM to predict the skull shape of craniosynostotic patients following surgery was highlighted |
CI, cephalic index; FE, finite element; FEM, finite element method; NA, not applicable; SAS, spring-assisted surgery.
Overall, there was a lack of detailed validation of the FE results. For example, Weickenmeier et al. [2017] compared their modelling findings quantitatively with clinical data only in terms of the cephalic index for different types of craniosynostosis. Similarly, the study of Nagasao et al. [2011] compared their FE prediction of orbital distance in 3 different groups (normal skull, metopic synostosis, and metopic synostosis following forehead reconstruction) with their clinical data. Perhaps, the most detailed validation study to date is that of Borghi et al. [2018], who developed a patient-specific model of sagittal synostosis and compared the skull shape based on their FE predictions versus postoperative 3D head scan of the same patient's head.
Discussion
The current biomechanical literature relating to craniosynostosis was reviewed. Several studies were found that directly developed FE models of craniosynostosis (n = 10). Whilst these studies all highlighted the potential of FEM to advance treatment of craniosynostosis, it is clear that there is more work to be done. Here, 2 key areas that can be improved are discussed: (1) addressing the modelling assumptions and (2) validating the FE results.
Firstly, there is a clear lack of detailed description of the methodologies used in these studies. The technical details and how the models have been developed can be significantly improved. Here perhaps, 4 areas can be highlighted: (1) loading - most of the studies have applied a constant pressure to load the calvaria with exception of study of Weickenmeier et al. [2017]. This approach allows for a comparison of different reconstructions at a single time point during the development. It does not, however, explain how the growing brain interacts with different calvarial reconstructions during the development. In this respect, intracranial volume or brain soft tissue can be modelled and expanded based on the changes in the intracranial volume to take into account the loading arising from the growing brain [Jin et al., 2014; Libby et al., 2017; Marghoub et al., 2018]; (2) modelling the sutures - it is well established that the sutures can release the local mechanical strain [e.g., Moss, 1954; Jaslow and Biewner, 1995; Moazen et al., 2013]. It is important to include the sutures to develop more realistic models of the craniofacial system [Jin et al., 2013; Libby et al., 2017; Weickenmeier et al., 2017; Marghoub et al., 2018]. Sutures can be segmented during the reconstruction of the model of the skull via image processing and incorporated into the FE simulation; (3) modelling dura mater and other soft tissues - including other soft tissues such as dura mater and muscles will evidently lead to more realistic FE models of the skull growth. You et al. [2010] included dura mater in their model, but it is not clear to us how this tissue was modelled. In this respect, head models developed to simulate head injuries include various soft tissues [e.g., Roth et al., 2010]. These models can provide insights for developing more representative models of craniosynostosis [for review, see Dixit and Liu, 2017]. It must be noted that while increasing the complexity of FE models is possible, further studies are required to investigate how much complexity is needed to develop a validated model of craniosynostosis, whereby, the outcome of different reconstructions can be reliably predicted; (4) material properties - our understanding of changes in mechanical properties of calvarial bones and other related tissues such as dura mater during the development is still limited. Few studies have quantified such changes during the development [e.g., McPherson and Kriewall, 1980; Margulies and Thibault, 2000; Henderson et al., 2005; Coats and Margulies, 2006; Wang et al., 2014; Moazen et al., 2015]. Clearly, soft tissues involved in the calvarial development are viscoelastic materials, and their properties change during the development. Most of the current studies have used linear elastic material models. It is encouraging that the recent study of Borghi et al. [2018] took into account the viscoelasticity effect of bone and sutures. In this respect, the models can improve including time-dependent changes during the growth. This perhaps also requires further experimental studies.
Second, detailed validation of the FE models is a key step to build confidence in the results of such models. To our understanding, most of the reviewed studies in this work lack a detailed validation of their simulation. The authors are clearly conscious of the importance of validation in such models. For example, the study by Nagasao et al. [2010] compared their FE results with clinical data in terms of orbital changes in different caniosynostosis groups that they modelled. Similarly, Weickenmeier et al. [2017] compared cephalic indices of their predicated 2D and 3D craniosynostotic skull shapes and compared their results with clinical measurements. While such simple measurements are reassuring, if the CT data of the whole skull are available, a full 3D comparison between the FE and in vivo data can be carried out [Libby et al., 2017] and provide a more comprehensive analysis of the size and shape differences. In the case of craniosynostosis and predicting the outcome of different surgical techniques, the FE results need to be compared against the follow-up CT data of the same child. A caveat to this is that there might be ethical or resource issues in obtaining such CT data. In this respect, (1) 3D surface scanners can provide invaluable information [e.g., Dai et al., 2017; Borghi et al., 2018] and (2) in vitro experimental studies can also be an alternative way to validate the FE models in a simpler condition [e.g., Szwedowski et al., 2011; Toro-Ibacache et al., 2016; Libby et al., 2017].
The present study focused on the FE models of craniosynostosis; however, there are a number of studies that have used computer-aided design and 3D printing to visualize different reconstructions of craniosynostosis for preoperative planning of this condition [e.g., Imai et al., 1999; Mommaerts et al., 2001; Meehan et al., 2003; Iyer et al., 2018]. These studies are clearly advancing the treatment of craniosynostosis, and models generated from these studies can be used to develop FE simulations of the skull growth to predict the outcomes of different reconstructions on a virtual platform.
In summary, a few studies to date have used FEM to optimize the reconstruction of craniosynostosis skulls. The reviewed studies clearly show the potentials of this technique; however, there are several limitations that need to be addressed in relation to their input parameters and validations. Nonetheless, they provide a strong foundation for future studies.
Disclosure Statement
The authors have no conflicts of interest to disclose.
Acknowledgements
This work was supported by the Royal Academy of Engineering Research Fellowship to M.M.
References
- Abbott A, Netherway DJ, Niemann DB, Clark B, Yamamoto M, et al. CT-determined intracranial volume for a normal population. J Craniofac Surg. 2000;11:211–223. doi: 10.1097/00001665-200011030-00002. [DOI] [PubMed] [Google Scholar]
- Al-Rekabi Z, Cunningham ML, Sniadecki NJ. Cell mechanics of craniosynostosis. ACS Biomater Sci Eng. 2017;3:2733–2743. doi: 10.1021/acsbiomaterials.6b00557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borghi A, Rodriguez-Florez N, Rodgers W, James G, Hayward R, et al. Spring assisted cranioplasty: a patient specific computational model. Med Eng Phys. 2018;53:58–65. doi: 10.1016/j.medengphy.2018.01.001. [DOI] [PubMed] [Google Scholar]
- Clayman MA, Murad GJ, Steele MH, Seagle MB, Pincus DW. History of craniosynostosis surgery and the evolution of minimally invasive endoscopic techniques: the University of Florida experience. Ann Plast Surg. 2007;58:285–287. doi: 10.1097/01.sap.0000250846.12958.05. [DOI] [PubMed] [Google Scholar]
- Coats B, Margulies SS. Material properties of human infant skull and suture at high rates. J Neurotrauma. 2006;23:1222–1232. doi: 10.1089/neu.2006.23.1222. [DOI] [PubMed] [Google Scholar]
- Cornelissen M, Ottelander Bd, Rizopoulos D, van der Hulst R, Mink van der Molen A, et al. Increase of prevalence of craniosynostosis. J Craniomaxillofac Surg. 2016;44:1273–1279. doi: 10.1016/j.jcms.2016.07.007. [DOI] [PubMed] [Google Scholar]
- Dai H, Pear N, Smith W, Duncan C. A 3D Morphable model of craniofacial shape and texture variation. IEEE International Conference on Computer Vision, Oct 22-29, Venice. 2017 [Google Scholar]
- Dekaban AS. Tables of cranial and orbital measurements, cranial volume, and derived indexes in males and females from 7 days to 20 years of age. Ann Neurol. 1977;2:485–491. doi: 10.1002/ana.410020607. [DOI] [PubMed] [Google Scholar]
- Dixit P, Liu GR. A review on recent development of finite element models for head injury simulations. Arch Computat Methods Eng. 2017;24:979–1031. [Google Scholar]
- Fagan MJ. Finite Element Analysis: Theory and Practice (Longman Scientific and Technical, Harlow 1992)
- Gerety PA, Basta MN, Fischer JP, Taylor JA. Operative management of nonsyndromic sagittal synostosis: a head-to-head meta-analysis of outcomes comparing 3 techniques. J Craniofac Surg. 2015;26:1251–1257. doi: 10.1097/SCS.0000000000001651. [DOI] [PubMed] [Google Scholar]
- Ghajari M, Hellyer PJ, Sharp DJ. Computational modelling of traumatic brain injury predicts the location of chronic traumatic encephalopathy pathology. Brain. 2017;140:333–343. doi: 10.1093/brain/aww317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy CH, Marcal PV. Elastic analysis of a skull. J Appl Mech. 1973;40:838–842. [Google Scholar]
- Henderson JH, Chang LY, Song HM, Longaker MT, Carter DR. Age-dependent properties and quasi-static strain in the rat sagittal suture. J Biomech. 2005;38:2294–2301. doi: 10.1016/j.jbiomech.2004.07.037. [DOI] [PubMed] [Google Scholar]
- Herring SW. Mechanical influences on suture development and patency. Front Oral Biol. 2008;12:41–56. doi: 10.1159/0000115031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopper RA, Grant GA, Ellenbogen RG. Controversies in the management of craniosynostosis. Sem Neurosurg. 2002;13:81–95. [Google Scholar]
- Horgan TJ, Gilchrist MD. The creation of three-dimensional finite element models for simulating head impact biomechanics. Int J Crash. 2003;8:353–366. [Google Scholar]
- Huiskes R, Chao EY. A survey of finite element analysis in orthopedic biomechanics: the first decade. J Biomech. 1983;16:385–409. doi: 10.1016/0021-9290(83)90072-6. [DOI] [PubMed] [Google Scholar]
- Imai K, Tsujiguchi K, Toda C, Enoki E, Sung KC, et al. Reduction of operating time and blood transfusion for craniosynostosis by simulated surgery using three-dimensional solid models. Neurol Med Chir (Tokyo) 1999;39:423–426. doi: 10.2176/nmc.39.423. [DOI] [PubMed] [Google Scholar]
- Iyer RR, Wu A, Macmillan A, Musavi L, Cho R, et al. Use of computer-assisted design and manufacturing to localize dural venous sinuses during reconstructive surgery for craniosynostosis. Childs Nerv Syst. 2018;34:137–142. doi: 10.1007/s00381-017-3601-0. [DOI] [PubMed] [Google Scholar]
- Jaslow CR, Biewener AA. Strain patterns in the horncores, cranial bones and sutures of goats (Capra hircus) during impact loading. J Zool. 1995;235:193–210. [Google Scholar]
- Jiang X, You J, Wang N, Shen Z, Li J. Skull mechanics study of PI procedure plan for craniosynostosis correction based on finite element method. 4th International Conference on Bioinformatics and Biomedical Engineering, June 10-12. Chengdu. 2010 [Google Scholar]
- Jimenez DF, Barone CM. Early treatment of coronal synostosis with endoscopy-assisted craniectomy and postoperative cranial orthosis therapy: 16-year experience. J Neurosurg Pediatr. 2013;12:207–219. doi: 10.3171/2013.4.PEDS11191. [DOI] [PubMed] [Google Scholar]
- Jin J, Shahbazi S, Lloyd J, Fels S, de Ribaupierre S, et al. Hybrid simulation of brain-skull growth. Simulation. 2014;90:3–10. [Google Scholar]
- Johnson D, Wilkie AOM. Craniosynostosis. Eur J Hum Genet. 2011;19:369–376. doi: 10.1038/ejhg.2010.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khonsari RH, Olivier J, Vigneaux P, Sanchez S, Tafforeau P, et al. A mathematical model for mechanotransduction at the early steps of suture formation. Proc Biol Sci. 2013;280:20122670. doi: 10.1098/rspb.2012.2670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larysz D, Wolański W, Kawlewska E, Mandera M, Gzik M. Biomechanical aspects of preoperative planning of skull correction in children with craniosynostosis. Acta Bioeng Biomech. 2012;14:19–26. [PubMed] [Google Scholar]
- Lee C, Richtsmeier JT, Kraft RH. A computational analysis of bone formation in the cranial vault using a coupled reaction-diffusion-strain model. J Mech Med Biol. 2017;17:1750073. doi: 10.1142/S0219519417500737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lestrel PE. Some approaches toward the mathematical modeling of the craniofacial complex. J Craniofac Gene Dev Bio. 1989;9:77–91. [PubMed] [Google Scholar]
- Li X, Zhu W, He J, Di F, Wang L, et al. Application of computer assisted three-dimensional simulation operation and biomechanics analysis in the treatment of sagittal craniosynostosis. J Clin Neurosci. 2017;44:323–329. doi: 10.1016/j.jocn.2017.06.032. [DOI] [PubMed] [Google Scholar]
- Libby J, Marghoub A, Johnson D, Khonsari R, Fagan MJ, Moazen M. Modelling human skull growth: a validated computational model. J R Soc Interface. 2017;14:20170202. doi: 10.1098/rsif.2017.0202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marghoub A, Libby J, Babbs C, Pauws E, Fagan MJ, Moazen M. Predicting calvarial growth in normal and craniosynostosis mice using a computational approach. J Anat. 2018;232:440–448. doi: 10.1111/joa.12764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies SS, Thibault KL. Infant skull and suture properties: measurements and implications for mechanisms of pediatric brain injury. J Biomech Eng. 2000;122:364–371. doi: 10.1115/1.1287160. [DOI] [PubMed] [Google Scholar]
- Mathijssen IMJ. Guideline for care of patients with the diagnoses of craniosynostosis: working group on craniosynostosis. J Craniofac Surg. 2015;26:1735–1807. doi: 10.1097/SCS.0000000000002016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy JG, Glasberg SB, Cutting CB, Epstein FJ, Grayson BH, et al. Twenty-year experience with early surgery for craniosynostosis: I. Isolated craniofacial synostosis-results and unsolved problems. Plast Reconstr Surg. 1995;96:272–283. doi: 10.1097/00006534-199508000-00004. [DOI] [PubMed] [Google Scholar]
- McPherson GK, Kriewall TJ. Fetal head molding: an investigation utilizing a finite element model of the fetal parietal bone. J Biomech. 1980;13:17–26. doi: 10.1016/0021-9290(80)90004-4. [DOI] [PubMed] [Google Scholar]
- Meehan M, Teschner M, Girod S. Three-dimensional simulation and prediction of craniofacial surgery. Orthod Craniofac Res 6 Suppl. 2003;1:102–107. doi: 10.1034/j.1600-0544.2003.242.x. [DOI] [PubMed] [Google Scholar]
- Moazen M, Curtis N, O';Higgins P, Evans SE, Fagan MJ. Biomechanical assessment of evolutionary changes in the lepidosaurian skull. Proc Nat Acad Sci USA. 2009;106:8273–8277. doi: 10.1073/pnas.0813156106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moazen M, Costantini D, Bruner E. A sensitivity analysis to the role of fronto-parietal suture in Lacerta bilineata: a preliminary finite element approach. Anat Rec (Hoboken) 2013;296:198–209. doi: 10.1002/ar.22629. [DOI] [PubMed] [Google Scholar]
- Moazen M, Peskett E, Babbs C, Pauws E, Fagan MJ. Mechanical properties of calvarial bones in a mouse model for craniosynostosis. PLoS One. 2015;10:e0125757. doi: 10.1371/journal.pone.0125757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mommaerts M, Jans G, Vander Stoten J, Staels PF, Van der Perre G, Gobin R. On the assets of CAD planning for craniosynostosis surgery. J Craniofac Surg. 2001;12:547–554. doi: 10.1097/00001665-200111000-00008. [DOI] [PubMed] [Google Scholar]
- Morriss-Kay GM, Wilkie AOM. Growth of the normal skull vault and its alteration in craniosynostosis: insights from human genetics and experimental studies. J Anat. 2005;207:637–653. doi: 10.1111/j.1469-7580.2005.00475.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moss ML. Growth of the calvaria in the rat, the determination of osseous morphology. Am J Anat. 1954;94:333–361. doi: 10.1002/aja.1000940302. [DOI] [PubMed] [Google Scholar]
- Nagasao T, Miyamoto J, Uchikawa Y, Tamaki T, Yamada A, et al. A biomechanical study on the effect of premature fusion of the frontosphenoidal suture on orbit asymmetry in unilateral coronal synostosis. Cleft Palate Craniofac J. 2010;47:82–91. doi: 10.1597/08-164.1. [DOI] [PubMed] [Google Scholar]
- Nagasao T, Miyamoto J, Jiang H, Kaneko T, Tamaki T. Biomechanical analysis of the effect of intracranial pressure on the orbital distances in trigonocephaly. Cleft Palate Craniofac J. 2011;48:190–196. doi: 10.1597/09-027. [DOI] [PubMed] [Google Scholar]
- O';Higgins P, Cobb SN, Fitton LC, Gröning F, Phillips R, et al. Combining geometric morphometrics and functional simulation: an emerging toolkit for virtual functional analyses. J Anat. 2011;218:3–15. doi: 10.1111/j.1469-7580.2010.01301.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Opperman LA. Cranial sutures as intramembranous bone growth sites. Dev Dyn. 2000;219:472–485. doi: 10.1002/1097-0177(2000)9999:9999<::AID-DVDY1073>3.0.CO;2-F. [DOI] [PubMed] [Google Scholar]
- Pan X, Qian Y, Yu J, Wang D, Tang Y, Shen G. Biomechanical effects of rapid palatal expansion on the craniofacial skeleton with cleft palate: a three-dimensional finite element analysis. Cleft Palate Craniofac J. 2007;44:149–154. doi: 10.1597/05-161.1. [DOI] [PubMed] [Google Scholar]
- Prado FB, Freire AR, Cláudia Rossi A, Ledogar JA, Smith AL, et al. Review of in vivo bone strain studies and finite element models of the zygomatic complex in humans and nonhuman primates: implications for clinical research and practice. Anat Rec (Hoboken) 2016;299:1753–1778. doi: 10.1002/ar.23486. [DOI] [PubMed] [Google Scholar]
- Rayfield EJ. Finite element analysis and understanding the biomechanics and evolution of living and fossil organisms. Ann Rev Ear Plan Sci. 2007;35:541–576. [Google Scholar]
- Remmler D, Olson L, Ekstrom R, Duke D, Metamoros A, et al. Pre-surgical CT/FEA for craniofacial distraction: I. Methodology, development, and validation of the cranial finite element model. Med Eng Phys. 1998;20:607–619. doi: 10.1016/s1350-4533(98)00053-8. [DOI] [PubMed] [Google Scholar]
- Richtsmeier JT, Flaherty K. Hand in glove: brain and skull in development and dysmorphogenesis. Acta Neuropathol. 2013;125:469–489. doi: 10.1007/s00401-013-1104-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth S, Raul JS, Willinger R. Finite element modelling of paediatric head impact: global validation against experimental data. Comput Methods Programs Biome. 2010;99:25–33. doi: 10.1016/j.cmpb.2009.10.004. [DOI] [PubMed] [Google Scholar]
- Scheuer L, Black S. New York: Elsevier Academic Press; 2004. The Juvenile Skeleton. [Google Scholar]
- Simpson A, Wong AL, Bezuhly M. Surgical correction of nonsyndromic sagittal craniosynostosis concepts and controversies. Ann Plast Surg. 2017;78:103–110. doi: 10.1097/SAP.0000000000000713. [DOI] [PubMed] [Google Scholar]
- Szwedowski TD, Fialkov J, Whyne CM. Sensitivity analysis of a validated subject-specific finite element model of the human craniofacial skeleton. Proc Inst Mech Eng H. 2011;225:58–67. doi: 10.1243/09544119JEIM786. [DOI] [PubMed] [Google Scholar]
- Tanne K, Miyasaka J, Yamagata Y, Sachdeva R, Tsutsumi S, Sakuda M. Three-dimensional model of the human craniofacial skeleton: method and preliminary results using finite element analysis. J Biomed Eng. 1988;10:246–252. doi: 10.1016/0141-5425(88)90006-4. [DOI] [PubMed] [Google Scholar]
- Taylor JA, Maugans TA. Comparison of spring-mediated cranioplasty to minimally invasive strip craniectomy and barrel staving for early treatment of sagittal craniosynostosis. J Craniofac Surg. 2011;22:1225–1229. doi: 10.1097/SCS.0b013e31821c0f10. [DOI] [PubMed] [Google Scholar]
- Thomas GP, Johnson D, Byren JC, Jayamohan J, Magdum SA, et al. Long-term morphological outcomes in nonsyndromic sagittal craniosynostosis: a comparison of 2 techniques. J Craniofac Surg. 2015;26:19–25. doi: 10.1097/SCS.0000000000001107. [DOI] [PubMed] [Google Scholar]
- Toro-Ibacache V, Fitton LC, Fagan MJ, O';Higgins P. Validity and sensitivity of a human cranial finite element model: implications for comparative studies of biting performance. J Anat. 2016;228:70–84. doi: 10.1111/joa.12384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Meulen J, van der Hulst R, van Adrichem L, Arnaud E, Chin-Shong D, et al. The increase of metopic synostosis: a pan-European observation. J Craniofac Surg. 2009;20:283–286. doi: 10.1097/scs.0b013e31818436be. [DOI] [PubMed] [Google Scholar]
- Wang J, Zou D, Li Z, Huang P, Li D, et al. Mechanical properties of cranial bones and sutures in 1-2-year-old infants. Med Sci Monit. 2014;20:1808–1813. doi: 10.12659/MSM.892278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang JW, Huang J, Li ZD, Zou DH, Li Z, et al. Research progress on biomechanics of craniocerebral injury in children (in Chinese) Fa Yi Xue Za Zhi. 2016;32:448–431. doi: 10.3969/j.issn.1004-5619.2016.06.014. [DOI] [PubMed] [Google Scholar]
- Wang Q, Wright BW, Smith A, Chalk J, Byron CD. Mechanical impact of incisor loading on the primate midfacial skeleton and its relevance to human evolution. Anat Rec (Hoboken) 2010;293:607–617. doi: 10.1002/ar.21123. [DOI] [PubMed] [Google Scholar]
- Weickenmeier J, Fischer C, Carter D, Kuhl E, Goriety A. Dimensional, geometrical, and physical constraints in skull growth. Phys Rev Lett. 2017;118:248101. doi: 10.1103/PhysRevLett.118.248101. [DOI] [PubMed] [Google Scholar]
- Wilkie AOM, Johnson D, Wall SA. Clinical genetics of craniosynostosis. Curr Opin Pediatr. 2017;29:622–628. doi: 10.1097/MOP.0000000000000542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolański W, Larysz D, Gzik M, Kawlewska E. Modeling and biomechanical analysis of craniosynostosis correction with the use of finite element method. Int J Numer Method Biomed Eng. 2013;29:916–925. doi: 10.1002/cnm.2506. [DOI] [PubMed] [Google Scholar]
- You J, Jiang X, Hu M, Wang N, Shen Z, et al. The bone slot effect study of PI procedure for craniosynostosis correction plan based on finite element method. 3rd International Conference on Biomedical Engineering and Informatics, Oct 16-18. Yantai. 2010:pp 605–608. [Google Scholar]
- Zhang G, Tan H, Qian X, Zhang J, Li K, et al. A systematic approach to predicting spring force for sagittal craniosynostosis surgery. J Craniofac Surg. 2016;27:636–643. doi: 10.1097/SCS.0000000000002590. [DOI] [PubMed] [Google Scholar]