Modified Wilcoxon-Mann-Whitney Test and Power against Strong Null

Abstract

The Wilcoxon-Mann-Whitney (WMW) test is a popular rank-based two-sample testing procedure for the strong null hypothesis that the two samples come from the same distribution. A modified WMW test, the Fligner-Policello (FP) test, has been proposed for comparing the medians of two populations. A fact that may be underappreciated among some practitioners is that the FP test can also be used to test the strong null like the WMW. In this paper we compare the power of the WMW and FP tests for testing the strong null. Our results show that neither test is uniformly better than the other and that there can be substantial differences in power between the two choices. We propose a new, modified WMW test that combines the WMW and FP tests. Monte Carlo studies show that the combined test has good power compared to either the WMW and FP test. We provide a fast implementation of the proposed test in an open-source software. Supplementary materials are available online.

1 Introduction

The two-sample location problem is a common one in many applied areas. Rank-based two-sample comparison procedures are popular because they make no assumptions about the distributions of data within each sample and because they are relatively powerful across a spectrum of scenarios (e.g. Blair and Higgins, 1980; van der Vaart, 2000, p. 198). One of the best known rank-based two-sample tests is the Wilcoxon-Mann-Whitney (WMW) test (Wilcoxon, 1945; Mann and Whitney, 1947). The test is based on the following statistic. Suppose that we have m independent and identically distributed (i.i.d.) observations X₁,…,X_m from population 1, and n i.i.d. observations Y₁,…, Y_n from population 2, and that the two sets of samples are independent of each other. Further assume the distributions of X and Y are continuous so that there are no ties in the data; this assumption can be easily relaxed, but it helps streamline the exposition of the main ideas of the paper. The WMW test statistic can be represented either by the sum of the ranks assigned to the Y’s in the combined samples or the U-statistic representation:

$$U=\frac{1}{\mathit{mn}}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j-1}^{n}I(X_i<Y_j).}}$$ (1)

The rank sum representation and the U-statistic representation are mathematically equivalent up to some constants (Hollander et al., 2013, equation 4.16). While the former lends itself to more efficient computation, the latter makes explicit the nature of the WMW statistic. As Equation (1) shows, U is an estimate, in fact a consistent, minimum variance unbiased estimate (Lehmann, 1951), of the probability that a randomly chosen Y is greater than a randomly chosen X. This measure, to be denoted by θ, has been called the relative marginal effect (Brunner et al., 2002) and probabilistic index (Acion et al., 2006). In the biomarker evaluation literature (Pepe, 2003; Zhou et al., 2002; Saha and Heagerty, 2010) it is known as the area under the receiver operating characteristic curve (AUC) and is a key classification performance criterion. More generally, θ is a measure of stochastic ordering.

One reason for the popularity of the WMW test is its distribution-free property. Under the strong null hypothesis that the distributions of X and Y are equal, the sampling distribution of U only depends on the sample sizes and has mean 1/2 and variance V_mn = {1/m + 1/n + 1/(mn)}/12, regardless of the distributions of X and Y. The p-value of the WMW test can be determined by comparing the observed value of U to its exact distribution. Alternatively, as the sample sizes increase, the sampling distribution of $(U-1/2)/\sqrt{V_{\mathit{mn}}}$ can be well approximated by the standard normal distribution (e.g. Hollander et al., 2013, Sec. 4.1).

In addition to the strong null, in many applications it makes sense to consider the weak null hypothesis, which states that the relative marginal effect θ = 1/2. The WMW test does not have the correct size for testing the weak null because the sampling distribution of U is not distribution-free under the weak null (e.g. Chung and Romano, 2016; Chung et al., 2013). Towards this end, Fligner and Policello (1981) proposed a modified WMW test, the Fligner-Policello (FP) test, that incorporates an estimate of the variance of U from the data. Let P_i be the number of Y ’s less than X_i and S_j be the number of X’s less than Y_j . Denote the average of P_i by $\overline{P}$ and the average of S_j by $\overline{S}$. ${\widehat{V}}^{\ast }=\{{\displaystyle {\sum }_{j=1}^n{(S_j-\overline{S})}^2}+{\displaystyle {\sum }_{i=1}^m{(P_i-\overline{P})}^2}+\overline{P}\overline{S}\}/{(\mathit{mn})}^2$ is then a consistent estimator of the variance of U. The test statistic of the Fligner-Policello test is $(U-1/2)/\sqrt{{\widehat{V}}^{\ast }}$ and the reference distribution can be either N (0,1), in the normal approximation, or the permutation distribution (e.g. Hollander et al., 2013, Sec. 4.4). Under the additional assumption that the distributions of X and Y are symmetric, the weak null is equivalent to testing the equality of the medians of the two populations.

For rank-based two-sample location tests, as for two-sample t-tests, whether or not the variances of the two samples are considered equal affects the appropriate choice of testing procedures. There are two ways variance equality affects the choice of rank-based testing procedures: (1) For testing the weak null, under which the variances are not assumed equal, it is well recognized that the FP test instead of the WMW test should be used (e.g. Siegel and Castellan, 1988; Zumbo and Coulombe, 1997; Mickelson, 2013). (2) For testing the strong null, under which the variances are assumed equal, both the WMW and FP tests can be used, but one may be more powerful than the other and we have a choice to make. The second scenario is understudied in the literature in our opinion and is the focus of this paper.

Our goals in this paper are three-fold: (1) to investigate the relationship between the variance of U and the distributions of X and Y, (2) to study the power trade-off between the WMW and FP tests for testing the strong null, and (3) to propose a new, modified WMW test that combines the WMW and FP tests to improve the overall power for testing the strong null.

2 Variance of the U statistic

Let the distribution functions of X and Y be denoted by F (x) and G (y). It is a useful fact to note that the relative marginal effect can be expressed in terms of F and G: θ = E_Y{F (Y)} = 1 − E_X{G (X)}, where E_X and E_Y are the notations for taking an average over the populations of X and Y, respectively. It can be shown through straightforward computation (supplementary materials Sec. A) that

$$\mathrm{Var}(U)=(1-1/n)\mathrm{Var}\{G(X)\}/m+(1-1/m)\mathrm{Var}\{F(Y)\}/n+\mathrm{Var}\{I(X<Y)\}/(\mathit{mn}).$$ (2)

To the first order of approximation, this can be simplified to

$$\mathrm{Var}(U)\approx \mathrm{Var}\{G(X)\}/m+\mathrm{Var}\{F(Y)\}/n.$$ (3)

To estimate the variance of U based on either (2) or (3), we can estimate Var {G (X)} by the sample variance of $\widehat{G}(X_i)$, where $\widehat{G}$ is the empirical distribution function of the observed Y’s; estimate Var {F (Y)} by the sample variance of $\widehat{F}(Y_j)$, where $\widehat{F}$ is the empirical distribution function of the observed X’s; and estimate Var {I (X < Y)} by $\widehat{\theta }(1-\widehat{\theta })$, where $\widehat{\theta }$ equals U, the sample average of I (X_i < Y_j).

To check the performance of the variance estimation, we simulate X’s from Logistic(μ_x, s_x), a logistic distribution with mean μ_x and scale s_x, and Y’s from Logistic(μ_y, s_y). We compute the true variance of U by numerical integration and compare the mean of the variance estimates based on formula (2) and (3), as well the original formula from Fligner and Policello (1981) to the theoretical value. The percent biases of the estimated variances from 10,000 replicates for μ_x = μ_y = 0, s_x = 1, and s_y ∈ {1, 2, 0.5} are summarized in Table 1. The results show that as the sample sizes increase, variance estimates based on all the formulae provide good estimates of the actual variance, whether or not s_x and s_y are equal. When the sample sizes m and n reach 30, the relative biases fall below 5%. We repeat the experiment with μ_y = 1 and obtain similar results (supplementary materials Table D.8); we also repeat the experiments using normal instead of logistic distributions and observe similar results (supplementary materials Table D.1 and D.9).

Table 1.

Percent bias of three variance estimators. FP*: the original variance estimator from Fligner and Policello (1981); (2) and (3): variance estimators based on formula (2) and (3). X ~ Logistic(0, 1), Y ~ Logistic(0, s_y).

m	n = m			n = 2m			n = 4m
	FP*	(2)	(3)	FP*	(2)	(3)	FP*	(2)	(3)
sy =1
5	10.5	10.5	9.1	5.3	8.2	5.9	−3.6	4.9	3.0
10	7.6	7.6	4.8	3.5	5.1	2.9	−1.3	3.0	1.6
20	4.3	4.3	2.3	2.1	2.9	1.5	−0.6	1.6	0.8
30	3.1	3.1	1.6	1.5	2.1	1.1	−0.3	1.2	0.6
50	1.9	1.9	1.0	1.0	1.3	0.7	−0.1	0.8	0.4
sy =2
5	7.8	7.8	7.3	11.9	8.6	6.2	7.2	7.0	4.4
10	6.1	6.1	4.0	7.0	5.4	3.1	4.1	4.0	2.1
20	3.5	3.5	2.0	3.9	3.0	1.6	2.2	2.2	1.1
30	2.5	2.5	1.4	2.6	2.1	1.1	1.6	1.5	0.8
50	1.5	1.5	0.7	1.6	1.3	0.7	1.0	1.0	0.5
sy = 0.5
5	7.6	7.6	7.1	−2.5	4.8	3.8	−10.5	2.3	1.6
10	5.8	5.8	3.7	−0.6	3.2	1.8	−5.0	1.5	0.7
20	3.3	3.3	1.8	−0.1	1.8	0.9	−2.4	0.9	0.4
30	2.4	2.4	1.3	0.1	1.4	0.7	−1.5	0.7	0.3
50	1.5	1.5	0.8	0.1	0.9	0.5	−0.8	0.5	0.3

We now examine the relationship between the variance of U and the distributions of X and Y, conditional on the ratio between the two sample sizes. Again we simulate X’s and Y’s from Logistic (0, 1) and Logistic (0, s_y), respectively, and vary s_y from 1/3 to 3. Three sets of (m, n) are explored: (50, 50), (50, 100) and (100, 50). Figure 1 shows that when m = n, the functional relationship between Var (U) and s_y is U-shaped. This changes when m ≠ n. When m < n, Var (U) decreases as s_y increases; and when m > n, we have the opposite trend. This sample ratio-dependent relationship has to do with the fact that the two components of Var (U) in formula (3) move in the opposite direction as s_y changes. As s_y increases, Var {F (Y)} increases, but Var {G (X)} decreases because G, the distribution function of Y, becomes flatter. These two trends are of similar magnitude, but when there are more Y’s than X’s (m = 50, n = 100), the decrease in m⁻¹ Var {G (X)} dominates the increase in n⁻¹ Var {F (Y)}, leading to a net effect of decreasing Var (U).

Figure 1.

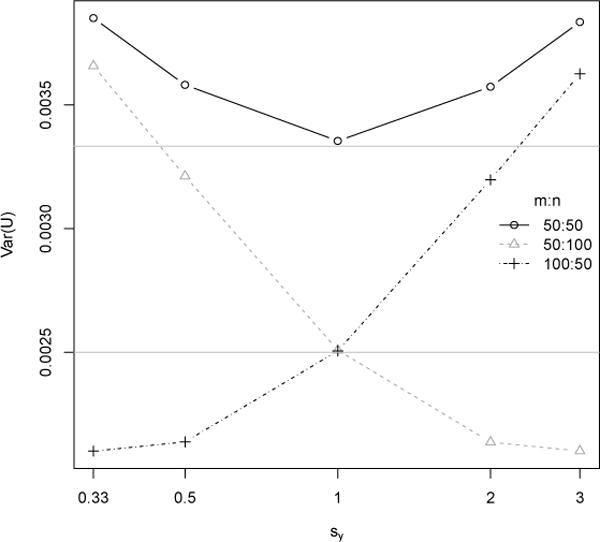
Relationship between Var(U) and s_y. X ~ Logistic(0, 1), Y ~ Logistic(0, s_y). The horizontal lines have heights V_mn, the theoretical variance of U when s_y = 1.

The relationship observed above can be summarized as when the sample with greater sample size also has greater variance, the variance of U tends to drop below V_mn. It is important to note that this pattern only reflects a snapshot of a potentially more complicated relationship between Var (U) and the distributions of X and Y. In particular, the two samples in this experiment have the same location. The same relationship may not hold if the locations of the two samples differ by a large amount.

3 Trade-off between the WMW and FP tests

Under the strong null hypothesis, the FP test based on the normal approximation should have the correct type 1 error rates when the sample sizes are large enough. When the sample sizes are small, a permutation-based method for determining significance may control the type 1 error rate better. To obtain the permutation distribution, we enumerate all possible ways of reshuffling the labels among the m + n samples, and compute a test statistic for each possibility. The number of ways to choose m out of m + n samples grows quickly with m and n, and if it is computationally infeasible to exhaustively compute the test statistic, a Monte Carlo method can be applied to obtain a large number, say 10⁴, of random reshuffles.

To examine the sizes of the FP tests, we simulate both X’s and Y’s from a logistic distribution with mean 0 and scale 1. Three ratios of m : n, 1:1, 1:2 and 1:4, are considered. Results from 10,000 Monte Carlo replicates are summarized in Table 2. The results show that when both sample sizes reach 30, the type 1 error rates of the normal approximation-based FP tests are fairly close to the nominal value. Of the three FP tests, the one using the variance estimator based on formula (2) has a slight advantage over the other two. That this test performs better than the test based on the variance formula (3) is somewhat surprising given that we see earlier in Table 1 the variance estimate based on formula (3) is a little less biased. This is because the main driver for the deviation from the nominal type 1 error rate is inadequacy of the normal approximation, which leads to a more liberal test. As the variance estimated from formula (3) tends to be smaller than the variance estimated from formula (2), it rejects more, leading the type 1 error rate further away from the nominal level. The type 1 error rates of the permutation-based FP tests appear to be close to the nominal level even when there are only five observations from each population. We repeat this experiment using normally distributed data (Table D.2) and arrive at the same conclusions. From here on, we will use the variance estimator based on formula (2), denoted by $\widehat{V}$, exclusively for the FP test.

Table 2.

Estimated size (%) of the WMW test and three FP tests: FP*, which uses the original variance estimator from Fligner and Policello (1981), and (2) and (3), which use the variance estimators based on formula (2) and (3), respectively. Nominal level 5%. X,Y ~ Logistic(0, 1).

m	n = m				n = 2m				n = 4m
	WMW	FP*	(2)	(3)	WMW	FP*	(2)	(3)	WMW	FP*	(2)	(3)
normal approx.
5	3.21	8.01	8.01	8.01	4.06	8.51	8.24	8.57	4.07	9.95	9.29	9.78
10	4.46	6.45	6.45	6.71	4.39	6.77	6.62	6.97	4.88	7.46	7.09	7.29
20	5.29	6.10	6.10	6.30	5.03	6.13	6.05	6.18	5.14	6.52	6.25	6.40
30	4.70	5.28	5.28	5.47	5.11	5.74	5.70	5.78	5.19	5.96	5.82	5.90
50	5.19	5.46	5.46	5.63	5.30	5.66	5.64	5.72	5.27	5.81	5.66	5.76
permutation
5	3.21	4.10	4.10	4.10	4.06	5.02	5.02	4.95	4.07	4.83	4.81	4.82
10	4.46	4.99	4.99	5.00	4.86	5.16	5.22	5.18	5.13	5.21	5.16	5.14
20	5.29	5.44	5.44	5.45	5.03	5.35	5.38	5.37	5.14	5.31	5.29	5.28
30	4.84	4.91	4.91	4.90	5.11	5.20	5.19	5.20	5.19	5.35	5.37	5.36
50	5.19	5.24	5.24	5.25	5.32	5.37	5.38	5.39	5.27	5.30	5.30	5.30

The WMW test does not suffer from inflated type 1 error rates when the sample sizes are small. But when the sample sizes are very small, e.g. m = n = 5, both the permutation-based and the normal approximation-based WMW tests are somewhat conservative, which is a consequence of the discreteness of the tail distributions of the statistic U at very small sample sizes (Mann and Whitney, 1947, Table 1).

To compare the power of the WMW and FP tests, we simulate the X’s and Y’s from Logistic(0,1) and Logistic (μ_y, s_y), respectively, and examine three levels of s_y: 1, 2 and 1/2. At m = 30, the μ_y’s are set to 1, 1.2 and 0.8 at the three levels of s_y so that the power is in the same general range across the different s_y’s. At m = 10, the μ_y’s are set to 2, 2.4 and 1.6, respectively. We look at three different m to n ratios: 1:1, 1:2 and 1:4. For determining the significance of the WMW test, we follow a common practice, e.g. as implemented in the R wilcox.test function, and use the N (0,1) reference distribution when either m or n is 50 or greater and the exact reference distribution otherwise. For determining the significance of the FP test, we look at both normal approximation and permutation at m = 30 and permutation only at m = 10.

Results from 10,000 Monte Carlo replicates are summarized in Table 3. The WMW and FP tests have similar power when s_y = 1 = s_x or m = n, but not when s_x = s_y and m = n, and the difference in power increases as sample sizes become more unbalanced between the two samples. There is a trade-off between the WMW and FP tests. When n > m, the FP test is more powerful when s_y > s_x and less powerful when s_y < s_x. In other words, the FP test is more powerful when the sample with a bigger sample size has a greater variance, and less powerful otherwise.

Table 3.

Estimated power (%) of the WMW and FP tests. The FP test uses the variance estimator based on formula (2). X ~ Logistic(0,1), Y ~ Logistic(μ_y,s_y). μ_y is set to 1, 1.2 and 0.8, respectively for the three s_y at m = 30 and 2, 2.4 and 1.6, respectively for the three s_y at m = 10 to achieve a comparable level of power.

sy	n = m		n = 2m		n = 4m
	WMW	FP	WMW	FP	WMW	FP
normal approx., m = 30
1	57	59	71	72	79	79
2	38	38	49	57	58	75
0.5	60	59	71	64	77	67
permutation, m = 30
1	58	58	71	71	79	78
2	39	37	49	55	58	73
0.5	60	58	71	63	77	65
permutation, m = 10
1	64	66	80	79	87	84
2	43	44	59	64	70	80
0.5	66	66	79	72	85	73

A connection can be made between the power study in this section and the variance study in the previous section. Figure 1 shows that under the scenario n > m, when s_y is greater than s_x, the variance of U drops below V_mn. Thus $(U-1/2)/\sqrt{\widehat{V}}$ will tend to be greater than $(U-1/2)/\sqrt{V_{\mathit{mn}}}$. When the p-values are determined by comparing to the standard normal distribution, the FP test will reject the null more often than the WMW test.

4 Combining the WMW and FP tests

That there is a trade-off between the WMW and FP tests should not come as a surprise. It is only natural that the power depends on the underlying distribution of the data. To improve the overall power, we propose a simple and effective way to combine the WMW and FP tests in a way that adapts to the underlying distribution (e.g. van der Vaart, 2000, p. 223). The idea is to divide U − 1/2 by the square root of min $(\widehat{V},V_{\mathit{mn}})$, the lesser value between $\widehat{V}$, the estimated variance of U based on the data and V_mn, the theoretical variance of U under the null hypothesis.

If the N (0,1) reference distribution is used, the combined test would produce a statistic that is always the greater between the WMW and FP test statistics, and the test will reject the null when either the WMW or FP test rejects. A potential pitfall with such an approach is the possible inflation of the type 1 error rate when the normal reference distribution is used because min $(\widehat{V},V_{\mathit{mn}})$ is downward biased in finite samples (supplementary materials Figure D.4); the degree of inflation should tend to 0, however, as the sample sizes increase, because min $(\widehat{V},V_{\mathit{mn}})$ is a consistent estimate of V_mn as shown in the following theorem.

Theorem 1

Under the strong null hypothesis, as m and n go to infinity,

$$\min (\widehat{V},V_{\mathit{mn}})-V_{\mathit{mn}}{\to }_{p}0,$$

and

$$\frac{U-1/2}{\sqrt{\min (\widehat{V},V_{\mathit{mn}})}}{\to }_{d}N(0,1).$$

The proof of the theorem is given in the supplementary materials Section 2. If the permutation reference distribution is used, the type 1 error rate should not be affected because the permutation reference distribution adapts to the combined test statistic.

We study the size of the combined test by repeating the size study from Section 3. The results are summarized in Table 4. The type 1 error rates of the normal approximation-based combined test are indeed slightly higher than the FP test when n > m, but the type 1 rates of both tests rapidly approach the nominal rate as the sample size increases. When using the permutation reference distribution, the type 1 error rates of the FP and combined tests show no systematic differences.

Table 4.

Estimated size (%) of the FP and combined (C) tests, nominal level 5%. X,Y ~ Logistic(0, 1).

m	n = m		n = 2m		n = 4m
	FP	C	FP	C	FP	C
normal approx.
5	8.01	8.01	8.24	8.24	9.29	9.35
10	6.45	6.45	6.62	6.65	7.09	7.26
20	6.10	6.11	6.05	6.13	6.25	6.38
30	5.28	5.29	5.70	5.81	5.82	6.04
50	5.46	5.47	5.64	5.73	5.66	5.93
permutation
5	4.10	4.10	5.02	5.02	4.81	4.81
10	4.99	4.99	5.22	5.15	5.16	5.13
20	5.44	5.44	5.38	5.34	5.29	5.19
30	4.91	4.89	5.19	5.15	5.37	5.34
50	5.24	5.24	5.38	5.38	5.30	5.41

To study the power of the combined test, we repeat the power study from Section 3. For comparison, we include the van der Waerden test (Van der Waerden, 1952), which is also known as a normal scores test. Like the WMW test, the van der Waerden test is also rank-based, and it is of special interest because its Pitman asymptotic relative efficiency versus the Student’s t test is 1 if both samples are normally distributed. The results for s_x ≠ s_y and n = 4m are presented in Table 5. The results show that at m = 30, the combined tests using both the normal approximation and the permutation distribution perform as well as the winner between WMW and FP. At m = 10, when s_y = 2, the permutation-based combined test performs nearly as well as the FP test, which outperforms the WMW test; when s_y = 0.5, its performance is appreciably better than the FP test although not as good as the WMW test.

Table 5.

Estimated power (%) of the van der Waerden (vdW), WMW (W), FP, and the combined (C) tests. X ~ N(0,1), Y ~ Logistic(μ_y, s_y). μ_y is set to 1, 1.2 and 0.8, respectively for the three s_y at m = 30 and 2, 2.4 and 1.6, respectively for the three s_y at m = 10 to achieve a comparable level of power.

Sy	n = m				n = 2m				n = 4m
	vdW	W	FP	C	vdW	W	FP	C	vdW	W	FP	C
normal approx., m = 30
1	57	57	59	59	70	71	72	73	78	79	79	80
2	34	38	38	39	40	49	57	57	44	58	75	75
0.5	55	60	59	60	70	71	64	71	79	77	67	77
permutation, m = 30
1	57	58	58	58	70	71	71	71	78	79	78	78
2	35	39	37	37	40	49	55	55	44	58	73	72
0.5	55	60	58	59	71	71	63	69	79	77	65	75
permutation, m = 10
1	65	64	66	66	79	80	79	80	87	87	84	85
2	43	43	44	44	52	59	64	64	59	70	80	79
0.5	65	66	66	66	79	79	72	75	86	85	73	79

To examine the power of the proposed test further, we repeat the comparison study using normal distributions, lognormal distributions, and gamma distributions (supplementary materials Table D.5, D.6 and D.7). Although the difference in power between the WMW and FP tests varies across the various scenarios, the power of the combined test is almost always closer, and often quite close, to the winner of the two.

The relative efficiency of the van der Waerden test versus the WMW test may be greater than or less than 1 depending on the distributions (Hollander et al., 2013, p. 150). This is confirmed in our simulation studies. For example, the WMW test performs better than the van der Waerden test when the data are generated from lognormal distributions and n = m (supplementary materials Table D.6), while the van der Waerden test performs better when the data are generated from gamma distributions and n = 4m (supplementary materials Table D.7).

5 Data examples

In this section we use three data examples to illustrate the application of the combined test. The first example comes from a study of the immunological biomarkers that are associated with mother-to-child transmission (MTCT) of HIV-1 (Permar et al., 2015). The study population is U.S. non-breastfeeding, HIV-1-infected, mother-infant pairs enrolled in the Women and Infants Transmission Study prior to the availability of antiretroviral prophylaxis (Rich et al., 2000). There are 55 caesarean section births in this dataset, 17 of which resulted in vertical transmission while 38 did not. The biomarker V3_BioV3B measures the abundance of binding antibodies in the serum that recognize the V3 region at the surface of the HIV envelope protein. Figure 2(a) gives a boxplot of the biomarker measurement by transmission status; the variance of V3_BioV3B appears smaller in the non-transmitters than in the transmitters. Since the sample size 17 borders on whether the normal approximation can be safely applied, we try both the normal approximation and the permutation distribution to determine statistical significance. Table 6 shows that regardless of the method, both the WMW and combined tests reject the strong null at level 0.05, but the FP test does not. These results suggest that the amount of V3-specific binding antibodies may be associated with HIV-1 mother-to-child transmission in this population.

Figure 2.

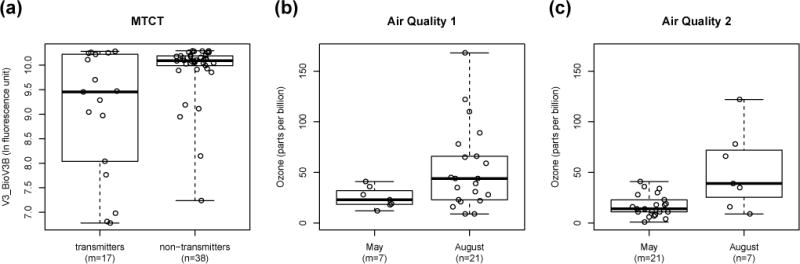
Boxplots for the data examples.

Table 6.

P-values for the data examples. For the WMW test, the p-value is determined by the normal approximation when either m or n exceeds 50 and by exact distribution otherwise; for the FP or combined (C) test, the p-value is determined by the method indicated for MTCT, and by permutation for air quality.

	WMW	FP	C
MTCT (normal approx.)	0.0396	0.0661	0.0405
MTCT (permutation)	0.0396	0.0707	0.0467
Air Quality 1	0.0711	0.0420	0.0422
Air Quality 2	0.0181	0.0333	0.0333

The second and third examples come from the New York City air quality measurements dataset (Chambers, 1983). It contains around 30 observations for each month between May and September of 1973. For our illustration we focus on May and August. For the second example, we compare the ozone readings from the first 7 days in May and the first 21 days in August. For our third example, we compare the ozone readings from the first 21 days in May and the first 7 days in August. The data are shown in Figure 2(b) and 2(c). The August observations appear to have a greater variability than the May observations. Since the number of observations in one of the samples is under 20, we use the permutation distribution in both examples. Table 6 shows that in the second example both the FP and combined tests reject the strong null at level 0.05, but the WMW test does not. In the third example, all three tests reject the strong null; however, the p-value from the combined test is closer to the FP test rather than the WMW test, and the latter is more significant. The third example reminds us of a lesson from the simulation studies that when the sample size is small, the combined test does not always match the power of the winner between WMW and FP. These results indicate that the ozone level in the New York City is different between May and September in 1973.

6 Discussion

Both the Wilcoxon-Mann-Whitney test and the Fligner-Policello test can be used to test the strong null hypothesis that two samples come from the same distribution. Motivated by the observation that neither test is uniformly more powerful than the other under all scenarios, we propose a new, modified WMW test that combines the WMW and FP tests. The combined test has the right size asymptotically, and Monte Carlo studies show that it has the right type 1 error rate when using the permutation reference distribution and only slightly inflated type 1 error rate when using the normal approximation. In the power study the combined test is as powerful as the winner between WMW and FP under a series of simulation scenarios when the sample size is high enough to warrant the normal approximation. When the sample size is smaller, the combined test sometimes matches the power of the winner between WMW and FP and sometimes falls in between. Taken altogether, the combined test offers the best overall solution for testing the strong null hypothesis.

When ties exist, both the WMW and FP tests can be adjusted accordingly. For completeness sake, we list the adjustments in the supplementary materials Section C. The definition of the combined test remains unchanged.

We provide an implementation of the combined test in the robustrank R package hosted at the Comprehensive R Archive Network. Computation of the test statistic as well as the permutation distribution are performed in C to gain speed. The implementation handles continuity correction and ties, as well as one- and two-sided alternatives.

While our proposed test is based on the WMW test, the underlying approach of studentization-and-combination is not limited to the WMW test and can have broader applications to the many other reasonable and interesting rank-based two-sample tests, including the van der Waerden test. Further research is required to investigate in detail the tradeoffs of such modifications.