Dose tailoring of human cell line‐derived recombinant factor VIII simoctocog alfa: Using a limited sampling strategy in patients with severe haemophilia A

Abstract

Aims

The use of factor VIII (FVIII) prophylaxis in haemophilia A is considered the standard of care, particularly in children. Despite adjustment of doses for body weight and/or age, a large pharmacokinetic (PK) variability between patients has been observed. PK‐tailored prophylaxis may help clinicians adjust coagulation factor FVIII activity (FVIII:C) to the desired level, which may differ in individual patients. The objective was to develop a population PK model for simoctocog alfa based on pooled clinical trial data and to develop a Bayesian estimator to allow PK parameters in individual patients to be estimated using a reduced number of blood samples.

Methods

PK data from 86 adults and 29 children/adolescents with severe haemophilia A were analysed. The FVIII data measured using 2 different assays (chromogenic and the 1‐stage clotting assay) were fit to separate develop population PK models using nonlinear mixed‐effect models. A Bayesian estimator was then developed to estimate the time above the threshold of 1%.

Results

The PK data for chromogenic and the 1‐stage clotting assays were both best described by a 2‐compartment models. Simulations demonstrated good predictive capacity. The limited sampling strategy using blood sample at 3 and 24 hours allowed an accurate estimation of the time above the threshold of 1% FVIII:C (mean bias 0.01 and 0.11, mean precision 0.18 and 0.45 for 2 assay methods).

Conclusion

In this study, we demonstrated that a Bayesian approach can help to reduce the number of samples required to estimate the time above the threshold of 1% FVIII:C with good accuracy.

What is already known about this subject

• A longer time above the threshold of 1% coagulation factor VIII activity is associated with a decrease in the numbers of spontaneous bleeding and haemarthroses

• Efficacy and safety of pharmacokinetics‐guided personalized prophylaxis with simoctocog alfa in patients with severe haemophilia A has been demonstrated

What this study adds

• Two pharmacokinetic models of simoctocog alfa in patients with severe haemophilia A were developed using chromogenic 1‐stage assays

• A Bayesian estimator was developed that can estimate the target time above the threshold of 1% using only 2 factor VIII plasma concentrations. This can be used to aid dosing decisions in the clinic.

1. INTRODUCTION

The use of factor VIII (FVIII) prophylaxis in haemophilia A is considered the standard of care, particularly in children.1, 2, 3 Several strategies have been proposed using different dosages and frequencies of FVIII administration.4, 5, 6, 7, 8 Despite adjustment of doses for body weight and/or age, a large pharmacokinetic (PK) variability between patients has been observed, which presents difficulties for maintaining the level of FVIII coagulant activity (FVIII:C) permanently above 1% in all patients, and at higher levels in some patients in certain situations.

PK‐guided prophylaxis dosing strategies may offer several advantages for better dose tailoring. Collins et al. demonstrated that a longer time above the threshold (TAT) of 1% FVIII:C was associated with a decrease in the numbers of spontaneous bleeding and haemarthroses.9 In addition, Carlsson et al. have shown that using a PK‐based approach could significantly reduce FVIII consumption and the cost of prophylaxis.10

Simoctocog alfa (Nuwiq) is a 4^th generation recombinant FVIII (rFVIII) produced in a human cell line.11, 12, 13, 14 The use of a human cell line ensures post‐translational modifications that are closer to human plasma‐derived FVIII compared to other rFVIII produced in hamster cell lines.11, 12 A higher affinity for von Wilbrandt factor (vWF) might also reduce the amount of free FVIII in plasma and therefore extend the half‐life of simoctocog alfa.12, 13

The efficacy and safety of PK‐guided personalized prophylaxis with simoctocog alfa in patients with severe haemophilia A was demonstrated in the NuPreviq study.15 In this study, the dosing regimen for prophylaxis was based on each individual's PK profile measured during an initial PK assessment using a 10‐point sampling approach with individual compartmental or non‐compartmental analysis. During 6 months of personalized prophylaxis, 83% of patients had no spontaneous bleeding, 57% of patients were treated with ≤2 infusions per week, and the dose was reduced by 7.2% compared to previous standard prophylaxis. In Italy, a modified NuPreviq approach that includes 6 sampling points and at‐home sampling has been used successfully.16

Population PK modelling offers the possibility to estimate the individual patient PK parameters using data obtained from limited or full sampling design and to simulate the impact of different dosing regimens on PK parameters.17, 18, 19, 20, 21, 22, 23, 24 Furthermore, by using this approach, probabilistic Bayesian analysis can be applied using the developed population PK model to estimate individual PK profiles based on limited samples.7, 25 Such information may be helpful to individualize the dose and the interval between infusions based on a patient's bleeding phenotype and lifestyle, particularly if a full sampling strategy PK analysis is not possible.17

The aims of this study were: (i) to develop a population PK model for simoctocog alfa based on pooled data from 3 clinical trials; (ii) to develop a Bayesian estimator to determine individual PK parameters using a limited blood sampling strategy; and (iii) to develop an interactive web application for individual Bayesian PK estimation using a limited blood sampling strategy.

2. PATIENTS AND METHODS

2.1. Population

Data from 3 clinical studies conducted in 115 previously treated patients with severe haemophilia A were used to generate the PK models. GENA‐01 (pivotal, phase II) included 20 adults and 2 adolescent patients treated on demand with 50 IU of simoctocog alfa per kg of body weight.26 GENA‐03 (pivotal, phase III) investigated the prophylactic efficacy of simoctocog alfa in 59 children27; 27 underwent a PK evaluation following administration of 50 IU kg⁻¹ simoctocog alfa. GENA‐21 (NuPreviq, phase IIIb) assessed the efficacy and safety of individually tailored PK‐guided prophylaxis in 66 adult patients.15 Simoctocog alfa was administered at a dose of 60 ± 5 IU kg⁻¹ for PK evaluation. The studies were conducted in compliance with Good Clinical Practice, the Declaration of Helsinki and national laws. Each patient provided a freely given written consent before commencing the study.

2.2. Sample collection and determination of FVIII plasma activity

Blood samples for PK analysis were collected in 5 mL citrated tubes. PK parameters were derived from FVIII:C time profiles obtained by serial blood sampling at predefined sampling time points for each study (Table 1). FVIII:C was measured in the blood samples using both the chromogenic (ChS) assay and the 1‐stage (OS) clotting assay. The Coamatest SP test (Chromogenix, Essen, Germany) and an OS assay (automated activated partial thromboplastin time) from Trinity Biotech, Siemens BCS‐XP (Siemens, Marburg, Germany) were used to determine FVIII:C. The lower limit of quantification for both methods was 0.9 IU dL⁻¹. Within‐run and between‐run coefficients of variation were below 4% and 8% for the ChS and OS methods, respectively.

Table 1.

Patients characteristics

Study	GENA‐01	GENA‐03	GENA‐21	Overall
Number of patients	22	27	66	115
Sampling time points (n)	12	7	10	7–12
Sampling time points	before infusion and at 15, 30 and 45 min and 1, 3, 6, 9, 12, 24, 30 and 48 h after the end of the infusion	before infusion and 30 min and 2, 5, 10, 24 and 48 h after the end of the infusion	before infusion and at 30 minutes and 1, 3, 6, 9, 24, 30, 48 and 72 h after the end of the infusion	‐
Weight (kg)	69 [48–105]	22 [13–73]	79 [50–140]	70 [13–140]
Age (years)	41 [12–65]	6 [2–12]	33 [18–67]	31 [2–67]
Height (cm)	177 [154–188]	115 [92–172]	177 [155–196]	174 [92–196]

Age, weight and height are expressed as median [range].

2.3. Pharmacokinetic analysis

Before analysis, the dataset was divided into 2 groups: (i) a learning set (n = 95) and (ii) a validation set (n = 20). A stratified randomization was used to allocate patients in each dataset according to their age. FVIII:C activity values measured by the ChS or OS assay were analysed separately because the difference in the potency measurements between assays was approximately 15% and affect significantly the estimation of PK parameters.15, 27

Data were analysed using MONOLIX, a nonlinear mixed effects modelling software (Lixoft, version 4.3.2)28 using the Stochastic Approximation Expectation–Maximization (SAEM) algorithm. The parameters of the model were assumed to be log‐normally distributed. We built our model according to a stepwise procedure, initially identifying the best structural model for simoctocog alfa PKs (base model) by estimating 1‐, 2‐ and 3‐compartment PK models.

In a second step, we examined the effect of covariates on simoctocog alfa exposure. The covariates tested were total body weight, ideal body weight, lean body weight, age, height and body surface area of patient. The covariates were included in the model using a stepwise method with forward inclusion and backward elimination. Covariates were kept in the model if they improved the fit, reduced interpatient variability and decreased the objective function, calculated as –2log likelihood, by at least 3.84 com‐ pared with the previous model (χ², P < .05 for 1 degree of freedom). The statistical significance of covariate was individually assessed during the stepwise deletion phase at the P < .001 level. Only covariates associated with an increase of at least 10.83 in OFV were retained in the model.

Data below the lower limit of quantification were simulated in a right‐truncated Gaussian distribution using the SAEM algorithm.29 All graphics were generated using R software.30 Model evaluation and selection were based on visual inspection of the goodness‐of‐fit plots, the precision of parameter estimates, and the decrease in objective function (calculated by importance sampling). The goodness‐of‐fit was established by plotting the population predictions of the model vs observations, the individual predictions vs observations, and the normalized prediction distribution errors (NPDE) vs time. The prediction‐corrected visual predictive check (pcVPC) was generated by simulating 1000 times datasets using the model of interest and the design of the observed data.31 The ability of the model to describe the observations was evaluated by visual inspection of the distribution of the simulated concentrations. The median parameter values and the 90% prediction interval of the pcVPC replicates were compared with the observations comprising the original dataset.

2.4. Simulations

From the variance–covariance matrix of the estimated PK parameters, Monte Carlo simulations were performed using R software. A total of 1000 datasets were generated according the patients characteristic (age, weight) of the study. In the simulation, all patients received a single dose of 50 IU kg⁻¹ of simoctocog alfa. For simulations, 90% of prediction interval of the model were superposed to a typical patient aged 2, 6, 12, 30 or 50 years.

2.5. Bayesian approach and model prediction

To optimize the blood sampling times, a global approach combining external validation and optimal design was used. For external validation, the individual parameters of 20 subjects included in the validation dataset were estimated by the maximum a posteriori probability method using the nonlinear mixed‐effects population PK model estimates for the ChS and OS assays. Individual parameters were estimated using 4 sampling scenarios and the (TAT of 1%, 3% and 5% FVIII:C were calculated. The reference sampling strategy used the full PK samples. Limited sampling strategy 1 (S1) was close to that recommended by Bjorkman (6, 24 and 48 hours),17 and strategy 2 (S2) used sampling times of 3, 9 and 24 hours. Limited sampling strategies 3 (S3) and 4 (S4) used only 2 samples, at 3 and 24 hours and 6 and 24 hours, respectively. The performance of Bayesian estimations was evaluated by comparing TAT of 1% estimated by limited sampling strategies (Bayesian) and by full sampling strategy (observed). Bias of Bayesian estimation was estimated by mean error (ME), and percentage of bias (PBIAS%). Precision of Bayesian estimation was estimated by root mean square error (RMSE) and mean absolute error (MAE).

$$\begin{array}{l}\mathit{ME}=\frac{1}{n}\sum _{i=1}^n\left(\mathit{TAT}1{\%}_{\mathit{\text{Bayesian}}}-\mathit{TAT}1{\%}_{\mathit{\text{observed}}}\right)\\ \mathit{\text{PBIAS}}\%=\frac{{\sum }_{i=1}^n\left(\mathit{TAT}1{\%}_{\mathit{\text{Bayesian}}}-\mathit{TAT}1{\%}_{\mathit{\text{observed}}}\right)}{{\sum }_{i=1}^n\mathit{TAT}1{\%}_{\mathit{\text{observed}}}}\\ \mathit{MAE}=\frac{1}{n}\sum _{i=1}^n\left|\mathit{TAT}1{\%}_{\mathit{\text{Bayesian}}}-\mathit{TAT}1{\%}_{\mathit{\text{observed}}}\right|\\ \mathit{\text{RMSE}}=\sqrt{\sum _{i=1}^n\frac{{\left(\mathit{TAT}1{\%}_{\mathit{\text{Bayesian}}}-\mathit{TAT}1{\%}_{\mathit{\text{observed}}}\right)}^2}{n}\times 100}\end{array}$$

As an extension of the design analysis, we evaluated the optimal sampling times using a Bayesian individual Fisher information matrix method. This approach optimally incorporates all the information available from the whole population to increase the ability to estimate individual parameters. Design for maximum a posteriori estimation of individual parameters was evaluated (S1–S4) and finally optimized for 2 or 3 samples. For a satisfactory strategy, the predicted root mean square error for all fixed parameters had to be lower than 30%. Evaluation and optimization were performed using PFIM 4.0 software.32

2.6. Development of interactive web application

The population PK model reported here has been established through a project initiated by the national reference centre for haemophilia in France and made available for haemophilia care centres as a free interactive tool (http://www.hemotik.org) to help physicians to tailor prophylaxis regimens for individual patients receiving simoctocog alfa using a limited blood sampling strategy. Hemotik is a Shiny application that allows the user to estimate individual PK parameters using a limited sampling strategy, to visualize FVIII activity over time, to estimate the time above different threshold, and finally to simulate individualized dosing regimens. With this application, individual PK were estimated using a Bayesian approach derived from a previous work.33 The posterior distributions and uncertainty of parameters were estimated with Markov Chain Monte Carlo simulations.

2.7. Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY, and are permanently archived in the Concise Guide to PHARMACOLOGY 2017/18.34

3. RESULTS

3.1. Population description and samples

PK data from 1114 FVIII:C assays of blood samples from 115 patients were included in the pooled population PK analysis. Patient characteristics are summarized in Table 1. The median patient was a 30‐year‐old male, weighing 70 kg. A total of 1107 ChS‐FVIII:C and 1114 OS‐FVIII:C results were included in the analysis. The BLQ were recorded for 80 samples (7.2%) and 41 samples (3.6%) for ChS and OS methods, respectively.

3.2. Population PK models

The final parameter estimates for the ChS and OS assays are reported in Table 2. Continuous covariates were log transformed and scaled or centred to a typical value; for example, the effect of body weight or age on the parameter V_C or Cl was evaluated as follows:

$$\begin{array}{l}log\left({\mathit{Cl}}_i\right)=\mathit{Cl}+b_{\mathit{BW}}^{\mathit{Cl}}\times log\left(\frac{{\mathit{BW}}_i}{70}\right)+b_{\mathit{AGE}}^{\mathit{Cl}}\times \left({\mathit{AGE}}_i-30\right)+{\omega }_i^{\mathit{Cl}}\\ log\left({\mathit{Vc}}_i\right)=V_c+b_{\mathit{BW}}^{\mathit{Vc}}\times log\left(\frac{{\mathit{BW}}_i}{70}\right)+{\omega }_i^{\mathit{Vc}}\\ log\left({\mathit{Vp}}_i\right)=V_p+b_{\mathit{BW}}^{\mathit{Vp}}\times log\left(\frac{{\mathit{BW}}_i}{70}\right)+{\omega }_i^{\mathit{Vp}}\end{array}$$

Table 2.

Population pharmacokinetic model parameters based on the chromogenic (ChS) and 1‐stage (OS) factor VIII:C assays

Parameter	ChS model		OS model
	Population mean (RSE %)	Interindividual variability, % (RSE %)	Population mean (RSE %)	Interindividual variability, % (RSE %)
Structure parameters
Cl (mL.h−1)	200 (4)	33.8 (8)	271 (4)	35.2 (8)
Vc (mL)	2700 (2)	22 (8)	3750 (3)	20.2 (8)
Vp (mL)	451 (9)	27.8 (56)	960 (7)	16 (51)
Q (mL.h−1)	80.2 (15)	—	349 (18)	—
Corr_Cl_Vc	—	35.1 (27)	—	9.8 (25)
Covariate effect
$log\left(\mathit{Cl}\right)=\mathit{Cl}+b_{\mathit{BW}}^{\mathit{Cl}}\times log\left(\frac{\mathit{BW}}{70}\right)+b_{\mathit{AGE}}^{\mathit{Cl}}\times \left(\mathit{AGE}-30\right)$
$b_{\mathit{AGE}}^{\mathit{Cl}}$	−0.00805 (26)	—	−0.0058 (39)	—
$b_{\mathit{WT}}^{\mathit{Cl}}$	0.75 FIX	—	0.75 FIX	—
$log\left(V_c\right)=V_c+b_{\mathit{BW}}^{V_c}\times log\left(\frac{\mathit{BW}}{70}\right)$
$b_{\mathit{WT}}^{V_C}$	1 FIX	—	1 FIX	—
$log\left(V_p\right)=V_c+b_{\mathit{BW}}^{V_p}\times log\left(\frac{\mathit{BW}}{70}\right)$
$b_{\mathit{WT}}^{V_p}$	0.546 (22)	—	0.613 (15)	—
Error model
Additive (SD) (IU dL−1)	0.0181 (7)	—	0.0236 (5)	—
Proportional (CV) (%)	0.0867 (5)	—	0.0831 (6)	—

ChS, chromogenic substrate assay; OS, 1‐stage assay; Cl, clearance; Vc, volume of central compartment; Vp, volume of peripheral compartment; Q, intercompartment clearance; BW, body weight; Corr_Cl_Vc, covariance of Cl and Vc. RSE, root square error; SD, standard deviation. The parameters $b_{\mathit{BW}}^{V_c}$, $b_{\mathit{BW}}^{\mathit{Cl}}$, $b_{\mathit{AGE}}^{\mathit{Cl}}$ correspond to the regression coefficient.

where Vc_i, Vp_i Cl_i, BW_i, and AGE_i denote respectively the volume of distribution of central and peripheral compartment, the clearance, the bodyweight, and age. Parameters ${\omega }_i^{\mathit{Vc}},{\omega }_i^{\mathit{Vp}},{\omega }_i^{\mathit{Cl}}$represent the and between subject variability of patient i. The parameter $b_{\mathit{BW}}^{V_c}$, $b_{\mathit{BW}}^{\mathit{Cl}}$, $b_{\mathit{AGE}}^{\mathit{Cl}}$ corresponds to the regression coefficient. The regression coefficient of size descriptor was fixed at 0.75 and 1 for Cl and Vc parameters, respectively.35, 36 The goodness‐of‐fit plots of the final models are presented in Figure 1. The data exhibited no apparent bias in model predictions. According to the pcVPC (Figure 2), the average observed values were well predicted. Only extreme profiles were not within 90% of the simulated values, demonstrating good predictive capacity of the models. Distributions of TAT 1%, 3% and 5% FVIII:C relative to the patient's age are presented in Figure 3.

Figure 1.

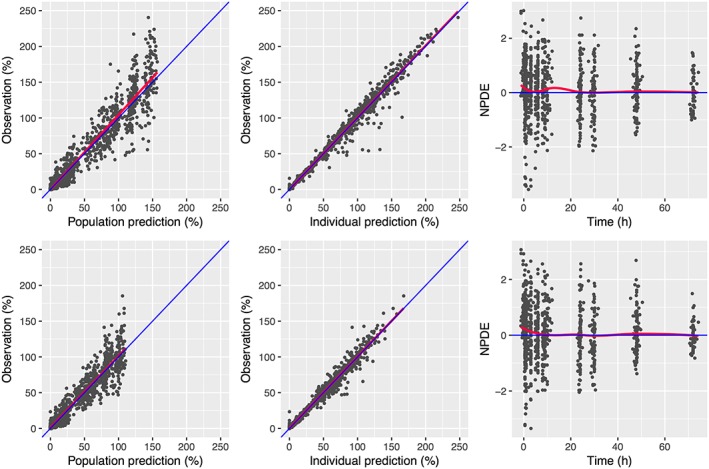
Goodness‐of‐fit plots for the pharmacokinetics of FVIII measured by chromogenic (ChS; top row) and 1‐stage (OS; bottom row) assays. Left: observed FVIII:C vs population predictions; centre: observed FVIII:C vs individual predictions (mode); right: normalized prediction distribution error (NPDE) vs time. The blue line corresponds to the identity line and the red line to the regression line

Figure 2.

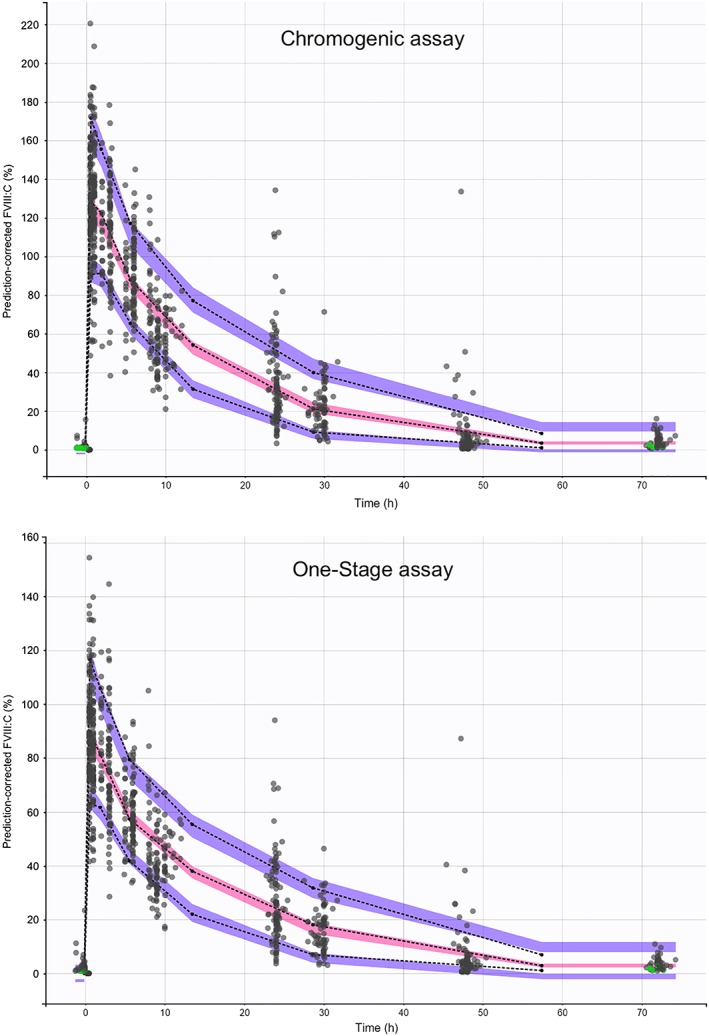
Prediction‐corrected visual predictive check. The black dash curve represents the 5, 50 and 95 empirical observed percentiles. The purple and pink shaded envelope represents the prediction interval for the simulations of 5, 50 and 95 percentiles. The grey dots represent the observed FVIII activities. The green dots represent the observed data below the lower limit of quantification

Figure 3.

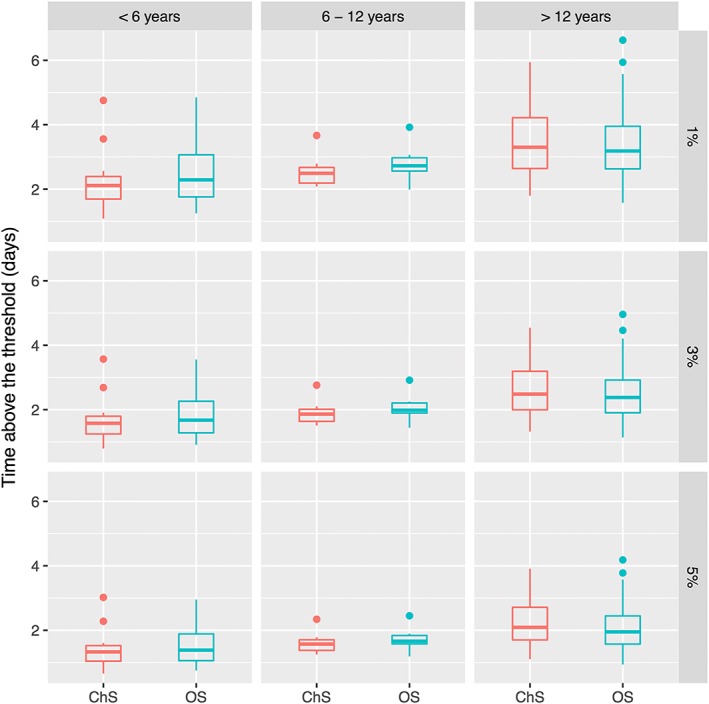
Estimated distribution of time above the threshold

3.3. Simulations

Using the parameters of the final estimated models, simulations were performed to illustrate the effect of covariates for patients receiving 50 IU kg⁻¹ of simoctocog alfa. The simulated PK profiles presented in supplementary data S1 demonstrate the impact of age and body weight on the half‐life and then on time above the threshold of 1% FVIII:C. These simulations demonstrated that a body weight‐adjusted dose was not sufficient to obtain comparable TAT 1% in children, adolescents and adults.

3.4. Bayesian estimation and limited sampling strategy

The results of the Bayesian estimations of TAT 1%, 3% and 5% FVIII:C are presented in Figure 4 and show the concordance of TAT obtained with 2‐ or 3‐sample PK estimates and those obtained with full sampling data (7–12 samples). A correlation coefficient (r) >0.89 was obtained between Bayesian estimated TAT 1% FVIII:C by 2 or 3 samples and a full sampling strategy (Table 3). The best sampling strategy for the ChS assay was based on the time points of 3 and 24 hours (RMSE = 0.18, r = 0.99). For the OS assay, the best sampling strategy was based on the time points of 3, 9, 24 hours (RMSE = 0.21, r = 0.98). Whichever limited sampling strategy was evaluated, the estimation of TAT 1%, 3% and 5% FVIII:C was accurate (Figure 5).

Figure 4.

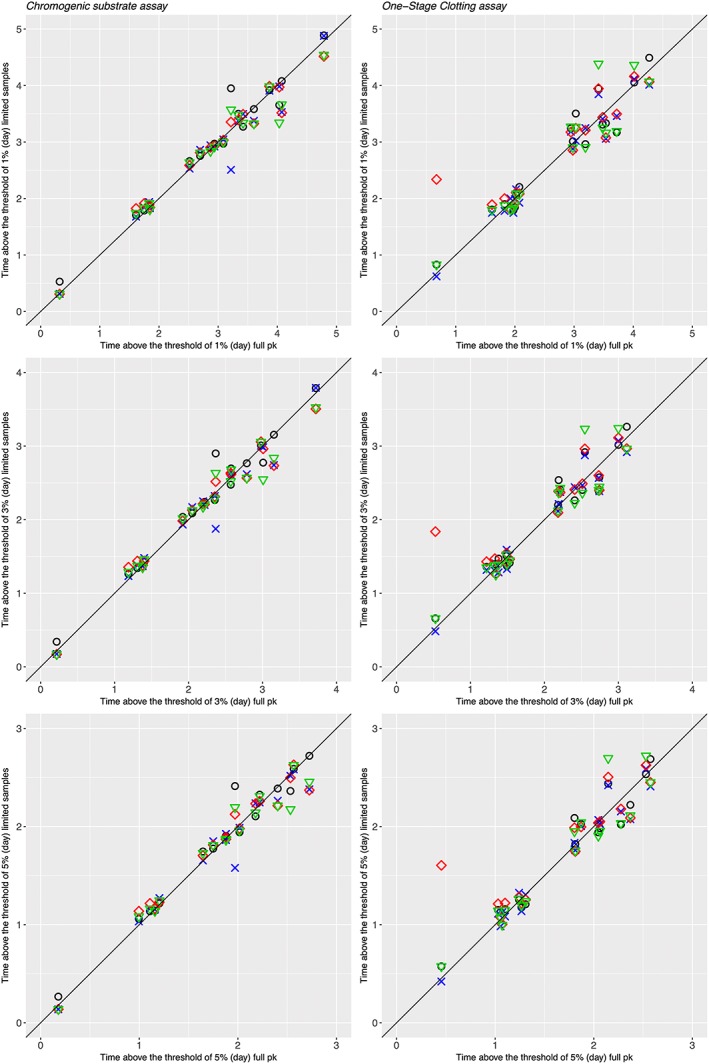
Relationship between estimated time above the threshold of 1%, 3% and 5% obtained by limited and full sampling strategies. Symbols: black open circle: 3‐sample determinations (t = 6, 24, 48 h), blue crosses: 3‐sample determinations (t = 3, 9, 24 h), red open diamonds: 2‐sample determinations (t = 3, 24 h), green open triangles: 2‐sample determinations (t = 9, 24 h). The black curve corresponds to the line of identity

Table 3.

Quantitative statistics for comparison of full vs 4 limited sampling strategies to estimate time above the threshold of 1% factor VIII:C

Parameter	Time above threshold of 1% estimated by ChS assay				Time above threshold of 1% estimated by OS assay
	S1	S2	S3	S4	S1	S2	S3	S4
ME	−0.06	0.05	0.01	0.04	−0.03	0.03	−0.11	−0.01
MAE	0.13	0.13	0.13	0.17	0.21	0.16	0.26	0.25
RMSE	0.22	0.23	0.18	0.24	0.26	0.21	0.45	0.33
PBIAS %	−1.90	1.70	0.40	1.50	−1.20	1.00	−3.90	−0.50
R	0.98	0.98	0.99	0.98	0.96	0.98	0.89	0.94

ChS, chromogenic; OS, 1‐stage; ME, mean error; MAE, mean absolute error; RMSE, root mean square error; PBIAS %, percent bias; R, coefficient of correlation; S1, sampling strategy 1 (t = 6, 24, 48 h); S2, sampling strategy 3 (t = 3, 9, 24 hours); S3, sampling strategy 1 (t = 3, 24 hours); S4, sampling strategy 1 (t = 9, 24 hours).

Figure 5.

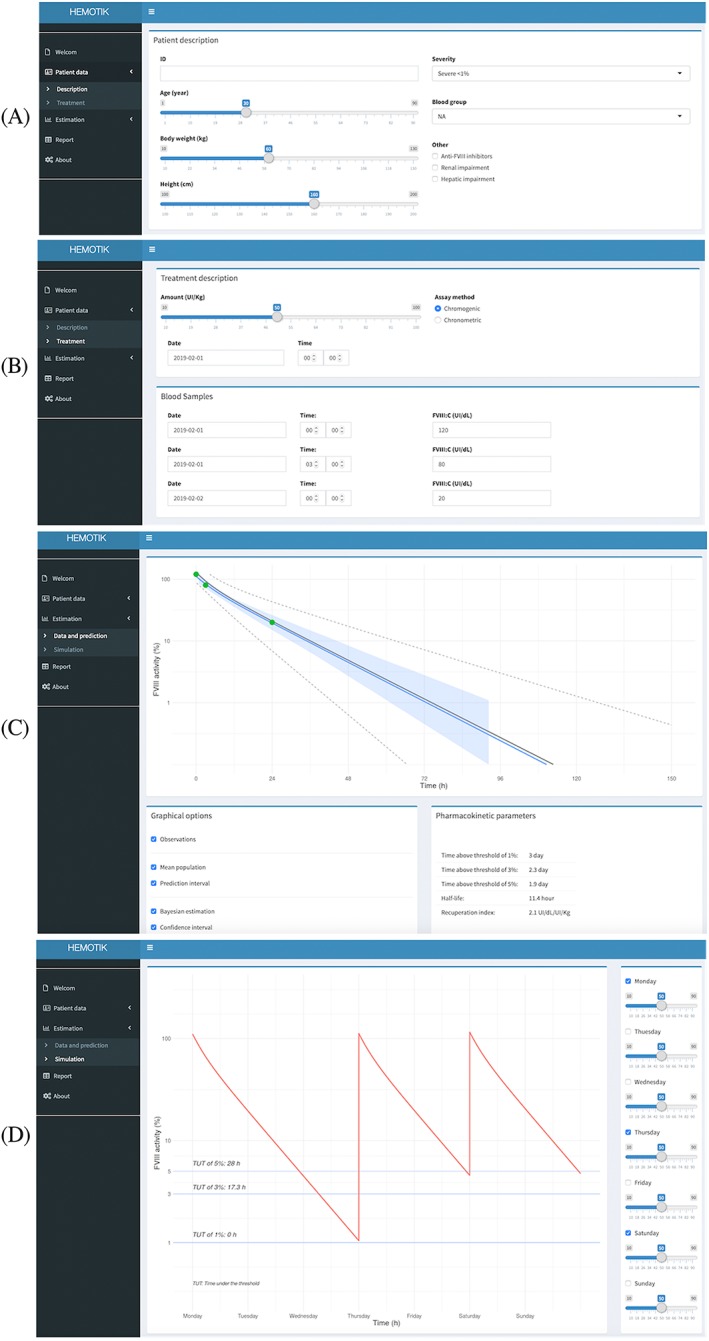
Using the Hemotik tool: (A) patient details, (B) treatment details, (C) pharmacokinetic estimation, (D) dosing simulation. The light grey shaded envelope represents the 90% confidence interval for the simulations. The grey shaded envelope represents the 50% interval for the simulation. The lines represent the median for different typical patients.

The evaluation of the relative standard errors of PK parameters by Bayesian Fisher information matrix of the different strategies is presented in supplementary data (S2). The best 2‐sample strategy was 0.1, 29.7 hours and 0.1, 26.4 hours ChS and OS method. For each parameter, whatever the design, the expected relative standard errors were quite similar and lower than 30%. The difference of the relative standard error between the 3, 9 hours strategy and optimal design was lower than 2.1% for each parameter and for each assay method. Finally, the optimization step, which determine the most informative sampling time, slightly improve the estimation of Q, Vc and Vp. This optimization did not improve the estimation of Cl, the most important PK parameter to estimate the time above the threshold (S3).

3.5. Development of interactive web application

An illustrative example of how the Hemotik tool can be used in clinical practice is given in Figure 5. In the first step, patient details (e.g. age, body weight; Figure 5a) and treatment details (e.g. sampling information, assay used; Figure 5b) are entered into predefined fields. By clicking the Data and prediction tab, predicted PK parameters are displayed (Figure 5c). By clicking the Simulation tab, FVIII:C profiles are shown for a chosen dose and dosing frequency (Figure 5d). In this example, a dose of 35 IU kg⁻¹ every 3 days would be expected to maintain FVIII:C above 1%. An important feature of the Hemotik tool is that target FVIII:C levels, as well as dose and frequency, can be personalized. This flexibility is in line with a recent Delphi Consensus Statement that recommended the use of different target plasma FVIII levels depending on a patient's physical activity levels and bleeding phenotype.37

4. DISCUSSION

The present paper describes a population PK modelling and Bayesian approach for simoctocog alfa, a 4^th generation rFVIII produced in a human cell line. We modelled FVIII PK using data measured with the ChS or OS assays and developed a Bayesian estimator for each assay to estimate PK parameters using a limited sampling strategy.

This study is the first report of a population PK analysis of simoctocog alfa using pooled studies of a large population of patients with a wide range of body weight and age. This analysis showed that the PK profile of simoctocog alfa in patients with severe haemophilia A was adequately described by a 2‐compartment model. The models were influenced by age and body weight, as reported previously with another rFVIII population PK analysis. The mean population parameters estimates were close to those presented in other studies.17, 18, 19, 20, 21, 38 For example, by using the OS assay, a typical 30‐year‐old and 70‐kg patient has an estimated clearance of 270 mL h^–1 and an estimated volume of the central compartment of 3.75 L.

The difference in the potency measurements between assays has been reported to be approximately 15% and is expected to significantly affect the estimation of PK parameters.15, 27 For this reason, we developed 2 separate models for the ChS and OS assays to obtain precise PK estimates for each patient and assay. The PK models allowed estimation of the TAT 1% FVIII:C, which is probably the most important PK parameter because a correlation has been reported between this parameter and the incidence of bleeding events.9 In our study, the median estimated TAT 1% was 3 days, with a range of 1–6 days for both assays. This result emphasizes the need for personalized prophylaxis for haemophilia A. For instance, some patients may need daily infusions, whilst others may need every other day or weekly infusions to maintain a chosen TAT target.

The simulations demonstrated that younger patients (age ≤2 years) have a shorter time above threshold of 1%. The most effective way to maintain the level of FVIII:C above 1% is to change the dosing interval. However, many other strategies are possible taking into account many parameters taking into account the dose level, the cost of treatment, lifestyle, bleeding phenotype, and individual PK parameters.39 For these reasons, many scenarios are possible and the Hemotik online tool could help to evaluate their PK effectiveness.

To estimate the TAT for individual patients, we developed Bayesian estimators based on previously obtained nonlinear mixed effect population PK model estimates of ChS and OS PK data. Our objective was to evaluate the performance of the Bayesian tool to estimate the TAT of 1%, 3% and 5% FVIII:C using a limited sampling strategy of 2 or 3 blood samples. The sampling strategies t = 3, 9, 24 hours and t = 3, 24 hours were found to be the optimal schedules for the OS and ChS assays, respectively. The sampling times were chosen to suit patient constraints. Our Bayesian approach, using 1 or 3 samples, provided an accurate prediction of PK parameters and gave an accurate estimation of individual TAT of 1%, 3% and 5% FVIII:C in an independent group of 20 patients with different characteristics. Surprisingly, the sampling strategy that included a late time point at 48 hours was not the best option in our study, in contrast to the results of previous studies from Bjorkman's group.17 In our study, strategies based on 2 or 3 blood samples were equivalent and only minor differences were observed between the 2 assays.

This work has some limitations. The most important is the absence of vWF measurements. Many studies have reported that vWF levels may explain a significant part of interindividual variability of the clearance of rFVIII.18, 40, 41 Blood group may also have an impact on the clearance of rFVIII.21, 42 However, the precision of the models remains adequate without this information. Moreover, the aim of this study was to develop a general model that does not depend on too many biological parameters.43 Another limitation is that we did not evaluate interoccasion variability of PK parameters. Divergent results have been reported and often this parameter was not properly estimated.19, 21, 37 However, a model including interoccasion variability would probably not improve model‐based therapeutic drug monitoring, as this variability remains unpredictable for a given patient and can only be observed a posteriori. The only way to deal with this issue is to repeat TDM and adjust the dosage when the patient is unstable.

In conclusion, we have constructed population PK models based on the ChS or OS FVIII:C assay data that should facilitate dose tailoring using Bayesian estimators for simoctocog alfa. The Hemotik on‐line tool demonstrated its value for estimating time above certain FVIII:C thresholds with simoctocog alfa using only 2 or 3 blood samples.

COMPETING INTERESTS

X.D. has received honoraria for participation in symposia by CSL Behring, Shire, Octapharma and Sobi. Y.D. has received grants/research support from Bayer, Baxter, Baxalta, Novo Nordisk, CSL Behring, LFB, Pfizer, Leo Pharma, Octapharma and Stago; and honoraria from Bayer, Baxter, Novo Nordisk, CSL Behring, Sobi and Octapharma. E.O. has no conflict of interest. C.N. has received grants/research support from Alnylam, Bayer, Baxalta/Shire, CSL Behring, LFB, Novo Nordisk, Octapharma, Pfizer, and Sobi/Biogen; and honoraria from Alnylam, Bayer, Baxalta/Shire, CSL Behring, LFB, Novo Nordisk, Octapharma, Pfizer, and Sobi/Biogen.

CONTRIBUTORS

Data analysis: X.D., E.O., C.N. Writing of manuscript: X.D., Y.D., C.N. Revision of manuscript: X.D., Y.D., E.O., C.N.

Supporting information

Data S1: Population model simulation of factor VIII activity for different patient characteristics.

Data S2: Optimization and expected relative standard error (%) of sampling time using 2 or 3 samples estimated by maximum a posteriori estimation of the Fischer information matrix

Data S3: Expected relative standard error (%) of individual pharmacokinetic parameter for 4 limited sampling strategies estimated by maximum a posteriori estimation of the Fischer information matrix

Delavenne X, Dargaud Y, Ollier E, Négrier C. Dose tailoring of human cell line‐derived recombinant factor VIII simoctocog alfa: Using a limited sampling strategy in patients with severe haemophilia A. Br J Clin Pharmacol. 2019;85:771–781. 10.1111/bcp.13858