Systematic external evaluation of published population pharmacokinetic models of mycophenolate mofetil in adult kidney transplant recipients co‐administered with tacrolimus

Abstract

Aims

Various mycophenolate mofetil (MMF) population pharmacokinetic (popPK) models have been developed to describe its PK characteristics and facilitate its optimal dosing in adult kidney transplant recipients co‐administered with tacrolimus. However, the external predictive performance has been unclear. Thus, this study aimed to comprehensively evaluate the external predictability of published MMF popPK models in such populations and investigate the potential influencing factors.

Methods

The external predictability of qualified popPK models was evaluated using an independent dataset. The evaluation included prediction‐ and simulation‐based diagnostics, and Bayesian forecasting. In addition, factors influencing model predictability, especially the impact of structural models, were investigated.

Results

Fifty full PK profiles from 45 patients were included in the evaluation dataset and 11 published popPK models were identified and evaluated. In prediction‐based diagnostics, the prediction error within ±30% was less than 50% in most published models. The prediction‐ and variability‐corrected visual predictive check and posterior predictive check showed large discrepancies between the observations and simulations in most models. Moreover, the normalized prediction distribution errors of all models did not follow a normal distribution. Bayesian forecasting demonstrated an improvement in the model predictability. Furthermore, the predictive performance of two‐compartment (2CMT) models incorporating the enterohepatic circulation (EHC) process was not superior to that of conventional 2CMT models.

Conclusions

The published models showed large variability and unsatisfactory predictive performance, which indicated that therapeutic drug monitoring was necessary for MMF clinical application. Further studies incorporating potential covariates need to be conducted to investigate the key factors influencing model predictability of MMF.

What is Already Known about this Subject

• Population pharmacokinetic analyses are widely used to describe mycophenolate mofetil pharmacokinetic characteristics in adult kidney transplant recipients co‐administered with tacrolimus and facilitate dose individualization.

• Model transferability can be influenced by centre‐related factors, and it is unclear whether these models can be appropriately extrapolated to other centres.

What this Study Adds

• We comprehensively evaluated the external predictability of published models using an independent dataset.

• The published models performed unsatisfactorily in prediction‐ and simulation‐based diagnostics.

• The investigation of the impact of model structure did not show that incorporating the EHC process could improve predictive performance.

Introduction

Mycophenolate mofetil (MMF), a pro‐drug of mycophenolic acid (MPA), exerts immunosuppressive effects via selective reversible inhibition of inosine 5′‐monophosphate dehydrogenase. It is generally used as a co‐therapy with tacrolimus (TAC) or cyclosporin (CSA) to prevent rejection following kidney transplantation 1. Moreover, during the past 20 years there has been a tendency to replace CSA with TAC 2, 3, 4.

After oral administration, MMF is extensively absorbed and rapidly hydrolysed to the active component MPA, which is highly protein bound (80–97%). MPA is primarily metabolized by UDP glucuronosyltransferase (UGT) to form the abundant but inactive 7‐O‐mycophenolic acid glucuronide (MPAG) and the relatively minor but active acyl‐glucuronide mycophenolic acid (AcMPAG) 5. The metabolite of MPAG also undergoes extensive enterohepatic circulation (EHC) through biliary excretion, intestinal deglucuronidation by the gut flora, and then reabsorption as MPA. It has been reported that EHC contributes to approximately 40% of the area under the time–concentration curve (AUC) of MPA and causes the appearance of multiple peaks in the concentration–time profile 5, 6.

The pharmacokinetics (PK) of MPA is characterized by high between‐subject variability (BSV) and time‐dependent variation within subjects 7, 8, 9, 10. A 10‐fold variation of MPA exposure has been reported even in patients administered the same dose. Furthermore, the MPA AUC was approximately 30–50% lower in the first few weeks post‐transplantation than in the later period at the same dose of MMF 8.

Previous studies 11, 12, 13, 14, 15, 16 have demonstrated that MPA AUC may predict the risk of acute rejection and toxicity; however, single‐point sampling at particular trough levels has shown poor correlation with the risk of acute rejection and toxicity 17. The wide variability and clear concentration–effect relationship are thought to be the most compelling arguments favouring therapeutic drug monitoring (TDM) for MPA, and individualization of MMF dose using TDM based on the MPA AUC 18.

However, the traditional approach has practical difficulties such as the unfeasibility of the intensive sampling strategy for transplant patients. Limited sampling strategies based on population pharmacokinetic (popPK) combined with Bayesian forecasting are recommended for facilitating an optimal MMF dosage regimen. As a superior approach to classical PK, popPK analysis requires only a few measurements per patient and allows quantification of inter‐ and intra‐subject variability, with the possibility of identifying relevant covariates for this variability 19. However, the model transferability could be influenced by centre‐related factors including study subjects, number of participants, treatment protocols, and analytical methods. Before the models are extrapolated to other centres, more rigorous and extensive evaluation with an independent dataset should be conducted to assess model transferability 20.

Although various popPK models have been developed to quantitatively describe the PK characteristics of MPA over the past decades, whether they can be appropriately extrapolated to other centres remains unclear 7, 21. Assessing the model transferability may also facilitate the identification of potential centre‐based factors influencing model predictability. Moreover, compared with performing a complete popPK study, it might be more effective to screen the most appropriate popPK model for guiding individualized therapy 22.

This study aimed to comprehensively evaluate the predictive performance of currently published popPK studies on co‐administration of MMF and TAC in adult kidney transplant recipients using an independent dataset. Additionally, potential factors influencing model predictability were analysed.

Methods

Review of published popPK studies on co‐administration of MMF and TAC

A systematic literature search for popPK studies of MMF in adult kidney transplant recipients administered both MMF and TAC was performed. The following electronic databases were searched from their inception up to June 30, 2018: PubMed, Web of Science, and Embase, with the language limited to English. The reference lists of identified studies were also screened, and studies were considered eligible if they developed a popPK model using a population approach.

Studies were excluded if the model parameters or formulas of MPA were missing, or if the covariate information was not available in our evaluation dataset. If models with overlapping datasets were developed using the same modelling strategies, only the most recent or those with the largest sample size were included.

Study cohort of external evaluation

Subjects

Adult patients who underwent their first kidney transplants at the First Affiliated Hospital of Sun Yat‐sen University from November 2000 to April 2011, and received MMF (CellCept^®, Roche Pharma Ltd., Shanghai, China), TAC (Prograf^®, Astellas, Dublin, Ireland) and corticosteroids were included in this study. Details of the subjects have been reported elsewhere 23. Recipients with severe gastrointestinal disorders, acute rejection or who were administered proton pump inhibitors were excluded from this study. Combined organ transplantation was also excluded. The study protocols were approved by the Ethics Committee of the First Affiliated Hospital of Sun Yat‐sen University ([2011]217), and all participants provided written informed consent before inclusion.

Immunosuppressive therapy

All recipients received triple maintenance immunosuppressive therapy comprising MMF, TAC and corticosteroids. MMF was orally administered at 0.75 or 0.5 g twice daily (within or after 12 months, respectively) for patients weighing <70 kg, and 1 or 0.75 g twice daily for those >70 kg. TDM of MPA was performed 2 weeks post‐operation, every 3 months between 1 and 12 months and yearly after 12 months.

TAC was initiated at 0.1–0.2 mg kg⁻¹ day⁻¹ every 12 h after transplantation and then adjusted to achieve the target whole blood trough concentration, which was 6–8 ng ml⁻¹, within 3 months post‐operation, 5–7 ng ml⁻¹ from 3 to 12 months, and 4–6 ng ml⁻¹ thereafter.

Methylprednisolone 500 mg was administered intravenously during the operation and daily in the following two days. On Day 3, treatment was switched to oral prednisone (30 mg day⁻¹) and the dose was decreased gradually until it reached the maintenance dose of 5–10 mg day⁻¹. All patients received either basiliximab (Simulect^®, Norvatis, Basel, Switzerland) or rabbit antithymocyte globulin (ATG, Thymoglobulin^®, Sanofi, Quebec, Canada) as an induction therapy. Basiliximab (20 mg) was administered during the operation and on Day 4 post‐operation, whereas ATG (50 mg) was administered during the operation and daily in the following two days.

Blood sample collection and bioassay

Whole blood samples were collected after the same dosage regimen was administered for at least seven days according to the following schedule: pre‐dose, and 0.5, 1, 1.5, 2, 3, 4, 6, 9 and 12 h following the morning MMF dose. Sodium heparin was used as the anticoagulant in the antecubital catheter. The blood samples were centrifuged to separate the plasma samples, which were stored at −20°C until analysis.

The MPA plasma concentration was measured using a validated high‐performance liquid chromatographic method 24. The calibration range was 0.1–50 mg l⁻¹ with the lowest limit of quantification of 0.1 mg l⁻¹. Precision was within 7.2% and accuracy was within 8.0% at the MPA control concentrations of 0.2, 5 and 50 mg l⁻¹.

External predictability evaluation

The external evaluation was conducted using NONMEM^® (version 7.4; ICON Development Solutions, Ellicott City, MD, USA) compiled with gfortran 4.6.0 and interfaced with PsN (version 4.7.0; uupharmacometrics.github.io/PsN) and Pirana (version 2.9.6; www.pirana‐software.com). The R software (version 3.4.4; www.r‐project.org) was used to post‐process the NONMEM output.

The final popPK models were re‐established based on the formulas and parameters reported for each identified article and were sent to the corresponding authors via email for crosschecking. Then the external predictive performance was evaluated using prediction‐ and simulation‐based diagnostics and Bayesian forecasting.

Prediction‐based diagnostics

Based on observed concentrations and population predictions (PRED), the observed and predicted AUCs within a 12 h dose‐interval [AUC_obs(0‐12h) and AUC_{pred(0‐12h)}, respectively], were calculated using the linear trapezoidal rule. Prediction error (PE%) and absolute prediction error (APE%) were calculated using equations (1) and (2), respectively.

$$\mathit{PE}\%=\frac{{\mathit{AUC}}_{\mathit{\text{pred}}\left(0-12\mathit{h}\right)}-{\mathit{AUC}}_{\mathit{obs}\left(0-12\mathit{h}\right)}}{{\mathit{AUC}}_{\mathit{obs}\left(0-12\mathit{h}\right)}}\times 100$$ (1)

$$\mathit{A}\mathit{PE}\%=\left|\frac{{\mathit{AUC}}_{\mathit{\text{pred}}\left(0-12\mathit{h}\right)}-{\mathit{AUC}}_{\mathit{obs}\left(0-12\mathit{h}\right)}}{{\mathit{AUC}}_{\mathit{obs}\left(0-12\mathit{h}\right)}}\right|\times 100$$ (2)

The median PE (MDPE) and median APE (MAPE) were used to evaluate the accuracy and precision of the predictive performance, respectively 25. As a combination predictor of both accuracy and precision, F₂₀ (PE% within ±20%) and F₃₀ (PE% within ±30%) were also calculated. The predictive performance of a candidate model was considered satisfactory if the standards of MDPE ≤ ±20%, MAPE ≤ 30%, F₂₀ ≥ 35% and F₃₀ ≥ 50% were met 22, 26.

Simulation‐based diagnostics

To evaluate the predictive performance of each model based on simulation, the statistics of the observed and simulated time–concentration profiles were compared using prediction‐ and variability‐corrected visual predictive check (pvcVPC) 27 and normalized prediction distribution error (NPDE) test 28. Moreover, a posterior predictive check (PPC) 29 was performed to investigate the accuracy of the models in predicting the AUC. The dataset was simulated 2000 times using the $SIMULATION block in NONMEM^® for pvcVPC, NPDE and PPC.

The pvcVPC assessed graphically whether simulations of a candidate model could reproduce both the central trend and the variability in the observed data. The 95% confidence intervals (CIs) of the median, and the 5th and 95th percentiles of the simulations at different sampling times were calculated and compared with the observations. The computations and graphical presentations for pvcVPC were performed with PsN.

NPDE accounted for the full predictive distribution of each individual observation and handled multiple observations within subjects. Under the null hypothesis that the data in the evaluation dataset could be described adequately by a candidate model, NPDE follows the standard normal distribution. The NPDE test was performed using the NPDE add‐on package in R (version 2.0; www.npde.biostat.fr).

To analyse the degree to which data distributions generated from the investigated model deviated from the observed data, a PPC was performed under the assumption that the replicated data generated from the model should be similar to the observed data if the model fitted. Using this approach, the posterior distributions, AUC within a 12 h dose‐interval of the simulations [AUC_sim(0‐12h)], were also calculated with simulated data from the investigated models using the linear trapezoidal rule. The probability that AUC_sim(0‐12h) ≥ AUC_obs(0‐12h) was computed and denoted as the Bayesian P‐value 30, 31. The median, 2.5th, 5th, 25th, 75th, 95th and 97.5th percentiles were investigated to identify systematic discrepancies between the observed and simulated data. A Bayesian P‐value close to 0 or 1 indicated that the model did not fit the data well 30, 31.

Bayesian forecasting

To evaluate the influence of prior observations on model predictability, maximum a posteriori Bayesian (MAPB) forecasting was performed using data from the patients with ≥2 full concentration–time profiles. The individual prediction (IPRED) was based on prior observations. The predicted AUCs within a 12 h dose interval [AUC_{ipred(0‐12h)}] were calculated using the linear trapezoidal rule, and then compared with the corresponding AUC_obs(0‐12h). Individual prediction error (IPE%) was calculated using equation (3).

$$\mathit{IPE}\%=\frac{{\mathit{AUC}}_{\mathit{\text{ipred}}\left(0-12\mathit{h}\right)}-{\mathit{AUC}}_{\mathit{obs}\left(0-12\mathit{h}\right)}}{{\mathit{AUC}}_{\mathit{obs}\left(0-12\mathit{h}\right)}}\times 100$$ (3)

Impact of structural models

Because the modelling strategies could affect the predictive performance, we reviewed the structural models used in previous studies. The prediction‐ and simulation‐based diagnostics mentioned above were conducted to evaluate the predictability of different structural models.

Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY 32, and are permanently archived in the Concise Guide to PHARMACOLOGY 2017/18 33.

Results

Review of published popPK studies on co‐administration of MMF and TAC

A total of 11 popPK models of MMF co‐administered with TAC 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44 were included for external evaluation after the literature retrieval. The details of the literature search process are provided in Appendix S1. Among them, seven were multicentre studies 36, 37, 38, 39, 40, 41, 44 and four were single‐centre studies 34, 35, 42, 43. Although >60% of the included models were conducted in multicentres, the sample size of kidney transplant recipients co‐administered with TAC was >100 in only one study 39, and 50–100 in two 35, 42. In addition, only one study 43 was conducted in Chinese individuals while the remaining 10 were mainly conducted in Caucasians. Liquid chromatography methods were used to detect the MPA concentrations in all studies (Table 1).

Table 1.

Summary of published population pharmacokinetic studies of mycophenolate mofetil in adult kidney transplant recipients co‐administered with tacrolimus

Study (publication year)	Country (Single/multiple sites)	Number of patients (Male/Female)	Sampling schedule (Number of samples)	Postoperative time mean ± SD/median (range)	Bioassay	Structural model	PK parameters and formulas		BSV% (BOV%)	Residual error
Cremers et al. (2005) 34	Netherlands (Single)	31 (23/8)	IS+SSa (2748 tMPA, 2648 tMPAG)	(2–52 weeks)	HPLC	2CMT (tMPA), 1CMT (tMPAG), Continuous EHC	CL/F (tMPA)	11.9	30 (/)	35%, tMPA 14%, tMPAG
							VC/F (tMPA)	10.3	74 (/)
							VP/F (tMPA)	183	330 (/)
							Q/F (tMPA)	11.2	51 (/)
							T1/2a	0.567	57 (/)
							VC/F (tMPAG)	8.91	20 (/)
							Ke (tMPAG)	0.122	28 (/)
							KT (tMPAG)	0.0410	78 (/)
Staatz et al. (2005) 35	Canada(Single)	> 55	SSb (1376 tMPA)	7 days (3–7)	HPLC	2CMT (tMPA)	CL/F (tMPA)	25.4 × [1–0.042 × (ALB‐26)]	32 (35)	41%, tMPA
							VC/F (tMPA)	65	/
							VP/F (tMPA)	496	/
							Q/F (tMPA)	30.7	78 (/)
							Ka	0.64	109 (/)
de Winter et al. (2009) 36	Belgium & Netherlands (multiple)	28 (18/10)	IS+SSc 45 profiles (489 tMPA, 489 fMPA, 488 tMPAG, 210 fMPAG)	11 days (4–115)	HPLC, LC/MS/MS	2CMT (fMPA), 1CMT (fMPAG), Intermittent EHC	CL/F (fMPA)	747	97 (/)	0.52, tMPA 0.993, fMPA 0.186, tMPAG 0.551, fMPAG log‐transformed additive model
							VC/F (fMPA)	189	116 (/)
							VP/F (fMPA)	34 300	/
							Q/F (fMPA)	2010	/
							Ka	4	/
							Tlag	0.231	161 (/)
							CL/F (fMPAG)	4.75 × (CLcr/45)1.36	106 (/)
							VC/F (fMPAG)	8.56	/
							BMAX	35 100 × (ALB/33)1.39	48 (/)
							KB (fMPA)	0.153	/
							KUB (bMPA)	169	/
							KB (fMPAG)	0.0133	/
							KUB (bMPAG)	93.1	/
							KCG (fMPAG)	0.0796	71 (/)
							KGB	10.0	/
							TGB	7.90	141 (/)
							DGB	1.00	/
de Winter et al. (2010) 37	Austria, Belgium, Germany & Netherlands (multiple)	17	ISd (not available)	6 days (3–8)	HPLC, LC/MS/MS	2CMT (tMPA)	CL/F (tMPA)	15.3 × (ALB/40)‐0.69	51 (/)	0.61, tMPA log‐transformed additive model
							VC/F (tMPA)	79.4	103 (/)
							VP/F (tMPA)	291	/
							Q/F (tMPA)	26.5	/
							Ka	4	/
							Tlag	0.293	/
Lamba et al. (2010) 38	USA(multiple)	9 (3/6)	SS Details of sampling were not available (406 tMPA)	(1 day −3.5 years)	LC/MS/MS	2CMT (tMPA)	CL/F (tMPA)	13.6 (if POT ≥ 30 days) or 17.0 (if POT < 30 days)	26.7 (/)	49.5%, tMPA 0.51 mg l−1, tMPA
							VC/F (tMPA)	61.8	/
							VP/F (tMPA)	518	/
							Q/F (tMPA)	22	/
							Ka	4.1	/
de Winter et al. (2011) 39	Belgium & Netherlands (multiple)	101 (73/28)	IS+SSc (7739 tMPA)	23 days (3–168)	HPLC, LC/MS/MS	2CMT (tMPA)	CL/F (tMPA)	17 × (1 + 0.5 × e‐0.04×POT)	31 (3.8)	0.45, tMPA log‐transformed additive model
							VC/F (tMPA)	68 × (1 + 3.2 × e‐0.045×POT)	71 (50)
							VP/F (tMPA)	229	/
							Q/F (tMPA)	38	/
							Ka	3.9	125 (117)
							Tlag	0.21	7.4 (/)
							F	1 × (MMFdose/1000)−0.41	41 (24)
de Winter et al. (2012) 40	France (multiple)	31	IS+SSe 147 profiles (4718 tMPA)	(1 week–6 months)	LC/MS/MS	2CMT (tMPA)	CL/F (tMPA)	13	62 (36)	37%, tMPA
							VC/F (tMPA)	34.9 (if POT ≥ 14 days) or 27.571 (if POT < 14 days)	105 (/)
							VP/F (tMPA)	4910	/
							Q/F (tMPA)	24.7	/
							Ka	1.9	36 (110)
							Tlag	0.24	/
							F	1	79 (/)
Colom et al. (2014) 41	Belgium & Spain (multiple)	10	ISf (2038 tMPA, 2054 tMPAG, 1043 tAcMPAG)	7 days–1 year	HPLC	2CMT (tMPA), 2CMT (tMPAG), 1CMT (tAcMPAG), Continuous EHC	CL/F (tMPA)	19.4	20.6 (/)	0.39, tMPA 0.202, tMPAG 0.472, tAcMPAG log‐transformed additive model
							VC/F (tMPA)	24.8	113.6 (/)
							VP/F (tMPA)	607	/
							Q/F (tMPA)	17.5	/
							Ka	1.22	/
							Tlag	0.206	/
							fm	0.85	/
							CL/F (tMPAG)	1.12 × (CLcr/59.51)0.977	46.0 (/)
							VC/F (tMPAG)	2.60	/
							VP/F (tMPAG)	3.75	/
							Q/F (tMPAG)	21.2	/
							KT (tMPAG)	0.341751	85.6 (/)
							CL/F (tAcMPAG)	38.5 × (CLcr/59.51)0.534	62.3 (/)
							VC/F (tAcMPAG)	13.5	/
Velickovic‐Radovanovic et al. (2015) 42	Serbia (single)	61	SS Details of sampling were not available (90 tMPA)	51.14 months (1–204)	HPLC	2CMT (tMPA)	CL/F (tMPA)	0.741 + 0.00165 × 0.72 × MMFddose + 0.0804 × AGE	24.7 (/)	35.07%, tMPA
							VC/F (tMPA)	0.653	24.3 (/)
							VSS/F (tMPA)	801	1241.1 (/)
							Q/F (tMPA)	52.1	216.1 (/)
							Ka	4.07	144.2 (/)
							Tlag	0.21	34.64 (/)
Yu et al. (2017) 43	China (single)	7	IS+SSg (783 tMPA)	Not availableh	HPLC	2CMT (tMPA)	CL/F (tMPA)	0.0916 × BW + 0.0417 × SCr + 7.98	34.2 (13.7)	15.8%, tMPA 0.15 mg l−1, tMPA
							VC/F (tMPA)	7.72 × UGT2B7 genotype+14.7	21.3 (13.7)
							KCP (tMPA)	0.915	31.2 (/)
							KPC (tMPA)	0.059	138 (/)
							Ka	1.89	51.3 (/)
Colom et al. (2018) 44	Belgium & Spain (multiple)	10	ISf (2038 tMPA, 2046 fMPA)	7 days–1 year	HPLC	2CMT (fMPA), Intermittent EHC	CL/F (fMPA)	410	26.81 (40.9)	46.9%, tMPA 58.3%, fMPA
							VC/F (fMPA)	18.3	99.45 (137.6)
							VP/F (fMPA)	29 100	/
							Q/F (fMPA)	749	/
							Ka	1.41	/
							Tlag	0.293	/
							KB (fMPA)	43.1 × (CLcr/59.51)0.394	24.10 (/)
							KCG (fMPA)	0.224	/
							KGB	10	/
							TGB	2.0	/
							DGB	1.5	/

ALB, albumin (g l⁻¹); B_MAX, maximum number of protein binding sites; bMPA, bound mycophenolic acid; bMPAG, bound 7‐O‐glucuronide mycophenolic acid; BOV, between‐occasion variability; BSV, between‐subject variability; BW, body weight (kg); CL/F, apparent clearance (l h⁻¹); CLcr, creatinine clearance calculated by the Cockcroft‐Gault formula (ml min⁻¹); CMT, compartment; co‐ad, co‐administration of mycophenolate mofetil and; D_GB, duration of gallbladder emptying (h); EHC, enterohepatic circulation; F, bioavailability; f_m, fraction of mycophenolic acid converted to 7‐O‐glucuronide mycophenolic acid; fMPA, free mycophenolic acid; fMPAG, free 7‐O‐glucuronide mycophenolic acid; HPLC, high performance liquid chromatography; IS, intensive sampling; Ka, absorption rate constant (h⁻¹); K_B, protein binding rate constant (h⁻¹); K_CG, transfer rate constant from the central compartment to gallbladder (h⁻¹); K_CP, transfer rate constant from the central compartment to peripheral compartment (h⁻¹); Ke, elimination rate constant (h⁻¹); K_GB, gallbladder emptying rate constant (h⁻¹); K_PC, transfer rate constant from the peripheral compartment to central compartment (h⁻¹); K_T, transfer rate constant describing biliary excretion (h⁻¹); K_UB, protein unbinding rate constant (h⁻¹); LC/MS/MS, liquid chromatography tandem‐mass spectrometry; MMF, mycophenolate mofetil; MMFdose, dose of mycophenolate mofetil (mg times⁻¹); MMFddose, daily dose of mycophenolate mofetil (mg day⁻¹); POT, postoperative time; Q/F, apparent inter‐compartmental clearance (l h⁻¹); SCr, serum creatinine (μmol l^−l); SD, standard deviation; SS, sparse sampling; T_1/2a, absorption half‐life (h); TAC, tacrolimus; Tlag, absorption lag time (h); tAcMPAG, total acyl‐glucuronide mycophenolic acid; T_GB, time of gallbladder emptying (h); tMPA, total mycophenolic acid; tMPAG, total 7‐O‐glucuronide mycophenolic acid; V_C/F, apparent volume of distribution of central compartment (l); V_P/F, apparent volume of distribution of peripheral compartment (l); V_SS/F, apparent volume of distribution in steady‐state (l)

^aAt weeks 2, 6, 12, 26, 39 and 52, intensive samples were taken around the morning dose at 0, 1, 2, 3, 4 and 6 h after drug administration. At weeks 4, 8, 10, 17 and 21, sparse samples were taken at 0, 2 and 3 h after drug administration

^bSparse samples were collected at 0, 1, 2, 3 and 4 h post‐dose on days 3, 5 and 7 post‐operation

^cFor patients co‐administered with tacrolimus, intensive samples were collected at 0, 0.5, 1, 2, 6 and 12 h post‐dose on day 6, and sparse samples were collected at 0, 0.5, 2 h post‐dose on days 21, 49 and 140 post‐operation

^dIntensive samples were collected at 0, 0.5, 1, 2, 6 and 12 h post‐dose for patients co‐administered with tacrolimus

^eIntensive samples were collected at 0, 0.33, 0.66, 1, 1.5, 2, 3, 4, 6 and 9 h post‐dose, and an extra sample was taken from hospitalized patients at 12 h post‐dose

^fIntensive samples were collected at 0, 20, 40, and 75 min and at 2, 3, 4, 6, 8, 10 and 12 h post‐dose on day 7 and months 1, 3, 6 and 12 post‐operation

^gIntensive samples were collected at 0, 0.5, 1, 1.5, 2, 4, 6, 8, 10 and 12 h after the morning dose. Sparse samples were collected at limited sampling times (0, 0.5, 2 h, or 0, 0.5, 2 and 8 h)

^hPostoperative time was not available in the article, and the duration of MMF therapy ranged between 2 and 209 days

Furthermore, both intensive and sparse samples were collected in five studies 34, 36, 39, 40, 43, only intensive samples were collected in three 37, 41, 44, and only sparse samples were obtained in the other three studies 35, 38, 42. Samples were obtained within 1 month post‐operation in two studies 35, 37, and 1–204 months post‐operation in another study 42. Moreover, samples collected within and after the first month post‐operation were simultaneously included in the remaining eight studies 34, 36, 38, 39, 40, 41, 43, 44.

The structural models adopted were either conventional two‐compartment (2CMT) models 35, 37, 38, 39, 40, 42, 43 or 2CMT models with an EHC process 34, 36, 41, 44. BSV was modelled using an exponential model. The median (range) values for BSV in apparent clearance of MPA were 31% (20.6–97%). The median (range) of residual variability (RUV) using a proportional model was 46.9% (35–84%) [n = 9]. For the two studies using combined RUV models (proportional/additive), the values were 15.8% and 0.15 mg l⁻¹ 43, and 49.5% and 0.51 mg l⁻¹ 38, respectively.

The most frequently identified covariate influencing MPA PK was postoperative time, which was incorporated in three studies 38, 39, 40. Other covariates identified were age, body weight (BW), serum creatinine, creatinine clearance, albumin, UGT2B7 genotype and MMF dose.

External evaluation cohort

A total of 50 full concentration–time profiles of 45 patients were included in this study. Among these patients, 41 had one full profile, three had two full profiles and one had three full profiles. The demographic and laboratory test data are summarized in Table 2. Since the UGT2B7 genotype was not collected in our dataset, the apparent volume of distribution of the central compartment was set to a fixed value (27.9 l) in the model of Yu et al. 43.

Table 2.

Characteristics of external evaluation dataset

Characteristics	Number or mean ± SD	Median (range)
No. of patients (Male/Female)	45 (33/12)	/
No. of samples (Male/Female)	500 (380/120)	/
Age (years)	39.9 ± 11.9	38.0 (21.0–65.0)
Body weight, BW (kg)	61.3 ± 12.8	61.7 (33.0–95.5)
Height (cm)	167.7 ± 8.2	169.5 (150.0–185.0)
Mycophenolate mofetil daily dose (g day −1 )	1.4 ± 0.4	1.5 (0.5–2.5)
AUC MPA(0‐12h) (mg h l −1 ) a	52.5 ± 24.5	51.9 (13.8–124.5)
Tacrolimus daily dose (mg day −1 )	5.9 ± 2.9	6.3(1.0–12.0)
Tacrolimus trough concentration (ng ml −1 )	8.1 ± 2.2	7.5 (4.1–14.2)
Postoperative time, POT (days)	539.7 ± 984.0	52.0 (9.0–3669.0)
Albumin, ALB (g l −1 )	41.4 ± 4.4	41.6 (27.1–49.5)
Hemoglobin, HB (g l −1 )	105.2 ± 25.3	100.0 (70.0–179.0)
Serum creatinine, SCr (μmol l −1 )	185.6 ± 148.8	133.5 (60.0–749.0)
Creatinine clearance, CLcr (ml min −1 ) b	56.5 ± 29.0	55.7 (8.2–119.0)

AUC_MPA(0‐12h), Area under the time–concentration curve of mycophenolic acid within 12 h dose‐interval; SD, standard deviation

^aCalculated using the linear trapezoidal rule via a pracma add‐on package in R

Calculated from serum creatinine using the Cockcroft‐Gault formula: CLcr = [140 – age (years)] × weight (kg)/[0.818 × SCr (μmol l⁻¹)] × (0.85, if female)

External predictability evaluation

Prediction‐based diagnostics

The results indicated an unsatisfactory predictive performance in the prediction‐based diagnostics (Figure 1A, and Table S1). None of the investigated models met all the aforementioned criteria (MDPE ≤ ±20%, MAPE ≤ 30%, F₂₀ ≥ 35% and F₃₀ ≥ 50%). The values of MDPE, an indicator of predictive accuracy, were within ±20% in five studies 34, 38, 39, 41, 44. The MAPE, an indicator of predictive precision, was less than 30% in three studies 34, 38, 39. As a combination predictor of both accuracy and precision, F₂₀ was no more than 35% in all studies and F₃₀ was over 50% in three studies 34, 38, 39. Taking both accuracy and precision into account, the studies by Cremers et al. 34, Lamba et al. 38 and de Winter et al. 39 showed preferable predictive performances than the others, in which three of four criteria were met with MDPE ≤ ±20%, MAPE ≤ 30% and F₃₀ ≥ 50%. In addition to the study by Cremers et al. 34, the other three EHC models 36, 41, 44 did not perform well.

Figure 1.

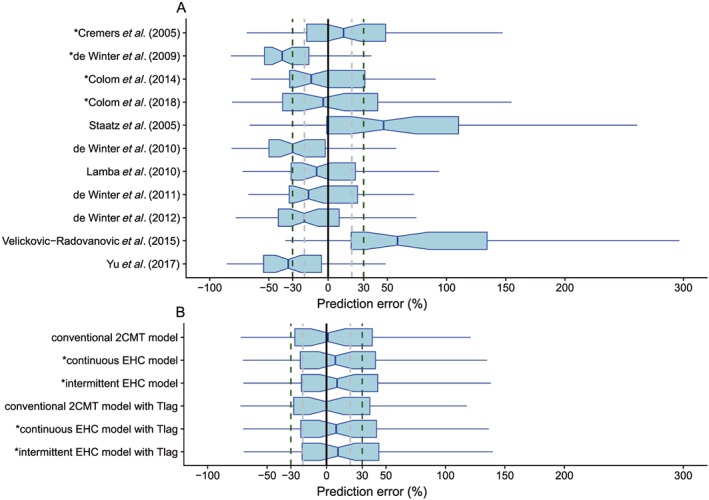
Box plots of the prediction error (PE%): (A) published population pharmacokinetic models, (B) investigated structural models. Black solid, grey and dark green dashed lines are reference lines indicating PE of 0%, ±20% and ±30%, respectively. The model with an asterisk (*) incorporates an enterohepatic circulation (EHC) process. 2CMT, two‐compartment; Tlag, absorption lag time

Simulation‐based diagnostics

In simulation‐based diagnostics, the pvcVPC showed a large discrepancy between the observations and simulations in most models (Figure S1). An obvious trend of over‐ or underprediction was observed, except in the study by Cremers et al. 34, which showed slight misspecifications in the absorption phase and 6 h post‐dose. Neither the two relatively superior models in the prediction‐based diagnosis 38, 39 nor the other three EHC models 36, 41, 44 performed well in the pvcVPC.

The NPDE results are shown in Figure S2 and Table S2. Only the model reported by de Winter et al. 39 showed a preferable performance with a global test P = 0.04, which indicated the simulation might have been appropriately applied. Furthermore, none of the NPDE distributions of the EHC models followed a normal distribution.

The PPC results are shown in Figure 2A and Table S3. Obvious discrepancies between the observations and simulations were observed and the Bayesian P‐values were close to 0 or 1 in most models, which suggested that the models did not fit the data well. The model reported by de Winter et al. 39 showed superiority over the others, and the posterior distribution (median, 2.5th, 5th, 25th, 75th, 95th and 97.5th percentiles of simulated AUC) showed no obvious deviation from those of the observed AUC with Bayesian P‐values ranging between 0.1 and 0.9. Furthermore, none of the EHC models were better than the others in the PPC analysis.

Figure 2.

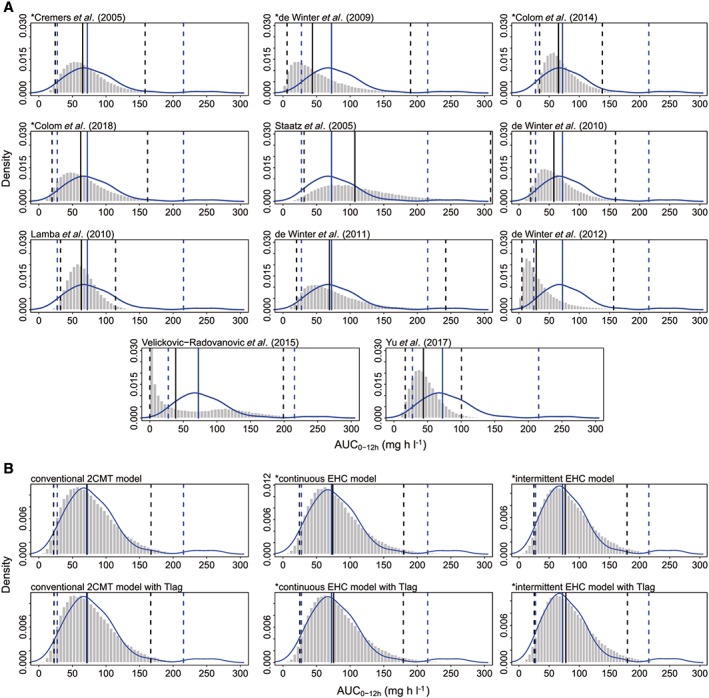
Posterior predictive check (PPC) graphics: (A) published population pharmacokinetic models, (B) investigated structural models. The histograms represent the distribution of simulations and the blue curves are the kernel density plots of observations. The blue and black solid lines represent the median observations and simulations, respectively. The observed 2.5th and 97.5th percentiles are represented by blue dashed lines, and the simulated 2.5th and 97.5th percentiles are represented by black dashed lines. The model with an asterisk (*) incorporates an enterohepatic circulation (EHC) process. 2CMT, two‐compartment; AUC_0‐12h, area under the time‐concentration curve within 12 h dose‐interval; Tlag, absorption lag time

Bayesian forecasting

Since only four patients with ≥2 full profiles were available in our dataset, the influence of only one prior observation was investigated in Bayesian forecasting. For all four patients, IPRED of the second profile was predicted by the first profile. In addition, IPRED of the third profile was also predicted by the second profile for the patient with three full profiles. IPEs of all 11 investigated models were pooled for analysis, and the result showed that both precision and accuracy of the model predictability could be improved by MAPB even with only one prior profile (Figure 3).

Figure 3.

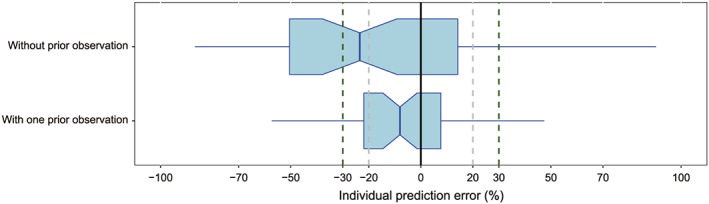
Box plots of the individual prediction error (IPE%). Black solid, grey and dark green dashed lines are reference lines indicating IPE of 0%, ±20% and ±30%, respectively

The impact of structural models

To characterize MPA PK, four studies 34, 35, 38, 43 used first‐order absorption, while the other seven studies 36, 37, 39, 40, 41, 42, 44 incorporated absorption lag time (Tlag) with first‐order absorption. Conventional 2CMT models were used in seven studies 35, 37, 38, 39, 40, 42, 43 and 2CMT models with an EHC process were employed in the other four studies 34, 36, 41, 44. EHC processes were modelled to be continuous in two studies 34, 41 and intermittent in the other two studies 36, 44. The continuous EHC process was described through a first‐order transfer rate constant from gallbladder to the absorption site, while the intermittent EHC process assumed that gallbladder emptying occurs at a specified time point with a first‐order process and over a specific period.

Therefore, from the review of the selected studies, six structural models without covariates were evaluated including the conventional 2CMT, continuous EHC and intermittent EHC models with and without Tlag. The schematics of the structural model are presented in Figure 4, and the estimated parameters of all models are shown in Table S4.

Figure 4.

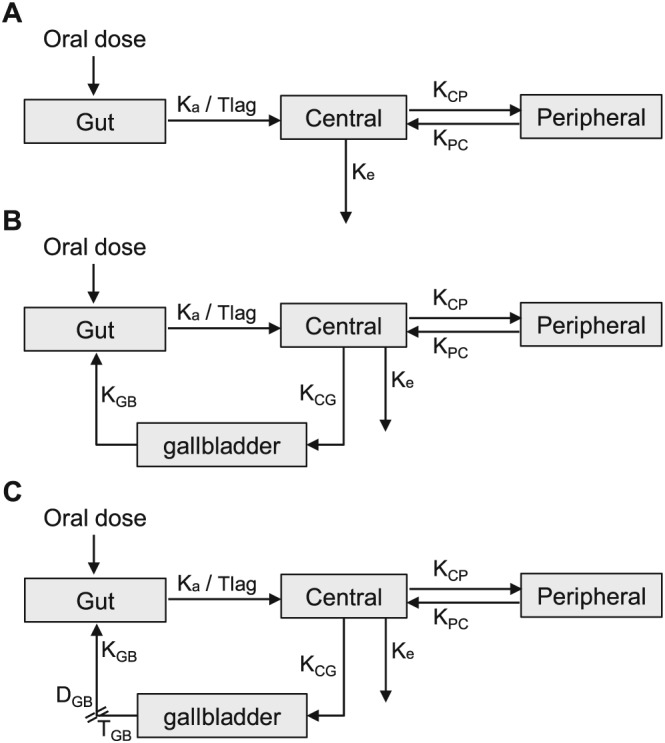
Schematics of mycophenolic acid (MPA) pharmacokinetic models. (A) conventional two‐compartment (2CMT) model with or without absorption lag time (Tlag), (B) continuous enterohepatic circulation (EHC) model with or without Tlag, (C) intermittent EHC model with or without Tlag. D_GB, duration of gallbladder emptying; K_a, absorption rate constant; K_CG, transfer rate constant from the central compartment to the gallbladder; K_CP, transfer rate constant from the central compartment to the peripheral compartment; K_e, elimination rate constant; K_GB, gallbladder emptying rate constant; K_PC, transfer rate constant from the peripheral compartment to the central compartment; T_GB, time of gallbladder emptying

In the prediction‐based diagnostics, no significant difference was found either in predictive accuracy (MDPE ranged from −0.21 to 9.77) or in predictive precision (MAPE ranged from 25.51 to 29.20) between the conventional 2CMT, continuous EHC and intermittent EHC models (Figure 1B and Table S1).

In the simulation‐based diagnostics, there was no significant difference between the conventional 2CMT, continuous EHC and intermittent EHC models. No obvious discrepancy between observations and simulations could be found in the pvcVPC (Figure S3). Furthermore, all investigated models showed P < 0.05 in global test (Table S2), which indicated that the NPDE did not follow a normal distribution (Figure S4). Moreover, the posterior distributions of the AUC_sim(0‐12h), except for the 97.5th percentiles, were consistent with those of the AUC_obs(0‐12h) (Figure 2B and Table S3).

Discussion

Although more than 10 popPK models of MMF co‐administered with TAC in adult kidney transplant recipients have been published over the past decades, their extrapolated predictability is unclear. To the best of our knowledge, this is the first comprehensive external evaluation of published popPK studies on MMF using an independent dataset. Although the evaluation dataset was taken from one centre and was relatively small, this study could be helpful to further investigating MMF PK characteristics including the complex EHC process.

The predictive accuracy was acceptable (MDPE ≤ ±20%) in five studies. However, large unexplained variability, as well as poor precision, was observed in the predictive performance. More than half of the PE% fell outside the ±30% in most published models. There was no obvious trend which indicated that the superior predictive performance was related to the sample size, region or race. Taking both accuracy and precision into account, both the continuous and intermittent EHC models did not significantly improve the predictive performance compared with the conventional 2CMT model.

MPA has been widely reported to undergo extensive EHC, and co‐administration with TAC does not influence the EHC process 45, 46. The EHC process related to the gallbladder filling and emptying is complex. In humans, a fraction of the bile is secreted continuously into the duodenum while most is concentrated and stored in the gallbladder 47. Gallbladder emptying is thought to be triggered by ingestion of a meal, fats and proteins, which results in the contraction of the gallbladder and relaxation of the sphincter of Oddi by the release of endogenous neurohormones such as cholecystokinin and secretin 47.

Furthermore, Clarke et al. 48 demonstrated the positive associations between dietary protein intake and gut microbial diversity, which plays a vital role in the deglucuronidation of MPAG to MPA in the distal gut. Therefore, this process could be influenced by patient characteristics, gut flora and other external factors such as meal time and food type 49, 50, 51, which makes predicting MPA PK even more difficult. In previous studies, the effects of meal time and food type were not accounted for. The EHC process had not been adequately characterized, which might be the major reason why the EHC models contributed little to predictive performance.

Insufficient samples were collected between 6 and 12 h post‐dose, which could be another important reason for the failure to characterize the EHC process. It has been reported that the secondary peak in MPA concentration profile resulting from EHC typically occurs approximately 6–12 h after oral administration of MMF 43, 49, which might be attributed to the gallbladder contraction stimulated by the second or third food intake. However, the intensive sampling within 4 h post‐dose in most previous studies could only cover the first food intake. Only two or three samples were collected after the 6 h post‐dose time point, which would not have captured the second or third food intake. Therefore, the data did not contain sufficient information to describe the discrete biliary excretion episodes.

The investigation of the impact of model structure did not show incorporating the EHC process could improve predictive performance. However, this could be confounded by the lack of sampling between 6 and 12 h post‐dose in the evaluation dataset and previous studies, which was not sufficient to estimate the observed AUC by non‐compartment analysis. In addition, the appropriate inclusion of covariates also plays an important role in predictive performance. Postoperative time was the most frequently identified covariate, followed by the co‐administration type, which represented the prevailing consensus in covariate selection.

Our results indicated that the two models 38, 39 which included postoperative time as a covariate influencing the apparent clearance showed preferable predictability. This time‐dependent clearance might be associated with a combination of improving kidney function, increasing albumin levels, improving gastrointestinal function, and decreasing corticosteroid dose during the first three months post‐transplantation 9, 52.

Furthermore, the large RUV and BSV from model misspecification and unknown covariates in most of the investigated studies may contribute to the poor predictive performance.

Moreover, it is expected that a model developed in a population similar to that in an evaluation dataset should have superior predictive performance due to similar genetics, prescribing and dietary habits of the subjects 26. Therefore, the model may have better predictive performance if the modelling and evaluation data were from the same centre. However, the model developed using Chinese subjects 43 showed no superiority, which might be explained by the fact that seven participants (<10%) were co‐administered with TAC while 72 were co‐administrated with CSA in this study. It is well known that CsA inhibits the MPA EHC process and thereby reduces MPA exposure. Thus, for patients who were co‐administered with TAC, an obvious underestimation by this model was observed.

The present study has some limitations. Firstly, an improvement of the model predictability could be observed as long as one prior profile was available. However, given the low number of patients with multiple full concentration–time profiles in the evaluation dataset, more data from multiple monitoring needed to be collected to adequately assess the effect of prior observations on model predictability. Secondly, most patients in our dataset were administered one dose of MMF and therefore the nonlinear relationship between MMF dose and MPA exposure that has been reported 39 could not be investigated.

In conclusion, 11 published popPK models of MMF co‐administered with TAC in adult kidney transplant recipients were externally evaluated using an independent dataset. The high degree of unexplained variability and unsatisfactory predictive performance of the published models indicated that TDM was necessary for optimization of MMF therapy in kidney transplant recipients. Moreover, further studies incorporating potential covariates need to be conducted to investigate the key factors influencing the model predictability of MMF.

Competing Interests

All authors have completed the United Competing Interest form at www.icmje.org/conflicts‐of‐interest (available on request from the corresponding author). C.X.W. had support from National Natural Science Foundation of China (No. 81670680), and Science and Technology Planning Project of Guangdong Province of China (2015B020226002). Z.J. received grants from National Natural Science Foundation of China (No. 81573505), Western Medicine Guidance Project (No. 15411968000) of Shanghai Science and Technology Committee, ‘Weak Discipline Construction Project’ (No. 2016ZB0301‐01), and ‘2016 Key Clinical Program of Clinical pharmacy’ of Shanghai Municipal Commission of Health and Family Planning. H.X.Z. was funded by National Natural Science Foundation of China (No. 81700655) and China Postdoctoral Science Foundation (2017 M622874). There are no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years, and no other relationships or activities that could appear to have influenced the submitted work. The other authors have no conflicts of interest to declare.

The authors would like to sincerely thank Dr Helena Colom from the Department of Pharmacy and Pharmaceutical Technology and Physical‐Chemistry, Biopharmaceutics and Pharmacokinetics Unit, School of Pharmacy, University of Barcelona (Spain), Dr Malek Okour from Clinical Pharmacology Modeling and Simulation, GlaxoSmithKline (USA), Dr Brenda C. M. de Winter from the Department of Hospital Pharmacy, Erasmus University Medical Center (Netherlands), and Dr Zi‐Cheng Yu from the Institute of Clinical Pharmacy and Pharmacology, Yangpu Hospital, School of Medicine, Tongji University (China) for providing details about the research and active discussions on the model code. The authors would also like to thank Editage [ www.editage.cn ] for English language editing.

Contributors

Z.J., C.X.W., H.X.Z. and C.C.S. conceptualized and planned the work that led to the manuscript. L.S.L., Q.F., Y.F.L., J.L. and R.H.D. acquired the data. H.X.Z., C.C.S., L.S.L., B.L. and Q.Z. analyzed and interpreted the data. C.C.S. and H.X.Z. drafted the manuscript. The final submitted version of manuscript was reviewed and approved by all the authors.

Supporting information

Appendix S1 Details of literature search and selection process

Table S1 Results of prediction‐based diagnostics

Table S2 Statistical test results of normalized prediction distribution error (NPDE) diagnostics

Table S3 Statistical test results of posterior predictive check (PPC)

Table S4 Estimated parameters of investigated structural models

Figure S1 Visual predictive check (VPC) plot of the published models: (A) plotted with logarithmic scale for y‐axis and linear scale for x‐axis, (B) plotted with linear scale for both x‐ and y‐axis. The red solid lines represent the median observed concentration, and the semitransparent red fields represent the simulation‐based 95% confidence intervals (CIs) for the median. The observed 5th and 95th percentiles are represented by red dashed lines, and the 95% CIs for the corresponding model predicted percentiles are shown as semitransparent blue fields. The observed concentrations are represented by blue dots. The model with an asterisk (*) incorporates an enterohepatic circulation process

Figure S2 Normalized prediction distribution error (NPDE) plots of the published models: (A) quantile–quantile plot of the NPDE distribution against theoretical distribution (semitransparent blue fields), (B) histogram of the NPDE distribution against theoretical distribution (semitransparent blue fields), (C) NPDE vs. time after last dose (h), (D) NPDE vs. predicted concentration. In plots C and D, the red solid lines represent the median NPDE of observations, and semitransparent red fields represent the simulation‐based 95% confidence intervals (CIs) for the median. Blue solid lines represent the NPDE of the observed 5th and 95th percentiles, and semitransparent blue fields represent the simulation‐based 95% CIs for the corresponding model‐predicted percentiles. The NPDE of observations are represented by blue dots. The model with an asterisk (*) incorporates an enterohepatic circulation process

Figure S3 Visual predictive check (VPC) plot of the investigated structural models: (A) plotted with logarithmic scale for y‐axis and linear scale for x‐axis, (B) plotted with linear scale for both x‐ and y‐axis. The red solid lines represent the median observed concentration, and the semitransparent red fields represent the simulation‐based 95% confidence intervals (CIs) for the median. The observed 5th and 95th percentiles are represented by red dashed lines, and the 95% CIs for the corresponding model predicted percentiles are shown as semitransparent blue fields. The observed concentrations are represented by blue dots. The model with an asterisk (*) incorporates an enterohepatic circulation (EHC) process. 2CMT, two‐compartment; Tlag, absorption lag time (h)

Figure S4 Normalized prediction distribution error (NPDE) plots of the investigated structural models: (A) quantile–quantile plot of the NPDE distribution against theoretical distribution (semitransparent blue fields), (B) histogram of the NPDE distribution against theoretical distribution (semitransparent blue fields), (C) NPDE vs. time after last dose (h), (D) NPDE vs. predicted concentration. In plots C and D, the red solid lines represent the median NPDE of observations, and semitransparent red fields represent the simulation‐based 95% confidence interval (CIs) for the median. Blue solid lines represent the NPDE of the observed 5th and 95th percentiles, and semitransparent blue fields represent the simulation‐based 95% CIs for the corresponding model‐predicted percentiles. The NPDE of observations are represented by blue dots. The model with an asterisk (*) incorporates an enterohepatic circulation (EHC) process. 2CMT, two‐compartment; Tlag, absorption lag time (h)

Zhang H.‐X., Sheng C.‐C., Liu L.‐S., Luo B., Fu Q., Zhao Q., Li J., Liu Y.‐F., Deng R.‐H., Jiao Z., and Wang C.‐X. (2019) Systematic external evaluation of published population pharmacokinetic models of mycophenolate mofetil in adult kidney transplant recipients co‐administered with tacrolimus, Br J Clin Pharmacol, 85, 746–761. 10.1111/bcp.13850.