Theoretical Simulation of Red Cell Sickling Upon Deoxygenation Based on the Physical Chemistry of Sickle Hemoglobin Fiber Formation

Abstract

The polymerization of the mutant hemoglobin S upon deoxygenation to form fibers in red blood cells of patients suffering from sickle-cell anemia results in changes in cell shape and rigidity, also known as sickling, which underlie the pathology of the disease. While much has been learned about the fundamental physical chemistry of the polymerization process, transferring these insights to sickling of red cells under in vivo conditions requires being able to monitor, and ultimately to predict, the time course of cellular sickling under physiological conditions of deoxygenation. To this end, we have developed an experimental technique for tracking the temporal evolution of the sickling of red blood cells under laboratory deoxygenation conditions, based on the automated analysis of sequences of microscope images and machine-learning analysis to characterize cell morphology. As an aid in the quantitative understanding of these experiments, we have developed a computational framework for simulating the time dependence of sickling in populations of red blood cells which incorporates the current theoretical and empirical understanding of the physical chemistry of the sickling process. In order to apply these techniques to our experiments, we have theoretically determined the time course of deoxygenation by solving the diffusion equation for oxygen in our experimental geometry. With this combined description we are able to reproduce our experimentally observed kinetics of sickling, suggesting that our theoretical approach should be applicable to physiological deoxygenation scenarios.

TOC graphic

Introduction

Sickle-cell disease arises from a single point mutation in the β subunits of hemoglobin (Hb), which causes the mutant sickle hemoglobin (HbS) to polymerize and form fibers upon deoxygenation. The presence of these fibers induces distortion and loss of flexibility of red blood cells; the pathology of the disease is largely due to the resulting occlusion of small blood vessels in the tissues, leading to chronic organ damage and episodes of severe pain.

The phenomenology of HbS polymerization has been the subject of intensive research over several decades, and the governing physical chemical principles underlying the process have been well established (reference 1 and references cited therein). In the heterogeneous nucleation picture,² under favorable conditions the polymerization is characterized by a delay time, related to the time to form a critical nucleus, which is exquisitely sensitive to the total Hb concentration; after this initial phase, the polymerization proceeds in a strongly auto-catalytic fashion. An understanding of the relevant features of this process has relied heavily on in vitro studies of HbS. However, the application of these principles to experimental situations of clinical relevance has lagged behind this fundamental understanding. For example, the detailed progression of the sickling of red blood cells under deoxygenation conditions present in the tissues is an essential element of the disease pathology, but a quantitative understanding of this process, with predictive power, has been challenging.

The approach to this problem relies first of all on the understanding of the progression of sickling under set deoxygenation conditions. This may be examined in a laboratory setting by monitoring the sickling of red blood cells from disease patients under controlled deoxygenation. We have adopted a general setting for such experiments in which the morphology of red blood cells is monitored by automated analysis of series of digital microscope images of prepared cell samples. These samples are managed as aliquots injected into the individual wells of a well-plate, which may be scanned in the horizontal plane under computer control to bring different wells into the image field of the microscope.

In these experiments, the red blood cells lie at the bottom of the solvent medium in each well, and control of the state of oxygenation of these cells is only indirect, by adjusting the atmosphere above this medium. The finite rate at which oxygen diffuses through the medium results in a time-dependent response of the oxygen concentration at the bottom of the well to any changes in the ambient atmosphere. We have exploited this feature in developing a passive-deoxygenation technique for inducing and monitoring the sickling process. In this technique, cell preparations are initially equilibrated with air; after injection of samples into the well-plate, the ambient air is rapidly replaced with pure nitrogen. This depletion of oxygen propagates with time from the surface of the solvent medium to the bottom of each well, as the oxygen diffuses out of the wells. The combination of the retarded response of the oxygen depletion at the bottom of the well with the intrinsic dependence of sickling delay times on the degree of oxygenation of the cells results in progressive sickling of the cells in the sample on a time scale which is easily resolved by our image-acquisition method.

A complete understanding of these experiments, in terms of the progression of sickling in response to changes in oxygen concentration, requires knowledge of the actual degree of oxygenation (which we will often refer to as simply the saturation) of the cellular Hb as a function of time. In principle, it is possible to monitor the saturation of Hb by exploiting the different optical absorption spectra of deoxygenated and oxygenated Hb and monitoring the changing absorption of light by the cells with time at certain wavelengths. This approach relies on the assumption that the effective optical path lengths of the cells remain constant with time. Unfortunately, this assumption fails badly in the case of sickling cells, because the sickling process involves major changes in cell shape and organization of Hb within the cell, and the resulting changes in effective path lengths swamp the expected changes in absorption due to changes in the saturation of the Hb.

An alternative is to monitor absorbance changes of normal red blood cells, which do not undergo such internal changes upon deoxygenation, under identical conditions, and assume that these results transfer over to the case of cells which do sickle. Even in this case, an accurate determination is made very difficult by the fact that in typical microscope systems, light arrives at a specific pixel of a detector by multiple paths due to reflected and refracted stray light³; in other words, the intensity measured for a specific point in the sample is not simply the light transmitted through the sample at that point. Quantitative corrections for this effect are very difficult, and have not yielded fractional saturations with oxygen we consider reliable.

We assume that diffusion is the operative mechanism for oxygen transport through the solvent medium, which means that oxygen concentrations at various positions in the medium as a function of time should be available from appropriate solutions of the diffusion equation; with this information, a theoretical calculation of the time course of deoxygenation of red blood cells in our experiments is possible, even in the absence of a reliable experimental description. This calculation, combined with theoretical and empirical machinery assembled from current understanding of the phenomenology of the sickling process,^1,4 provides the basis for a complete theoretical calculation of predicted sickling fractions vs. time under our experimental conditions, given only the geometry of the solvent medium. In this paper, we explore in detail the path to the fully theoretical calculation of sickling profiles in our experiments, and compare these predictions with typical experimental results. In light of the various experimental and computational uncertainties we encounter during this process, the goal is not to provide a definitive and parametrically complete theoretical analysis, but rather to lay out a conceptual framework which, in combination with a careful characterization of the experimental system, offers some insight into the relative importance of different features in determining the observed sickling profiles, and which may be applied to physiological conditions.

The study reported here deals exclusively with samples from donors who possess the so-called sickle trait—that is, they are heterozygous for the genes for HbA (normal Hb) and HbS. Because of the resulting dilution in total HbS concentrations, the delay times for sickling are much longer for cells from these individuals, to the extent that their condition is medically benign. The use of these cells in our experiments is advantageous because the longer delay times result in time-dependent sickling profiles which are easily resolved by our image-acquisition procedures.

Methods

Experimental measurement of fractions sickled vs. time

Sample preparation and image acquisition.

Anonymized blood samples with EDTA anticoagulant were obtained through the Phlebotomy Unit of the NIH Clinical Center. Sickle trait donors gave their consent under NIH protocol 08-DK-0004. The mean corpuscular hemoglobin concentrations (MCHC) of the blood from all donors were determined to be in the normal range, differing by no more than 1 g/dl.

For the well-plate experiments, whole blood from each donor was diluted 3000-fold into 20 mM phosphate, pH 7.4, 295 mOsm buffer containing 5.5 mM dextrose. The cell suspension was dispensed into 384-well plates (Corning 3770) using a 16-channel pipette (Capp). Columns 1–8 contained 10 μl of the cell suspension. Columns 9–16 contained 10 μl of the cell suspension and an additional 2 μl of buffer added on top, for a final volume of 12 μl. Columns 17–24 contained 10 μl of the cell suspension and an additional 4 μl of buffer added on top, for a final volume of 14 μl. After the blood suspension and extra buffer were added to the plate, the plate was horizontally shaken at 1000 rpm for 1 minute to ensure an even distribution of cells throughout each well. After shaking, the plates were kept on the lab bench at room temperature for 15 minutes to allow the cells to settle to the bottom of the plate. The plates were then inserted into a BioTek Lionheart FX automated microscope with an enclosed atmosphere pre-equilibrated to 37 °C and fully humidified.

The plates were equilibrated at 37 °C for 15 minutes inside the microscope, after which the autofocus/autoexposure algorithm within the BioTek Gen5 software was executed to optimize imaging conditions. All images were collected with a 20x objective using a white light source passed through a 430 nm filter (Thorlabs, full width at half maximum absorbance ± 10 nM) prior to interacting with the sample. The imaging protocol was then initiated, in which the plates were incubated at 37 °C under air for two hours. During that period, one image was collected at the center of every well at 30-minute intervals. This incubation period was followed by a 15-minute gas recharge period during which pure nitrogen gas was pumped into the well-plate chamber at a flow rate of 12 SCFH (standard cubic feet per hour). During this gas recharge, the oxygen pressure inside the sample chamber was monitored, reaching a value of less than 0.5% oxygen by the end of this period. Following the gas recharge, images were continuously collected for 12 hours. During this image collection step, one image was collected at the center of every well every 15–16 minutes, which is the time it takes to make a single scan through a 384-well plate. Pure nitrogen gas was pumped into the chamber throughout the image collection, with the measured oxygen pressure reaching 0.1% after ~30 minutes.

Oxygen binding curves of diluted whole-blood samples were measured using a Hemox Analyzer (TCS Scientific Corp).

Summary of the basic image-analysis procedure.

During data acquisition, the microscope field was digitized as a series of 16-bit gray-scale, 1224 × 904-pixel images, with each image saved as a TIFF file for subsequent analysis. For each series of images, a detailed intensity-population analysis was first conducted on a small number of images in order to determine the gray-scale ranges to be identified with background and object (cell) pixels, respectively. Based on these initial assignments, the pixel values for all images were transformed and inverted to maximize the dynamic range of the values assigned to image features and provide a simple threshold value for classifying every pixel in any transformed image in the series as either “background” or “cell”. Using this classification, a list of cells was compiled as contiguous regions of pixels classified as cell pixels, using the first image of the series. Regions deemed too small to represent a cell profile were culled at this stage. Regions initially too large to represent a single cell were processed in an attempt to decompose them into smaller valid cell images; regions for which this procedure failed were retained in their original form or eliminated from consideration, depending on their overall size. The set of pixels assigned to each remaining cell was tracked unambiguously by flowing and expanding overlapping regions of object pixels from one image to the next. Cells which moved between successive images to the extent that there was no overlap with the cell footprint in the previous image were marked lost and removed from consideration. Moreover, even for cells which were successfully tracked, periods in the experiment during which a cell was deemed to overlap an edge of the image were excluded from the analysis, because of the expected distortion of various measures of cell shape by pixel loss at the edge.

Extraction of sickling profiles from sequences of images.

The basic image-analysis procedure, when applied to a series of images measured on a single well, identifies a set of cells from the first image in the series and attempts to track them throughout the series. For those cells which are successfully tracked in this way, the net result is a frame-by-frame compilation of the set of contiguous pixels, including position and intensity, belonging to each cell. From these pixel sets a variety of geometric quantities may be computed, which together provide a thorough description of the evolution of the position and shape of the cell with time; these quantities include projected area (number of pixels), various population and geometric moments, and estimates of the density contrast between peripheral and central pixels.

Among these geometric properties of individual cells, several have been shown to be useful, taken together or separately, as indicators of cell morphology. For example, the dimensionless ratio of the square of the perimeter of the cell to the projected area of the cell (i.e., the number of pixels) is a direct measure of the complexity of the cell outline, and values of this quantity greater than some threshold may in many cases be interpreted as a signature of a sickled shape. Another example is the eccentricity of the equivalent ellipse of the cell’s shape, computed from the spatial distribution of pixels intensities; this is a measure of the elongation of the cell, and values above a certain threshold may again be considered diagnostic of a sickled shape. The difficulty in using these geometric properties in morphological analysis is that there is no universally applicable choice of the best property or set of properties to use. Moreover, even with a specific set of quantities, the choice of appropriate thresholds to apply to these quantities may differ depending on the type of system being studied. For example, different types of cell preparations may exhibit very different morphological changes upon sickling, calling for different combinations and/or thresholds of geometric properties for accurate identification.

One method of assembling a sickling profile which avoids some of these problems uses frame-by-frame geometric information about each cell to detect possible abrupt changes (relative to the time scale of the experiment) in certain key quantities, of sufficient magnitude and in an appropriate direction to represent a potential signature of a sickling event. The appearance of coincident transitions in two or more of these quantities for a single cell is taken to be a definitive signature of a sickling event for that cell, and a single-cell temporal likelihood profile for the event is generated from the temporal profiles of the transitions in the individual quantities. The sickling time for a single cell is estimated from the midpoint of this composite profile, and a full sickling temporal profile for the entire cell population is computed by summing the profiles of the individual cells.

This event-based approach to creating a sickling profile from a series of images has proved to be quite useful and robust in previous applications.⁵ As a complement to this method, and in some cases to avoid certain of its shortcomings, we have also adopted an approach which solidifies the use of multiple geometric properties to perform morphological classification of cells, based on machine learning.^6,7 This method assembles for each cell a vector of geometric quantities which individually have some potential for discriminating between morphological classes, and processing these vectors using a support-vector machine (SVM)⁸ specifically trained on sets of images measured under similar conditions on similar cellular systems. The training procedure requires a human trainer to examine a series of reference images and visually classify cells in these images as either “normal” or “sickled”; the vectors of geometric quantities for all such cells, combined with their respective class assignments, constitute the training set for subsequent processing to create a SVM classification model. The interactive training procedure, as well as the creation of models based on the resulting training set, was performed using custom software, based on the LIBSVM library.⁹

In principle, the training procedure need only be performed once for a specific image type and cell preparation, with the goal of providing useful samples of the set of all possible morphologies, as characterized by the chosen vector of geometric properties, for the two distinct classes of cells under these conditions. The creation of SVM models from these samples allows for the generalization of the original visual classification procedure to apply to vectors of geometric quantities for cells not in the original training set. The details of this model-creation procedure are controlled by adjustable parameters,⁹ which need to be varied in order to create models which optimally define the boundaries which delimit the two classes in the complex multi-dimensional space of geometric properties. Such an optimal model, based on a single reference image set, may then be used to perform automatic classification of cell morphologies in other image sets.

In this study, a single training set was generated from a set of images for a single patient, and the resulting optimized SVM model was applied to sets of images, all distinct from the reference set, measured for each well of a 384-well sample for each of several patients. For a sequence of images from a given well, the model classification procedure was applied to all cells which could be tracked throughout the image sequence (see above) to produce a frame-by-frame count of normal and sickled cells, from which the sickling profile (fraction of cells sickled for each frame) for that well was computed.

Theoretical modeling of experimental fraction sickled vs. time

Because of structural constraints on the incorporation of HbS into polymer, the concentration of Hb which can remain in solution and thus not incorporate into polymer, referred to as the solubility, depends on the fraction of the available heme binding sites to which oxygen is actually bound, also known as the fractional saturation; the pathophysiology of the disease is intrinsically linked to this rapid decrease in solubility upon the release of oxygen to the cells in the microcirculation. Moreover, in mixtures of HbS with other Hb variants which do not incorporate into the polymer, the solubility is itself strongly dependent on the total Hb concentration. These properties of the solubility have been well characterized both experimentally and theoretically^1,10. In general terms, our approach to computationally predicting our experimental sickling fractions combines these insights with computational modeling of the temporal evolution of the fractional saturation of the cellular HbS with oxygen under our experimental conditions.

The experimental results reported here are from samples provided by sickle-trait (AS) donors—i.e., individuals heterozygous for the mutation, with gene copies for the production of both normal (HbA) and mutated (HbS) hemoglobin. Therefore, these samples contain a mixture of HbA and HbS, in addition to possible other Hb variants. The resulting dilution of the HbS variant compared to concentrations found in homozygous (SS) patients results in a much higher solubility for a given total Hb concentration, which dramatically slows the polymerization process and produces sickling times easily accessible to the passive-desaturation technique described here. This sensitivity of polymerization delay times to the actual concentration of HbS in the cells makes the relative concentrations of HbS and other non-polymerizing variants an important input to the calculations. The overall goal of the calculation is to produce, for a population of cells which is large in a statistical sense, an estimated temporal dependence of the fraction of sickled cells—or equivalently, the time-dependent survival probability for unsickled cells. This requires some operational definition of the characteristic time required for a sickling “event”, which is typically taken to be the delay time between the onset of polymerizing conditions (e.g., deoxygenation of the sample) and the onset of the formation of polymer. Under conditions being considered here, this delay time will generally be long compared to the additional time required for the autocatalytic polymerization process, once initiated, to pass a specified threshold of completion.^a Moreover, an important element of the procedure relies on an empirical relation which directly yields values for this delay time (see below).

For a given single value of the total Hb concentration, a specification of the relative concentrations of HbS and other variants, and a value of the fractional saturation, the procedure described here provides a single calculated solubility, leading to a single estimated delay time for polymerization. By design, our experiments induce a fractional saturation—and therefore a solubility and delay time--which are themselves time-dependent, so the procedure also provides a method for distilling, from a continuously evolving saturation-dependent delay time, a single overall estimated delay time. The key elements of this procedure are now described.

The total Hb concentration.

It will be seen below that saturation-dependent delay times are very sensitive to the total Hb concentration. A collection of red blood cells exhibits a distribution of such concentrations. A prototype discrete distribution of cell population vs. Hb concentration was taken from Lew et al.¹¹ and approximated by a continuous Gaussian distribution; this made parametric adjustments in the distribution possible (e.g., shifts in the peak concentration), to determine the sensitivity of the final computed results to the properties of the distribution. The adjusted form of this distribution used in all calculations presented here is shown in Fig. 1.

Figure 1.

Distribution of total Hb concentrations used in the calculations. This is derived from a Gaussian fit to the data of Lew et al.¹¹, followed by an upward shift of the peak position by 3%.

Calculation of a time-dependent delay time.

We assume that a calculated fractional saturation as a function of time is provided; this calculation is described in detail below. Section 1 of the Supplementary Information (SI-1) presents a detailed description of the calculation of the solubility c_s for a given fractional saturation. A value of this solubility less than the total Hb concentration is associated with polymer formation.

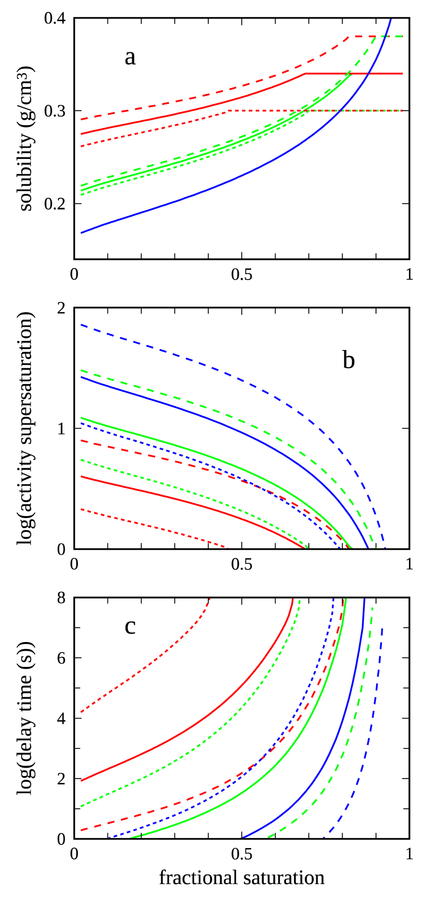
Fig. 2a shows a sample calculation of the dependence of the solubility on fractional saturation for two distinct HbS/HbA mixtures and several distinct total Hb concentrations, as well as a sample calculation of this dependence for pure HbS by direct application of eq. SI-1.1; all calculations use a simple representation of the binding curves of Hb in solution and in the polymer. Unlike for pure HbS, the solubility of the HbS/HbA mixtures depends also on the total Hb concentration, with this dependence diminishing as the fraction of HbS in the mixture approaches 1.

Figure 2.

Computed dependence of solubility and derived quantities on the fractional saturation with oxygen. In all panels, color indicates the assumed HbS/HbA mixture: our standard 38%HbS/62%HbA mixture (red), a hypothetical 70%HbS/30%HbA mixture (green), and 100%HbS (blue). Line type indicates the total Hb concentration: 0.34 g/cm³, which is near the peak of our standard concentration distribution shown in Fig. 1 (solid), 0.30 g/cm³ (short dashed), and 0.38 g/cm³ (long dashed). The latter two concentration are ~1.5σ from the peak of the concentration distribution shown in Fig. 1. a) Solubility, computed as described in SI-1. In our computational method, the solubility for the mixtures by definition can not exceed the total Hb concentration. The solubility for pure HbS (blue curve) is independent of the total Hb concentration. b) Activity supersaturation, computed as described in the text. c) Delay time, computed using the empirical relation between delay time and activity supersaturation described by (1).

The rate of polymer formation depends on the amount by which the total concentration exceeds the solubility. If c₀ is the total Hb concentration, one measure of this excess is the simple ratio of the two concentrations, the so-called supersaturation, given by c₀/c_s. Given the highly non-ideal conditions in the intracellular milieu, it is perhaps not surprising that a more useful measure of the excess is the ratio of the activities rather than the concentrations, the so-called activity supersaturation, given by S=(γ₀c₀)/(γ_sc_s) .Here the γ quantities are the activity coefficients at the respective concentrations, which are themselves concentration-dependent; the form taken by these quantities is described in detail in SI-1. Fig. 2b shows the dependence of the activity supersaturation on the fractional saturation for the same sets of conditions as for Fig. 2a. In this case, the activity supersaturation of pure HbS, as well as that of the mixtures, is strongly dependent on the total Hb concentration for a fixed fractional saturation. For a given total Hb concentration and fraction HbS, decreasing the fractional saturation to the point where the solubility falls below the total concentration, with the activity supersaturation therefore becoming greater than 1, leads to the onset of polymerization; the rate of polymer formation, reflected in the delay time, and the extent of polymer formation are sensitive functions of the activity supersaturation beyond this point.

The final step of computing a time-dependent delay time τ(t) makes use of a striking approximate empirical relation between the activity supersaturation and the polymerization delay time, described by Cellmer et al.⁴. We adopt a simple functional form expressing this relation

$$\begin{array}{c}\log \left(\text{τ}\right)=f\left(\log \left(S\right)\right)\text{}\\ f\left(x\right)=\frac{\exp \left(-67.9x\right)}{x}+11.2\exp \left(-1.49x\right)-2.64\end{array}$$ (1)

while acknowledging its approximate nature by allowing possible ranges of acceptable delay times bracketing this computed value. Fig 2c shows the dependence of the time-dependent delay time on the fractional saturation for the same sets of conditions as for Figs. 2a-b. As the fractional saturation decreases below that for which the activity supersaturation begins to exceed 1, a further decrease in saturation is required, the size of which depends on the specific conditions, before the delay time becomes small enough to become relevant on the time scale of our experiments.

To summarize, for a specified total Hb concentration c₀ and mixture of HbS with other Hb variants, a time-dependent delay time τ(t) is calculated from a fractional saturation by computing a solubility c_s and corresponding activity supersaturation S using the methods detailed in SI-1, and using (1) to compute a delay time from S.

Calculation of a single overall delay time from a time-dependent delay time.

The overall delay time τ_d is that time which satisfies the equation

$${\displaystyle \underset{0}{\overset{{\text{τ}}_d}{\int }}\frac{dt}{\text{τ}\left(t\right)}}=1$$ (2)

A derivation of this is given by Cellmer, et al. (in preparation). The solution of (2) requires that the time-dependent delay time in the denominator be computable for any value of the time t; this may be accomplished by either a complete calculation “on demand”, incorporating all the steps described above, or by interpolation on a set of values pre-computed at a discrete set of times.

Calculation of the final fraction sickled vs. time.

Fig. 2 and the calculations summarized in (1) and (2) indicate that the computed overall delay time should be very sensitive to the total Hb concentration. We have adopted the probability distribution of total Hb concentrations shown in Fig. 1 for all calculations reported here. With the availability of such a distribution, two distinct approaches to computing the final sickling profile are possible. One method is to step through the probability distribution at discrete intervals in the concentration and use the above procedure to compile a set of probability-weighted (concentration,delay time) pairs. An alternative “Monte Carlo” method generates a series of random concentration values from the distribution, which may be viewed as creating a finite random sample of red blood cells with a distribution of Hb concentrations approximating the original distribution, and performs an independent delay-time calculation for each concentration sample.

The net result of both approaches is a probability distribution of overall sickling delay times, which is then used to compute an approximate cumulative survival probability (fraction remaining unsickled) as a function of time, the desired result.

Theoretical calculation of fractional saturation vs. time

Prior to the beginning of the experiment, the solvent in each well is equilibrated with atmospheric oxygen; the fractional saturation of the Hb in the red blood cells at the bottom of the well is assumed to be that determined by equilibrium binding at that oxygen concentration. Upon replacement of the atmosphere above the well with pure nitrogen, the oxygen in solution begins to diffuse away through the upper solvent-atmosphere interface. The resulting progressive depletion of oxygen in the well propagates with time downward from the interface to the bottom of the well and continues with the oxygen concentration at all positions within the well approaching zero. During the course of this depletion, the fractional saturation of Hb in the red blood cells responds to the current oxygen concentration at the bottom of the well, and this desaturation drives the eventual polymerization of the Hb in each cell.

For simplicity, we separate the calculation of the fractional saturation vs. time of Hb in red blood cells into two independent steps: the calculation of the time-dependent oxygen concentration at the bottom of the well, and the determination of the fractional saturation from this concentration using equilibrium binding properties of Hb. The former is more demanding, requiring a theoretical analysis of diffusion within the well; the latter requires a model description of the oxygen binding curve of Hb in the cells.

The temporal evolution of the oxygen concentration $\varphi \left(\overrightarrow{\mathit{\text{r}}},t\right)$ at various positions within the solvent in the well is governed by the diffusion equation

$$D{\nabla }^2\varphi =\frac{\partial \varphi }{\partial t}$$ (3)

which has been written to reflect the assumption that the diffusion coefficient D is independent of position. The application of this equation to the current problem, and possible methods of solution, are treated in more detail in section 2 of the Supplementary Information (SI-2). In order to proceed with such an analysis, it is necessary to specify the region over which the equation is to be solved, as well as boundary conditions which the resulting solution must satisfy on this region.

The geometry of the solution region.

As discussed in SI-2, methods available to solve the diffusion equation depend on the region over which the equation is defined. For an idealized geometry which only approximates the true region, analytical methods of solution are possible. For the realistic region prescribed by the true shape of the well and the expected shape of the solvent-atmosphere interface, only numerical methods of solution are possible; these methods are orders-of-magnitude more computationally demanding than the analytical methods.

From the manufacturer’s data sheet, a single well in a 384-well plate is only approximately cylindrical, with a height of 1.156 cm, a radius at the bottom of 0.141 cm, and a radius at the top of 0.1815 cm. Moreover, because the solvent medium forms a meniscus with the outer walls of the well, the actual interface between solvent and the atmosphere is distinctly non-planar. The shape of this meniscus was estimated by taking a series of microscope images of a pure dye solution with a known absorption spectrum at various positions within a well, and computing position-dependent solution depths from the overall transmitted intensities of these images. These measurements indicate that the effect of the meniscus is such that the depth of the solution at the outer edge of the well is approximately 20% greater than the depth at the center. For a given solution volume, corresponding to the actual pipetted volume for a given experiment, the documented geometry of the well and a simple functional form for the deduced shape of the meniscus were sufficient to define the simulation region used for the numerical simulations.

The assumed idealized approximate geometry for a well, which lends itself to analytical solution of the diffusion equation, is a perfect cylinder, with a planar interface between the solvent and the surrounding atmosphere. For the purpose of computing an analytical solution to directly compare with numerical calculations, an “equivalent cylinder” was constructed with a fixed radius given by the average radius of, and the same volume as, the solution region used for the numerical simulation; the height of the cylinder computed from these assumed properties was taken as the height of the cylindrical diffusion region in the analytical calculations. In addition, a “minimal cylinder” was constructed with the same radius as the equivalent cylinder, but with height given by the minimum depth (i.e., at the center of the well) of the meniscus in the numerical solution region, effectively flattening the meniscus; the volume of this cylinder is necessarily less than that of the other two solution regions.

Boundary conditions on the solution.

Because the walls of a well are assumed to be impermeable to oxygen, a zero-flux boundary condition is prescribed for the bottom and sides of the near-cylindrical solution region; this takes the form of a requirement that the component of the gradient of the solution normal to the boundary is zero. The more interesting boundary condition is that applicable to the solvent/atmosphere interface. As discussed in SI-2, there are two basic classes of boundary conditions, consistent with a zero oxygen concentration outside the region, which are accessible to both analytical and numerical solution in this case. The first of these is the simple requirement that the value of the solution be everywhere zero at the solvent-atmosphere interface. This creates a very strong sink for (or equivalently, an infinitely permeable barrier to) oxygen at the interface, which is reflected in very abrupt depletion of oxygen, and accompanying abrupt desaturation of red blood cells, at the bottom of the well. The predicted speed of desaturation in this case is inconsistent with the much more gradual desaturations observed by monitoring the optical densities of desaturating samples of normal blood in the same experimental geometries.

An alternative boundary condition which provides some control over the “permeability” of the solvent-atmosphere interface to oxygen is a so-called mixed boundary condition coupling the normal component of the gradient of the solution to the solution value at the boundary. A computationally tractable form of this condition is the simple linear form

$$n\cdot \nabla \varphi =c\varphi$$ (4)

where the gradient and the value of the solution ϕ are evaluated on the boundary, and n is the local normal to the boundary; in the case of the ideal cylindrical geometry this assumes the form in eq SI-2.7. The constant c < 0 provides control over the effective permeability of the interface; as c →0 eq (4) becomes a zero-flux condition, and as c → −∞ the behavior of the solution approaches that of the zero-value condition considered above.

The parameter c is related to the diffusive mass transfer coefficient for oxygen across the solvent-atmosphere boundary, and has the dimensions of 1/distance. The best guidance regarding the order of magnitude of this parameter is provided by the mass transfer coefficient of oxygen across a water/air interface¹², determined to be D_s/l_s = 0.13 × 10⁻³ cm/s at 20 °C; here D_s is a diffusion constant, and l_s is related to a “surface layer” thickness. Using simple dimensional considerations, we adopt the approximate diffusion coefficient of oxygen through water at 20 °C (1.8 × 10⁻⁵ cm²/s) to arrive at a value of c (≈ l_s⁻¹) of about 7 cm⁻¹. As a characteristic of a clean interface between pure water and air, this value should be considered an upper bound for values appropriate for “dirtier” interfaces, such as those likely to be present in our experiments. For example, the same authors¹² cite from various sources diffusion conductivity values for wastewater surface layers consistent with values of c from 3- to 6-fold smaller than the clean-interface value cited above.

Methods of solution of the diffusion equation.

Methods applicable to the solution of the diffusion equation are developed in some detail in SI-2. In all calculations the initial (t=0) oxygen concentration was uniform throughout the solution region, with a value of 1; the linearity of the equations allows for the generation of actual oxygen concentrations (partial pressures) by simply multiplying the resulting solution by the atmospheric partial pressure of oxygen in the required units.

With this simple initial condition, the analytic solution (SI-2.27) takes the form

$$\varphi \left(z,t\right)={\displaystyle \sum _{i=0}^n{c}_i\cos \left({\text{μ}}_{\text{i}}z\right)\exp \left(-D{\text{μ}}_{\text{i}}^{2}t\right)}$$ (5)

where

$$c_i=\frac{{\displaystyle \underset{0}{\overset{L}{\int }}\cos \left({\text{μ}}_{\text{i}}z\right)dz}}{{\displaystyle \underset{0}{\overset{L}{\int }}{\cos }^2\left({\text{μ}}_{\text{i}}z\right)dz}}=\frac{2\sin \left({\text{μ}}_{\text{i}}L\right)}{{\text{μ}}_{\text{i}}L+\frac{1}{2}\sin \left({\text{2μ}}_{\text{i}}L\right)}$$ (6)

The eigenvalues μ_i are determined by the choice of boundary condition at the solvent-atmosphere interface. In practice, a minimum of n = 100 terms are included in the evaluation of (5); this truncation adequately reproduces the t = 0 value and incurs rapidly decaying errors for t>0 because of the exponential factors.

For the finite-element method used for the numerical solution, custom software was created based on the deal-II finite-element library¹³. In formulating the problem, a minimum of 30,000 degree-1 elements (piece-wise linear functions with local support) were used as basis functions covering the solution region. Time-dependent solutions were obtained using a step-wise second-order-accurate scheme, with a time step of 0.02 s. The stability and acceptable accuracy of the calculation with this choice of mesh refinement and time step were checked by performing a similar numerical calculation on an equivalent idealized cylindrical geometry, for which an analytical solution is available, and comparing the results of the numerical and analytical solutions.

Unless otherwise noted, for all analytical and numerical solutions computed, the diffusion constant D was taken to be that of oxygen through water at 37 °C (=2.6 × 10⁻⁵ cm²/s), from the documented temperature dependence of this quantity.¹⁴

Calculation of fractional saturations from predicted oxygen concentrations.

As noted above, we compute the fractional saturation with oxygen as a function of time by applying equilibrium models for the cooperative binding of oxygen to Hb directly to the time-dependent oxygen concentrations. Several parametric descriptions of the saturation y as a function of the oxygen partial pressure p are available. The simplest is a two-parameter empirical description of the form

$$y\left(p\right)=\frac{{\left(p/p_{50}\right)}^n}{1+{\left(p/p_{50}\right)}^n}$$ (7)

where p₅₀ is the pressure corresponding to 50% saturation, and n is the Hill constant (0 < n < 4 for tetrameric Hb).

Other prescriptions for the oxygen binding curve are provided by mechanistic models which have been proposed to explain the functionally important cooperative binding of oxygen by Hb. The classic allosteric model of Monod, Wyman and Changeux (MWC)¹⁵ explains the oxygen binding in terms of a progressive shift with increasing saturation by oxygen in the equilibrium between two quaternary states (T and R) which have different binding affinities for oxygen, with the low-affinity T state favored at low saturations and the high-affinity R state favored at high saturations. The partition function for this model is completely described by three parameters, which generally depend on temperature and solution conditions: the equilibrium constant L between the T and R states at zero saturation and the binding affinities K_R and K_T of the R and T states, respectively, for oxygen. In terms of these parameters, the binding curve for oxygen assumes the form

$$y\left(p\right)=\frac{L{K}_{\text{T}}p{\left(1+K_{\text{T}}p\right)}^3+K_{\text{R}}p{\left(1+K_{\text{R}}p\right)}^3}{L{\left(1+K_{\text{T}}p\right)}^4+{\left(1+K_{\text{R}}p\right)}^4}$$ (8)

Finally, the Tertiary Two-State (TTS) model^16,17 describes the binding properties in terms of binding affinities of two tertiary structural states (r and t) of the four subunits in the Hb tetramer. The relative stabilities of these tertiary states differ between the two quaternary structures and whether or not oxygen is bound, with the low-affinity t state favored by low saturations and the T quaternary structure, and the high-affinity r state favored by high saturations and the R quaternary structure; the configuration of subunit tertiary states in the tetramer determines the relative stabilities of the two quaternary structures. The model defines five parameters: the equilibrium constant L between the T quaternary structure with four unliganded t subunits and the R quaternary structure with four unliganded r subunits, equilibrium constants l_R and l_T between unliganded t and unliganded r subunits in the R and T quaternary structures, respectively, and affinities K_r and K_t for the binding of oxygen to subunits in the r and t tertiary states, respectively. The TTS partition function as a function of the oxygen partial pressure in terms of these parameters is

$$\Xi \left(p\right)=\frac{L}{l_T^4}{\left(1+K_{r}p+l_T\left(1+K_{t}p\right)\right)}^4+{\left(1+K_{r}p+l_R\left(1+K_{t}p\right)\right)}^4$$ (9)

from which a binding curve may be derived.

The sensitivity of the calculation to the fractional saturation, illustrated in Fig. 2, argues against the use of a simplified description of the binding curve (e.g., (eq 7)); a model-based description of the binding curve, such as those in (8) and (9), is more likely to accurately reproduce the actual saturations over a wider pressure range. We have therefore analyzed oxygen-binding curves of diluted samples of normal human blood measured on a clinical instrument at 37 °C under the same solvent conditions as in our well-plate experiments, using the MWC prescription (8); implicit in the use of these curves is the well-founded assumption that the oxygen-binding curves for HbA and HbS are essentially indistinguishable for our purposes. The best estimates we have derived from these curves for the MWC parameters are L = 4.3 × 10⁵, K_R = 1.042 torr⁻¹ and K_T = 0.0093 torr⁻¹. This parametrization of the MWC partition function is used as the basis for all desaturation and solubility calculations required by the simulated sickling profiles reported here.

Results and Discussion

Sources of uncertainty in the simulation procedure.

In using the methods developed here to attempt to reproduce experimentally measured time-dependent sickling profiles, there are a number of possible distinct and unrelated sources of uncertainty in the computed results. These arise both from assumptions intrinsic to the calculation of solubilities and delay times from fractional saturations, and from the method for computing time-dependent fractional saturations in our experimental geometry.

The copolymerization model for computing the solubility (SI-1) of mixtures of HbS with HbA and other possible Hb variants assumes a best estimate of 0.4 for the overall probability of incorporation of hybrid tetramers α₂β^Aβ^S into the polymer, based on measured solubilities of mixtures.¹ For mixtures being considered here, in which HbA is present in large proportions, the computed solubilities, and therefore delay times, are demonstrably sensitive to the value of this probability. In the interest of simplifying our analysis, we use the above estimate for all calculations; small variations in this parameter might be appropriate in the event that other sources of uncertainty, discussed below, become sufficiently small.

The calculation of time-dependent delay times relies on the empirical relation between activity supersaturations and delay times⁴ represented by (1). In addition to the approximate nature of the fit underlying this representation, it should be noted that this relation is determined from a large set of experimental measurements on macroscopic samples of HbS; it is not clear a priori what, if any, adjustments to the relation would be necessary for it to be applicable to polymer formation in individual red blood cells. In light of these unknowns, we have introduced an “uncertainty” in the relation, in the form of a range of possible scale factors to be applied to the delay times computed using (1), when computing sickling profiles to be compared with experimental measurements.

For the purpose of simulating the time-dependent oxygen concentration at the bottom of the well, we adopt the natural choice of a diffusional modeling framework, where we assume a position- and time-independent diffusion coefficient D. Moreover, based on the unavailability or inadequacy of alternative assumptions, we assume a mixed boundary condition of the form (4) at the solvent-atmosphere interface. Because of uncertainties in the properties of this interface in our experimental samples, we regard the permeability parameter c in this boundary condition as broadly delimited by estimates for a pure water-air interface,¹² but otherwise adjustable within perhaps an order of magnitude of these limits.

There is no information to motivate an assumed value of D other than the known diffusion coefficient of oxygen in pure water at 37 °C; the medium through which the oxygen diffuses in the well is a highly diluted blood sample, so departures from these ideal conditions should be relatively small. However, it should also be noted that even small changes in this constant can have significant effects on the evolution of the fractional saturation, and therefore the computed sickling profiles. This is demonstrated in Fig. 3a, in which the value of D is scaled by varying amounts, with all other aspects of the calculation kept fixed. However, it is interesting to note (Fig. 3b) that scaling D downward by some factor and simultaneously scaling c upward by the same factor dramatically suppresses the differences between computed profiles. This simultaneous adjustment with little ultimate effect would introduce ambiguity into the process of trying to determine values of the two parameters separately; however, we wish to determine the validity of our computational approach by only explicitly varying c, so a positive result--i.e., a value of c which leads to computed sickling profiles comparable to measured profiles—could be viewed as incorporating (assumed minor) adjustments in D as well.

Figure 3.

Sensitivity of computed sickling profiles to the value of the diffusion coefficient D. In both panels, the red curves are for the unscaled value of D at 37 °C (=2.6 × 10⁻⁵ cm²/s), blue curves result from scaling this value by 0.8, and green curves from scaling by 0.5. a) For all curves, the value of c, the permeability parameter for the solvent-atmosphere interface in eq. (4), is set to −1.5. b) The value of c for each curve is adjusted so that the product Dc is a constant: c = −1.5 (red), c = −1.875 (blue), c = −3 (green), demonstrating that variations in D may be largely offset by compensating adjustments in c to yield very similar sickling profiles.

Comparison of analytical and numerical solution methods.

Within this modeling framework, the principal remaining uncertainty lies in possible consequences of different choices of solution method, either a numerical method applied to the actual geometry of the well or an analytical method applied to idealized approximations of that geometry. As discussed in Methods, the true geometry of the solvent in the well, with departures from ideal cylindrical well geometry and a non-planar solvent-atmosphere interface, lends itself only to numerical methods for solving the diffusion equation. For a given true solvent region, an “equivalent cylinder” (volume-matched with the numerical solution region) and a “minimal cylinder” (height-matched with the minimum depth of the numerical solution region) may be constructed which attempt to mimic the true region, and to which analytical methods of solution are applicable. The results from either the numerical or the analytical solution method may be used for the calculation of theoretical sickling profiles. The analytical solution is computationally efficient, and computed oxygen concentrations at the bottom of the well may be incorporated directly into the framework for computing time-dependent delay times. On the other hand, a single instance of a numerical solution requires many hours to compute, so it is necessary to save the resulting oxygen concentrations at a discrete set of times and compute the time-dependent oxygen concentrations required by the delay-time calculation by interpolating on this discrete set of values.

While incorporation of the results of either solution method into the overall calculation is possible, it is instructive to inquire whether the differences between the results are sufficiently large to warrant giving special consideration to the computationally burdensome numerical results. In Fig. 4a we show a comparison between results for the oxygen concentration at the bottom of the well computed numerically for specific solvent regions and analytically for the corresponding equivalent and minimal cylinders. Overall, the results are quite similar, with the decays of the oxygen concentration in the three cases exhibiting a clear hierarchy: The decay of the numerical solution for the realistic region is systematically faster than that for the equivalent cylinder, and systematically slower than that for the minimal cylinder. This may be attributed to the high sensitivity of the depletion rate to the liquid depths encountered in a region. The minimum depth of the true meniscus, and therefore also the depths over a significant central portion of the true region, are necessarily somewhat less than the single height assigned to the equivalent cylinder; the enhanced depletion rate through these lower depths leads, in balance, to a slightly faster overall depletion rate. By the same reasoning, the fact that the height of the minimal cylinder is everywhere less than or equal to the depth of the surface of the realistic region (with equality only at the center of the cylinder) results in a higher overall depletion rate for the minimal cylinder than for the true solution region.

Figure 4.

Comparison of calculations based on numerical and analytical solutions of the diffusion equation. In both panels, all curves of a single color correspond to a specific choice of a realistic geometry and associated idealized geometries (see text), combined with a specific choice of diffusional parameters. For each color the solutions are identified by line type: numerical solution on a realistic geometry (solid), analytical solution on the corresponding equivalent cylinder (short dashed) and analytical solution on the corresponding minimal cylinder (long dashed). Red curves refer to a realistic region with volume 10 μl and a permeability parameter c of the solvent/atmosphere interface of −5 (cf. Eq 4), green curves refer to a realistic region with volume 10 μl and c = −2, and blue curves refer to a realistic region with volume 14 μl and c = −5. Realistic regions with volume 10 μl have a minimum well depth (depth at the center of the meniscus, and also the height of the minimal cylinder) of 0.140 cm, and a height of the equivalent cylinder of 0.155 cm. Realistic regions with volume 14 μl have a minimum well depth of 0.192 cm, and a height of the equivalent cylinder of 0.214 cm. a) Oxygen partial pressure at the bottom of the well vs. time. b) Fraction sickled vs. time, computed as described in Methods. As discussed in the text, the numerical solutions for realistic geometries are incorporated into the calculations by interpolating on pre-computed values saved at discrete time intervals; the relative lack of smoothness of the corresponding (solid) curves arises from potential instabilities in the solution of eq. (2) arising from this interpolation process.

For our purposes, the significance of these small observed differences in the oxygen-depletion curves computed for the realistic and idealized geometries depends on their effect on the predicted sickling profiles. Fig 4b shows an example comparison of the profiles computed from the oxygen-depletion curves for all three geometries under otherwise identical assumptions. The first thing to note is the distinct lack of smoothness in certain profiles computed from the numerical solution. This arises from the need to compute oxygen concentrations at the bottom of the well by interpolating on a set of tabulated values output by the solution procedure for a discrete set of times; when the solution of (2) requires values at times outside the range of this discrete set, the results become unstable. Taking into account this deficiency of using numerical solutions, the small differences in the rate of oxygen depletion in all cases would be expected to lead to sickling profiles which are themselves quite similar.

Based on these observations, combined with the much greater speed of the analytical solution method and the unconditional stability of the resulting simulated sickling profiles, we have chosen to conduct all subsequent calculations of sickling profiles using analytical solutions computed for the equivalent cylinder. The differences between these results and those which would be obtained from calculations on the realistic region are small and consistent with a small systematic upward correction of sickling rates computed from the analytical solution.

Sensitivity of results to other assumptions.

As described in Methods, we have adopted a single fixed distribution of total Hb concentrations, as well as a single fixed description of the oxygen binding curve, for our calculations. Computed sickling profiles will certainly be sensitive to both of these properties, and there is no a priori reason to assume that they will be identical for all patients. However, it is difficult to characterize typical deviations from these assumed properties, and in attempting to compare measured and computed sickling profiles we prefer to vary as few adjustable features of the calculations as possible, at least initially.

For illustrative purposes, we consider one experimental property required for the calculation which may in principle vary between patients. This property is the precise mixture of HbS with other Hb variants, which directly affects the calculation of solubility vs. fractional saturation described in SI-1. A choice of mixture which closely approximates that actually determined for the patients in this study is 38% HbS/62% HbA, which we have adopted as our standard assumption for all calculations here. The principal deviation seen from this is some small amount of an additional variant, HbA₂, substituted for the same amount of either HbS or HbA; the behavior of this variant with respect to incorporation into the polymer is discussed in SI-1. We present in Fig. 5 a comparison of simulated sickling profiles with and without substitution by HbA₂. The effect relative to the standard mixture (red curve) from substitution of 4% HbS by HbA₂ (blue curve) is the largest, because of the effective removal of some portion of the species (HbS) with the highest polymerization probability; the smaller effect arising from substitution of HbA by HbA₂ (green curve) is due to the relatively innocuous replacement of a species (HbA) which may only copolymerize at a reduced probability via hybridization with HbS by a species (HbA₂) whose hybrids with HbS are assumed to have zero probability of copolymerization.

Figure 5.

Effect of the mixture of Hb variants on simulated sickling profiles. Desaturation profiles are computed in all cases using a value of the solvent-atmosphere permeability parameter c of −1.5. The red curve is for a mixture of 38% HbS/62% HbA, the green curve for a mixture of 38% HbS/58% HbA/4%HbA₂, and the blue curve for a mixture of 34% HbS/62% HbA/4% HbA₂.

Comparison between computed and experimental sickling profiles.

Of the available data sets measured on different patients over a period of several days, two were chosen for subsequent analysis; data sets were rejected based on artifactual distortions of the sickling profiles (due to fluctuations in the instrumental focus) and/or large inconsistencies in the sickling profiles measured for different wells, likely due to deficiencies in the image quality for those measurements. The two chosen data sets reflect the typical patient-to-patient variability in sickling profiles measured under comparable conditions using our passive-desaturation protocol. The measured profiles most likely incorporate some small systematic error in sickling yields due to the limitations of the machine-learning analysis; one indication of these errors is the small non-zero fractions sickled evident at even the shortest times.

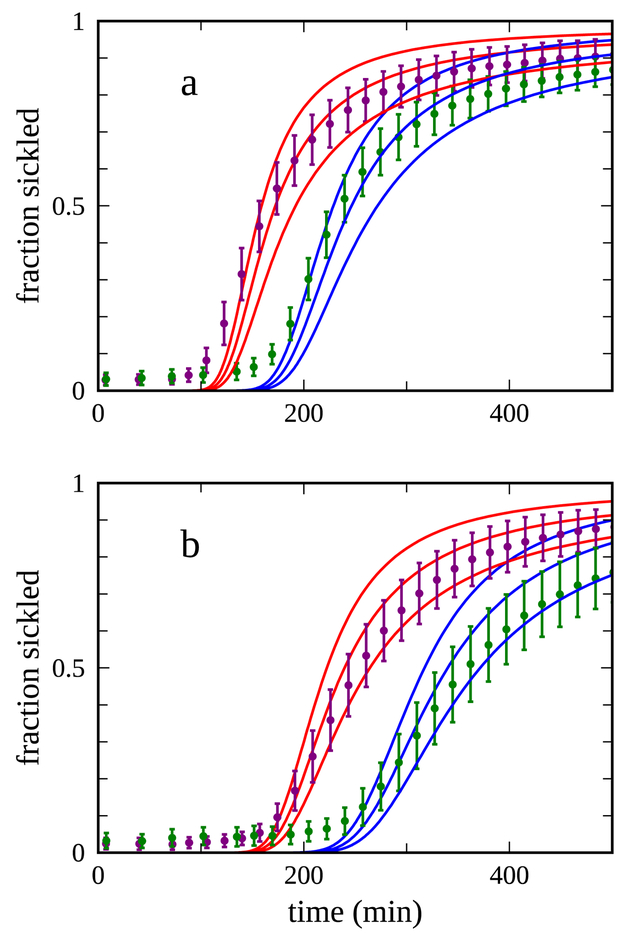
These data sets incorporate measurements at several sample volumes, ranging from 10 μl to 14 μl, and the appropriate comparison is between experimental profiles measured at a single volume and simulations performed assuming the same volume. As a first attempt to address the differences between the two data sets, we performed two distinct sets of simulations of the sickling profile in which the only difference was the assumed value of the permeability parameter c for the solvent/atmosphere interface ((eq 4)) in the analytical solution of the diffusion equation. The two distinct values of this parameter were varied by trial-and-error until the envelopes of profiles computed for the two values—with an “envelope” defined by allowing reasonable deviations from the empirical relation (1)--reproduced the experimental profiles acceptably well for the 10 μl sample volumes. The results of this comparison are shown in Fig. 6a. As a follow-up to bracket the experimental sample volumes, a comparison was made between the experimental profiles for the 14 μl sample volumes and a set of simulated profiles computed for this volume, using the same two values of the parameter c. The results of this comparison are shown in Fig. 6b.

Figure 6.

Comparison between experimental and computed sickling profiles. In each panel, the sets of points and error bars colored purple and green represent experimentally determined fractions from data sets measured on samples from two different donors. The two panels show comparisons between data and simulations for two distinct sample volumes a) 10 μl and b) 14 μl. The simulated results appear in each panel as triples of like-colored continuous curves, with each triple displaying results for the volume in that panel, derived from the analytical solution of the diffusion equation for the oxygen concentration at the bottom of the well using the equivalent cylinder corresponding to that volume. The colors of the continuous curves represent results assuming a value of the permeability parameter c for the solvent-atmosphere interface (see text and eq. 4) of −1.6 (red) and −1.05 (blue). Each triple represents three calculations which are identical except for an overall scale factor applied to every time-dependent delay time computed using the parametrized empirical relation (2); these scale factors are intended to represent the inexact nature of this relation as reflected in the analysis by Cellmer et al. ⁴. The middle curve in each triple is unscaled, and the upper and lower curves are computed using delay times scaled by factors of 1/3 and 3, respectively. The experimental fractions sickled for each patient and for each volume are distilled from the time-dependent sickling profiles determined from 128 wells, weighted by the number of cells in each well. Each set of well profiles is “sigma-trimmed” to remove outliers, by computing the weighted mean and standard deviation of each profile frame-by-frame and culling any well profile whose value at any frame deviates from the average value at that frame by more than three times the standard deviation. The weighted mean and standard deviation of the remaining profiles are recomputed, and the culling process repeated. Out of the 128 wells at the start of this procedure, the number of wells remaining after two cycles of culling were a) 99 (purple) and 105 (green), and b) 105 (purple) and 103 (green). The weighted means and standard deviations of the sickling profiles from these surviving wells, computed frame-by-frame, are plotted as the points and error bars for each frame. Times assigned to each frame are the simple mean of the experimental times assigned to that frame for all the surviving wells, where the experimental time is computed relative to the measurement time of the first frame of the first well scanned. The average time assigned to each plotted data point represents a distribution of measurement times for individual wells with a typical standard deviation of ~5 min.

It is evident that the same two values of c result in computed profiles which reproduce the measured profiles acceptably well at two different sample volumes. On the whole, the computed profiles for the 14 μl sample volume slightly overestimate the yields of the measured profiles relative to the fidelity with which the 10 μl profiles are reproduced, but given the large number of experimental and computational uncertainties which factor into these comparisons, the results are encouraging.

The two values of c (−1.6 and −1.05) required to produce a consistent treatment of two data sets for two different sample volumes are sufficiently similar that it is tempting to accept these comparisons at face value and rationalize the different parameter values in terms of variations in solvent properties of the two samples. However, as was noted earlier, there are several other properties required by the calculation to which the results are clearly sensitive and which may also vary from patient to patient. Prominent among these properties are the distribution of total Hb concentrations, and the precise HbS/HbA mixture, in the red blood cells. Unfortunately, there is insufficient information of this sort available for these donors to incorporate the possible effects of differences in these properties directly into the calculations.

Nevertheless, it is straightforward to examine the plausibility of at least one alternative scenario, in which the value of c is in fact the same for the two samples, and the differences in characteristic time scales for the two measured sickling profiles arise from differences in the total Hb concentration between cells from the two patients. Fig. 7 shows the results of such an examination, in which a single intermediate value of c is assumed and the peak position of the analytical representation of the Hb concentration distribution, normally fixed at 3% greater than that of the original empirical distribution¹¹, is instead assigned values equal to, and 6% greater than, that of the original distribution. The 6% difference in mean Hb concentration between the two patients implied by this distinction, while not implausible, is somewhat larger than is seen when comparing information actually compiled for the patient cohort available to us.

Figure 7.

Similar to Fig. 6, except that a single value of c = −1.3 is assigned for both sets of calculations in each panel, and the two samples are distinguished by assigning to them different peak positions for the distribution of total Hb concentrations: 6% greater than that of the analytical form of the empirical distribution¹¹ (red), and equal to that of the empirical distribution (blue).

The comparison in this case does not appear to reproduce the experimental time courses quite as effectively as that in Fig. 6. However, it does serve to broadly frame the sensitivity of the calculations to plausible variations in the distribution of total Hb concentrations, with all other features being equal. Along with the demonstrated sensitivity of the calculation to small variations in HbS/HbA mixture (Fig. 5), this sensitivity underscores the desirability of precise characterization of the various properties of the system subject to patient-to-patient variation, as an adjunct to using this computational framework to make quantitative deductions.

Concluding Remarks

In this work we have demonstrated an elegant technique for tracking the temporal evolution of the sickling of red blood cells from sickle-cell anemia patients under controlled desaturating conditions, based on the automated analysis of sequences of microscope images and machine-learning analysis to characterize cell morphology. This technique begins to emulate in vitro the physiological processes underlying the pathology of the disease and provides a powerful laboratory for examining the effects of different chemical environments on these processes.

As an aid in understanding these experiments in more quantitative detail, we have developed a computational framework for simulating time-dependent sickling profiles, based on the extensive current theoretical and empirical understanding of the physical chemistry of the sickling process^1,4. A specific application of this core framework requires an appropriate description of the time dependence of the fractional saturation of hemoglobin with oxygen; we have provided such a description which requires solving the diffusion equation for oxygen in our experimental geometry. Our success in thereby reproducing the observed time scale for sickling in our experiments suggests that this core framework will also be applicable to other desaturation scenarios, such as those which underlie the actual pathology of the disease. In its present form, the framework should be applicable to any desaturation scenario for which a quantitative description is available, ranging from the slow desaturation accomplished in the present work to the essentially instantaneous desaturation accomplished in the laser-photolysis method.⁵ Moreover, the framework relies in a fundamental way on a calculation of solubility as a function of fractional saturation, so should be applicable both to pure HbS (based on the solution of SI-1.1) and mixtures of HbS with other Hb variants (using methods described in SI-1). Therefore, the application of the framework to the physiological problem further requires only an estimate of the time-dependent saturations of red blood cells during unloading of oxygen to the tissues, for which definitive information is still not available.