Abstract
We develop a robust coarse-grained model for single- and double-stranded DNA by representing each nucleotide by three interaction sites (TIS) located at the centers of mass of sugar, phosphate, and base. The resulting TIS model includes base-stacking, hydrogen bond, and electro-static interactions as well as bond-stretching and bond angle potentials that account for the polymeric nature of DNA. The choices of force constants for stretching and the bending potentials were guided by a Boltzmann inversion procedure using a large representative set of DNA structures extracted from the Protein Data Bank. Some of the parameters in the stacking interactions were calculated using a learning procedure, which ensured that the experimentally measured melting temperatures of dimers are faithfully reproduced. Without any further adjustments, the calculations based on the TIS model reproduce the experimentally measured salt and sequence-dependence of the size of single-stranded DNA (ssDNA), as well as the persistence lengths of poly(dA) and poly(dT) chains. Interestingly, upon application of mechanical force, the extension of poly(dA) exhibits a plateau, which we trace to the formation of stacked helical domains. In contrast, the force–extension curve (FEC) of poly(dT) is entropic in origin and could be described by a standard polymer model. We also show that the persistence length of double-stranded DNA, formed from two complementary ssDNAs, is consistent with the prediction based on the worm-like chain. The persistence length, which decreases with increasing salt concentration, is in accord with the Odijk-Skolnick-Fixman theory intended for stiff polyelectrolyte chains near the rod limit. Our model predicts the melting temperatures of DNA hairpins with excellent accuracy, and we are able to recover the experimentally known sequence-specific trends. The range of applications, which did not require adjusting any parameter after the initial construction based solely on PDB structures and melting profiles of dimers, attests to the transferability and robustness of the TIS model for ssDNA and dsDNA.
Graphical Abstract

INTRODUCTION
DNA, the blueprint of life, accomplishes its functional roles through highly orchestrated motions, spanning a hierarchy of time and length scales.1 Evolution has endowed DNA with high adaptability, allowing it to undergo conformational changes in response to cellular cues, without being irreversibly damaged. The advances in experimental methodology, in particular, single molecule techniques, have provided critical insight into DNA biophysics, including various aspects of its structural organization and sequence-dependent mechanical tensegrity.2 Nonetheless, the physical principles that underlie key attributes of DNA at all length scales, ranging from a few hundred base pairs to large scale chromatin organization, are not well understood.3 The growing interest in DNA nanotechnology and the need to formulate design rules for self-assembly, as well as nano-fabrication, further necessitate an understanding of DNA thermodynamics and mechanics.4,5 In all these areas well-designed computational models with sufficient accuracy are needed to provide not only insights into the biophysics of DNA but also for making predictions, especially where experiments cannot fully decipher the sequence-dependent properties of DNA.
A reliable structural model of DNA is required to accurately describe the key features of DNA biophysics at the molecular level. It is always tempting to use an all-atom representation of the DNA molecule, as well as the surrounding solvent, and counterions in order to glean microscopic insights into DNA dynamics.6,7 However, the innumerable degrees of freedom, which are coupled together in a complex fashion, often render it practically impossible to probe DNA dynamics over biologically relevant time scales and length scales using current computer hardware. Although there is some optimism regarding the level of accuracy that can be attained with current force fields, poor correlation with some key experimental results leaves room for skepticism. Some of the underlying force field deficiencies become even more apparent when simulations are extended to longer time scales. All-atom force fields routinely used in DNA simulations, such as AMBER and CHARMM, do not provide a reliable description of the denatured state and produce overtly compact structures, compared to experiment.8,9 Some of these deficiencies are also inherent in coarse-grained models10 that are developed based on benchmarking with respect to all-atom simulations. A particularly well-known deficiency of the AMBER force field is its systematic overestimation of base-stacking free energies compared to experiment.11,12 Several ad hoc corrections have been proposed to resolve this discrepancy,13–15 though with limited success. The latest version of the AMBER force field, parmbsc1, considered the current gold-standard in all-atom simulations, recapitulates some experimental results; nonetheless, recent work has brought to light some key deficiencies.16,17
While the concerted efforts of several groups to improve the force field quality for all-atom simulations are gaining ground, there is much left to be desired. Instead, it is often prudent to use a level of description depending on the length scale of DNA and the accuracy of the measurements.18 For example, characterization of the organization of chromosome structure can only be done using copolymer models in which each bead represents ~1000 base pairs (bps), whereas assembly of DNA hairpins needs a more refined model. In some cases, such as the polymerase-DNA complex, much can be learned using a single bead per base pair representation.19,20 Inspired by the success of simplified models there have been continued efforts toward the development of coarse-graining (CG) procedures, which reduce the number of degrees of freedom significantly. Despite their simplicity, CG models are often accurate at the molecular, as well as the chemical level and are built with the aim to embody the underlying physics of nucleic acid mechanics, thermodynamics, and kinetics.10,21–28
In a broad sense, DNA CG models are built either using a “top-down” or a “bottom-up” approach.29–31 While the former is constructed to reproduce experimental trends and large scale behavior, the latter exploits systematic coarse-graining to match distributions32,33 or fluctuations34 computed using a more detailed model. Some coarse-grained models often use a combination of both approaches.10
In recent years, CG models of different resolutions have been introduced to probe the mesoscale properties of DNA. Schatz and co-workers introduced a two beads per site DNA model to study the sequence-dependent melting behavior of dsDNA.35,36 As electrostatic interactions were not included explicitly, the model could not describe the salt-dependent mechanical properties of DNA. Subsequently, several CG models of higher resolution have been proposed.10,25,31,37,38 Notably, the model of Scheraga and co-workers25 has been used to study the assembly of the DNA double helix, from two single strands. However, the mechanical properties of both single-stranded and double-stranded DNA were not correctly reproduced. The recently introduced MARTINI DNA model fails to provide a faithful description of ssDNA and, surprisingly, even the thermodynamic stability of the dsDNA structure in the absence of an auxiliary elastic network.10 The applicability of the other models has also been rather limited, with most studies focusing on only a small subset of DNA properties, such as structural dynamics around the native state or conformational dynamics occurring over short time scales.37,38
The three interaction site (TIS) representation, first introduced by Hyeon and Thirumalai21 in the context of RNA folding, provides a reasonable resolution to probe key aspects of DNA biophysics, including sequence-dependent thermodynamics and mechanical response in the presence of an external force or torque. Several coarse-grained DNA models, which heavily borrow from the mapping scheme formulated by Hyeon and Thirumalai, have been introduced in recent years. Among these, the SPN model39 provides a sufficiently accurate description of sequence-dependent thermodynamic24,40 and mechanical properties40 of dsDNA. Nonetheless, ssDNA chains are predicted to be too rigid compared to experiment.40 Although Plotkin and co-workers22 adopted a somewhat different strategy by using anisotropic potentials to account for the nonsymmetric nature of the nucleobases, their model fails to reproduce the experimentally known persistence lengths of both single-stranded, and double-stranded DNA. On the other hand, the oxDNA model,23 in its original form, neither distinguished between AT and GC base pairs nor described salt-dependent behavior, although thermodynamic and mechanical properties were captured in an “average” sense. Subsequently, sequence41 and salt-dependence42 have been introduced, but a unified parametrization scheme that describes both is still lacking.
In this work, we adopt a largely “top-down” strategy to develop a new coarse-grained model for DNA based on the TIS representation. The TIS-DNA model includes sequence-dependent stacking, hydrogen-bonding, and electrostatic interactions that contribute to the overall stability of the DNA structures. We show that the TIS-DNA model provides a robust description of both ssDNA and dsDNA, a trait that is lacking in existing coarse-grained DNA models. The accuracy of our predictions, even in applications outside the realm of parametrization, attests to the transferability of our model and sets the stage for applications for a wide range of problems involving DNA on not too large a length scale.
METHODOLOGY
The Three Interaction Site (TIS) DNA Model.
In the TISmodel for nucleic acids,21 each nucleotide is represented by three spherical beads (interaction sites), corresponding to the phosphate (P), sugar (S), and the base (B). The mapping scheme from all-atom to the TIS representation is illustrated in Figure 1, and the explicit grouping of atoms is shown in the Supporting Information (SI), Figure S1. The beads are positioned at the center of mass of the chemical groups. The energy function describing the interactions between the interaction sites in DNA has the same functional form as the TIS-RNA model, developed by Denesyuk and Thirumalai (DT).43,44 The total energy, UT, for a given conformation of the polynucleotide is expressed as a sum of contributions from six components, denoting the bond (UB), angular (UA), single-stranded stacking (US), hydrogen-bonding (UHB), excluded volume (UEV), and electrostatic (UE) interactions:
| (1) |
Figure 1.
Coarse-graining procedure underlying the TIS-DNA model. Each nucleotide is represented by three beads: one for the sugar, base, and the phosphate. These residues are represented using the same color code in the all-atom and the TIS-DNA representations. As shown above, in the case of a 12 base pair duplex, the number of degrees of freedom reduces from 1458 to 210 upon coarse-graining.
We use harmonic potentials to describe the bond and angular interactions:
| (2) |
| (3) |
In eqs 2 and 3, r0 and α0 denote the equilibrium bond lengths and bond angles respectively, and kr and kα are the corresponding force constants.
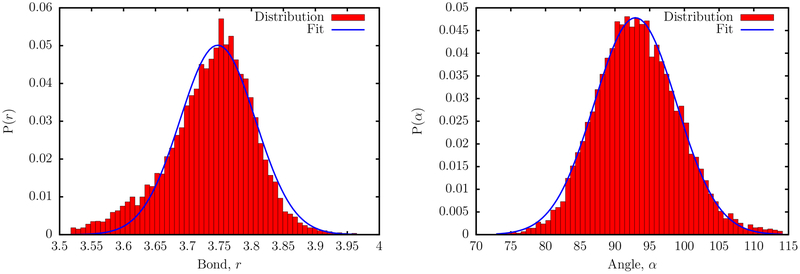
The values r0 and α0 were obtained by coarse-graining an ideal B-form DNA helix. To obtain the initial guesses for kr, and kα, we carried out Boltzmann inversions of the corresponding distributions obtained from experimental structures. The statistics were collected from three-dimensional structures of DNA helices deposited in the PDB database. We exclude all X-ray structures with a resolution lower than 2.5 Å, DNA molecules consisting of unnatural bases, and DNA-ligand complexes. The PDB ids of the 284 structures, which met the selection criteria, are tabulated in the SI. Some representative distributions corresponding to the coarse-grained bonds and angles obtained from the PDB database mining are shown in Figure 2.
Figure 2.
Distribution of the SP bond length (left) and SPS bond angle (right) from PDB database mining (red bars). The blue curves are fits to Gaussian functions.
Bond Stretch Potential.
The distribution of the bond lengths can be fit to a Gaussian function
| (4) |
where the parameter σ is obtained from the fit; kB is the Boltzmann factor; and T denotes the absolute temperature. Taking the logarithm on both sides of (4) and dropping the arbitrary constant, we get
| (5) |
We estimate kr with T set to 298 K. The values of kr for the different bonds are largely insensitive to the choice of T, within a broad range.
Bond Angle Potential.
Following earlier work,45,46 the distribution of bond angles, α, were weighted by a factor sin α and renormalized. The distribution of bond angles is expressed as
| (6) |
In (6), fn is a normalization factor, while p(α), and P(α) denote the unnormalized and normalized distribution functions, respectively. The angular potential is obtained using
| (7) |
Excluded Volume.
To account for volume exclusions between the sites, we use the Weeks–Chandler–Andersen (WCA) potential:47
| (8) |
The excluded-volume interaction term vanishes if the interacting sites are separated by a distance greater than D0, thereby making the WCA potential computationally efficient. Following DT,43 we set D0 = 3.2 Å and ϵ0 = 1 kcal/mol. All the interaction sites are assigned the same D0 and ϵ0 to keep the parametrization as simple as possible. As discussed by DT,43 this particular choice of D0 and ϵ0 somewhat underestimates the distance of closest approach between the interaction sites, with the exception of stacked bases, but has little effect on the folding thermodynamics.
Stacking Interaction.
Stacking interactions, between two consecutive nucleotides along the DNA chain, are described using the function
| (9) |
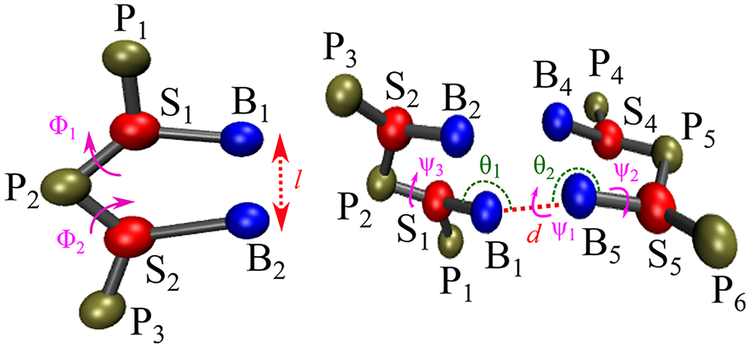
The strength of the stacking interaction is modulated by deviations from the equilibrium geometry, described by the stacking distance l0 and backbone dihedrals and . In a previous work, Dima et al. showed that an accurate description of stacking in RNA is necessary for fold recognition and structure prediction.48 The geometric parameters in terms of which the stacking interactions are represented in the TIS model are described in Figure 3. The equilibrium values for stacking distances and dihedrals are obtained by coarse-graining an ideal B-DNA helix We calculated kl and kϕ, by performing a Boltzmann inversion of the distributions corresponding to the distances between stacked bases (l) and backbone dihedrals (ϕ1, and ϕ2) computed from the experimental structures.
Figure 3.
Schematic of a coarse-grained dimer based on the TIS model, with l, ϕ1, and ϕ2 labeled. Right: Illustration of the structural parameters in eq 13. The hydrogen-bonding distance d is between sites B1 and B5; ϕ1 (S1, B1, B5) and ϕ2 (S5, B5, B1) are the angles; ψ1 (S1, B1, B5, S5), ψ2 (P6, S5, B5, B1), and ψ3 (P2, S1, B1, B5) are the dihedral angles.
In eq 9, describes the stacking interaction for a particular dimer and is calibrated to reproduce the thermodynamics, as described by the nearest-neighbor model.49,50 In this formalism, the overall stability of DNA duplexes is expressed as a sum over contributions from individual base pair steps. Here, we use the unified nearest-neighbor parameters from SantaLucia and Hicks (Table 1),50 which describes the overall stability of duplexes at 1 M monovalent salt in terms of enthalpic (ΔH) and entropic contributions (ΔS).
Table 1.
Nearest-Neighbor Thermodynamic Parameters for Watson–Crick Base Pairs in DNA in 1 M NaCl and 310 K50
| ΔH (kcal/mol) | ΔS (cal/(mol K)) | |
|---|---|---|
| −7.6 | −21.3 | |
| −7.2 | −20.4 | |
| −7.2 | −21.3 | |
| −8.5 | −22.7 | |
| −8.4 | −22.4 | |
| −7.8 | −21.0 | |
| −8.2 | −22.2 | |
| −10.6 | −27.2 | |
| −9.8 | −24.4 | |
| −8.0 | −19.9 |
We assume that the ΔH and ΔS of each base pair dimer step can be decoupled into separate contributions arising from single-stranded stacking and interstrand hydrogen-bonding:
| (10) |
| (11) |
In eqs 10 and 11, and denote the enthalpy and entropy associated with the stacking of x over w in the 3′ → 5′ direction. Based on previous experimental data,51 it is reasonable to assume that the contribution from hydrogen-bonding, ΔH(x−y), is purely enthalpic in nature. To obtain the thermodynamic parameters for all the dimers, we need to solve (10) and (11) for , , and ΔH(x−y). Since the number of unknowns exceeds the number of equations, we make some additional assumptions based on previous experimental and simulation data.
The thermodynamic parameters corresponding to AT/TA and TA/AT, CA/GT and GT/CA, CT/GA and GA/CT, and CG/GC and GC/CG, as described by eqs 10 and 11 can be averaged, as these values are similar within experimental uncertainty.50 This enables us to assign and for all the dimer steps. Experiments by Olsthoorn et al.52 indicate that the stacking enthalpy of a deoxyadenylate dimer is virtually identical to the ribo analogue. Hence, we set equal to −3.53 kcal/mol, which is the enthalpy value computed for an adenine–adenine stack in the RNA model.43 The melting temperature (Tm) of the dimer is estimated to be 322 K by CD spectroscopy experiments.52 Furthermore, experiments53 show that the free energy of stacking for a dimer at 298 K is around 0.1 kcal/mol. From the above assumptions, and using eqs 10 and 11, we can compute , , , , and ΔH(A−T). Using ΔH(A−T), and are computed from the appropriate thermodynamic equations. The enthalpies of hydrogen-bonding are related as ΔH(G−C) = 1.5ΔH(A−T). Once ΔH(G−C) is known, and are computed from eqs 10 and 11.
To evaluate the thermodynamic parameters for the remaining dimers, we need to make additional simplifications. Experiments by Sollie and Schellman,53 as well as recent simulations,54–56 indicate that and have similar stacking propensities. Therefore, we can describe them by the same set of thermodynamic parameters: and . Using the enthalpy and entropy of stacking for the dimer, we estimate the corresponding values for the dimer using the appropriate set of equations from (10) and (11). We also assume that , , and dimers can be described by the same set of thermodynamic parameters, as experiments and simulations show that they have very similar stacking propensities.53,55,57 This simplification allows us to evaluate , , , , , and . The results are summarized in Table 2.
Table 2.
Enthalpies ΔH, Entropies ΔS, and Melting Temperatures Tm of Single-Stranded DNA Stacks Derived in This Worka
| ΔH (kcal/mol) | ΔS (cal/(mol K)) | Tm (K) | |
|---|---|---|---|
| −3.53 | −10.96 | 322.0 | |
| ; | −3.06 | −10.43 | 293.0 |
| ; | −3.76 | −11.26 | 333.6 |
| ; | −3.06 | −10.43 | 293.0 |
| −3.39 | −9.56 | 353.9 | |
| ; | −4.28 | −12.90 | 331.9 |
| ; | −4.03 | −12.13 | 332.6 |
| −2.98 | −10.33 | 288.3 | |
| ; | −2.98 | −10.33 | 288.3 |
| −2.98 | −10.33 | 288.3 |
ΔH(A−T) = −1.09 kcal/mol; ΔH(G−C) = −1.64 kcal/mol.
Using Melting Temperature of Dimers To Learn the Value.
In order to calibrate the stacking interactions , we simulated the stacking of coarse-grained dimers’ similar to that shown in Figure 3. We use the expression for Us in eq 9, with . Here, h and s are adjustable parameters, and Tm is the melting temperature of a given dimer, as tabulated in Table 2. In simulations, the free energy of stacking for each dimer can be computed using
| (12) |
where p is the fraction of sampled configurations for which US < −kBT, and ΔG0 is a correction factor that accounts for any difference in the definition of stacking, and hence ΔG, between experiment and simulation. Since the thermodynamic parameters for the dimer were derived to explicitly match the stacking free energy at 298 K, we set ΔG0 = 0 for this dimer, as well as for , , and dimers, all of which are thermodynamically equivalent within our parametrization scheme. For the rest of the dimers, we choose ΔG0 such that stacking free energy at 298 K, as estimated by osmometry experiments, is reproduced.
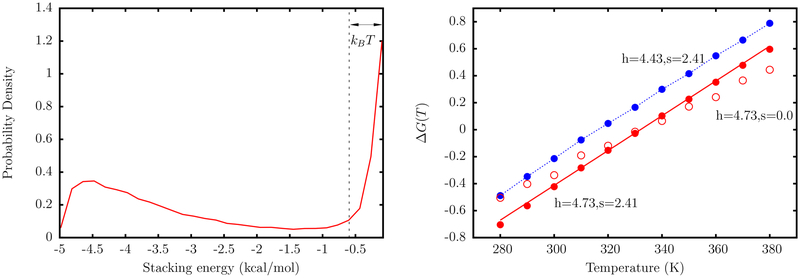
Figure 4 shows the results from the simulation of a dimer. For ΔG0 = 0 and s = 0, the melting temperature Tm systematically increases with h and is equal to the value in Table 2 for h = 4.73. If s = 0, the entropy of stacking, given by the slope of ΔG(T) versus T, is underestimated compared to the value in Table 2. To correct for the entropic contribution, we use , with s > 0. This readjustment does not change Tm but allows us to reproduce the entropy and hence the temperature dependence of ΔG(T), in accordance with Table 2. We find that s = 2.41 is an optimal choice for the dimer. The fitting procedure described above is carried out for all 16 dimers using the TIS representation. The final set of parameters is tabulated in Table 3. Some of the dimers, which have equivalent thermodynamic parameters according to our model, have somewhat different h and s values due to differences in their equilibrium geometry.
Figure 4.
Left: A representative distribution of stacking energies, US from simulations of a dimer represented by the TIS model. All configurations with US < −kBT are considered as stacked. Right: The free energy of stacking for dimer as a function of temperature. The red solid line corresponds to the experimental line, with free energies given by the parameters in Table 2. The red filled circles represent simulation results, with h and s chosen such that the experimental temperature dependence is reproduced. These values correspond to the case where ΔG0 = 0. The red open circles correspond to the case where Tm is reproduced, but the entropy is underestimated. The blue circles are simulation data for h and s where the free energy is shifted by a constant factor.
Table 3.
Parameters h and s are Computed from the Simulations of Coarse-Grained Dimersa
| h (kcal/mol) | s | ΔG0 | |
|---|---|---|---|
| 5.69 (4.67) | 0.94 | 0.60 | |
| ; | 4.95 (4.18); 5.02 (4.28) | 0.87; 0.65 | 0.49 |
| ; | 4.98 (4.21); 5.03 (4.24) | 0.92; 0.79 | 0.49 |
| ; | 5.43 (4.83); 5.42 (4.82) | 1.06; 0.98 | 0.39 |
| ; | 4.13; 4.18 | 0.71; 0.94 | 0.00 |
| 4.15 | 0.98 | 0.00 | |
| ; | 5.22 (4.81); 5.13 (4.73) | 2.33; 2.41 | 0.26 |
| ; | 5.28 (4.70); 5.43 (4.86) | 1.69; 1.73 | 0.38 |
| 5.66 (5.13) | −0.29 | 0.38 | |
| 4.17 | 0.89 | 0.00 |
ΔG0 is chosen such that the experimental stacking free energies at 298 K are reproduced. The values of h before the inclusion of the correction term, ΔG0, are shown in parentheses.
Hydrogen-Bonding Interactions.
Hydrogen-bonding interactions are only considered between the canonical base pairs (Watson–Crick) in the DNA structure. In some instances, noncanonical base pairs may play a role in stabilizing the DNA structure.58,59 Nonetheless, these interactions are excluded from the current model. The CG interaction describing hydrogen-bonding is given by
| (13) |
where d, θ1 θ2, ψ1 ψ2, and ψ3 are described in Figure 3. The corresponding equilibrium values are obtained from the coarse-grained structure of an ideal B-DNA helix The coefficients kd, kθ, and kψ were determined in a fashion similar to the other harmonic constants, using a Boltzmann inversion of the statistics accumulated from experimental structures. The parameter controls the strength of the hydrogen-bonding. Similar to base-stacking, hydrogen-bonding is sensitive to deviations from the equilibrium geometry.
Eq 13 denotes the UHB for a single hydrogen bond and is multiplied by a factor of 2 or 3 depending on the type of base pair (A-T or G-C) connecting the coarse-grained sites.
Electrostatic Interactions.
The electrostatic interactions are computed using the Debye–Hückel approximation, in conjunction with the concept of Oosawa-Manning counterion condensation. The electrostatic free energy is given by60
| (14) |
where |ri−rj| is the distance between two phosphates i and j, ϵ is the dielectric constant of water, and λD is the Debye-screening length. The Debye length λD is related to the ionic strength of the solution and is given by
| (15) |
In eq 15, qn is the charge for an ion of type n, and ρn is the number density of the ion in solution.
The magnitude of phosphate charge, Q, is determined using the Oosawa-Manning theory.61 The bare charge on the phosphate is renormalized due to propensity of ions to condense around the highly charged polyanion. The Oosawa-Manning theory predicts that the renormalized charge on the phosphate is
| (16) |
where b is the length per unit charge, and lB is the Bjerrum length. The length per unit charge for DNA, as estimated by Olson and co-workers,62 is approximately 4.4 Å, which leads to a reduced charge of −0.6 for the phosphates at 298 K. As the dielectric constant is also a function of temperature, the temperature dependence of Q is nonlinear63 with
| (17) |
In eq 17, T is the temperature in Celsius. Following DT, the charges are placed on the center of mass of the phosphate beads,43 which is somewhat comparable to atomistic representations where the charges are localized on the two oxygen atoms of the phosphate group.
Calculation of Persistence Length.
The persistence length, a measure of stiffness of DNA, is calculated using the decay of the autocorrelation of tangent vectors along the backbone. For a worm-like chain (WLC), such as DNA64
| (18) |
In eq 18, 〈…〉 denotes an average, s denotes the position along the DNA strand, and lp is the persistence length. For ssDNA, the tangent was calculated by taking the distance vector from the sugar bead on nucleotide i to the sugar bead on nucleotide i+1 and normalizing it to unity. For dsDNA, the tangent vector was calculated by taking the distance vector from the midpoint of the bases involved in hydrogen-bonding at position i along the chain, to the midpoint of the bases at position i+5, and normalizing it to unity. We found that the values of the correlations were quite insensitive to our particular definition of tangent vectors.
Although the relationship described by eq 18 is quite robust for dsDNA, it breaks down when the decay of the autocorrelation function becomes nonexponential. This situation typically arises for charged flexible polymers, such as ssDNA.64 Hence, we use the following relationship to estimate lp for ssDNA, following Doi and Edwards64
| (19) |
where R is the end-end distance, and l is the contour length of the ssDNA chain.
The persistence length of a polyelectrolyte chain exhibits a strong dependence on the ionic strength of the solution.65,66 It is known that polyelectrolytes (PEs), such as DNA, become more flexible with an increase in ionic strength due to a more effective screening of the phosphate–phosphate charge repulsion resulting from counterion condensation. Nonetheless, interplay between the DNA geometry and PE effects in determining the overall chain stiffness is not known. For a stiff PE near the rod limit, the Odijk-Skolnick-Fixman (OSF) theory67,68 provides a very good description of the electrostatic contribution to persistence length69,70
| (20) |
where lp0 is the bare persistence length, which depends on the intrinsic geometric properties of the chain, and λD and lB denote the Debye length and Bjerrum length, respectively. In the OSF theory, whose validity extends to flexible polyelectrolytes as well, it is assumed that lp0 > lOSF.
Langevin Dynamics Simulations.
The equations of motion of each bead is described by Langevin dynamics, which for bead i can be expressed as a stochastic differential equation: , where mi is the mass of the bead, γi is the drag coefficient, Fi denotes the conservative force acting on bead i due to interactions with the other beads, and gi is a Gaussian random force. The random force satisfies 〈gi(t) gj(t′)〉 = 6kBTγiδijδ(t−t′). A variant of the velocity-Verlet version of the algorithm for Langevin dynamics,71 with a time step of 2.5 fs, was used to integrate the equations of motion. For the mechanical pulling simulations, we use a time step of 1.25 fs to maintain the stability of the system. The drag coefficient corresponding to each bead, γi, is calculated using the Stokes′ formula, γi = 6πηRi, where η is the viscosity of the surrounding environment, and Ri is the Stokes’ radius. We used a value of 10−5 Pa·s for η, which is around 1% of the viscosity of water. This choice does not affect the thermodynamic properties but is critical for an efficient exploration of the conformational space.43,71 The values for Ri are 2 Å for the phosphate beads, 2.9 Å for sugar beads, 3 Å for guanine beads, 2.8 Å for adenine beads, and 2.7 Å for cytosine and thymine beads. All the simulations were carried out using an in-house code. Each simulation was carried out for at least 4 × 108 time steps. To obtain meaningful statistics for any given observable, we carried out at least five simulations for each data point, with different initial conditions.
PARAMETRIZATION OF THE DNA MODEL
Bonded Interactions.
The range of harmonic constants (kr, kα) was obtained using eqs 5 and 7. To parametrize the coarse-grained DNA model, in terms of mechanical properties, we chose a heterogeneous single-stranded DNA sequence (CATCCTCGACAATCGGAACCAGGAAGCGCCCCGCAACTCTGCCGCGATCGGTGTTCGCCT) with 60 nucleotides. The objective was to optimize the angular bending constants (kα), in particular, such that the persistent lengths, computed at different monovalent salt concentrations, fell within the experimental range.72–75 The choice of this particular ssDNA sequence ensured that all the kα values were properly tuned, with much of the simulation effort being focused on parameter optimization rather than exploration of a vast sequence space. Furthermore, this sequence has also been considered in parametrizing previously published CG models20,22 and persistence length calculations, which enabled us to set relevant upper and lower bounds for our model during the optimization process.
During the parametrization process, we switched off the stacking interactions. Besides eliminating the complexity arising due to base-stacking, this choice enabled us to compare our simulated results with persistence length estimates for unstructured ssDNA available from recent experiments.75 The choice of bond-stretching constants, kr, had practically no effect on the persistence length estimates. Once an optimal set of harmonic constants was identified, the stacking interactions were parametrized using the procedure described earlier. The final set of parameters, employed in our coarse-grained model, is tabulated in Table 4.
Table 4.
Optimal Values for the Various Harmonic Force Constants in the DNA Modela
| bond type | force constant, kr(kcal/mol/Å2) | equilibrium value, r0 (Å) |
|---|---|---|
| SP | 62.59 | 3.75 |
| PS | 17.63 | 3.74 |
| SA | 44.31 | 4.85 |
| SG | 48.98 | 4.96 |
| SC | 43.25 | 4.30 |
| ST | 46.56 | 4.40 |
| angle type | force constant, kα (kcal/mol/rad2) | equilibrium value, α0 (deg) |
| PSP | 25.67 | 123.30 |
| SPS | 67.50 | 94.60 |
| PSA | 29.53 | 107.38 |
| PST | 39.56 | 97.18 |
| PSG | 26.28 | 111.01 |
| PSC | 35.25 | 101.49 |
| ASP | 67.32 | 118.94 |
| TSP | 93.99 | 123.59 |
| GSP | 62.94 | 116.90 |
| CSP | 77.78 | 121.43 |
| parameter | value | |
| kl (Å−2) | 1.45 | |
| kϕ (radians−2) | 3.00 | |
| kd (Å−2) | 4.00 | |
| kθ (radians−2) | 1.50 | |
| kψ (radians−2) | 0.15 | |
The kr, kl, kϕ, kd, kθ, and kψ values correspond to those which are obtained directly from the Boltzmann inversion of distributions obtained from database mining. No further optimization of these parameters was necessary. The angle-specific kα values correspond to those that reproduce the experimental persistence lengths of ssDNA and were obtained after fine-tuning of the initial parameters obtained from Boltzmann inversion.
Calibration of Hydrogen-Bonding Interaction.
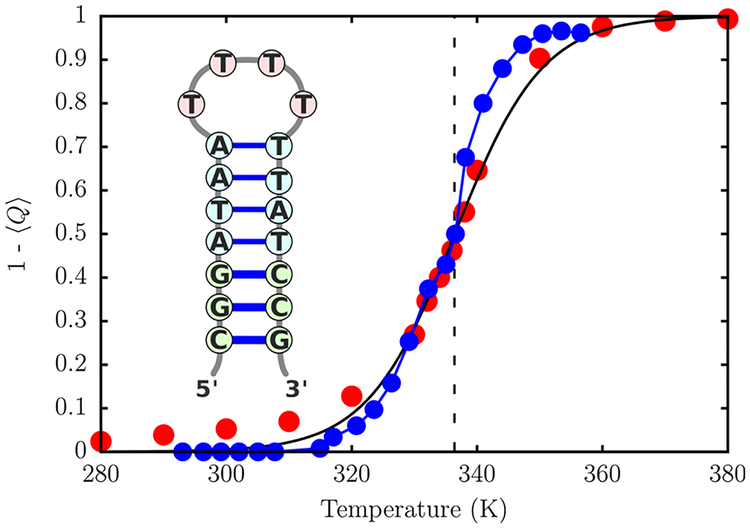
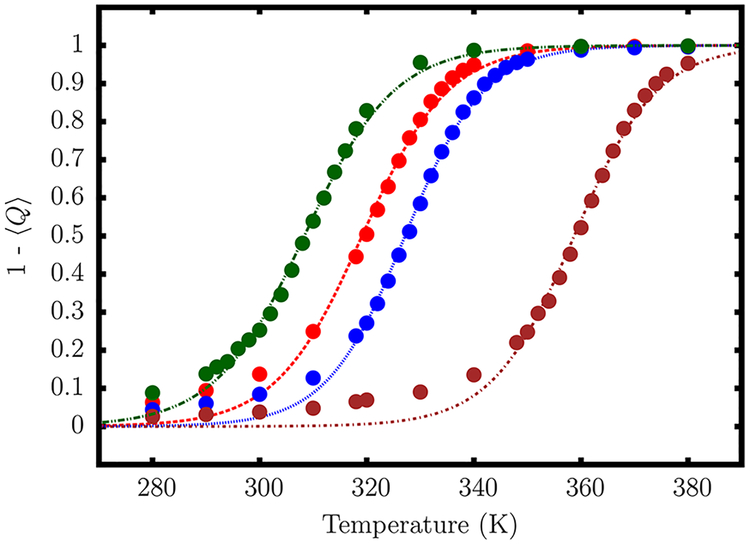
After the optimization procedure, the only free parameter in the model is . We chose its value to reproduce the experimental melting curve for a DNA hairpin (shown in the inset of Figure 5).76 The relatively small size of the hairpin and heterogeneity of the stem composition, as well as extensive thermodynamic data available for this hairpin,76,77 make it an ideal candidate for our calibration procedure.
Figure 5.
Variation of the fraction of broken base pairs, 1 − 〈Q〉, with temperature. A quantitative agreement with experimental melting profile is obtained for kcal/mol. The simulation results are given in red circles. The experimental estimates76 correspond to blue circles. The solid line is a sigmoidal fit to the simulation data, which gives Tm = 336.4 K. The dashed vertical line indicates the experimental melting temperature.76
In the experiment, the increase of the relative absorbance with temperature corresponds to both unstacking of bases, as well as breakage of hydrogen bonds. For the hairpin sequence considered here, the former effect is minimized due to the weak stacking interactions between the thymine bases.76 The loss of hydrogen-bonding occurs in a largely cooperative fashion, and at the melting temperature approximately half of the base pairs are broken. The strength of a hydrogen bond is determined both by the donor–acceptor distance, as well as the relative orientation. In the TIS-DNA model, the precise functional form of UHB (eq 13) is such that it subsumes both the distance and orientational requirements. We consider a hydrogen bond to be formed between the coarse-grained sites if UHB < − nkBT, where n = 2 for a A-T base pair and 3 for a G-C base pair. As shown in the Supporting Information (Figure S2), these cutoffs are reasonable and allow us to unequivocally distinguish between intact and melted base pairs. Using this definition for a hydrogen bond, we can compute 〈Q〉, the fraction of native contacts as a function of temperature. Assuming that 〈Q〉 is an appropriate order parameter for describing DNA hairpin thermodynamics, we can determine the melting temperature, Tm, from the following sigmoidal fit:
| (21) |
In the above equation, σ is the width of the melting transition. We find that for kcal/mol, the TIS-DNA model reproduces the experimental curve (Figure 5). Using eq 21, we estimate Tm = 336.4 K, which exactly corresponds to the experimental estimate.76 The width of the transition is slightly overestimated compared to experiment. This discrepancy is likely caused by the neglect of non-native base pairs, as well as anisotropy in the excluded volume term of our model. Similar deviations were also observed in previous studies by Dorfman and co-workers.78,79
RESULTS AND DISCUSSION
It should be pointed out that the parameters in our TIS-DNA model were determined using statistics generated from PDB structures and thermodynamic properties of dimers. This is the same learning procedure used by DT to probe the thermodynamic properties of RNA folding.43 The TIS-DNA force field was not calibrated using experimental data in the applications described below. Therefore, the results are genuine predictions of the model. The success, as assessed by comparison to experiments, provides the much needed validation.
Description of Single-Stranded DNA.
In the following sections, we describe the applications of the TIS-DNA model to obtain the sequence and salt-dependent mechanical, as well as thermodynamic properties of single-stranded DNA. We compare the predictions of our model to available experimental data or well-established theoretical results.
Radius of Gyration: Salt-Dependent Scaling Behavior.
The dependence of radius of gyration (Rg) on the length of a flexible polymer chain is often described by a universal Flory scaling law,80 Rg = A0Nν, where N is the number of segments, and ν is the Flory exponent. An ideal chain with ν = 0.5 and a rigid rod with ν = 1 denote two limiting cases. For a random coil, with excluded volume, the scaling exponent is predicted to be ~0.6, based on renormalization group based approaches.64,81
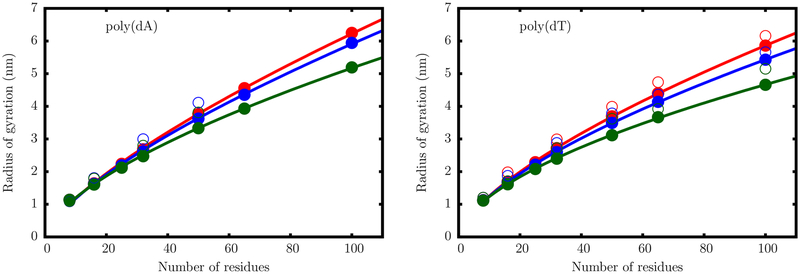
In Figure 6, we illustrate the dependence of Rg on the chain length, for single-stranded dA and dT sequences, as described by the TIS-DNA model. Data are shown for three salt concentrations. As the salt concentration is increased, the power law dependence becomes weaker for both the ssDNA sequences. This trend is typical of charged polymers, where an increase in chain collapsibility at high ionic strengths results from a more effective screening of the backbone charges. Overall, the predicted values are in good agreement with the estimates from small-angle X-ray scattering (SAXS) experiments,82 in contrast to most currently available DNA models,8,10 which lead to overcompaction of ssDNA.
Figure 6.
Dependence of the radius of gyration Rg on the number of nucleotides for a dA (left) and dT oligomer (right). The filled circles are the simulation results at salt concentrations of 0.125 M (red), 0.225 M (blue), and 1.025 M (green). The open circles are experimental data from Sim et al.82 The solid lines are fits to the scaling law with Rg = A0Nν.
It is clear that the TIS-DNA model provides an excellent description of the sequence-dependent variation of the scaling exponents,82 ν, with salt concentration (Figure 7). For the dT sequence, a fit of the simulation data to the scaling law yields ν ~ 0.67, at 0.125 M. The effective scaling exponent decreases in an exponential fashion with increasing salt concentration and falls below the random coil limit (ν = 0.588) at around 1 M. Therefore, our model predicts that, in the moderate to high salt regime, poly(dT) behaves as a random coil, which is in accord with recent experimental findings.82,83
Figure 7.
Variation of the effective scaling exponent, ν, with salt concentration. The filled circles correspond to ν obtained from power law fits of Rg = A0Nν. The scaling exponents for both poly(dA) and poly(dT) decrease exponentially with salt concentration. The open circles denote ν at different salt concentrations, reported by Sim et al.82 The dashed line is the scaling exponent (ν = 0.588) for a random coil, with excluded volume interactions.
The effective scaling exponents for the poly(dA) sequence are consistently higher than those for poly(dT) at all salt concentrations. Interestingly, even at 1 M, the poly(dA) chain does not display random coil-like behavior, unlike poly(dT). Within the Debye–Hückel approximation employed in our model, the two ssDNA sequences have the same charge densities for a given chain length, and therefore electrostatics is unlikely to result in such disparate behavior. Previous work84,85 suggests that the origin of this contrasting flexibilities lies in the chemical difference between adenine and thymine, with the former exhibiting significantly higher stacking propensity.
The pre-exponential factors, A0, obtained from the power law fits, lie within the experimental range.82,86,87 In the salt concentration range from 0.1 to 1 M, A0 varies from 0.26 to 0.32 nm for poly(dT) and from 0.22 to 0.27 nm for poly(dA) sequences. The specific values usually depend on the chemical and geometric details of the monomer. For the poly(dA) sequence, the systematically lower A0 values at all salt concentrations imply that the effective monomer–monomer bond length (in this particular case, the distance between two consecutive nulceobases) is shortened as a consequence of base stacking. On the other hand, the preponderance of unstacked monomers in poly(dT) chains results in higher A0 values and consequently leads to a stronger dependence of Rg on salt concentration.
The distinct stacking property exhibited by adenine and thymine is an emergent feature of the TIS-DNA model, as it accounts for base step dependent stacking thermodynamics. The presence of base-stacking interactions reduces the collapsibility of the poly(dA) chain, and therefore the Rg dependence on chain length follows a stronger power law compared to poly(dT). In subsequent sections, we discuss in more detail how the presence of persistent helical stacks along the poly(dA) chain could affect its mechanical tensegrity and lead to signatures (“plateau”) in the force–extension profile.
Sequence Dependent Stiffness.
Despite the ongoing efforts, some ambiguity exists regarding the persistence length (lp) of ssDNA in solution. The reported values of lp span a wide range, from 1.0 to 6.0 nm, and are often sensitive to theexperimental setup.72,73,75,88 To further validate the robustness of the TIS-DNA model in describing ssDNA, we compute lp using eq 19 for a homogeneous poly(dT) and a poly(dA) sequence, each of which is 40 nucleotide long.
As outlined in the Methodology section, exponential fits to the decay of tangent correlations provide another means to estimate persistence lengths. Nonetheless, we find that this method of computing lp breaks down for ssDNA, as noted in previous studies.89,90 The polyelectrolyte nature of DNA is primarily responsible for this deviation. In a previous work, Toan and Thirumalai90 showed that tangent correlations decay as a power law, rather than in an exponential fashion, over length scales shorter than the characteristic Debye length.
The autocorrelation function of the tangent vectors computed at different salt concentrations (Figure 8) shows dramatic differences in the equilibrium conformations adopted by the two ssDNA sequences. For poly(dA), the decay of the tangent correlations exhibits oscillatory behavior, which is characteristic of helical structure formed by base-stacking interactions within the chain.83 No such signatures are observed for the poly(dT) sequence, within a range of salt concentration, suggesting that the corresponding equilibrium ensemble is largely unstructured. The tangent correlations decay in a nonexponential fashion, particularly at low salt concentrations (~0.02 to 0.10 M), where electrostatic effects are dominant. From Figure 9, it is evident that the decay of the tangent correlations becomes exponential over long length scales but exhibits substantial curvature at short distances. Specifically, the power law behavior postulated by Toan and Thirumalai90 becomes apparent when the data is plotted on the logarithmic scale.
Figure 8.
Decay of tangent correlations with the contour length in ssDNA for the dT40 sequence (left) and dA40 sequence (right). The correlation function corresponding to dA40 shows oscillatory behavior indicating the presence of the helical structure within the chain.
Figure 9.
Left: The decay of tangent correlations with contour length for the poly(dT), at different ionic strengths. The dashed curves denote fits to a single exponential. The solid lines denote fits to a double exponential. Middle: A semilog plot of the data, showing the exponential decay at large length scales. Right: Log–log plot of the tangent correlations, showing evidence of power law behavior.
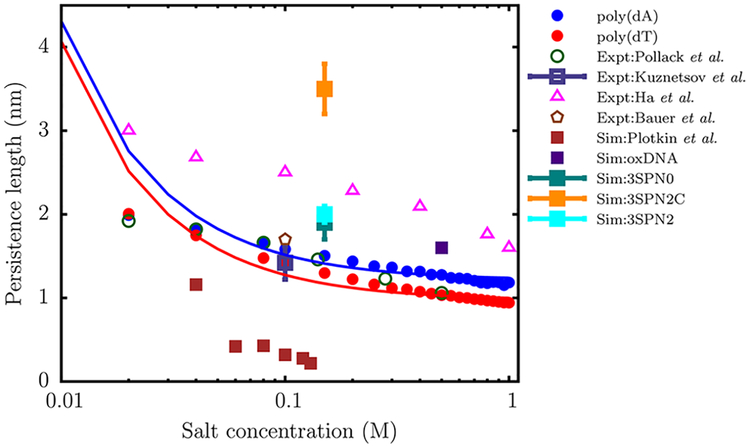
As shown in Figure 10, the persistence length, lp, of ssDNA predicted by the TIS-DNA model falls within the range of experimentally reported values, over the entire range of salt concentration. In particular, the agreement between our estimates for poly(dT) (red circles) and those reported in a recent study by Pollack and co-workers75 using a combination of SAXS and smFRET experiments (green open circles) is remarkable. At a salt concentration of 0.1 M, our model predicts lp to be 1.45 nm, which lies within the error bars of the values determined by Kuznetsov et al. (1.42 nm)73 and Bauer and co-workers (1.7 nm),74 respectively. Our results for the dT40 sequence deviate from the experimental values of Ha and co-workers,72 particularly at low salt concentrations. This discrepancy was also noted in the experimental study of Pollack and co-workers,75 who ascribed the reason to the disparate boundary conditions. In their experiment, Ha and co-workers72 measured lp for a ssDNA construct, which was attached to the end of a long DNA duplex. This tethering impedes the motion of the ssDNA segment and likely alters the values of lp. In contrast, in the experiment of Pollack and co-workers,75 the ssDNA molecules diffuse freely, and this setup is commensurate with the boundary conditions employed in our simulations. Besides agreement with the experimental data, the variation of lp with salt concentration is in accord with the OSF theory. A fit to the OSF equation yields a bare persistence length lp0 of 0.98 nm for poly(dT), which is within the range (0.6 to 1.3 nm) of values reported by different experiments.75,88,92,93
Figure 10.
Variation of the persistence length (lp) with salt concentration for the dT40 (red) and dA40 (blue) sequences computed from the simulation. The solid curves are fits of the simulation data to the OSF theory (eq 20). The lp values reported by Pollack and co-workers,75 using a combination of SAXS and smFRET experiments, are shown as green open circles. The triangles denote the experimental data of Ha and co-workers.72 The open square with an error bar represents the experimental data of Kuznetsov et al.,73 for a dT hairpin at 0.1 M. The brown polygon denotes the lp value reported by Bauer and co-workers74 for a dT100 sequence at 0.1 M using FCS experiments. The filled squares denote the persistence lengths estimated by using coarse-grained models with a resolution similar to ours: data in brown are from Plotkin and co-workers,22 oxDNA (purple),23 3SPN0 (teal),39 3SPN2 (cyan),24 and 3SPN2C(orange).40 We do not include the data for 3SPN191 as it lies outside the experimental range.
The poly(dA) sequence is stiffer than poly(dT), particularly at high salt concentration, where the electrostatics are effectively screened, and the intrinsic geometric nature of the chain manifests itself. A fit to the OSF theory yields a bare persistence length of 1.22 nm. The organization of neighboring bases into stacked helices in poly(dA) endows the ssDNA chain with additional bending rigidity, leading to systematically larger lp values. Our prediction is also consistent with the experiment of Goddard et al.,94 who found that hairpin formation in poly(dA) involves a larger enthalpic cost, compared to poly(dT). The contrasting persistence lengths estimated for poly(dT) and poly(dA) further explain why these sequences exhibit entirely different salt-dependent collapse, as explained in the earlier section.
It should not go unstated that the results of the TIS-DNA model represent a significant improvement over other currently available coarse-grained DNA models of similar resolution in describing the flexibility of ssDNA. The success of the TISDNA model in predicting the sequence-dependent stiffness is due to a careful calibration of the dimer stacking thermodynamics. However, we note that this prediction is truly an emergent property of the TIS-DNA model, as it was not specifically tuned to distinguish between poly(dA) and poly(dT) strands. As shown in Figure 10, the model of Plotkin and co-workers22 severely underestimates the lp of ssDNA over the entire range of salt concentration. On the other hand, the latest version of the 3SPN model,40 which was optimized for DNA duplex structures, predicts ssDNA to be too stiff. Although the older versions of the 3SPN model24,39 and oxDNA23 estimate lp values that fall within the experimental range, the bare persistence lengths, lp0’s, are overestimated. These discrepancies would produce incorrect force–extension behavior and severely limit the use of such models in applications where a correct description of ssDNA flexibility is important.
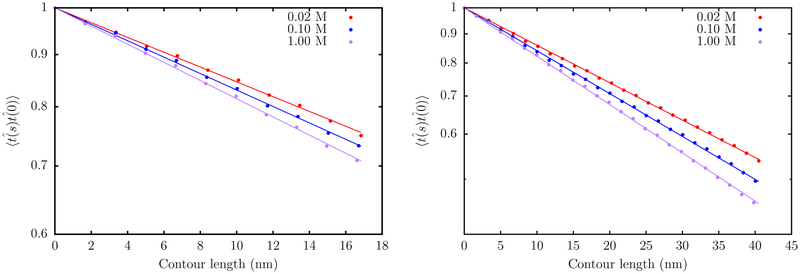
Sequence-Dependent Force–Extension Profiles of ssDNA.
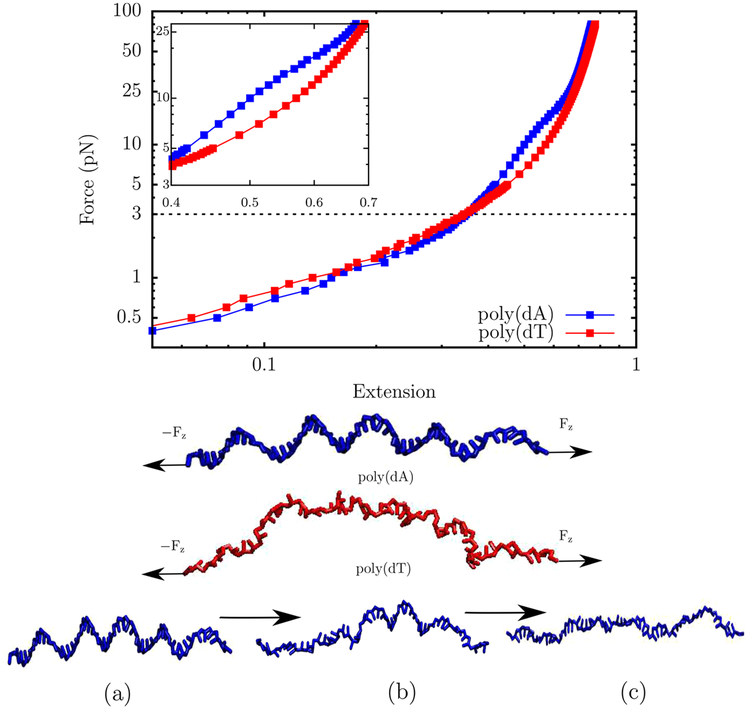
Single-molecule pulling experiments provide a viable route toward determining the mechanical properties, as well as the thermodynamics of base-stacking in DNA. The applied force, in conjunction with electrostatic repulsion between the backbone phosphates destabilizes base-stacking, and the subtle interplay between competing interactions lead to a variety elastic regimes. Several studies report that the tensile response of ssDNA is dictated by sequence composition, as well as ionic strength.85,95,96 Recently it was shown that in designed homogeneous sequences, such as poly(dA), which exhibit substantial base-stacking, the elastic response deviates substantially from the predictions of the standard polymer models.97,98 Specifically, a plateau in the low-force regime of the force–extension profile is thought to be the “mechanical footprint” of base-stacking.85,95
To investigate how the TIS-DNA model captures sequence-specific effects on the force–extension behavior of ssDNA, we simulated the mechanical stretching of poly(dA) and poly(dT) strands consisting of 50 nucleotides, at a salt concentration of 0.5 M. The force–extension curves are depicted in Figure 11. While the mechanical response of poly(dT) is purely entropic, the force–extension profile of poly(dA) exhibits a concave feature between ~7 and 22 pN, which corresponds to the plateau reported in experiments.85,95,96 A substantial fraction of bases in poly(dA) is stacked and forms helical domains, at forces below ~7 pN. At higher forces, a helix-to-coil transition (Figure 11) unravels the helical domains. At low forces, the largely unstacked poly(dT) sequence typically has a shorter extension, compared to poly(dA), as it is more flexible and has a propensity to collapse. On the other hand, the poly(dA) strand is more extensible in this force regime because stacked helical domains are associated with a smaller entropic cost of aligning in the direction of the applied force. The strands align with the force with greater ease, as the force increases, and the curves cross at around ~3 pN. The critical force for this crossover is in excellent agreement with the experimental estimate (~4 pN) of Saleh and co-workers.96
Figure 11.
Top: The force extension behavior of ssDNA. The profiles correspond to a salt concentration of 0.5 M. The z-axis denotes the extension, z, normalized by the contour length, L. The red curve denotes the force extension profile for poly(dT). The blue curve denotes the profile for poly(dA). A distinct plateau appears in the force–extension profile due to helix–coil transition (see inset). In contrast, the force–extension curve for poly(dT) follows the conventional worm-like chain behavior. The dashed line corresponds to the critical force (~3 pN) at which the extension of the poly(dT) chain exceeds that of poly(dA). Middle: Representative snaphots of the poly(dA) and poly(dT) sequences at 3 pN. The arrows represent the direction of the applied force. While poly(dA) consists of stacked helical domains, poly(dT) is mostly unstacked. Bottom: Helix-to-coil transition in the poly(dA) sequence that results in a plateau in the force–extension profile. In snapshot (a) the strand is under a tension of 3 pN, and helical domains persist throughout the chain. Snapshot (b) corresponds to a tension of 17 pN, where approximately two helical domains remain. In snapshot (c), the strand experiences a tension of 30 pN, and no visible helical domains exist in the chain.
Stacking Thermodynamics of ssDNA.
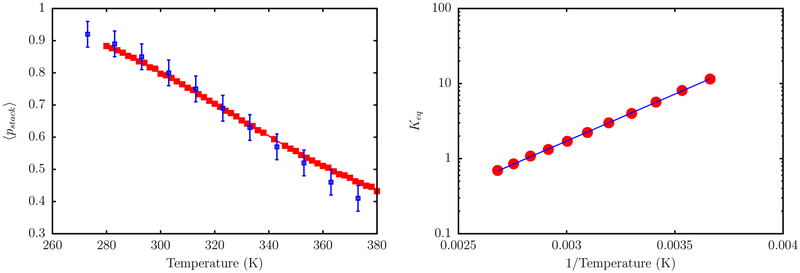
To assess whether the TIS-DNA model provides a robust description of stacking thermodynamics, over a wide range of temperature, we consider a 14 nucleotide long ssDNA with the sequence, 5GCGTCATACAGTGC3′, for which experimental data is available from Holbrook et al.99 In the experiment, stacking probability is described in terms of relative absorbance, with unstacked regions showing a higher absorbance compared to stacked bases. In our model, we consider a dimer to be stacked if US < −kBT. The average stacking probability, 〈pstack〉, as a function of temperature, for the ssDNA sequence is shown in Figure 12. As expected, 〈pstack〉 decreases linearly with temperature. Our estimates lie within the error bars of the experimental values, particularly in the low temperature regime.
Figure 12.
Left: The red curve shows the evolution of stacking probability, 〈pstack〉, with temperature. The blue squares are experimental data from Holbrook et al.99 The simulation and experimental data correspond to a salt concentration of 0.12 M. Right: A van’t Hoff plot depicting the variation of Keq with T. The red circles are the estimated equilibrium constants from simulations, and the blue solid line denotes a linear fit. From the fit, we estimate ΔHstack = −4.8 kcal/mol, ΔSstack = −13.3 cal/mol/K, and Tm = 363 K. These values are in very good agreement with the corresponding experimental estimates, which are ΔHstack = −5.7 kcal/mol, ΔSstack = −16.0 cal/mol/K, and Tm = 356 K.
Assuming a two-state model, we can define the equilibrium constant, Keq, for stacking in terms of stacking probability:
| (22) |
A van’t Hoff analysis (Figure 12), based on eq 22, yields stacking enthalpy, ΔHstack = −4.8 kcal/mol, entropy, ΔSstack = −13.3 cal/mol/K, and the transition midpoint temperature Tm = 363 K. These values are in good agreement with those reported by Holbrook et al. at the same salt concentration (see Figure 12).
Elasticity of Double-Stranded DNA.
To assess the accuracy of the TIS-DNA model in describing the elasticity of dsDNA, we consider two DNA sequences of length 60 and 130 base pairs, considered in an earlier study.22 The sequences of the leading strands for the two sequences are as follows:
Seq1: 5′-CATCCTCGACAATCGGAACCAGGAAGCGCCCCGCAACTCTGCCGCGATCGGTGTTCGCCT-3′
Seq2: 5′-GCATCCTCGACAATCGGAACCAGGAAGCGCCCCGCAACTCTGCCGCGATCGGTGTTCGCCTCCAAGCTAGAACCTGGCGATACGGCCTAAGGGCTCCGGAACAAGCTGAGGCCTTGGCCGTTTAAGGCCG-3′
Compared to ssDNA, the decay of the tangent autocorrelations is exponential, and dsDNA exhibits a worm-like chain behavior over the entire range of salt concentration (Figure 13). Hence, eq 18 was used to compute the persistence lengths.100,101
Figure 13.
Decay of the tangent correlations with the contour length in Seq1 (left) and Seq2 (right), at three different salt concentrations. The correlations decay exponentially in contrast to ssDNA.
As expected, the presence of hydrogen-bonding interactions (UHB) between complementary strands induces additional bending rigidity. For both the dsDNA sequences, the lp values predicted by the TIS-DNA model are in good agreement with the various experimental estimates (see Figure 14).100,102–104 In particular, we obtain very good agreement with the data of Bustamante and co-workers100 over the ion concentration range spanning an order of magnitude. At low salt concentrations, our lp estimate for Seq2 is close to the value reported by Sobel and Harpst for bacteriophage DNA.103 In the regime corresponding to moderate salt concentration, our results are in very good agreement with the values reported in separate studies by Harrington et al.102 and Maret and Weill.104
Figure 14.
Variation of persistence length with salt concentration for the 60 bp duplex, Seq1 (red) and 130 bp duplex, Seq2 (blue) from simulations. The solid curves denote fits of the simulation data to the OSF theory. The green open circles are lp values reported by Bustamante and co-workers.100 The triangles denote experimental data of Harrington et al.102 The open squares are data from the experiments of Sobel and Harpst103 on bacteriophage DNA. The brown polygon corresponds to the measurement of Maret and Weill.104 The filled squares denote the persistence lengths estimated by other groups: 3SPN1 (teal),91 3SPN2 (orange),24 and oxDNA (purple).42 We do not show the data from Plotkin and co-workers,22 because the estimated lp values are too low and lie outside the experimentally reported range.
For both Seq1 and Seq2, the variation of lp with salt concentration is in accord with the OSF theory. A fit to eq 20 yields a bare persistence length, lp0, of 49.3 nm for Seq1 and 51.5 nm for Seq2. These estimates fall within the range suggested by Bustamante and co-workers.100 Although sequence-dependent variations in lp are to be expected in general,105,106 the results predicted by the TIS-DNA model already look promising, considering that we did not parametrize the model explicitly to reproduce the dsDNA persistence lengths.
Sequence-Dependent Melting Temperatures of DNA Hairpins.
The accuracy of the TIS-DNA model in describing sequence-dependent thermodynamics is further assessed by computing the melting curves of select DNA hairpin sequences (Figure 15). The hairpins share the same loop sequence and vary only in terms of stem composition. Therefore, the melting temperatures (Tm) primarily depend on the strength of the base-pairing interactions, which in our model is described by UHB. The sequences were chosen such that the dependence of Tm on the GC content, as well as the nature of the closing base pair, could be carefully examined. To provide an objective assessment of our model, we computed all the melting curves at a salt concentration of 0.1 M, which is commensurate with the ionic strength of the buffer used in the experiments.107,108
Figure 15.
Hairpin sequences considered for predicting the sequence-dependent melting behavior with the TIS-DNA model. The GC content, and consequently Tm, increases from H1 to H4.
The fraction of native contacts, 〈Q〉, is computed as before, and the Tm is obtained by fitting the melting profile to a sigmoidal function (eq 21). We find that for all the hairpin sequences, the Tm values are in excellent agreement with the corresponding experimental estimates (Table 5), and the maximum error in our prediction is 2.5%. As illustrated in Figure 16, Tm increases monotonically in going from hairpin H1 (least GC content) to hairpin H4 (highest GC content). This trend is in accord with previous observations110,111 and indicates that the TIS-DNA model accurately captures the sequence-dependent thermodynamics of DNA hairpins. Interestingly, even at temperatures as low as 280 K the hairpin stem does not fully form for H1 owing to the plasticity of the AT base pair near the terminii. On the other hand, some base pairing is retained for H4, even at temperatures as high as 380 K, due to the higher enthalpic cost associated with disrupting GC base pairs.
Table 5.
Simulated and Experimental Values of Melting Temperatures for the Different Hairpin Constructsa
| sequence name | GC content | Tm(sim) (K) | Tm(expt) (K) |
|---|---|---|---|
| H1 | 0.16 | 308.3 | 316.6 |
| H2 | 0.30 | 319.1 | 321.4 (323.3) |
| H3 | 0.50 | 327.1 | 332.8 (329.4) |
| H4 | 1.00 | 357.8 | 358.7 |
For H2, the experimental Tm is available from the study of Ansari and co-workers.107 For H3, we show the estimate from calorimetric measurements of Benight and co-workers.108 The values shown in parentheses correspond to Tm calculated using the OligoAnalyzer 3.1 toolbox,109 which uses the SantaLucia–Hicks nearest-neighbor model. For H1 and H4, values from experimental measurements are not available, hence we compare the TIS-DNA predictions with the OligoAnalyzer estimates at the same salt concentration.
Figure 16.
Melting curves for the DNA hairpin sequences, H1 (green), H2 (red), H3 (blue), and H4 (brown). The closed circles represent the simulation data, and the dashed lines denote sigmoidal fits to the data. 〈Q〉 is the fraction of native contacts within the hairpin stem.
As highlighted in previous work, the closing base pair plays a prominent role in modulating hairpin folding thermodynamics and kinetics.108,112,113 We find that the TIS-DNA model is quite sensitive to these minimal variations in stem composition. Changing the closing base pair from AT (in H2) to CG (in H3) increases the Tm by 8 K, in agreement with the calorimetric and spectroscopic measurements of Benight and co-workers.108
CONCLUSIONS
In this work, we have introduced a robust coarse-grained model of DNA based on the TIS representation of nucleic acids, which reproduces the sequence-dependent mechanical, as well as thermodynamic properties of both single-stranded and double-stranded DNA. The model represents a significant improvement over current coarse-grained DNA models, particularly in the description of single-stranded DNA flexibility. In particular, we are able to reproduce experimental trends in sequence and salt-dependent persistence lengths, Flory scaling exponents, and force–extension behavior. Once the various interaction strengths are optimized for ssDNA, an appropriate choice of a single parameter (UHB) is able to reproduce the melting profile of a DNA hairpin, as well as the persistence length of dsDNA. Furthermore, the TIS-DNA model correctly captures the sequence-specific shifts of the melting temperatures for select DNA hairpin sequences, without any further adjustments to the parameters. In particular, we are able to recapitulate the effect of different closing base pairs (AT vs CG) and GC content on the melting temperatures.
Due to its balanced description of both single and double-stranded DNA, the TIS-DNA model in its current form should be well suited for providing the much needed molecular insight into biophysical problems of contemporary interest. For example, many aspects of sequence and salt-dependent behavior of dsDNA when subject to mechanical pulling, in particular the nature of the overstretched state, are yet to be fully resolved,114–116 and we believe that the TIS-DNA model can provide key insight in order to resolve the existing conundrum. In addition, our model should find several novel applications in DNA self-assembly and material design, where a robust description of sequence-dependent thermodynamics and elasticity is critical.117,118
The current version of the model does not include counterions explicitly and only provides a description at the Debye–Hückel level. However, this approach has some limitations; several key facets of DNA’s polyelectrolyte behavior critically hinge upon a proper description of the counterion atmosphere, particularly when multivalent ions arepresent.119,120 Therefore, a more sophisticated treatment of electrostatics will be required to understand the more subtle correlations between ion binding and flexibility and explore effects such as DNA swelling induced by overcharging.121,122 Recently, such extensions have been included in the RNA version of the TIS model, and it dramatically improves the description of RNA folding thermodynamics, ion binding, and assembly.123
In conjunction with the protein and RNA models introduced previously by our group,21,43,124 the TIS-DNA model should be well-suited to explore the structural dynamics of complex biomolecular machinery, such as nucleosomes125 and ssDNA–protein complexes.126 Studies on these and related systems are still in their nascent stages.
Supplementary Material
ACKNOWLEDGMENTS
We are grateful to Upayan Baul, Hung Nguyen, and Huong Vu for fruitful discussions. The authors acknowledge the Texas Advanced Computing Center (TACC) at the University of Texas at Austin for providing the computational resources.
Funding
The research was supported by the National Science Foundation (CHE 16-36424), the National Institutes of Health (GM089685), and the Collie-Welch Regents Chair (F-0019).
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00091.
PDB ids of sequences used in database mining, figure showing the grouping of atoms into coarse-grained interaction sites, and figure illustrating how an energy criterion is used for the definition of a hydrogen-bond in the TIS-DNA model (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Saenger W Principles of Nucleic Acid Structure; Springer-Verlag: Berlin, 1984; DOI: 10.1007/978-1-4612-5190-3. [DOI] [Google Scholar]
- (2).Reif M; Clausen-Schaumann H; Gaub HE Sequence-dependent mechanics of single DNA molecules. Nat. Struct. Biol 1999, 6, 346–349. [DOI] [PubMed] [Google Scholar]
- (3).Bonev B; Cavalli G Organization and function of the 3D genome. Nat. Rev. Genet 2016, 17, 661–678. [DOI] [PubMed] [Google Scholar]
- (4).Seeman NC Nanomaterials based on DNA. Annu. Rev. Biochem 2010, 79, 65–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Chen YJ; Groves B; Muscat RA; Selig G DNA nanotechnology from the test tube to the cell. Nat. Nanotechnol 2015, 10, 748–760. [DOI] [PubMed] [Google Scholar]
- (6).Beveridge DL; Barreiro G; Byun KS; Case DA; Cheatham TE; Dixit SB; Giudice E; Lankas F; Lavery R; Maddocks JH; Osman R; Seibert E; Sklenar H; Stoll G; Thayer KM; Varnai P; Young MA Molecular Dynamics Simulations of the 136 Unique Tetranucleotide Sequences of DNA Oligonucleotides. I. Research Design and Results on d(C(p)G) Steps. Biophys. J 2004, 87, 3799–3813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Lavery R; Zakrzewska K; Beveridge D; Bishop TC; Case DA; Cheatham T; Dixit S; Jayaram B; Lankas F; Laughton C; Maddocks JH; Michon A; Osman R; Orozco M; Perez A; Singh T; Spackova N; Sponer J A systematic molecular dynamics study of nearest-neighbor effects on base pair and base pair step conformations and fluctuations in B-DNA. Nucleic Acids Res 2010, 38, 299–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Guy AT; Piggot TJ; Khalid S Single-stranded DNA within nanopores: conformational dynamics and implications for sequencing; a molecular dynamics simulation study. Biophys. J 2012, 103, 1028–1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Yoo J; Aksimentiev A New tricks for old dogs: improving the accuracy of biomolecular force fields by pair-specific corrections to non-bonded interactions. Phys. Chem. Chem. Phys 2018, 20, 8432–8449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Uusitalo JJ; Ingólfsson HI; Akhshi P; Tieleman DP; Marrink SJ Martini Coarse-Grained Force Field: Extension to DNA. J. Chem. Theory Comput 2015, 11, 3932–3945. [DOI] [PubMed] [Google Scholar]
- (11).Häse F; Zacharias M Free energy analysis and mechanism of base pair stacking in nicked DNA. Nucleic Acids Res 2016, 44, 7100–7108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Banáš P; Mládek A; Otyepka M; Zgarbová M; Jurečka P; Svozil D; Lankaš F; Šponer J Can We Accurately Describe the Structure of Adenine Tracts in B-DNA? Reference Quantum-Chemical Computations Reveal Overstabilization of Stacking by Molecular Mechanics. J. Chem. Theory Comput 2012, 8, 2448–2460. [DOI] [PubMed] [Google Scholar]
- (13).Chen AA; Garcia AE High-resolution reversible folding of hyperstable RNA tetraloops using molecular dynamics simulations. Proc. Natl. Acad. Sci. U. S. A 2013, 110, 16820–16825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Yang C; Lim M; Kim E; Pak Y Predicting RNA Structures via a Simple van der Waals Correction to an All-Atom Force Field. J. Chem. Theory Comput 2017, 13, 395–399. [DOI] [PubMed] [Google Scholar]
- (15).Yang C; Kim E; Pak Y Free energy landscape and transition pathways from WatsonCrick to Hoogsteen base pairing in free duplex DNA. Nucleic Acids Res 2015, 43, 7769–7778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Lindahl V; Villa A; Hess B Sequence dependency of canonical base pair opening in the DNA double helix. PLoS Comput. Biol 2017, 13, e1005463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Zgarbová M; Jurečka P; Šponer J; Otyepka M A- to B-DNA Transition in AMBER Force Fields and Its Coupling to Sugar Pucker. J. Chem. Theory Comput 2018, 14, 319–328. [DOI] [PubMed] [Google Scholar]
- (18).Hyeon C; Thirumalai D Capturing the essence of folding and functions of biomolecules using coarse-grained models. Nat. Commun 2011, 2, 1481. [DOI] [PubMed] [Google Scholar]
- (19).Chen J; Darst SA; Thirumalai D Promoter melting triggered by bacterial RNA polymerase occurs in three steps. Proc. Natl. Acad. Sci. U. S. A 2010, 107, 12523–12528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Fosado YAG; Michieletto D; Allan J; Brackley C; Henrich O; Marenduzzo D A single nucleotide resolution model for large-scale simulations of double stranded DNA. Soft Matter 2016, 12, 9458–9470. [DOI] [PubMed] [Google Scholar]
- (21).Hyeon C; Thirumalai D Mechanical unfolding of RNA hairpins. Proc. Natl. Acad. Sci. U. S. A 2005, 102, 6789–6794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Morriss-Andrews A; Rottler J; Plotkin SS A systematically coarse-grained model for DNA and its predictions for persistence length, stacking, twist, and chirality. J. Chem. Phys 2010, 132, 035105. [DOI] [PubMed] [Google Scholar]
- (23).Ouldridge TE; Louis AA; Doye JPK Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model. J. Chem. Phys 2011, 134, 085101. [DOI] [PubMed] [Google Scholar]
- (24).Hinckley DM; Freeman GS; Whitmer JK; de Pablo JJ An experimentally-informed coarse-grained 3-Site-Per-Nucleotide model of DNA: structure, thermodynamics, and dynamics of hybridization. J. Chem. Phys 2013, 139, 144903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Maciejczyk M; Spasic A; Liwo A; Scheraga HA DNA duplex formation with a coarse-grained model. J. Chem. Theory Comput 2014, 10, 5020–5035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Cho SS; Pincus DL; Thirumalai D Assembly mechanisms of RNA pseudoknots are determined by the stabilities of constituent secondary structures. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 17349–17354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Savelyev A; Papoian G Chemically accurate coarse graining of double-stranded DNA. Proc. Natl. Acad. Sci. U. S. A 2010, 107, 20340–20345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Markegard CB; Fu IW; Reddy A; Nguyen HD Coarse-Grained Simulation Study of Sequence Effects on DNA Hybridization in a Concentrated Environment. J. Phys. Chem. B 2015, 119, 1823–1834. [DOI] [PubMed] [Google Scholar]
- (29).Brini E; Algaer EA; Ganguly P; Li C; Rodriguez-Ropero F; van der Vegt NFA Systematic coarse-graining methods for soft matter simulations a review. Soft Matter 2013, 9, 2108–2119. [Google Scholar]
- (30).Drukker K; Wu G; Schatz GC Model simulations of DNA denaturation dynamics. J. Chem. Phys 2001, 114, 579–590. [Google Scholar]
- (31).Dans PD; Zeida A; MacHado MR; Pantano S A coarse grained model for atomic-detailed DNA simulations with explicit electrostatics. J. Chem. Theory Comput 2010, 6, 1711–1725. [DOI] [PubMed] [Google Scholar]
- (32).Moore TC; Iacovella CR; McCabe C Derivation of coarse-grained potentials via multistate iterative Boltzmann inversion. J. Chem. Phys 2014, 140, 224104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Maffeo C; Ngo TTM; Ha T; Aksimentiev A A Coarse-Grained Model of Unstructured Single-Stranded DNA Derived from Atomistic Simulation and Single-Molecule Experiment. J. Chem. Theory Comput 2014, 10, 2891–2896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Bruant N; Flatters D; Lavery R; Genest D From Atomic to Mesoscopic Descriptions of the Internal Dynamics of DNA. Biophys. J 1999, 77, 2366–2376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Drukker K; Schatz GC A Model for Simulating Dynamics of DNA Denaturation. J. Phys. Chem. B 2000, 104, 6108–6111. [Google Scholar]
- (36).Drukker K; Wu G; Schatz GC Model simulations of DNA denaturation dynamics. J. Chem. Phys 2001, 114, 579–590. [Google Scholar]
- (37).Edens LE; Brozik JA; Keller DJ Coarse-Grained Model DNA: Structure, Sequences, Stems, Circles, Hairpins. J. Phys. Chem. B 2012, 116, 14735–14743. [DOI] [PubMed] [Google Scholar]
- (38).Li G; Shen H; Zhang D; Li Y; Wang H Coarse-Grained Modeling of Nucleic Acids Using Anisotropic GayBerne and Electric Multipole Potentials. J. Chem. Theory Comput 2016, 12, 676–693. [DOI] [PubMed] [Google Scholar]
- (39).Knotts TA; Rathore N; Schwartz DC; de Pablo JJ A coarse-grained model for DNA. J. Chem. Phys 2007, 126, 084901. [DOI] [PubMed] [Google Scholar]
- (40).Freeman GS; Hinckley DM; Lequieu JP; Whitmer JK; de Pablo JJ Coarse-grained modeling of DNA curvature. J. Chem. Phys 2014, 141, 165103. [DOI] [PubMed] [Google Scholar]
- (41).Šulc P; Romano F; Ouldridge TE; Rovigatti L; Doye JPK; Louis AA Sequence-dependent thermodynamics of a coarse-grained DNA model. J. Chem. Phys 2012, 137, 135101. [DOI] [PubMed] [Google Scholar]
- (42).Snodin BEK; Randisi F; Mosayebi M; Šulc P; Schreck JS; Romano F; Ouldridge TE; Tsukanov R; Nir E; Louis AA; Doye JPK Introducing improved structural properties and salt dependence into a coarse-grained model of DNA. J. Chem. Phys 2015, 142, 234901. [DOI] [PubMed] [Google Scholar]
- (43).Denesyuk NA; Thirumalai D A Coarse-Grained Model for Predicting RNA Folding Thermodynamics. J. Phys. Chem. B 2013, 117, 4901–4911. [DOI] [PubMed] [Google Scholar]
- (44).Denesyuk NA; Thirumalai D Crowding Promotes the Switch from Hairpin to Pseudoknot Conformation in Human Telomerase RNA. J.Am. Chem. Soc 2011, 133, 11858–11861. [DOI] [PubMed] [Google Scholar]
- (45).Xia Z; Gardner DP; Gutell RR; Ren P Coarse-grained model for simulation of RNA three-dimensional structures. J. Phys. Chem. B 2010, 114, 13497–13506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (46).Agrawal V; Arya G; Oswald J Simultaneous iterative boltzmann inversion for coarse-graining of polyurea. Macromolecules 2014, 47, 3378–3389. [Google Scholar]
- (47).Chandler D; Weeks JD; Andersen HC Van der waals picture of liquids, solids, and phase transformations. Science 1983, 220, 787–794. [DOI] [PubMed] [Google Scholar]
- (48).Dima RI; Hyeon C; Thirumalai D Extracting stacking interaction parameters for RNA from the data set of native structures. J. Mol. Biol 2005, 347, 53–69. [DOI] [PubMed] [Google Scholar]
- (49).SantaLucia J; Allawi HT; Seneviratne PA Improved nearest-neighbor parameters for predicting DNA duplex stability. Biochemistry 1996, 35, 3555–3562. [DOI] [PubMed] [Google Scholar]
- (50).SantaLucia J; Hicks D The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct 2004, 33, 415–440. [DOI] [PubMed] [Google Scholar]
- (51).Yakovchuk P; Protozanova E; Frank-Kamnetskii MD Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res 2006, 34, 564–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Olsthoorn S; Bostelaar LJ; De Rooij JF; Van Boom JH; Altona C Circular Dichroism Study of Stacking Properties of Oligodeoxyadenylates and Polydeoxyadenylate: A ThreeState Conformational Model. Eur. J. Biochem 1981, 115, 309–321. [DOI] [PubMed] [Google Scholar]
- (53).Solie TN; Schellman JA The interaction of nucleosides in aqueous solution. J. Mol. Biol 1968, 33, 61–77. [DOI] [PubMed] [Google Scholar]
- (54).Florián J; Šponer J; Warshel A Thermodynamic Parameters for Stacking and Hydrogen Bonding of Nucleic Acid Bases in Aqueous Solution: Ab Initio/Langevin Dipoles Study. J. Phys. Chem. B 1999, 103, 884–892. [Google Scholar]
- (55).Jafilan S; Klein L; Hyun C; Florian J Intramolecular base stacking of dinucleoside monophosphate anions in aqueous solution. J. Phys. Chem. B 2012, 116, 3613–3618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (56).Brown RF; Andrews CT; Elcock AH Stacking Free Energies of All DNA and RNA Nucleoside Pairs and Dinucleoside-Monophosphates Computed Using Recently Revised AMBER Parameters and Compared with Experiment. J. Chem. Theory Comput 2015, 11, 2315–2328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (57).Ts’o POP; Melvin IS; Olson AC Interaction and Association of Bases and Nucleosides in Aqueous Solutions. J. Am. Chem. Soc 1963, 85, 1289–1296. [DOI] [PubMed] [Google Scholar]
- (58).Nikolova EN; Zhou H; Gottardo FL; Alvey HS; Kimsey IJ; Al-Hashimi HM A historical account of Hoogsteen base-pairs in duplex DNA. Biopolymers 2013, 99, 955–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Jissy AK; Dutta A Design and Applications of Noncanonical DNA Base Pairs. J. Phys. Chem. Lett 2014, 5, 154–166. [DOI] [PubMed] [Google Scholar]
- (60).Sharp KA; Honig B Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem 1990, 94, 7684–7692. [Google Scholar]
- (61).Manning GS Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions I. Colligative Properties. J. Chem. Phys 1969, 51, 924–933. [Google Scholar]
- (62).Olson WK; Manning GS A configurational interpretation of the axial phosphate spacing in polynucleotide helices and random coils. Biopolymers 1976, 15, 2391. [DOI] [PubMed] [Google Scholar]
- (63).Hasted JB Liquid water: dielectric properties In Water, a Comprehensive Treatise; Plenum Press: New York, 1972; DOI: 10.1007/978-1-4684-8334-5_7. [DOI] [Google Scholar]
- (64).Doi M; Edwards SF The Theory of Polymer Dynamics; Clarendon Press: Oxford, 1986. [Google Scholar]
- (65).Brunet A; Turdin C; Salome L; Rousseau P; Destainville N; Manghi M Dependence of DNA Persistence Length on Ionic Strength of Solutions with Monovalent and Divalent Salts: A Joint TheoryExperiment Study. Macromolecules 2015, 48, 3641–3652. [Google Scholar]
- (66).Ha BY; Thirumalai D Electrostatic Persistence Length of a Polyelectrolyte Chain. Macromolecules 1995, 28, 577–581. [Google Scholar]
- (67).Odijk TJ Polyelectrolytes near the rod limit. J. Polym. Sci., Polym. Phys. Ed 1977, 15, 477. [Google Scholar]
- (68).Skolnick J; Fixman M Electrostatic Persistence Length of a Wormlike Polyelectrolyte. Macromolecules 1977, 10, 944. [Google Scholar]
- (69).Ha BY; Thirumalai D Persistence length of flexible polyelectrolyte chains. J. Chem. Phys 1999, 110, 7533. [Google Scholar]
- (70).Netz R; Orland H Variational theory for a single polyelectrolyte chain. Eur. Phys. J. B 1999, 8, 81. [DOI] [PubMed] [Google Scholar]
- (71).Honeycutt JD; Thirumalai D The nature of folded states of globular proteins. Biopolymers 1992, 32, 695–709. [DOI] [PubMed] [Google Scholar]
- (72).Murphy M; Rasnik I; Cheng W; Lohman T; Ha T Probing single stranded DNA conformational flexibility using fluorescence spectroscopy. Biophys. J 2004, 86, 2530–2537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (73).Kuznetsov SV; Shen Y; Benight AS; Ansari A A semiflexible polymer model applied to loop formation in DNA hairpins. Biophys. J 2001, 81, 2864–2875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Doose SS; Barsch H; Sauer M Polymer properties of polythymine as revealed by translational diffusion. Biophys. J 2007, 93, 1224–1234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Chen H; Meisburger SP; Pabit SA; Sutton JL; Webb WW; Pollack L Ionic strength-dependent persistence lengths of single-stranded RNA and DNA. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 799–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (76).Shen Y; Kuznetsov SV; Ansari A Loop Dependence of the Dynamics of DNA Hairpins. J. Phys. Chem. B 2001, 105, 12202–12211. [Google Scholar]
- (77).Kuznetsov SV; Ansari A A Kinetic Zipper Model with Intrachain Interactions Applied to Nucleic Acid Hairpin Folding Kinetics. Biophys. J 2012, 102, 101–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Linak MC; Dorfman KD Analysis of a DNA simulation model through hairpin melting experiments. J. Chem. Phys 2010, 133, 125101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Linak MC; Tourdot R; Dorfman KD Moving beyond Watson Crick models of coarse grained DNA dynamics. J. Chem. Phys 2011, 135, 205102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (80).de Gennes PG Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, 1979. [Google Scholar]
- (81).Le Guillou JC; Zinn-Justin J Critical Exponents for the n-Vector Model in Three Dimensions from Field Theory. Phys. Rev. Lett 1977, 39, 95–98. [Google Scholar]
- (82).Sim AYL; Lipfert J; Herschlag D; Doniach S Salt dependence of the radius of gyration and flexibility of single-stranded DNA in solution probed by small-angle x-ray scattering. Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys 2012, 86, 021901. [DOI] [PubMed] [Google Scholar]
- (83).Plumridge A; Meisburger SP; Andresen K; Pollack L The impact of base stacking on the conformations and electrostatics of single-stranded DNA. Nucleic Acids Res 2017, 45, 3932–3943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Isaksson J; Acharya S; Barman J; Cheruku P; Chattopadhyaya J Single-Stranded Adenine-Rich DNA and RNA Retain Structural Characteristics of Their Respective Double-Stranded Conformations and Show Directional Differences in Stacking Pattern. Biochemistry 2004, 43, 15996–16010. [DOI] [PubMed] [Google Scholar]
- (85).Ke C; Humeniuk M; S-Gracz H; Marszalek PE Direct Measurements of Base Stacking Interactions in DNA by Single-Molecule Atomic-Force Spectroscopy. Phys. Rev. Lett 2007, 99, 018302. [DOI] [PubMed] [Google Scholar]
- (86).Kohn JE; Millett IS; Jacob J; Zagrovic B; Dillon TM; Cingel N; Dothager RS; Seifert S; Thiyagarajan P; Sosnick TR; Hasan MZ; Pande VS; Ruczinski I; Doniach S; Plaxco KW Random-coil behavior and the dimensions of chemically unfolded proteins. Proc. Natl. Acad. Sci. U. S. A 2004, 101, 12491–12496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (87).Wilkins DK; Grimshaw SB; Receveur V; Dobson CM; Jones JA; Smith LJ Hydrodynamic Radii of Native and Denatured Proteins Measured by Pulse Field Gradient NMR Techniques. Biochemistry 1999, 38, 16424–16431. [DOI] [PubMed] [Google Scholar]
- (88).Tinland B; Pluen A; Sturm J; Weill G Persistence Length of Single-Stranded DNA. Macromolecules 1997, 30, 5763–5765. [Google Scholar]
- (89).Gubarev A; Carrillo J-M; Dobrynin YAV Scale-Dependent Electrostatic Stiffening in Biopolymers. Macromolecules 2009, 42, 5851–5860. [Google Scholar]
- (90).Toan NM; Thirumalai D On the origin of the unusual behavior in the stretching of single-stranded DNA. J. Chem. Phys 2012, 136, 235103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (91).Sambriski E; Schwartz D; de Pablo JJ A Mesoscale Model of DNA and Its Renaturation. Biophys. J 2009, 96, 1675–1690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (92).McIntosh DB; Ribeck N; Saleh OA Detailed scaling analysis of low-force polyelectrolyte elasticity. Phys. Rev. E 2009, 80, 041803. [DOI] [PubMed] [Google Scholar]
- (93).Jacobson DR; McIntosh DB; Stevens MJ; Rubinstein M; Saleh OA Single-stranded nucleic acid elasticity arises from internal electrostatic tension. Proc. Natl. Acad. Sci. U. S. A 2017, 114, 5095–5100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (94).Goddard NL; Bonnet G; Krichevsky O; Libchaber A Sequence dependent rigidity of single stranded DNA. Phys. Rev. Lett 2000, 85, 2400. [DOI] [PubMed] [Google Scholar]
- (95).Seol Y; Skinner GM; Visscher K Stretching of Homopolymeric RNA Reveals Single-Stranded Helices and Base-Stacking. Phys. Rev. Lett 2007, 98, 158103. [DOI] [PubMed] [Google Scholar]
- (96).McIntosh DB; Duggan G; Gouil Q; Saleh OA Sequence-dependent elasticity and electrostatics of single-stranded DNA: signatures of base-stacking. Biophys. J 2014, 106, 659–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (97).Marko JE; Siggia ED Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar]
- (98).Buhot A; Halperin A Effects of stacking on the configurations and elasticity of single-stranded nucleic acids. Phys. Rev. E 2004, 70, 020902. [DOI] [PubMed] [Google Scholar]
- (99).Holbrook JA; Capp MW; Saecker RM; Record MT Enthalpy and Heat Capacity Changes for Formation of an Oligomeric DNA Duplex: Interpretation in Terms of Coupled Processes of Formation and Association of Single-Stranded Helices. Biochemistry 1999, 38, 8409–8422. [DOI] [PubMed] [Google Scholar]
- (100).Baumann CG; Smith SB; Bloomfield VA; Bustamante C Ionic effects on the elasticity of single DNA molecules. Proc. Natl. Acad. Sci. U. S. A 1997, 94, 6185–6190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (101).Smith SB; Cui Y; Bustamante C Overstretching B-DNA: The Elastic Response of Individual Double-Stranded and Single-Stranded DNA Molecules. Science 1996, 271, 795–799. [DOI] [PubMed] [Google Scholar]
- (102).Harrington RE Opticohydrodynamic properties of high-molecular-weight DNA. III. The effects of NaCl concentration. Biopolymers 1978, 17, 919–936. [Google Scholar]
- (103).Sobel ES; Harpst JA Effect of Na+ on the persistence length and excluded volume of T7 bacteriophage DNA. Biopolymers 1991, 31, 1559–1564. [DOI] [PubMed] [Google Scholar]
- (104).Maret G; Weill G Magnetic birefringence study of the electrostatic and intrinsic persistence length of DNA. Biopolymers 1983, 22, 2727–2744. [DOI] [PubMed] [Google Scholar]
- (105).Mitchell JS; Glowacki J; Grandchamp AE; Manning RS; Maddocks JH Sequence-Dependent Persistence Lengths of DNA. J. Chem. Theory Comput 2017, 13, 1539–1555. [DOI] [PubMed] [Google Scholar]
- (106).Geggier S; Vologodskii A Sequence dependence of DNA bending rigidity. Proc. Natl. Acad. Sci. U. S. A 2010, 107, 15421–15426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (107).Ansari A; Kuznetsov SV; Shen Y Configurational diffusion down a folding funnel describes the dynamics of DNA hairpins. Proc. Natl. Acad. Sci. U. S. A 2001, 98, 7771–7776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (108).Vallone PM; Paner TM; Hilario J; Lane MJ; Faldasz BD; Benight AS Melting studies of short DNA hairpins: influence of loop sequence and adjoining base pair identity on hairpin thermodynamic stability. Biopolymers 1999, 50, 425–442. [DOI] [PubMed] [Google Scholar]
- (109).Owczarzy R; Tataurov AV; Wu Y; Manthey JA; McQuisten KA; Almabrazi HG; Pedersen KF; Lin Y; Garretson J; McEntaggart NO; Sailor CA; Dawson RB; Peek AS IDT SciTools: a suite for analysis and design of nucleic acid oligomers. Nucleic Acids Res 2008, 36, W163–W169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (110).Marmur J; Doty P Determination of the Base Composition of Deoxyribonucleic Acid from its Thermal Denaturation Temperature. J. Mol. Biol 1962, 5, 109–118. [DOI] [PubMed] [Google Scholar]
- (111).Sambriski EJ; Ortiz V; de Pablo JJ Sequence effects in the melting and renaturation of short DNA oligonucleotides: structure and mechanistic pathways. J. Phys.: Condens. Matter 2009, 21, 034105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (112).Moody EM; Bevilacqua PC Thermodynamic coupling of the loop and stem in unusually stable DNA hairpins closed by CG base pairs. J. Am. Chem. Soc 2003, 125, 2032–2033. [DOI] [PubMed] [Google Scholar]
- (113).Moody EM; Bevilacqua PC Folding of a stable DNA motif involves a highly cooperative network of interactions. J. Am. Chem. Soc 2003, 125, 16285–16293. [DOI] [PubMed] [Google Scholar]
- (114).Williams MC; Rouzina I; McCauley MJ Peeling back the mystery of DNA overstretching. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 18047–18048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (115).van Mameren J; Gross P; Farge G; Hooijman P; Modesti M; Falkenberg M; Wuite GJL; Peterman EJG Unraveling the structure of DNA during overstretching by using multicolor, single-molecule fluorescence imaging. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 18231–18236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (116).Zhang X; Chen H; Fu H; Doyle PS; Yan J Two distinct overstretched DNA structures revealed by single-molecule thermodynamics measurements. Proc. Natl. Acad. Sci. U. S. A 2012, 109, 8103–8108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (117).Li Z; Wang J; Li Y; Liu X; Yuan Q Self-assembled DNA nanomaterials with highly programmed structures and functions. Mater. Chem. Front 2018, 2, 423–436. [Google Scholar]
- (118).Wei X; Nangreave J; Liu Y Uncovering the Self-Assembly of DNA Nanostructures by Thermodynamics and Kinetics. Acc. Chem. Res 2014, 47, 1861–1870. [DOI] [PubMed] [Google Scholar]
- (119).Drozdetski AV; Tolokh IS; Pollack L; Baker N; Onufriev AV Opposing effects of Multivalent Ions on the Flexibility of DNA and RNA. Phys. Rev. Lett 2016, 117, 028101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (120).Dai L; Mu Y; Nordenskiold L; van der Maarel JRC Molecular Dynamics Simulation of Multivalent-Ion Mediated Attraction between DNA Molecules. Phys. Rev. Lett 2008, 100, 118301. [DOI] [PubMed] [Google Scholar]
- (121).Hsiao PY; Luijten E Salt-induced collapse and reexpansion of highly charged flexible polyelectrolytes. Phys. Rev. Lett 2006, 97, 148301. [DOI] [PubMed] [Google Scholar]
- (122).Deserno M; Jiminez-Angeles F; Holm C; Lozada-Cassou M Overcharging of DNA in the Presence of Salt: Theory and Simulation. J. Phys. Chem. B 2001, 105, 10983–10991. [Google Scholar]
- (123).Denesyuk N; Thirumalai D How do metal ions direct ribozyme folding? Nat. Chem 2015, 7, 793–801. [DOI] [PubMed] [Google Scholar]
- (124).Reddy G; Thirumalai D Dissecting Ubiquitin Folding Using the Self-Organized Polymer Model. J. Phys. Chem. B 2015, 119, 11358–11370. [DOI] [PubMed] [Google Scholar]
- (125).McGinty RK; Tan S Nucleosome Structure and Function. Chem. Rev 2015, 115, 2255–2273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (126).Dickey TH; Altschuler SE; Wuttke DS Single-Stranded DNA-Binding Proteins: Multiple Domains for Multiple Functions. Structure 2013, 21, 1074–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.