Likelihood-based analysis of outcome-dependent sampling designs with longitudinal data

Abstract

The use of outcome-dependent sampling with longitudinal data analysis has previously been shown to improve efficiency in the estimation of regression parameters. The motivating scenario is when outcome data exist for all cohort members but key exposure variables will be gathered only on a subset. Inference with outcome-dependent sampling designs that also incorporates incomplete information from those individuals who did not have their exposure ascertained has been investigated for univariate but not longitudinal outcomes. Therefore, with a continuous longitudinal outcome, we explore the relative contributions of various sources of information toward the estimation of key regression parameters using a likelihood framework. We evaluate the efficiency gains that alternative estimators might offer over random sampling, and we offer insight into their relative merits in select practical scenarios. Finally, we illustrate the potential impact of design and analysis choices using data from the Cystic Fibrosis Foundation Patient Registry.

1 |. INTRODUCTION

Because of the natural constraint of limited financial and patient resources, the development of novel and statistically efficient study designs continues to be a priority for scientific investigators. For example, patient registries and other cohorts can provide readily accessible sources of longitudinal data; however, when novel candidate biomarkers are discovered, limited availability of biological specimens together with financial constraints may require investigators to target only a subset of patients for detailed additional study. In such cases, outcome-dependent sampling (ODS) designs, which collect new covariate data on a subset of individuals who are selected based on characteristics of their outcome variables, can provide an efficient and cost-effective strategy to conduct biomarker substudies that leverage existing cohort information.

Methods that selectively subsample highly informative individuals have a long history of offering efficiency gains over simple random sampling. The fundamental case-control study has been frequently used as a cost-effective way to study the association between rare binary outcomes and key exposures.¹ In the more general regression setting, ODS designs typically require appropriately tailored estimation to account for purposeful subsample selection, and a naïve analysis may yield biased estimation. To avoid this complexity, continuous outcomes are sometimes dichotomized and then simply analyzed using logistic regression. However, dichotomization will generally yield reduced power to detect an association and makes comparisons across different studies difficult if there is not a standardly accepted and meaningful cutpoint.^2–4 When the association of an exposure with a continuous longitudinal outcome is of primary interest, ODS designs and analysis strategies offer the prospect of valid inference and increased efficiency at a reduced cost compared with traditional methods.^5,6

Although ODS designs and analysis methods have been proposed in the statistical literature, there is incomplete applied guidance regarding how to choose a specific sampling design, and limited study of the statistical information that is recovered using various analysis approaches. In particular, some strategies may not use covariate information or outcome information on nonsubsampled subjects. Therefore, we provide a careful mathematical and numerical characterization of both the design and the likelihood-based analysis choices.

We focus in this manuscript on detailing all of the candidate elements that could be used for a full likelihood or Bayesian analysis. We recognize that alternative estimation approaches could be used to account for the design-based biased sample such as inverse probability weighting (IPW)⁷ or regression calibration approaches.^8,9 However, these semi-parametric strategies generally sacrifice potential efficiency gains for protection against model violation (robustness), and our primary goal in this manuscript is to evaluate the full information potential of various design choices. Therefore, likelihood-based analysis provides a theoretical bound for efficiency comparisons. Future work that compares likelihood-based and semiparametric alternatives is certainly of interest.

In this manuscript, we first detail the information that is potentially available from all aspects of the data including the conditional distribution of covariates given a subject was sampled. For the first time in the statistical literature, we explicitly consider the likelihood contribution for the longitudinal outcomes of those subjects not selected for detailed exposure evaluation. In addition, we provide new results clarifying when the conditional distribution of covariates given sampling contains any information relevant to target parameters. Second, we consider the relative efficiency of these analysis alternatives under sampling design choices where different thresholds that trigger sampling are considered or where different sampling fractions are considered. Our comprehensive evaluation of design and likelihood-based analysis options provides insight for applied statisticians who may wish to consider use of ODS with longitudinal cohort data and for researchers seeking to use collected data more completely.

2 |. MOTIVATION AND BACKGROUND

Cystic fibrosis (CF), a genetic disease manifesting primarily in pulmonary dysfunction, affects about 30 000 people in the United States. The Cystic Fibrosis Foundation Patient Registry (CFFPR) collects detailed longitudinal data on health outcomes, clinical care, and demographics of CF patients receiving care at accredited centers.¹⁰ Many patients also contribute biological specimens upon enrollment in the registry. When a novel biomarker is discovered, the registry can provide a rich resource for studying the association between new markers or exposures and relevant longitudinal outcomes such as lung function over time.

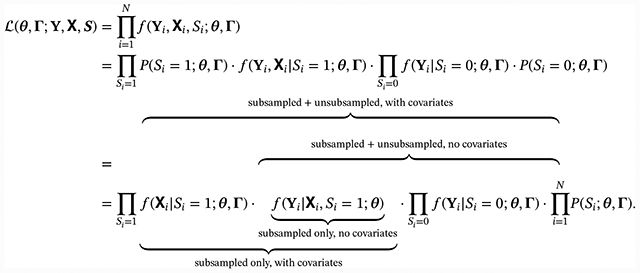
Within the CFFPR, suppose we wish to study the association of lung function denoted as Y_i = vec(Y_ij), measured repeatedly at times T_i = vec(T_ij), with a novel marker M_i to be ascertained at baseline; call this collection of covariates X_i = [T_i, M_i], and suppose the marginal distribution of covariates is indexed by a parameter Γ. Moreover, we assume that for practical reasons, M_i can only be ascertained in a subset of patients for whom Y_i is already known. We denote the subset with the indicator S_i = 1 for sampled subjects and S_i = 0 for nonsampled subjects. We also assume that we choose the subset based strictly on the outcome or some summary of the outcome that is conditionally independent of covariate values or ω(Y_i) = P(S_i = 1|Y_i, X_i) = P(S_i = 1|Y_i). If θ is the collection of regression parameters and variance components of interest from the greater CFFPR population, we can write the likelihood from the observed subset data using Bayes rule:

$$\begin{gathered} L(\mathit{\theta },\mathbf{\Gamma };\mathbf{\text{Y}},\mathbf{\text{X}},\mathit{S})=\prod _{s_i\in 1}f\left({\mathbf{\text{Y}}}_i,{\mathbf{\text{X}}}_i|S_i=1;\mathit{\theta },\mathbf{\Gamma }\right) \\ =\prod _{s_i\in 1}\frac{P\left(S_i=1|{\mathbf{\text{Y}}}_i,{\mathbf{\text{X}}}_i\right)\cdot f\left({\mathbf{\text{Y}}}_i|{\mathbf{\text{X}}}_i;\mathit{\theta }\right)\cdot g\left({\mathbf{\text{X}}}_i;\mathbf{\Gamma }\right)}{P\left(S_i=1;\mathit{\theta },\mathbf{\Gamma }\right)} \\ =\prod _{S_i\in 1}\frac{\omega \left({\mathbf{\text{Y}}}_i\right)\cdot f\left({\mathbf{\text{Y}}}_i|{\mathbf{\text{X}}}_i;\mathit{\theta }\right)\cdot g\left({\mathbf{\text{X}}}_i;\mathbf{\Gamma }\right)}{P\left(S_i=1;\mathit{\theta },\mathbf{\Gamma }\right)}. \end{gathered}$$ (1)

By design, ω(Y_i) is strictly a function of the observed outcome, so it does not depend on θ and can be ignored in maximizing the likelihood. The scaling factor P(S_i = 1), however, involves both the distributions of X_i and S_i|X_i (henceforth written simply as [X_i] and [S_i|X_i]), and since the latter is related to θ under biased sampling, this term must be taken into account for valid inference on θ. While the marginal distribution g(X_i) is unrelated to θ, g(X_i) is involved in the scaling factor P(S_i = 1) and cannot be ignored in analysis as is typically done under random sampling designs.

Previous work has analyzed ODS designs using likelihood approaches similar to that outlined above. Zhou et al^11–13 and Weaver and Zhou¹⁴ demonstrated the potentially increased efficiency of ODS designs relative to a random sample for cross-sectional data with scalar continuous outcomes. For cross-sectional data, Zhou et al^11,15 used an empirical likelihood estimate of g(X_i); a profile likelihood for the same problem was used for clustered data by Neuhaus et al.^16,17 For longitudinal data, Schildcrout et al⁵ sidestepped the issue of modeling or estimating g(X_i) by further conditioning on the exposure X_i, possibly at the expense of a loss of additional information, and then maximizing an “ascertainment-corrected” likelihood to produce an estimator of θ. Importantly, Schildcrout et al⁵ showed that the sampling design options have potentially large impacts on regression parameter estimation efficiency and could lead to a doubling in efficiency compared with a random sample for targeted parameters.

The approaches discussed above all analyzed only those individuals whose exposure was ascertained (S_i = 1) and discarded all unsubsampled subjects (S_i = 0). However, including unsubsampled individuals in the analysis would yield an expanded likelihood function that could also be maximized to obtain valid and possibly more efficient estimators of θ. While unsubsampled subjects do not have their exposure measured and cannot directly provide information on the relationship between the expensive covariate and the outcome, the observed outcomes of unsubsampled individuals provide information on the population-level mixture of covariate-specific mean outcomes or marginal means. Thus, including these individuals in estimation and inference has the potential to improve inference on some parameters or combinations of parameters, at added computational but no additional logistical cost. A complete likelihood was explored by Weaver and Zhou¹⁴ for univariate outcome data using an estimated likelihood approach. Later work by Song et al¹⁸ similarly produced a “restricted maximum likelihood” estimator for cross-sectional data that used all individuals. Pseudoscore¹⁹ and semiparametric maximum likelihood estimation²⁰ methods that included unsubsampled individuals were also found to perform well in simulations. More recently, Schildcrout et al⁶ examined the ability of imputation strategies to recover information from unsubsampled individuals for ODS designs with longitudinal data.

Likelihood-based ODS methods are not the only analysis approach for longitudinal data with covariates that are missing by design. In particular, weighting methods, such as the classic Horvitz-Thompson estimator⁷ and augmented IPW estimators,²¹ provide a class of alternatives that may be used that are robust to model misspecification and may in some cases achieve semiparametric efficiency. The likelihood-based ODS methods we consider here rely on characterization of the tails of the normal distribution; given this fact, concerns about balancing robustness with efficiency are reasonable and worthy of investigation. However, we restrict the focus of the current work to likelihood-based estimators only, with the goal of characterizing the parametric efficiency that may come from various sources of information toward the estimation of key regression parameters in a likelihood framework.

Collectively, this body of work has demonstrated that likelihood-based ODS designs can provide substantial efficiency gains for regression parameters of interest compared with a random sample. However, approaches to creating valid likelihood-based estimators have varied with respect to both the specific design and the choice of analysis for the resulting biased subsample. Decisions about which likelihood to maximize and whether to include information from the exposure and/or unsubsampled individuals have been explored in some circumstances, but not systematically for longitudinal data. Hence, researchers are likely unsure of which estimator to implement and under what specific ODS design. For a continuous longitudinal outcome, this paper explores the contributions of various sources of information toward the estimation of key regression parameters in a likelihood framework. For simplicity, we assume the ascertained exposure to be binary in simulations, although the statistical arguments extend easily to exposures with an arbitrary number of levels.

The following framework could easily accommodate the presence of additional inexpensive covariates that are measured for all subjects; for simplicity, these are omitted here. Section 3 introduces 6 likelihood-based regression parameter estimators that we compare, while Section 4 presents operating characteristics of these estimators and guidance on selecting design parameters. In Section 5, we illustrate the results with an application to a hypothetical biomarker substudy using the CFFPR dataset and finally offer a discussion of our results in Section 6.

3 |. METHODS

3.1 |. Notation and design

In this section, we explore a collection of valid candidate likelihood-based estimators of the regression parameters of interest based on the usual linear mixed model for longitudinal data. Specifically, suppose we have a cohort of N subjects, each measured n_i times, so that for the n_i × 1 continuous outcome vector Y_i, i = 1, …, N, the linear mixed model of interest as proposed by Laird and Ware²² is

$${\mathbf{\text{Y}}}_i={\mathbf{\text{X}}}_i\mathit{\beta }+{\mathit{\text{Z}}}_i{\mathbf{b}}_i+{ϵ}_i,$$

where X_i = [1, T_i, M_i, M_i × T_i] is the n_i × 4 design matrix. We define the vector of times T_i = vec(T_ij), j = 1, …, n_i, and M_i the retrospectively ascertained time-invariant covariate. The 4 × 1 vector β contains the regression parameters of interest, while Z_i is the design matrix for the intercept and slope random effects. The vector b_i = (b_i0, b_i1)^T is assumed to be multivariate normally distributed with 2 × 1 mean vector 0 and covariance matrix D consisting of diagonal elements ${\left({\sigma }_{b_0}^2,{\sigma }_{b_1}^2\right)}^T$ and off-diagonal covariance $Cov\left(b_{i0},b_{i1}\right)=\rho {\sigma }_{b_0}{\sigma }_{b_1}$. The n_i × 1 vector of errors ϵ_i is assumed to be conditionally independent and normally distributed with common variance ${\sigma }_e^2$. We transform the variance components to $\gamma ={\left(\text{log}\left({\sigma }_{b_0}^2\right),\text{log}\left(\frac{1+\rho }{1-\rho }\right),\text{log}\left({\sigma }_{b_1}^2\right),\text{log}\left({\sigma }_e^2\right)\right)}^T$ for ease of estimation, and the parameter vector on which we focus is denoted θ = (β, γ)^T.

For this work, we assume that all N members of the cohort have completely observed outcome vector Y_i and that M_i is an expensive covariate that is ascertained only for a subsample of N_S individuals. We consider a simple time-invariant covariate, such as a novel marker retrospectively measured on a stored biological sample. For subjects who are subsampled, the complete information vector on (Y_i, T_i, M_i) is available; for the remaining N − N_S = N_NS subjects who are not subsampled, only the vector (Y_i, T_i) is known.

For longitudinal or clustered data, specification of the biased ODS sampling design presents an added level of complexity compared to cross-sectional data, since different aspects of the vector Y_i can be chosen to indicate sampling. One simple way to define an ODS scheme for longitudinal data is to transform the outcome vector into a low-dimensional summary that provides a natural ordering for subsampling. For example, for binary outcome data, this has been accomplished by preferentially sampling based on the number of cases in a cluster^16,17 or based on clusters whose members are not all 0 or 1.²³ For continuous longitudinal outcomes considered here, we follow the example of Schildcrout et al⁵ by defining a class of subsampling variables Q_i, which is a low-dimensional summary of the outcome vector Y_i and often would be chosen as a linear combination of the longitudinal outcome, Q_i = W_iY_i for some m×n_i matrix W_i. Briefly, we consider subsampling based on a regression feature using the vector $Q_i={\left({\mathbf{\text{X}}}_{ti}^T{\mathbf{\text{X}}}_{ti}\right)}^{-1}{\mathbf{\text{X}}}_{ti}^T{\mathbf{\text{Y}}}_i$, where X_ti = [1, T_i]. Here, the summary is simply the result of regressing outcome vector Y_i on time for each cohort member. We choose to focus subsampling on only one element of Q_i, either the individual intercept or slope, although bivariate subsampling based on Q_i is also possible.⁵ The resulting values of the sampling variable $q_i\in {ℝ}^1$ will fall into 1 of 3 regions: region 1 (−∞, a₁), region 2 [a₁, a₂), or region 3 [a₂, ∞), where a₁ and a₂ are predetermined constants. Within each region, subjects are subsampled with constant probability ω_k(q) = P(S_i = 1|q_i ∈ R_k), k = 1, 2, 3, which may differ by stratum but is assumed to be a constant chosen by design. As in previous work, we generally wish to oversample subjects with extreme values of q_i. Although we choose to examine only ODS designs based on these 2 simple features, other approaches to biased sampling could be equally valid provided the design is adequately considered in the analysis stage.

3.2 |. Likelihood

Under the longitudinal data scenario described above, the complete observed data likelihood can be written as

(2)

As seen in Equation 2, the unconditional observed data likelihood can be factored into terms corresponding to several conditional likelihoods that could be used to yield estimators of θ. For the present, we consider only complete balanced designs; T_i may be assumed to be independent of other variables in this case. Under random sampling, the distributions of [X_i|S_i] and [S_i] do not depend on θ and add no information to inference; conventional regression approaches condition upon X_i and S_i for this reason. Under biased sampling, however, both may contain information about θ and could potentially be incorporated in the maximization to yield efficiency gains. Similarly, including unsubsampled individuals in the analysis, either conditionally upon or jointly with covariate information, would yield a likelihood function that could also be maximized to obtain valid estimators of θ.

3.3 |. Analysis: subsampled only

Equation 2 shows that a variety of valid likelihoods derived from the complete data likelihood could be used as a basis for inference. One simple analysis option would be to consider the conditional likelihood (which we refer to as “subsampled only, no covariates”, or SO,NC)

$${\mathcal{L}}_{SO,NC}(\mathit{\theta };\mathbf{\text{Y}},\mathbf{\text{X}},\mathit{S})=\prod _{S_i=1}f\left({\mathbf{\text{Y}}}_i|{\mathbf{\text{X}}}_i,S_i=1;\mathit{\theta }\right),$$ (3)

considered by Schildcrout et al,⁵ which uses information from subsampled individuals only, conditional upon the marker value and sampling. The resulting conditional log-likelihood can be written as a term that treats subsampled data as if it had come from a random sample, together with an “ascertainment-correction” term AC₀(M_i, T_i; θ) ≡ P(S_i = 1|M_i, T_i; θ), which accounts for the biased sampling design.

A second option for analyzing only subsampled individuals is to add information from the marker value conditional on sampling by analyzing the joint conditional likelihood (“subsampled only, with covariates”, or SO,WC). This approach may be attractive since the conditional distribution [X_i|S_i] may contain additional statistical information that could potentially increase efficiency; however, it additionally requires estimating the parameter Γ that indexes the marginal distribution of X_i (for binary marker M_i, this is simply the marker population prevalence p). We can write the joint conditional likelihood as

$${\mathcal{L}}_{SO,WC}(\mathit{\theta },\mathbf{\Gamma };\mathbf{\text{Y}},\mathbf{\text{X}},\mathit{S})=\prod _{S_i=1}f\left({\mathbf{\text{X}}}_i|S_i=1;\mathit{\theta },\mathbf{\Gamma }\right)\cdot f\left({\mathbf{\text{Y}}}_i|{\mathbf{\text{X}}}_i,S_i=1;\mathit{\theta }\right).$$ (4)

The bias induced by the sampling design can again be corrected through an ascertainment correction; in contrast to SO,NC, in this case, Γ must also be estimated. Moreover, the distribution upon which the SO,WC likelihood is based can be related to the SO,NC likelihood in the following way:

$$\begin{gathered} f\left(Y_i,{\mathbf{\text{X}}}_i|S_i=1;\mathit{\theta },\mathbf{\Gamma }\right)=f\left(Y_i|{\mathbf{\text{X}}}_i,S_i=1;\mathit{\theta }\right)\cdot P\left({\mathbf{\text{X}}}_i|S_i=1;\mathit{\theta },\mathbf{\Gamma }\right) \\ =f\left(Y_i|{\mathbf{\text{X}}}_i,S_i=1;\mathit{\theta }\right)\cdot \frac{P\left(S_i=1|{\mathbf{\text{X}}}_i;\mathit{\theta }\right)\cdot P\left({\mathbf{\text{X}}}_i;\mathbf{\Gamma }\right)}{P\left(S_i=1;\mathit{\theta },\mathbf{\Gamma }\right)} \\ =f\left(Y_i|{\mathbf{\text{X}}}_i,S_i=1;\mathit{\theta }\right)\cdot \frac{A{C}_0\left(M_i,T_i;\mathit{\theta }\right)\cdot P\left({\mathbf{\text{X}}}_i;\mathbf{\Gamma }\right)}{A{C}_1\left({\mathit{T}}_i;\mathit{\theta },\mathbf{\Gamma }\right)}. \end{gathered}$$ (5)

The marginal probability of being sampled, AC₁, can be viewed as the expectation of the covariate-specific ascertainment correction AC₀(M_i, T_i; θ) taken over the distribution of M_i conditional on T_i and assuming T_i is fixed by design, since

$$\begin{gathered} A{C}_1\left({\mathit{T}}_i;\mathit{\theta },\mathbf{\Gamma }\right)=\int P\left(S_i=1,M_i=m;{\mathit{T}}_i,\mathit{\theta },\mathbf{\Gamma }\right)dm \\ =\int P\left(S_i=1|M_i=m,{\mathit{T}}_i;\mathit{\theta }\right)\cdot f\left(M_i|{\mathit{T}}_i;\mathbf{\Gamma }\right)dm \\ =\int A{C}_0\left(M_i=m,{\mathit{T}}_i;\mathit{\theta }\right)\cdot f\left(M_i|{\mathit{T}}_i,\mathit{\theta },\mathbf{\Gamma }\right)dm \\ ={\mathbb{E}}_{M_i|{\mathit{T}}_i}\left[A{C}_0\left(M_i,{\mathit{T}}_i;\mathit{\theta },\mathbf{\Gamma }\right)\right]. \end{gathered}$$

It can be shown (Appendix S1) that in complete and balanced design situations (ie, when all individuals are observed n_i ≡ n times and those observation times are the same across all individuals), the second term in Equation 5 is essentially a reparameterization of Γ, the parameters that index the marginal distribution of M_i. As such, this term provides no information about θ for complete and balanced designs, and the resulting estimators SO,NC and SO,WC will be the same with respect to the target parameter θ, although SO,WC additionally estimates the marginal distribution parameter Γ (the marker population prevalence p = P(M_i = 1) for binary M_i). When the design is not balanced, and cohort members may be observed at times that differ from one another, AC₀(M_i, T_i; θ) may vary by marker/time combination, and the inclusion of covariates in inference may offer some additional information in this case.

3.4 |. Analysis: inclusion of unsubsampled subjects

While estimators SO,NC and SO,WC exclusively use information from subsampled individuals, the inclusion of unsubsampled subjects may provide additional statistical information. While unsubsampled subjects do not have the marker measured and cannot directly provide information on the relationship of the expensive covariate with the outcome, the observed outcomes of unsubsampled individuals provide information on the population-level mixture of marker-specific mean outcomes. For example, for a binary marker M_i, at baseline, the mean outcomes for subjects with M_i = 0 and M_i = 1 under the usual linear mixed model are β₀ and β₀ + β_M, respectively. If p is the prevalence of the marker, observing the mean of Y among all cohort members at baseline would then give an estimate of $\mathbb{E}\left({\mathbf{\text{Y}}}_{i1}|T_{i1}=0\right)={\beta }_0+{\beta }_{M}p$; the variance of Y_i1 is likewise related to combinations of regression parameters.

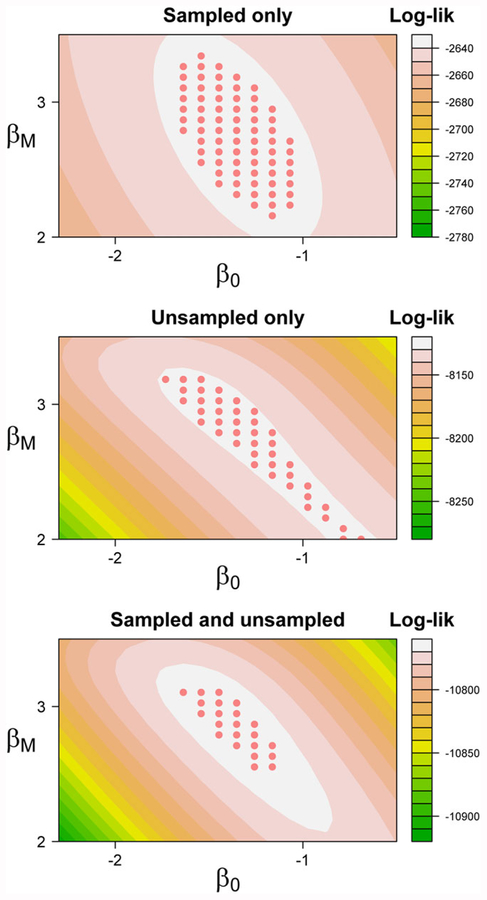
To illustrate the potential contributions of subsampled and unsubsampled subjects to inference, we generated simulated data under regression parameters β^T = (β₀, β_T, β_M, β_M×T) = (−1.5, −0.15, 3, −0.15) for N = 1000 cohort members each with n_i = 6 observations, of whom N_S = 250 were randomly subsampled; the marker population prevalence was 25%. Figure 1 shows representative contours from subsampled and unsubsampled subjects’ contributions to the profile log-likelihood for these parameters under random sampling and illustrates the possible impact of including these individuals in the analysis. Notably, the log-likelihood contribution of unsubsampled subjects (middle panel of Figure 1) describes a ridge of linear combinations of the parameters related to the baseline mean of Y among all subjects, subject to constraints imposed by the observed variance. Adding information from the unsubsampled subjects to the usual log-concave likelihood contributions from subsampled subjects (top panel of Figure 1) has the potential to affect both estimation (ie, orientation) and precision (the area of a 95% confidence region obtained by inversion), as seen in the bottom panel.

FIGURE 1.

Profile log-likelihood contours showing the contribution of unsubsampled subjects under random sampling and true regression parameter β^T = (β₀, β_T, β_M, β_M×T) = (−1.5, −0.15, 3, −0.15). Marker prevalence for the cohort of 1000 was 25%, and 250 subjects were subsampled. The characteristic “ridge” in the middle panel reflects the fact that only the estimated population-level mean outcome is observed in these subjects. While many different combinations of regression parameters could give rise to the observed data, adding this information to an analysis based on subsampled subjects alone (top panel) may potentially improve inference for some parameters. The inclusion of unsubsampled individuals both changes the precision and orientation of a 95% confidence region obtained by inversion (bottom panel)

Incorporating the entire cohort of subsampled and unsubsampled subjects into the analysis and without including covariate information, we obtain estimator SU,NC (“subsampled/unsubsampled, no covariates”) by maximizing over the following likelihood:

$${\mathcal{L}}_{\mathit{S}U,NC}(\mathit{\theta },\mathbf{\Gamma };\mathbf{\text{Y}},\mathbf{\text{X}},S)=\prod _{S_i=1}f\left({\mathbf{\text{Y}}}_i|{\mathbf{\text{X}}}_i,S_i=1;\mathit{\theta }\right)\cdot \prod _{S_i=0}f\left({\mathbf{\text{Y}}}_i|S_i=0;\mathit{\theta },\mathbf{\Gamma }\right).$$

Maximizing this conditional likelihood involves estimating the marginal marker distribution’s parameter Γ; however, information on Γ is available only through the mixture distribution contributed by unsubsampled individuals. While this parameter is formally identifiable, it may not be easily estimable. To address this concern, for binary M_i, we also evaluated another version of this estimator (denoted SU,NC + PI) that maximizes the same likelihood but uses a plug-in estimator of Γ = p based on inverse probability of sampling weighting, $\widehat{p}=\sum _{i=1}^N\frac{M_i\cdot \mathbb{I}\left(S_i=1\right)}{N\cdot \omega \left(q_i\right)}$. Via the weak law of large numbers, we expect the plug-in estimator to be consistent for p, since it has the proper expectation and finite variance.

$${\mathbb{E}}_{M,Q,S,T}\left[M\cdot \frac{\mathbb{I}(S=1)}{\omega (q)}\right]={\mathbb{E}}_{M,Q,T}\left[\frac{M}{\omega (q)}{\mathbb{E}}_S[\mathbb{I}(S=1|M,\mathit{T},Q\in R_K)]\right]={\mathbb{E}}_M[M]=p.$$

Just as estimator SO,WC added the covariate information to the conditional likelihood of estimator SO,NC, we could likewise add covariate information to estimator SU,NC. In contrast to the analyses that considered only subsampled individuals, including covariate information may prove beneficial when analyzing the entire cohort, since the covariate information from subsampled individuals can help to inform about the mixture distribution of unsubsampled subjects, which in turn informs inference about θ. Therefore, we also consider maximizing the likelihood conditioning only on sampling status (“subsampled/unsubsampled, with covariates”, or SU,WC):

$${\mathcal{L}}_{\mathit{S}U,WC}(\mathit{\theta },\mathbf{\Gamma };\mathbf{\text{Y}},\mathbf{\text{X}},S)=\prod _{S_i=1}f\left({\mathbf{\text{X}}}_i|S_i=1;\mathit{\theta },\mathbf{\Gamma }\right)\cdot f\left({\mathbf{\text{Y}}}_i|{\mathbf{\text{X}}}_i,S_i=1;\mathit{\theta }\right)\cdot \prod _{S_i=0}f\left({\mathbf{\text{Y}}}_i|S_i=0;\mathit{\theta },\mathbf{\Gamma }\right).$$

Finally, we could analyze the unconditional likelihood (Equation 2), incorporating information from all subjects, marker values, time, and sampling status. We refer to the resulting estimator as “UC” (unconditional).

In summary, we have delineated a series of likelihood-based estimators of θ that exploit different parts of the unconditional likelihood and hence differ in the information used. Each conditional and unconditional likelihood $\mathcal{L}$ may then be maximized to produce a valid estimator of θ by solving the system $\sum _{i=1}^N\frac{d{\mathcal{L}}_i(\widehat{\mathit{\theta }})}{d\mathit{\theta }}=0$ (or $\sum _{i=1}^N\frac{d{\mathcal{L}}_l(\widehat{\mathit{\theta }},\widehat{\mathbf{\Gamma }})}{d(\mathit{\theta },\mathbf{\Gamma })}=0$ for likelihoods that additionally estimate Γ) using the Newton-Raphson algorithm; the covariance of $\widehat{\mathit{\theta }}$ can then be estimated by $\sum _{i=1}^N\left(\frac{d{\mathcal{L}}_i(\widehat{\theta })}{d\theta }\cdot {\frac{d{\mathcal{L}}_i(\widehat{\theta })}{d\theta }}^T\right)$. Intuitively, we expect that including unsubsampled individuals in inference will result in additional statistical efficiency, while utilizing covariate information among subsampled subjects will not add precision under balanced designs. A careful evaluation of the gains in efficiency, balanced against the complexity of implementation, that are available for this class of designs is necessary to inform practice; we provide a comparison of these estimators with respect to consistency and efficiency in Section 4.

4 |. ASSESSMENT OF OPERATING CHARACTERISTICS

4.1 |. Setup and data-generating mechanism

Previous work by Schildcrout et al⁵ showed large efficiency gains from an ODS design compared with a random sample of the same size, while Weaver and Zhou¹⁴ demonstrated the added utility of analyzing unsampled individuals for cross-sectional data. Here, we evaluate the added incremental benefit of including information about covariates and/or information about unsubsampled subjects for longitudinal data with a continuous outcome and an expensive binary time-invariant covariate. We compare the behavior of the likelihood-based estimators described in Section 3 to a random sample of the same size with respect to bias and efficiency, both analytically and through simulation.

For each replication, we generated independent and identically distributed data for N = 1000 subjects from the linear model

$${\mathbf{\text{Y}}}_{ij}={\beta }_0+{\beta }_T{t}_{ij}+{\beta }_M{m}_i+{\beta }_{M\times T}{t}_{ij}{m}_i+b_{0i}+b_{1i}{t}_{ij}+e_{ij},$$

where β = (β₀, β_T, β_M, β_M×T) = (10, −0.25, −0.75, 0.5), i = 1, …, 1000, j = 1, …, n_i, where n_i was either 6 or 11 and observation times were equally spaced. The expensive binary time-invariant marker, M_i, had a prevalence of 10%. Random effects b_i = (b_0i, b_1i) were multivariate normally distributed with mean 0 and 2 × 2 covariance matrix variance D, with variances ${\sigma }_{b_0}^2$ and ${\sigma }_{b_1}^2$ on the diagonal and covariance off-diagonal element of 0 (ρ = 0). Errors e_ij were generated to be conditionally independent and normally distributed with mean 0 and variance ${\sigma }_e^2$. We examined estimator performance under 2 variance component scenarios: one with low subject-to-subject heterogeneity $\left({\sigma }_{b_0}^2=4,{\sigma }_{b_1}^2=0.25,{\sigma }_e^2=1\right)$ and one with high subject-to-subject heterogeneity $\left({\sigma }_{b_0}^2={\sigma }_{b_1}^2={\sigma }_e^2=4\right)$. Simulation results reported here are based on 1000 replications.

Subjects were selected for marker ascertainment based on the 2×1 vector of subject-specific regression coefficients $Q_i={\left({\mathbf{\text{X}}}_{ti}^T{\mathbf{\text{X}}}_{ti}\right)}^{-1}{\mathbf{\text{X}}}_{ti}{\mathbf{\text{Y}}}_i$, where X_ti = [1, T_i]. We considered 2 sampling schemes, selecting either subjects for subsampling based on the value of their subject-specific intercept or their subject-specific slope, both of which we derived from regressing each cohort member’s outcome vector on observation times. In each case, we selected a subsample of 250 on average, with an average of 100 individuals from the lowest 20th percentile, 50 individuals from the middle 60%, and 100 individuals from the highest 20th percentile of the subsampling variable q_i (either individual intercept or slope). Both intercept- and sloped-based outcome-dependent samples were analyzed using the approaches described in Section 3. To ensure that estimates obeyed parameter constraints such as positive variance, we transformed the variance components as described in Section 3.1 and used the Newton-Raphson algorithm to maximize over the parameter vector θ = (β, γ)^T, plus the transformed population marker prevalence, logit(p), for estimators that required it. We compare the estimates resulting from each ODS design/analysis combination with the estimate obtained from a random sample of 250 individuals and with the estimate obtained from a usual linear mixed model using all 1000 individuals from the original simulated cohort. Although the prospect of more efficient estimation of regression parameters is the primary motivation for this class of designs, we compare results of each estimator over the entire parameter vector θ, to more completely characterize the possible benefits; in some applications in which characterizing the heterogeneity of participant outcomes, the parameters in γ may likewise be of interest.

4.2 |. Validity and relative efficiency: simulation

We evaluated each estimator in terms of the average percent relative bias and efficiency relative to a random sample of the same size (on average). Results are presented for a constant cluster size of n_i = 6; results when n_i = 11 were qualitatively similar and are not shown. For all design and analysis methods, and under both low and high subject-to-subject heterogeneity, estimates for regression and variance parameters showed little bias, generally <5% (Tables S1 and S2). Analysis methods that additionally estimated the population prevalence p of the expensive covariate were likewise unbiased, with the exception of estimator SU,NC. This method experienced convergence issues related to the parameter p a substantial fraction of the time, which led to widely variable estimates of p, although the other parameters of interest continued to be correctly estimated.

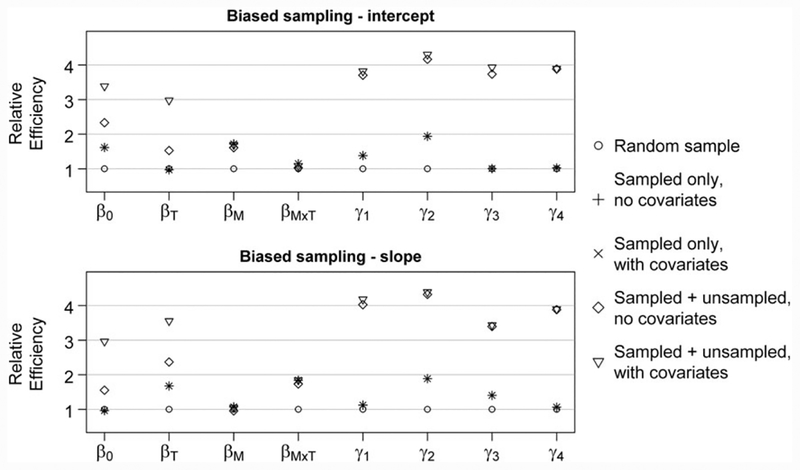
Consistent with results seen by Schildcrout et al,⁵ estimator SO,NC offered major efficiency gains over random sampling for selected regression parameters, which depended on the subsampling design used (Figure 2). When the subject-specific intercept was chosen as the subsampling variable, the greatest efficiency gains occurred for time-invariant covariate parameters β₀ and β_M (relative efficiencies up to 3.44 and 1.56, respectively; see Table S1), while time-varying covariate parameters β_T and β_M×T had the greatest gains when a subject-specific slope was used (relative efficiencies up to 3.43 and 1.48, respectively). As previously discussed, when only subsampled individuals’ information was analyzed, incorporating covariate information (estimator SO,WC) into inference did nothing to change the relative efficiency of the estimator compared with the conditional version (estimator SO,NC). In fact, these 2 estimators were numerically equivalent, up to convergence of the respective algorithms, as expected.

FIGURE 2.

Relative efficiencies of outcome-dependent sampling estimators via simulation, under low subject-to-subject heterogeneity, compared with a random sample of N_S = 250. The vector γ represents transformed variance components, where $\mathit{\gamma }={\left(\text{log}\left({\sigma }_{b_0}^2\right),\text{log}\left(\frac{1+\rho }{1-\rho }\right),\text{log}\left({\sigma }_{b_1}^2\right),\text{log}\left({\sigma }_e^2\right)\right)}^T$. For comparison, note that analyzing full cohort (N = 1000) would give a true relative efficiency of 4

Adding unsubsampled individuals to the analysis produced substantial gains in efficiency for some regression parameters and for all variance components, regardless of the ODS design. For variance components, estimators that included unsubsampled subjects (estimators SU,NC, SU,WC, and UC) recovered nearly all the information from the full cohort; for regression parameters, only β₀ and β_T had improved efficiency. Augmenting information from unsubsampled individuals without also considering covariate information (estimator SU,NC) produced an estimator that often had convergence issues. Unlike the situation when only subsampled individuals were considered, analyzing the joint likelihood improved efficiency over the conditional likelihood when unsubsampled individuals were included (Estimators SU,WC vs SU,NC). However, using a plug-in estimator of p (estimator SU,NC + PI) was nearly as efficient as incorporating covariate information formally into the likelihood (estimator SU,WC). Almost no benefit was seen in analyzing the unconditional likelihood (estimator UC) over a likelihood approach that conditioned on sampling status and time (estimator SU,WC).

We also evaluated the benefit of ODS design and analysis choices for the time-specific difference in expected outcome, ${\Delta }_t={\mu }_1(t)-{\mu }_0(t)\equiv \mathbb{E}(\mathbf{\text{Y}}\left|M=1,T=t)-\mathbb{E}(\mathbf{\text{Y}}\right|M=0,T=t)={\beta }_M+{\beta }_{M\times T}\cdot t$. Percent bias and relative efficiency for Δ_t under high subject-to-subject heterogeneity are summarized in Table S3. For baseline (t = 1) comparisons, the highest relative efficiency came from intercept-based designs; for t = 6, when Δ_t is more highly weighted toward the time-related parameter β_M×T, the greater efficiency came from slope-based designs. In neither case did the analysis approach appear to have a substantial impact on the relative efficiency. Results were similar under low subject-to-subject heterogeneity, as seen in Table S4.

4.3 |. Evaluation of design features

Each of the estimators examined here is a maximum likelihood estimator and as such will be asymptotically unbiased for θ under correct model specification. The asymptotic relative efficiency of the estimators can likewise be found through an analytical comparison of the information in each estimator. For estimators that included only subsampled individuals, we calculated this directly; for estimators involving all cohort members, we used a numerical approach to ascertain relative efficiency. In addition to the intercept- and slope-based ODS designs described above, we also investigated the relative efficiency obtained from an ODS design that used the intercept-based criterion to choose half of the subsample and the slope-based criterion to choose the other half.

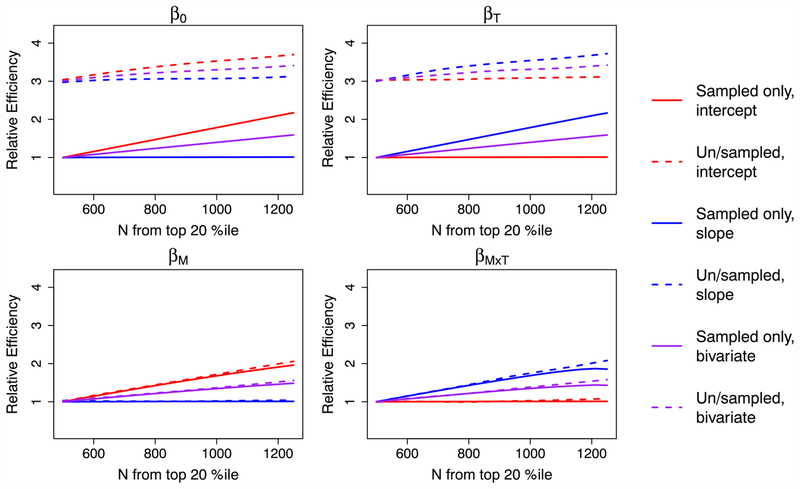
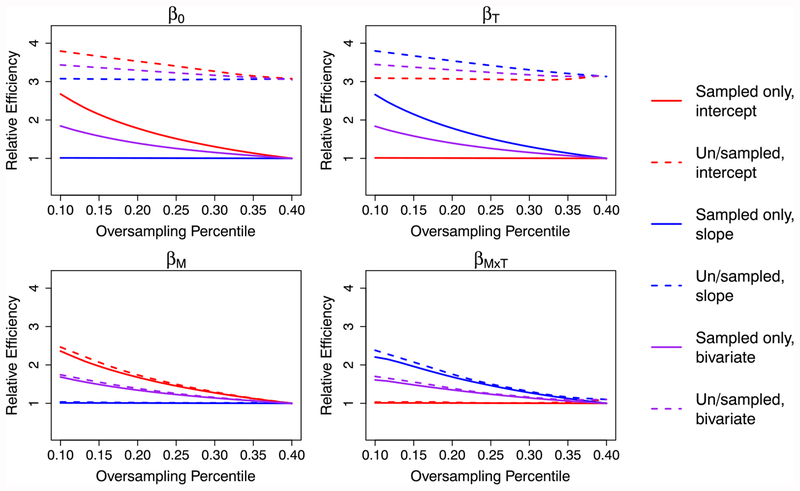
Intuitively, sampling more individuals with extreme subject-specific intercepts and/or slopes should yield larger efficiency gains and would change the sampling probabilities used in each region. The relative efficiency of the ODS designs considered here depends not only on θ itself but also on 2 key ODS design parameters, where the oversampling regions are defined to be (eg, cutpoints for q_i) and the sampling fractions (ω(q)) for each region. For a simulated cohort of 10 000 individuals and for estimators SO,NC and SU,WC, Figures 3 and 4 show the relative efficiency for regression parameters obtained when varying these key ODS design parameters. In Figure 3, the oversampling region is kept constant and we illustrate the effect of varying the number oversampled in that region. As expected, sampling more subjects from the top 20th percentile increases efficiency for parameters related to the subsampling variable. Alternatively, one may fix the sampling number in each region but vary how extreme those regions are; Figure 4 shows the effect of this. Again, the greatest efficiency gains occur for parameters the design has specifically targeted (ie, β₀ and β_M for intercept-based designs and β_T and β_M×T for slope-based designs) and for designs that have a large number of individuals subsampled from the most extreme regions of q. These illustrations demonstrate the impact that design choices, as well as analytical strategy, may have on regression parameter efficiency.

FIGURE 3.

Relative efficiencies of estimators SO,NC and SU,WC for various outcome-dependent sampling designs, varying the number subsampled from the top/bottom 20th percentiles. The “bivariate” sampling design subsampled half of subjects based on subject-specific intercept and half based on subject-specific slope. Note that here, N = 500 corresponds with a random sampling design

FIGURE 4.

Relative efficiencies of estimators SO,NC and SU,WC for various outcome-dependent sampling designs, varying the oversampling percentile from which 1000 subjects are subsampled. The “bivariate” sampling design subsampled half of subjects based on subject-specific intercept and half based on subject-specific slope. Note that here, an oversampling percentile of 40% corresponds with a random sampling design

5 |. APPLICATION TO CFFPR DATA

We illustrate the relative merits of the likelihood-based estimators discussed here with an application to data from the CFFPR, which collects detailed information on the health outcomes, clinical care, and demographic characteristics of patients with CF receiving care at accredited centers.¹⁰ We mimic a project that would selectively evaluate stored baseline specimens for a subset of patients and link these data to longitudinal trajectories of lung function. For this illustration, we identified a cohort of 3141 CFFPR patients between the ages of 8 and 16 who had at least 6 consecutive annual longitudinal spirometry measurements available and whose initial spirometry measurement after the age of 8 occurred between 1990 and 2006. The average age of participants at the first visit considered was 8.8 years old, with the cohort split equally between boys and girls. Seventy percent of the cohort tested positive for the bacterium Staphylococcus aureus at the first visit; selected summary statistics for this cohort can be found in Table S5. We evaluated the impact of ODS design and analysis of a hypothetical substudy to investigate the longitudinal association between the presence of the bacterium S aureus at baseline and FEV₁ (L), a measure of lung function. We assume that only a subsample would be assayed for S aureus.

In this context, the parameters of interest include the effect of the presence of S aureus at baseline and the difference in the slopes of lung function trajectory between those with and without baseline S aureus. Since assaying in reality was conducted on all patients for this cohort of 3141, we can evaluate the performance of hypothetical substudies that use ODS design and analysis relative to the gold standard of analyzing the entire cohort. For substudies in a large cohort such as the CFFPR cohort, covariate information such as an expensive or technologically complex biomarker assay will generally be ascertained only in a small subset; hence, ODS techniques can be of use in choosing and analyzing the cohort subset. We evaluated ODS design and analysis approaches for conducting a substudy of 600 patients on average, selected either by random or biased sampling based on subject-specific intercept or slope. Average parameter estimates and standard errors over 1000 resamplings of the data are presented in Table 1.

TABLE 1.

Parameter estimates and empirical standard errors of likelihood-based estimators for the Cystic Fibrosis Foundation Patient Registry dataset (N = 3141)

	β0		βT		βS aureus		βS aureus×T
Estimator	Est. (SE)	P	Est. (SE)	P	Est. (SE)	P	Est. (SE)	P
Full cohort	1.200 (0.012)	<.001	0.184 (0.0029)	<.001	−0.013 (0.015)	.39	−0.011 (0.0035)	.001
Random sample	1.201 (0.025)	<.001	0.185 (0.0061)	<.001	−0.013 (0.030)	.67	−0.012 (0.0073)	.11
SO,NC intercept	1.213 (0.019)	<.001	0.181 (0.0057)	<.001	−0.014 (0.023)	.54	−0.012 (0.0066)	.06
SU,NC + PI intercept	1.202 (0.014)	<.001	0.184 (0.0042)	<.001	−0.013 (0.020)	.52	−0.011 (0.0060)	.07
SU,WC intercept	1.201 (0.014)	<.001	0.184 (0.0041)	<.001	−0.013 (0.020)	.52	−0.011 (0.0059)	.06
UC intercept	1.200 (0.013)	<.001	0.184 (0.0042)	<.001	−0.012 (0.019)	.52	−0.011 (0.0060)	.06
SO,NC slope	1.191 (0.024)	<.001	0.185 (0.0041)	<.001	0.013 (0.029)	.67	−0.013 (0.0049)	.007
SU,NC + PI slope	1.185(0.017)	<.001	0.185 (0.0032)	<.001	0.009 (0.024)	.71	−0.012 (0.0046)	.007
SU,WC slope	1.185 (0.017)	<.001	0.185 (0.0032)	<.001	0.009 (0.025)	.70	−0.013 (0.0046)	.007
UC slope	1.185(0.017)	<.001	0.185 (0.0032)	<.001	0.009 (0.025)	.71	−0.012 (0.0046)	.007
	$\text{log}\left({\sigma }_{b_0}^2\right)$		$\text{log}\left(\frac{1+\rho }{1-\rho }\right)$		$\text{log}\left({\sigma }_{b_1}^2\right)$		$\text{log}\left({\sigma }_e^2\right)$
Full cohort	−2.06 (0.029)	<.001	0.10 (0.042)	.02	−5.00 (0.030)	<.001	−3.94 (0.013)	<.001
Random sample	−2.07 (0.140)	<.001	0.10 (0.110)	.35	−5.01 (0.067)	<.001	−3.94 (0.050)	<.001
SO,NC intercept	−1.87 (0.110)	<.001	0.08 (0.073)	.25	−4.91 (0.057)	<.001	−3.84 (0.047)	<.001
SU,NC + PI intercept	−2.03 (0.016)	<.001	0.09 (0.008)	<.001	−5.01 (0.005)	<.001	−3.94 (0.006)	<.001
SU,WC intercept	−2.03 (0.009)	<.001	0.09 (0.005)	<.001	−5.01 (0.005)	<.001	−3.94 (0.003)	<.001
UC intercept	−2.06 (0.008)	<.001	0.10 (0.009)	<.001	−5.01 (0.005)	<.001	−3.94 (0.003)	<.001
SO,NC slope	−1.83 (0.110)	<.001	0.12 (0.072)	.09	−4.96 (0.052)	<.001	−3.78 (0.041)	<.001
SU,NC + PI slope	−2.06 (0.014)	<.001	0.10 (0.008)	<.001	−5.00 (0.008)	<.001	−3.94 (0.005)	<.001
SU,WC slope	−2.06 (0.011)	<.001	0.10 (0.006)	<.001	−5.00 (0.008)	<.001	−3.94 (0.003)	<.001
UC slope	−2.06 (0.011)	<.001	0.10 (0.005)	<.001	−5.01 (0.004)	<.001	−3.94 (0.002)	<.001

Abbreviations: S aureus, Staphylococcus aureus. For “full” estimator, standard errors are derived from analysis of full Cystic Fibrosis Foundation Patient Registry cohort. All other estimators are based on an average subsample of 600 patients, and results are averaged over 1000 resamplings. Empirical standard errors are the estimator’s standard deviation over all resamplings.

As shown in Table 1, patients infected with S aureus at baseline had FEV₁ scores that were about 13 mL lower at baseline (indicating worse lung function) than patients who were not infected, although not significantly so. On average, patients’ lung function tended to improve over time, probably as a result of physical growth. However, lung function for patients infected by S aureus at baseline improved 11 mL less than those who were bacteria free at baseline, a small but statistically significant effect present in the full cohort (P = .03) that was not detected by a random sampling design. In fact, only slope-based substudy designs that targeted the interaction regression parameter detected this difference. Likewise, only ODS designs that incorporated information from unsubsampled individuals detected a statistically significant nonzero value of ρ, the correlation between an individual’s baseline lung function and change in lung function over time. Thus, those with higher lung function at baseline tended to have somewhat more of an increase in lung function over the time analyzed here.

In general, the inclusion of unsubsampled individuals in the analysis produced smaller standard errors for all parameters; however, the smallest standard errors overall corresponded to the design (estimator SU,WC with slope-based design) that both targeted the parameter of interest and incorporated unsubsampled individuals. Overall, the patterns observed in the empirical standard errors from the CFFPR analysis tended to agree with simulation results in Section 4.2. Diagnostic plots of subject-specific intercepts and slopes (Figure S1) suggest that the distribution of random effects was not inconsistent with bivariate normality, the violation of which may impact the expected performance of likelihood-based ODS estimators.

6 |. DISCUSSION

In this paper, we have explored the incremental utility of multiple sources of information in the analysis of ODS designs in the longitudinal data setting. In the case of a simple binary marker, we have shown benefit, sometimes substantial, of incorporating additional sources of information into inference. All of the likelihood-based estimators investigated here accounted for the biased sampling design through an ascertainment correction approach. Other valid strategies of estimation exist: for example, the inverse IPW approach,⁷ which produces estimators that are valid under mild conditions but often inefficient in modest samples.²¹ Previous work by Neuhaus et al²⁴ and our own preliminary simulations (not shown) suggest that misspecification of the random effects distribution not involving covariates leads to little bias in regression coefficient estimates. When the random effects distribution depends on a covariate the bias in estimated regression coefficients has been shown to be potentially large²⁵; we speculate this problem may be worse under ODS designs since misspecification occurs in multiple components of the likelihood. An exploration of estimators that balance robustness to misspecification and efficiency in the ODS setting, and comparison with likelihood-based estimators, merits investigation in future work.

While we have chosen to examine the operating characteristics of a simple binary covariate, we expect the lessons learned here to be broadly similar for a categorical or continuous covariate; estimation in these cases should be mostly straightforward. For a k-level marker, the same strategy could easily be applied as for the binary case, estimating the k-1 parameters that index Γ instead of the single parameter we have considered here. For markers with a large number of levels, or for continuous markers, a strategy that adopts a parametric model for the marker and then integrates over the missing covariate using estimates from the parametric model could be used as a natural extension of the work presented here. Finally, although we have not considered here the effect of multiple exposures or confounders, these too could be accommodated under the proposed framework; in this scenario, a profile likelihood approach may be used to good effect in order not to estimate the marginal joint likelihood of exposures and confounders.

In evaluating these estimators, we have followed the example of Schildcrout et al⁵ and conditioned on the marginal sampling status S_i. In contrast, some previous work^11,17 conditioned on being sampled from stratum k. Although not considered explicitly here, we expect that finer conditioning would produce a loss of information relative to the conditioning explored here.

We have observed that ODS analysis choices have the potential to improve efficiency for targeted regression parameters, sometimes dramatically, at minimal cost. However, the utility of incorporating covariate information into inference depends on the choice of subjects to analyze. When analyzing subsampled individuals only, we have shown that in the case of complete and balanced designs, there is no benefit. When there is variability in measurement times across categories of the marker, there may be a small amount of information to be gained by adding in covariate information. When all cohort members are analyzed, however, we have observed sometimes substantial increases in efficiency, as observed covariate information among subsampled individuals allows for a more precise characterization of the mixture distribution among unsubsampled subjects.

The benefit of including unsubsampled individuals in inference has been previously explored for univariate outcomes and suggested for longitudinal data. We formally found this benefit to carry over to longitudinal data, albeit for selected regression parameters only. Analysis of all subjects allowed nearly full information to be recovered for the variance components, which may be of interest in some applications. This type of analysis also improved inference on some regression parameters, although minimally for those related to the unobserved covariate; greater efficiency for these parameters will need to be addressed primarily through careful choice of ODS designs that promote efficiency for them, not through analysis. We have additionally illustrated the effects of some ODS design choices; a more thorough examination of these practical design parameters in the future will be helpful to the researcher implementing these methods. For researchers planning substudies based on existing longitudinal data, there appears to be utility in both careful design and analysis of biased sampling approaches. Overall, our results suggest that thoughtfulness at both design and analysis stages will be rewarded, sometimes substantially.