Abstract
The effectiveness of deep brain stimulation (DBS) therapy strongly depends on precise surgical targeting of intracranial leads and on clinical optimization of stimulation settings. Recent advances in surgical targeting, multi-electrode designs, and multi-channel independent current-controlled stimulation are poised to enable finer control in modulating pathways within the brain. However, the large stimulation parameter space enabled by these technologies also poses significant challenges for efficiently identifying the most therapeutic DBS setting for a given patient. Here, we present a computational approach for programming directional DBS leads that is based on a non-convex optimization framework for neural pathway targeting. The algorithm integrates patient-specific pre-operative 7T MR imaging, post-operative CT scans, and multi-objective particle swarm optimization (MOPSO) methods using dominance based-criteria and incorporating multiple neural pathways simultaneously. The algorithm was evaluated on eight patient-specific models of subthalamic nucleus (STN) DBS to identify electrode configurations and stimulation amplitudes to optimally activate or avoid six clinically relevant pathways: motor territory of STN, non-motor territory of STN, internal capsule, superior cerebellar peduncle, thalamic fasciculus, and hyperdirect pathway. Across the patient-specific models, single-electrode stimulation showed significant correlations across modeled pathways, particularly for motor and non-motor STN efferents. The MOPSO approach was able to identify multi-electrode configurations that achieved improved targeting of motor STN efferents and hyperdirect pathway afferents than that achieved by any single-electrode monopolar setting at equivalent power levels. These results suggest that pathway targeting with patient-specific model-based optimization algorithms can efficiently identify non-trivial electrode configurations for enhancing activation of clinically relevant pathways. However, the results also indicate that inter-pathway correlations can limit selectivity for certain pathways even with directional DBS leads.
Keywords: Deep Brain Stimulation, Particle Swarm Optimization, Subthalamic Nucleus, Pathway Activation Models
1. Introduction
Deep brain stimulation (DBS) is an effective neurosurgical therapy for movement disorders [1] and a promising interventional option for a range of neuropsychiatric disorders [2,3]. In recent years, there has been a surge of technological developments to further optimize and individualize DBS therapy on a patient-specific basis. A major area of development has focused on improving the spatial precision of targeting stimulation within the brain, which is especially relevant given the likelihood of surgical targeting errors [4] and the association of targeting errors with variability in responses to DBS within and across clinical centers [5]. Toward this end, there have been notable improvements in imaging to guide surgical targeting [6,7], in computational models to predict clinical outcomes [8–10], in current steering capabilities [11,12], and in directional DBS lead technology [13,14]. With the growing availability of directional DBS systems that incorporate such functionality, experimental [15] and recent clinical [16,17] investigations have reported increased therapeutic windows, suggesting a much wider range of programming options available to optimize therapy on a patient-specific basis.
In spite of the potential for directional DBS systems to optimize therapy, there remain several challenges to fully utilize this technology. One challenge is the large stimulation parameter space, which includes the increased number and arrangement of stimulation electrodes that can be individually addressed in terms of amplitude, pulse width, waveform shape, and pulse pattern among other parameters. Currently, programming for conventional four-channel DBS lead systems involves traversing this parameter space through an iterative trial-and-error process [18] across multiple visits [19,20], which can be time-consuming, strenuous for the patient, and result in potentially suboptimal therapy. By adding more electrodes and the capability to simultaneously activate multiple independent electrodes, directional DBS systems complicate the clinical challenge of identifying optimal stimulation settings amidst an even larger parameter space [21].
Another challenge is the complexity of effects that stimulation can have (both therapeutic and side effects), and the lack of definitive clarity regarding how those effects relate to specific neural targets. Not only do the therapeutic effects of DBS vary across signs and symptoms [22], but in some cases improvement in one sign may co-occur with worsening of another [23]. Overt side effects can also be diverse, being comprised of muscle pulling, dysarthria, and transient paresthesia, among others [24,25]. Furthermore, effects with long wash-in times (e.g. tonic components of dystonia [26] and tics in Tourette’s syndrome [27]) and less overt side effects (e.g. mood [28] and dual-task performance [10]) further complicate conventional programming approaches. Results from previous studies in Parkinson’s disease [10,23], Essential Tremor [29], and depression [30] suggest that incorporating subject-specific anatomy of pathways and target regions may have value in addressing the range of possible DBS effects and optimizing therapy. Directional DBS systems provide an opportune platform for targeting such pathways and for facilitating further investigations into the role of these pathways in DBS mechanisms. However, incorporating subject-specific region and pathway anatomy further complicates the programming process, such that identifying the optimal stimulation settings becomes non-intuitive and even more time consuming. Computational methods are ideally suited to simplify this problem.
In order to reduce the complexity of the programming problem and make it clinically feasible, computational methods must be able to (1) predict the effects of DBS in terms of subject-specific neural activation, and (2) efficiently traverse the parameter space to identify clinically optimal stimulation settings. Over the past decade, models of DBS-induced neural activation have been used to provide insights into DBS mechanisms [9,31–33] and to evaluate new stimulation paradigms [11,12]. Many of the models implemented in studies to date have used the paradigm of “volume of tissue activated” (VTA) [8,14,34–39], which estimates the effects of stimulation in terms of its spatial extent. As subject-specific imaging, and particularly diffusion tractography, have become more prevalent, the use of pathway activation models (PAM) has come to replace VTAs as a more precise way to predict the effects of DBS on specific neural pathways [11,40– 42].
To transition computational models of DBS from retrospective to prospective functionality, it is essential to couple such neural activation models with efficient optimization algorithms. Previously, we developed a convex optimization approach for programming an experimental directional DBS lead with 32 electrodes and tested the algorithm in an anatomical thalamic model of DBS for treating Essential Tremor [43]. Extended formulations of such convex optimization approaches have also been proposed [44]. While such convex formulations can identify settings within seconds, the simplifying assumption of convexity may not necessarily hold for arbitrary fiber trajectories, since activation of an axon can occur at multiple spatially disparate nodes. We subsequently developed a programming approach based on particle swarm optimization [45], which is well suited to solving such non-convex problems. By weighting the different pathways modeled to specify regions to activate and to avoid, this programming algorithm identified optimal, non-intuitive solutions within minutes.
In the present study, our objective was to evaluate the utility of a pathway-driven optimization framework for identifying optimal electrode configurations in subject-specific human models of DBS targeting the subthalamic nucleus (STN). Further, we improved the optimization algorithm developed in [45] to handle a higher number of pathways using dominance-based criteria to evaluate candidate solutions, which negate the need to predefine weighting values in the objective function. Through computational models of a retrospective imaging dataset and clinical notes from eight STN DBS implants, we evaluated clinically activated pathways in our cohort, assessed targeting capabilities of directional DBS systems for these pathways, and used those targeting capabilities as a baseline to evaluate the utility of the optimization algorithm for enhancing pathway targeting.
2. Methods
2.1. Clinical Imaging and DBS Programming Data Sets
This study included retrospective analysis of imaging data (Fig. 1A) from seven subjects (six males and one female), who had a clinical diagnosis of Parkinson’s disease and who had received a DBS lead implant in the subthalamic nucleus (STN). Pre-operative anatomical imaging data included the standard clinical imaging protocols (1 mm isotropic) at 1.5T or 3T, and T2-weighted (0.4 × 0.4 × 1 mm), diffusion-weighted (1.5 mm isotropic), and susceptibility-weighted (SWI, 0.4 × 0.4 × 0.8 mm) imaging at 7T [46]. A Medtronic 3389 (Minneapolis, MN, USA) DBS lead had been implanted in the STN bilaterally for one subject and unilaterally for six subjects, comprising a total of eight STN DBS leads in the cohort. Subject leads were labeled S1 to S8, corresponding to the eight implants.
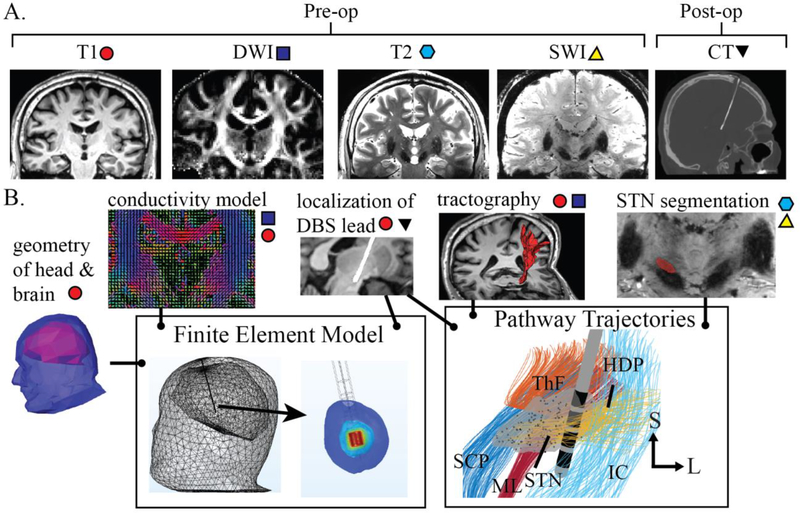
Figure 1:
Subject-specific modeling overview of STN-DBS therapy. (A) For each subject, the pre-operative imaging acquired included T1 (at 1.5T or 3T) and T2, susceptibility-weighted imaging, and diffusion-weighted imaging (at 7T). Post-operative CT was also obtained. (B) Preoperative imaging data were used to construct a head and brain geometry, build an inhomogeneous anisotropic conductivity model, segment the STN, and create fiber tractography models of axonal pathways within and around the STN. Implanted DBS lead positions and orientations with respect to the STN were determined through co-registration of pre-operative T1 with post-operative CT imaging. A finite element model was built to estimate DBS-induced electric potentials in neural tissue. Seven clinically relevant pathways were constructed and simulated in the context of conventional and directional DBS leads. Pathways included motor and non-motor STN (MT and NMT; substructure not shown), superior cerebellar peduncle (SCP), hyperdirect pathway (HDP), thalamic fasciculus (ThF), medial lemniscus (ML), and internal capsule corresponding to the corticospinal tract from all of motor cortex (IC).
During a post-surgical follow-up visit, typically four weeks post-surgery, each subject underwent a CT scan (≤ 1 mm isotropic) to identify the DBS lead position and trajectory through the STN. In addition, each subject met with a movement disorders specialist, who performed a monopolar review in which stimulation amplitude was increased incrementally from a low, baseline level to a higher level until one or more persistent side effects were elicited (e.g. involuntary muscle contractions, paresthesia, and dysarthria). Clinically optimized DBS settings for each lead were identified as those stimulation parameters and electrode configurations that delivered therapy on bradykinesia, rigidity, and tremor, while staying below the threshold for inducing overt side effects. The study was approved by the Institutional Review Board at the University of Minnesota, and all subjects gave written informed consent in accordance with the Declaration of Helsinki.
2.2. Modeling the DBS Lead
The trajectories of the implanted Medtronic 3389 leads were extracted from post-operative CT and co-registered to the T1-weighted images (Fig. 1B). While the imaging for this study was obtained from subjects who were implanted with a Medtronic 3389 DBS lead (conventional lead), we also incorporated a virtual model of the Boston Scientific Cartesia (directional lead) for modeling purposes in place of each subject’s preexisting DBS lead position. As a directional DBS system with eight electrodes and multiple independent current-controlled stimulation capabilities, the Boston Scientific Cartesia lead has sufficiently complex electrode configuration options to benefit from model-driven spatial optimization. The modeled directional leads were positioned within the same extracted trajectory as the conventional leads, such that the superior (i.e. most dorsal) cylindrical electrodes of the two lead types were aligned. Geometric models were built in COMSOL Multiphysics v5.3a. The geometric model for the conventional lead comprised of a 1.27 mm diameter, and insulating tip of length 1.5 mm, four cylindrical electrodes of length 1.5 mm, and inter-row spacing of 0.5 mm. The directional lead was modeled with a diameter of 1.3 mm, a tip electrode of length 1.5 mm (including a spherical tip of radius 0.635 mm), two rows of directional electrodes of length 1.5 mm and 0.34 mm circumferential inter-electrode spacing, a superior cylindrical electrode of length 1.5 mm, and 0.5 mm inter-row spacing. An encapsulation layer of 0.15 mm was modeled for all DBS leads, in accordance with histological measurements of encapsulation layer thickness [48].
2.3. Finite Element Modeling
We constructed an inhomogeneous, anisotropic conductivity model (Fig. 1B) to estimate DBS-induced electric potentials in neural tissue. Subject-specific imaging was used to model four different tissue types: white matter, gray matter, cerebrospinal fluid (CSF), and lumped head tissue. To classify the tissue as white matter, gray matter, or CSF, the brain was manually segmented from T1-weighted anatomical images. These images were then classified automatically by FSL’s FAST tool. Lumped head tissue was defined as all tissue within the head residing outside the brain. Conductivity tensors were then estimated for gray and white matter using diffusion tensor imaging, as described by [49] and [50]. The isotropic electrical properties used to calculate the conductivity tensors were derived at the median frequency of the applied stimulus waveform (4.294 kHz) (white matter: σ = 0.066184 S/m, ɛr = 23361; gray matter: σ = 0.10836 S/m, ɛr = 48617) [51–53]. All other tissue types were modeled using isotropic electrical properties (CSF: σ = 2.00 S/m, ɛr = 109; encapsulation layer [54]: σ = 0.066184 S/m, ɛr = 23361; lumped tissue: σ = 0.23 S/m [55], ɛr = 1)).
To define the boundaries of our model, the geometry of the head and brain were manually extracted from the T1-weighted imaging (Fig. 1B). The head surface and brain surface were imported into COMSOL models with the DBS leads. Delaunay triangulation was used to generate a multi-resolution mesh, such that tetrahedral element spatial resolution was 0.07–0.2 mm near the DBS lead, and up to 20 mm at the surface of the scalp. The resulting volumes were meshed using 686,600 ± 26,655 quadratic tetrahedral elements with 125,431 ± 4,778 vertices. A normal current density (directional) or electric potential (conventional) was then applied on the electrode surfaces such that each simulation comprised of a single electrode with 1 mA (directional) or 1 V (conventional) of stimulation, enabling the subsequent use of superposition to estimate the voltage distribution of arbitrary combinations of electrodes and stimulation amplitudes. The caudal base of the head model was assigned as ground (i.e. 0 V, Dirichlet boundary condition), while the rest of the scalp surface and the DBS lead shaft were assigned zero current density (i.e. Neumann boundary condition). To estimate the spatial distribution of electric potential, simulations were run at a single AC frequency corresponding to the median frequency (4.294 kHz) of the stimulus waveform applied on our axon models, at which conductivity properties were also estimated. The finite element analysis was performed within the electric currents physics of COMSOL’s AC/DC module, and the solution was obtained with the BiCGStab iterative solver.
2.4. Modeling Fiber Tracts and STN Projection Neurons
We leveraged diffusion-weighted imaging and probabilistic tractography (Fig. 1B) to extract subject-specific trajectories of the internal capsule (IC) (i.e. corticospinal tracts from across motor cortex), dentate-rubro-thalamic tract coursing through superior cerebellar peduncle (SCP), medial lemniscus (ML), and pallidothalamic projections coursing through the lenticular fasciculus and joining the thalamic fasciculus (ThF) [56]. The tractography termination mask for IC was derived from FreeSurfer’s cortical parcellation of precentral gyrus using the Destrieux atlas, while the seedpoint mask was set to be the ipsilateral crus cerebri. For SCP, the seedpoint mask was the decussation of SCP, the waypoint mask was a dilated mask of the ipsilateral red nucleus, and the termination was the lateral extent of the ipsilateral thalamus. For ML, the seedpoint mask was the region just anterior and lateral to the decussation of SCP, the waypoint was the region just posterior and lateral to the red nucleus, and the termination mask was the lateral extent of the ipsilateral thalamus. Finally, the pallido-thalamic tract was obtained by joining tractography streamlines for the lenticular fasciculus with streamlines for the thalamic fasciculus. The joining was defined to occur at the region medial to the substantia nigra and lateral to the anterior portions of red nucleus. This region was used as a seedpoint mask for tractography for both the lenticular fasciculus and for the thalamic fasciculus, with the globus pallidus and the thalamus used as termination masks, respectively. After generating the fiber tract trajectories, the tracts were populated with myelinated axons of 2 μm fiber diameter (FLUT length 10 μm; STIN length 57.7 μm; MYSA length 3 μm; node diameter 1.4 μm; axon diameter 1.6 μm; node length 1 μm; number lamellae 30; passive first and last nodes) using the threshold-contour mapping procedure described in [41]. Axons that overlapped with the DBS lead were removed from subsequent simulations.
We also modeled projection neurons of the STN. The STN was manually segmented from T2-weighted or SWI coronal images taken at 7T (Fig. 1B), as performed in previous studies imaging the basal ganglia [6,46]. The STN was subsequently populated with neurons consisting of realistic morphologies of dendrites, somas, and axons derived from staining experiments in non-human primates [32] with axonal projections extended with curved trajectories for human scale. The axons of these STN neurons were oriented such that the main axis of the STN axonal projections were parallel to a line connecting the centroid of the globus pallidus to the centroid of the STN. These STN neurons were further categorized as either motor or non-motor STN. This was done first by using the procedure described in [47] to obtain parcellation of functional territories of STN based on their white matter connectivity to cortical areas (Fig. 2A). The percentage of tractography streamlines from each cortical region was then used as a probability for classifying each STN cell (e.g. cells in a region of STN with 80% connectivity from motor cortex had an 80% chance of being classified as motor STN cells) (Fig. 2B).
Figure 2:
STN parcellation in a sample subject. (A) Axial view of STN mask, with percentage of tractography streamlines represented by intensity within STN. Tractography streamlines originated from cortical areas (motor, associative, limbic, and other) and arrived at various regions of STN. (B) Probabilistic classification of STN neurons based on the percentage of streamlines. Classification method was adapted from [47].
In addition to modeling SCP, IC, ML, ThF, and STN, we also constructed the hyperdirect pathway (HDP) given its potential relevance to DBS therapy for Parkinson’s disease [39,40,57]. The hyperdirect pathway was modeled as a set of collaterals emanating from IC [58] into random points in the STN. Axons were generated within IC, and random nodes at the superior-inferior level of STN were selected as seed points for the collateral branches to STN. Random points within the STN were subsequently selected as terminal points for the collateral, such that the end points did not overlap with the DBS lead or its encapsulation layer. Trajectories with strong superior-toinferior components were iteratively revised. Random curvature was added to the trajectories at evenly spaced points along each trajectory, followed by a cubic spline to produce a smooth curved trajectory. Fibers that overlapped with the DBS lead were removed from further simulations. The simulated fibers were subsequently modeled as myelinated axons with 1 μm fiber diameter (parameters adapted from [31,59]: FLUT length 10 μm; STIN length 57.7 μm; MYSA length 3 μm; node diameter 0.7 μm; axon diameter 0.8 μm; node length 1 μm; number lamellae 20), and with passive nodes at first and last nodes to prevent low-threshold terminal activation.
2.5. Activation Prediction
Membrane activity of the multicompartment cable models were simulated in the programming environment, NEURON [60], in the context of monopolar stimulation through each electrode on the conventional and directional DBS leads. The biophysical axon models consisted of multicompartment axons, and the multicompartment STN neuron models included cell bodies, dendrites, and axons [59]. The biophysical effects of DBS were modeled using NEURON’s e_extracellular function, which calculates transmembrane current that is derived from finite element analysis results of extracellular potentials at each membrane compartment. To drive activation, we applied a square current-controlled (directional) or voltage-controlled (conventional) waveform consisting of a 60 μs cathodic pulse, a 400 μs interphase delay, and a 2 ms anodic phase. Waveforms were filtered as described previously to generate voltage waveforms consistent with those found in tissue [61]. The median frequency of the waveform was 4.294 kHz, and this median frequency was used to estimate the electrical properties for finite element modeling. A binary search algorithm was used to compute threshold currents for each simulated axon and neuron for monopolar stimulation through each of the electrodes on the DBS lead. Additionally, as performed in [45], a modified activating function (MAF) value at threshold was computed by scaling the FEM-derived distribution of electric potentials using the threshold current value. The maximum MAF value along each axon at activation was taken to be the MAF threshold (MAFT), and the median MAFT value across axons within a given pathway was used as an approximation threshold for activation of any axon in that pathway. This MAFT value was supplied to the particle swarm optimization algorithm for activation prediction.
2.6. Particle Swarm Optimization
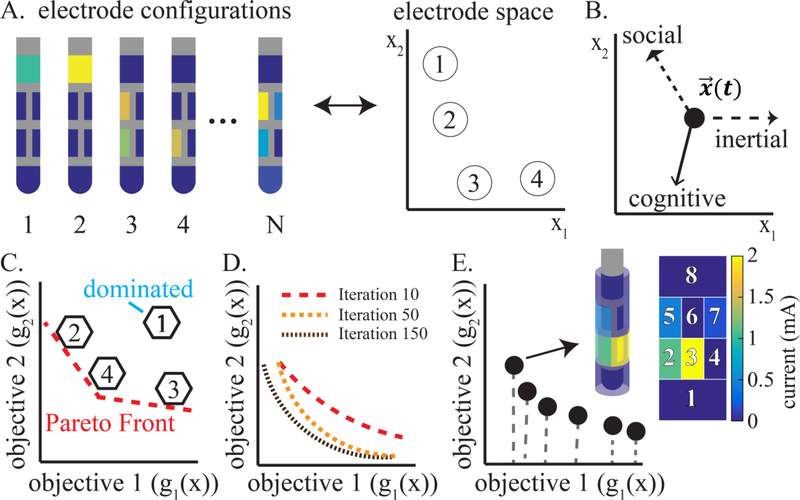
Particle swarm optimization (PSO) was first proposed by Kennedy and Eberhart in 1995 as a means of solving nonlinear optimization problems by modeling the social behavior of swarms of simple organisms [62]. Through cooperation over many iterations, the members of a swarm explore their problem space to identify the best (i.e. optimal) solutions to complex problems. This emergent behavior, or swarm intelligence, has since been applied widely across fields, including the training of neural networks, design applications, and others [63]. In this study, we implemented the PSO algorithm to identify the set of optimal electrode configurations (i.e. electrodes and currents) for activating targets of STN DBS using the directional DBS lead in the presence of multiple neighboring tracts. We defined a population of 262 “particles”, where each particle was an instance of a DBS lead initialized with a distinct electrode configuration representing its initial position in “electrode space” (Fig. 3A). Initial positions of the particles were defined such that all equally-distributed current combinations were represented in the initial population. Particles were then allowed to move stochastically within the electrode space. At each iteration, each particle gained a new electrode configuration corresponding to its new location in electrode space, and the “success” of each electrode configuration was evaluated and stored. The particles’ movement through electrode space was guided by three components (Fig. 3B): (1) a “social” component attracting the particles toward a point that the swarm has collectively deemed as most “successful” (i.e. global best), (2) a “cognitive” component, attracting each individual particle toward a point deemed most “successful” based on its own history (i.e. personal best), and (3) “inertia”, based on the actual velocity of each particle at any given iteration. Mathematically, particle positions and movement were represented as follows:
| (1) |
| (2) |
| (3) |
where i is the index of the particle, t is iteration number, x is particle position, v is velocity, j is electrode index, y is a personal best as of the given iteration, is a global best as of the given iteration, c1 is weighting of the cognitive component, c2 is the weighting of the social component, w is the weighting of the inertial component, n is the total number of iterations, and r1 and r2 are random variables that help promote exploration. The inertial weighting w was set to be highest at initial iterations to promote initial exploration. In our previous work [45], a range of social, cognitive, and inertial parameters were explored, and the parameters used in this current study followed those found to best balance convergence with robust exploration of the parameter space. We thus defined the social, cognitive, and inertial parameters as follows: c1 = 4.5, c2 = 0.2, w(0) = 0.9, w(n) = 0.4, r1~U(0,1), r2 = 1.
Figure 3:
Overview of the multi-objective particle swarm optimization algorithm. (A) “Particles” were defined as N instances of DBS lead configurations, each with a different electrode and stimulation amplitude setting, corresponding to an eight-dimensional point in electrode space (schematic projection into 2D shown). (B) Each particle explored the electrode space with stochastic movement that was guided by location designated as personal leaders (cognitive), locations designated as global leaders (social), and inertia. (C) Each particle was mapped onto objective space, and non-dominated particles were tracked to generate a Pareto front. (D) The Pareto front improved over the course of the iterative exploration. (E) The final output Pareto front was set after reaching the pre-defined iteration limit. Each point on the Pareto front represented a distinct Pareto optimal electrode configuration, given tradeoff objectives in the multi-objective space.
2.7. Dominance-based Criteria
At each iteration, the personal best and global best were determined based on an evaluation of the electrode configurations at the current iteration and in the context of all prior iterations. In optimization problems having only one objective, particles can be evaluated based on their objective function value. However, in the present work, we defined a multi-objective problem consisting of seven objectives. We designed the following optimization problem: Given a certain power budget, find the best ways to distribute current across the electrodes (i.e. the best electrode configurations) to maximize activation in target pathways (SCP, ThF, motor STN, HDP) while minimizing activation in pathways associated with side effect (IC, ML, and non-motor STN including associative, limbic, and “other”-designated STN neurons)). Mathematically, this was represented as follows:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where x is electrode configuration constrained to be cathodal stimulation only, to are functions that predict number of axons activated in SCP, ThF, motor STN, HDP, IC, ML, and non-motor STN respectively, R is an eight-by-eight matrix describing how electric potential at each electrode is influenced by current applied at every other electrode, P is the power budget, H is the Heaviside function, l is the tract index, k is the axon index within the tract, U is the total number of axons in a tract, C is the matrix that maps electrode configurations to activating function values, and α is the MAFT value for a given tract. The R matrix was computed individually for each subject through the finite element models by extracting the electric potential at all eight electrodes on the directional DBS lead resulting from 1 mA cathodal stimulation applied separately at each electrode. The mean impedance for all directional lead models across non-directional electrodes was 1.77 kΩ, and across directional electrodes was 4.77 kΩ. Cross-electrode interaction terms ranged from as high as 0.75 kΩ to as low as 0.09 kΩ. In contrast to a purely current-based approach, this power-based approach enabled the consideration of differences in impedances between directional and non-directional electrodes when evaluating electrode configurations for programming.
Evaluating electrode configurations for multi-objective problems poses a unique challenge compared to single-objective problems due to the lack of a clear objective function. In our previous implementation of PSO for DBS programming [45], we addressed this issue by constructing an aggregate objective function through a weighted sum of each of the objectives:
| (9) |
| (10) |
where A 1, A2, A3, and An are weightings applied to each objective, M is the cathodal current bound, is the vector of amplitudes applied to each electrode, and K is the number of electrodes. This objective function enabled the selection of personal best and global best points to guide exploration of the particles. We furthermore tracked the evaluated solutions in terms of their dominance (Fig. 3C), removing any candidate solutions for which another solution existed that was better in all objectives. This collection of non-dominated solutions, referred to as the Pareto front, enabled us to track multi-objective information in spite of having a single aggregate objective function to guide the search. While such a hybrid approach to multi-objective optimization can be expanded to a higher number of objectives, selecting the weightings for each objective can be subject to arbitrary criteria.
To accommodate multiple pathways of interest and avoidance, we extended our original PSObased approach (Supp. Fig. 1) using a purely Pareto dominance-based approach [64]. The dominance-based method contrasts with the previously described approach in that its aim is solely to enhance the Pareto front, rather than trying to optimize for a single aggregate objective function. The dominance-based method bypasses the linear aggregate function by constructing an objective vector from the objectives:
| (11) |
where B1, B2, B3, and Bn are not weights, but simply set to −1 or +1 depending on whether the region or pathway is one to target (−1) or avoid (+1). At each iteration, objective vectors are compared in terms of their dominance, and those that are not dominated are appended to the Pareto front. Furthermore, objective vectors are removed from the Pareto front as a new objective vector dominates them. The goal of the optimization, then, is to continually find new dominant objective vectors. Pareto fronts were calculated for each particle, which provided the seeds to generate a population-based Pareto front using an adapted version of the Moore Chapman approach [64]. In this approach, the Pareto front represents the best solutions obtained so far, based on Pareto-dominance. A random point on the Pareto front is selected as the global best, and each particle is attracted to this global best at each iteration. Additionally, each particle has its own Pareto front corresponding to the best points it has traversed. The personal best is chosen from among each personal Pareto front. The personal and global bests are each used to drive Pareto front exploration further. This technique contrasts with the previously implemented PSO technique in its ability to select personal and global best solutions based on randomly picking points designated as dominant, rather than relying on an objective function with arbitrarily defined weightings. In this manner, the dominance-based PSO enables multiple pathways to be added for optimization without prior knowledge of how to weight each pathway.
We ran the multi-objective PSO (MOPSO) for each of the eight STN DBS models, obtaining a Pareto front for each model (Fig 3D). Each point on the Pareto front represented an activation profile and a corresponding electrode configuration. To evaluate targeting capabilities, we established a targeting metric that reflected the clinical pathway activation patterns observed in our models of the conventional DBS lead, as well as the anticipated side effect pathways. Specifically, the targeting metric for comparison was the following:
| (12) |
All comparisons were performed with a subject-specific power constraint, such that the MOPSO for each subject was constrained to use the same power as each subject’s clinically optimized setting. Power was computed by Equation 7 for electrode configurations . To further facilitate comparison across the conventional lead and the directional lead simulations, we ran current-controlled simulations in the conventional lead at the clinically chosen electrode, and then identified a scaling factor that minimized the difference between activation thresholds in the voltage-controlled simulations and the current-controlled simulations. This scaling threshold was identified using a linear regression (i.e. fitlm in MATLAB v2016a) with automated, iteratively reweighted least squares fitting to minimize the impact of outliers. The resulting current was set as the basis for calculating power limits in the directional lead simulations. Due to differences in the waveform shape between voltage- and current-controlled activation that resulted in slight difference in pathway selectivity across waveforms (Supp. Fig. 2), we also used the threshold-matched current-controlled simulations for comparing conventional lead settings to the directional lead settings. Finally, to quantify the spread of the power across electrodes in the MOPSO solutions, we adapted a heuristic metric based on the Kullback-Leibler divergence for calculating differences between two discrete distributions:
| (13) |
where KL denotes the Kullback-Leibler divergence, N is the number of electrodes, Pi is the power dissipated by electrode i, normalized by the sum of power across all electrodes, and Qi is the power that electrode i would have under a fully uniform distribution that is also normalized by the sum across all electrodes, corresponding to a value of 0.125 for a lead with eight electrodes.
3. Results
3.1. Relationship between Pathway Modulation and Clinical Ratings
The clinical monopolar review process through the conventional DBS lead engaged a range of pathways during the programming process as indicated by the subject-specific computational models (Fig. 4A-C). These included SCP, ThF, HDP, motor STN (MT), and non-motor STN (NMT). ML activation occurred infrequently and in small amounts. Across all subjects (Fig. 4D), the final therapeutic setting consistently activated MT, NMT, and HDP. In some subjects, there was also activation in ThF, IC, and SCP at the clinically optimized therapeutic settings.
Figure 4:
Retrospective analysis of clinical programming with the conventional DBS lead. (A) Sample monopolar review for subject S3, whose motor sign assessments included rest tremor, postural tremor, and upper extremity rigidity. The clinical monopolar review (shown in terms of current applied) across all four electrodes yielded multiple therapeutic settings. The highlighted setting (circled) was selected by the clinician as the clinically optimized DBS setting. (B) Percentage of axons activated within each pathway for the same sample subject, based on biophysical models. Pathways engaged during the monopolar review process for the subject shown included SCP, IC, HDP, MT, and NMT (clinically optimized setting highlighted by dotted red line). (C) Spatial visualization of predicted activation due to highlighted setting from (B). Activated fibers bolded. Activated MT (purple dots) and NMT (green dots) also bolded. Inset shows lead and active electrode without fibers plotted. (D) Biophysical model predictions of percent activation of axons in each pathway during voltage-controlled stimulation at clinically optimized settings across all subjects. At the clinically chosen settings, the pathways that were consistently activated were MT, NMT, and HDP.
3.2. Single-electrode Biophysical Simulations in Directional DBS Leads
To evaluate the directional lead’s selectivity for pathways within and near the STN, computational models of a directional lead were simulated in the exact position of the actual implanted trajectory of the conventional lead for each subject. In single-electrode simulations of the directional leads, applying currents between 0.5 to 4 mA on each electrode revealed significant correlations across all except three pairs of pathways (i.e. activation in one pathway was associated with activation in another) (Fig. 5). The strongest correlations occurred between MT & NMT, ThF & SCP, and MT & HDP. Significant correlation coefficients were as follows (p < 0.01, non-parametric Spearman correlation, correcting for multiple comparisons): MT/NMT, 0.75; SCP/ThF, 0.73; MT/HDP, 0.70; HDP/NMT, 0.67; ThF/MT, 0.47; HDP/IC, 0.39; ThF/NMT, 0.38; SCP/MT, 0.36; MT/IC, 0.32; SCP/NMT, 0.23; SCP/HDP, 0.21; ThF/HDP, 0.21.
Figure 5:
Correlations of pathway activation across MT, NMT, SCP, ThF, HDP, and IC, based on biophysical models of a current sweep from 0.5 mA to 4 mA across all electrodes of the directional lead in all subjects. ML pathway not shown due to low occurrence of activation. Each dot is semitransparent, such that sections with overlapping dots appear darker. Plots sorted by descending correlation strength from left to right and top to bottom (non-parametric Spearman correlation coefficients).
Pathway selectivity with the directional lead is illustrated in (Fig. 6) for power levels equivalent to the power dissipated by each subject’s cylindrical electrode with 2.5 mA applied. Selectivity quantified the activation of a given pathway relative to activation across all pathways (i.e. relative to the L2 norm of percent activations). In the seven subjects who had ThF activation at the directional rows of the DBS lead, the medially facing electrodes exhibited higher selectivity for ThF compared to other directional electrodes (Fig. 6B, leftmost plot). Furthermore, in seven of eight subjects, the superior (i.e. dorsal) rows of the DBS lead had higher selectivity for ThF compared to the inferior (i.e. ventral) rows (Fig. 6B, middle plot). The five subjects with IC activation had higher selectivity in laterally facing electrodes compared to other directional electrodes (Fig. 6B, second plot), and in inferior rows compared to superior rows (Fig. 6B, fourth plot), albeit at relatively low overall selectivity levels compared to HDP, NMT, and MT. In six of eight subjects, HDP selectivity was highest in the middle two directional rows, and was highest in the most superior row for the other two subjects (Fig. 6B, rightmost plot). The described selectivity patterns were also reflected in the percent activation patterns (Supp. Fig. 2–3). Additionally, across all pathways and particularly MT and NMT, there were subject-specific variations in selectivity patterns along and around the DBS lead which did not follow specific trends (Fig. 6A; Supp. Fig. 4–5).
Figure 6:
Selectivity for pathway activation at each electrode of the directional DBS lead, based on biophysical models and a power level equal to the power dissipated by 2.5 mA applied on each subject’s cylindrical (superior) electrode. (A) Selectivity visualized as a stacked bar plot for each electrode for all subjects (S1 to S8). The area of each pathway in the bar plots is proportional to its percent activation relative to other pathways. (B) Selectivity trends around (plots 1–2) and along (plots 3–5) the directional lead across subjects. For selectivity with respect to position along the DBS lead (plots 3–5), the plotted points for C2-C4 and C5-C7 show the highest value among those electrodes. ThF and IC selectivity peaked at medial and lateral electrodes, respectively. ThF, IC, and HDP selectivity peaked at superior, inferior, and either middle or superior electrodes, respectively. A: Anterior, M: Medial, P: Posterior, L: Lateral, I: Inferior, S: Superior.
3.3. MOPSO Output
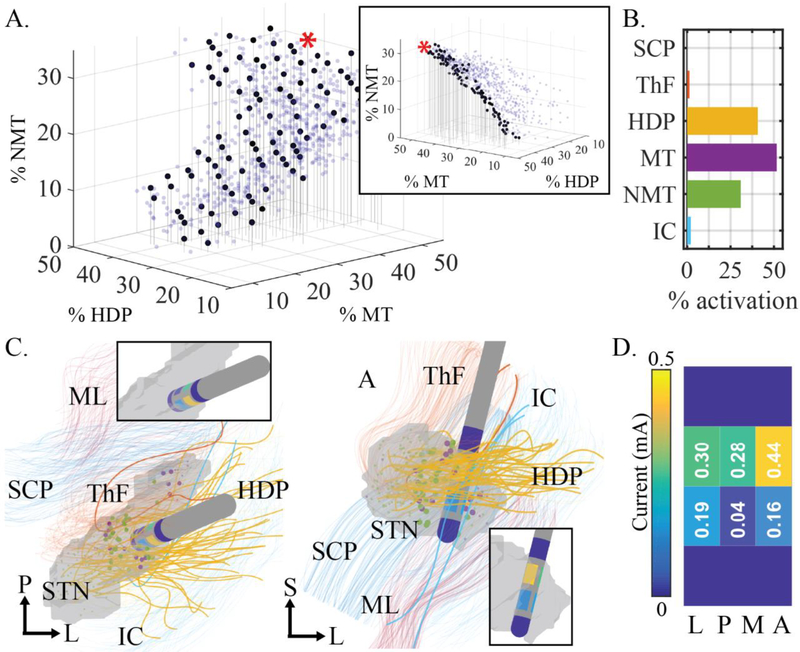
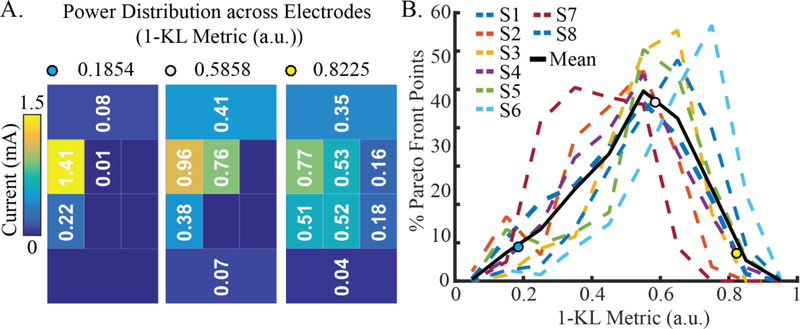
A sample MOPSO result is shown in (Fig. 7) for model S6 constrained to a power of 2.78 mW (according to Equation 7) to match the power level computed for the clinically chosen settings. The result of running the MOPSO algorithm was a seven-dimensional Pareto front (Fig. 7A, 7B), in which every point corresponded to an activation profile (Fig. 7B; ML not shown due to infrequent or low activation across subjects). As shown in the sample Pareto front result (Fig. 7A), plotting the entire high-dimensional Pareto front along only three dimensions results in a cloud of points representing candidate solutions. The point cloud can be simplified to a discernable front by highlighting only those points that are non-dominated in the dimensions of the plot. The activation profiles represented on the Pareto front reflect the subject-specific placement of the lead and its adjacent fiber pathways (Fig. 7C). The power levels for all subjects, as computed from the clinically chosen settings, finite element models, and Equation 7 were as follows for subjects S1S8, respectively (in mW): 2.77, 2.49, 1.81, 10.25, 1.51, 2.78, 4.97, 3.81. The MOPSO results from these clinical power level constraints were used for all subsequent comparisons across models. The majority of optimal electrode configurations were comprised of a combination of electrodes (Fig. 7D, Fig. 8), with power distributed preferentially around a single electrode at varying levels of spread. Median values of the power spatial distribution, based on the metric defined by Equation 13, were as follows for subjects S1-S8, respectively: 0.5211, 0.4777, 0.5782, 0.5125, 0.5767, 0.6867, 0.4066, 0.6127 (Fig. 8).
Figure 7:
Sample MOPSO output for subject S6 using MAFT-based activation prediction and power constrained to 2.78 mW. (A) The seven-dimensional Pareto front, with all points shown (semi-transparent blue dots) and only those points that are non-dominated with respect to the NMT, HDP, and MT objectives (opaque black dots). The range of solutions presented exhibit tradeoffs. A different view (inset) indicates that the black dots form a non-dominated subset of the Pareto front along the three dimensions plotted. (B) Activation profile corresponding to the red highlighted point on the sample Pareto front from (A). (ML not shown due to low, infrequent activation across subjects.) (C) Visualization of the DBS lead placed in the STN and surrounded by modeled pathways. Activated fibers are bolded. Activated MT (purple dots) and NMT (green dots) are also bolded. The DBS lead and active electrodes are highlighted in the insets. (D) Unfolded view of electrode configuration at red highlighted point from (A). P: posterior, L: lateral, S: superior, M: medial.
Figure 8:
Distribution of power across active electrodes for each MOPSO-derived electrode configuration on the Pareto fronts across all subjects. (A) Power distributions, as measured by the metric described in Equation 13, reflect higher values for more distributed power (yellow dot) and lower values for less distributed power (blue dot). (B) Across all subjects, the Pareto front points exhibited a range of power distributions, with the majority of configurations consisting of multi-electrode settings.
3.4. Comparing Pathway Targeting across Models
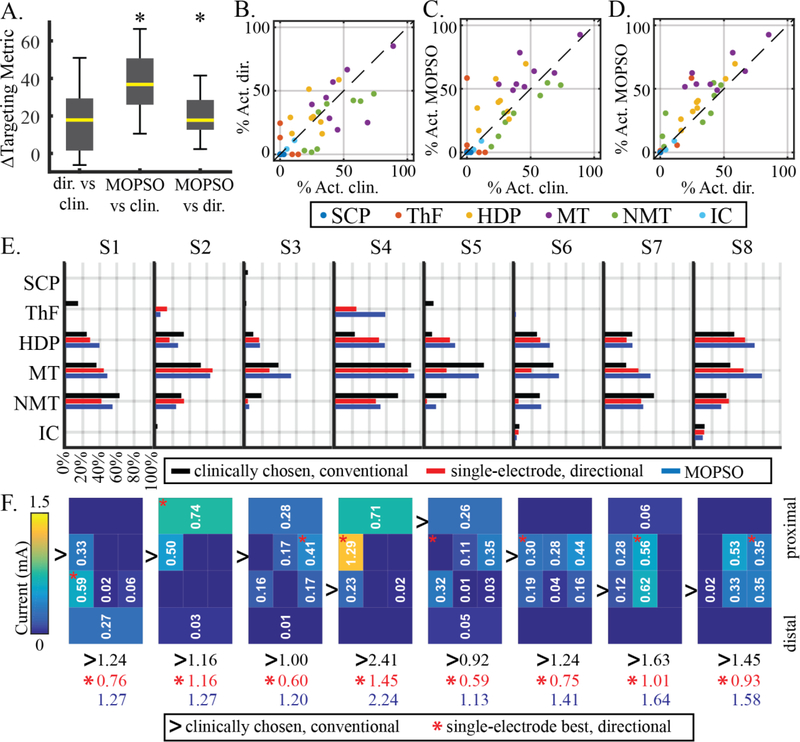
We selected a point from each subject’s Pareto front that maximized the targeting metric (Equation 12), and compared that point to the single-electrode directional lead configuration that maximized the same targeting metric, as well as to the clinically optimized setting in the conventional lead. In all subjects, the selected MOPSO-derived multi-electrode configurations achieved a higher targeting metric than either the single-electrode directional lead configurations or the clinically optimized conventional lead configurations (Fig. 9A, Supp. Fig. 6). Additionally, compared to the clinically optimized settings in the conventional lead, the single-electrode directional configurations achieved a larger targeting metric in most (S1, S3, S4, S6, S7, S8), but not all (S2, S5) subjects (Supp. Fig. 6). These differences across individuals were reflected in group differences, with significant differences being evident only between the MOPSO-derived settings and setting derived from either the single-electrode directional or the conventional lead settings (Friedman test: p < 0.001; post-hoc Wilcoxon signed rank test: directional minus clinical: p = 0.0391; MOPSO minus clinical: p = 0.0078; MOPSO minus directional: p = 0.0078; Bonferroni corrected threshold at 5% significance level: 0.0167; Fig. 9A). In terms of pathway activation underlying these targeting metrics, the MOPSO-derived multi-electrode configurations generally achieved higher MT (7 of 8 subjects) and HDP (6 of 8 subjects) activation and lower NMT (7 of 8 subjects) activation than the clinically optimized setting (Fig. 9C), as well as generally higher MT (7 of 8 subjects) and HDP (8 of 8 subjects) activation than the single-electrode directional lead settings (Fig. 9D). The directional lead single-electrode configurations had 5 of 8 subjects with higher HDP activation, 6 of 8 subjects with lower NMT activation, but also an equal mix of subjects with lower and higher MT activation (i.e. 4 of 8 for each), compared to the clinically optimized conventional lead configuration.
Figure 9:
Comparison of pathway activation and electrode configurations across models. (A) Differences in targeting metric across all subjects and across all three model types. Black asterisks denote a pairwise difference across subjects that was significantly different from zero. (B) Summary of percent activation across each pathway for the conventional lead at clinically optimized settings and the single-electrode directional lead settings at maximal targeting metric. (C) Same as (B), but comparing clinically optimized conventional lead to MOPSO at maximal targeting metric. (D) Same as (C), but comparing directional single-electrode to MOPSO multi-electrode settings. (E) Activation profiles for each subject for the three model types. Activation due to clinically optimized settings (black bars) were predicted using biophysical models of current-controlled stimulation that best matched the thresholds of voltage-controlled stimulation. Activation due to single-electrode and multi-electrode directional lead settings were predicted using MAFT (red and blue bars). (F) Electrode configurations for all three model types. For the MOPSO-derived multi-electrode configurations, current distribution is shown (total sum of current in milliamps shown in blue). For the single-electrode directional lead settings, the electrode that maximized the targeting metric is denoted by the red asterisk (current in milliamps shown in red). For the clinically optimized conventional lead setting, the chosen electrode is denoted by the black arrow (current in milliamps shown in black). All single- and multi-electrode configurations were constrained to a power that was equivalent to that used in the respective subject’s conventional lead setting.
In terms of activation profiles and dominance (i.e. improvement in all objectives simultaneously) (Fig. 9E), particularly in the MT, NMT, and HDP pathways considered by the targeting metric, tradeoffs were evident across the three model types. The MOPSO approach dominated the single-electrode directional approach in only one subject (S8), given that the single-electrode setting in other subjects achieved either lower NMT activation (S1, S3, S4, S5, S6, S7) or higher MT activation (S2). Compared to the conventional lead settings, the MOPSO approach dominated in five subjects (S1, S3, S4, S7, S8), with other subjects at conventional lead settings having either higher HDP activation (S2), higher MT activation (S5), or lower NMT activation (S6). Meanwhile, the single-electrode directional lead configurations only dominated the conventional lead settings in one subject (S1), while exhibiting a mix of tradeoffs in other subjects, including lower MT activation (S3, S4, S5, S6), higher NMT activation (S8), lower HDP activation (S7), and both lower HDP and higher NMT activation (S2).
The total current of the multi-electrode configurations was greater than that of the single-electrode directional lead configurations for all subjects, with the distribution of current overlapping spatially with the best single electrode on the directional lead for all subject except S5 (Fig. 9F).
3.5. Influence of Modifying the DBS Lead Orientation Estimate
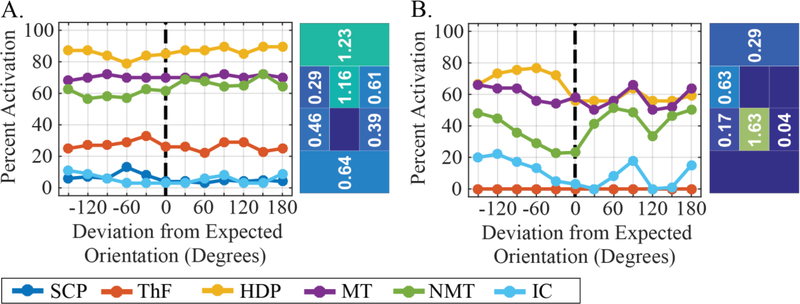
To gauge the influence of DBS lead orientation estimates on pathway activation, we simulated the activation profiles of two sample electrode configurations from the Pareto front of model S5, but rotated the DBS lead by 30° increments over a 360° range. As illustrated in (Fig. 10), when modifying the orientation for the more distributed electrode configuration (Fig. 10A), the effect on the activation profile was small, with changes of less than 8% within 30° deviations, and less than 10% for any deviation. In comparison, for more focal electrode configurations (Fig. 10B), orientation shifts caused larger changes in the activation profile, with changes up to 20% within 30° deviations, and changes up to 28% across other deviations.
Figure 10:
Influence of DBS lead orientation estimate on predicted activation due to two sample electrode configurations from a sample Pareto front of Subject S5. (A) For a distributed electrode configuration, activation profiles exhibited small changes relative to changes in orientation estimation. (B) For a more focal electrode configuration, activation profiles exhibited larger differences relative to changes in orientation estimation.
4. Discussion
In this study, our models of neural pathway activation prediction showed that the range of pathways coursing within and around the STN are correlated in their activation when stimulating with commercial DBS systems. Within the confines of these correlations, the multi-objective particle swarm optimization framework presented here was able to identify multi-electrode configurations that solve the multi-objective DBS programming problem of modulating one or more pathways with the goal of maximizing therapeutic efficacy and minimizing the emergence of stimulation-induced side effects.
4.1. Relationship between Pathway Modulation and Clinical Ratings
In developing methods to program DBS systems, it is important to understand the neural pathways involved in both therapy and side effects of stimulation. In our models with the conventional DBS lead, we found that a number of pathways were predicted to be activated during the programming process. During the clinical monopolar review, reduction in parkinsonian motor signs occurred along with predicted activation of modeled pathways that included MT, NMT, HDP, ThF, SCP, and to some extent IC (Fig 4A-D). Across all subjects, the final therapeutic setting selected by the clinician was consistently associated with high MT, NMT, and HDP activation, with relatively low and infrequent activation of other pathways (Fig. 4D). It is important to note that the choice of the final setting did not necessarily indicate a causal relationship between the pathways (MT, NMT, HDP) and the greatest reduction in parkinsonian motor signs, since selection of final settings often reflects a combination of delivering therapy with a large therapeutic window [18]. Indeed, the clinical implication of the retrospective modeling results for the monopolar review data is that stimulation of several different pathways may generate therapeutic effects. This is consistent with previous retrospective VTA-based visualization models that suggested DBS target regions may be located both within and outside of STN [9]. Previous work has also suggested the potential role of cerebello-thalamic pathways (SCP & ThF) in tremor and gait [29,65,66], and even to some degree the role of IC in rigidity [23], though there was minimal activation of these pathways in this subject cohort. ML activation was infrequent and low in amplitude due to its distant posterior location relative to the implanted DBS leads in this study, suggesting a limited role in STN DBS programming settings in this cohort. Together, the results indicate that conventional DBS lead designs with monopolar single-contact electrode configurations can make it challenging to selectively activate individual pathways within and around the STN [67]. The results suggest that directional DBS lead designs should improve targeting of individual pathways within and around the STN.
4.2. Single-electrode Biophysical Simulations in Directional DBS Lead
Our single-electrode biophysical models of the directional DBS lead showed that most pathways were inter-related in their activation to some degree (i.e. a correlation was found between strength of activation in one pathway and strength of activation in another) (Fig. 5). In particular, for the placement of the DBS leads considered in the present study, the most highly correlated pairs of pathways were the anatomically adjacent MT and NMT, SCP and ThF [56], and MT/NMT and HDP. This is consistent with the concept that pathways with similar spatial orientations relative to the electric field will have similar activation profiles [67,68]. The presence of such correlated pathway activation poses challenges to targeting those pathways individually with current DBS lead designs, implant trajectories, and stimulation settings. This issue is of particular clinical relevance for pathways such as MT and NMT, in which the ideal stimulation would activate one at the exclusion of the other [10]. However, previous clinical studies have noted that some degree of separation may be possible [10].
A number of anatomical trends in selectivity emerged around and along the DBS lead (Fig. 6B). These included higher ThF selectivity in posteromedial electrodes, higher IC selectivity in lateral electrodes (when IC activation was present), higher ThF selectivity in seven of eight subjects in superior electrodes, higher IC selectivity in more inferior electrodes, and higher HDP selectivity in either middle or superior electrodes. The lateral electrodes’ affinity for IC selectivity is consistent with a previous simulation study using VTAs [14]. However, in spite of these anatomical trends, selectivity profiles across MT, NMT, and around the lead for HDP did not exhibit such trends (Fig. 6A). Instead, there were variations in selectivity around and along the lead that reflected subject-specific DBS lead placement and pathway trajectories. Furthermore, as shown in (Fig. 9A), while single-electrode directional stimulation did improve the targeting metric result over single-electrode stimulation through conventional DBS leads, the pairwise comparison was not statistically significant. This suggests that directional DBS leads can provide improved targeting in some patients, but this largely depends on the position and orientation of the DBS lead relative to the targeted pathways [16,17]. Taken together with our computational findings, these outcomes highlight the contribution of subject-specific anatomical variability and DBS lead placement to pathway selectivity, as well as its importance in developing programming approaches that target individual pathways.
4.3. MOPSO Output
In this study, we ran the MOPSO algorithm to solve the programming problem posed by Eqs. 4–8, with the goal of finding a distribution of current that optimized for seven objectives: maximize activation of purported therapeutic regions (SCP, ThF, MT, HDP), and minimize activation of regions associated with side effects (IC, ML, NMT). The result for each run was a seven-dimensional Pareto front (Fig. 7A), consisting of a range of candidate solutions that exhibited trade-offs in pathway activation. Each point on the Pareto front corresponded to an electrode configuration (Fig. 7D) and a resulting activation profile (Fig. 7B). Furthermore, each point on the Pareto front was comprised of an activation profile that was better than other points in at least one objective, at the expense of at least one other objective (e.g. more MT activation in exchange for less HDP activation). Therefore, this range of solutions comprised the best possible electrode configurations for stimulating in a pathway-driven manner, enabling the flexible selection and prioritization of pathway targets to tailor activation toward the programmer’s particular goals.
The points on this Pareto front consisted of distributed current electrode configurations across all subjects and across the majority of points on the Pareto front (Fig. 8). Notably, these multi-electrode configurations had a total sum of current that exceeded that of their single-electrode counterparts, due principally to the total power constraint rather than constraining the total current. This was due to the lower impedance present in a multi-electrode configuration, even after accounting for the higher impedance of the directional electrodes. As such, the optimal configurations were found to be non-intuitive distributions of current across multiple electrodes.
4.4. Comparing Pathway Targeting across Model Types
Given that the results generated for multi-objective pathway targeting included a collection of solutions rather than a single solution (Fig. 7A), our comparison across model types was facilitated by defining a targeting metric (Equation 12). In this comparison, we found that the multi-electrode configurations generated by the MOPSO approach achieved larger targeting metric values than either the clinically optimized conventional lead or the single-electrode directional lead alone. This was generally manifested in the form of tradeoffs involving greater overall activation across pathways in the multi-electrode configurations. While such tradeoffs are inherent in multi-objective problems, the degree to which a particular desired activation profile can be achieved is fundamentally limited by how well an underlying system can isolate one pathway over another.
MT and NMT were found to be highly correlated (Fig. 5), making it difficult to orthogonally stimulate one pathway while avoiding the other. Furthermore, while multi-electrode cathodal stimulation can readily enable increased activation of particular pathways, the problem of activating a desired pathway while avoiding a highly correlated adjacent pathway is not readily solved with redistribution of cathodal current alone. Indeed, such a redistribution of cathodal current to increase activation in one pathway would increase activation in the correlated pathway, as reflected by the generally increased MT and NMT activation in multi-electrode settings compared to single-electrode settings (Fig. 9D). Notably, this finding applies to combinations of cathodes and to the commercial DBS leads considered here. Selectivity can be improved by increasing the DBS system’s ability to de-correlate pathways, either through novel DBS electrode designs or through the introduction of simultaneous anodal stimulation to further shape electric fields in the vicinity of the leads [67,68]. The multi-objective approach developed here can be extended to address such additional stimulation capabilities.
The distribution of current across multi-electrode directional lead settings overlapped to varying degrees with the corresponding single-electrode directional lead settings in seven subjects (S1-S4, S6-S8). However, while there was also some degree of overlap between the multi-electrode current distributions and the clinically optimized electrode chosen on the conventional lead, there are two important factors that limit the ability to interpret such overlap or lack thereof. First, therapeutic stimulation can occur at any one of the electrodes and at a number of amplitudes on the conventional lead (Fig. 4A). The clinically chosen setting among these is more reflective of the measured motor benefit and the threshold for overt side effects, rather than reflecting a particular activation profile. Second, there is not yet a clearly established relationship between activation of particular pathways and the resulting clinical outcome. Indeed, the targeting metric used here was heuristically derived from a literature-driven assumption that HDP and MT are relevant to therapy and that NMT induces cognitive side effects. We showed that the pathway-driven approach to DBS programming identified multi-electrode combinations that can enhance activation of clinically relevant target pathways and the defined targeting metric. Nevertheless, the establishment of a clinically optimal targeting metric in future prospective studies are needed, and such studies can both leverage and inform the pathway-targeting tools developed here in order to compare outcomes across electrode configurations within a directional DBS lead.
The study described here formulates and efficiently solves (within minutes) a non-convex optimization problem using a computational model of DBS that includes subject-specific axonal morphologies. By allowing axons to be activated at any location along the fiber trajectory, this problem captures the non-convex nature of stimulation, which can be explored and solved using particle swarm optimization and likely other non-convex optimization algorithms. Other approaches based on convex optimization have also been advanced [43,44], and these techniques are useful for identifying candidate electrode configurations very quickly (within seconds). Like the present approach, convex optimization approaches have been applied to specific fiber trajectories [43] and to models based on subject-specific human imaging [44]. However, these convex optimization frameworks rely on the intensity of the second spatial difference in one [43] or all [44] directions as proxies for amount of activation, and this relaxation therefore neglects the non-convex nature of axonal activation. VTA-based modeling approaches [36,69] have also been developed that can facilitate programming and analysis by visually representing the extent of activation around the DBS lead. However, while the relatively lower complexity of such VTA-based approaches makes them more amenable for dissemination since diffusion-weighted imaging data is not required, specific pathway trajectories are not used in the calculation of activation and thus creates inaccuracies in the activation predictions [70]. Previous work, which developed a PSO approach to improving pathway targeting of DBS therapy [45], implemented an aggregate objective function with predefined weights to address the non-convex, pathway-informed optimization problem. The MOPSO approach used in the current study, however, only requires defining pathways as either therapeutic (−1) or side effect (+1) and effectively integrates a broad range of different objective function weights into the calculation of the Pareto front. This approach thus provides the user with a Pareto front in which (1) one can select an electrode setting that best targets pathways of interest without having to predefine specific objective function weights and (2) does not require re-running the algorithm and simulations should one wish to evaluate an objective function that weights pathway activation differently.
4.5. Influence of Modifying the DBS Lead Orientation Estimate
As shown in (Fig. 10), estimation errors of DBS lead orientation can lead to errors in predicted activation. When the optimal electrode configuration consists of a more focal distribution of current, a deviation as low as 30° can lead to large deviations in pathway activation (up to 28% in Fig. 10B). Meanwhile, optimal electrode configurations consisting of more distributed current have a smaller deviation in predicted activation (less than 8% within 30° in Fig. 10A). Beyond the deviations in activation profile, the optimality of the applied stimulation is reduced by errors in orientation estimation, highlighting the importance of proper estimation in order to target desired pathways. Such errors in DBS lead localization can be compounded by registration errors involved in building subject-specific models [71]. Nevertheless, recent efforts to develop accurate techniques for orientation estimation have demonstrated promising approaches to address the problem of orientation estimation to within several degrees of consistency [72,73], which may be sufficiently precise for the scale of electrodes used commercially. Given such ongoing developments to develop increasingly accurate characterizations of DBS implants orientations, the subject-specific pathway targeting approach presented here becomes more relevant as a tool for assessing the clinical role of pathways and maximizing desired activation profiles.
4.6. Limitations
While the presented pathway-driven approach for DBS programming suggested the potential for improved activation profiles in the modeled pathways, important gaps remain to validate the use of such approaches clinically. First, the present study made a number of predictions regarding activation based on computational models of both conventional and directional DBS leads. These predictions were not accompanied with experimental evidence of activation. For investigating the effects of stimulation in the conventional lead and the directional lead alone, we implemented “gold standard” biophysical models [59,70], which incorporate non-linear dynamic interactions between stimulation and activation. Furthermore, in the MOPSO approach itself, we predicted activation using an “activating function” paradigm that was calibrated to the specific pathway geometry modeled as done in [45] in order to mitigate the sensitivity of this approach to parameters such as axonal geometry, distance from the lead, and temporal parameters [74,75] (Supp. Fig. 7–8). A notable consequence of this tuning was that our findings regarding targeting metric remained even after calculating activation of the multi-electrode configurations using biophysical models (Supp. Fig. 9–10). In spite of these efforts to accurately predict activation with biophysical models (active) and calibrated cable models (passive), the need for validation in activation prediction remains an important gap at the pathway-specific level. Furthermore, errors associated with lead localization, pathway trajectory modeling, and neuron biophysical parameter estimation all contribute to this challenge.
A related limitation, noted previously, involves the question of what the best targeting metric is. We demonstrated the ability to enhance activation profiles that target MT and HDP while penalizing NMT activation, under the heuristically derived supposition that MT and HDP are therapeutic and that NMT activation produces side effects. However, this remains an open question, and a number of studies have aimed to probe the roles of these and other modeled pathways in therapy for Parkinson’s disease [10,23,57,76], Essential Tremor [29,77,78], and Dystonia [79]. While the dominance-based optimization approach presented here does not rely on the specific targeting metric weightings used, an increased understanding of each pathway’s role would inform the selection of electrode configurations along the Pareto front. Toward the aim of investigating these roles, the pathway-driven programming approach presented here provides a powerful tool for identifying points on the Pareto front that most selectively activate pathways under consideration, thus providing a small number of points for clinical testing. Importantly, prospective studies will be needed to evaluate this framework, ideally involving the quantification of clinical outcomes of DBS relative to each single dimension along a subject’s Pareto front. Such intra-subject studies that leverage the proposed pathway targeting approach in in vivo settings can therefore clarify the clinical relevance of Pareto front dimensions while also helping to address gaps in knowledge regarding the role of different pathways in therapy.
As a note on efficiency, the MOPSO runtime for the seven objectives discussed here was under two minutes for each model on a relatively standard PC. Such a short runtime is not restrictive, and is therefore amenable to implementation as part of a larger framework of subject-specific modeling for DBS programming. It is important to consider, however, that while the algorithm was designed to run efficiently, the process of building the subject-specific finite element models and generating the axonal pathway models remains a largely manual process and requires access to high-field MR imaging [47,80]. A full clinical implementation of the presented approach for high-volume DBS centers will therefore require an increased availability of high quality imaging data (i.e. through the increased clinical use of 7T scanners and through improved processing algorithms for extracting needed structural data from lower quality images [81]), as well as additional advances in automating the co-registration of imaging data sets, segmentation of nuclei and fiber pathways, and reconstruction of axonal trajectories from diffusion weighted imaging.
4.7. Conclusion
In summary, we developed a multi-objective framework for pathway-targeted programming of DBS leads that leverages subject-specific anatomy to efficiently provide a range of electrode configurations for therapy. Future studies that apply this framework in vivo are necessary to facilitate experimental validation of the model predictions and test specific hypotheses about the clinical relevance of targeting individual pathways around a DBS lead. The optimization framework is also poised for future developments to extend the relevant solution space traversed, incorporating mixed anode-cathode configurations, multimodal objectives such as electrophysiological signals, as well as more intelligent particle exploration of solution space to more efficiently search the larger space introduced by such developments.
Supplementary Material
5. Acknowledgements
We thank our funding sources: Michael J. Fox Foundation, NIH (R01-NS081118, R01- NS094206, P50-NS098573, R01-NS085118, P41-EB015894, P30–076408, U54-MH091657), NSF Graduate Research Program (00039202 to E.P.), and NSF-IGERT Program (DGE1069104).
References
- 1.Lozano AM, Hutchison WD, Kalia SK. What Have We Learned About Movement Disorders from Functional Neurosurgery? Annu Rev Neurosci. 2017;40:453–477. [DOI] [PubMed] [Google Scholar]
- 2.Crowell AL, Riva-Posse P, Garlow SJ, Mayberg HS. Toward an Understanding of the Neural Circuitry of Major Depressive Disorder Through the Clinical Response to Deep Brain Stimulation of Different Anatomical Targets. Curr Behav Neurosci Rep. 2014;1(2):55–63. [Google Scholar]
- 3.Wichmann T Deep-Brain Stimulation for Neurologic and Neuropsychiatric Disorders In: Handbook of Behavioral Neuroscience [Internet]. Elsevier; 2017. [cited 2017]. p. 971–95. Available from: http://linkinghub.elsevier.com/retrieve/pii/B9780128022061000490 [Google Scholar]
- 4.Okun MS, Tagliati M, Pourfar M, et al. Management of referred deep brain stimulation failures: a retrospective analysis from 2 movement disorders centers. Arch Neurol. 2005;62(8):1250–1255. [DOI] [PubMed] [Google Scholar]
- 5.Kleiner-Fisman G, Herzog J, Fisman DN, et al. Subthalamic nucleus deep brain stimulation: Summary and meta-analysis of outcomes. Mov Disord. 2006;21(S14):S290–304. [DOI] [PubMed] [Google Scholar]
- 6.Duchin Y, Abosch A, Yacoub E, Sapiro G, Harel N. Feasibility of Using Ultra-High Field (7 T) MRI for Clinical Surgical Targeting. Bankiewicz K, editor. PLoS ONE. 2012;7(5):e37328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gross RE, McDougal ME. Technological Advances in the Surgical Treatment of Movement Disorders. Curr Neurol Neurosci Rep [Internet]. 2013. [cited 2017];13(8). Available from: http://link.springer.com/10.1007/s11910-013-0371-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shamir RR, Dolbert T, Noecker AM, Frankemolle AM, Walter BL, McIntyre CC. A method for predicting the outcomes of combined pharmacologic and deep brain stimulation therapy for Parkinson’s disease. Med Image Comput Comput-Assist Interv MICCAI Int Conf Med Image Comput Comput-Assist Interv. 2014;17(Pt 2):188–95. [DOI] [PubMed] [Google Scholar]
- 9.Butson CR, Cooper SE, Henderson JM, Wolgamuth B, McIntyre CC. Probabilistic analysis of activation volumes generated during deep brain stimulation. NeuroImage. 2011;54(3):2096–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Frankemolle AMM, Wu J, Noecker AM, et al. Reversing cognitive-motor impairments in Parkinson’s disease patients using a computational modelling approach to deep brain stimulation programming. Brain. 2010;133(3):746–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chaturvedi A, Foutz TJ, McIntyre CC. Current steering to activate targeted neural pathways during deep brain stimulation of the subthalamic region. Brain Stimulat. 2012;5(3):369–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Butson CR, McIntyre CC. Current Steering to Control the Volume of Tissue Activated During Deep Brain Stimulation. Brain Stimulat. 2008;1(1):7–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Keane M, Deyo S, Abosch A, Bajwa JA, Johnson MD. Improved spatial targeting with directionally segmented deep brain stimulation leads for treating essential tremor. J Neural Eng. 2012;9(4):046005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.van Dijk KJ, Verhagen R, Bour LJ, Heida C, Veltink PH. Avoiding Internal Capsule Stimulation With a New Eight-Channel Steering Deep Brain Stimulation Lead: EIGHT CHANNEL STEERING-DBS LEAD. Neuromodulation Technol Neural Interface [Internet]. 2017. [cited 2017]; Available from: http://doi.wiley.com/10.1111/ner.12702 [DOI] [PubMed] [Google Scholar]
- 15.Pollo C, Kaelin-Lang A, Oertel MF, et al. Directional deep brain stimulation: an intraoperative double-blind pilot study. Brain. 2014;137(7):2015–26. [DOI] [PubMed] [Google Scholar]
- 16.Steigerwald F, Müller L, Johannes S, Matthies C, Volkmann J. Directional deep brain stimulation of the subthalamic nucleus: A pilot study using a novel neurostimulation device: Horizontal Current Steering in DBS. Mov Disord [Internet]. 2016. [cited 2016]; Available from: http://doi.wiley.com/10.1002/mds.26669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dembek TA, Reker P, Visser-Vandewalle V, et al. Directional DBS increases side-effect thresholds-A prospective, double-blind trial: Directional Dbs Increases Side-Effect Thresholds. Mov Disord [Internet]. 2017. [cited 2017]; Available from: http://doi.wiley.com/10.1002/mds.27093 [DOI] [PubMed] [Google Scholar]
- 18.Volkmann J, Moro E, Pahwa R. Basic algorithms for the programming of deep brain stimulation in Parkinson’s disease. Mov Disord. 2006;21(S14):S284–9. [DOI] [PubMed] [Google Scholar]
- 19.Moro E, Poon Y-YW, Lozano AM, Saint-Cyr JA, Lang AE. Subthalamic nucleus stimulation: improvements in outcome with reprogramming. Arch Neurol. 2006;63(9):1266–1272. [DOI] [PubMed] [Google Scholar]
- 20.Hunka K, Suchowersky O, Wood S, Derwent L, Kiss ZHT. Nursing time to program and assess deep brain stimulators in movement disorder patients. J Neurosci Nurs J Am Assoc Neurosci Nurses. 2005;37(4):204–10. [DOI] [PubMed] [Google Scholar]
- 21.Schüpbach WMM, Chabardes S, Matthies C, et al. Directional leads for deep brain stimulation: Opportunities and challenges: Directional Leads For DBS. Mov Disord. 2017;32(10):1371–5. [DOI] [PubMed] [Google Scholar]
- 22.Krack P, Batir A, Van Blercom N, et al. Five-year follow-up of bilateral stimulation of the subthalamic nucleus in advanced Parkinson’s disease. N Engl J Med. 2003;349(20):1925–1934. [DOI] [PubMed] [Google Scholar]
- 23.Xu W, Miocinovic S, Zhang J, Baker KB, McIntyre CC, Vitek JL. Dissociation of motor symptoms during deep brain stimulation of the subthalamic nucleus in the region of the internal capsule. Exp Neurol. 2011;228(2):294–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fytagoridis A, Åström M, Wårdell K, Blomstedt P. Stimulation-induced side effects in the posterior subthalamic area: Distribution, characteristics and visualization. Clin Neurol Neurosurg. 2013;115(1):65–71. [DOI] [PubMed] [Google Scholar]
- 25.Tommasi G, Krack P, Fraix V, et al. Pyramidal tract side effects induced by deep brain stimulation of the subthalamic nucleus. J Neurol Neurosurg Psychiatry. 2008;79(7):813–9. [DOI] [PubMed] [Google Scholar]
- 26.Krauss JK, Yianni J, Loher TJ, Aziz TZ. Deep brain stimulation for dystonia. J Clin Neurophysiol. 2004;21(1):18–30. [DOI] [PubMed] [Google Scholar]
- 27.Servello D, Porta M, Sassi M, Brambilla A, Robertson MM. Deep brain stimulation in 18 patients with severe Gilles de la Tourette syndrome refractory to treatment: the surgery and stimulation. J Neurol Neurosurg Psychiatry. 2008;79(2):136–42. [DOI] [PubMed] [Google Scholar]
- 28.Antosik-Wójcińska A, Święcicki Ł, Dominiak M, Sołtan E, Bieńkowski P, Mandat T. Impact of STN-DBS on mood, drive, anhedonia and risk of psychiatric side-effects in the population of PD patients. J Neurol Sci. 2017;375:342–7. [DOI] [PubMed] [Google Scholar]
- 29.Coenen VA, Allert N, Mädler B. A role of diffusion tensor imaging fiber tracking in deep brain stimulation surgery: DBS of the dentato-rubro-thalamic tract (drt) for the treatment of therapy-refractory tremor. Acta Neurochir (Wien). 2011;153(8):1579–85. [DOI] [PubMed] [Google Scholar]
- 30.Riva-Posse P, Choi KS, Holtzheimer PE, et al. Defining Critical White Matter Pathways Mediating Successful Subcallosal Cingulate Deep Brain Stimulation for TreatmentResistant Depression. Biol Psychiatry. 2014;76(12):963–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McIntyre CC. Cellular Effects of Deep Brain Stimulation: Model-Based Analysis of Activation and Inhibition. J Neurophysiol. 2004;91(4):1457–69. [DOI] [PubMed] [Google Scholar]
- 32.Johnson MD, McIntyre CC. Quantifying the Neural Elements Activated and Inhibited by Globus Pallidus Deep Brain Stimulation. J Neurophysiol. 2008;100(5):2549–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Miocinovic S Computational Analysis of Subthalamic Nucleus and Lenticular Fasciculus Activation During Therapeutic Deep Brain Stimulation. J Neurophysiol. 2006;96(3):1569–80. [DOI] [PubMed] [Google Scholar]
- 34.Butson CR, Cooper SE, Henderson JM, McIntyre CC. Patient-specific analysis of the volume of tissue activated during deep brain stimulation. Neuroimage. 2007;34(2):661–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Maks CB, Butson CR, Walter BL, Vitek JL, McIntyre CC. Deep brain stimulation activation volumes and their association with neurophysiological mapping and therapeutic outcomes. J Neurol Neurosurg Psychiatry. 2009;80(6):659–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chaturvedi A, Luján JL, McIntyre CC. Artificial neural network based characterization of the volume of tissue activated during deep brain stimulation. J Neural Eng. 2013;10(5):056023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Martens HCF, Toader E, Decré MMJ, et al. Spatial steering of deep brain stimulation volumes using a novel lead design. Clin Neurophysiol. 2011;122(3):558–66. [DOI] [PubMed] [Google Scholar]
- 38.Baumgarten C, Zhao Y, Sauleau P, Malrain C, Jannin P, Haegelen C. Improvement of Pyramidal Tract Side Effect Prediction Using a Data-Driven Method in Subthalamic Stimulation. IEEE Trans Biomed Eng. 2017;64(9):2134–41. [DOI] [PubMed] [Google Scholar]
- 39.Akram H, Sotiropoulos SN, Jbabdi S, et al. Subthalamic deep brain stimulation sweet spots and hyperdirect cortical connectivity in Parkinson’s disease. NeuroImage. 2017;158:332–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gunalan K, Chaturvedi A, Howell B, et al. Creating and parameterizing patient-specific deep brain stimulation pathway-activation models using the hyperdirect pathway as an example. PLoS ONE [Internet]. 2017. [cited 2017];12(4). Available from: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC5404874/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zitella LM, Teplitzky BA, Yager P, et al. Subject-specific computational modeling of DBS in the PPTg area. Front Comput Neurosci [Internet]. 2015. [cited 2016];9 Available from: http://journal.frontiersin.org/Article/10.3389/fncom.2015.00093/abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Howell B, McIntyre CC. Analyzing the tradeoff between electrical complexity and accuracy in patient-specific computational models of deep brain stimulation. J Neural Eng. 2016;13(3):036023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Xiao Y, Pena E, Johnson MD. Theoretical Optimization of Stimulation Strategies for a Directionally Segmented Deep Brain Stimulation Electrode Array. IEEE Trans Biomed Eng. 2016;63(2):359–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Anderson DN, Osting B, Vorwerk J, Dorval A (Chuck), Butson CR. Optimized programming algorithm for cylindrical and directional deep brain stimulation electrodes. J Neural Eng [Internet]. 2017. [cited 2017]; Available from: http://iopscience.iop.org/article/10.1088/1741-2552/aaa14b [DOI] [PubMed] [Google Scholar]
- 45.Peña E, Zhang S, Deyo S, Xiao Y, Johnson MD. Particle swarm optimization for programming deep brain stimulation arrays. J Neural Eng. 2017;14(1):016014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lenglet C, Abosch A, Yacoub E, De Martino F, Sapiro G, Harel N. Comprehensive in vivo Mapping of the Human Basal Ganglia and Thalamic Connectome in Individuals Using 7T MRI. Bankiewicz K, editor. PLoS ONE 2012;7(1):e29153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Plantinga BR, Temel Y, Duchin Y, et al. Individualized parcellation of the subthalamic nucleus in patients with Parkinson’s disease with 7T MRI. NeuroImage [Internet]. 2016. [cited 2017]; Available from: http://linkinghub.elsevier.com/retrieve/pii/S1053811916304864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nielsen MS, Bjarkam CR, Sørensen JC, Bojsen-Møller M, Sunde NA, Østergaard K. Chronic subthalamic high-frequency deep brain stimulation in Parkinson’s disease ? a histopathological study. Eur J Neurol. 2007;14(2):132–8. [DOI] [PubMed] [Google Scholar]
- 49.Schmidt C, van Rienen U. Modeling the Field Distribution in Deep Brain Stimulation: The Influence of Anisotropy of Brain Tissue. IEEE Trans Biomed Eng. 2012;59(6):1583–92. [DOI] [PubMed] [Google Scholar]
- 50.Güllmar D, Haueisen J, Reichenbach JR. Influence of anisotropic electrical conductivity in white matter tissue on the EEG/MEG forward and inverse solution. A high-resolution whole head simulation study. NeuroImage 2010;51(1):145–63. [DOI] [PubMed] [Google Scholar]
- 51.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys Med Biol. 1996;41(11):2251–69. [DOI] [PubMed] [Google Scholar]
- 52.Gabriel S, Lau RW, Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys Med Biol. 1996;41(11):2271–93. [DOI] [PubMed] [Google Scholar]
- 53.Cole KS, Cole RH. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J Chem Phys. 1941;9(4):341–51. [Google Scholar]
- 54.Yousif N, Bayford R, Bain PG, Liu X. The peri-electrode space is a significant element of the electrode–brain interface in deep brain stimulation: A computational study. Brain Res Bull. 2007;74(5):361–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Howell B, McIntyre CC. Role of Soft-Tissue Heterogeneity in Computational Models of Deep Brain Stimulation. Brain Stimulat. 2017;10(1):46–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Gallay MN, Jeanmonod D, Liu J, Morel A. Human pallidothalamic and cerebellothalamic tracts: anatomical basis for functional stereotactic neurosurgery. Brain Struct Funct. 2008;212(6):443–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gradinaru V, Mogri M, Thompson KR, Henderson JM, Deisseroth K. Optical deconstruction of parkinsonian neural circuitry. science. 2009;324(5925):354–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kita T, Kita H. The Subthalamic Nucleus Is One of Multiple Innervation Sites for LongRange Corticofugal Axons: A Single-Axon Tracing Study in the Rat. J Neurosci. 2012;32(17):5990–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.McIntyre CC, Richardson AG, Grill WM. Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle. J Neurophysiol. 2002;87(2):995–1006. [DOI] [PubMed] [Google Scholar]
- 60.Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9(6):1179–209. [DOI] [PubMed] [Google Scholar]
- 61.Yousif N, Bayford R, Liu X. The influence of reactivity of the electrode–brain interface on the crossing electric current in therapeutic deep brain stimulation. Neuroscience. 2008;156(3):597–606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kennedy J, Eberhart R. Particle swarm optimization. In IEEE; 1995. [cited 2017]. p. 1942–8. Available from: http://ieeexplore.ieee.org/document/488968/ [Google Scholar]
- 63.Engelbrecht AP. Fundamentals of computational swarm intelligence. Hoboken, NJ: Wiley; 2005. 599 p. [Google Scholar]
- 64.Reyes-Sierra M, Coello CC. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int J Comput Intell Res. 2006;2(3):287–308. [Google Scholar]
- 65.Fournier-Gosselin M-P, Lipsman N, Saint-Cyr JA, Hamani C, Lozano AM. Regional anatomy of the pedunculopontine nucleus: Relevance for deep brain stimulation: Anatomy of the Pedunculopontine Nucleus. Mov Disord. 2013;28(10):1330–6. [DOI] [PubMed] [Google Scholar]
- 66.Stover NP, Okun MS, Evatt ML, Raju DV, Bakay RAE, Vitek JL. Stimulation of the subthalamic nucleus in a patient with Parkinson disease and essential tremor. Arch Neurol. 2005;62(1):141–3. [DOI] [PubMed] [Google Scholar]
- 67.Slopsema JP, Peña E, Patriat R, et al. Clinical deep brain stimulation strategies for orientation-selective pathway activation. J Neural Eng [Internet]. 2018. [cited 2018]; Available from: http://iopscience.iop.org/article/10.1088/1741-2552/aad978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lehto LJ, Slopsema JP, Johnson MD, et al. Orientation selective deep brain stimulation. J Neural Eng. 2017;14(1):016016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Horn A, Li N, Dembek TA, et al. Lead-DBS v2: Towards a comprehensive pipeline for deep brain stimulation imaging. 2018. [cited 2018]; Available from: http://biorxiv.org/lookup/doi/10.1101/322008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Gunalan K, Howell B, McIntyre CC. Quantifying axonal responses in patient-specific models of subthalamic deep brain stimulation. NeuroImage. 2018;172:263–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Chaturvedi A, Butson CR, Lempka SF, Cooper SE, McIntyre CC. Patient-specific models of deep brain stimulation: Influence of field model complexity on neural activation predictions. Brain Stimulat. 2010;3(2):65–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Reinacher PC, Krüger MT, Coenen VA, et al. Determining the Orientation of Directional Deep Brain Stimulation Electrodes Using 3D Rotational Fluoroscopy. Am J Neuroradiol [Internet]. 2017. [cited 2017]; Available from: http://www.ajnr.org/lookup/doi/10.3174/ajnr.A5153 [DOI] [PMC free article] [PubMed]
- 73.Sitz A, Hoevels M, Hellerbach A, et al. Determining the orientation angle of directional leads for deep brain stimulation using computed tomography and digital x-ray imaging: A phantom study. Med Phys. 2017;44(9):4463–73. [DOI] [PubMed] [Google Scholar]
- 74.Peterson EJ, Izad O, Tyler DJ. Predicting myelinated axon activation using spatial characteristics of the extracellular field. J Neural Eng. 2011;8(4):046030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Moffitt MA, McIntyre CC, Grill WM. Prediction of Myelinated Nerve Fiber Stimulation Thresholds: Limitations of Linear Models. IEEE Trans Biomed Eng. 2004;51(2):229–36. [DOI] [PubMed] [Google Scholar]
- 76.van Wouwe NC, Pallavaram S, Phibbs FT, et al. Focused stimulation of dorsal subthalamic nucleus improves reactive inhibitory control of action impulses. Neuropsychologia. 2017;99:37–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Schlaier J, Anthofer J, Steib K, et al. Deep Brain Stimulation for Essential Tremor: Targeting the Dentato-Rubro-Thalamic Tract?: The DRTT in ET-DBS. Neuromodulation Technol Neural Interface. 2015;18(2):105–12. [DOI] [PubMed] [Google Scholar]
- 78.Chazen JL, Sarva H, Stieg PE, et al. Clinical improvement associated with targeted interruption of the cerebellothalamic tract following MR-guided focused ultrasound for essential tremor. J Neurosurg. 2017;1–9. [DOI] [PubMed] [Google Scholar]
- 79.Rozanski VE, da Silva NM, Ahmadi S-A, et al. The role of the pallidothalamic fibre tracts in deep brain stimulation for dystonia: A diffusion MRI tractography study: A Diffusion MRI Tractography Study. Hum Brain Mapp. 2017;38(3):1224–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Duchin Y, Shamir RR, Patriat R, et al. Patient-specific anatomical model for deep brain stimulation based on 7 Tesla MRI. Toft M, editor. PLOS ONE 2018;13(8):e0201469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kim J, Duchin Y, Kim H, Vitek J, Harel N, Sapiro G. Robust Prediction of Clinical Deep Brain Stimulation Target Structures via the Estimation of Influential High-Field MR Atlases In: Navab N, Hornegger J, Wells WM, Frangi A, editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Cham: Springer International Publishing; 2015. p. 587–594. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.