Abstract
Health risks from cigarette smoking — the leading cause of preventable death in the United States — can be substantially reduced by quitting. Although most smokers are motivated to quit, the majority of quit attempts fail. A number of studies have explored the role of self-reported symptoms, physiologic measurements, and environmental context on smoking risk, but less work has focused on the temporal dynamics of smoking events, including daily patterns and related nicotine effects. In this work, we examine these dynamics and improve risk prediction by modeling smoking as a self-triggering process, in which previous smoking events modify current risk. Specifically, we fit smoking events self-reported by 42 smokers to a time-varying semi-parametric Hawkes process (TV-SPHP) developed for this purpose. Results show that the TV-SPHP achieves superior prediction performance compared to related and existing models, with the incorporation of time-varying predictors having greatest benefit over longer prediction windows. Moreover, the impact function illustrates previously unknown temporal dynamics of smoking, with possible connections to nicotine metabolism to be explored in future work through a randomized study design. By more effectively predicting smoking events and exploring a self-triggering component of smoking risk, this work supports development of novel or improved cessation interventions that aim to reduce death from smoking.
1. Introduction
Cigarette smoking is responsible for over 480,000 deaths per year in the United States, with total yearly economic cost exceeding 4300 billion (Centers for Disease Control and Prevention (CDC), 2014). Quitting smoking quickly and substantially lowers the risk of heart attack, stroke, and cancer (Centers for Disease Control and Prevention (CDC), 2010), and most adult smokers are motivated to quit (Jamal et al., 2018). Unfortunately, fewer than one in three smokers who attempt to quit use evidence-based methods — often due to barriers to access — and there is a large divide between yearly quit attempts (>50%) and successful quitting (<10%) (Babb et al., 2017). Consequently there is an ongoing and urgent need to develop novel, effective, and accessible cessation interventions.
To more effectively support cessation, we can seek to better understand the immediate causes (or precursors) of smoking events. Currently, there is limited understanding of the factors leading to lapse (i.e. smoking during a quit attempt), and the process through which a single lapse becomes a relapse (i.e. failed quit attempt). If moments of high lapse risk can be identified, possible interventions include accessing self-help materials (Siu, 2015), telephone support/counseling (Siu, 2015; Stead et al., 2013), or use of short-acting pharmacologic treatment such as a nicotine lozenge (Kotlyar et al., 2017), oxytocin (Miller et al., 2016), or a nicotine film (Du et al., 2015). Smoking risk has been estimated based on passive physiologic measurements (Chatterjee et al., 2016), self-reported symptoms (e.g. urge, stress) (Businelle et al., 2016), and previously observed daily patterns (Chandra et al., 2011). Studies in controlled settings have also suggested that the surrounding environment plays an important role (McClernon et al., 2016; Stevenson et al., 2017). However, less emphasis has been placed on the underlying temporal dynamics of smoking events — in other words, the natural rhythms and patterns of smoking within and between days. The goal of this work is to improve prediction and knowledge of smoking risk by utilizing a prediction model that can learn these dynamics.
Temporal patterns of smoking have been studied since the 1970s, when Frederiksen and Frazier (1977) and Robinson and Young (1980) independently observed consistent daily patterns of smoking in several small cohorts of smokers. These patterns were even more striking when considering individual participants, whose behaviors were more consistent than the cohorts as a whole. More recent work by Chandra et al. (2007) has strengthened and extended this line of research with much larger study (n=351) that identified four common daily smoking patterns (e.g. daily decline, morning high). Subsequently these patterns were confirmed and additionally tied to craving, including evidence that craving tends to precede smoking (Chandra et al., 2011). The connection between smoking patterns and craving — a factor which also predicts failure to quit (Killen and Fortmann, 1997) — is strong motivation for predicting craving (Chatterjee et al., 2016) as a proxy for smoking risk to inform an intervention. Nevertheless risk and craving are distinct, and their relative merits in predicting smoking and/or lapses are currently unknown.
Related to daily patterns, smoking is influenced by plasma and saliva nicotine concentrations, which peak within minutes of smoking and return to baseline over several hours (~2hr plasma half-life) (Benowitz et al., 2009). Plasma nicotine concentration and craving are negatively correlated, suggesting that craving is driven in part by nicotine seeking (Jarvik et al., 2000). Gomeni et al. (2001) directly studied the relative effects of nicotine and circadian patterns on craving with a blinded study design, finding that nicotine replacement can attenuate craving. Indeed, this effect is the motivation for nicotine-based cessation treatment, which has been shown to be effective (Kotlyar et al., 2017; Du et al., 2015). Given the strong relationship between craving and smoking itself (Chandra et al., 2011), these results suggest that cigarette smoking is a self-triggering (i.e. self-reinforcing) process in which the probability of smoking is modulated by previous smoking events.
To our knowledge, this self-triggering dynamic has not yet been incorporated in smoking prediction models. For example, Rathbun and Shiffman (2016) model smoking events as a Poisson process with intensity function (i.e. rate of smoking) modulated by self-reports of affect, arousal, attention, and restlessness; but in their model, previously observed smoking events do not directly modify the current intensity. Here we propose to explore the self-triggering nature of smoking with a Hawkes process, wherein the intensity is influenced not only by exogenous factors — such as demographics or self-reports — but also the accumulating influence of previous smoking events.
Specifically, we develop the time-varying semi-parametric Hawkes process (TV-SPHP), then fit it to smoking events reported by smokers (n=42) over a >1 week period. This approach allows us to capture the effects of the following predictors on current smoking intensity (i.e. risk): (a) fixed covariates such as demographics; (b) time-varying covariates, including speed as measured by GPS; and (c) previous smoking events. The relationship between recent smoking and current risk is modeled with a semi-parametric impact function, which is itself a sum of parametric basis functions.
From a clinical perspective, this approach offers two important advantages. First, it allows us to investigate the self-triggering nature of smoking in the real world by examining the learned impact function. We hypothesize that the impact function will exhibit daily periodicity and peak within 1–4 hours of smoking, which may reflect increased nicotine seeking. Second, it may improve prediction performance compared to alternative approaches by modeling the effect of previous events on current risk. We hypothesize that the TV-SPHP will improve prediction performance — measured as the mean absolute error over periods ranging from 10 minutes to 1 hour — compared to baseline and existing models.
Technical Significance
This work develops the time-varying, semi-parametric Hawkes process (TV-SPHP) and its associated learning/inference algorithm. The TV-SPHP extends previous Hawkes process variants by modeling the intensity function as a sum of exogenous and endogenous factors. The exogenous factors include both time-invariant and time-varying participant features, while the endogenous factors capture the self-triggering nature of smoking using a semi-parametric impact function.
Clinical Relevance
The clinical significance of this work is twofold. First, we improve on existing smoking prediction models and establish a new performance baseline. Smoking prediction models can identify high risk contexts either (a) in real-time to trigger a just-intime adaptive intervention, or (b) in advance to help smokers avoid these contexts. Second, we connect the self-triggering nature of smoking to nicotine metabolism as a hypothesis to be explored further in future work.
2. Related Work
2.1. Smoking Prediction
Compared to the smoking detection literature — which is intimately connected to the large, rapidly progressing activity (Ordóñez and Roggen, 2016) — less work has focused on smoking prediction. Dumortier et al. (2016) compared the performance of several machine learning classifiers (Naive Bayes, discriminant analysis, decision tree) to discriminate between high-urge and low-urge states based on self-reported contextual information. Chatterjee et al. (2016) also predicted high and low craving with an approach based on conditional random fields, but their system was based on physiologic measurements passively collected with wearable devices.
The work of Rathbun and Shiffman (2016) is most closely related to the current work. A total of 304 smokers self-reported all smoking events along with contextual information with a hand-held device. These events were fitted to an inhomogeneous Poisson process with intensity modified by the time-varying contextual predictors. In contrast to our work, (a) the focus was model interpretation and not prediction; (b) their model did not include a self-triggering component; and (c) time-varying covariates were self-reported contextual information rather than GPS measurements.
2.2. Temporal point processes and Hawkes processes
Temporal point processes (Daley and Vere-Jones, 2007) have been widely used to model real-world event sequences. In the simplest 1D case, given an individual’s sequence of events and the corresponding counting process a point process model characterizes the sequence by modeling the expected instantaneous event occurrence rate over time:
| (1) |
Where contains all historical events happening before or at time t and computes the expected number of events in [t, t + dt) conditioned on the history. Generally, we call λ(t) the intensity function. The key to the point process model is modeling and learning λ(t) based on observed data.
A important kind of point process called the Hawkes process (Hawkes, 1971) is useful for explicitly modeling sequences whose events are self- and mutually-triggering. Mathematically, the intensity function of a 1D Hawkes process has the following form:
| (2) |
where μ(t) corresponds to the background intensity caused by exogenous factors (Xu et al., 2018), which can be modeled as homogeneous or inhomogeneous Poisson process. The term represents the accumulation of endogenous intensity caused by the history (Farajtabar et al., 2014). The nonnegative function ∅(t − s), where t ≥ s, is called the impact function. It represents the influence of an historical event at time s on the intensity at time t.
Recently, Hawkes processes have attracted many researchers, and a number of variants have been proposed. These include the mixture of Hawkes processes (Xu and Zha, 2017), the nonlinear Hawkes process (Xu et al., 2017b), and the locally-stationary Hawkes process (Roueff et al., 2016; Xu et al., 2017a). Applications include network analysis (Zhao et al., 2015), quantitative finance (Da Fonseca and Zaatour, 2014; Bacry et al., 2015), and e-health (Xu et al., 2017b). Maximum likelihood estimation (MLE) is one of the most popular approaches for learning Hawkes processes (Lewis and Mohler, 2011; Zhou et al., 2013a). In addition to MLE, least squares methods (Eichler et al., 2017), Wiener-Hopf equations (Bacry et al., 2015), and the Cumulants-based method (Achab et al., 2016) have been applied. However, stochastic optimization for Hawkes processes has not been studied systematically. For nonparametric Hawkes processes, online learning methods were proposed in (Hall and Willett, 2016; Yang et al., 2017), but they use time-consuming discretization or kernel-estimation when learning models, and thus have poor scalability. The risk bound and the sample complexity of learning a single Hawkes process are investigated in (Daneshmand et al., 2014; Eichler et al., 2017; Yang et al., 2017).
3. Cohort
3.1. Participants and Study Design
Adult smokers (N=60) were recruited from the Durham, NC area. All participants completed an IRB-approved informed consent form. Participant characteristics (age, sex, race, ethnicity, marital status, highest education completed, number of years smoked, and cigarettes smoked per day) were collected during a baseline study visit. After the visit, smokers carried a small, rechargeable GPS tracker for approximately one week. The trackers are smaller than a cigarette pack and fit easily in a pocket or purse. Participants were required to keep the tracker on their person at all times except when it could become wet (e.g. while bathing or swimming), and they received detailed instructions on tracker use and recharging.
A button on the front of the tracker can be pressed to indicate the times of events of interest. Participants were instructed to manually log all cigarettes smoked by pressing this button just before lighting the cigarette. Shiffman et al. (2002) showed that smoking events self-reported with a button press were highly correlated with cotinine and exhaled CO levels as well as participant recall on timeline follow-back assessment. Nevertheless, we took additional steps (see Section 3.3) to validate these data.
3.2. Inclusion and exclusion criteria
Participants were required to be generally healthy and between the ages of 18 and 55. They were also required to have smoked at least 5 cigarettes with normal nicotine content (>0.5mg) per day for at least a year, with an afternoon expired CO concentration >8 ppm.
Those with current or previous significant health problems (e.g. chronic hypertension, COPD, seizure disorder, liver or kidney disorder, coronary heart disease, myocardial infarction, arrhythmia) were excluded. Other exclusion criteria included use of psychoactive medications, use of smokeless tobacco, current alcohol or drug abuse (confirmed by urine drug screen), and use of nicotine replacement therapy or other smoking cessation treatment.
3.3. Data collection and pre-processing
Raw data downloaded from the GPS trackers included GPS coordinates, GPS performance level (coordinate accuracy), estimated speed, the time of measurement, and a button press indicator. These data were collected at 30 second intervals throughout the collection period with two exceptions. First, the trackers incorporate a “smart tracking” functionality that prevents GPS collection when no movement is detected to conserve battery life. Second, each logged smoking event (button press) prompted an additional measurement at that time. Available features are summarized in Table 1.
Table 1:
The list of collected features
| Feature Domain | Options |
|---|---|
| Exhaled CO (ppm) | 1. < 10; 2. [10, 20]; 3. [20, 30]; 4. > 30 |
| # Years Smoked | 1. < 10; 2. [10, 20]; 3. > 20 |
| Age | 1. < 25; 2. [20, 25]; 3. > 50 |
| Sex | 1. Male; 2. Female |
| Race | 1. White; 2. American India; 3. Asian; 4. Black; 5. Hispanic; 6. Other |
| Ethnicity | 1. Non-Hispanic; 2. Hispanic; 3. Unknown |
| Education | 1. Elementary; 2. Middle; 3. High; 4. Coll/Tech; 5. College Graduate |
| Marital Status | 1. Single; 2. Separated; 3. Widowed; 4. Married; 5. Divorced |
| GPS Measurements | Longitude; Latitude; Speed (km/h); Distance (m) |
| Time of Day | 1. Night; 2. Morning; 3. Afternoon; 4. Evening |
The raw data from all N=60 participants were first pre-processed to exclude participants for whom there was strong evidence of unreliable button presses. This was determined by partitioning each participant’s data into individual days and comparing (a) the rate of daily button presses to the expected daily rate (based on self-reported cigarettes per day) by nonparametric two-sample proportion test; and (b) comparing the rate of button presses over the entire collection period to the expected rate. Participants were excluded when p < 0.01 for two or more days — an event expected to occur with approximately 0.002 probability given 7 days of collection (21 pairs of days) — or when p < 0.01 for the collection period as a whole.
As a final pre-processing step, repeated button presses (<60 seconds apart) were removed. Multiple rapid sequences of presses were observed in several participants. Since the tracker does not provide feedback/confirmation when the button is pressed, these sequences may reflect the participant’s uncertainty as to whether their button presses have been recorded. The 60 second threshold was chosen was a reasonable lower bound on the time between successive cigarettes. We assume that these sequences do represent a smoking event, however, so the final button press in each such sequence was retained.
4. Proposed method
4.1. Time-varying Semi-parametric Hawkes processes
Consider N individuals’ smoking behaviors, i.e., records the timestamps of the n-th individual’s smoking behaviors. Participant characteristics (e.g., race, gender, age and education) are recorded as a time-invariant feature A participant’s motion status (e.g., location and speed) is also recorded as a time-varying feature vector
For each individual, the sequence of his/her smoking behaviors is an instantiation of a temporal point process system. As previously mentioned, the dynamics of the system (i.e., the occurrence of a smoking behavior at certain time) are influenced by three factors: an intrinsic propensity of that individual, the current environment and status, and the triggering from historical smoking events. From the viewpoint of Hawkes processes, the first two factors are history-independent, and may be viewed as exogenous factors of the system; while the remaining factor depends on historical behaviors, and is the endogenous factor of the system. As this analysis suggests, the Hawkes process is well-suited for capturing factors affecting smoking behavior in its intensity function. In particular, we propose the following semi-parametric Hawkes process model for smoking behaviors. For each individual n, the intensity function is written as:
| (3) |
where are parameters corresponding to time-invariant and time-varying features, respectively. The μTI, μTV, and impact function ∅(t) are the parameters of our model, which are shared across all subjects.
In contrast to traditional parametric or nonparametric Hawkes process models (Zhou et al., 2013a,b; Eichler et al., 2017), here we design a time-varying semi-parametric Hawkes process (TV-SPHP) model: the exogenous intensity μ(t) in (2) is parametrized as to take advantage of all available features, while the impact function ∅(t) is modeled nonparametrically to reduce the risk of model misspecification. In particular, we use the basis representation method to model the impact function as
| (4) |
Where are predefined basis functions (e.g., wavelets, Gabor, Gaussian kernel, etc.) and are the corresponding coefficients. Given our training event sequences, we apply the basis selection method proposed in (Xu et al., 2016) to decide the number and bandwidth of the basis functions.
4.2. Learning algorithm
Given training event sequences from N subjects and the proposed model mentioned above, we can learn the parameters of the model via maximum likelihood estimation (MLE), which is a common method used in many existing works (Lewis and Mohler, 2011; Zhou et al., 2013a; Luo et al., 2015). In particular, the learning problem of our model is the following optimization problem:
Algorithm 1.
Learning Time-varying Semi-parametric Hawkes Processes (TV-SPHP)
| 1: Input: Event sequences . Weight γ. Learning rate δ. Iteration number J. |
| 2: Output: Parameters θ = [μTI; μTV; a]. |
| 3: Initialize θ(0) randomly from uniform distribution, z(0) = θ(0), y(0) = 0. |
| 4: for j = 1, ..., J do |
| 5: Gradient descent: θ(j) = (θ(j−1) − δ(|θ(j−1) + ρ(θ − z(j−1) + y(j−1))))+. |
| 6: min ‖θ(j) + y(j−1) − z + γ‖ z ‖1 by soft-thresholding: z(j) = Sγ/ρ(θ(j) + y(j−1)). |
| 7: Update dual variable: y(j) = y(j−1) + θ(j) − z(j). |
| 8: end for |
| 9: θ = θ(J). |
| (5) |
where are the parameters of our model. According to Daley and Vere-Jones (2007), the negative log-likelihood function is
| (6) |
where T is the length of training event sequence, and In is the number of events of the n-th sequence. Based on (3) and (4), it is easy to prove that (6) is convex (Zhou et al., 2013a). is an arbitrary convex regularizer and its significance is controlled by the weight γ. In this work, we only impose sparsity on the parameters, i.e., where denotes the norm.
Similar to the algorithms in (Zhou et al., 2013a), we introduce an auxiliary variable and a dual one for θ, denoted as y and z, and rewrite (5) as a Lagrangian form:
| (7) |
This problem can be solved iteratively by the alternating direction method of multipliers (ADMM) (Zhou et al., 2013a). In particular, the scheme of our learning algorithm is shown in Algorithm 1, where the function (•)+ in line 5 sets all negative elements to zeros and the function Sτ(•) in line 6 is the soft-thresholding function with threshold τ. The derivation details of the gradient of are shown in Appendix A.
4.3. Simulation-based prediction
Given the learned point process model and historical observations, we can predict the expected number of events in future time intervals. In particular, for the target interval, we can simulate a set of synthetic event sequences based on Ogata’s modified thinning method (Ogata, 1981). The expected number of events in this interval can be estimated by the mean of the numbers of the events in these synthetic event sequences.
Algorithm 2.
Predicting the expected number of events in [t0, t0 + T]
| 1: Input: History . Learned model θ Features f0 and f(t0). Simulation trials J. |
| 2: Output: The expected number of events . |
| 3: Initial |
| 4: for j = 1, ..., J do |
| 5: t = t0. |
| 6: repeat |
| 7: Compute m(t) = Generate Uniform([0,1]). |
| 8: t = t + s. If t < t0 + T and |
| 9: until t > t0 + T |
| 10: end for |
| 11: |
It should be noted that when predicting future events based on our TV-SPHP model, we do not have access to the time-varying features for the future time interval. Fortunately, for predictions in a short interval (e.g., next 20 minutes or next one hour), we may assume that the time-varying features are relatively stable, allowing them to be approximated as the features corresponding to the last observed event. In summary, the scheme of our prediction method is shown in Algorithm 2, in which the supremum of the intensity function in [t, t0+T] is approximated by discretization: where the step size Δ is predefined.
5. Experimental Results
There were 42 subjects with valid data who jointly recorded a total of 5483 smoking events. Individual participants logged between 37 and 389 smoking events (1.9–19.5 packs), with a median of 113 (5.7 packs) and an interquartile range of 79 to 152 (4.0–7.6 packs).
The dataset was divided into 54 smoking event sequences. Each sequence records the timestamps of a subject’s smoking behaviors over a 4 day period. The first 3 days’ events are used for training and the remaining events are used for testing. Based on different learned models, we predict the expected number of smoking events in the next time interval given the history of observations. The length of the time interval ranges from 10 minutes to 1 hour in 10 minute increments, as shown in Table 2, to explore how the different models are affected. We feel that different windows in this range may be appropriate depending on the specific intervention (see Discussion).
Table 2:
Prediction performance of all models
| Method | LogLike. | 10 mins MAE |
20 mins MAE |
30 mins MAE |
40 mins MAE |
50 mins MAE |
1 hr MAE |
|---|---|---|---|---|---|---|---|
| Poisson | −2132.7 | 0.080 | 0.173 | 0.259 | 0.381 | 0.570 | 0.802 |
| Multi-task HP | −2093.9 | 0.075 | 0.169 | 0.246 | 0.356 | 0.530 | 0.751 |
| TI-SPHP | −2095.6 | 0.074 | 0.174 | 0.247 | 0.364 | 0.545 | 0.763 |
| TV-SPHP | −2058.4 | 0.074 | 0.167 | 0.243 | 0.365 | 0.523 | 0.733 |
To demonstrate the feasibility and superiority of our time-varying semi-parametric Hawkes process (TV-SPHP) method, we test it on our dataset and compare its performance with its variants and other state-of-the-art methods, including the parametric inhomogeneous Poisson process (Poisson) (Rathbun and Shiffman, 2016), the multi-task Hawkes process (Multi-task HP) (Xu et al., 2018), and the time-invariant semi-parametric Hawkes process (TI-SPHP). In particular, the Poisson method was designed for smoking event analysis, but only considers time-invariant and time-varying features while ignoring triggering patterns caused by previous smoking events. The multi-task HP does not utilize features and relies solely on temporal information, so that the exogenous part for each subject n is represented as a value and learned directly. The TI-SPHP utilizes only the time-invariant features, i.e. it ignores the term. in (3).
As previously mentioned, the time-invariant features include participant characteristics, which can be represented as 31-dimensional (C = 31) binary vectors. Each time-varying feature is an 8-dimensional (D = 8) vector consisting of a 4-dimensional real-valued vector containing the participant’s location (latitude and longitude), their speed, and the distance from their location to their home; and a 4-dimensional binary vector representing the time of day. The basis {km} are the Gaussian basis, with their number and bandwidth set using the method in (Xu et al., 2016). In all of the above models, we apply an iterative optimization method to learn the parameters. For our learning algorithm (Algorithm 1), the number of iterations is J = 30 and the learning rate is δ = 0.01. The weight γ = 0.2 is decided by cross-validation. For our prediction algorithm (Algorithm 2), the number of simulation trials is 20, the step size Δ is 10 minutes.
5.1. Model Performance
For each testing sequence k, k = 1, ..., K, the true number of smoking events in a specific testing interval is Nk, and the expected number obtained from a certain learned model is . Note that for the current dataset, K is 54, the number of test sequences. We then calculate the following performance measures:
- MAE. The mean absolute error of the estimated number:
Testing Log-Likelihood. The log-likelihood values of the testing sequences are calculated for each model.
Performance of all models is compared in Table 2. TV-SPHP performance was superior to the other models except for the 40-minute prediction window, and was superior to the Poisson model for all windows. Table 3 shows the standard deviation of the MAE across all simulation trials, demonstrating that results are consistent across testing sequences. In most cases, standard deviation is lowest for the TV-SPHP.
Table 3:
Standard deviation of prediction performance across simulation trials
| Method | 10 mins SD |
20 mins SD |
30 mins SD |
40 mins SD |
50 mins SD |
1 hr SD |
|---|---|---|---|---|---|---|
| Poisson | 0.011 | 0.009 | 0.010 | 0.017 | 0.014 | 0.008 |
| Multi-task HP | 0.007 | 0.008 | 0.010 | 0.008 | 0.010 | 0.013 |
| TI-SPHP | 0.005 | 0.012 | 0.011 | 0.011 | 0.015 | 0.016 |
| TV-SPHP | 0.005 | 0.005 | 0.007 | 0.011 | 0.012 | 0.011 |
Binary classification accuracy (i.e. will smoke, will not smoke) was identical for all models-values were 92.6%, 85.2%, 77.8%, 64.8%, and 53.7% for 10–60 minute windows, respectively-because smoking is a rare event with respect to these prediction windows, so all models heavily favor not smoking over smoking. For this reason, the MAE is the more appropriate measure of smoking risk in this application (see Discussion).
5.2. Model Interpretation
Model parameters are summarized and compared in Figure 1. Among the time-varying parameters, time of day was weighted much more heavily than the GPS measurements. The impact function, visualized in Figure 2, peaks within the first hour then decays over several hours, with marked daily periodicity.
Figure 1:
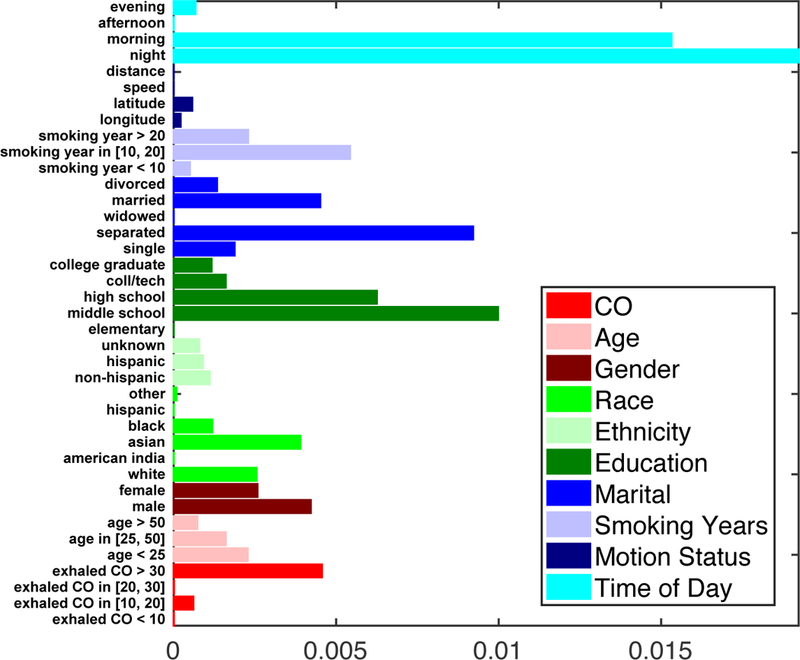
Standardized coefficients for all exogenous factors
Figure 2:
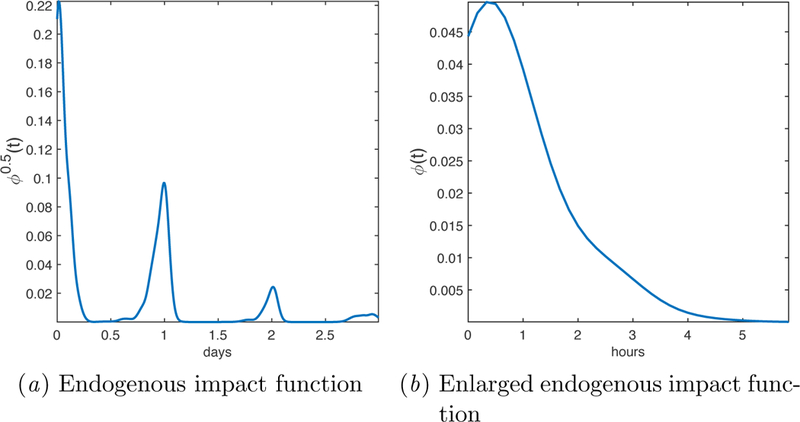
Visualization of (a) the learned impact function with length 3 days, and (b) an enlarged view of the first 6 hours. For better visual effect, we show the square root of the impact function, i.e., ∅0.5(t), in the time domain
6. Discussion
To our knowledge, this study is the first to model smoking as a self-triggering process, and among the first to evaluate the performance of smoking event prediction. Moreover, we have developed the time-varying semi-parametric Hawkes process (TV-SPHP), an extension of previous Hawkes process variants that is well-suited to this application. These methods and performance statistics can serve as baselines for future prediction models, leading to improved prediction of smoking risk. Effective prediction can be used to identify moments of high lapse risk and their causes/precursors, ultimately supporting more effective cessation strategies that could reduce death from smoking.
As hypothesized, prediction performance favored the TV-SPHP over its variants and previous methods, validating the advantages of modeling smoking as a self-triggering process. The models with and without time-varying features were similar over shorter prediction windows, but the TV-SPHP was superior over longer windows, most notably the 1 hour window. This suggests that time-varying features — such as speed and time of day - offer greater predictive advantage as the time since the last known smoking event increases.
The most appropriate prediction window depends on the application or intervention. A 10-minute window might fit a nicotine lozenge intervention due to its fast effect, whereas a longer window might be more appropriate for a self-help or peer support intervention. We feel that prediction windows longer than an hour are less reasonable, because (a) the time-varying features may change substantially during the window, and (b) smoking events occurring during the window affect the expected number of subsequent events.
Smoking is a rare event with respect to our prediction windows, therefore all models predict that the participant will not smoke in a given window. For this reason, accuracy (and other binary prediction measures) is a misleading measure of performance. The TV-SPHP most closely estimates the true number of cigarettes smoked (i.e. lowest MAE), which may be used as a measure of smoking risk. When placing a threshold on model output to trigger an intervention, a low threshold would be needed to achieve high sensitivity. This would also result in a high false positive rate, which may be acceptable given the importance of avoiding a lapse. The appropriate trade-off between these measures is intervention-specific.
The Hawkes process impact function is capable of capturing both short-term temporal dynamics, which may relate to nicotine metabolism and/or nicotine seeking, as well as longer-term daily patterns. For example, the peak ~30 minutes after smoking may reflect nicotine seeking as plasma nicotine levels decline. This hypothesis could be explored in future work by testing how the learned impact function differs between groups with/without nicotine replacement. The location of this peak, which we hypothesized would occur within 1–4 hours of smoking, occurred earlier than expected. On average, plasma nicotine levels remain above of their peak value when the impact function peaks, but importantly, they are declining sharply.
The peaks 1 and 2 days after smoking, on the other hand, more likely reflect daily patterns and preferences rather than direct effects of nicotine. The clear daily periodicity of the impact function is striking, and corroborates previous observations that individual smokers exhibit consistent daily patterns of smoking (Frederiksen and Frazier, 1977; Robinson and Young, 1980; Chandra et al., 2007). The nature of the factors underlying these patterns (e.g. physiologic versus environmental) remains to be explored.
6.1. Limitations and Future Work
A first and arguably most important limitation of this work is the uncertain reliability of self-reported smoking events. This problem is a well-known difficulty of detecting or predicting real-world smoking. Our pre-processing excluded participants with an unreasonable (high or low) number of button presses, but knowing the number is consistent with the participant’s smoking habits does not guarantee that it is accurate. This step eliminated almost a third of participants (18/60), which underscores the difficulty of relying on self-report. Further, there is also no way to know whether the timing of individual presses is accurate, which is particularly important given our focus on temporal dynamics. Research in smoking risk prediction will benefit from technologies that reliably detect smoking, bypassing the problems of self-report.
This pre-processing was essential to the goals of this study, but it also introduces a potential source of bias: participants with unpredictable smoking patterns may have been excluded because they appeared to be unreliable self-reporters. We have tried to mitigate this possibility by using a conservative exclusion threshold.
Finally, the measurements and participant populations in the parent studies were tailored to the objectives of those studies. We intend to extend this work with new data collection that includes a more comprehensive set of physiologic, self-report, and environmental measures. Many such factors are known to be associated with smoking risk and would be expected to improve prediction performance. A broader cohort of participants will be recruited, including those with significant health problems. These participants may be good candidates for intervention due to their more frequent interaction with the healthcare system. Follow-up work will also explore more meaningful incorporation of location information via a hierarchical model that converts raw GPS coordinates to personal activity space (e.g. distinct locations visited by the participant throughout their day).
Future work will also explore relationships between nicotine metabolism (e.g. nicotine metabolite ratio) and the self-triggering nature of smoking, as quantified by the Hawkes process impact function. Nicotine metabolism is known to affect the relative efficacy of varenicline versus nicotine patch in smoking cessation (Lerman et al., 2015), for example. With our approach, the effect of pharmacologics and/or lapses on subsequent smoking risk could be explored through simulation, which may have important implications for cessation interventions.
7. Conclusion
In this work, we have developed the time-varying semi-parametric Hawkes process and applied it to the important problem of smoking prediction using data collected by 42 smokers. Motivated by the known influence of daily patterns and plasma nicotine levels on smoking behaviors, our approach models smoking as a self-triggering process. Results illustrate the temporal dynamics of smoking and demonstrate improved prediction performance compared to previous methods. Future work will extend the approach to a more comprehensive dataset and explore the effects of interventions such as nicotine replacement on temporal smoking dynamics.
Effective smoking prediction models can pinpoint moments of high lapse risk in order to trigger a just-in-time intervention, for example with a mobile device. Modeling smoking as a self-triggering process may help to explain how a single lapse can progress to a failed quit attempt, thereby supporting cessation and reducing death from smoking.
Appendix A.
The gradient is composed of , where and are elements of μTI and μTV, c = 1,…,C, d = 1,…,D, and m = 1,…,M. In particular, in the j-th iteration we have
Where is calculated based on (3) given the parameters in previous iteration and are elements of and Additionally, here we assume that the element of time-varying features are piecewise-constant functions over time, so we approximate
Contributor Information
Matthew Engelhard, Department of Psychiatry and Behavioral Sciences, Duke University School of Medicine, Durham, NC, USA.
Hongteng Xu, Department of Electrical and Computer Engineering, Duke University, InfiniaML, Inc., Durham, NC, USA.
Lawrence Carin, Department of Electrical and Computer Engineering, Duke University, Durham, NC, USA.
Jason A Oliver, Department of Psychiatry and Behavioral Sciences, Duke University School of Medicine, Durham, NC, USA.
Matthew Hallyburton, Department of Psychiatry and Behavioral Sciences, Duke University School of Medicine, Durham, NC, USA.
F Joseph McClernon, Department of Psychiatry and Behavioral Sciences, Duke University School of Medicine, Durham, NC, USA.
References
- Achab Massil , Bacry Emmanuel, Gaïffas Stephane, Mastromatteo Iacopo, and Muzy Jean-Francois. Uncovering Causality from multivariate Hawkes integrated Cumulants. arXiv preprint arXiv:1607.06333, 2016. [Google Scholar]
- Babb Stephen, Malarcher Ann, Schauer Gillian, Asman Kat, and Jamal Ahmed. Quitting Smoking Among Adults United States, 20002015. MMWR. Morbidity and Mortality Weekly Report, 65(52):1457–1464, January 2017. ISSN 0149–2195. doi: 10.15585/mmwr.mm6552a1. URL http://www.cdc.gov/mmwr/volumes/65/wr/mm6552a1.htm. [DOI] [PubMed] [Google Scholar]
- Bacry Emmanuel, Mastromatteo Iacopo, and Muzy Jean-Frangois. Hawkes processes in finance. Market Microstructure and Liquidity, 1(01):1550005, 2015. [Google Scholar]
- Benowitz Neal L., Hukkanen Janne, and Jacob Peyton. Nicotine Chemistry, Metabolism, Kinetics and Biomarkers In Nicotine Psychopharmacology, pages 29–60. Springer Berlin Heidelberg, Berlin, Heidelberg, 2009. doi: 10.1007/978-3-540-69248-5-2. URL http://link.springer.com/10.1007/978-3-540-69248-5{_}2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Businelle Michael S Ma Ping, Kendzor Darla E, Frank Summer G, Vidrine Damon J, and Wetter David W. An ecological momentary intervention for smoking cessation: Evaluation of feasibility and effectiveness. Journal of Medical Internet Research, 18 (12):e321, December 2016. ISSN 14388871. doi: 10.2196/jmir.6058. URL http://www.jmir.Org/2016/12/e321/http://www.ncbi.nlm.nih.gov/pubmed/27956375http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC5187451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention (CDC). How Tobacco Smoke Causes Disease. How Tobacco Smoke Causes Disease: The Biology and Behavioral Basis for Smoking-Attributable Disease: A Report of the Surgeon General, pages 1–16, 2010. ISSN 0149–2195. doi: Dec12014. URL https://www.cdc.gov/tobacco/data{_}statistics/sgr/2010/consumer{_}booklet/pdfs/consumer.pdfhttp://www.ncbi.nlm.nih.gov/pubmed/21452462 [PubMed]
- Centers for Disease Control and Prevention (CDC). Smoking and Tobacco Use; 50th Anniversary Surgeon General’s Report. Technical report, 2014. URL https://www.cdc.gov/tobacco/datai_Jstatistics/sgr/50th-anniversary/index.htmhttp://www.cdc.gov/tobacco/data{_}statistics/sgr/50th-anniversary/index.htm.
- Chandra Siddharth, Shiffman Saul, Scharf Deborah M., Dang Qianyu, and Shadel William G. Daily smoking patterns, their determinants, and implications for quitting. Experimental and Clinical Psychopharmacology, 15(1):67–80, 2007. ISSN 1936–2293. doi: 10.1037/1064-1297.15.1.67. URL http://doi.apa.org/getdoi.cfm?doi=10.1037/1064-1297.15.1.67 [DOI] [PubMed] [Google Scholar]
- Chandra Siddharth, Scharf Deborah, and Shiffman Saul. Within-day temporal patterns of smoking, withdrawal symptoms, and craving. Drug and alcohol dependence, 117(2–3):118–25, September 2011. ISSN 1879–0046. doi: 10.1016/j.drugalcdep.2010.12.027. URL http://www.ncbi.nlm.nih.gov/pubmed/21324611http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC3123683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee Soujanya, Nakajima Motohiro, Spring Bonnie, Wetter David W., Kumar Santosh, Hovsepian Karen, Sarker Hillol, Saleheen Nazir, Mustafa Al’Absi Gowtham Atluri, Ertin Emre, Lam Cho, and Lemieux Andrine. mCrave: Continuous Estimation of Craving During Smoking Cessation. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing - UbiComp ‘16, volume 2016, pages 863–874, New York, New York, USA, September 2016. ACM Press; ISBN 9781450344616. doi: 10.1145/2971648.2971672. URL http://dl.acm.org/citation.cfm?doid=2971648.2971672http://www.ncbi.nlm.nih.gov/pubmed/27990501http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC5161415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Da Fonseca José and Zaatour Riadh. Hawkes process: Fast calibration, application to trade clustering, and diffusive limit. Journal of Futures Markets, 34(6):548–579, 2014. [Google Scholar]
- Daley Daryl Jand Vere-Jones David. An introduction to the theory of point processes: volume II: general theory and structure, volume 2 Springer Science & Business Media, 2007. [Google Scholar]
- Daneshmand Hadi, Manuel Gomez-Rodriguez Le Song, and Schoelkopf Bernhard. Estimating diffusion network structures: Recovery conditions, sample complexity & soft-thresholding algorithm. In International Conference on Machine Learning, pages 793–801, 2014. [PMC free article] [PubMed] [Google Scholar]
- Du Daniel, Borders James, Selmani Alex, and Waverczak William. A Pilot Study to Investigate the Efficacy of Nicotine Oral Soluble Film, Lozenge and Gum in Relief of Acute Smoking Cue-provoked Craving for Cigarette in Low Dependence Smokers. Journal of Smoking Cessation, 10(02):87–95, December 2015. ISSN 1834–2612. doi: 10.1017/jsc.2014.5. URL http://www.journals.cambridge.org/abstracti_jS183426121400005X. [DOI] [Google Scholar]
- Dumortier Antoine, Beckjord Ellen, Shiffman Saul, and Ervin Sejdić. Classifying smoking urges via machine learning. Computer Methods and Programs in Biomedicine, 137:203–213, December 2016. ISSN 18727565. doi: 10.1016/j.cmpb.2016.09.016. URL http://www.sciencedirect.com/science/article/pii/S0169260716304904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichler Michael, Dahlhaus Rainer, and Dueck Johannes. Graphical modeling for multivariate Hawkes processes with nonparametric link functions. Journal of Time Series Analysis, 38(2):225–242, 2017. [Google Scholar]
- Farajtabar Mehrdad, Du Nan, Manuel Gomez Rodriguez Isabel Valera, Zha Hongyuan, and Song Le. Shaping social activity by incentivizing users. In NIPS, 2014. [PMC free article] [PubMed] [Google Scholar]
- Frederiksen Lee W. and Frazier Mark. Temporal distribution of smoking. Addictive Behaviors, 2(4):187–192, January 1977. ISSN 0306–4603. doi: 10.1016/0306-4603(77)90016-8. URL https://www.sciencedirect.com/science/article/pii/0306460377900168. [DOI] [PubMed] [Google Scholar]
- Gomeni Roberto, Teneggi Vincenzo, Iavarone Laura, Squassante Lisa, and Bye Alan. Population Pharmacokinetic-Pharmacodynamic Model of Craving in an Enforced Smoking Cessation Population: Indirect Response and Probabilistic Modeling. Pharmaceutical Research, 18(4):537–543, 2001. ISSN 07248741. doi: 10.1023/A:1011070814530. URL http://link.springer.com/10.1023/A:1011070814530. [DOI] [PubMed] [Google Scholar]
- Hall Eric C and Willett Rebecca M. Tracking dynamic point processes on networks. IEEE Transactions on Information Theory, 62(7):4327–4346, 2016. [Google Scholar]
- Hawkes Alan G. Point spectra of some mutually exciting point processes. Journal of the Royal Statistical Society. Series B (Methodological), pages 438–443, 1971. [Google Scholar]
- Jamal Ahmed, Phillips Elyse, Gentzke Andrea S., Homa David M., Babb Stephen D., King Brian A., and Neff Linda J. Current Cigarette Smoking Among Adults United States, 2016. MMWR. Morbidity and Mortality Weekly Report, 67(2):53–59, January 2018. ISSN 0149–2195. doi: 10.15585/mmwr.mm6702a1. URL http://www.cdc.gov/mmwr/volumes/67/wr/mm6702a1.htm?s{_}cid=mm6702a1{_}w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarvik Murray E, Madsen Damian C, Olmstead Richard E, Iwamoto-Schaap Paula N, Elins Julie L, and Benowitz Neal L. Nicotine Blood Levels and Subjective Craving for Cigarettes. Pharmacology Biochemistry and Behavior, 66(3):553–558, July 2000. ISSN 0091–3057. doi: 10.1016/S0091-3057(00)00261-6. URL https://www.sciencedirect.com/science/article/pii/S0091305700002616. [DOI] [PubMed] [Google Scholar]
- Killen JD and Fortmann SP. Craving is associated with smoking relapse: findings from three prospective studies. Experimental and clinical psychopharmacology, 5(2):137–42, May 1997. ISSN 1064–1297. URL http://www.ncbi.nlm.nih.gov/pubmed/9234050. [DOI] [PubMed] [Google Scholar]
- Kotlyar Michael, Lindgren Bruce R, Vuchetich John P, Le Chap, Mills Anne M, Amiot Elizabeth, and Hatsukami Dorothy K. Timing of nicotine lozenge administration to minimize trigger induced craving and withdrawal symptoms. Addictive Behaviors, 71:18–24, August 2017. ISSN 03064603. doi: 10.1016/j.addbeh.2017.02.018. URL http://www.ncbi.nlm.nih.gov/pubmed/28235705http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC5449230http://linkinghub.elsevier.com/retrieve/pii/S0306460317300837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerman Caryn, Schnoll Robert A, Hawk Larry W, Cinciripini Paul, George Tony P, Wileyto E Paul, Swan Gary E, Benowitz Neal l, Heitjan Daniel F and Tyndale Rachel F. Use of the nicotine metabolite ratio as a genetically informed biomarker of response to nicotine patch or varenicline for smoking cessation: a randomised, double-blind placebocontrolled trial. The Lancet Respiratory Medicine, 3(2):131–138, February 2015. ISSN 2213–2600. doi: 10.1016/S2213-2600(14)70294-2. URL https://www.sciencedirect.com/science/article/pii/S2213260014702942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis Erik and Mohler George. A nonparametric EM algorithm for multiscale Hawkes processes. Journal of Nonparametric Statistics, 1(1):1–20, 2011. [Google Scholar]
- Luo Dixin, Xu Hongteng, Zhen Yi, Ning Xia, Zha Hongyuan, Yang Xiaokang, and Zhang Wenjun. Multi-task multi-dimensional Hawkes processes for modeling event sequences. In IJCAI, 2015. [Google Scholar]
- McClernon F Joseph, Conklin Cynthia A, Kozink Rachel V, Adcock R Alison, Sweitzer Maggie M, Addicott Merideth A, Chou Ying-hui, Chen Nan-kuei, Hallybur-ton Matthew B, and DeVito Anthony M. Hippocampal and Insular Response to Smoking-Related Environments: Neuroimaging Evidence for Drug-Context Effects in Nicotine Dependence. Neuropsychopharmacology, 41(3):877–885, February 2016. ISSN 0893–133X. doi: 10.1038/npp.2015.214. URL http://www.ncbi.nlm.nih.gov/pubmed/26179147http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC4707833http://www.nature.com/articles/npp2015214 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller Melissa A Bershad Anya, King Andrea C Lee Royce, and Harriet de Wit. Intranasal oxytocin dampens cue-elicited cigarette craving in daily smokers: a pilot study. Behavioural pharmacology, 27(8):697–703, 2016. ISSN 1473–5849. doi: 10.1097/FBP.0000000000000260. URL http://www.ncbi.nlm.nih.gov/pubmed/27661192http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC5089916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogata Yosihiko. On Lewis’ simulation method for point processes. IEEE Transactions on Information Theory, 27(1):23–31, 1981. [Google Scholar]
- Ordonez Francisco Javier and Roggen Daniel. Deep convolutional and lstm recurrent neural networks for multimodal wearable activity recognition. Sensors, 16(1):115, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rathbun Stephen L and Shiffman Saul. Mixed effects models for recurrent events data with partially observed time-varying covariates: Ecological momentary assessment of smoking. Biometrics, 72(1):46–55, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson JC and Young JC. Temporal patterns in smoking rate and mouth-level nicotine exposure. Addictive Behaviors, 5(2):91–95, January 1980. ISSN 0306–4603. doi: 10.1016/0306-4603(80)90024-6. URL https://www.sciencedirect.com/science/article/pii/0306460380900246. [DOI] [PubMed] [Google Scholar]
- Roueff Francois, Von Sachs Rainer, and Sansonnet Laure. Locally stationary Hawkes processes. Stochastic Processes and their Applications, 126(6):1710–1743, 2016. [Google Scholar]
- Shiffman Saul, Gwaltney Chad J, Balabanis Mark H, Liu Kenneth S, Paty Jean A, Kassel Jon D, Hickcox Mary, and Gnys Maryann. Immediate antecedents of cigarette smoking: an analysis from ecological momentary assessment. Journal of abnormal psychology, 111 (4):531, 2002. [DOI] [PubMed] [Google Scholar]
- Siu Albert L. Behavioral and Pharmacotherapy Interventions for Tobacco Smoking Cessation in Adults, Including Pregnant Women: U.S. Preventive Services Task Force Recommendation Statement. Annals of Internal Medicine, 163(8):622, October 2015. ISSN 0003–4819. doi: 10.7326/M15-2023. URL http://annals.org/article.aspx?doi=10.7326/M15-2023. [DOI] [PubMed] [Google Scholar]
- Stead Lindsay F Hartmann-Boyce Jamie, Perera Rafael, and Lancaster Tim. Telephone counselling for smoking cessation. Cochrane Database of Systematic Reviews, August 2013. ISSN 14651858. doi: 10.1002/14651858.CD002850.pub3. URL http://doi.wiley.com/10.1002/14651858.CD002850.pub3. [DOI] [PubMed] [Google Scholar]
- Stevenson Jennifer G., Oliver Jason A., Hallyburton Matthew B., Sweitzer Maggie M., Conklin Cynthia A., andMcClernon F. Joseph. Smoking environment cues reduce ability to resist smoking as measured by a delay to smoking task. Addictive Behaviors, 67:49–52, April 2017. ISSN 18736327. doi: 10.1016/j.addbeh.2016.12.007. URL http://www.sciencedirect.com/science/article/pii/S0306460316304427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Hongteng and Zha Hongyuan. A Dirichlet mixture model of Hawkes processes for event sequence clustering. In NIPS, 2017. [Google Scholar]
- Xu Hongteng, Farajtabar Mehrdad, and Zha Hongyuan. Learning Granger causality for Hawkes processes. In ICML, 2016. [Google Scholar]
- Xu Hongteng, Luo Dixin, and Zha Hongyuan. Learning Hawkes processes from short doubly-censored event sequences. In ICML, 2017a. [Google Scholar]
- Xu Hongteng, Wu Weichang, Nemati Shamim, and Zha Hongyuan. Patient flow prediction via discriminative learning of mutually-correcting processes. IEEE transactions on Knowledge and Data Engineering, 29(1):157–171, 2017b. [Google Scholar]
- Xu Hongteng, Luo Dixin, Chen Xu, and Carin Lawrence. Benefits from superposed hawkes processes. In AISTATS, 2018. [Google Scholar]
- Yang Yingxiang, Etesami Jalal, He Niao, and Kiyavash Negar. Online learning for multivariate Hawkes processes. In NIPS, 2017. [Google Scholar]
- Zhao Qingyuan, Erdogdu Murat A, He Hera Y, Rajaraman Anand, and Leskovec Jure. SEISMIC: A self-exciting point process model for predicting tweet popularity. In KDD, 2015. [Google Scholar]
- Zhou Ke, Zha Hongyuan, and Song Le. Learning social infectivity in sparse low-rank networks using multi-dimensional Hawkes processes. In AISTATS, 2013a. [Google Scholar]
- Zhou Ke, Zha Hongyuan, and Song Le. Learning triggering kernels for multi-dimensional hawkes processes. In ICML, 2013b. [Google Scholar]


