Light Spread Manipulation in Scintillators Using Laser Induced Optical Barriers

Abstract

We are using the Laser Induced Optical Barriers (LIOB) technique to fabricate scintillator detectors with combined performance characteristics of the two standard detector types, mechanically pixelated arrays and monolithic crystals. This is done by incorporation of so-called optical barriers that have a refractive index lower than that of the crystal bulk. Such barriers can redirect the scintillation light and allow for control of the light spread in the detector. Previous work has shown that the LIOB technique has the potential to achieve detectors with high transversal and depth of interaction (DOI) resolution simultaneously in a single-side readout configuration, suitable for high resolution PET imaging. However, all designs studied thus far present edge effect issues similarly as in the standard detector categories. In this work we take advantage of the inherent flexibility of the LIOB technique and investigate alternative barrier patterns with the aim to address this problem. Light transport simulations of barrier patterns in LYSO:Ce, with deeper barrier walls moving towards the detector edge show great promise in reducing the edge effect, however there is a trade-off in terms of achievable DOI information. Furthermore, fabrication and characterization of a 20 mm thick LYSO:Ce detector with optical barriers forming a pattern of 1 × 1 × 20mm³ pixel like structures show that light channeling in laser-processed detectors in agreement with optical barriers with refractive index between 1.2 and 1.4 is achievable.

I. INTRODUCTION

SPATIAL information of the incident radiation is of great importance in radiation imaging systems such as clinical and pre-clinical Positron Emission Tomography (PET), Single Photon Emission Computed Tomography (SPECT), and Computed Tomography (CT). Scintillation crystals are the main radiation detector type in the majority of these imaging modalities, where upon interaction of incident radiation, a bundle of scintillation photons is generated and then collected by single or multiple photosensors such as photomultiplier tubes (PMTs) or Silicon photomultipliers (SiPMs) for further processing and image generation.

In applications such as PET where the incident gamma-ray has high-energy (511 keV), the scintillator needs to be thick (e.g > 20 mm) for improved stopping power and high system sensitivity essential for practical image acquisition times. Providing spatial information in these scintillation-based detectors requires special means (such as optical structures) to confine the spread of the scintillation light and thereby achieve spatial resolution. This has been conventionally realized by fabricating arrays of individual scintillators, where each scintillator element (pixel) can be used as an indicator for the position of the radiation interaction. Mechanical pixelation is the industry standard to fabricate scintillator arrays, and the pixelation is typically accomplished through near complete optical isolation from neighboring pixels using reflectors between adjacent pixels. While such isolation reduces light spread beyond the pixel boundaries, it may cause light loss, especially for high aspect ratio pixels, due to increased number of trapped photons. Furthermore, this approach results in material loss, processing yield issues, pixel size inconsistency, and high cost, especially for large scintillator arrays with many small pixels.

For high resolution PET detectors, not only the transversal radiation interaction position is of interest, but also Depth of Interaction (DOI) information is important to avoid blurring at the edge of the field of view caused by mapping all the events to the center of each detector element. Achieving DOI information in mechanically cut arrays is not straightforward but often requires more complex detector setups like double side readout or depth dependent reflector arrangements [1], [2]. There are recent promising efforts to introduce simple mechan-ical DOI detector configurations where the crystal array is sandwiched between a light guide and the photodetector (PD) [3]. It however still remains to be demonstrated that such detector can be used in practical cases (i. e. with thicker crystals and larger number of pixels per PD element). In recent years, a few innovative approaches have been introduced to fabricate fine pixel pitch scintillator arrays, such as growing crystals in the form of pixels [4] or introducing micro-grooves in thin scintillator plates [5]. While these techniques prove to be useful for low X- or gamma-ray energy applications, they are not practical for 511 keV applications that require thick crystals. Also, a number of research groups have explored alternative methods to achieve high spatial resolution with monolithic scintillators (instead of pixelated arrays) for medical imaging applications [6]–[8]. One advantage of using a monolithic detector is that DOI information is inherent due to depth dependent light spread functions in the detector. In these efforts, however, the required transversal spatial resolution is achieved by utilizing thin monolithic scintillator plates, which causes loss of sensitivity, or by utilizing sophisticated electronics and event positioning algorithms that result in higher detector cost and complexity. Furthermore, one of the techniques proposed to control or modify the light spread function in continuous scintillators is to apply surface treatments (by mechanical means) to the scintillator or the light guide between the scintillator and the photosensor [9]. While these techniques provide some improvements, their benefits are marginal and typically lead to the so-called edge effect problem where the detector resolution is greatly worsened near the detector edge. It should be mentioned that the edge effect issue exists in all detector types including the pixelated types but is less severe and can be compensated for by using more sophisticated calibration and positioning estimator algorithms.

In our group, we work on novel techniques to suppress the limitations associated with the standard mechanical array fabrication and the monolithic detectors. Our scintillator fabrication technique, called laser-induced optical barriers (LIOB), is based on local modifications of the scintillator crystal structure to control the light spread and thus achieve spatial resolution [10], [11]. In this paper, we report on simulations and experimental results of cerium-doped lutetium yttrium orthosilicate (LYSO:Ce) processed by the LIOB technique for PET applications. The goal of this work is the fabrication of a LYSO:Ce detector with high transversal (XY) and DOI resolution in a single side readout configuration.

II. SCINTILLATOR PROCESSING USING LIOB

Detailed descriptions of the LIOB technique as well as the similar Sub-Surface Laser Engraving (SSLE) technique are given by our group and others [10]–[14]. The basic concept of the LIOB technique is illustrated in Fig 1a. Interaction of laser light with crystal material is a function of many parameters including laser pulse energy, duration, repetition rate, crystal thermal expansion, and crystal structure. The energy transfer at the laser focal spot results in permanent local modifications of the crystal structure manifested as a change in refractive index (RI). The resulting so-called optical barriers (OB) can redirect the scintillation light and hence be used to control the light spread in the detector. The difference between LIOB and SSLE is that with LIOB the aim is to engineer the refractive index of the material without causing cracks, while with SSLE micro-cracks are placed inside the crystal to act as light diffusers/scatterers. Fig. 1b shows optical barriers created by 3 individual laser pulses in LYSO:Ce. It is apparent that there are other applications that can benefit from optical barriers that are strategically placed throughout the crystal volume. For example, the entrance window of photosensors such as PMTs can be processed by the LIOB technique such that the barriers redirect the incident light to the photocathode and minimize the reflection. This can greatly enhance the light collection efficiency, which can improve the spectroscopic capabilities of the setup.

Fig. 1.

a) LIOB concept. The laser beam is focused within the crystal volume using an objective lens. Local alteration to the crystal structure which we refer to as optical barrier is a function of key parameters such as the crystal thermal and optical properties, laser pulse energy, repetition rate, pulse duration, etc. The optical barriers show refractive index smaller than the crystal bulk. b) OB’s in LYSO created by 3 individual pulses from a 532 nm Nd:YAG laser.

In our earlier experiments, we applied the LIOB technique to CsI:Tl to fabricate detectors for SPECT imaging [10]. It is noteworthy that CsI:Tl has a cubical structure and also is tolerant with respect to intense laser pulse energy, and therefore we did not observe any processing problems. However, LYSO:Ce, which is the mainstay for PET detectors, behaves differently when exposed to intense laser light. LYSO:Ce has a monoclinic structure and presents anisotropy in many of its properties [15], [16]. The anisotropy in constant of thermal expansion (CTE) may lead to non-uniform crystal fabrication quality as well as cracking issues [13], [17]. The anisotropy in refractive index (LYSO:Ce has 3 refractive indices) will change the laser focus depth depending on the crystal orientation. These issues together with LYSO:Ce’s brittle and hard nature that causes it to easily crack under thermo-mechanical stress can lead to low material yield and thus increased processing cost especially in fine pixel arrays. Given these constraints efficient fabrication of LYSO:Ce detectors using LIOB requires thorough work to optimize the laser parameters and will involve changing the settings depending on the write direction as well as the crystal depth. Fig. 2b shows how crack formation appears in the crystal depending on write direction. Laser parameter optimization is further important since it allows control over the properties of the optical barriers created in the crystal. In Ref. [18] and Fig. 2a we show that by changing the laser pulse duration the roughness of the interface between the optical barriers and the crystal bulk can be altered. Fig. 2a also highlights how the optical barrier properties vary with pulse energy.

Fig. 2.

60 μm long lines written in LYSO:Ce bulk. (a) Varying pulse duration and pulse energy. Smoother interfaces are achieved with shorter pulse duration, and cracks appear for lower pulse energy at longer pulse duration. (b) Varying write direction showing preferential crack formation along certain crystal orientations due to the material anisotropy.

Since the modified sites inside the scintillator volume have smaller refractive index compared with the crystal bulk, they will reflect and refract light depending on the angle of incidence. This behavior is similar, to some extent, to mechanically cut arrays where the inter-pixel gaps are filled with reflecting materials. Therefore, the RI mismatch between the optical barriers and the crystal bulk plays an important role in light channeling effect in that the larger the RI difference the larger the light channeling.

III. SIMULATION STUDY

Given the flexibility of the LIOB technique in terms of barrier patterns that can be incorporated into the crystal, light transport simulations are important and useful tools that can be used to determine a suitable barrier pattern for a given application, and ultimately guide the experimental work. We here present light transport simulations of laser-processed detectors performed using the Monte Carlo code DETECT2000 [19].

A. Behavior of optical photons impinging on optical barriers

The shape, size and refractive index of an optical barrier depend on the laser parameters used during processing, as well as on the crystal structure. A barrier created by one single laser pulse typically has a spherical or rather elliptical shape, extending in the direction parallel to the laser beam. Many closely packed barriers can form a wall similar to the reflectors in mechanically cut arrays. Fig. 3 shows how the reflectivity of a 50 μm optical barrier placed in LYSO:Ce (RI=1.82) depends on the angle of incidence of the optical photon, and the shape and RI of the barrier. The critical angle for total reflection (θ_c) is the same regardless of the barrier shape, and increases when the RI approaches that of the crystal bulk, as expected. The discrepancies between the two geometries are further explained in the Fig 3c. In the remainder of this paper the barriers are modeled as slabs, and the surface roughness is varied in order to account for the range of barrier behaviors that might be present in real detectors.

Fig. 3.

(a) Simulation setup. A unidirectional beam of optical photons impinging on the surface of the optical barrier with varying angle of incidence θ. The barrier was placed in a 0.01×1×1m³ LYSO:Ce crystal. The number of photons being reflected back and collected at the top crystal surface were recorded. A wide crystal was chosen such that the effect from crystal edges was negligible. (b) Resulting reflectivity (R) as a function of θ.. (c) Schematic explanation of features seen in (b). For the slab R is dominated by light reflected at the first (blue arrow) and second interface (red arrow). For the sphere the behavior can be divided into 4 cases with increasing value of θ, indicated in (b) for n=1.0. 1: R is dominated by the same two components as the slab. 2: R is lowered compared to the slab due to loss of the second reflected component (red) which is directed downwards due to the curvature of the OB. 3: The curve is characterized by a sharp increase in R due to the upward direction of the light transmitted through the second interface (green). After the peak R decreases with θ since the magnitude of the green component decreases faster than the blue component increases. 4: Just before reaching θ_c, R again increases with θ due to recovery of the second reflected component (red).

B. Light channeling effect of optical barriers

The most straightforward optical barrier pattern is walls arranged to form a pixel-like pattern similar to a conventional pixel array. In order to evaluate the light channeling potential of such configuration we simulated a 25.4×25.4×20 mm³ LYSO:Ce crystal with 50 μm thick slab shaped optical barriers placed with 1 mm separation to form a 24×24 pixel array with 1.05 mm pixel pitch. The outer crystal surface was polished and 5 sides were wrapped in an external diffuse reflector (RC=0.98). The crystal was coupled to an 8×8 Multi-Pixel Photon Counter (MPPC) array with 3.2 mm pixel pitch and 3.0×3.0 mm² active pixel area, through a 100 μm thick entrance window (RI=1.55) as described in [20]. An isotropic source of 420 nm optical photons was placed at different depths in one central pixel-like volume, and the number of photons detected in a 1×1 mm² square directly underneath the source was recorded, as well as the total signal from all MPPC pixels. A total of 100k optical photons were started in each location. Fig. 4 shows the resulting light confinement for different barrier RI and barrier/crystal interface roughness combinations, compared to a monolithic crystal and a mechanically pixelated array, where the latter had varying pixel surface roughness. The barrier/crystal interface roughness, as well as the outer pixel surface in the mechanical array, was described using the UNIFIED surface model in DETECT2000. The σ_α parameter was varied to account for different surface roughness, as explained in [21], [22].

Fig. 4.

Number of photons detected in a 1.0×1.0 mm² area underneath the source location, normalized to the total number of photons collected by the complete MPPC array. The statistical errors in the simulations are negligible.

Fig. 4 shows that a lower barrier RI leads to less light leakage to adjacent pixels. Furthermore, a rough interface will result in depth dependent light leakage, which could be exploited for DOI extraction.

C. Detector performance evaluation

We further study the expected performance characteristics of a detector containing optical barriers, with the goal of achieving high XY and DOI resolution simultaneously in a singleside readout configuration. Here we implement LYSO:Ce detectors with the same dimensions as in Section B, again coupled to an 8×8 MPPC array [20]. Two sets of simulations were performed for each barrier pattern, as illustrated in Fig. 5.

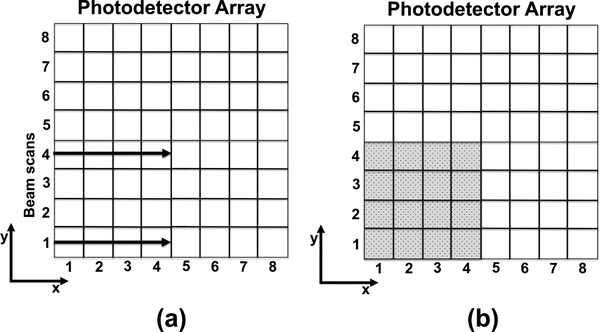
Fig. 5.

Schematic figures of the simulation setup used for the detector performance evaluation. (a) shows beam scans along a central and an edge pixel row. 300 gamma events were simulated with increments of 0.35 mm in the x direction. (b) illustrates the flood map simulations. 400 gamma events were randomly distributed over each crystal pixel cross section. Due to symmetry events were only generated in one quarter of the detector as illustrated by the grey area in (b). Both procedures were repeated with 3 mm separation in z. Depending on the geometry this 3 mm pitch in z was modified to avoid source generation on or very close to discontinuities in the geometry

In all simulations one gamma event was simulated as an isotropic source of 5000 optical photons, in combination with a SiPM quantum efficiency of 1. Only photopeak events were simulated and the inherent energy resolution of LYSO:Ce was neglected. Similar to other work the simulations were carried out at 420 nm being the peak emission wavelength of LYSO: We do not expect this simplification to change the trends observed in this paper. The beam scans were used to generate light response functions (LRF) for individual MPPC pixels. These were calculated as the signal in the MPPC pixel normalized to the emitted number of photons for each event location. Normalization to the total number of collected photons instead does not change the shape (i. e. width) of the LRF significantly, but only the absolute values. The width of the LRF was analyzed as a function of depth in order to assess the DOI capabilities of each design. This was done by Gaussian fitting and determination of the Full Width at Half Maximum (FWHM). The second set of simulations was used to create position histograms using a center of gravity estimator. These simulations were also used to calculate the light collection efficiency as an average over all source locations, for each detector configuration. Further details regarding the simulation setup can be found in [21].

1). Comparison LIOB, monolithic, and mechanical:

In previous work we performed simulations to compare the performance characteristics of laser-processed detectors with the two standard detector types being mechanically pixelated arrays and monolithic crystals [21]. For this baseline study we implemented laser-processed detectors with simple optical barrier patterns (1.05 mm pitch) extending all the way or half way through a 20 mm thick LYSO:Ce crystal, and the results of this study are summarized in Fig. 6.

Fig. 6.

Comparison of the characteristics of the four detector categories. The Mechanical array and the all-way barrier patterns were simulated with a 1 mm thick light guide (RI=1.5). A, C, and D show the results for polished crystal/pixels for the mechanical array and the monolithic crystal, and barrier RI=1.0 and interface roughness characterized by σ_α=20° for the laser-processed detectors. A: LRF for four adjacent MPPC pixels under a beam scan through the center of the detector. B: FWHM of the LRF, for a central MPPC pixel, as a function of DOI and the characteristics of the optical barriers in the case of laser-processed detectors, and surface roughness of the crystal/pixels in the case of the mechanical array and the monolithic crystal. The error bars correspond to the 95% confidence interval of the fitting parameter. C: Flood maps showing the sum of 7 (8 in the case of half- way barriers) discrete interaction depths. D: Line profiles through a central and an edge row in the above flood maps. For the monolithic detector and the half way barriers the depth dependence of the flood map is large making the line profiles not illustrative. The results presented here are compiled from Ref. [21]

A mechanical array is characterized by good transversal resolution, as manifested in the flood map and line profiles, but no DOI information. A monolithic detector has poor transversal resolution but inherent DOI information given by the depth dependent LRF.

A laser-processed detector can combine the features of the other two detector types and provide a pixel map similar to that of the mechanical array, and depth dependent LRF like what is observed for the monolithic detector. As expected the all-way barrier pattern shows a behavior closer to that of the mechanical array, while the half-way barrier pattern is closer to the monolithic crystal. Both designs do however clearly show combined features from the two detector extremes. Furthermore, all designs under study show edge effect issues, where the edge pixels are somewhat merged when the center of gravity estimator is used for gamma-ray event positioning. This edge effect is most pronounced for the half-way barrier pattern and the monolithic crystal, as expected.

2). Deeper barriers close to the detector edge:

One approach to address the edge effect issue is to design a barrier pattern where the barriers close to the detector edge has different properties compared to the rest. This difference may be in terms of barrier RI or interface roughness, which affects the opacity of the barriers, or in the barrier shape or pattern. Here we investigate the characteristics of a detector with barriers half-way through the detector thickness in the center of the detector, but deeper barriers close to the detector edge, as illustrated in Fig. 7a. We chose to modify the halfway barrier pattern given that this presented the worst edge effect issues in Fig. 6.

Fig. 7.

(a) Schematic figure of the geometry with barriers half-way (10 mm) through the crystal thickness, and 16 mm barriers closest to the crystal edge. (b) Barrier pattern where the barrier depth decreases gradually towards the center of the detector.

Fig. 8 shows flood maps for this design compared to the half-way barrier pattern studied in [21]. These results showcase one way of using the LIOB technique to address the edge effect issues common to many detector designs.

Fig. 8.

Flood maps with 8 discrete interaction depths combined, as well as at 3 individual interaction depths. Top: Half-way barrier pattern. Bottom: Half-way barrier pattern with deeper barriers close to the detector edge. In both cases the barrier RI=1.0 and the barrier crystal interface is rough with σ_α = 20°.

Fig. 9 shows the DOI dependence of the same geometry, compared to the all-way and half-way barrier patterns. It is apparent that this geometry provides less DOI information compared to the half-way barrier pattern, both along the center and close to the detector edge.

Fig. 9.

FWHM width of the LRF as a function of depth. The error bars correspond to the 95% confidence interval of the fitting parameter. Left: Beam scans along a central pixel row. Right: Beam scans along an edge row.

3). Gradual barriers:

Following the promising results with the deeper edge barriers, we implemented the design shown in Fig. 7b. Here the barrier depth changes gradually from 17 mm close to the edge to 5 mm at the center of the detector.

Fig 10 shows the resulting flood maps obtained with this geometry, for four combinations of barrier RI and barrier/crystal interface roughness. The impaired light confinement for higher barrier RI causes shrinking of the flood maps regardless of barrier/crystal interface roughness. One can also sense a depth dependent response in the flood maps, especially in the case of a rough barrier/crystal interface.

Fig. 10.

Flood maps for the gradual detector geometry as a function of barrier RI and barrier/crystal interface roughness. It should be noted that these flood maps contains the summation of 7 discrete interaction depths.

The depth dependence is further demonstrated in Fig. 11, showing LRF as a function of depth for a central MPPC pixel, for the same four configurations. A rough interface results in a clear depth dependence throughout the detector thickness, while a smooth interface yields essentially constant LRF below 10 mm DOI. Fig. 12 shows the FWHM width of the LRF for the rough barrier-crystal interface compared to the half-way and all-way barrier patterns. The smooth barrier crystal interface was not further analyzed due to the poor DOI information manifested in Fig. 11, and the non-Gaussian shapes of their LRF’s making them unsuitable for the FWHM analysis chosen here. It can bee noted that for the gradual barrier pattern the DOI dependence resembles that of the halfway barriers in the center of the detector, but the all-way barriers close to the edge.

Fig. 11.

LRF for a central MPPC pixel as a function of depth for four barrier RI/interface roughness combinations. z increases with DOI in the detector.

Fig. 12.

FWHM of the LRF for the gradual barrier pattern as well as allway and half-way barriers. The error bars correspond to the 95% confidence interval of the fitting parameter. Left: Beam scan along a central pixel row. Right: beam scan along an edge pixel row.

Given the superior DOI dependence for rough interfaces, in combination with the higher light confinement for a low barrier RI, we chose to study the configuration with barrier RI=1.0 and a rough barrier/crystal interface (σ_α = 20°) in more detail. Fig. 13 shows flood maps and line profiles at 3 individual interaction depths for this configuration. Noteworthy is that the edge pixel-like volumes are separated at all depths shown here. However, the transversal resolution in the center of the detector is impaired when the centroid method is used for event positioning. The performance is expected to improve if a statistical positioning algorithm such as Maximum Likelihood is employed. The overall performance of this barrier pattern is characterized by high transversal resolution and weaker DOI at the edge of the detector, but low transversal resolution and strong DOI dependence in the center of the detector.

Fig. 13.

Flood maps and line profiles for RI=1.0 and σ_α = 20° for 3 individual interaction depths. Shown are also line profiles along the edge pixel row.

For all 3 partial barrier patterns studied, the LRF width as a function of DOI is not a bijective function, and events in the top and bottom of the detector can have the same FWHM. Figure 11 however highlights how such events could be distinguished based on different magnitude of the MPPC signal for the two regions.

4). Light Collection Efficiency:

The light collection efficiency was calculated as an average over all events in the flood map simulations. The results for the gradual detector design are presented in Table 1, together with the corresponding values for a monolithic detector, a mechanical array, and the all-way and half-way barrier patterns. The light collection efficiency for the gradual pattern is comparable to the other laser-processed designs and higher than both the monolithic crystal and the mechanically pixelated array.

TABLE 1.

Light Collection Efficiencies

Configuration	Polished	σα=20°
Monolithic	39.5 ±0.8	71.6 ±0.9
Mechanical	35.5 ±1.2	59.1 ±7.1
All-way, RI=1.0	42.5 ± 1.4	74.3 ±2.6
Half-way, RI=1.0	45.2 ±1.2	73.6 ±3.9
Gradual, RI=1.0	45.0 ±1.0	75.8 ±1.6
Gradual, RI=1.4	46.9 ±1.1	76.2 ±1.8

Light collection efficiencies. The values for the monolithic crystal, the mechanical array, as well as the all-way and half-way barrier patterns are taken from Ref. [21]. The uncertainties correspond to the one σ variations in light collection efficiency over the detector volume.

IV. DETECTOR FABRICATION AND CHARACTERIZATION

A. Laser processing setup

For this study we used a picosecond Nd:YAG laser with maximum repetition rate of 1 MHz and 532 nm wavelength. The beam was focused inside the scintillator using an objective lens. We jogged the beam focus in the scintillator volume using XYZ translation stage to create a pixel-like pattern in the crystal. Being the most straightforward pattern, we chose to fabricate an array with barriers extending all the way through the crystal thickness. The pixel dimensions were 1×1×20 mm³.This array was processed in a single run (~100 min) without rotation or human involvement. The measured width of the optical barriers was ~ 0.03 mm on average

B. Detector evaluation setup

To evaluate the performance of the fabricated scintillator array, we utilized silicon photomultipliers from SensL Corporation (Cork, Ireland). We used SensL Array4 SiPM which is a 4×4 array of 3.0×3.0mm² SiPMs with 3.36 mm pixel pitch. The SiPM directly sits on the preamplifier board, which is a low profile and small footprint PCB board used to amplify the signals from SPMArray4 photosensor. The preamp board is then connected to the breakout board, which is an interface board for fast evaluation of SensL SiPM arrays. The breakout board also provides a sum signal from all 16 channels. Fig. 14 shows the schematic of the data acquisition. The LYSO array was coupled to the SiPM using Dow Corning Q2–3067 optical grease. Light sharing between neighboring SiPM elements was used to calculate centroid of gamma-ray interaction. A position histogram (2D) was generated as a response to a point-like Cs-137 source at ~12 cm distance from the crystal surface. It should be noted that all experiments were carried out at room temperature and no temperature feedback control was used to correct for the related known effects on SiPM performance. Measures were however taken to keep the temperature in the experimental box constant and the effect is expected to be minor.

Fig. 14.

Data acquisition setup for generating 2D position histogram.

C. Detector performance

The 2D position histogram, generated using a center of gravity estimator, and 1D line profile through a central column of pixels in the LYSO array is shown in Fig. 15. Despite the relatively large thickness of the LYSO sample, the pixels are resolved in the position histogram. This means that the optical barriers in the scintillator in fact contribute to light channeling and reflect the scintillation light back to the pixel volume. The peak to valley ratio for the pixels in the line profile is 2.2.

Fig. 15.

Top: side and top view of a 10×10×20³ LYSO:Ce with 1×1 mm² pixels processed by LIOB technique. Bottom: flood map of the array as a response to Cs-137 source, and a 1D line profile through a column of pixels.

Due to the unfavorable geometry of our detector (thick with small cross-section), we chose to wrap the detector in only 2 thin Teflon layers, in order to improve the performance at the detector edge and avoid pixel merging in this region. This is similar to some other efforts that use absorbers or black paint on the crystal sides to improve spatial resolution. With the use of more robust positioning algorithms such as statistical based techniques, it is apparent that the detector performance is expected to improve even with complete wrapping.

D. DOI measurement

Light channeling in the pixel-like structures of a laser-processed array is expected to lead to non-isotropic light propagation in the crystal, which, in the case of a non-perfect outer reflector, would lead to variations in photon escape from the entrance surface of the detector, depending on DOI. We verified this by exposing a laser-processed detector and a monolithic crystal, with the same dimensions and reflector arrangement as the previous experiment, to a collimated Co-57 source at different crystal depths. This low energy source was chosen for increased interaction probability in the relatively thin crystal. Fig. 16 shows the resulting pulse height spectra where the photopeak location varies with DOI for the laserprocessed detector, but not for the monolithic crystal. This feature could be used to extract DOI information through pulse height discrimination. We further compare these results to light transport simulations of the same setups. The detectors were here wrapped in an external diffuse reflector with a reflection coefficient of 0.5, and point sources where placed along a central pixel column at different depths. As seen in Fig. 16 there is no observed depth dependence for the monolithic detector, in agreement with the experiment. For a laser-processed detector with barrier RI=1.4 and rough barrier/crystal interface (σ_α = 20°), a linear dependence is observed. The photopeak location in the corresponding experiment is found to move with ~18% from 3 to 17 mm DOI. This is to be compared to ~13% in the simulations. Both experiments and simulations thus show the same trend, but a more methodical study is required. However, we believe that a barrier RI~1.4 and a rough barrier/crystal interface describes our fabricated crystal well.

Fig. 16.

Top: Pulse height spectra as a function of interaction depth for a laser-processed detector and a monolithic crystal. Bottom left: Simulated light collection efficiencies as a function of depth for the same two cases. The laserprocessed detector is here characterized by RI=1.4 and (σ_α = 20°). Bottom right: Signal strength normalized to DOI=3 mm for the laserprocessed case. The figure is generated using the photopeak locations from the experimental data, as those are directly related to the light collection efficiency.

V. DISCUSSION AND CONCLUSIONS

In the light collection efficiency simulations, we observed that the laser-processed scintillators may collect larger fraction of scintillation photons compared with the other detector types. Also, given that much of the light is collected by the photodetector underneath the radiation interaction site, one can expect that the timing resolution of the laser-processed scintillators can be potentially better than the other two detector types. However more methodical study needs to be done with experiments. We also observed that the so-called edge effect can be mitigated by using the LIOB technique. This is however the subject of future work to simulate and fabricate detectors with uniform resolution across the detector face. Specifically, with more optimized pattern for the optical barriers in combination with statistical based positioning estimator, we expect to achieve detectors with sub-mm transverse resolution and multiple DOI levels. By comparing the simulation and experimental position histograms and line profiles, we believe that the refractive index of the barriers obtained thus far is between 1.2 and 1.4. A more methodical study is required to achieve RI of 1.0 which can lead to a better pixel separation and approaching values reported by the current mechanically fabricated arrays. It is noteworthy that in the effort to increase the fill factor in more recent mechanically cut arrays, the inter-pixel gap is 0.07 mm or smaller. However the interpixel optical crosstalk in these arrays is not negligible and considerable fraction of light leaks to the neighboring pixels [23]. Therefore, we believe that by using the LIOB technique especially for those applications that require small pixel crosssection and large crystal thickness, the laser-processed arrays may provide better performance, and more design flexibility at lower cost.