Upper Airway Reconstruction Using Long-Range Optical Coherence Tomography: Effects of Airway Curvature on Airflow Resistance

Abstract

Objectives:

Adenotonsillectomy (AT) is commonly used to treat upper airway obstruction in children, but selection of patients who will benefit most from AT is challenging. The need for diagnostic evaluation tools without sedation, radiation, or high costs has motivated the development of long-range optical coherence tomography (LR-OCT), providing real-time cross-sectional airway imaging during endoscopy. Since the endoscope channel location is not tracked in conventional LR-OCT, airway curvature must be estimated and may affect predicted airway resistance. The study objective was to assess effects of three realistic airway curvatures on predicted airway resistance using computational fluid dynamics (CFD) in LR-OCT reconstructions of the upper airways of pediatric patients, before and after AT.

Methods:

Eight subjects (five males, three females, aged 4–9 years) were imaged using LR-OCT before and after AT during sedated endoscopy. Three-dimensional (3D) airway reconstructions included three airway curvatures. Steady-state, inspiratory airflow simulations were conducted under laminar conditions, along with turbulent simulations for one subject using the k-v turbulence model. Airway resistance (pressure drop/flow) was compared using two-tailed Wilcoxon signed rank tests. Results: Regardless of the airway curvatures, CFD findings corroborate a surgical end-goal with computed postoperative airway resistance significantly less than pre-operative (P <0.01). The individual resistances did not vary significantly for different airway curvatures (P >0.25). Resistances computed using turbulent simulations differed from laminar results by less than ~5%.

Conclusions:

The results suggest that reconstruction of the upper airways from LR-OCT imaging data may not need to account for airway curvature to be predictive of surgical effects on airway resistance.

INTRODUCTION

Upper airway obstruction in children is most commonly caused by adenotonsillar hypertrophy (AH) [1]. The AH condition also contributes to the development of obstructive sleep apnea (OSA) [2,3], leading to significantly lower quality of life from neurocognitive [4], behavioral [3,4], and cardiovascular [5] concerns. Adenotonsillectomy (AT; the surgical removal of the adenoids and tonsils) is commonly used to treat AH and AH-related sleep disorders [6], but guidelines are lacking to aid surgical decision-making [1]. While patient-reported improvement following surgery is between 70% and 80%, persistent symptoms of sleep-related breathing disorders have been reported in as many as 25% of normal-weight and 75% of obese children after surgical management [2,3,7–9]. Hence, there is ongoing debate among pediatric otolaryngologists on improvement of AH-related sleep disorders, and sufficiency of AT alone to relieve symptoms in the absence of an established tool for evaluating this disorder [9–14].

Computed tomography (CT) and magnetic resonance imaging (MRI) studies can provide anatomical information, but are expensive, often require sedation in children, and involve radiation exposure from CT imaging. Though these modalities produce high- resolution images that facilitate computational modeling of airway obstructions, for example [15–18], the diagnostic benefits of CT and MRI must be weighed against the potential risk for cancer from ionizing radiation and sedation, especially in a pediatric population [19]. Endoscopy furnishes information on internal airway abnormalities and helps localize the level(s) of obstruction, but does not provide quantitative information sufficient for computational modeling [20]. The need for diagnostic evaluation tools without radiation, sedation, or high costs has motivated the development of long-range optical coherence tomography (LR-OCT) [21].

Optical coherence tomography (OCT) is an imaging technique using a low-coherence optical interferometer and reflected light to generate information on spatial structures based on differences in optical absorption and scattering [22]. The objective of conventional OCT is the use of penetrating light over a short range of several millimeters to obtain images of tissue components like confocal microscopy [23]. Long-range OCT (LR-OCT) is the use of this technique with an emphasis on longer range capture of airway wall location [24,25] to quantify size and shape of hollow organs including the upper airway [26,27] and can provide real-time cross-sectional airway imaging during endoscopy [28]. Our group has successfully used LR-OCT to generate images in the upper airways of adults [29,30] and pediatric patients [21,31], and developed methods to process LR-OCT images into three-dimensional (3D) reconstructions [32].

Airway reconstructions can be used to relate airway obstruction and AT outcomes to measureable anatomic characteristics such as cross-sectional area (CSA). One initial study used 3D airway reconstructions from acute, intra-operative LR-OCT images in pediatric patients before and after AT to demonstrate that naso- and oropharyngeal CSAs were measurably larger post-operatively [21]. LR-OCT reconstructions could also be used for computational fluid dynamics (CFD) simulations of airflow through upper airways to quantify airflow characteristics such as resistance and wall shear. [27,33].

Airway resistance may be sensitive to airway shape, and hence to airway curvature or degree of flexure. Since the location of the LR-OCT fiber optic tip was not tracked during imaging in our previous studies [21,32], sequential airway images were initially stacked vertically and the resulting 3D reconstructions were curved or bent to reflect the general curvature of the upper airways in three control subjects [32]. The main objective of the current study was to use CFD-based airflow simulations in these pediatric LR-OCT reconstructions to test the hypothesis that airway resistance varies with curvatures. Since airway resistance is sensitive to the width of the airway’s narrowest segment, the relationship between airway resistance and minimal CSA (mCSA) was also studied.

Additionally, we noted that the narrow airways, prevalent especially before AT, could induce turbulent flow downstream of the constriction. This motivated us to test the hypothesis that airway resistance computed using a turbulent flow solver can differ from the resistance obtained assuming laminar flow. The test was done representatively for one curvature in one subject.

MATERIALS AND METHODS

Patients

Eight pediatric patients (five males, three females, ages 4–9 years, weight 18.2–53.5 kg; Table 1), with a diagnosis of adenotonsillar hypertrophy and who were candidates for AT, were selected from the pediatric otolaryngology practice at Children’s Hospital of Orange County, CA. Parents were informed of the study and provided written consent on their children’s behalf. This study was conducted with Institutional Review Board approval from the Children’s Hospital of Orange County and the University of California, Irvine [21]. All patients underwent AT under normal standards of care and had unremarkable post-operative recoveries.

TABLE 1. Study Subjects.

Table 1 presents a description of the eight subjects imaged in this study using long-range optical coherence tomography before and after adenotonsillectomy. Minute volume ${\dot{V}}_E$ was estimated using ${\dot{V}}_E$ =(1.36) (M)^0.44, where M=body weight in kg, from Garcia et al [32].

Subject ID	Gender	Age (years)	Weight (kg)	Estimated resting minute volume (${\dot{V}}_E$, L/min)	Steady-state inspiratory airflow rate (= 2 × ${\dot{V}}_E$, L/min)
Subject 1	F	8	53.5	7.83	15.67
Subject 2	M	7	20.1	5.09	10.19
Subject 3	M	4	18.2	4.87	9.75
Subject 4	F	6	21.6	5.26	10.51
Subject 5	M	9	28.0	5.89	11.78
Subject 6	M	4	18.3	4.89	9.77
Subject 7	M	6	35.7	6.56	13.11
Subject 8	F	7	25.9	5.69	11.39

LR-OCT Imaging

The imaging system and protocol were described in detail in previous publications [21,29]. Briefly, LR-OCT imaging was conducted with a Fourier domain swept source system in which a 1,310nm swept source laser with 26mW average power, 50 kHz A-scan rate, and 5mm coherence length in air was used with an acousto-optic modulator generating a 100 MHz carrier frequency on a probe with an extended working distance of 20 mm. The system had an axial resolution of 10 mm in tissue and a lateral resolution of 112 mm at the focal point of the probe, with sensitivity roll offs of 6 and 10 dB at 9.5 and 14mm total offsets (imaging ranges), respectively [29]. Due to the experimental nature of LR-OCT imaging at this time, the imaging protocol for this study was incorporated into airway endoscopy exams conducted as part of the standard of care immediately before and after surgery while the subject was sedated. Thus, each patient was sedated, intubated, and positioned with the head slightly tilted back, less so than the position used for surgical procedure. The imaging probe was inserted into a single-use fluorinated ethylene propylene sheath, distally heat-sealed. The sheath and probe were passed through the nose to the oropharynx using a Robinson catheter, and then guided to the esophageal introitus. The catheter was removed and the probe was drawn up through the sheath, leaving the sheath in place for two additional imaging passes. Three passes from esophageal introitus to nares were completed for optimal image quality pre- and immediately post-operatively. Imaged regions spanned 10–25 cm, and 250–1,000 cross-sectional images were taken during each imaging pass (20–40 seconds each) [21].

Airway Reconstruction

The process of creating 3D airway reconstructions from the LR-OCT images was previously described [21,32]. Briefly, each image set was examined for quality based on signal intensity, distortion from irregular rotation of the probe, effects of airway size and shape, and artifacts and noise such as specular reflection [21]. Among the three passes, the image set with the best signal-to-noise ratio, the best contrast between air and tissues, and the least loss of structure owing to probe line-of-sight limitations was selected for analysis in each patient pre- and post-surgery. Selected raw image sets were then cropped to the appropriate field of view, converted to polar coordinates, re-aligned, and imported into the medical image analysis software Mimics™ (Materialise, Inc., Plymouth, MI). In Mimics™, airway outlines were traced by hand with manual interpolation of structures missed during imaging or obscured by the endotracheal (ET) tube (Fig. 1A). A 3D rendering of the airway surface was created by stacking the images vertically and using the “wrap” function in Mimics™ to generate a smooth surface around the airway tracings (Fig. 1B) [32].

Fig. 1.

Method for creating 3D airway reconstruction from LR-OCT images. (A) The contour of the tissue in each LR-OCT image was manually segmented. (B) The stack of outlined images was converted to a 3D straight tube model (figure modified slightly from Lazarow et al. [21] and used with permission).

The vertical airway surface was then subjected to a bending algorithm implemented in Visual Basic (Microsoft, Inc., Redmond, WA) to curve the vertical reconstruction into a more anatomically-correct position [32]. The algorithm was based on planar curves fitted to sagittal CT and MRI images of the upper airways of three normal pediatric patients, representing three possible curvatures (Fig. 2A) [21]. Each curve was then used by the bending algorithm to reposition axial cross sections of each vertical airway reconstruction so that the cross sections were at right angles to the curved common axis (Fig. 2B). This process produced pre- and post-surgery reconstructions for three different curves in each of eight patients, generating a total of 48 models (Fig. 2C) [32].

Fig. 2.

Method for curving the vertical LR-OCT reconstructions to represent three normal neck curvatures. (A) Curvature 1 was obtained from a CT of an 8-year-old male, Curvature 2 (inset=fitting of curve to Curvature 2) was obtained from a CT of a 7-year-old female, and Curvature 3 was obtained from an MRI of an 8-year-old female [21] (figure used with permission). (B) Curved common axes were truncated to the imaging region from piriform sinus to choanae (dotted inset). Axial cross-sections from vertical reconstructions were realigned along and perpendicular to curved common axis (Curvature 2 shown) to produce curved reconstructions. Example of curved reconstruction shown with curved common axis superimposed. (C) All reconstructions from pre- and post-surgery LR-OCT images in one subject after curving the vertical reconstructions using the curvatures shown in (A).

Cross-Sectional Area Calculation

CSA values were obtained for axial cross sections spanning each vertical LR-OCT airway reconstruction, before bending, using the area calculation function in MimicsTM. mCSA values were calculated by averaging the areas of five consecutive CSAs corresponding to a 1- or 2-mm thick slab of the OCT data surrounding the smallest CSA value. This averaging protocol was used to smooth the section-to-section variations in CSA in the raw OCT data. Curve fits of resistance as a function of mCSA were implemented using Excel 2010 (Microsoft, Inc.).

Computational Fluid Dynamics Simulations

Model preparation and meshing.

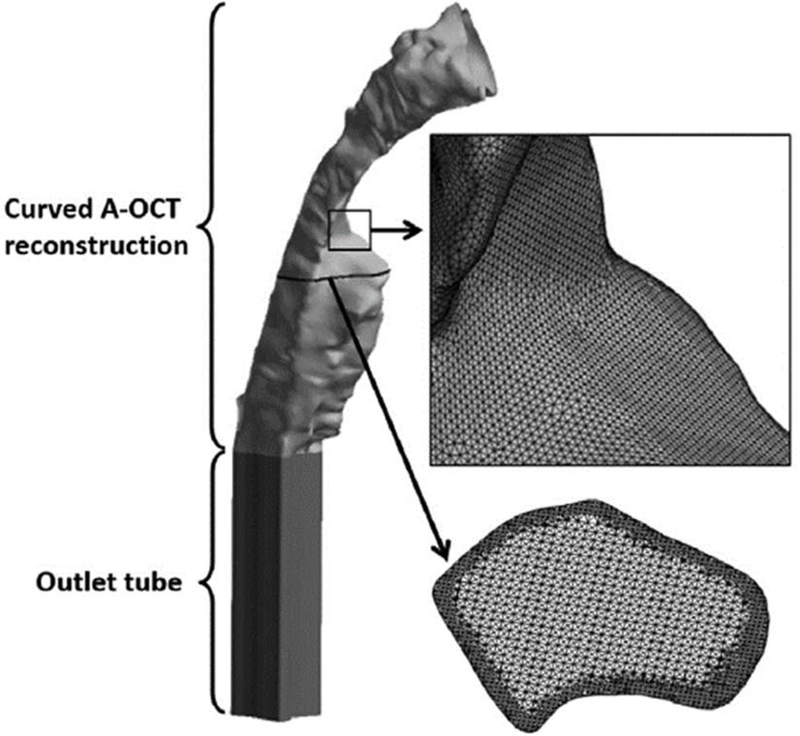
Stereolithography (STL) files for each of the three pre- and post-operative airway curvatures for each subject were exported from Mimics™ and imported into the computer-aided design and meshing software ICEM-CFDTM (ANSYS, Inc., Canonsburg, PA). Separate inlet, outlet, and airway wall surfaces were created, and a 4-cm straight tube was extruded from the distal end of the reconstructions to aid with flow stabilization. Computational meshes (unstructured grids) comprising approximately four million graded, tetrahedral elements [34,35] were developed (Fig. 3) and smoothed until the quality (aspect ratio) of all elements was greater than 0.3, to ensure robust numerical performance.

Fig. 3.

LR-OCT airway reconstruction for one neck curvature in one subject with an outlet tube added for numerical stability and illustrations of the computation mesh. Small black box shows an area of enlargement (indicated by short arrow) illustrating the density of the surface mesh. Horizontal black line shows the level of an enlarged axial cross section (indicated by long arrow) illustrating the interior mesh.

For turbulent flow simulations, additional mesh structures are needed to resolve potentially higher velocity gradients near airway walls. Therefore, hybrid prism-and-tetrahedral-element meshes were constructed for the pre-and post-operative geometries of Subject 1 with one airway curvature (Curvature 1, Fig. 2A) by adding four 0.1-mm layers of prism elements to the tetrahedral mesh adjacent to airway walls.

Airflow simulations.

Steady-state inspiratory airflow simulations were conducted using Fluent™ v.14 (ANSYS, Inc.) for flow rates based on individual resting minute volumes which were estimated from body weight using allometric scaling (Table 1) [36]. Laminar simulations were conducted for all models. Airway resistance from the inlet to the last airway section was computed as the pressure drop in Pascals (Pa) divided by the flow rate in ml/sec.

Turbulent flow simulations were conducted in the hybrid mesh for Subject 1 using the shear-stress transport (SST) k-ω turbulence model [37,38]. The turbulence length scale was assumed to be 1mm, and turbulent intensity was assumed to be 5% at the inlet. Adequacy of the hybrid mesh parameters for the representative simulation using the turbulence model was authenticated by computing the y⁺ values in the regions adjacent to the wall. The y⁺ value, a ratio between the turbulent and laminar influences in a mesh element, is represented by

$$y^{+}=\frac{u*\Delta }{v}=\frac{\Delta }{v}\sqrt{\frac{{\tau }_w}{\rho }},$$

where u* is the friction velocity, τ_w is wall shear stress, D is the normal distance of the control volume center from wall, υ is the kinematic viscosity of air, and ρ is air density [39]. y⁺ can be interpreted as a dimensionless distance from the wall, with a smaller value implying the predominance of laminar sub-layers in the near-wall region and a higher value implying the occurrence of turbulent structures in the wall proximity. Typically the following ranges are assumed to identify the flow characteristics at the wall [40]:

• y⁺< 5: laminar sub-layers with viscous stress dominating the wall shear;

• 5 < y⁺ < 30: transition layers;

• y⁺> 30: fully turbulent,

where y⁺ is a function of the numerical solution. In our turbulence simulations (Table 2), the mean y⁺ values were consistently ~0.6–1.2, both pre- and post-surgery. This implies that the preeminent flow behavior at the near-wall control volumes corresponded to the laminar sub-layer regime [41]. Mesh refinement was also considered sufficient, as the maximum values for y⁺ were less than 5.0 for all the simulation set-ups, with the target steady state inspiration rate of 15.67 L/min (Table 1).

TABLE 2. Turbulence Simulation Results and Comparison With Viscous–Laminar Modeling.

Table 2 presents wall y⁺, pressure drop (Pa), and inspiratory airflow (L/min) obtained from simulations in the Curvature 1 model of Subject 1 using the shear-stress transport k-ω turbulence model [33,34], both with and without low Reynolds number (Re) corrections. The turbulence and laminar model results are compared with respect to the airway resistance. ReC, with low-Re-correction; NReC, without low-Re-correction; SD, standard deviation.

Simulation.	Mean y+	Peak y+	SD on y+	Pressure drop (Pa)	Achieved inspiratory airflow rate (L/min)	Airway resistance from turbulence simulations (Pa.sec/ml)	Airway resistance from laminar simulations (Pa.sec/ml)	Percentage change in resistance (relative to the laminar results)
Pre-surgeiy
ReC	1.22	4.38	0.735	−356.65	15.67	1.365	1.347	+1.34%
NReC	1.21	4.41	0.737	−359.36	15.67	1.375		+2.08%
Post-surgery
ReC	0.56	2.83	0.368	−45.46	15.64	0.174	0.176	−1.14%
NReC	0.58	2.85	0.380	−48.71	15.75	0.186		+5.68%

Statistical Analysis

Since the sample size in this study was small, non-parametric statistical analyses were conducted. Airway resistances computed from the laminar simulations in LR-OCT subjects were compared among curvatures using the Kruskal–Wallis test [42] and between pre- and post-surgery states using two-tailed non-parametric Wilcoxon signed rank tests [43]. A P-value <0.05 was taken to imply statistical significance. Statistical analyses were performed using Microsoft Excel 2010 (Microsoft Corp.), and the Excel add-in Real Statistics Resource Pack (www.real-statistics.com) was used to conduct the non-parametric Kruskal–Wallis and Wilcoxon Signed-Rank tests.

Experimental Validation of the Computational Techniques

Validation methods.

A 3D reconstruction of the nasal cavity of a healthy adult subject was created in Mimics™, based on CT scans. A plastic replica of the nasal cavity was printed with a resolution of 0.10mm in the coronal direction and 0.25mm transverse to it, using the Accura 25 material in the SLA iPro-8000 3D printer at the Milwaukee School of Engineering Rapid Prototyping Center. The plastic nasal replica was used in an experimental setup to measure the pressure-flow curve. To reproduce the protocol for rhinomanometry, one nostril was occluded with tape (Microfoam 3M). Air pressure was measured with a pressure catheter (Millar Mikro-Cath, Millar, Inc.) that was pierced through the tape. Since this nostril was occluded with the tape, the pressure reading reflected the pressure drop across the nasal cavity (i.e., the gauge pressure at the end of the nasal septum). Steady flow through the contralateral nasal cavity was generated by connecting a plastic hose from the model outlet at the nasopharynx to house vacuum. The flowrate was measured using a flowmeter (Model 4045, TSI Inc.) in series with the plastic hose. Pressure was measured for steady flowrates from 0 to 70 L/min in steps of 10 L/min.

A tetrahedral mesh of the same nasal geometry was created in ICEM-CFDTM using approximately seven million elements. Steady-state airflow simulations were performed with both the laminar model and the standard k-ω model. The inlet boundary conditions for the k-ω model were 5% turbulence intensity and a turbulent length scale of 1 mm. The no-slip boundary condition was applied at all walls. To reproduce the experimental setup, separate simulations were performed to obtain the pressure-flow curves of the left and right cavities by setting one nostril as the inlet, while the other nostril was assumed occluded (wall boundary condition).

To compare CFD predictions and experimental measurements, the unilateral nasal resistance was estimated for an inhalation rate of 15 L/min, which corresponds to an adult person breathing at rest. Unilateral nasal resistance was defined as NR = ΔP/Q, where ΔP is the transnasal pressure drop and Q = 15 L/min = 250 ml/s is the unilateral flowrate. The pressure drop corresponding to the flowrate of 15 L/min was obtained by fitting a power law curve to the experimental or numerical data, namely Q = a(ΔP)^b, where a and b are constants. Once the coefficients a and b were obtained from linear regression, the pressure drop was calculated from Δ P = (250/a)^1/b.

Validation results.

A good agreement was observed between the pressure-flow curve measured experimentally and simulated with CFD (Fig. 4). The laminar model and the k-v turbulence model provided similar results, but the laminar model predicted flowrates that were somewhat higher than k-ω model. For unilateral flowrates greater than 30 L/min, CFD simulations with the k-ω model were in better agreement with the experimental measurements than the laminar simulations for the right cavity. However, the two CFD models provided similar predictions for the lower ranges of flowrates. In particular, nasal resistance at a flowrate of 15 L/min predicted by the laminar model had a better agreement with the experimental measurements than nasal resistance estimated with the k-ω model (Table 3).

Fig. 4.

Experimental measurements of the pressure-flow curve in a 3D-printed plastic replica of the human nasal cavity compared to CFD simulations using the laminar model or the standard k-ω turbulence model. (A) Left cavity. (B) Right cavity.

TABLE 3. Validation Data for the Numerical Methods.

Table 3 presents the unilateral nasal resistance (Pa.s/ml) at a flowrate of 15 L/min measured in a 3D-printed plastic replica and the corresponding estimates from CFD simulations using the laminar model and the k-ω turbulence model.

Nasal resistance (Pa.s/ml)
	Experiment	CFD laminar	CFD k-ω to turbulent
Left cavity	0.127	0.135	0.150
Right cavity	0.104	0.116	0.128

RESULTS

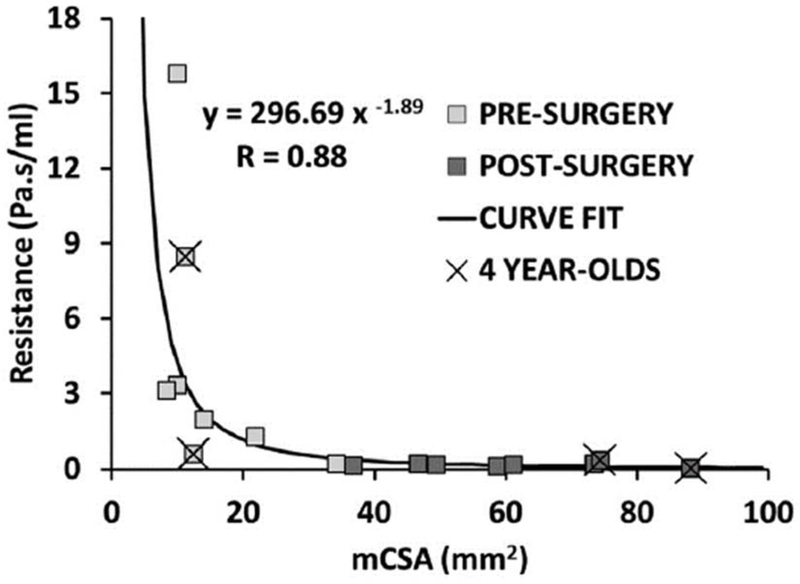
mCSA increased from an average of 15.2±8.7mm² before surgery to an average of 61.1±16.9mm2 after surgery in LR-OCT subjects. A strong inverse relationship was observed between airway resistance and mCSA (R= −0.88, P < 0.005), with low values of mCSA associated with high values of airway resistance (Fig. 5).

Fig. 5.

Airway resistance as a function of minimal cross-sectional airway (mCSA). Black curve shows fit to data (y = resistance, x = mCSA) with correlation coefficient of −0.88 (P < 0.005).

For each airway curvature, airway resistance before surgery varied substantially (up to 77-fold) over the study cohort. A similar trend was also seen for the post-surgery airway resistance, with up to 17-fold variation over the study cohort. Statistically, airway resistance was significantly less post-surgery than pre-surgery for all subjects and all curvatures (P<0.01; Fig. 6). Average variation of airway resistance with curvature was 5% before surgery (up to 13%, in Subjects 2 and 6) and 8% after surgery (up to 28%, in Subject 3). Statistically, however, curvature did not significantly affect resistance (P>0.25). These results contradicted our hypothesis that curvature would significantly affect airway resistance.

Fig. 6.

Effect of neck curvature on pre- and post-operative airway resistance. AT, adenotonsillectomy.

An estimate of percent airway blockage was computed by comparing the mCSA with the CSA near the choana through which imaging was done in each subject (Fig. 7). Percent blockage, estimated by 1-(mCSA/choanal CSA) as a percentage, ranged from 69.4% to 95% (averaging 86.3%) before surgery, and ranged from −33.7% to 75.6% (averaging 54.3%) postoperatively. Surgery reduced percent blockage in all subjects.

Fig. 7.

Effect of surgery on percent airway blockage as calculated by taking 1– (mCSA/choanal cross-sectional area) as a percentage. mCSA, minimal cross-sectional area.

Just before the airways widened out, the Reynolds number (Re) of the airflow approximated to 2,470 in the pre-surgery model and 2,100 in the post-surgery model, for target breathing rates in the representative Curvature 1 reconstructions of Subject 1. Re, a ratio of the convective inertia of the flow to its viscosity, is a key predictive marker for the onset of turbulence in a flow domain. For example, airflow in a pipe, purportedly a simplistic idealization of airway flow, develops turbulence beyond Re ≈2,700 [44–46]. Thus, the estimated Re in Subject 1 suggested transitional airflow regimes in the airways. One major feature of such flow physics transitioning from laminarity to turbulence is the formation of separation bubbles and eddies at the airway-tissue interfaces [47,48]. To account for such phenomena, the turbulence modeling scheme (SST-based k-ω) was implemented with low-Re-correction to the turbulent viscosity [40], and the simulation output was compared with results generated from: (a) SST k-ω model without the low-Re-correction and (b) laminar-viscous modeling. Turbulence models produced airway resistances that were similar to laminar simulations (see Table 2). Resistances obtained with low-Re-correction differed from the laminar modeling results by less than 2% both for pre- and post-surgery bends. Such trends contradicted our hypothesis that airway resistance computed using a turbulent flow solver would differ from computations under laminar flow conditions, thereby justifying the adequacy of the viscous-laminar model for this study.

DISCUSSION

The airflow simulations presented here are the first in pediatric airways reconstructed from LR-OCT images. These results demonstrate the ability of airway reconstructions based on LR-OCT imaging to capture a significant difference in airway size and resistance in the vicinity of the tonsils and adenoids before and after AT in eight pediatric patients. These results also demonstrate the potential of LR-OCT as a significant sleep study tool. Currently sleep studies yield only systemic variables without information on site or extent of anatomic obstructtion, which is critical for treatment decision-making. LR-OCT imaging can add this information to sleep studies without radiation or high costs, and could be conducted continuously during sleep as well, providing airway shape changes during the breathing cycle. Airway reconstructions based on LR-OCT images can help quantify airway compliance as well as the effects of potential operations to treat OSA, and aid in selecting patients who would benefit most from these surgeries.

LR-OCT imaging is currently possible during awake endoscopy in adults as demonstrated by our group [29,30]. With the constraints of the current study, the use of LR-OCT was limited to sedated endoscopy, requiring the presence of an ET tube. Sedation may be avoided with stand-alone use of the LR-OCT device. However, imaging in awake children can become challenging as the probe becomes bigger with the need for tracking, and may require the use of fiber Bragg grating [49]. As noted by Lazarow et al. [21] one of the limitations of the present study was anatomic distortion of the airway reconstructions owing to sedation and ET tube presence. If airway distortions from sedation and ET tube effects were similar before and after surgery, then differences between pre- and post-surgery simulations may not be significantly affected, but further study is needed to determine if this is the case.

Another limitation of this study was a lack of consistently high image quality throughout the entire length of the airway. As discussed in detail by Lazarow et al. [21] image quality was adversely affected by fragile LR-OCT probes suffering damage and diminished performance over time, distortions due to irregular probe rotation, missing airway contours due to large airway size and line-of-sight limitations, and artifacts due to specular reflection. Work is ongoing in our lab to improve probe quality and durability, maximize signal intensity, and interpolate missing sections from adjacent structures via hardware, software, and reconstruction methods development. Another major limitation of current methods in LR-OCT image reconstruction is the lack of information on probe tip position during pull-back which necessitated estimating airway curvature by a curved common axis. Although airway resistance varied by as much as 28% among the three curvatures in one subject in our study, we were unable to show significant differences in airway resistance either before or after AT among three curvatures. These results suggest that reconstruction of the upper airways from LR-OCT images may not need to account for airway curvature to be predictive of surgical effects on airway resistance. However, accurately knowing the position of the probe tip as it traverses the airway during imaging would improve model accuracy and address current challenges in matching pre- and post-surgery locations in the airway, especially since the superficiality of LR-OCT imaging does not provide many landmarks to allow co-registration of reconstructions [21]. Probe tip tracking technology has been described previously [50], and implementation in vivo is ongoing.

As in many 3D airway reconstruction applications, smoothing was used here to generate airway surfaces that mimic the smooth walls generally observed during endoscopic examination. Smoothing can affect the pressure drops predicted by CFD computations [51], but for the average flow rate used in the simulations presented here (11.5 L/min), pressure drops among three nasal CFD models of varying smoothness differed by only 3 Pa,[51] which was insufficient to change any of the statistical conclusions of the present work. However, additional work to determine how much smoothing can be done on geometries such as those modeled here before conclusions are affected would be valuable.

Our cohort included patients with an age range of 4–9 years. It may be argued that the shape of the upper airway can be significantly different in 4- and 9-year-old children. To address this potential confounding concern of age-based upper airway maturation changes not being incorporated into the models, we explored the study trend when the two 4-year old were omitted from the analysis. The exclusion diminished the age range of the truncated cohort to 6–9 years, with a largely unchanged weight range of 21.6–53.5 kg. Interestingly, the conclusions from statistical comparisons of resistance among curvatures before and after surgery did not change when the two 4-years old were excluded. Airway resistance was statistically smaller before surgery than post-operatively with P < 0.01 for all subjects, P<0.05 without 4-years old; curvature effects on resistance were not statistically significant before or after surgery with P > 0.25 for all subjects, P > 0.20 without 4-years old. Airway resistance in the two 4-years old differed from each other before surgery, commensurate with the pre-surgery trends seen in the cohort.

Subjects portraying comparable improvements in the airway blockage (Fig. 7) sometimes underwent quite different drops in resistance (Fig. 6). To explain this inconsistency, we note that the percent blockage was a localized calculation with regard to the airway anatomy, involving only the mCSA and the choanal CSA. In contrast, the airway resistance was influenced by cross-sectional variations throughout the airway. Narrower sections raised the wall shear, it being proportional to the square of the airflow velocity [52,53], which is higher at such sites. Such subject-specific wall effects cumulatively increase the passage resistance. Thus, inter-individual differences in airway anatomy influence the resistance in ways that are not captured by mCSA and choanal CSA alone.

The inverse relationship found between airway resistance and mCSA is expected for laminar flow in circular tubes. The Poiseuille equation states that during laminar flow the hydrodynamic resistance of a circular tube is inversely proportional to the square of the CSA (resistance ~(mCSA)⁻²) [54]. Fitting a power curve to the data in Figure 5 estimated that resistance ~mCSA)^−1.89, indicating that the Poiseuille equation is a reasonable estimate of the relationship between minimal airway diameter and airway resistance, despite the complex shape of pharyngeal anatomy.

Differences between airway resistances from turbulent vs. laminar simulations were relatively small (Table 2), suggesting that the simpler and quicker laminar simulations may be adequate for capturing pre- and post-surgery changes. Altogether, these results suggest that the assumption of laminar airflow does not appreciably affect CFD estimates of airway resistance, particularly when large surgical changes are observed as in our cohort. However, we should still note the caveat that a faster airflow or narrower airways might push the Re values, which presently lie in the transitional zone, beyond the threshold limit for sustained turbulence. To generate a realistic flow profile, the simulations would then require an exclusive implementation of turbulence modeling schemes [55].

The need to overcome current limitations such as line-of-sight data collection and airway curvature estimation is driving additional research on probe design and the use of magnetic tracking devices, which will lead to improved LR-OCT reconstructions in future [21]. LR-OCT has distinct potential as an emerging imaging modality to become a relatively low-cost method of obtaining quantitative airway information without requiring sedation or ionizing radiation exposure suitable for use in native sleep. The potential for LR-OCT to enable monitoring of residual OSA during post-AT sleep studies without additional sedation [17] is compelling.