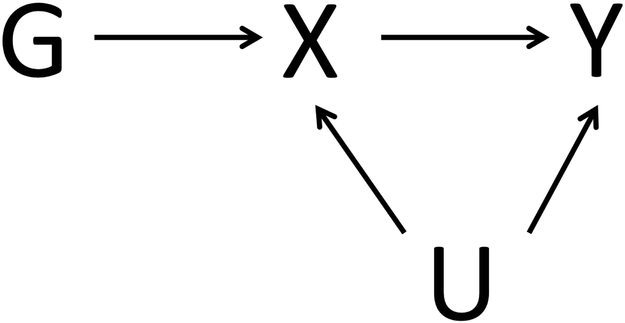Conducting a Reproducible Mendelian Randomization Analysis using the R analytic statistical environment

Abstract

Mendelian randomization (MR) is defined as the utilization of genetic variants as instrumental variables to assess the causal relationship between an exposure and an outcome (Davey Smith & Ebrahim, 2003). By leveraging genetic polymorphisms as proxy for an exposure, the causal effect of an exposure on an outcome can be assessed while addressing susceptibility to biases prone to conventional observational studies, including confounding and reverse causation, where the outcome causes the exposure (Davey Smith & Ebrahim, 2007). Analogous to a randomized controlled trial where patients are randomly assigned to subgroups based on different treatments, in an MR analysis, the random allocation of alleles during meiosis from parent to offspring assigns individuals to different subgroups based on genetic variants (Davey Smith & Ebrahim, 2007). Recent methods use summary statistics from genome-wide association studies to perform MR, bypassing the need for individual-level data (Burgess et al., 2015). Here, we provide a straightforward protocol for using summary-level data to perform MR and provide guidance for utilizing available software.

INTRODUCTION

The aim of many, if not all, observational studies is to associate an exposure and a disease or phenotype to eventually collect evidence to discern a causal relationship. However, observational associations are influenced by biases such as measured and unmeasured confounding, which can occur when an outside variable is associated with the exposure and the disease, and reverse causality and therefore can lack ability to establish a directional effect(Greenland, Robins, & Pearl, 1999). The principle underlying Mendelian randomization (MR) methodology is that such biases can be circumvented by leveraging genetic variants associated with an exposure as an “instrumental variable” (IV) to estimate the effect of genetic variation within an exposure on an outcome(Davey Smith & Ebrahim, 2007). An IV is defined as an external variable G that is associated with the exposureXand independent of outcome Yas well as any factors associated with outcome Y, other than via X(Greenland, 2018). Genetic variants can be utilized as “IVs”, thereby serving the role of randomizing “exposure”.

To utilize a genetic variant as an IV, three assumptions must be satisfied(Davey Smith & Hemani, 2014) (see Figure 1): (i) the genetic variant must be associated with the exposure, (ii) the genetic variant must be independent of any confounder of the exposure-outcome, and (iii) the genetic variant must be independent of the outcome, except via a possible association with the exposure.

Figure 1.

Directed acyclic graph depicting the IV assumptions for conducting Mendelian randomization. G, the genetic variant, must be (i) associated with exposure X, (ii) independent of any confounder U, and (iii) independent of outcome Y.

In the simplest MR technique (for one genetic variant), the presence of an association between a genetic variant and an exposure and the genetic variant and an outcome may imply causal effect of the exposure on the outcome(D. A. Lawlor, Harbord, Sterne, Timpson, & Davey Smith, 2008). MR can be performed with individual-level participant data, obtained from the genetic data for each participant, or with summary-level data, which usually contains per-allele regression coefficients and standard errors analyzed over all individuals within a study(Haycock et al., 2016; D. A. Lawlor, 2016). In summary data MR, summary-level data can either be obtained from publicly available summary level data or by consortia of genome-wide association studies (GWAS), or can be calculated from individual-level participant information(Burgess et al., 2015).

MR can be performed in a “one-sample” or a “two-sample” setting. One-sample MR is performed when the data on the exposure and the outcome are derived from a single dataset(Burgess, Davies, & Thompson, 2016). Two-sample MR is performed when the data on the exposure and the outcome are derived from two non-overlapping and independent datasets, allowing one dataset to be used for performing the summary-level instrument-exposure analysis and the other dataset for performing the instrument-outcome association analysis(Burgess et al., 2016; Hartwig, Davies, Hemani, & Davey Smith, 2016).

Here, we present a protocol to perform MR using summary-level data, which can be performed in the one-sample or two-sample setting, and we provide an RStudio markdown file to demonstrate how to use the TwoSampleMR package in R. The code and implementation of MR in the protocols below are inspired by and utilize resources provided by the MRC Integrative Epidemiology Unit and the MR-Base Collaboration(Hemani, Haycock, Zheng, Gaunt, & Elsworth, n.d.; Hemani et al., 2018).

BASIC PROTOCOL 1: Performing a Mendelian randomization analysis in R using summarized genetic data

In this protocol, we show how to perform MR using summary statistics using different methods of analysis. In the simplest method, the causal effect of the exposure on the outcome can be calculated by a “2-stage least-squares” (2SLS) regression, where the exposure is regressed on the genetic instrument, and the outcome is regressed over the exposure values (where linear or logistic regression is used for continuous or binary outcome variables, respectively)(Haycock et al., 2016).

In the inverse variance weighted (IVW) method, the causal effect of the exposure on the outcome for a single genetic variant can be estimated as a ratio of the association estimate for the outcome and the exposure (Bowden, Davey Smith, Haycock, & Burgess, 2016; Burgess & Thompson, 2017). For multiple independent genetic variants, the ratio estimates from each genetic variant can be meta-analyzed to form the overall causal estimate (Bowden, Davey Smith, et al., 2016; Burgess & Thompson, 2017).

MR-Egger can be used when the IV assumptions do not hold or weakly hold, and entails a modification to the IVW estimate calculation where the intercept term is calculated as part of the MR-Egger estimate, instead of setting the intercept term of the regression to zero (Bowden, Davey Smith, & Burgess, 2015). In MR-Egger, the intercept serves as a test for directional pleiotropy (meaning the genetic variants exert pleiotropic effects on the outcome)(Burgess & Thompson, 2017). In the protocol below, we describe how to conduct an MR analysis using these methods and provide guidance for utilizing MR software in R in order to perform, interpret, and visualize results of MR analyses.

Necessary Resources

Hardware

Computer running Linux, Mac OS, or Windows

Software

R package version >= 3.1.0 (Team, 2014)

Files

GWAS summary statistics (including SNP, major allele, minor allele, allele frequency, effect size, standard error, p-value, and sample size) for the exposure and outcome of interest.

Note that GWAS summary statistics may be available in different kinds of formats-- in this case, look at the header of the GWAS summary statistics file and identify if the following data are included, at a minimum: SNP, major allele, minor allele, allele frequency, effect size, standard error, p-value, and sample size. Remember that some information that may be missing from your summary statistics file, may be present in the paper referencing the GWAS.

The protocol and code below was inspired by the short course offered in the Mendelian Randomization Conference on July 10, 2017 by the MRC Integrative Epidemiology Unit.

Protocol steps —Step annotations

• 1.Obtain GWAS summary statistics for your exposure (Figure 1, X) and outcome (Figure 1, Y) of interest. Resources such as the NHGRI-EBI Catalog(Burdett et al., n.d.) can be leveraged to search for and download publicly-available GWAS summary statistics.
• 2.In this approach, genetic variants are utilized as instrumental variables (IVs), or “instruments” for the exposure. Determine usability of GWAS summary statistics from Step 1 by ensuring that the instrument-exposure data and the instrument-outcome data have listed the effect allele, allele frequency, beta, standard error, p-value, and sample size (as shown in Figure 2).
• 3.Determine if the IV assumptions hold for conducting an MR analysis. The first assumption can be evaluated by linear regression of the exposure on the instrument and calculating the F-statistic for your instrument (Palmer et al., 2011; Teumer, 2018). This can be calculated as,$F=\frac{N-K-1}{K}*\frac{R^2}{1-R^2}$, for N sample size, Knumber of genetic variants, and R²the proportion of the variance of the exposure explained by the IV (Burgess, Thompson, & CRP CHD Genetics Collaboration, 2011). An F statistic less than 10 denotes a weak instrument (Teumer, 2018).

  The second and third assumptions are more challenging to formally validate due to the possibility of unknown effects(Palmer et al., 2011; Teumer, 2018). In assessing the second assumption, consider any potential confounding variables (Figure 1, U) that may play a role in the association between your exposure and outcome, and in assessing the third assumption, consider potential issues such as pleiotropy or population substructure that may serve as a violation (Palmer et al., 2011; Teumer, 2018).

• 4.
  Run R package. Input exposure and outcome GWAS summary statistic data, using the read.table function.

  exposure_data<-read.table(“exposure_filename.txt”, head=T,
  sep=“\t”) outcome_data<-read.table(“outcome_filename.txt”,
  head=T, sep=“\t”)
  

Figure 2.

Shown are the first few rows of the body mass index GWAS summary statistics published from the UK Biobank and The Genetic Investigation of ANthropometric Traits (GIANT) Consortium meta-analysis(Yengo et al., 2018).

• 5.Identify instruments. Find independent SNPs that are GWAS significant (P < 5.0 × 10⁻⁸) for the exposure and identify the effects for these “instrument” SNPs from the outcome GWAS. Independent SNPs that are GWAS significant for the exposure are “instruments” – or proxies for exposure -- in this analysis.
• 6.Harmonize the exposure and outcome datasets. Ensure that the effect alleles from both files are the same. If not, then “flip” the log odds ratio of the effect allele of one of the datasets (multiply by −1). Ensure that the effect in the exposure file reflects the trait-increasing allele.

Note that the steps listed below for the ratio of coefficients (Steps 7-8), the inverse-variance weighted method (Step 9), and MR-Egger (Step 10) are independent and do not have to be performed consecutively (the results from one analysis do not affect the results of another analysis).

Ratio of coefficients (or Wald) method

• 7.
  Calculate the ratio of coefficients, or the Wald ratio. This is the simplest method for estimating the causal effect of the exposure on the outcome, and is the coefficient of the genetic variant in the regression of the outcome (represented here as outcome_data$beta) divided by the coefficient of the genetic variant in the regression of the exposure (represented here as exposure_data$beta)(Burgess, Small, & Thompson, 2017).

  wald_ratio <- outcome_data$beta/exposure_data$beta
  wald_ratio_standard_error <- outcome_data$SE/exposure_data$beta
  z_statistic <- wald_ratio/wald_ratio_standard_error
  p_value <- 2*pnorm(abs(z_statistic) ,lower.tail=F)
  

Note: The Wald ratio corresponds to the log odds ratio for the outcome per unit change of the exposure.

• 8.
  Perform a fixed-effects meta-analysis using the Wald ratio.

  effect <- sum(wald_ratio*wald_ratio_standard_error^−2)/
  (sum(wald_ratio_standard_error^−2))
  standard_error <- sqrt(1/sum(wald_ratio_standard_error^−2))
  Z_statistic <- effect/standard_error
  p_value <- 2*pnorm(abs(Z_statistic) ,lower.tail=F)
  

Inverse-variance weighted (IVW) method

• 9.
  Perform an inverse-variance weighted (IVW) linear regression to estimate the effect of the exposure on the outcome.

  IVW_weights <- outcome_data$SE^−2
  inverse_weighted_LR <- lm(outcome_data$beta ~ exposure_data$beta
  - 1 ,weights=IVW_weights)
  

The command summary(inverse_weighted_LR) displays the effect, standard error, and p-value of the exposure on the outcome.

Note that the intercept term here is zero in order to calculate the IVW estimate (Burgess & Thompson, 2017). In the case that a single genetic variant satisfies the IV assumptions, the effect of the exposure on the outcome can be estimated as a ratio of the estimated coefficient for the outcome to the estimated coefficient for the exposure for the genetic variant (Burgess & Thompson, 2017).

MR-Egger Regression

• 10.
  Perform an MR-Egger regression to estimate the effect of the exposure on the outcome.

  MR_egger_regression <- lm(outcome_data$beta ~ exposure_data$beta,
  weights=1/IVW_weights)
  

The command summary(MR_egger_regression) displays the effect, standard error, and p-value of the exposure on the outcome. Note that the intercept term here is calculated in the MR-Egger analysis (Bowden et al., 2015; Burgess & Thompson, 2017).

ALTERNATE PROTOCOL 1: Performing Mendelian randomization using the TwoSampleMR package in R.

The TwoSampleMR package in R facilitates conducting two-sample MR analyses by offering access to the large MR-Base repository of GWAS summary statistics and providing easy-to-use software for proper harmonization of datasets, estimating the causal effect using a range of MR methods, conducting sensitivity analyses, and visualizing results (Hemani et al., n.d., 2018).

This protocol and code below was inspired by the TwoSampleMR documentation provided by the MRC Integrative Epidemiology Unit and the MR-Base Collaboration, which can be found on https://mrcieu.github.io/TwoSampleMR/(Hemani et al., n.d., 2018).

Necessary Resources

Hardware

Computer running Linux, Mac OS, or Windows

Software

R package version >= 3.1.0 (Team, 2014) with the following libraries installed: devtools(Wickham, Hester, & Chang, 2018), TwoSampleMR(Hemani et al., n.d., 2018), MRInstruments(Hemani’, n.d.),and tidyverse(Wickham, 2017).

Files

GWAS summary statistics (including SNP, major allele, minor allele, allele frequency, effect size, standard error, p-value, and sample size) for the exposure and outcome of interest OR these files can be obtained by browsing through existing catalogues from the MR Base databases accessible through the MRInstruments package(Hemani’, n.d.). Note that some information that may be missing from your summary statistics file, may be present in the paper referencing the GWAS or may be calculated using the information in the file. Further note that your data can be formatted in the correct manner for use in the TwoSampleMR package by using the function format_data (as described in step #2 of the protocol below)(Hemani et al., n.d., 2018).

The .Rmd file “TwoSampleMR_protocol.Rmd” included in this manuscript will serve as a guide through the protocol below.

Protocol steps—Step annotations

• 1.
  Load the TwoSampleMR package in R (Hemani et al., n.d., 2018). You can install the

  devtools package from CRAN-like repositories with the
  install.packages(“devtools”) command in order to utilize the
  install_github function(Wickham et al., 2018).
  install.packages(“devtools”)
  library(devtools)
  install_github(“MRCIEU/TwoSampleMR”)
  library(TwoSampleMR)
  

• 2.Identify and obtain GWAS summary statistics. You can either obtain your own summary statistics or browse through the MR Base GWAS database(Hemani et al., 2018) (available_outcomes() can show the list of available GWASs).

External summary statistics can be read in and converted to the correct format using format_data. For example, the body mass index (BMI) GWAS summary statistics as shown in Figure 2 can be converted as follows:

• exposure_converted_dataframe <- format_data(exposure_dataset,
  type = “exposure”, snp_col = “SNP”, beta_col = “BETA”, se_col =
  “SE”, effect_allele_col = “Tested_Allele”, other_allele_col =
  “Other_Allele”, eaf_col = “Freq_Tested_Allele_in_HRS”, pval_col =
  “P”, samplesize_col = “N”)
  

The R package MRInstruments contains data sources to search for genetic instruments that can be used for your MR analysis(Hemani’, n.d.). In this demonstration, we use data from the gwas_catalog to search for the instruments from the 2010 GWAS on BMI published in Nature Genetics by Speliotes et al (Speliotes et al., 2010). This data can be searched for and installed as follows:

• devtools::install_github(“MRCIEU/MRInstruments”)
  library(MRInstruments)
  data(gwas_catalog)
  exposure_data <- subset(gwas_catalog, PubmedID == “20935630”)
  

• 3.
  Ensure that your data is presented in the correct input format as required by the package by running the format_data function and perform linkage disequilibrium (LD) clumping to remove any non-independent SNPs.

  exposure_data <- format_data(exposure_data)
  exposure_data <- clump_data(exposure_data)
  

• 4.
  Extract the instrumental SNPs for your outcome of interest. In this example, we are using the 2014 GWAS summary statistics for type 2 diabetes susceptibility as published in Nature Genetics by the DIAbetes Genetics Replication And Meta-analysis (DIAGRAM) consortium (DIAbetes Genetics Replication And Meta-analysis (DIAGRAM) Consortium et al., 2014).

  outcome_data <- extract_outcome_data(
       snps = exposure_data$SNP,
       outcomes = 23
  )
  

• 5.
  Harmonize exposure and outcome datasets to ensure the reference alleles from both datasets match. Prune your harmonized dataset. Here, the exposure and outcome datasets are harmonized (shown in Figure 3) and renamed as dat.

  dat <- harmonise_data(
      exposure_dat = exposure_data,
      outcome_dat = outcome_data
  )
  
  dat <- power.prune(dat)
  

• 6.
  Perform an MR analysis (results shown in Figure 4) and specify the types of method in method_list() of the mr()function.

  results <- mr(dat)
  

  It is conventional to report results from multiple methods. The full list of available MR methods can be identified from mr_method_list().

• 7.
  Conduct sensitivity analyses. Check for heterogeneity and test for directional horizontal pleiotropy.

  mr_heterogeneity(dat)
  mr_pleiotropy_test(dat)
  

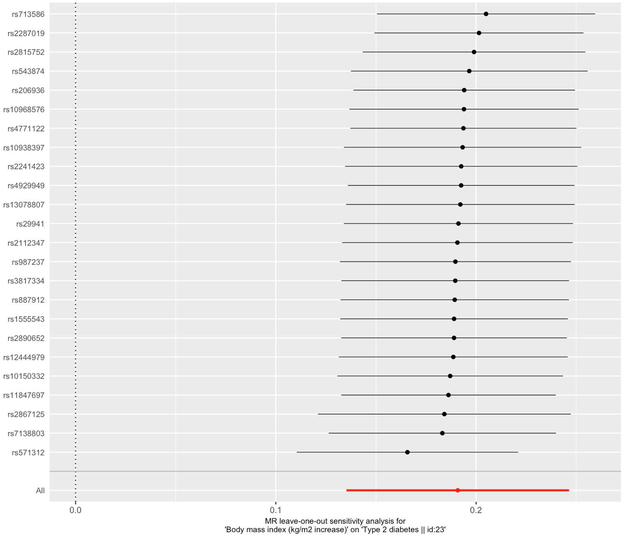
• 8.
  Perform a leave-one-out sensitivity analysis (by sequentially removing each SNP from the MR analysis and running MR) and visualize results from this sensitivity analysis (shown in Figure 5).

  results_leaveoneout <- mr_leaveoneout(dat).
  mr_leaveoneout_plot(results_leaveoneout)
  plot_leaveonout[[1]]
  

• 9.
  Visualize MR results.

  scatter_plot <- mr_scatter_plot(results, dat)
  scatter_plot[[1]]
  

Figure 3.

Shown are the first few rows of the harmonized dataset.

Figure 4.

The causal effects, standard errors, and p-values obtained from the MR analysis using the default methods of MR Egger, weighted median, inverse variance weighted, simple mode, and weighted mode, are shown.

Figure 5.

The results from the leave-one-out sensitivity analyses are shown on the scatterplot. The estimated causal effect is shown for each excluded SNP and the overall estimate using all the SNPs is shown in red. The error bars represent the 95% confidence intervals.

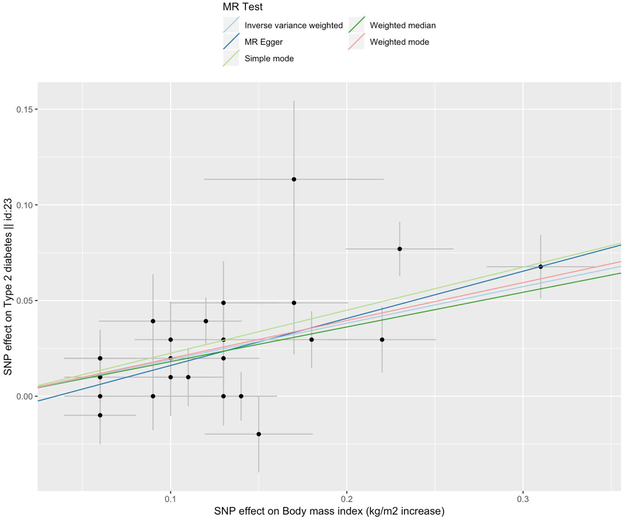
The command mr_scatter_plot(results, dat) creates a scatterplot for each exposure-outcome association (shown in Figure 6). A specification of the method in method_list() visualizes the estimated causal effect according to the specified MR method.

Figure 6.

The scatterplot suggests a positive causal relationship of the SNP effects on BMI against the SNP effects on type 2 diabetes. Each point displayed on the graph represents a single genetic variant. The horizontal and vertical lines extending from each point represent the 95% confidence interval for the genetic associations. The horizontal axis of the graph displays the estimated genetic associations with the exposure (BMI), and the vertical axis displays the estimated genetic associations with the outcome (type 2 diabetes). The color of the lines indicate the type of MR test used (light blue for inverse variance weighted, dark blue for MR Egger, light green for simple mode, dark green for weighted median, and red for weighted mode).

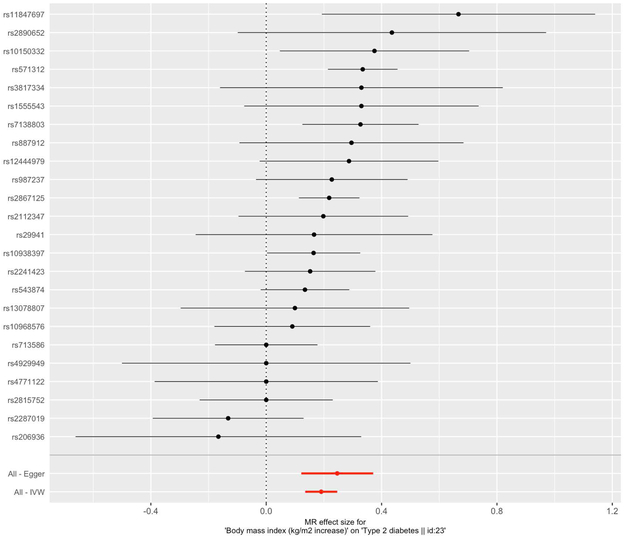
Additionally, a forest plot can be made to compare the MR estimates derived from the different MR methods (shown in Figure 7).

Figure 7.

The forest plot shows the causal estimate using each SNP alone as well as the overall causal estimate using all the SNPs with MR-Egger and IVW. The error bars represent the 95% confidence intervals.

• single_snp_analysis <- mr_singlesnp(dat)
  forest_plot <- mr_forest_plot(single_snp_analysis)
  forest_plot[1]
  

GUIDELINES FOR UNDERSTANDING RESULTS

By leveraging a genetic approach as demonstrated in our example above, we were able to provide evidence in support of a positive causal effect of BMI on type 2 diabetes, which was consistent across all MR methods. We obtained effect sizes of 0.25, 0.18, and 0.19 for MR Egger, weighted median, and inverse variance weighted, respectively, which correspond to the estimated causal effect on type 2 diabetes per unit increase in BMI (kg/m²). In a “leave-one-out” sensitivity analysis, where we sequentially excluded a SNP and performed MR, we observe that the causal estimate remains robust. The forest plot compares the estimated causal effects for all the SNPs as determined by MR-Egger and IVW to the estimated causal effect as determined per each SNP. While the MR-Egger and IVW estimates agree in our demonstrated example, the IVW estimate can substantially differ from the MR-Egger estimate, suggesting the possibility of directional pleiotropy (Burgess & Thompson, 2017). Directional pleiotropy is the phenomena when genetic variants affect multiple traits on different causal pathways, potentially resulting in a violation of the instrumental variable assumptions necessary for conducting an MR analysis (Burgess & Thompson, 2017). In summary, we highlight the utility of MR in assessing causal relationships, while accounting for limitations prone to many conventional observational epidemiological studies.

COMMENTARY

Background Information

The concept of utilizing IVs to examine causal effects was first introduced in econometrics 90 years ago, and applied to disease outcomes in 1986 by Martijn Katan (Thomas & Conti, 2004). In assessing the causal role of low serum cholesterol levels and cancer, Katan explained that the relationship was likely not affected by diet or other confounding factor, but that the relationship can be elucidated by observation of the number of cancer patients who carry the E-2 isoform of the apolipoprotein (ApoE) gene, which is associated with lower serum density lipoprotein than major isoforms E-3 and E-4 (Katan, 1986). Since then, there have been many studies that have attempted to assess causal relationships using MR for a range of exposures and outcomes, including biomarkers (i.e. C reactive protein in association with coronary heart disease (C Reactive Protein Coronary Heart Disease Genetics Collaboration (CCGC) et al., 2011)), clinical traits (i.e. BMI in association with cardiometabolic traits (Holmes, Lange, et al., 2014)), disease phenotypes (i.e. a range of biomarkers in association with coronary heart disease (Bennett & Holmes, 2017)), socioeconomics (i.e. educational attainment in association with coronary heart disease (Tillmann et al., 2017)), behavioral characteristics (i.e., alcohol consumption in association with cardiovascular disease (Holmes, Dale, et al., 2014)), and intrauterine effects on offspring outcomes (D. Lawlor et al., 2017) (i.e., maternal homocysteine levels in association with offspring birthweight (Lee et al., 2013)).Results from these studies attempt to assess causality for a broad range of exposures and have shown feasibility of use of MR to explore promising areas for therapeutic intervention.

For example, an MR study demonstrated that genetic variants in the gene encoding the target of statin therapy, HMG-CoA reductase or HMGCR, is associated with increased risk for type 2 diabetes and related traits such as higher body weight and waist circumference, highlighting a potential pharmacological application of MR(Swerdlow et al., 2015). In another example, MR was used to determine that tobacco smoking may cause a reduced BMI and a higher resting heart rate, but did not find a strong causal association between smoking and adverse blood pressure, serum lipids, and glucose levels(Åsvold et al., 2014). MR promises to be a valuable method for identifying disease risk factors and areas for intervention and can be leveraged to inform public health policy.

Critical Parameters

There are a number of statistical and methodological challenges and limitations to MR that have been discussed at length in other articles (Burgess, 2012; Haycock et al., 2016; VanderWeele, Tchetgen Tchetgen, Cornelis, & Kraft, 2014). Possible limitations include linkage disequilibrium (i.e., when different loci within a population have correlated allelic states(D. A. Lawlor et al., 2008)), population stratification (i.e., when a population can be broken into subpopulations that exhibit different frequencies of genetic variants or disease(D. A. Lawlor et al., 2008)), or pleiotropy (i.e., when a genetic variant is associated with more than one phenotype(D. A. Lawlor et al., 2008)). Challenges may arise from utilizing a weak instrument (F statistic less than 10), or from situations where the core assumptions are violated or weakly satisfied, and even from cases where the core assumptions are satisfied, but an external factor is at play (i.e., canalization) (Zheng et al., 2017). In fact, the development of novel MR approaches and extensions to the conventional methodology to account for these limitations is a rapidly growing field (Bowden, Del Greco M, et al., 2016; Bowden et al., 2017, 2018; van Kippersluis & Rietveld, 2017; Verbanck, Chen, Neale, & Do, 2018).

For a description of potential limitations that may affect interpretation of MR findings and recommended practices in those situations, we recommend referring to Table 2 from a review article by Zheng (Zheng et al., 2017) and Table II from Lawlor (D. A. Lawlor et al., 2008). We also recommend referring to Table 2 from the review article by Burgess for descriptions of various sensitivity analyses and situations where they would be of relevance (Burgess, Bowden, Fall, Ingelsson, & Thompson, 2017).

Significance Statement.

Conventional observational epidemiological studies aimed at assessing the effect of a modifiable exposure on a disease phenotype can be subject to confounding such as reverse causation, where the disease precedes the exposure(Smith & Ebrahim, 2002). A technique termed ‘Mendelian randomization’ (MR) can overcome this limitation by leveraging genetic variants such as single-nucleotide polymorphisms (SNPs) as instrumental variables to estimate exposure-outcome associations (Smith & Ebrahim, 2004). Summary statistics from genome-wide association studies (GWAS) facilitate conducting an MR analysis without the need for costly direct genotyping or obtaining individual-level data (Burgess et al., 2015). We describe here a protocol for assessing exposure-outcome associations in an MR framework using published GWAS summary statistics.