Abstract
Knowledge of the exact tumor location and structures at risk in its vicinity are crucial for neurosurgical interventions. Neuronavigation systems support navigation within the patient's brain, based on preoperative MRI (preMRI). However, increasing tissue deformation during the course of tumor resection reduces navigation accuracy based on preMRI. Intraoperative ultrasound (iUS) is therefore used as real-time intraoperative imaging. Registration of preMRI and iUS remains a challenge due to different or varying contrasts in iUS and preMRI. Here, we present an automatic and efficient segmentation of B-mode US images to support the registration process. The falx cerebri and the tentorium cerebelli were identified as examples for central cerebral structures and their segmentations can serve as guiding frame for multi-modal image registration. Segmentations of the falx and tentorium were performed with an average Dice coefficient of 0.74 and an average Hausdorff distance of 12.2 mm. The subsequent registration incorporates these segmentations and increases accuracy, robustness and speed of the overall registration process compared to purely intensity-based registration. For validation an expert manually located corresponding landmarks. Our approach reduces the initial mean Target Registration Error from 16.9 mm to 3.8 mm using our intensity-based registration and to 2.2 mm with our combined segmentation and registration approach. The intensity-based registration reduced the maximum initial TRE from 19.4 mm to 5.6 mm, with the approach incorporating segmentations this is reduced to 3.0 mm. Mean volumetric intensity-based registration of preMRI and iUS took 40.5 s, including segmentations 12.0 s.
Keywords: IGNS, Image-guided neurosurgery, Intra-operative ultrasound, MRI, Registration, Segmentation
Highlights
-
•
We demonstrate that our segmentation-based registration increases accuracy, robustness, and speed of multi-modal image registration of preoperative MRI and intraoperative ultrasound images for improving intraoperative image guided neurosurgery.
-
•
For this we provide a fast and efficient segmentation of central anatomical structures of the perifalcine region on ultrasound images.
-
•
We demonstrate the advantages of our method by comparing the results of our segmentation-based registration with the initial registration provided by the navigation system and with an intensity-based registration approach.
1. Introduction
In glioma surgery residual tumor has a great impact on the overall survival rate but also on progression-free survival (Coburger et al., 2016; Moiyadi, 2016; Petridis et al., 2015). For the optimal outcome after surgery a balance has to be established between maximization of surgical cytoreduction and minimization of new permanent neurological deficits to preserve and prolong the patient's resulting quality of life (Prada et al., 2016; Renovanz et al., 2014; Yong and Lonser, 2011). Preoperative image data are acquired a few days before surgery. However, the difference between these preoperative scans and the current intraoperative situation, due to brain-shift after craniotomy and tissue deformation, increases with the extent of tumor tissue removal (Prada et al., 2015b; Prada et al., 2015a; Reinertsen et al., 2014). The preoperative MRI (preMRI) data set, usually shown on a separate screen in the operating room for the medical staff, is now merely a rough estimate. For this reason, intraoperative imaging is crucial to maximize the gross-total resection but with greatest accuracy, precision and care of eloquent brain areas. Therefore, intraoperative imaging, such as MRI, have great importance during surgery but are not affordable or available in every neurosurgical department. On the contrary, intraoperative ultrasound (iUS) offers real-time information, it is widely available at relatively low costs, and does not cause radiation (Prada et al., 2015a). Moreover, tumor boundaries are even better distinguishable within iUS, which is an enormous benefit compared to other intraoperative imaging for safe gross-total resection (Moiyadi et al., 2017; Selbekk et al., 2013; Unsgård et al., 2011). However, several factors during resection degrade the quality of iUS. For example, additional structures or tissue boundaries are visible in iUS imaging than in preMRI, which are induced during surgery through creating and extending the resection borders, by filling the resection cavities with saline water, by small air bubbles, and by blood clotting agents. Moreover, this increases reflection that diminishes the general ultrasound penetration depth. All the above-mentioned gravely impedes a solely intensity-based iUS and preMRI registration.
Registration algorithms in this field of ultrasound and MRI fusion can be categorized in non-deformable (Coupe et al., 2012; Prada et al., 2015a; Presles et al., 2014; Schneider et al., 2012) or deformable (Farnia et al., 2015; Laurence et al., 2013; Reinertsen et al., 2014; Rivaz et al., 2015; Rivaz et al., 2014b; Rivaz et al., 2014a; Rivaz and Collins, 2015a, Rivaz and Collins, 2015b) approaches that further split into feature-based and intensity-based methods. Feature-based methods find corresponding points or structures in both modalities and use correspondences to conclude the registration transformation (Modersitzki, 2003). Intensity-based methods rely on similarity measures, methods commonly used are: sum of squared differences (SSD), normalized mutual information (NMI), normalized cross-correlation (NCC), and normalized gradient-field (NGF) measures (Boehler et al., 2011; Modersitzki, 2009; Modersitzki, 2003; Nesch et al., 2001). Proposed solutions in the context of this registration problem are landmark-based methods that register points (Gobbi et al., 2000), lines or tubes, e.g. of vasculature (Bucki et al., 2012; Porter et al., 2001; Reinertsen et al., 2007) or surfaces (King et al., 2000), and methods that attempt to transform and simulate the intensities within preMRI to iUS in order to make both imaging modalities more comparable for a subsequent registration (Kuklisova-Murgasova et al., 2013; Letteboer et al., 2003; Wein et al., 2013). For instance, segmentations are used for this by Arbel et al. (Arbel et al., 2004) and by Mercier et al. (Mercier et al., 2012) who registered preMRI to a probabilistic atlas. The atlas was used to segment the preMRI and they assigned different intensity transformations to different regions within the MRI to create a pseudo-US image. Our proposed combined segmentation and registration approach would fit into this registration category where segmentations are used to transfer additional information to the overall registration process.
Most 2D segmentation methods can be expanded to 3D segmentation approaches. (Mozaffari and Lee, 2018) describe them as being as powerful as 3D methods. For slice-wise US acquisition 2D image segmentation relies on contrast and image resolution, whereas 3D approaches add the supplementary issue of reconstruction quality. This is why we chose 2D image segmentation in order to segment the slice-wise acquired, thin and line-type structures of the falx and tentorium in highest image resolution. (Mozaffari and Lee, 2018) distinguish none of the reviewed segmentation strategies as gold standard or even trend-setting for every purpose in image processing. It is even more emphasized that this is an active field with numerous methods and segmentation strategies that are tailored for each scope of application.
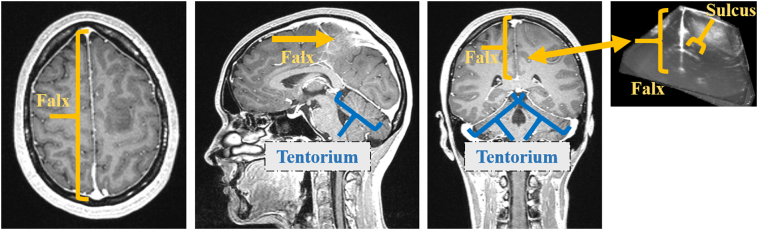
Based on this account, we propose a novel approach that combines automatic segmentations of central anatomical structures that can act as guiding-frame for a subsequent registration approach. The falx cerebri and the tentorium cerebelli as prominent, corresponding, and central anatomical structures of the perifalcine region are just examples of structures fulfilling the above prerequisites as both structures are visible in gadolinium-enhanced T1-weigthed preMRI and in B-mode iUS images (Fig. 1). The segmentations are utilized as additional spatial information for the registration to enable an alignment of selected structures – and, respectively, for masking out possible disruptive structures – for supporting fast, automatic, and robust iUS/preMRI fusion in order to improve real-time image guidance during neurosurgery.
Fig. 1.
Anatomical structures of falx cerebri, tentorium cerebelli, and adjacent gyri (sg. gyrus) and sulci (sg. sulcus) in MRI and US imaging. This figure also gives an impression about the central position and thinness of these anatomical structures.
This paper has two main contributions. First, we propose a 2D region-based segmentation method in order to segment the acquired iUS scans slice-wise and a Random Forest classifier is used to classify the candidate regions. To our best knowledge our paper publishes the first iUS segmentation approach applicable within the process of glioma surgery in order to increase registration accuracy, speed, and robustness of preMRI and iUS images for improving intraoperative image guided therapy (IGT).
The second contribution of this paper is the introduction of an initial registration approach which demonstrates how valuable an incorporation of segmentations is in reducing the overall computation time and in increasing registration accuracy.
2. Material and methods
2.1. Data sets used for preMRI and iUS image fusion
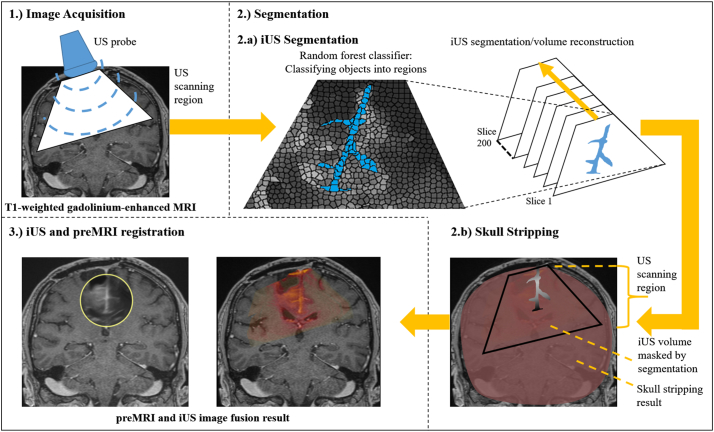
For this work we acquired corresponding preMRI and iUS images from 11 patients with low-grade and high-grade gliomas who underwent tumor resection in the neurosurgical department at Essen University Hospital. Each patient had at least one T1-weighted gadolinium-enhanced preMRI for surgical planning acquired a few days before tumor surgery. In Fig. 2. an overview of our entire method for preMRI and iUS image fusion is given. Navigated and tracked freehand B-mode iUS sweeps were made in a parallel, non-fan-like manner, before tumor resection. The iUS scans were acquired using an US system (Alpha 10, Hitachi Aloka Medical, Japan) connected to a neuronavigation system (Curve, Brainlab AG, Munich, Germany) via a video cable. We used a micro-convex multifrequency probe with a mean frequency of 7.5 MHz and a fixed penetration depth for all patients of 8 cm. For navigated freehand US acquisition an adapter was mounted onto the US probe for optical tracking. The navigation system saved 200 2D B-mode US images (slices) per sweep together with their tracking information. The slices were reconstructed to a 3D volume for volumetric preMRI and iUS image registration, but the original 2D slices were used for iUS image segmentation.
Fig. 2.
Overview of the entire segmentation and registration method for preMRI and iUS image fusion. Basically, the method consists of three steps: 1.) Image Acquisition (see Chapter 2.1): Acquisition of preoperative T1-weighted gadolinium-enhanced MRI and intraoperative B-mode ultrasound images. The iUS images are acquired freehand with a micro-convex US probe. 2.) Segmentation: 2.a) iUS segmentation (see Chapter 2.2): The falx cerebri and the tentorium cerebelli with their adjacent gyri and sulci are segmented slice-wise in 2D before the segmentation results are reconstructed to a 3D volume. Each US volume consists of 200 slices. For iUS segmentation an object-based image analysis approach is used that classifies objects into regions; 2.b) Skull stripping (see Chapter 2.3): The brain segmentation is essentially used to reduce complexity within the registration task in order to speed-up the computation and to prevent erroneous registrations. The skull stripping could be done prior to surgical intervention to avoid adding intraoperative computation time. 3.) iUS and preMRI registration (see Chapter 2.4): The masked preMRI brain image and the corresponding reconstructed iUS volume masked with the falx, tentorium, and adjacent gyri segmentations are used for registration in order to solely employ these anatomical structures for an initial alignment of both modalities.
Our registration approach incorporates segmentations of the falx cerebri and the tentorium cerebelli. Additionally, for further reduction of the computation time needed for multi-modal image registration, a skull stripping is performed on the preMRI. In the following the aforementioned segmentation algorithms for preMRI and iUS image segmentation are described separately, before we introduce our segmentation-based registration approach.
2.2. Automatic segmentation of Falx Cerebri and Tentorium cerebelli with adjacent gyri and sulci
As central anatomical structures within the perifalcine region of the brain the falx cerebri and the tentorium cerebelli are almost always visible within the operative field or at least visible in part. The falx is a thin meningeal fold of the dura mater that separates the hemispheres. The tentorium is an arched, meningeal fold that is partly connected to the falx, separating the cerebrum from the cerebellum. Therefore, segmentations of these structures are chosen for our approach to support the proposed multi-modal image registration. To add supplemental spatial image information to the otherwise line-type falx and tentorium segmentations, these structures are also segmented together with adjacent sulci and gyri (see Fig. 1).
In T1-weighted gadolinium-enhanced MRI the falx and tentorium are filled with contrast agent and are highlighted with high intensities. Fig. 1 shows the falx and the tentorium in both modalities. In the subsequent section the falx and tentorium segmentation algorithm for B-mode iUS is described.
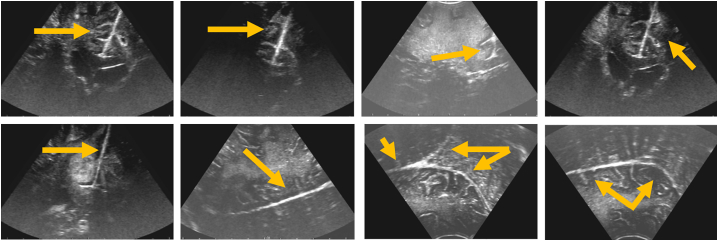
As mentioned above, the input data for our segmentation method are freehand and tracked series of 2D US scans which are segmented slice-wise. The delicate anatomical structures of the falx, tentorium, and their adjacent sulci and gyri are segmented in 2D in order to provide a segmentation within images of maximal resolution and quality which would be reduced by a previously applied reconstruction. For each patient US scans with 200 slices are acquired and subsequently segmented prior to volume reconstruction. The image extent of each slice is 531 × 376 pixels. Basically, the method described here is an object-based image analysis approach that classifies candidate regions within the US image series (Homeyer et al., 2010). Compared to pixel-based classification it is advantageous that a region-based approach offers more expressive features describing the specific target structures or objects within the image. Especially if differences between target objects and background are subtle – as they are for falx, tentorium, sulci, and gyri –it is important to define sufficiently specific features to characterize the target objects. This is the reason why we chose the object-based image analysis approach because the target structures here appear line-like for the human eye but are in fact discontinuous lines with enormous changes in their intensity along their extent even within the same iUS slice. Classic segmentation algorithms rely on homogeneous regions within and/or similar strong edges around the target structure. Both of these criteria are not given in this particular segmentation task. The object-based image analysis approach is a powerful method to locate different, discontinuous regions of the target structure within an over-segmented image. Accordingly, the region-based segmentation requires a good initial over-segmentation of the whole image that captures the boundaries of the target structures. To facilitate a good initial clustering of image regions the US image slices are preprocessed with two subsequently applied stick filters by adopting (Nitsch et al., 2015). The stick filters sustain and strengthen line-type structures, while smoothing homogeneous regions and reducing characteristic speckles in US images. The falx and the tentorium may be scanned from different angles but the line-type character remains still present. Fig. 3 shows the falx and the tentorium and their different representation in iUS images.
Fig. 3.
Falx and Tentorium in iUS images showing their different representation as line-type structures scanned from different angles by the US probe.
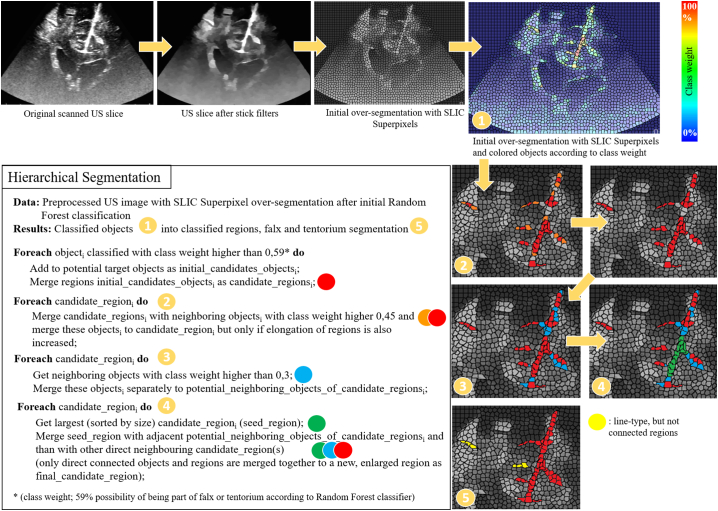
In order to generate the over-segmentation, watersheds – as suggested by Schwier et al. (Schwier et al., 2013) – and the SLIC Superpixel (Achanta et al., 2012) approach are tested and compared, resulting in the conclusion that the SLIC Superpixel approach provides a more precise and robust parcellation of target objects of the falx, tentorium, gyri, sulci, and their boundaries. An example of an initial over-segmented US image can be seen in Fig. 4. For the classification process a Random Forest classifier with 25 trees is used to classify the candidate regions. The classifier is trained with 686 positive samples and 824 negative samples from characteristic iUS slices of patient 1 that were excluded from the test data set. The training samples were selected manually by a human expert in order to guarantee that different examples with changing intensities as well as different perspectives of the target structures are covered by the training data. The scanned iUS volume of patient 1 was especially acquired as training data set to fit these criteria and almost every slice within the US sweep represents an example of falx and tentorium with adjacent gyri and sulci. In the first step of the segmentation algorithm, all objects generated by the initial over-segmentation are classified. Hereafter, the region-based features are listed that are used for initial classification of these objects as originally proposed by Schwier et al. (Schwier et al., 2013): Intensity-based features (lower and upper quartile, mean, median, minimum, maximum, standard deviation), shape-based features (size, eccentricity, elongation, circularity), and direct neighbor relation features (connectivity to other objects and their features). In addition to those, a subsequent classification process is applied that uses the initial classification result as basis to further analyze the connectivity of objects classified as potential candidate objects of the structures to be segmented and takes their neighbor relations to further analyze their probability of being part of the falx and tentorium in order to generate a more precise characterization of the overall anatomical structures of falx, tentorium, and their adjacent gyri and sulci. This hierarchical segmentation approach first classifies objects and then merges objects into regions and is described in pseudo code and visualized in Fig. 4.
Fig. 4.
Pseudo code of the hierarchical classification and segmentation process. The segmentation approach first classifies objects and then objects into regions.
2.3. Skull stripping of MRI as preprocessing prior registration
To prevent initial fitting to prominent pressure artifact or other artifacts of the US probe in iUS images onto the skull or brain surface in gadolinium-enhanced preMRI and in order to reduce the total computation time, a skull stripping is performed on the head and neck scans of the 11 patients prior to registration. A profound review of methods on skull stripping on non-contrast-enhanced images is given by Kalavathi et al. in (Kalavathi and Prasath, 2016) in which methods are distinguished in five different categories: mathematical morphology-based, intensity-based, deformable surface-based, atlas-based, and hybrid methods. Kleesiek et al. (Kleesiek et al., 2016) used Convolutional Neural Networks (CNNs) trained for skull stripping of 53 patient data sets consisting of T1-weighted images with and without contrast agent, T2-weighted and FLAIR images. For our field of application of image guidance during glioma surgery, contrast-enhanced T1-weighted images are used as basic preMRI for navigation and were acquired a couple of days prior to surgery for planning and intraoperative image guidance. These contrast-enhanced images come with additional difficulties such as varying uptakes of contrast agents due to different time points the MRI scan was performed after exposition to the contrast agent and also varying contrast uptakes of pathological brain tissues, creating patient specific-boundaries within the brain to be skull-stripped.
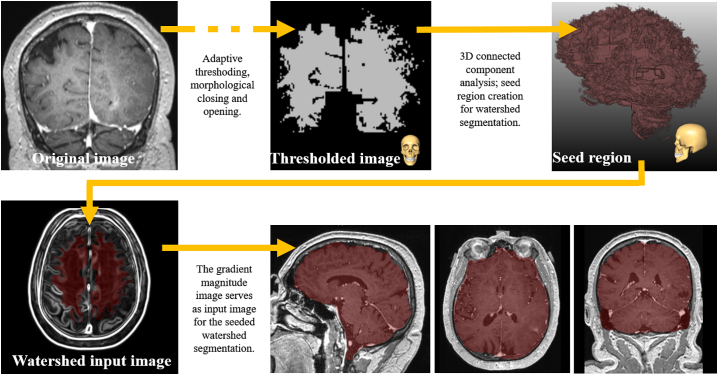
According to Kalavathi et al. (Kalavathi and Prasath, 2016) the proposed segmentation method for brain extraction can basically be categorized as a hybrid method using mathematical morphology-based as well as intensity-based segmentation methods. As initial step a non-parametric method for automatic correction of intensity non-uniformity is used as described by Sled et al. (Sled et al., 1998). Afterwards, a threshold is applied that focuses on filtering out lower intensities such as the cerebrospinal fluid and partly gray matter in order to increase the immediate gap between the center of the brain and the skull. Subsequently, a morphological opening is employed that separates the thresholded image roughly in two different components: Brain and skull/neck. Successionally, a 3D connected components analysis is performed using a 3D-18-neighborhood. Simultaneously, the center of gravity is calculated and the component that is closest to it is taken as a rough estimate of an initial coarse brain segmentation. The previously mentioned threshold, that roughly separates the brain from the skull and neck, is adaptive, increasing continuously, starting from the experimentally determined value of 200 with a step size of 10 as long as there are less than two components after connected component analysis. The non-uniformity intensity corrected image is then smoothed with a 3D Gauss smoothing using a sigma of 1 voxel on which the gradient magnitude is calculated with identical sigma before it serves as input image for a seeded watershed transformation. The applied watershed transformation method was proposed by Hahn et al. (Hahn and Peitgen, 2000). In our case, the previously attained, jagged segmentation of the brain serves as seed region. Remaining gaps within the brain mask are removed after watershed segmentation and are shut by morphological closing with a kernel of 3 × 3 × 3. Finally, a rolling ball closing with a radius of 5 mm is applied to remove residual holes and to smooth the overall surface of the segmented brain. Fig. 5. shows the main image processing steps of the skull stripping approach.
Fig. 5.
Shows the main image processing steps within the outlined skull stripping approach. At the end of the processing pipeline the resulting brain mask of patient 4 is shown and overlayed on the original preMRI in sagittal, axial, and coronal view.
2.4. Registration of iUS with preMRI
Before both imaging modalities can be registered, the iUS scans of 200 slices per patient and the corresponding 2D segmentations must be reconstructed into a 3D volume. The reconstructed volumes are attained through accumulating the scanned or segmented 2D slices/volumes. Besides trilinear interpolation, intersecting volumes are combined by means of weighted averaging. For multi-modal image fusion we used the MERIT registration framework (Boehler et al., 2011). As a preprocessing step, the original gadolinium-enhanced T1-weighted image is resampled with a Lanczos filter to an isotropic voxel size of 1 mm. The corresponding reconstructed iUS volume is masked with the falx, tentorium and adjacent gyri segmentations to solely use these anatomical structures for an initial alignment of both imaging modalities. Simultaneously, the head scan is masked by its skull stripping segmentation result to reduce the image content and computations needed for registration. Prior to registration all images masked by segmentations are resampled to the same isotropic voxel size of 1 mm. The MERIT framework includes multiple significantly different image similarity measures. For our purpose we used the local cross-correlation (LCC) similarity measure that evaluates the local cross-correlation in a local window of 3 × 3 × 3 around each voxel. LCC is robust to non-linear intensity relations which proved advantageous for our rigid iUS and preMRI registrations and has similar properties as the Normalized Mutual Information (NMI) similarity measure which is considered a standard similarity measure for robust multi-modal image registration. Furthermore, we used a multi-level registration approach consisting of three levels which allows a downscaling of the image to be registered with the following scaling factors 0.632, 0.63 and 1. This allows the deformed image to be registered from coarse to finer resolutions.
2.5. Evaluation methods for segmentation and registration results
In this section we shortly describe the methods for quality measurement of the segmentation and registration results that are applied in the following results chapter.
2.5.1. Evaluation of segmentation results
The employed similarity criteria are here briefly described that are used to measure the quality of our results. The Dice coefficient and the Hausdorff distance are established and commonly used methods for the evaluation of 2D and 3D segmentation results. The two methods provide numerical values that allow both a comparison of different segmentation results as well as an immediate assessment of the achieved quality of the segmentation at hand in regard to a reference segmentation. The following formula determines the calculation of the Dice coefficient, where P and Q represent the sets of pixels or voxels of two compared segmentation masks:
According to the formula the Dice coefficient represents the size of the union of two sets divided by the average size of the two sets. The coefficient is a value between 0 and 1, where a value of 0 indicates no overlap of the sets of two compared segmentation masks and a value of 1 indicates an exact match between two sets.
The Hausdorff distance quantifies the maximum distance between two 2D or 3D segmentations and allows a comparison of contours or surfaces of the segmented objects. Subsequently, the formula defines the Hausdorff distance, where S and T are the two different sets of pixels or voxels of the compared segmentations:
The maximum distance dmax is defined as:
According to the previously given formula the maximum calculated distance is not symmetric, because the following applies:
The Hausdorff distance is a symmetric measurement of both distances by considering the maximum of both distances. The Hausdorff is measured in mm and should be as small as possible by measuring the distance between a segmentation result and the corresponding reference masks of an expert or other gold standard.
2.5.2. Evaluation of the iUS and preMRI registration
In order to quantitatively measure the performance of our registration approach in comparison with the initial registration provided by the navigation system and a solely intensity-based registration, we use the commonly applied mean target registration error (mTRE) as metric. The mTRE measures the average distance between landmarks x (here: landmarks within the iUS that represent the ground truth landmarks) and x′ (here: landmarks after multi-modal image registration within the deformed preMRI). The mTRE can be computed as follows for a number of landmarks n:
3. Results
In the following we evaluate the previously described segmentation methods of the falx cerebri, the tentorium cerebelli, and adjacent gyri and sulci in 2D B-mode US images and the skull stripping method on gadolinium-enhanced T1-weighted preMRI. To assess the quality of the segmentation, we use standard quality measurements by means of the Dice coefficient and Hausdorff distance. Furthermore, we analyze our implemented registration approach for multi-modal image fusion of iUS and preMRI with distance measurements to landmarks placed by a human expert. We evaluate our registration results by comparing the initial registration from the navigation system with a solely intensity-based registration and with our segmentation-based registration approach that incorporates the prior attained segmentation results. An overview of the whole segmentation and registration approach is given in Fig. 2.
3.1. Evaluation of segmentation results
In this chapter we first evaluate the segmentation results before we measure the quality of preMRI and iUS iamage fusion.
3.1.1. Evaluation of segmentations in 2D B-mode US images
Table I shows the 2D segmentation results of the 11 patients for segmenting the falx cerebri and the tentorium cerebelli in B-mode US images which is illustrated in Fig. 4. The automatic segmentation results are compared to reference segmentations attained by segmenting the falx and the tentorium manually by an expert in 2D B-mode US slices. Consequently, the segmentations are also evaluated slice-wise. Average Dice coefficient and Hausdorff distances per US scan (set of 200 slices) or patient, respectively, are shown in Table I. The proposed method achieved an average Dice coefficient of 0.74 and an average Hausdorff distance of 12.2 mm over all 11 patients with an average computation time of 79 s for processing 200 US slices.
Table I.
Automatic falx cerebri and tentorium cerebelli segmentation of 2D B-mode US images.
| Patient | Dice coefficient | Hausdorff Distance (mm) | Computation time (s) |
|---|---|---|---|
| 1 | 0.89 | 6.3 | 103 |
| 2 | 0.69 | 15.9 | 88 |
| 3 | 0.67 | 12.0 | 84 |
| 4 | 0.88 | 7.3 | 96 |
| 5 | 0.86 | 7.8 | 93 |
| 6 | 0.72 | 14.2 | 70 |
| 7 | 0.65 | 15.9 | 75 |
| 8 | 0.63 | 16.0 | 62 |
| 9 | 0.65 | 15.2 | 58 |
| 10 | 0.73 | 13.0 | 65 |
| 11 | 0.77 | 11.1 | 78 |
| Mean | 0.74 | 12.2 | 79 |
Segmentation results of the implemented automatic 2D segmentation approach for falx cerebri and tentorium cerebelli segmentation.
3.1.2. Evaluation of the automatic skull stripping for gadolinium-enhanced T1-weighted MRI
Furthermore, we evaluated our skull stripping method (Fig. 5) and compared it to a reference segmentation by an expert. The subsequent Table II gives an overview of the segmentation results and the computation times for each patient. We focused our segmentation approach on a balance between speed and accuracy. A manual correction can be done as post-processing step in which the resulting mask is interpolated between two indicated corrections. Corrections are only necessary if the segmentation is not accurate enough in the required region where the acquisition of B-mode US scans is planned during the intervention. Automatic and manual correction times are also displayed in Table II. The skull stripping method attained an average Dice coefficient of 0.82 and an average Hausdorff distance of 33.8 mm with an average computation time of 106 s.
Table II.
Automatic skull stripping of gadolinium-enhanced T1-weighted MRI images.
| Patient | Dice coefficient | Hausdorff distance (mm) | Computation time (s) | correction (s) |
|---|---|---|---|---|
| 1 | 0.86 | 28.4 | 112 | * |
| 2 | 0.79 | 33.8 | 100 | 118 |
| 3 | 0.72 | 54.9 | 104 | 45 |
| 4 | 0.82 | 32.9 | 92 | * |
| 5 | 0.84 | 25.1 | 118 | * |
| 6 | 0.82 | 48.2 | 110 | 58 |
| 7 | 0.83 | 19.7 | 90 | 11 |
| 8 | 0.83 | 27.9 | 124 | * |
| 9 | 0.84 | 34.8 | 108 | 67 |
| 10 | 0.87 | 38.6 | 113 | * |
| 11 | 0.83 | 27.7 | 99 | * |
| Mean | 0.82 | 33.8 | 106 |
Segmentation results of the automatic 3D skull stripping method for gadolinium-enhanced T1-weighted MRI. * Indicates that no manual correction was needed.
3.2. Evaluation of the iUS and preMRI registration
Results of the different registrations methods are compared in Table III. For each patient ten to twelve corresponding landmarks between iUS and preMRI were defined by an expert. Moreover, we compare the computation time of the purely intensity-based method and the registration using the prior attained segmentations of the falx cerebri and the tentorium cerebelli in US images and the skull stripping from preMRI. An overview is given in Table IV. Registration results for iUS and preMRI image fusion are illustrated in Fig. 6. All segmentations and registrations are performed on an Intel Core i7 PC with 2.60 GHz and a 16 GB RAM.
Table III.
mTRE values with initial registration, Intensity-based Registration, and with Registration incorporating segmentations.
| Patient | Initial registration | Intensity-based registration | Registration with Segmentations |
|---|---|---|---|
| 1 | 10.3(9.6–11.2) | 3.3(2.5–5.6) | 2.3(1.9–3.1) |
| 2 | 5.8(3.0–8.0) | 3.0(2.0–4.3) | 1.7(1.0–2.3) |
| 3 | 4.8(2.7–5.6) | 3.2(2.3–4.0) | 2.0(1.6–2.6) |
| 4 | 6.2(4.0–8.3) | 5.9(3.8–7.6) | 3.2(2.2–4.3) |
| 5 | 16.1(11.8–19.9) | 3.0(2.4–4.3) | 2.1(1.8–2.8) |
| 6 | 24.3(22.0–25.7) | 3.7(2.1–5.6) | 2.1(1.7–2.7) |
| 7 | 10.5 (7.9–13.1) | 3.6(2.6–5.5) | 2.0(0.9–2.5) |
| 8 | 31.1(30.1–34.0) | 4.5(2.3–6.3) | 2.2(0.9–3.0) |
| 9 | 22.8(19.2–28.2) | 3.0(1.3–4.8) | 1.5(0.5–2.6) |
| 10 | 36.1(31.9–40.1) | 5.7(4.2–7.5) | 3.1(2.0–4.3) |
| 11 | 17.6(15.9–19.3) | 3.6(1.7–5.7) | 2.2(1.3–3.2) |
| Mean | 16.9(14.4–19.4) | 3.9(2.5–5.6) | 2.2(1.5–3.0) |
Overview of registration results of the proposed registration approach. For each patient ten to twelve landmarks were used to evaluate the registration accuracy. Within the brackets the lowest and the highest landmark distances within each patient are displayed.
Table IV.
Computation time for intensity-based registration and registration approach incorporating segmentations.
| Patient | Intensity-based registration | Registration with Segmentations |
|---|---|---|
| 1 | 32 | 9 |
| 2 | 31 | 9 |
| 3 | 45 | 19 |
| 4 | 30 | 7 |
| 5 | 28 | 11 |
| 6 | 30 | 12 |
| 7 | 84 | 20 |
| 8 | 30 | 13 |
| 9 | 45 | 15 |
| 10 | 48 | 8 |
| 11 | 42 | 9 |
| Mean | 41 | 12 |
Comparison of computation time (s) needed in order to compute the registrations.
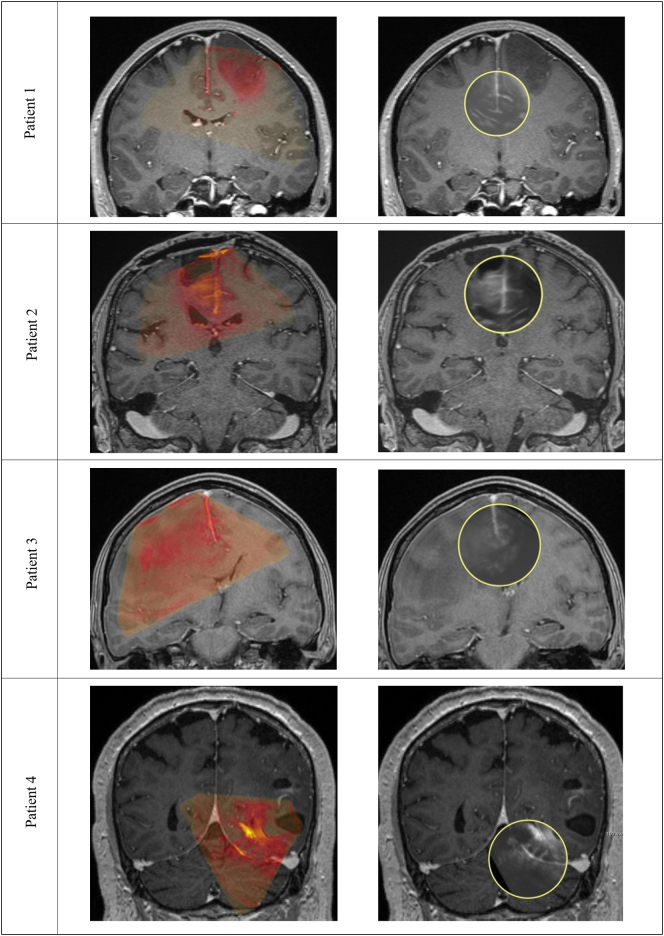
Fig. 6.
Registration results represented in a coronal view with a colored overlay (preMRI in red; iUS in green) within the left column. Furthermore, an additional view for image fusion is proposed within the right column of images. Here the clinical staff can move the lens over the region of interest in order to inspect the registration result and image fusion. Patient 1 and patient 3 show average registration results with a mTRE of 2.3(1.9–3.1) and a mTRE of 2.0(1.6–2.6). Patient 4 shows the registration with highest mTRE of 3.2(2.2–4.3) which is due to immediate tissue deformation during the iUS scan after dura opening. This causes initial deformations the here presented non-deformable registration approach cannot compensate. Patient 2 shows one of the best alignments of iUS and preMRI with a mTRE of 1.7(1.0–2.3).
3.3. Evaluation of inter-observer variability of Falx and Tentorium reference segmentations
Moreover, we analyzed the inter-observer variability of the combined falx, tentorium, sulci, and gyri reference segmentations in iUS images. For this we compared the reference segmentations from three different experts and used the Dice coefficient to access similarities. We included this comparison in our evaluation in order to spotlight how complex the segmentation task is even for human experts for these central anatomical structures within iUS images. The Dice coefficient in Table V is calculated between our segmentation result and the three different references. In Table VI the Dice coefficient is computed between the references of Expert 1 and Expert 2 as well as between Expert 1 and Expert 3 in order to determine the resemblance of the expert's segmentations.
Table V.
Inter-observer variability (dice coefficients).
| Patient | Expert 1 | Expert 2 | Expert 3 |
|---|---|---|---|
| 1 | 0.89 | 0.92 | 0.79 |
| 2 | 0.69 | 0.73 | 0.58 |
| 3 | 0.67 | 0.57 | 0.45 |
| 4 | 0.88 | 0.82 | 0.76 |
| 5 | 0.86 | 0.72 | 0.60 |
| 6 | 0.72 | 0.53 | 0.48 |
| 7 | 0.65 | 0.66 | 0.38 |
| 8 | 0.63 | 0.71 | 0.43 |
| 9 | 0.65 | 0.70 | 0.52 |
| 10 | 0.73 | 0.69 | 0.47 |
| 11 | 0.77 | 0.74 | 0.55 |
| Mean | 0.74 | 0.71 | 0.55 |
Inter-Observer variability of the falx cerebri and tentorium cerebelli using three different expert's segmentations to evaluate our iUS segmentation approach. Results are compared using the Dice coefficient. Segmentations from Expert 1 were used to assess the quality of the here proposed perifalcine region segmentation, see Table I for comparison.
Table VI.
Inter-observer variability (dice coefficients).
| Patient | Expert 1 compared to Expert 2 | Expert 1 compared to Expert 3 |
|---|---|---|
| 1 | 0.93 | 0.70 |
| 2 | 0.84 | 0.42 |
| 3 | 0.96 | 0.53 |
| 4 | 0.82 | 0.75 |
| 5 | 0.78 | 0.65 |
| 6 | 0.72 | 0.44 |
| 7 | 0.83 | 0.31 |
| 8 | 0.85 | 0.41 |
| 9 | 0.74 | 0.49 |
| 10 | 0.72 | 0.45 |
| 11 | 0.94 | 0.54 |
| Mean | 0.83 | 0.52 |
Inter-Observer variability in comparison to the chosen reference of Expert 1. The Dice coefficient represent the difference of the chosen reference to Expert 2 and 3.
4. Discussion
In general, the automatic segmentation of the perifalcine region is especially challenging due to the variance of tumor locations and neighboring anatomical structures, size, and image representation that correlates with the number of tumor patients. Nevertheless, we proposed two segmentation methods that are used to support multi-modal image registration of preMRI and iUS images and showed that we can reduce the overall computation time needed for registration from 40.53 s to 18.38 s. One could argue that the computation time for the segmentation of the scanned iUS images with on average 79 s must be added to the 18.38 s but the slice-wise segmentation can be performed in parallel to the volume reconstruction process of the 2D US images, which is essentially needed to register the scanned iUS volume to the corresponding region within the preMRI volume. In our case, no additional computation time is needed to perform the segmentations that would prolong the overall registration process. The automatic skull stripping could be accomplished during surgical planning prior to surgery. The overall methods achieved an average Dice score of 0.82, which leaves some areas (especially in regions adjacent to the eyes and areas nearing the brain stem and spinal cord) within the brain segmented incorrectly. However, in half of our 11 cases no manual correction was needed because the segmentation errors are not in the same brain region as the iUS scans are expected later during the neurosurgical intervention and these errors could be neglected.
The segmentation of the iUS images revealed another important issue that seriously influenced our evaluation and the here represented results: The inter-observer variability of the slice-wise segmentations of the perifalcine region. All experts have more than 10 years' experience in image analysis of cerebral structures. In Table V and in Table VI the variabilities can be seen between the three different experts. The experts discussed their segmentation strategy before each of them generated reference segmentations in order to find rules to which extent they would segment the structures of the perifalcine region. Expert 3 tends to segment more volume of the target structures than Expert 1 and 2 which includes regions Expert 1 and 2 were uncertain of belonging to the target structures. A slightly better correlation between the segmentations of Expert 1 and 2 can be observed. It can be seen that the results may differ based on which reference is used. To evaluate our segmentation results we used solely the references from Expert 1 who segmented the target structures more reproducibly than the other experts, which can be observed by inspecting segmentations of adjacent slices within the overall scanned iUS volume. Finding merging criteria to generate a ground truth from all three experts was discussed but it would lead to inconsistencies in how the structures would be segmented from slice to slice. This would lead to further conflicts in training the machine learning algorithm how to segment the structures of interest. According to the presented variabilities between the expert segmentations, the overall segmentation results of the perifalcine region with a Dice coefficient of 0.74 and an average Hausdorff distance of 12.2 mm is a reasonable and acceptable segmentation result.
The segmentation of patient 1 is evaluated as the best segmentation result which is due to the fact that the training slices are drawn from this patient data set by using iUS data sets from during and after surgery in order to train the Random Forest classifier. With our proposed approach we show a significant benefit by integrating segmentations into the registration process. The solely intensity-based registration decreases the mTRE comparing the initial registration from 16.9 mm to 3.9 mm which is further reduced by the segmentation-based registration to 2.2 mm. The maximum initial mTRE is reduced from 19.4 mm to 5.6 mm by the intensity-based registration and further decreased to 3.0 mm by the segmentation-based registration. In Fig. 6 characteristic registration results of the segmentation-based registration are shown. Nonetheless, the mTREs of the proposed registration may seem high with 2.2 mm on average to the ground truth landmarks. But this is due to the fact that the ground truth registration is deformable whereas the here proposed algorithms for registration used a non-deformable registration approach to initially demonstrate the usefulness of segmentations within the registration process of this use case in glioma surgery.
5. Conclusions
IUS is an imaging modality of low cost and usually already present in many neurosurgical units, iUS holds great potential in improving intra-operative image guidance and would improve considerably the quality of treatments of a large number of patients, i.e. higher survival rate or improved patient's quality of life. Being able to calculate the correct brain shift and tissue deformation from iUS and transferring this deformation to preMRI will support additional surgery planning. For instance, the deformation could also be applied to preoperative fMRI or DTI sequences and the shift of structures at risk within the operative field could be displayed on a screen within the operating room during glioma surgery.
The here described approach showed to increase robustness, accuracy, and speed of the registration process. It is demonstrated that the proposed segmentation-based registration can serve as initial registration right after craniotomy and before dura opening. The proposed approach could be used for further refinements with additional affine registrations to adapt and update the preMRI to local deformations within the operational field during the process of glioma resection.
Declarations of interest
None
Acknowledgements
We wish to thank Brainlab AG, Munich, Germany, especially Uli Mezger, for the support of our project concerning data export and technical matters. Likewise, we would like to thank Bernadette Kleist from Department of Neurosurgery, University Hospital Essen for her valuable support of our study. This work is part of a research project supported by the Wilhelm Sander-Stiftung (grant no. 2013.109.1). Moreover, Prof. Dr. Kikinis is supported by the following National Institutes of Health (NIH) grants: P41 EB015902 Neuroimage Analysis Center, P41 EB015898 National Center for Image-Guided Therapy, U24 CA180918 Quantitative Image Informatics for Cancer Research.
References
- Achanta R., Shaji A., Smith K., Lucchi A., Fua P., Süsstrunk S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012;34(11):2274–2282. doi: 10.1109/TPAMI.2012.120. [DOI] [PubMed] [Google Scholar]
- Arbel T., Morandi X., Comeau R., Collins D. Automatic non-linear MRI-ultrasound registration for the correction of intra-operative brain deformations. Computer Aided Surgery. 2004;9(4):123–136. doi: 10.3109/10929080500079248. [DOI] [PubMed] [Google Scholar]
- Boehler T., van Straaten D., Wirtz S., Peitgen H.-O. A robust and extendible framework for medical image registration focused on rapid clinical application deployment. Comput. Biol. Med. 2011;41(6):340–349. doi: 10.1016/j.compbiomed.2011.03.011. [DOI] [PubMed] [Google Scholar]
- Bucki M., Palombi O., Bailet M., Payan Y. Doppler ultrasound driven biomechanical model of the brain for intraoperative brain-shift compensation: A proof of concept in clinical conditions. In: Payan Y., editor. Soft Tissue Biomechanical Modeling for Computer Assisted Surgery. Springer Berlin Heidelberg; Berlin, Heidelberg: 2012. pp. 135–165. [Google Scholar]
- Coburger J., Merkel A., Scherer M., Schwartz F., Gessler F., Roder C., Pala A., König R., Bullinger L., Nagel G., Jungk C., Bisdas S., Nabavi A., Ganslandt O., Seifert V., Tatagiba M., Senft C., Mehdorn M., Unterberg A.W., Rössler K., Wirtz C.R. Low-grade glioma surgery in intraoperative magnetic resonance imaging: results of a multicenter retrospective assessment of the German study Group for Intraoperative Magnetic Resonance Imaging. Neurosurgery. 2016;78(6):775–786. doi: 10.1227/NEU.0000000000001081. [DOI] [PubMed] [Google Scholar]
- Coupe P., Hellier P., Morandi X., Barillot C. 3D rigid registration of intraoperative ultrasound and preoperative MR brain images based on Hyperechogenic structures. Int. J. Biomed. Imaging. 2012;2012 doi: 10.1155/2012/531319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farnia P., Ahmadian A., Shabanian T., Serej N.D., Alirezaie J. Brain-shift compensation by non-rigid registration of intra-operative ultrasound images with preoperative MR images based on residual complexity. Int. J. Comput. Assist. Radiol. Surg. 2015;10(5):555–562. doi: 10.1007/s11548-014-1098-5. [DOI] [PubMed] [Google Scholar]
- Gobbi D.G., Comeau R.M., Peters T.M. Ultrasound/MRI overlay with image warping for neurosurgery. In: Delp S., DiGioia A.M., Jaramaz B., editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2000. Proceedings. Springer; Berlin, London: 2000. pp. 106–114. [Google Scholar]
- Hahn H.K., Peitgen H.-O. The skull stripping problem in MRI solved by a single 3D watershed transform. In: Delp S., DiGioia A.M., Jaramaz B., editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2000. Proceedings. Springer; Berlin, London: 2000. pp. 134–143. [Google Scholar]
- Homeyer A., Schwier M., Hahn H.K. Proceedings of the International Conference on Computer Vision Theory and Applications. Vol. 2. 2010. A generic concept for object-based image analysis; pp. 530–533. [Google Scholar]
- Kalavathi P., Prasath V.B.S. Methods on skull stripping of MRI head scan images-a review. J. Digit. Imaging. 2016;29(3):365–379. doi: 10.1007/s10278-015-9847-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King A.P., Blackall J.M., Penney G.P., Edwards P.J., Hill D.L.G., Hawkes D.J. Bayesian estimation of intra-operative deformation for image-guided surgery using 3-D ultrasound. In: Delp S.L., DiGoia A.M., Jaramaz B., editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2000. Proceedings. Springer Berlin Heidelberg; Berlin, Heidelberg: 2000. pp. 588–597. [Google Scholar]
- Kleesiek J., Urban G., Hubert A., Schwarz D., Maier-Hein K., Bendszus M., Biller A. Deep MRI brain extraction: a 3D convolutional neural network for skull stripping. NeuroImage. 2016;129:460–469. doi: 10.1016/j.neuroimage.2016.01.024. [DOI] [PubMed] [Google Scholar]
- Kuklisova-Murgasova M., Cifor A., Napolitano R., Papageorghiou A., Quaghebeur G., Rutherford M.A., Hajnal J.V., Noble J.A., Schnabel J.A. Registration of 3D fetal neurosonography and MRI. Med. Image Anal. 2013;17(8):1137–1150. doi: 10.1016/j.media.2013.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurence Mercier, David Araujo, Claire Haegelen, Rolando F. Del Maestro, Kevin Petrecca, D. Louis Collins. Registering Pre- and Postresection 3-Dimensional ultrasound for improved visualization of residual brain tumor. Ultrasound Med. Biol. 2013;39(1):16–29. doi: 10.1016/j.ultrasmedbio.2012.08.004. [DOI] [PubMed] [Google Scholar]
- Letteboer M.M.J., Willems P.W.A., Viergever M.A., Niessen W.J. Non-rigid registration of 3D ultrasound images of brain Tumours acquired during neurosurgery. In: Ellis R.E., Peters T.M., editors. Medical Image Computing and Computer-Assisted Intervention - MICCAI 2003. Proceedings. Springer Berlin Heidelberg; Berlin, Heidelberg: 2003. pp. 408–415. [Google Scholar]
- Mercier L., Fonov V., Haegelen C., Del Maestro R.F., Petrecca K., Collins D.L. Comparing two approaches to rigid registration of three-dimensional ultrasound and magnetic resonance images for neurosurgery. Int. J. Comput. Assist. Radiol. Surg. 2012;7(1):125–136. doi: 10.1007/s11548-011-0620-2. [DOI] [PubMed] [Google Scholar]
- Modersitzki J. Oxford University Press; 2003. Numerical Methods for Image Registration. [Google Scholar]
- Modersitzki J. Society for Industrial and Applied Mathematics (SIAM 3600 Market Street Floor 6 Philadelphia PA 19104); Philadelphia, PA: 2009. FAIR: Flexible Algorithms for Image Registration; p. 189. [Google Scholar]
- Moiyadi A.V. Intraoperative ultrasound technology in neuro-oncology practice-current role and future applications. World Neurosurg. 2016;93:81–93. doi: 10.1016/j.wneu.2016.05.083. [DOI] [PubMed] [Google Scholar]
- Moiyadi A.V., Shetty P., Degaonkar A. Resection of pediatric brain tumors: intraoperative ultrasound revisited. J. Pediatr. Neurosci. 2017;12(1):19–23. doi: 10.4103/jpn.JPN_141_16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesch Thomas, Rösch Peter, van Muiswinkel Arianne, Weese Jürgen. IEEE Computer Society; Los Alamitos, Calif: 2001. Eighth IEEE International Conference on Computer Vision: July 7–14, 2001, Vancouver, British Columbia, Canada; p. 12. [Google Scholar]
- Nitsch J., Klein J., Miller D., Sure U., Hahn H.K. Automatic segmentation of the cerebral Falx and adjacent gyri in 2D ultrasound images. In: Handels H., Deserno T.M., Meinzer H.-P., Tolxdorff T., editors. Bildverarbeitung für die Medizin 2015. Springer Berlin Heidelberg; Berlin, Heidelberg: 2015. pp. 287–292. [Google Scholar]
- Petridis A.K., Anokhin M., Vavruska J., Mahvash M., Scholz M. The value of intraoperative sonography in low grade glioma surgery. Clin. Neurol. Neurosurg. 2015;131:64–68. doi: 10.1016/j.clineuro.2015.02.004. [DOI] [PubMed] [Google Scholar]
- Porter B.C., Rubens D.J., Strang J.G., Smith J., Totterman S., Parker K.J. Three-dimensional registration and fusion of ultrasound and MRI using major vessels as fiducial markers. IEEE Trans. Med. Imaging. 2001;20(4):354–359. doi: 10.1109/42.921484. [DOI] [PubMed] [Google Scholar]
- Prada F., Del Bene M., Mattei L., Lodigiani L., DeBeni S., Kolev V., Vetrano I., Solbiati L., Sakas G., DiMeco F. Preoperative magnetic resonance and intraoperative ultrasound fusion imaging for real-time neuronavigation in brain tumor surgery. Ultraschall in der Medizin (Stuttgart, Germany: 1980) 2015;36(2):174–186. doi: 10.1055/s-0034-1385347. [DOI] [PubMed] [Google Scholar]
- Prada F., Del Bene M., Moiraghi A., Casali C., Legnani F.G., Saladino A., Perin A., Vetrano I.G., Mattei L., Richetta C., Saini M., DiMeco F. From Grey scale B-mode to Elastosonography: multimodal ultrasound imaging in meningioma surgery-pictorial essay and literature review. Biomed. Res. Int. 2015;2015 doi: 10.1155/2015/925729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prada F., Bene M.D., Fornaro R., Vetrano I.G., Martegani A., Aiani L., Sconfienza L.M., Mauri G., Solbiati L., Pollo B., DiMeco F. Identification of residual tumor with intraoperative contrast-enhanced ultrasound during glioblastoma resection. Neurosurg. Focus. 2016;40(3):E7. doi: 10.3171/2015.11.FOCUS15573. [DOI] [PubMed] [Google Scholar]
- Presles B., Fargier-Voiron M., Biston M.-C., Lynch R., Munoz A., Liebgott H., Pommier P., Rit S., Sarrut D. Semiautomatic registration of 3D transabdominal ultrasound images for patient repositioning during postprostatectomy radiotherapy. Med. Phys. 2014;41(12) doi: 10.1118/1.4901642. [DOI] [PubMed] [Google Scholar]
- Reinertsen I., Lindseth F., Unsgaard G., Collins D.L. Clinical validation of vessel-based registration for correction of brain-shift. Med. Image Anal. 2007;11(6):673–684. doi: 10.1016/j.media.2007.06.008. [DOI] [PubMed] [Google Scholar]
- Reinertsen I., Lindseth F., Askeland C., Iversen D.H., Unsgard G. Intra-operative correction of brain-shift. Acta Neurochir. 2014;156(7):1301–1310. doi: 10.1007/s00701-014-2052-6. [DOI] [PubMed] [Google Scholar]
- Renovanz M., Hickmann A.-K., Henkel C., Nadji-Ohl M., Hopf N.J. Navigated versus non-navigated intraoperative ultrasound: is there any impact on the extent of resection of high-grade gliomas? A retrospective clinical analysis. J. Neurol. Surgery. 2014;75(3):224–230. doi: 10.1055/s-0033-1356486. [DOI] [PubMed] [Google Scholar]
- Rivaz H., Collins D.L. Deformable registration of preoperative MR, pre-resection ultrasound, and post-resection ultrasound images of neurosurgery. Int. J. Comput. Assist. Radiol. Surg. 2015;10(7):1017–1028. doi: 10.1007/s11548-014-1099-4. [DOI] [PubMed] [Google Scholar]
- Rivaz H., Collins D.L. Near real-time robust non-rigid registration of volumetric ultrasound images for neurosurgery. Ultrasound Med. Biol. 2015;41(2):574–587. doi: 10.1016/j.ultrasmedbio.2014.08.013. [DOI] [PubMed] [Google Scholar]
- Rivaz H., Karimaghaloo Z., Collins D.L. Self-similarity weighted mutual information: a new nonrigid image registration metric. Med. Image Anal. 2014;18(2):343–358. doi: 10.1016/j.media.2013.12.003. [DOI] [PubMed] [Google Scholar]
- Rivaz H., Karimaghaloo Z., Fonov V.S., Collins D.L. Nonrigid registration of ultrasound and MRI using contextual conditioned mutual information. IEEE Trans. Med. Imaging. 2014;33(3):708–725. doi: 10.1109/TMI.2013.2294630. [DOI] [PubMed] [Google Scholar]
- Rivaz H., Chen S.J.-S., Collins D.L. Automatic deformable MR-ultrasound registration for image-guided neurosurgery. IEEE Trans. Med. Imaging. 2015;34(2):366–380. doi: 10.1109/TMI.2014.2354352. [DOI] [PubMed] [Google Scholar]
- Schneider R.J., Perrin D.P., Vasilyev N.V., Marx G.R., Del Nido P.J., Howe R.D. Real-time image-based rigid registration of three-dimensional ultrasound. Med. Image Anal. 2012;16(2):402–414. doi: 10.1016/j.media.2011.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwier M., Chitiboi T., Hülnhagen T., Hahn H.K. Automated spine and vertebrae detection in CT images using object-based image analysis. Int. J. Numerical Methods Biomed. Eng. 2013;29(9):938–963. doi: 10.1002/cnm.2582. [DOI] [PubMed] [Google Scholar]
- Selbekk T., Jakola A.S., Solheim O., Johansen T.F., Lindseth F., Reinertsen I., Unsgård G. Ultrasound imaging in neurosurgery: approaches to minimize surgically induced image artefacts for improved resection control. Acta Neurochir. 2013;155(6):973–980. doi: 10.1007/s00701-013-1647-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled J.G., Zijdenbos A.P., Evans A.C. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imaging. 1998;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Unsgård G., Solheim O., Lindseth F., Selbekk T. Intra-operative imaging with 3D ultrasound in neurosurgery. Acta Neurochir. Suppl. 2011;109:181–186. doi: 10.1007/978-3-211-99651-5_28. [DOI] [PubMed] [Google Scholar]
- Wein W., Ladikos A., Fuerst B., Shah A., Sharma K., Navab N. Global registration of ultrasound to MRI using the LC2 metric for enabling neurosurgical guidance. Med. Image Computing Computer Assisted Intervention MICCAI. 2013;16(Pt 1):34–41. doi: 10.1007/978-3-642-40811-3_5. [DOI] [PubMed] [Google Scholar]
- Yong R.L., Lonser R.R. Surgery for glioblastoma multiforme: striking a balance. World Neurosurgery. 2011;76(6):528–530. doi: 10.1016/j.wneu.2011.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]