Functional Role of Solvent Entropy and Conformational Entropy of Metal Binding in a Dynamically Driven Allosteric System

Abstract

Allostery is a regulatory phenomenon whereby ligand binding to one site influences the binding of the same or a different ligand to another site on a macromolecule. The physical origins of allosteric regulation remain under intense investigation. In general terms, ligand-induced structural changes, perturbations of residue-specific dynamics, and surrounding solvent molecules all potentially contribute to the global energetics of allostery. While the role of solvent is generally well understood in regulatory events associated with major protein structural rearrangements, the degree to which protein dynamics impact solvent degrees of freedom is unclear, particularly in cases of dynamically driven allostery. With the aid of new crystal structures, extensive calorimetric and residue-specific dynamics studies over a range of time scales and temperatures, we dissect for the first time the relative degree to which changes in solvent entropy and residue-specific dynamics impact dynamically driven, allosteric inhibition of DNA binding by Zn in the zinc efflux repressor, CzrA (chromosomal zinc-regulated repressor). We show that non-native residue-specific dynamics in allosterically impaired CzrA mutants are accompanied by significant perturbations in solvent entropy that cannot be predicted from crystal structures. We conclude that functional dynamics are not necessarily restricted to protein residues but involve surface water molecules that may be responding to ligand (Zn)-mediated perturbations in protein internal motions that define the conformational ensemble, rather than major structural rearrangements.

Graphical Abstract

INTRODUCTION

Proteins are dynamic entities that interact strongly with their environment; therefore, internal protein motions and the dynamics of the hydration shell can significantly impact protein function.^1–6 Despite compelling evidence in support of the idea that biological regulation in proteins is achieved though fine-tuning of both structural and dynamic properties,^2–8 the structural paradigm remains dominant in the description of ligand binding and allosteric mechanisms. As a result, the analysis of the underlying thermodynamics of biological systems has largely focused on the contribution that enthalpy makes to function.^9–14 For example, the enthalpy of ligand binding (ΔH_TOT) is readily determined from calorimetric experiments and its molecular origins often interpreted in the context of atomic resolution structural models. The total change in entropy (ΔS_TOT) can also be derived from the calorimetric experiments through a simultaneous or independent determination of the equilibrium association constant (K_binding):

$$\begin{gathered} -T\Delta S_{\text{TOT}}=\Delta G_{\text{TOT}}-\Delta H_{\text{TOT}} \\ =-RT\text{ln}{K}_{\text{binding}}-\Delta H_{\text{TOT}} \end{gathered}$$ (1)

Quantifying the degree to which different processes contribute to the total entropy change in aqueous solution remains a challenging task. Three main contributors to ΔS_TOT are generally considered in the context of molecular recognition in proteins:

$$-T\Delta S_{\text{TOT}}=-T\Delta S_{\text{CONF}}^{\text{protein+ligand}}-T\Delta S_{\text{RT}}-T\Delta S_{\text{SOLV}}$$ (2)

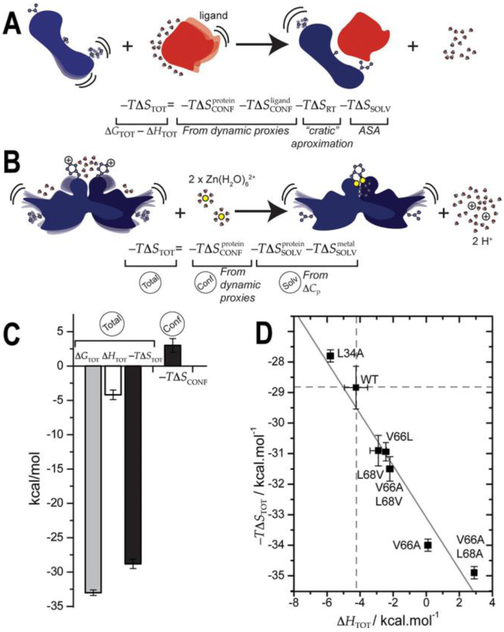
This dissection of the total entropy of molecular recognition is particularly well suited for protein–ligand complexes where the ligand is a small molecule or another protein (Figure 1A). The rotational-translation entropy (−TΔS_RT) or the entropy cost of forming a complex between two independent molecules in solution, can be determined using a number of models,^5,15,16 with the “cratic” entropy most often used (5 kcal mol⁻¹ at 25 °C¹⁵). Generally, the entropy of solvent water molecules (−TΔS_SOLV) ¹¹, ¹⁷, ¹⁸ can be estimated from changes in solvent-accessible surface area (ΔASA) derived from a comparison of the crystal structures of the free protein, the free ligand, and the protein–ligand complex, when available.¹⁹ Finally, recent NMR efforts have made it possible to obtain quantitative empirical information on the change in conformational entropy (ΔS_CONF) by measuring the methyl-terminated side chain order parameters as a dynamical proxy.^5,20,21 This methodology has evolved from the “oscillator inventory”²¹ to the “entropy-meter”²² and measures overall changes in protein dynamics using a small percentage of the atoms as representative probes.

Figure 1.

Stylized representation of the thermodynamics of molecular recognition (A) and metal binding (B) used to illustrate the rotational–translational (RT), conformational (CONFf), and solvent (SOLV) contributions to the total (TOT) entropy of binding. (C) Calorimetric (−TΔS_TOT) and conformational (−TΔS_CONF) contributions to total (TOT) energetics of Zn binding to wild-type CzrA. (D) Overall entropy and enthalpy contributions to the free energy of Zn(II) binding to all CzrA variants studied here.

This approach has been successfully applied to many different protein–ligand complexes^3,45,20,21 and reveals that conformational entropy plays a central role in the thermodynamics of ligand binding and molecular recognition. However, methods to obtain conformational entropy from internal protein and environmental water dynamics are still being developed. In the work described here, we make what is to our knowledge the first attempt to employ these approaches to quantify the extent to which distinct processes contribute to the total entropy of transition metal (Zn) binding to a folded apoprotein (Figure 1B). In this case, the metal ion (Zn; the ligand) generally displaces protons from the residues that form first-shell coordination bonds to the metal ion and the change in solvent-accessible surface area (ΔASA) inferred from the crystal structures does not necessarily reflect the total change in solvent entropy; in addition, in many cases, the structures of both states are not known.^14,23 Thus, we recast the general expression for the change in total entropy, ΔS_TOT, that more appropriately describes metal binding to a folded protein as follows:

$$\begin{gathered} -T\Delta S_{\text{TOT}}=-T\Delta S_{\text{CONF}}^{\text{protein}}-T\Delta S_{\text{SOLV}}= \\ -T\Delta S_{\text{CONF}}^{\text{protein}}-T\Delta S_{\text{SOLV}}^{\text{protein}}-T\Delta S_{\text{SOLV}}^{\text{metal}-\text{dehydration}} \end{gathered}$$ (3)

The rotational-translation entropy (−TΔS_RT) from eq 2 is omitted here because metal binding effectively occurs as a simple exchange process. This term is replaced by the metal dehydration, $-T\Delta S_{\text{SOLV}}^{\text{metal}-\text{dehydration}}$, which occurs upon coordination of metal by the protein and is defined by the difference in the entropies of hydration between displaced protons and metal ions. These values can be derived from conventional standard molar entropies of the hydration of metal ions.^24,25 The additional contribution to the entropy of the solvent in eq 3, $-T\Delta S_{\text{SOLV}}^{\text{protein}}$, is defined by the differential hydration of the unligated vs metalated states. Unfortunately, in some cases, this cannot be readily determined by the crystal structures alone since metal binding to a structured protein does not lead to a significant ΔASA.²⁶ Quantifying the differential hydration of two conformational states that share very similar crystal structures and then correlating this with $-T\Delta S_{\text{SOLV}}^{\text{protein}}$ constitutes a very challenging problem, since even up-to-date approaches that provide site-specific dynamic information^27–37 cannot currently be used to estimate the total change in solvent entropy of the system. Here, we aim to bridge the gap between protein functional dynamics and solvent dynamics by describing in detail how perturbations in internal protein motions can tune solvent reorganization in a model dynamically driven allosteric system where metal (ligand) binding does not lead to significant structural rearrangements.

Staphylococcus aureus CzrA is a paradigmatic member of the ArsR family of metalloregulators¹⁴ that has been the subject of detailed structural,^26,38,39 dynamic,^3,40 and thermodynamic studies.^3,39,41 The binding of two zinc ions to the CzrA homodimer triggers an allosteric response, i.e., in a physically distinct site, that results in a decreased affinity for the operator DNA. This negative heterotropic allosteric regulation of DNA binding allows S. aureus to maintain zinc homeostasis under conditions of host-imposed zinc toxicity by expressing a zinc export pump.^3,26,39,42 Zn binding to CzrA has been shown by calorimetry to be entropically driven,⁴¹ consistent with what has been observed in other Zn-binding biological macro-molecules.⁴³ Moreover, a detailed equilibrium dynamics study of different allosteric states of CzrA reveals that Zn induces a characteristic entropy redistribution that, when perturbed, results in near allosteric uncoupling; however, this change in conformational entropy makes only a small net contribution to the total calorimetric entropy³ (Figure 1C). This significant difference between the change in conformational entropy vs calorimetric entropy of Zn binding implicates a significant contribution of solvent molecule rearrangements to this equilibrium. However, the absence of a major structural rearrangement^26,38,39 suggests that solvent rearrangements occur mainly on the protein surface and/or from Zn desolvation, concomitant with a dynamical redistribution of conformational entropy.³ our previous results also suggest that changes in dynamics within the solvation shell of CzrA impact coupling between Zn and DNA binding, since the allosteric “hotspots” identified involve partially solvent exposed, “interfacial” residues.^3,39 These observations suggest that Zn binding not only leads to a redistribution of protein internal dynamics but also can lead to the release of waters from the protein surface, which may make a significant contribution to the allosteric response that results in dissociation from the DNA.

In previous studies, we investigated the structures and residue-specific dynamics contributions to heterotropic allostery of Zn-dependent regulation of DNA operator binding.^3,38,39 In this work, we address the degree to which solvent entropy and protein correlated motions contribute to Zn-induced allosteric inhibition of DNA binding (Figure 1A). We report a detailed analysis of a surface methyl group substitution far from the ligand binding sites (L34A CzrA) that strongly perturbs allosteric coupling of Zn and DNA binding by virtue of non-native side chain dynamics with minimal local structural perturbation in the dimer. Using the approach outlined above (eq 3), we quantify the extent to which individual contributions from residue-specific internal dynamics and solvent rearrangements make to the total entropy change of Zn binding. A comprehensive analysis of three additional methyl substitution mutants provides strong support for a model where dynamic changes within protein and the surrounding water molecules are key features of allosteric regulation of DNA binding by Zn.

MATERIALS AND METHODS

Protein Preparation.

Overexpression plasmids encoding L34A, V66A/L68A, V66A/L68V, V66A and V66L S. aureus CzrAs were constructed by PCR-based site-directed mutagenesis using pET3a-CzrA as template^26,39 and verified using DNA sequencing. Plasmids used for the expression of wild-type, V66A, and V66A/L68V were reported previously.^26,39 Proteins were expressed in E. coli BL21-(DE3)/pLysS cells and purified as previously described.²⁶ Chelex resin (Bio-Rad) was used throughout to remove trace metals from all final buffers. Protein samples for backbone and methyl group assignments of L34A were isotopically labeled using published procedures for wild-type CzrA,^3,44 with all isotopes for NMR experiments purchased from Cambridge Isotope Laboratories. All of the CzrAs eluted as a dimer by Superdex 75 (GE Healthcare) gel filtration chromatography (25 mM HEPES, 0.4 M NaCl, 2 mM EDTA, pH 7.0, 25 °C).

X-ray Crystallography.

V66L and L34A CzrAs were extensively dialyzed into 10 mM HEPES and 50 mM NaCl (pH 7.0). The calculated protein concentration after dialysis was 500 μM. (protomer or subunit). Both protein stocks were loaded 1:1 with Zn(II). V66L mutant was crystallized under conditions used previously for Zn₂ wild-type CzrA,²⁶ containing 100 mM CHES (pH 9.5), 200 mM NaCl, and 10% polyethylene glycol 8000 (Wizard I, Emerald Biosystems) at 20 °C by hanging-drop vapor diffusion method. L34A CzrA was crystallized in similar conditions but the mother liquor contained 0.1 M bis-tris propane (pH 9) and polyethylene glycol 550 20–22%. For cryoprotection, crystals were transferred for a few seconds into a reservoir solution supplemented with 20% (v/v) glycerol and were subsequently flash-frozen in liquid nitrogen. Diffraction data were collected at 100 K at the 4.2.2 beamline at the Advanced Light Source (Berkeley, CA). The data were indexed, integrated, and scaled using the XDS package.

Phase calculations were performed using Phaser in PHENIX Auto MR module.⁴⁵ The Zn-bound CzrA V66A/L68V structure (PDB code 4GGG) was used as search model,³⁹ and an initial model was produced using the PHENIX Auto Build module. The refined model was obtained by iterative cycles of refinement in Phenix-refine module and manual building in Coot⁴⁶ MolProbity software⁴⁷ was used to assess the geometric quality of the models and PyMol (http://www.pymol.org) to generate images. Table S4 summarizes data collection and refinement statistics.

NMR Spectroscopy.

$S_{\text{axis}}^2$ values of the Ile δ1, Leu δ1/δ2, Val γ1/γ2, Ala β, and Met ε methyl groups in apo and Zn(II)₂ states were determined using ¹H spin-based relaxation experiments at 600 MHz at 25.0, 30.0, 35.0, and 40.0 °C.⁴⁸ $S_{\text{axis}}^2$ values, cross-correlated relaxation rates, η, between pairs of ¹H−¹H vectors in ¹³CH₃ methyl groups were measured using eq 4:

$$\eta =\frac{R_{2,\mathrm{H}}^{\mathrm{F}}-R_{2,\mathrm{H}}^{\mathrm{S}}}{2}\approx \frac{9}{10}{\left(\frac{{\mu }_0}{4\pi }\right)}^2[P_2(\cos {\theta }_{\text{axis,HH}}){]}^2\frac{S_{\text{axis}}{}^{{}^2}\gamma _{{}_{\mathrm{H}}}{}^{{}^4}\hslash _{}{}^2\tau _{\mathrm{c}}}{{r_{{}_{\text{HH}}}}^{{}^6}}$$ (4)

where τ_c is the tumbling time of the protein; $R_{2,\mathrm{H}}^{\mathrm{F}}$ and $R_{2,\mathrm{H}}^{\mathrm{S}}$ are the fast and slow relaxing magnetization, respectively; γ_H is the gyromagnetic ratio of the proton; and r_HH is the distance between pairs of methyl protons.

In order to obtain an approximation of the differences in fast and slow relaxation rates (2η), we measured the time-dependence of the crosspeak intensities in a correlated pair of single and double quantum (2Q) experiments.⁴⁸ Using various delay time, T, values (3, 5, 8, 12, 17, 22, and 27 ms, recorded in an interleaved manner), the rates of η were obtained by fitting ratios of peak intensities measured in pairs of experiments (I_a and I_b, spin-forbidden and spin-allowed, respectively) with eq 5:

$$\frac{I_{\mathrm{a}}}{I_{\mathrm{b}}}=\frac{-0.5\eta \tanh (\sqrt{n^2+{\delta }^2}T)}{\sqrt{n^2+{\delta }^2}-\delta \tanh (\sqrt{n^2+{\delta }^2}T)}$$ (5)

where T is the variable delay time, δ is a parameter that is related to the ¹H spin density around the methyl group, and I_a and I_b are the time dependencies of differences and sums, respectively, of magnetization derived from methyl ¹H single-quantum transitions, as described.⁴⁸ Peak heights and spectral noise were measured in Sparky.⁴⁹ A python script was used to fit the peak height ratios to η values and to determine $S_{\text{axis}}^2$ values in the apo- or Zn-bound state, as described previously.^{3, 48, 50}

For apo and Zn(II) L34A-CzrA states, τ_c was obtained from T₁ T₂, and heteronuclear NOE (hNOE) obtained at 40 °C and 10% D₂O (data not shown) and adjusted for changes in solvent and temperature (nickanthis.com/tools/tau). Backbone amide relaxation experiments (¹⁵N R₁ and R₂) were performed at 800 MHz under the same conditions (10 mM MES, pH 6.0, 50 mM NaCl, 0.02% NaN₃ in 10% D₂O).³⁸ The values obtained for τ_c obtained from Monte Carlo simulations with tensor2⁵¹ software using the reported structures for Zn-L34A and apo-WT-CzrA for each state were comparable to what was previously reposted for other CzrAs.^3,38

For the apo and Zn L34A CzrA, the methyl-specific lambda (Λ) values were obtained for each state from eq 6:⁵²

$${\Lambda }_{\text{state},i}=\frac{\mathrm{d}\text{ln}(1-S_{\text{state},i})}{\mathrm{d}\text{ln}(T∕K)}$$ (6)

by fitting the T-dependence of the order parameter for T = 25.0, 30.0, 35.0, and 40.0 °C. The 25.0 and 40.0 °C were collected in duplicate to ensure that irreversible changes in the sample were not being misinterpreted as a temperature dependence.

The change in conformational entropy difference between Zn and apo states was obtained using a methyl order parameters, $S_{\text{axis}}^2$, as dynamical proxy:⁵

$$\begin{gathered} -T\Delta S_{\text{CONF},a\to b}=-T(-0.00116{\text{kcal mol}}^{-1}{\mathrm{K}}^{-1})N_{\chi }^{\text{prot}} \\ [\langle S_{\mathrm{b}}{}^2\rangle -\langle S_a{}^2\rangle ] \end{gathered}$$ (7)

where $N_{\chi }^{\text{prot}}$ is the total number of side-chain torsion angles in the protein dimer (212 in the case of CzrA).

Relaxation dispersion measurements were acquired using a ¹H−¹³C HMQC-based Carr–Purcell–Meiboom–Gill (CPMG) pulse sequence.⁵³ For L34A CzrA, experiments were performed at 25 °C at 600 and 800 MHz ¹H frequencies using constant time interval T = 40 ms with CPMG field strengths (ν_CPMG) of 50, 100, 150, 200, 250, 300, 350, 400, 450, 500, 600, 700, 850, and 1000 Hz. As a consequence, this experiment can capture processes occurring between 0.5 and 5 ms. Data were fitted to the two-site fast exchange limit equation, as discussed previously.³

Isothermal Titration Calorimetry.

ITC experiments were carried out using a MicroCal VP-ITC calorimeter using 2.50 mM ZnSO₄ as titrant in the syringe and solution conditions of 50 mM HEPES, 5.0 mM NTA as a Zn(II) competitor, 0.40 M NaCl (pH 7.0), and 100 μM CzrA homodimer. The raw ITC data were integrated, concentration normalized, and plotted as heat versus metal/protein ratio using Origin. All data were fit to a sequential twosite binding model included in the data analysis software provided by MicroCal, obtaining the binding constants and molar enthalpies of each Zn binding event (K_ITC,1 and K_ITC,2 and ΔH_ITC,1 and ΔH_ITC,2, respectively). NTA-independent binding constants, K_Zn,1 and K_Zn,2, were determined using NIST approved equilibrium constants accounting for the competition from 5.0 mM NTA as described in detail previously:⁴¹

$$K_{\mathrm{Z}n}=K_{\text{ITC}}{K}_{\text{comp}}=K_{\text{ITC}}(1+K_{\mathrm{Z}n-\text{NTA}}[{\text{NTA}}_{\text{base}}])$$ (8)

Under these conditions, K_comp is 6.0 × 10⁵ as calculated from the NIST approved values for NTA Zn binding constant and pK_a⁵⁴ and application of eq 8 generates NTA-independent values of NTA-corrected metal binding constants K_Zn,1 and K_Zn,2 (Table S1). The ΔG_Zn,1 and ΔG_Zn,2 are calculated from the K_Zn,1 and K_Zn,2 values following eq 1 and ΔG_tot results from the addition of those two values. The buffer independent molar enthalpies (ΔH_Zn,1 and ΔH_Zn,2, in Table S1) are obtained similarly after correction with the ionization enthalpy of HEPES and enthalpy of the Zn binding to NTA.⁵⁴ Finally, ΔS_tot for the Zn-binding process is calculated from eq 1. The standard deviation of the mean values from triplicate experiments in are given for all thermodynamic parameters.

The temperature-dependence of the enthalpy of Zn binding to NTA was also studied by calorimetry using 2.50 mM ZnSO₄ as titrant in 50 mM HEPES 0.40 M NaCl (pH 7.0) and 0.1 mM NTA at 15.0 20.0, 25.0, 30.0, and 35.0 °C. The heat capacity for Zn binding in the solution condition was determined to be 15 ± 3 cal K⁻¹ mol⁻¹; this value is comparable with the apparent heat capacities for complex-ation reported for other divalent metal ions.⁵⁵

Fluorescence Anisotropy-Based DNA-Binding Experiments.

DNA binding affinities were measured for V66L CzrA in the absence and presence of Zn in order to extract ΔG_c. Briefly, a fluorescein-labeled 28-bp DNA duplex harboring a single 12-2-12 DNA operator³⁸ was obtained by annealing to fully complementary single strands and employed to measure the change in fluorescence anisotropy upon CzrA addition to the DNA solution. Experiments were carried out at 25 (±0.1) °C on a PC1 spectrofluorometer (excitation wavelength of 495 nm, 1 mm slit; with the emission collected through a 515 nm bandpass filter) as described previously.³ The duplex DNA concentration in all cases was 10.0 nM in 10 mM Hepes, pH 7.0 buffer. For the Zn₂–CzrAs measurements, the DNA buffer contained 0.23 M NaCl and 3 μM ZnCl₂. For the apo-CzrA measurements, the DNA buffer contained 0.4 M NaCl and 1 mM EDTA. The DNA binding isotherms were fit to a single-binding site model (one dimer to DNA) coupled to a monomer–dimer equilibrium (K_dimer = 1.7 × 10⁵ M⁻¹ and 4.5 × 10⁵ M⁻¹ for apo and Zn₂–CzrAs respectively)⁵⁶ using Dynafit.⁵⁷

RESULTS

Structure and Thermodynamics of Zn Binding to CzrA Variants.

In order to quantify the contribution that each component makes to ΔS_TOT in eq 3, we first estimated that dehydration of the two Zn ions and corresponding hydration of two protons contributes a $-T\Delta S_{\text{SOLV}}^{\text{metal}-\text{dehydration}}$ of −11.4 kcal mol⁻¹ (Appendix 1, Supporting Information, eq S6). Meanwhile, the change in solvent entropy derived from the crystal structures of wild-type apo and Zn-bound CzrAs, $-T\Delta S_{\text{SOLV}}^{\text{protein}-\text{ASA}}$, contributes only −0.5 kcal mol⁻¹ (Table S2, eq S6). Taken together, these contributions are not large enough to account for the change in solvent entropy inferred from the total and the conformational entropies of Zn binding (Figure 1C). This suggests that other solvent entropy terms must play a substantial role in the favorable entropy of Zn binding in this system that cannot be derived from a net conformational stiffening of the protein side chains, −TΔS_CONF (Figure 1C).

We previously reasoned that internal and solvent dynamics can be tuned by small changes in “hotspots”, which we define as residues that significantly impact biological function. We also proposed that measuring these changes can contribute to our understanding of the impact that each entropy term has on the overall thermodynamics of metal binding CzrA. We therefore measured the thermodynamics of Zn binding and the allosteric coupling free energies of previously characterized methyl side chain “cavity” mutants that impact protein dynamics in the Zn-bound state (Figure 1D). We extend these studies to a CzrA mutant harboring a cavity substitution distal to the Zn binding site (L34A CzrA) and to an anticipated “overfill” substitution mutant, which in contrast to a cavity mutant exchanges a smaller methyl-bearing side chain for a larger one, V66L CzrA.

The different substitution mutants of CzrA analyzed here and in previous work impact allosteric connectivity to varying degrees without strongly affecting the affinity of apo-CzrA for DNA or Zn; this allows us to directly probe functionally important entropy terms. These variants share identical Zn binding affinities (K_Zn,1) and K_Zn,2,) and free energies (ΔG_Zn,1 and ΔG_Zn,2,) but have distinct quantitative effects on negative regulation of DNA binding by Zn(II) (Tables S1 and S3), i.e., allosteric coupling. While the L68V and V66L CzrA substitutions have little effect on DNA binding affinity in the apo- and Zn-bound states (Figure S1),³⁹ L34A CzrA binds tightly to DNA in both the absence and presence of Zn and is therefore an allosterically impaired mutant.¹⁴ Although each mutant has a variable impact on DNA binding affinity, each has essentially wild-type Zn binding affinities yet highly distinct underlying energetics and thus presents a clear case of entropy-enthalpy compensation over a relatively narrow range of binding free energies (Figure 1D).

Since these mutations are distant from the first coordination shell of the metal, they have no impact on those entropy terms that derive directly from formation of metal coordination bonds; as a consequence, their impact on the entropy term must be restricted to some combination of the conformational entropy and/or a net disordering of water molecules on the protein surface upon Zn binding. Although probably not informative in and of itself,^58–60 entropy–enthalpy compensation strongly motivates further studies of the structure, dynamics, and thermodynamics on these mutants because it suggests that the mutations affect the different contributions to the entropy with minimal effect on the affinity (Figure 1D). We hypothesize that these largely “interfacial” methyl substitutions create subtle perturbations in the protein structure, dynamics, and/or solvation that will allow us to identify major contributors to the overall entropy of Zn binding to CzrA and to understand the role of protein dynamics and solvent degrees of freedom on heterotropic allosteric coupling of Zn and DNA binding.

In order to elucidate any perturbations in protein structure and buried water molecules, we solved the crystal structures of the Zn₂ V66L (to 1.9 Å resolution) and Zn₂ L34A (to 2.0 Å resolution) CzrA homodimers. The global structures of wild-type,²⁶ V66L, and L34A CzrAs are essentially identical, with an rmsd of 0.5 Å over 185 Cα atoms (see Figure S2 and Table S4 for structure statistics). In addition, the first coordination shell around the Zn(II) ion and the previously described interprotomer hydrogen bonding pathway^23,39,40 that links the first coordination shell to the rest of the molecule are both intact and nearly indistinguishable in the mutants (Figure 2A,B). This was also the case for the previously characterized V66A/L68V (AV) CzrA and confirms that these substitution mutants do not show changes in Zn coordination chemistry and retain an overall wild-type like structure, findings consistent with wild-type zinc binding affinities (Table S1).

Figure 2.

(A) Global Cα wireframe superposition of wild-type (orange) and L34A (magenta, right) and V66L (green, left) CzrAs, with the positions of the zinc atoms shown as spheres. (B) Spacefilling representations of the van der Waals packing region in the vicinity of either the second coordination shell hydrogen bond^23,26,39 (top) or the L34 surface (bottom) in Zn₂ wild-type (orange), L34A (magenta), V66L (green), and V66A/L68V (light green) CzrAs. Summary of the allosteric coupling free energies measured by fluorescence anisotropy (ΔG_c, Figure S1) and stepwise Zn(II) binding free energies for the binding of the first (ΔG_1,Zn) and second (ΔG_2,Zn) Zn ions to each CzrA homodimer.

Closer inspection of Zn-bound L34A CzrA reveals a hydrophobic cavity that traps two water molecules, thus significantly affecting the chemical environment and hydrophobic packing in the immediate microenvironment of residue 34 (Figure 2B). In the case of the “overfill” mutant, V66L CzrA, the mutation actually perturbs packing in the hinge region formed by the V66 and L68 side chains, thus creating a cavity and trapping a surface water that forms a hydrogen bond with the C=O of R61. It is interesting to note that the V66L substitution appears to induce a structural perturbation that is similar to that of the V66A/L68V substitution (Figure 2B); however, the V66L substitution does not impact the allosteric coupling free energy, ΔG_c, while allostery is nearly completely crippled in the V66A/L68V mutant (Figure 2B and Table S3). These findings reinforce the idea that it is not possible to predict the functional impact solely on the basis of a structural perturbation. In fact, these trends are fully consistent with the predictions of an entropy redistribution model.³ A leucine-to-alanine substitution mutant would be predicted to be less functionally responsive from a dynamics perspective,^21,61 whereas substitution of a residue with one characterized by more χ angles is predicted to result in a minor functional perturbation, as established here for V66L CzrA and a V66Q variant published previously.³⁹

In an effort to explain the differences in the thermodynamics of Zn binding and coupling free energies, we compared the available crystal structures in terms of solvent-accessible area and buried water molecules. Although the solvent entropy estimated from the change in polar and nonpolar accessible surface area⁵ is negligible for wild-type CzrA (Table S2), closer inspection of buried waters in apo- and Zn-bound CzrA crystal structures²⁶ suggests an unfavorable entropy contribution (−TΔS = 1.6 kcal mol⁻¹)^5,62,63 from the addition of one extra water molecule per protomer upon Zn binding (Figure S3). This water is present in all of the crystal structures of Zn-bound V66L, L34A, and V66A/L68A CzrAs. Moreover, these substitutions in CzrA do not introduce significant differences in the polar and nonpolar areas exposed to solvent (Table S2). A net disordering of waters tightly bound to the protein surface in the apo-state can also contribute to the ligand binding entropy.^63,64 The buried waters are mostly conserved in a more peripheral region encompassing the α3 helix and the β-wing (Figure S3), with the exception of L34A CzrA that features an additional buried water molecule in the A34 peripheral cavity (Figure 2). We note that methyl substitutions do not affect the accessible surface area but can affect solvation by changes in either buried waters (L34A) or superficial waters (V66L and V66A/L68A).

This analysis of the wild-type crystal structures suggests only a minimal unfavorable solvent entropy contribution that cannot account for the value inferred from the total favorable entropy of metal binding (Figure 1C); further, the analysis of the available high resolution structures of CzrA mutants suggests that subtle structural differences introduced by mutations are likely insufficient to explain the differences in the thermodynamics of Zn binding and coupling free energies. These inconsistencies highlight the difficulties of using crystal structures to calculate solvent entropies when binding occurs with little structural rearrangement, as well as the need for further characterization of the protein hydration layer in these processes. The mutations described here and in previous reports^3,39 affect packing and solvation in distinct ways and these in turn, impact solvent and protein conformational dynamics. In order to gain additional insights on the effect of cavity mutations on conformational dynamics changes upon Zn binding, we focused on allosterically impaired CzrA mutants and assessed changes in protein dynamics introduced by the L34A substitution.

Conformational Dynamics of the L34A CzrA Substitution Mutant.

We first obtained backbone and stereospecific methyl group assignments of the L34A CzrA homodimer in the apo and Zn₂-bound states using previously published isotopic labeling schemes.⁴⁴ Examination of ¹H-¹⁵N and ¹H-¹³C HSQC spectra of Zn-bound L34A CzrA confirms that in solution the mutation gives rise to largely local perturbations of the structure immediately around the site of the substitution relative to Zn₂ wild-type CzrA (Figures S4A and S5). Moreover, this mutant shows comparable trends in the change in chemical shift between the apo and Zn₂-states indicating that the Zn-induced changes in chemical shift in the mutant are globally similar to that of wild-type CzrA (Figures S4B and S5). The similarity in chemical shift perturbations induced by Zn binding to WT and L34A CzrAs is consistent with the observation that metal affinities and coordination geometries are indistinguishable from that of wild type CzrA (Tables S1 and S3 and Figure 2).

In order to determine the degree to which the L34A mutation impacts internal dynamics and conformational entropy of Zn binding, we employed NMR dynamics experiments. We measured the axial order parameters ($S_{\text{axis}}^2$) of methyl bearing side chains (58 reporters per protomer) of the L34A mutant in the apo and Zn₂-states (Figures S6–S8). It is interesting to note that changes in the side chain dynamics in the C-terminal α5 helical residues show a pattern that is very similar to wild-type CzrA, i.e., increased flexibility of residues in the core of the helix coupled with decreased flexibility in methyl-bearing side chains closer to the first coordination shell of the Zn ion, at the extrema of the α5 helix. This was also observed in other allosterically compromised mutants previously characterized using these methods (Figure S9). This conservation of a “local dynamics signature” is consistent with similar Zn binding affinities and geometries among all CzrAs (Table S1 and Figure 2).

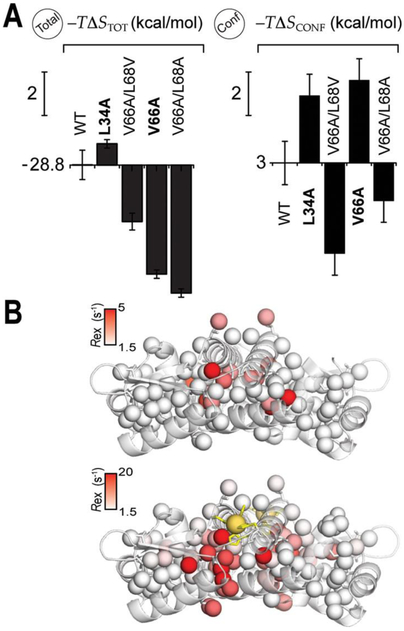
Beyond these Zn-centered local dynamics, L34A CzrA is clearly characterized by a non-native redistribution of fast internal dynamics relative to wild-type CzrA, as previously found for other allosterically impaired mutants (Figure 3A).³ As opposed to the mutants that were previously characterized,³ this mutation is in the periphery of the molecule and yet has an impact that is not restricted to the site of the mutation (Figures 3A and S7). This suggests that a distal methyl substitution on the protein surface can potentially affect how a signal can be transmitted to the core of the protein. Similar results have been reported in other systems^65–67 and contrast with the proposed role for surface residues as the sources or sinks of allosteric signals, instead of participating in the transmission of such signals.⁶⁸

Figure 3.

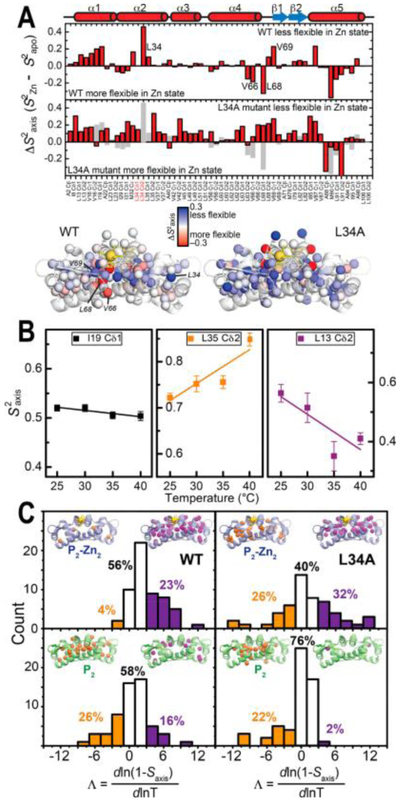
(A) Effect of the L34A mutation on the dynamic signatures of Zn binding; ¹³C-methyl side-chain changes in $S_{\text{axis}}^2$, $\Delta S_{\text{axis}}^2$, upon Zn binding measured at 25.0 °C for wild-type CzrA (upper)³ and the L34A CzrA cavity mutant (lower; WT in gray) with the corresponding changes and perturbations plotted on to the structure of Zn-bound CzrAs. (B) Effect of temperature changes on the axial order parameters ($S_{\text{axis}}^2$) of representative ILVMA residues in Zn₂-loaded L34A CzrA. (C) Represented as the Λ value, and shaded according to the class (orange: inverse T-dependence of $S_{\text{axis}}^2$; white: typical T-dependence behavior expected for a harmonic or mildly anharmonic potential; purple: T- dependence of a highly anharmonic potential) for Zn₂-loaded (top) and apo-states (bottom) for wild-type and L34A CzrAs.

To further investigate how non-native dynamics in L34A CzrA impair allostery, we took advantage of the increased thermal stability of L34A CzrA in the apo-state relative to other allosteric mutants studied previously³ and measured the temperature dependence of the $S_{\text{axis}}^2$ (Figures S7 and S8). In brief, the temperature dependence of each $S_{\text{axis}}^2$ reports on the degree of deviation from a simple harmonic rotor model for which $S_{\text{axis}}^2$ is expected to show a slight decrease over the temperature range measured (Figure 3B, shaded black). This can be reflected by a dimensionless parameter, namely Λ (eq 6), that is expected to be ≤1 for simple harmonic rotors.⁶⁹ The anharmonicity can be interpreted with different models depending on the values of Λ.^52,70,71 A mild deviation from harmonicity explains Λ values between 0 and 3, and Λ values ≥3 can be explained by a stepped angular potential^52,72 (Figure 3B, shaded purple). Λ < 0 are less frequent and are indicative of a high degree of conditional motion (Figure 3B, shaded orange), readily explained by excluded volumes effects⁵² and possibly other correlated motional regimes.⁷⁰ While it remains true that $S_{\text{axis}}^2$ values tend to decrease with higher temperature, which translates to a general increase in local conformational disorder and a positive conformational ΔC_p (Table S5),⁷¹ L34A CzrA is characterized by residues in all three motional regimes (Figure 3C), as observed previously for wild-type CzrA³. Anharmonicity is expected, particularly for low order parameter sites ($\Delta S_{\text{axis}}^2\le 0.6$) where rotameric interconversion is necessary^52,72 (see Figure S7 for reference to the different motional regimes). However, most of the anharmonicity for CzrAs is observed for higher order parameter side-chains (Figure S9), suggesting some degree of connection to correlated motion.

We recently demonstrated that Zn binding in wild type CzrA affects the degree of correlation of side chain dynamics, as reported by the temperature-dependence of the $S_{\text{axis}}^2$ (Λ<0), and allosteric mutations can potentially influence this effect.³ These correlated motions have been implicated in high affinity binding to DNA by apo wild-type CzrA. In the apo-form, L34A CzrA shows an inverse temperature-dependence of $S_{\text{axis}}^2$ within the dimer core, consistent with what was previously observed for the wild type protein by molecular dynamics⁴⁰ and NMR spectroscopy³ (Figure 3C). Upon binding Zn, the L34A mutant retains a degree of correlated motion that is comparable or higher to that of the apoprotein, whereas Zn quenches the correlated motions in wild-type CzrA (Figure 3C, percentage of residues with inverse temperature dependence). This result highlights the profound impact on fast internal dynamics of this cavity mutation by a solvent-exposed distal residue, in the absence of structural changes, while emphasizing the predictive power of the dynamically driven allosteric model.

Moreover, the dynamical signature of this mutant reveals a global “stiffening” derived from a net unfavorable conformational entropy, −TΔS_CONF = 6 kcal mol⁻¹, similar to what was observed previously for another single point cavity mutation (V66A CzrA; Table S1).³ The other allosteric mutations, V66A, V66A/L68V (AV), and V66A/L68A (AA) also influence the underlying energetics of Zn binding to CzrA (Figure 1D) as anticipated from strong perturbations in $\Delta S_{\text{axis}}^2$ (Figure 4A). However, the sign and magnitude of global Δ(−TΔS_TOT) vs Δ(−TΔS_CONF) differ strongly for each of the four mutants (Figure 4A). These observations contrast sharply with previously described cases, in particular E. coli CAP,⁴ which suggests that some of the assumptions made in the conformational entropy calculation are not valid in the case of CzrA. As discussed above, one likely explanation is the change in solvent entropy is not properly modeled by ΔASA alone and that changes in site-specific hydration may contribute significantly to this term.

Figure 4.

(A) Graphical illustration of the entropy terms associated with Zn binding to the wild- type vs CzrA variants derived from calorimetric (total, eq 1; resulting for binding two Zn equivalent per dimer) and internal protein dynamics measurements ($\Delta S_{\text{axis}}^2$, Conf, eq 7) by NMR spectroscopy. The vertical scale bar corresponds to a change of 2.0 kcal mol⁻¹. The variants marked in bold show conformational exchange in the Zn-bound state. (B) Site-specific methyl R_ex in the apo- and Zn₂-loaded in L34A CzrA homodimers mapped onto the structure of apo- and Zn₂-loaded, respectively.

The measure of ΔS_CONF (change in conformational entropy) through methyl terminated amino acids as dynamical proxies requires that the coupling of a small percentage of the atoms with their surroundings reports on the changes in overall protein dynamics.⁷³ However, coupling is expected to be weak,⁷³ whereas strong coupling originating with concerted motions could potentially obscure a linear dependence of −TΔS_CONF with −TΔS_TOT.⁷⁴ We previously showed that Zn binding quenches a collective mode in the millisecond time scale in wild-type CzrA and two cavity mutants (V66A/L68A and V66A/L68V) via conventional relaxation dispersion NMR experiments. The same experiments conducted on L34A and V66A CzrAs³ suggest that these concerted motions are not quenched by Zn but are enhanced in the Zn-bound state (Figure 4B and Figure S11). This slow conformational exchange is also reflected in the broadening of the crosspeak that reports on the quaternary structural hydrogen bond that connects the Zn coordination and DNA binding sites in Zn₂-L34A CzrA (Figure S12). L34A and V66A CzrAs have a – TΔS_CONF that is significantly more unfavorable than wild-type CzrA (Figure 4A), which can be explained by the fact that this collective mode remains present in their Zn states (Figure 4B); as a result, the degree of coupling does not decrease, nor does the entropy increase to the same extent.⁷⁴ This suggests that the methyl dynamics signatures in CzrAs are capturing the favorable conformational entropy associated with quenching collective modes in WT, V66A/L68A and V66A/L68V CzrAs that is not present in L34A and V66A CzrAs.

It is interesting to note that besides sharing the same conformational entropy and similar protein dynamics from ps–ns to μs–ms time scales, V66A and L34A CzrAs are characterized by markedly distinct total entropies of Zn binding (Figure 4A). This observation suggests that distinct degrees of freedom of surface water molecules in L34A and V66A CzrAs strongly impact the overall energetics of Zn binding. If this were the case, the dynamic effect of mutations that affect function would not be restricted to internal protein dynamics but could also perturb the solvation shell of the protein. To test this hypothesis, we measured the solvent contributions to entropy of structurally conserved and allosterically impaired mutants.

Solvent Entropy of Allosterically Impaired Mutants.

Historically, the change in solvent entropy upon protein (ligand) binding or protein folding can be calculated from the hydration heat capacity contributions,^5,75 generally classified into polar and apolar, and an experimentally determined reference temperature at which solvation entropies extrapolate to 0 (T_s).^18,76 However, as discussed above, it is not possible to use this approach with CzrA since ΔASA derived from the crystal structures are minimal and not representative of the overall thermodynamics (Table S4, Figure 1C, Appendix 1, Supporting Information). To avoid the complication of dissecting the solvent entropy term for each mutant, we took a simpler formulation of the change in solvent entropy, ΔS_SOLV, that readily allows a comparison of all CzrA variants with wild-type protein (eq 9):

$$-T\Delta S_{\text{SOLV}}=-T\left[\Delta C_{p,\text{SOLV}}\text{ln}\left(\frac{T}{T_{\mathrm{S}}}\right)\right]$$ (9)

where ΔC_p,S0LV is estimated from the calorimetric ΔC_p for each CzrA variant and T_s = 395 K is derived from total entropy of Zn binding to wild-type CzrA and internal conformational dynamics measurements at different temperatures. Equation 9 is valid if the contributions to ΔC_p from sources other than solvation are small, which is well supported on the wealth of structures obtained from this system as well as associated dynamics data. A full description of the assumptions and details of the approach are presented in Appendix 2 (Supporting Information). This approach is particularly well suited to studying the perturbation of solvent dynamics that originate with methyl substitution,⁷⁷ thus providing a simple and powerful tool to connect functional protein dynamics to solvent entropies in allosterically impaired CzrA mutants that involve no large-scale structural rearrangements.

To determine ΔC_p, we measured the molar enthalpies of each Zn binding event, ΔH_1,Zn and ΔH_2,Zn by isothermal titration calorimetry (ITC) by conducting otherwise identical titrations of ZnSO₄ into wild-type, L34A, V66A, V66A/L68V (AV), V66A/L68A (AA) CzrAs at 15.0, 25.0, and 35.0 °C (Figures 5A and S13). We used a previously reported^41,78 competition experiment using nitrilotriacetic acid (NTA) to bring the observed binding affinities, K_1,Zn and K_2,Zn, within a measurable range while inhibiting adventitious Zn binding. All mutants conserve the slight negative cooperativity of Zn binding to each of the two sites of the homodimer at the measured temperatures (Table S1), thus allowing us to estimate a value of ΔC_p for each binding event, ΔC_p1,Zn and ΔC_p2,Zn. The ΔC_p values obtained from this approach are significantly higher than both the ΔC_p of formation of the Zn(II)–NTA complex (15 ± 3 cal K⁻¹ mol⁻¹) as well as the conformational contribution to ΔC_p (Table S5). These results confirm that in this case ΔC_p reflects essentially only changes in solvent entropy with other contributions insignificant (<8%).

Figure 5.

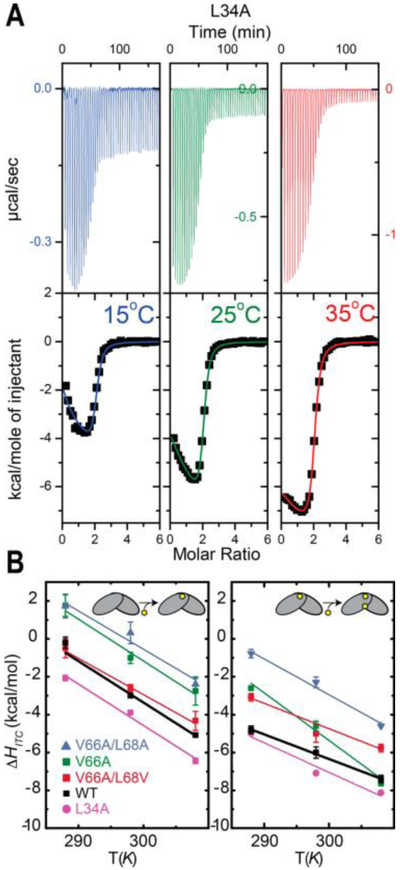
(A) Thermograms and representative ITC-derived Zn binding curves obtained for L34A CzrA homodimers at 15.0, 25.0, and 35.0 °C from left to right (data for the other variants are presented in Figure S13). (B) Temperature-dependence of the ΔH of binding of Zn to the CzrA homodimer in steps. Binding of the first Zn(II) (left) and binding of the second Zn (right) to the homodimer. The continuous lines are linear fits that define the slope ΔC_p = dΔH/ dT for each variant.

The ΔC_p for the first Zn binding event is significantly larger than the second, which suggests that most of the increase in solvent degrees of freedom occurs upon binding of the first zinc ion to the homodimer. Previous results hinted that the conformational restriction upon zinc binding occurs upon binding the second Zn,⁷⁹ which suggests that the conformational restriction of the protein can be associated with a decrease of the ΔC_p. This is consistent with previous reports that link altered heat capacities with disorder-to-order transitions.⁷⁷ In accordance with this, ΔC_p of the first Zn binding event, ΔC_p1,Zn, is very similar among all measured CzrAs, reinforcing the idea that changes in protein internal dynamics do not impact the solvent molecule degrees of freedom. In contrast, significant differences are detected in ΔC_p2,Zn (Figure 5B), which suggests that the solvent water dynamics are affected by differences in protein dynamics. Thus, our data suggest protein internal dynamics impact primarily the solvent reorganization associated with the second Zn binding event.

All of the mutants characterized here show a significant impact in the solvent entropy as determined from the ΔC_p (Figure 5B). However, the effect is strikingly distinct for each mutant, similar to what we found for the conformational entropy term, ΔS_CONF. The case of V66A CzrA is particularly noteworthy in that the effect on solvent entropy is 2-fold larger than the effect on the total entropy term, suggesting an entropy–entropy compensation is occurring with this mutation. Additional mutations superimposed on V66A CzrA, as in V66A/L68V and V66A/L68A CzrAs, attenuate the dramatic increase in solvent entropy, which is also accompanied by restriction of internal protein dynamic changes upon Zn binding.³ Further, although V66A and L34A CzrAs share the same impact on the conformational entropy term, i.e., global “stiffening” (Figure 4A), the effect on the solvent degrees of freedom is markedly different. Although our ITC-derived measurements of the solvent entropy do not provide site-specific information, we propose that the marked effect of the V66A substitution on the changes in solvent entropy may be attributed to the role of V66 as a “hinge” residue positioned between the α4 reading heads and the β-wings of the homodimer.

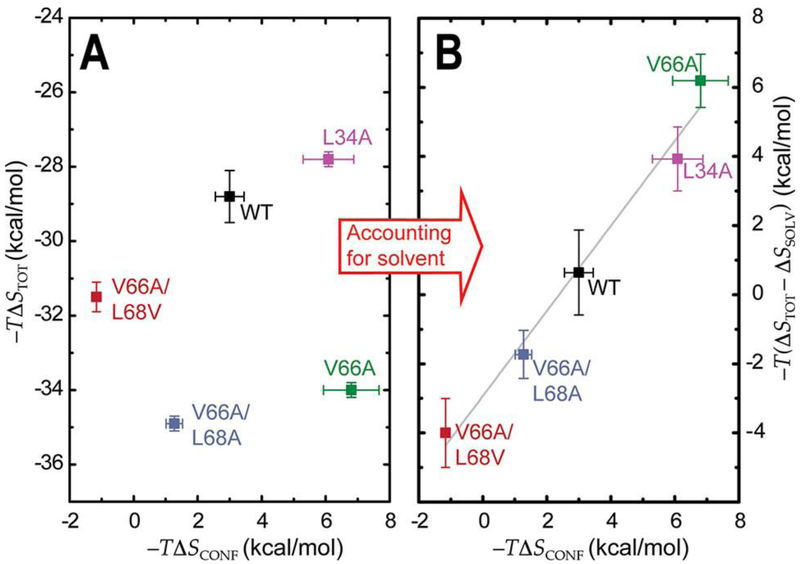
When one takes into account these empirically determined solvent entropies derived from the ΔC_p values, it is now possible to successfully recapitulate the anticipated correlation between the calorimetric and the conformational entropies, as determined from ITC and the axial order parameter differences, respectively (Figure 6).^{4, 5} This correlation provides important validation of the “entropy meter” and suggests that in dynamically driven macromolecular processes, water–protein interactions escape the superficial treatment of changes in solvent entropy based simply on changes in accessible surface area obtained from crystal structures. Furthermore, these differences in the contribution that changes in solvent entropy make to the overall change in entropy in each of the mutants further suggest that non-native protein dynamics significantly impact solvent reorganization beyond what can be inferred from inspection of crystal structures alone. We show here and in previous work that these mutants are allosterically impaired as a result of these non-native dynamics.³ Thus, these data provide strong support for the hypothesis that non-native protein dynamics and a non-native reorganization of solvent molecules significantly impact heterotropic allostery and ultimately, biological function.

Figure 6.

Buffer-independent changes in calorimetric entropies (ΔS_TOT, eq 1) and conformational entropies (ΔS_CONF, eq 7) upon binding two dimer●equiv of Zn to CzrAs before (A) and after (B) accounting for differences in solvent entropy (ΔS_SOLV, eq 9) in each CzrA mutant.

CONCLUSION

In this work, we investigate the role of internal protein and solvent dynamics on Zn binding to the model metal-loregulatory protein CzrA that leads to allosteric inhibition of DNA operator binding. We first establish that the overall entropy contribution to this free energy can be precisely tuned by single-point mutations distal to the site of metal coordination, while maintaining nearly identical Zn binding affinities. Our detailed structural and dynamics experiments demonstrate that dynamically driven heterotropic allostery in CzrA can be negatively affected by a “cavity” substitution of an interfacial (partially solvent-exposed) methyl-bearing side chain (L34) that fails to narrow the conformational ensemble upon Zn binding, while strongly perturbing solvent dynamics. Moreover, a comprehensive analysis of allosterically impaired “cavity” mutants provides strong evidence in support of differential solvent rearrangement on wild-type vs mutant CzrAs as a major contributor to the free energy of Zn binding to CzrAs. These results suggest a model where a dynamic redistribution between protein and hydration layer occurs without significant perturbations in the protein structure and acts as a key feature of Zn-mediated allosteric inhibition of DNA binding by CzrA.

Although the concept of functional dynamics in allostery is well established and has been extensively discussed in the literature,^{2–8,80–84} the number of structured systems where the fast-internal dynamics have been analyzed to establish their functional role remains limited.⁷³ The cAMP-binding transcriptional regulator, catabolite activator protein (CAP), is arguably the best characterized example of dynamically driven homotropic allostery. Here the allosteric ligand cAMP quenches slow- and fast-time scale dynamics, resulting in activation of DNA binding through a mechanism where conformational selection plays a major role,⁸⁰ superimposed on measurable changes in conformational entropy.⁴ In this case, mutations that negatively impact internal dynamics to the detriment of DNA binding appear to show no effect in the solvent entropy contribution.⁴ In contrast, solvent-coupled dynamics have been shown to play a major role in the PDZ (PSD-95/SAP90 PDZ3) domain, where ligand binding promotes an entropy change that results in signal transmission through solvent;^7,85 further, residues that are solvent-exposed are clearly integrated into the defined dynamical pathways.⁷ Overall, the apparently contradictory findings of the PDZ domain and CAP systems suggest that simultaneous changes in internal dynamics and the hydration shell upon ligand binding may well be a significant feature of functional dynamics in some allosteric systems. Here we show that perturbations in protein internal dynamics can have a compensatory impact on solvent entropy that cannot be inferred from crystal structures alone (Figure 6). Moreover, in other systems where functional dynamics have been investigated, mutations that impact internal motions have a compensatory effect on the hydrophobic effect⁷⁷ or on the solvent accessible surface area.⁸⁶ In those cases, changes in conformational entropy have not yet been reported but clearly suggest the possibility that protein sequence impacts the conformational ensemble by both tuning functional protein dynamics and rearranging superficial solvent molecules. Our findings with CzrA provide significant support for this hypothesis.

Nonetheless, discussions of the true origins that poise certain conformational states for ligand binding are often obscured by the inherent connection between structural and dynamical changes in both the protein itself and its hydration layer. For example, in the case of the PDZ domain, the underlying dynamics behavior has recently been suggested to arise from subtle changes in electrostatic interactions inferred from crystal structures;⁸ however, this cannot imply that dynamics properties are nonfunctional or entirely passive, “enslaved” to attendant structural changes. Instead, it could be argued that this observation reinforces the idea that changes in structure can occur concomitantly with changes in dynamics, particularly in the case of globally “entropically-driven” processes.^10,87 In a similar way, the interdependence of solvent and internal dynamics has been recently illustrated by measurements on how cosolvents affect dynamically driven allostery.⁸⁸ Here, we provide compelling evidence that the protein hydration layer impacts the overall Zn binding thermodynamics in CzrA and that mutations that affect functional internal dynamics strongly impact solvent entropy, in the absence of a significant change in structure. We therefore conclude that both internal and solvent dynamics have functional roles, consistent with previous findings that “cavity” mutations in CzrA that do not directly impact solvent interactions show wild-type coupling free energies.³

Although this work provides support for the hypothesis that changes in the hydration layer of apo- vs Zn-bound CzrA variants, perhaps involving “long-lived” or site-specifically bound water molecules, is a major contributor to the thermodynamics of Zn binding, where such waters might reside is not yet known. We suggest that a compelling candidate solvent reservoir is the “top” of the CzrA homodimer, in the cleft between the C-terminal α5 helices that provide ligands to the Zn, that may be more “open” in the apo-state conformational ensemble. This is consistent with previous hydrogen–deuterium solvent exchange experiments that show increased solvent exchange in the apo-CzrA backbone, notably in the C-terminal α5 helices,²⁶ relaxation dispersion data for the methyl groups in apo wild-type CzrA³ and a structural model of the apo-CzrA-DNA complex based on NMR data.³⁸ Zn coordination to both metal sites here would displace this water reservoir into bulk solvent along with those derived from dehydration of the Zn cation, thus providing a strong entropic contributor to Zn binding; internal protein dynamics are then redistributed in a way that impairs DNA binding.³ Newly developed methods to study site-specific water dynamics in the protein hydration layer have recently been described^29,30,33,34 and can be combined with more established strategies^35,89 to test this hypothesis in CzrA. These experiments constitute an exciting future research direction in this and other metal binding proteins and will provide residue-specific insights on how internal dynamics might be coupled to solvent dynamics.

Allosteric systems have an enhanced ability to acquire new functions.⁸¹ This is particularly the case for the arsenic repressor (ArsR) protein repressor family studied here.¹⁴ Members of the family have evolved to sense a remarkably diverse range of stimuli in different sites scattered throughout an essentially unchanging molecular scaffold.^3,14 We propose that these solvent and protein dynamics mapped here function as entropy reservoirs in CzrA that can be tapped to drive both high affinity Zn and DNA binding. We further propose that these dynamic properties are likely conserved in other ArsR family repressors, even as new specific structural features have evolved to respond to other binding events that redistribute internal and solvent dynamics to inhibit DNA binding. We do however recognize that it may not be possible to easily distinguish those features that represent a true evolutionary adaptation from others that arise from an inevitable physicochemical outcome of that adaptation. In any case, a careful accounting of the specific contributions to the overall thermodynamics of ligand binding may allow us to consider this interconnectedness of internal and solvent dynamics in the context of the evolution of new biological outcomes.^81,90 Indeed, the connection between protein dynamics and molecular evolution has recently been experimentally investigated for a number of enzymes,^86,91,92 and it remains to be fully explored in the context of homotropic and heterotropic allostery in biological regulation.