Bivariate Spatio-Temporal Shared Component Modeling: Mapping of Relative Death Risk due to Colorectal and Stomach Cancers in Iran Provinces

Abstract

Background:

Gastrointestinal cancers make for nearly half fatal cancers with colorectal and stomach cancers’ being listed among the ten most common in Iran. This research aims to determine the spatial pattern and temporal trend of death risk due to colorectal and stomach cancers among provinces of Iran and estimate the effect of shared and specific components as surrogates of risk factors for the aforementioned cancers on changes of death due to the cancers over time and place.

Methods:

In this ecological study, the data regarding death causes in colorectal and stomach cancers during 2006–2011 were obtained from the death registration system of the Iranian Ministry of Health. The estimation of relative risk (RR) of death due to the target cancers was performed applying Bayesian spatiotemporal shared component (SC) model in OpenBUGS software.

Results:

North-Western provinces ranked first regarding stomach cancer RR of death (RR >1.75). Furthermore, some North-Western and central provinces had the highest RR of death due to colorectal cancer (RR >1.5). The SC surrogating the risk factor shared between both cancers had the most effect in Northern, North-Western and western provinces, and the least effect in Southern and South-Eastern ones.

Conclusions:

North and North-West of Iran found to be the high-risk area for death due to both stomach and colorectal cancers and South-East and South provinces shown to have the lowest RR. The obtained results can be illuminating to health resource allocation to the health policymakers.

Introduction

Cancer is one of the most important death causes around the world. According to the declaration of the World Health Organization, more than 13 million people will die due to cancer in 2030.[1] Cancer is the third cause of mortality after car accident and cardiovascular disease in Iran, so cancer is an important problem in public health in Iran.[2] Gastrointestinal cancers make for nearly half of fatal cancers[3] with colorectal and stomach cancers as examples. According to the estimations of International Agency for Research on Cancer, stomach cancer was the fifth most common cancer and the third main death cause in 2012.[4] Geographical distribution has shown to have no pattern; for instance in Asia, along with high-risk countries such as Japan, Korea, and China, there stands the very low-risk India. This may due to different factors such as age, food culture, race but does not follow a strict geographical pattern.[5,6] As stated by 2008–2009 report of Cancer Registry System in Iran, stomach cancer is the third most common cancer in Iran, which happens to be more occurring in the northern parts of the country.[3] It, as well, was a cause of 15.5 percent of deaths in Iran in 2012 and has been the deadliest cancer.[4]

Colorectal cancer is the third most fatal after lung and stomach cancers[7] and in Iran, it ranks as the third and fourth cause of death in men and women, respectively.[8] Iran's Cancer Registry System indicates that the disease occurrences are more frequent in the northern provinces, compared to the central and southern ones.[9] Regarding the soaring rate of occurrences of cancer in Iran and the distribution of the occurrences in differing provinces, as well as the pressing importance of prevention regarding the disease, recognition and identification of the risk factors along with the high-risk geographical regions seem to be inevitable.

The important role geographical distribution of disease scales play in identifying the relative risk (RR) factors has led to intensive use of spatial statistics tools (a branch of Statistics for analyzing spatial data) in performing the analysis.[10] Disease mapping is an example, which is defined as a collection of statistic methods to obtain exact estimations of occurrence, prevalence or death rates of the disease and organizing them in the form of geographical maps.[11]

Since in numerous studies in Medicine and Hygiene, Preventive Medicine and Epidemiology, data is obtained in temporal courses over some years, it is only logical to take into account the analysis of disease mapping which include the time aspect. Doing so, the available spatial models have expanded to different spatiotemporal models.[12,13,14,15] The advantages of spatiotemporal modeling over pure spatial analysis approach is the fact that the former makes it possible to simultaneously investigate the trends over a course of time and single out the uncommon trends. Spatial patterns of diseases risks with fixed or increasing trends over time, provide more convincing clues compared to analysis of spatial patterns in a specific point in time.[16]

To date, the major part of cancer research body in Iran has been descriptive while very few has ever glanced over the role of risk factors. There were a few studies maneuvering over joint cancer mapping in Iran. However, none of these studies used joint spatiotemporal modeling.[17,18,19,20,21,22]

Recent years have seen more and more cases of cancer occurrence and the distribution seems to be geographically-bound in different parts of the country. Considering the shared risk factors between colorectal and stomach cancers and the fact that the very limited body of research regarding cancer mortality in Iran is purely descriptive and solely touches death rates in a specific region over a single time course, the researchers decided to implement bivariate spatiotemporal shared component (SC) modeling to investigate shared and distinct temporal and spatial death causes regarding the two cancers.

Methods

Study design and data

The present ecological study used the data for death due to colorectal and stomach cancers in all provinces in Iran except for Tehran province from 2006 to 2011 with no regard to the cases’ age, gender, etc. The researchers obtained the required data from death and cause of death registration system of the Iranian Ministry of Health. The Ethical Committee of Isfahan University of Medical Sciences, in Isfahan, Iran approved the current study (Project number: 395002).

Here, Y_ijk indicates the number of deaths due to k^th cancer (k = 1, 2) in the i^th region (i = 1,…, 29) and j^th temporal course (j = 1,…, 6) while E_ijk indicates the expected death record due to each of the aforementioned cancers which is reached by multiplying the k^th death probability of target cancer into j^th year into the population of the i^th province during the j^th year. The provinces’ populations were estimated based on the national census of 2006 reported by the Iran Statistical Center. The annual population growth trend of each province was used to estimate the population in the years 2007–2011. The country's incidence of the death due to the k^th cancer was obtained through dividing the number of deaths due to that specific cancer during the desired period of time across the country by the country's population.

Statistical analysis

We implemented joint spatiotemporal mapping using bivariate spatiotemporal SC model.[16] In addition to entering the time dimension, spatiotemporal interaction effects and spatial correlated heterogeneities were also added to the model and four bivariate spatiotemporal mapping models were introduced. The models differed in whether or not to enter the spatiotemporal interaction and heterogeneity value.

The models were performed in Bayesian modeling framework. First, it was assumed that the number of deaths due to k^th cancer, in the i^th region, during the j^th temporal course complies with Poisson distribution Y_ijk~poisson (θ_ijkE_ijk) where stands for unknown relative death risk of k^th cancer in the i^th region during the j^th temporal course.

Second, the latent variables (SCs) were introduced and variability of observed distribution around unknown RRs (θ_ijk) were modeled. The spatiotemporal structure was introduced based on modeling log of RR.

Among the four mentioned models, for the sake of parsimony, only the most complex model consisting of all parameters, intercepts, spatial and temporal shared and specific components along with their scale parameters, spatiotemporal interaction effects, and heterogeneity effects is introduced here:

Here, θ_ij1, θ_ij2 are respectively expressing the RR of death due to stomach and colorectal cancers in the i^th province, during the j^th temporal course.

α_k indicates disease-specific intercept of the k^th cancer while λ_i, λ_1i, λ_2i and t_j, t_1j, t_2j respectively refer to the spatial and temporal effects of shared and specific components suggesting the risk factors of the specific cancer.

Spatial and temporal scale parameters (δ > 0,ψ > 0) respectively indicate the weight of SCs on spatial and temporal changes of the cancers and can be different for each of related cancers.

Finally, ξ_ij is the space-time interaction effect and ξ_ijk indicates the heterogeneity effects.

To perfect the Bayesian model, all unknown parameters were assigned prior distribution. The random spatial effects (λ_i, λ_1i, λ_2i) were assigned normal conditional autoregressive prior distribution with weights equal 1 to the neighboring regions, where adjacency matrix is defined according to this neighboring structure. Accordingly, first order random walk priors were implemented for temporal trends (t_j, t_1j, t_2j).[12,16] For space-time interaction effects ξ_ij, simple interchangeable hierarchical structures for were taken into consideration.[14] For heterogeneity expression (ξ_ij1, ξ_ij2)² multivariate normal distribution was assigned with mean of zero Σ^-1 and covariance matrix. Flat noninformative distribution was also assigned to disease-specific intercepts(α_k). A normal distribution was, as well, assigned to the logarithm of temporal and spatial scale parameters (logδ and logψ). The hyper-parameters of shared elements (τ's) were separately assigned the weakly informative Gamma hyperprior distributions.[23] For the precision matrix of disease-specific heterogeneity effects (Σ^-1), Wishart prior distribution (Q, 2) was used, where Q is the 2-dimensional identity matrix (I₂).

The suitability of all models to the data was assessed through Bayesian estimation software, OpenBUGS. Posterior distribution estimations for the model parameters were obtained from simulation methods of Monte Carlo Markov Chain. Markov chain was administered 50,000 times for each model and Brooks-Gelman-Rubin diagnostic tool, as well as observing the autocorrelation figures were implemented to assess the convergence of all parameters. Burn-in was repeated 20,000 times and the results were reported based on the remaining 30,000 posterior sample with thin 10 to decrease correlation.[24,25] The comparison between the spatiotemporal models SC was done using deviance information criterion (DIC) where the lower values indicated the model's being more suitable.[23,24,26,27]

Results

Table 1 includes the death due to stomach and colorectal cancers from 2006 to 2011, based on the information obtained from the death causes registration and classification system in the Iranian Ministry of Health and Medical Education. This indicates that, in spite of minor fluctuations in some years, the number of the deceased due to the two aforementioned cancers has increased in the country.

Table 1.

The number of the deceased due to stomach and colorectal cancers from 2006 to 2011

Year	2006	2007	2008	2009	2010	2011	Total
Number of death due to the stomach cancer	5446	5621	5594	5674	5596	5510	33,439
Number of death due to the colorectal cancer	820	989	1099	1172	1096	1169	6345

As mentioned earlier, this study was designed to investigate 4 forms of SC bivariate spatiotemporal models, based on having or not having the spatiotemporal interaction effects as well as the disease-specific heterogeneity effects. To compare the suitability of the 4 main models and to choose the optimized model, the DIC was used and the related information can be found in Table 2.

Table 2.

The results of deviance information criterion to compare bivariate spatiotemporal shared component models

Model	DIC
Model 1: No interaction + no heterogeneity	3012.0
Model 2: Intrraction + no heterogeneity	2589.0
Model 3: No interaction + heterogeneity	2309.0
Model 4: Interaction + heterogeneity	2328.0

DIC=Deviance information criterion

As shown in Table 2, the model with disease-specific heterogeneity effect which does not have the spatiotemporal interaction effect (Model 3) is the best and thus chosen for the modeling.

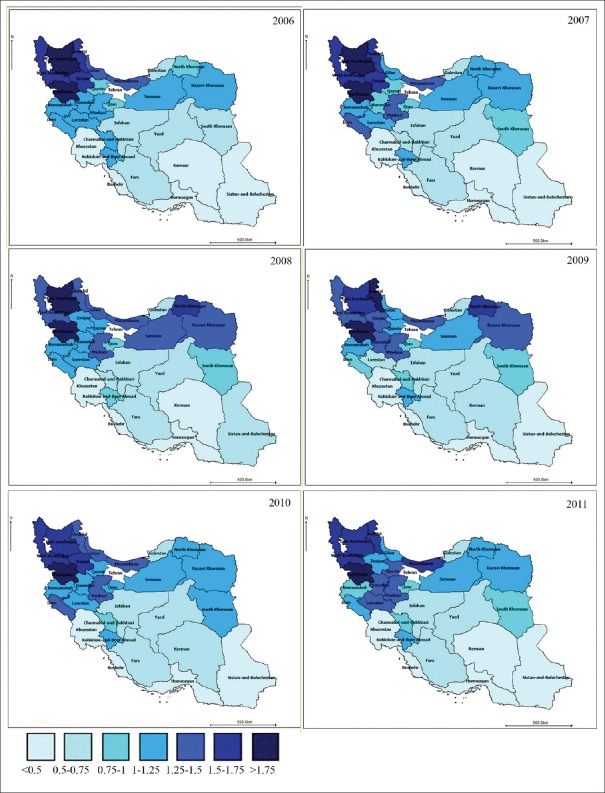
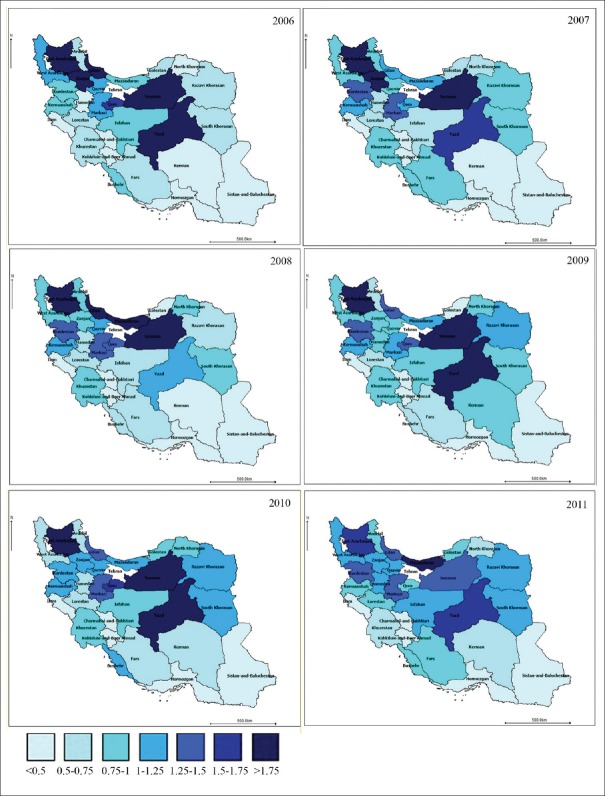
Then, the RR of death due to stomach and colorectal cancers was estimated using the bivariate spatiotemporal SC model [Figures 1 and 2]. It indicated that stomach cancer is of higher relative death risk in Northern, North-Western and western provinces. Southern, South-Eastern and South-Western provinces were of the lowest risk in all 5 temporal periods. Some North-Western and central provinces found to have the highest relative death risk due to colorectal cancer in all 5 temporal periods.

Figure 1.

The map of estimated relative death risk due to stomach cancer according to bivariate spatiotemporal shared component model: 2006–2011

Figure 2.

The map of estimated relative death risk due to colorectal cancer according to bivariate spatiotemporal shared component model: 2006–2011

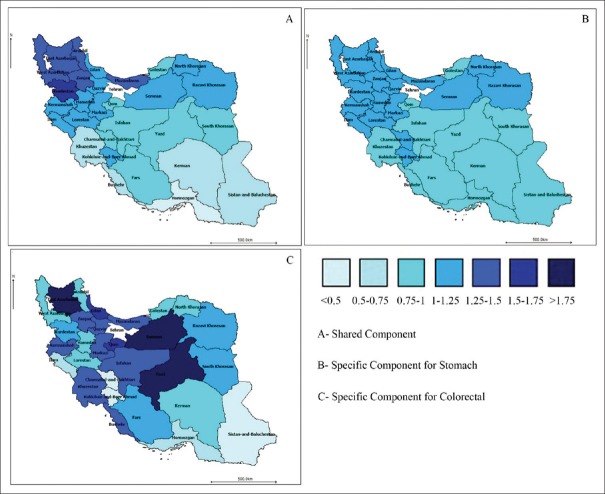
Then, the estimation map of RR of the effect of SCs of risk factors was designed based on spatial distribution of each cancer across the temporal course (λ_i, λ_1i, λ_2i) [Figure 3]. The values indicate the effect of each component surrogating the risk factors on the geographical distribution of RR due to the cancers’ death cause related in all investigated temporal courses. The SC surrogating the risk factor shared between stomach and colorectal cancers had the most dominant effect in Northern, North-Western and western provinces, and the least dominant effect in Southern and South-Eastern ones [Figure 3A]. Generally speaking, the map of effect of stomach cancer specific component has almost always been steady and a specific pattern cannot be traced among the effects of this component across provinces [Figure 3B]. The pattern noticed regarding the colorectal cancer-specific component effect, on the other hand, is a bit different. This specific component has the highest effect in Yazd (center of country), Semnan (center), and East-Azerbaijan (North-West) and the least effect in two central provinces, Kohgiluyeh and Boyerahmad, and Chaharmahal and Bakhtiyari provinces [Figure 3C].

Figure 3.

The map of estimated relative risk of spatial effect of shared and specific components based on bivariate spatiotemporal shared component model

Table 3 shows the estimate of RR of the temporal effect of the components across the country. All the obtained values are similar and really close to 1 and all the intervals include 1. This shows that the effects of the components representing the risk factors on the temporal trend of relative death risk due to the cancers is not meaningful. This indicates that as the time progresses, RRs are not decreasing or increasing for.

Table 3.

The estimated relative risk of temporal effects of shared and specific components: Posterior median (95% CI) per year

Year	2006	2007	2008	2009	2010	2011
Shared component	0.994 (0.94-1.04)	0.998 (0.96-1.04)	0.999 (0.96-1.03)	1.001 (0.97-1.03)	1.005 (0.97-1.05)	1.004 (0.96-1.06)
Specific component for stomach cancer	0.994 (0.94-1.04)	0.997 (0.96-1.04)	1.000 (0.97-1.03)	1.003 (0.97-1.04)	1.003 (0.97-1.05)	1.002 (0.95-1.05)
Specific component for colorectal cancer	0.995 (0.94-1.04)	0.997 (0.94-1.05)	0.996 (0.94-1.04)	1.000 (0.95-1.05)	1.006 (0.97-1.07)	1.007 (0.94-1.08)

The relative weight of these effects was estimated, so that the role of the components in spatial changes of the related cancers could be compared more precisely. 1.27 indicates the ratio between the magnitudes of SC for stomach and colorectal cancers and reveals that the role of shared risk factor in geographical distribution of death due to stomach cancer plays is more pervasive compared to that of colorectal cancer but the value interval (0.590–-3.086) which, as well, includes 1, indicates that the relative magnitude of SC in spatial changes of the two cancers is not meaningful.

To better compare the magnitude of temporal effects of risk factor components in related cancers, the relative magnitude of these effects was estimated. The estimations talk of the magnitude of risk factors in changes of deaths due to the relevant cancers across the studied regions, during the temporal period. The results showed that the ratio of weight of SC for stomach cancer to the same weight for colorectal cancer in 0.935 with value interval of (0.475–1.809) which, in turn, indicates that the relative weight of SC s of temporal changes in both cancers is not meaningful.

Discussion and Conclusions

Bivariate spatiotemporal SC model is a latent-variable model which does not need real data on risk factors. By entering the components as surrogates of risk factors, the model can clarify not only the spatial pattern and temporal trend of investigated diseases, but also the spatial and temporal effects of these components as well as the relative weight of temporal and spatial effects of the components on each of the related diseases.[10,23,24,28,29]

In this study, we applied the mentioned model in Iran for the first time. The previous studies in the field of joint disease mapping in Iran does not take time effect into account and there were not possible to evaluate temporal trend of disease and their risk factors.[18]

In addition to its superiority over the pure spatial models, this model has some advantages over other multivariate spatiotemporal disease mapping models: The possibility to separately estimate of shared and specific components as surrogates of risk factors, while other models only map the general RR of each disease; the expanded possibility to recognize the high risk regions; having temporal and spatial scale parameters and so estimating the relative weight of each SC for all related disease; the possibility to have spatial-temporal, spatial-disease, temporal-disease, and spatial-temporal-disease interaction effects; no need to limiting constraint of considering the similar correlation between the diseases across all regions.[16,30]

Applying this model needs for the number of risk factors and the disease linked to each risk factor in advance. The final results would highly depend on the way the risk factors are defined. To identify the related risk factors of each disease, the epidemiological history of diseases need to be taken into consideration.[13,29]

In this model, it is assumed that effects of shared and specific components are independent from one another. This assumption is not constant in many of the observations and epidemiologic documents.[29,31,32]

Compared to raw mapping or mapping standardized values, this model has proved to be more efficient when the number of desired observed cases is rare. Hence, the higher the level of access to information such as the counties, cities, urban areas, and postal areas, the more efficient the model will be.

We found that two South-Eastern and Southern provinces, Sistan and Baluchistan and Hormozgan have lowest RR for both cancers. Northe and North-West part of country including Mazandaran, East-Azerbaijan, and Kurdistan are the highest risk areas regarding the two stomach and colorectal cancers and these obtained results are consistent with those of Mahaki et al.,[17] Kavousi et al.,[33] Rastaghi et al.[34] and Nasrazadani et al.[35]

This study has some limitations:

1. We only have five short time periods in this study. As a result we found that there is not any significant temporal effect of the shared and specific components across the country. This is because cancers are long latency chronic diseases and so we do not expect “bursts” of short-term clusters

2. Data were available only for provincial level and not for counties, districts, etc., so we had to consider the provinces as our geographical areas

3. As age and sex information was not available, we did not used age-standardized rates of deaths and data for each sex separately. This is a major limitation of the study

4. In addition to age and sex, we did not have access to data about other risk factors of the cancers or death due to. Hence, the model does not contain any covariates

5. We used the prior distributions only based on suggestion from the published papers.

Based on the results and the mentioned limitation, there are some suggestions:

It is suggested that this model be implemented for longer time period to better evaluate the temporal trend. In addition, having smaller regions such as counties, towns, areas or neighborhoods helps showing the advantages of the model over mapping raw data. It is recommended to adjust for age, sex, and the most known factors affecting the incidence and death rates of the cancer to make the results more interpretable.

It is also suggested sensitivity analysis for different prior distributions be taken in to consideration and the results of the distributions be compared. This will help to estimate the sensitivity of the model to the prior distributions allocated to the parameters. Finally, this study provides useful information, on areas requiring more attention, for policy makers and medical experts. It is seen fit to perform more epidemiological studies in high risk regions, so that prevention policies are grounded in such high risk areas.[36]

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.