Abstract
Deep learning methods have shown great success in pixel-wise prediction tasks. One of the most popular methods employs an encoder-decoder network in which deconvolutional layers are used for up-sampling feature maps. However, a key limitation of the deconvolutional layer is that it suffers from the checkerboard artifact problem, which harms the prediction accuracy. This is caused by the independency among adjacent pixels on the output feature maps. Previous work only solved the checkerboard artifact issue of deconvolutional layers in the 2D space. Since the number of intermediate feature maps needed to generate a deconvolutional layer grows exponentially with dimensionality, it is more challenging to solve this issue in higher dimensions. In this work, we propose the voxel deconvolutional layer (VoxelDCL) to solve the checkerboard artifact problem of deconvolutional layers in 3D space. We also provide an efficient approach to implement VoxelDCL. To demonstrate the effectiveness of VoxelDCL, we build four variations of voxel deconvolutional networks (VoxelDCN) based on the U-Net architecture with VoxelDCL. We apply our networks to address volumetric brain images labeling tasks using the ADNI and LONI LPBA40 datasets. The experimental results show that the proposed iVoxelDCNa achieves improved performance in all experiments. It reaches 83.34% in terms of dice ratio on the ADNI dataset and 79.12% on the LONI LPBA40 dataset, which increases 1.39% and 2.21% respectively compared with the baseline. In addition, all the variations of VoxelDCN we proposed outperform the baseline methods on the above datasets, which demonstrates the effectiveness of our methods.
Keywords: Deep learning, voxel deconvolutional layer, voxel deconvolutional networks, volumetric brain image labeling
1. INTRODUCTION
In recent years, deep learning methods play an important role in various computer vision tasks such as image classification [14], data completion [17], action recognition [12] and pixel-wise prediction [4, 11, 26]. Some key network layers like convolutional layers [15], pooling/unpooling layers [21, 34], deconvolutional layers [28] and some well-known models like generative models [9] and encoder-decoder architectures [21, 23] are frequently used for these tasks. In pixel-wise prediction tasks, U-Net [23] with and encoder-decoder architecture is commonly used. The encoder path contains convolutional and down-sampling operations to extract high-level feature maps from raw images, while the decoder path recovers feature maps to the original spatial size using up-sampling operations. The architecture of an encoder is very similar to a classic convolutional neural networks which have been studied extensively [16, 23]. On the other hand, less attention is paid to the decoder path. There are three primary ways to up-sample feature maps; namely deconvolution, unpooling and resampling with interpolation [2]. In practice, deconvolutional layers are the most commonly used. However, a key problem with the deconvolutional layer is the presence of the checkerboard artifact issue [1, 22], which is caused by the independence among the adjacent pixels on the output feature maps.
To solve the checkerboard artifact problem, some studies focused on improving the post-processing [5], which made the whole process not fully trainable. Some other work focused on adding smooth constraints [13], which resulted in a more complex process. In contrast, the pixel deconvolutional networks [7] solved the checkerboard artifact problem by generating the intermediate feature maps sequentially, thereby building direct relationships among adjacent pixels on output feature maps. This is an effective way while keeping the learning process trainable. However, it only solved this issue in 2D deconvolutional layers. The checkerboard artifact issue also exists in 3D deconvolutional layers, and it is more challenging due to the fact that the number of intermediate maps needed to generate one deconvolutional layer grows exponentially with dimensionality. There are a total of 2d intermediate feature maps needed when generating a deconvolutional layer given a d dimensional input.
In this paper, we propose the voxel deconvolutional layer (VoxelDCL) to address the checkerboard artifact of 3D deconvolutional layers. We build four variations of VoxelDCLs, which are known as iVoxelDCLc, iVoxelDCLa, VoxelDCLc, and VoxelDCLa, based on different approaches when generating the intermediate feature maps. The iVoxelDCLc and iVoxelDCLa use the input along with the generated intermediate feature maps to generate new intermediate feature maps by concatenation and addition, respectively. The VoxelDCLc and VoxelDCLa only use the generated intermediate feature maps to generate new intermediate feature maps. We also provide an efficient implementation method to improve the computational efficiency by reducing unnecessary dependencies among the intermediate feature maps. To demonstrate the effectiveness of the proposed VoxelDCL, we build the voxel deconvolutional networks (VoxelDCN) based on the U-Net with four variations of VoxelDCL and apply them to the volumetric brain image labeling task [6, 29, 31, 33, 37] using the Alzheimer’s disease neuroimaging initiative (ADNI) [20] and the LONI LPBA40 [25] datasets. The results show that our methods outperform the U-Net with regular deconvolutional layers significantly in terms of dice ratio. Specifically, the iVoxelDCLa achieves the best performance on both the ADNI and LONI LPBA40 datasets with 83.34% and 79.12% dice ratio, respectively.
2. RELATED WORK
2.1. Deep Learning for Pixel-Wise Prediction
In computer vision, many problems can be formulated as assigning a label to every pixel of an image, such as semantic segmentation [11, 21, 23, 26]. The goal of semantic segmentation is to label each pixel of the image so that pixels belonging to the same class get the same label. In recent years, convolutional neural networks (CNNs) have had great success in computer vision and brought great improvement in semantic segmentation tasks. The fully convolutional network (FCN) [26] can generate segmentation maps with an input image of any size. It is much faster and more effective than the traditional patch-wise classification methods [3]. Multiple encoder-decoder based architectures [16, 23] are also proposed. The encoder part reduces the spatial sizes with pooling layers and extracts high-level feature maps while the decoder part recovers them to the original spatial size. U-Net [23] is one of the most widely used networks in natural and medical image segmentation tasks.
2.2. Operations for Up-Sampling
To recover the spatial size of the extracted feature maps to the original size as the input image, up-sampling layers are essential in the decoder path of a dense prediction network. Unpooling, resampling with interpolation, and deconvolution are the most commonly used operations for up-sampling. Unpooling layers [21, 34] put each activation back to its original location based on the recorded location of maximum activation selected during the corresponding pooling operations. Up-sampling layers using resampling with interpolation [2] scales an feature map to the desired size and calculates the value of each pixel using an interpolation method such as bilinear interpolation. In the above two methods, there is no learning parameters required in the operation. The third method, known as the deconvolutional layer [1, 22, 28], is the most popular method for up-sampling tasks. It up-samples feature maps by using operations that can be formulated as convolutional operations with learned kernels. More details are explained in Section 3.1. However, deconvolutional layers suffer from the checkerboard artifact issue. This is because there is no direct relationship among adjacent pixels on the output feature map. To solve this problem, pixel deconvolutional networks [7] built direct relationship among adjacent pixels on the output of a deconvolutional layer by generating intermediate feature maps sequentially. This process is different in traditional deconvolutional layers where the intermediate feature maps are generated independently. Details of the concepts of intermediate feature maps and the sequential process are given in Section 3. The dependencies among the intermediate feature maps add direct relationships among adjacent pixels on the output feature map, thereby alleviating the checkerboard artifact in 2D deconvolutional layers.
2.3. 3D Brain Image Labeling
3D brain image labeling is an important task since plenty of quantitative brain image analysis often relies on it. It becomes a popular topic in the medical image analysis field. In computer vision area, this task can be seen as a 3D semantic segmentation task [35, 38]. Some existing methods [8, 18, 24, 30, 32, 36] use multi-atlas based labeling models to predict the labels of new images. These methods first transfer the segmentation labels from pre-labeled atlases to a new image and then apply the label fusion method to combine the transferred labels as predicted results. There are also several learning-based labeling methods using random forests, support vector machine, and neural networks [19] to train a prediction model. Among these methods, neural networks have an unique advantage in that it does not require hand-crafted feature extraction in advance. It enables end-to-end learning, which improves efficiency of the training process. In this work, we introduce a novel deep neural network architecture and apply the variations of this network on the 3D brain image labeling task.
3. VOXEL DECONVOLUTIONAL NETWORKS
In this section, we introduce the concept of deconvolutional layers and other related operations, including transposed convolutional layers [28] and sub-pixel convolutional layers [1, 22, 28]. We show the equivalence among these concepts in the 1D case. After that, we describe 2D and 3D deconvolutional layers in the form of sub-pixel deconvolutional layer and show the checkerboard artifact that they suffer [22]. We discuss existing approaches to solve the checkerboard artifact and propose the voxel deconvolutional layers and networks, which can overcome the checkerboard problem of 3D deconvolutional layers. We show that our methods achieve better labeling performance on the Alzheimer’s disease Neuroimaging Initiative (ADNI) [20] and the LONI LPBA40 [25] datasets as compared with other baseline methods.
3.1. Deconvolutional Layer
Deconvolutional layers can be viewed as a form of convolutional layers. The relationship between convolutional and deconvolutional layers can be best understood when both of them are considered as fully connected layers. Specifically, convolutional layers can be considered as fully connected layers with sparse connection matrices. Let us consider the following example in 1D. Given an input vector x ∈ ℝ8, we pad the input by adding two zeros to both ends of x, yielding the padded input . We then apply a 1D convolution with a stride of 2 and a kernel of size 4 to produce an output vector y ∈ ℝ5. This convolution operation can be equivalently viewed as a fully connected operation as
| (1) |
with a 5 × 12 sparse connection matrix C, defined as follows:
| (2) |
In this example, y can be cropped by one pixel from the right end to make the down-sampling factor to be 2.
The above example reduces x to a lower-dimension by a convolution of stride 2. A similar operation can be used to convert a lower-dimensional input to a high-dimensional output, resulting in the deconvolutional operation. Specifically, assume y is the input and is the output, then their relationship can be expressed as
| (3) |
where C is defined in Eq. (2). It can be seen from Eq. (3) that, given a lower-dimensional input, a higher-dimensional output can be obtained via a fully connected layer with a sparse connection matrix. This results in the so-called deconvolutional layer. Since deconvolution layers use the transposed weight matrix of its corresponding convolutional operation C, it is also known as transposed convolutions.
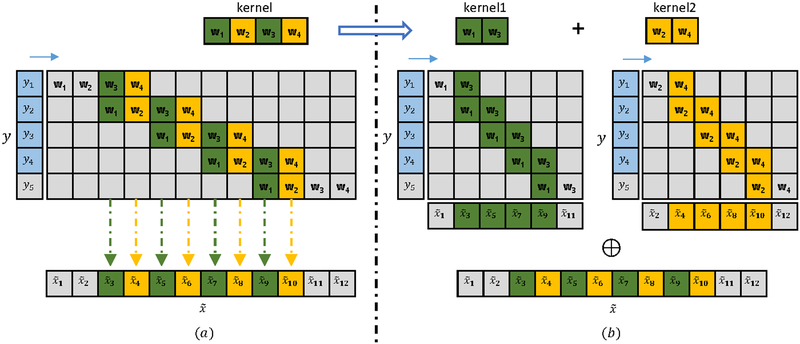
Since C is a sparse matrix, another way to understand the deconvolutional layer is to interpret it as a standard convolution. Specifically, it can be considered as performing multiple independent convolutions on the input followed by a periodical shuffling operation [27]. An example is given in Figure 1 to illustrates this idea.
Figure 1:
Illustration of a 1D deconvolutional layer. The green and yellow colors represent the odd and even columns of the kernel, respectively. ⊕ denotes the periodical shuffling and combination operation. y is the input and is the output from the deconvolutional layer. By multiplying each column of the weight matrix C with y, we can obtain its corresponding output i (see (a)). Since all the odd columns of are computed only by w 1 and w 3 and all the even columns of are computed by w2 and w4, the operation can be decomposed into two convolutions with two independent kernels of sizes 1×2, resulting in kernel1 and kernel2. The intermediate results are then shuffled and combined to obtain the final output can be cropped by two pixels from both ends to make the up-sampling factor to be 2.
3.2. 3D Deconvolutional Layer
In the previous section, we describe how to understand deconvolutional layers as a form of convolutional layers in 1D space. The same strategy can be used in 2D and 3D spaces as well. In 2D case, the first step is to generate 4 intermediate feature maps from padded input. This step simply requires 2D convolutional operations. Next, these feature maps are periodically shuffled and combined together to form the output. The same steps can be applied to perform deconvolutional operations in 3D space, which will be discussed next.
Assume X ∈ ℝl×m×n is the input and Y ∈ ℝ2l×2m×2n is the output of a deconvolutional layer. Here the up-sampling factor is 2. We first perform eight 3D convolutional operations on the input. Each of such operation generates one intermediate feature map Yi with size l ×m × n given by
| (4) |
where ⊗ denotes the convolutional operation, Yi denotes the ith feature map and ki denotes the corresponding kernel. We add padding to the input in order to make sure that spatial size remains the same. Finally, these 8 feature maps are periodically shuffled and combined together as
| (5) |
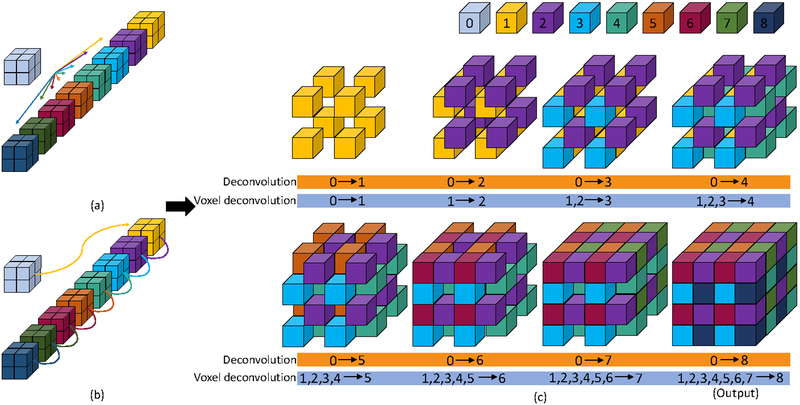
where ⊕ denotes the periodical shuffling and combination operation, as illustrated in Figure 2.
Figure 2:
Illustration of the 3D deconvolutional layer and voxel deconvolutional layer. For convenience, we use number 0 to denote the input, and number 1 – 8 to denote the eight intermediate feature maps which are generated from convolutional operations. The input size is 2 × 2 × 2 and the desired out size is 4 × 4 × 4. The size of each intermediate feature map is also 2×2×2. (a) shows how the intermediate feature maps are generated independently from eight different kernels in a regular 3D deconvolutional layer. This independent generation process is also indicated in the lower orange bar in (c). (b) shows how the intermediate feature maps are generated sequentially in a voxel deconvolutional layer. The ith feature map are built on the 1st, …,(i −1)th feature maps. In iVoxelDCLa and iVoxelDCLc layers, input data is also included in this process. This sequential generation process is also indicated in the lower blue bar in (c). (c) displays the periodically shuffling and combination process of eight feature maps to form the final output of a deconvolutional layer.
Compared to deconvolutional layers in 2D space, the number of feature maps needed in 3D space grows exponentially. In general, assume the up-sampling factor is 2 and the dimensionality is d, the number of intermediate feature maps need to generate one deconvolutional layer is 2d. This indicates that deconvolutional layers in higher dimensional space are much more complex and computationally expensive than those in lower dimensional space. These are factors to consider when we introduce voxel deconvolutional layers in Section 3.3.
3.3. Voxel Deconvolutional Layer
When we consider a deconvolutional layer as the shuffled combination of several intermediate feature maps, discontinuities among adjacent pixels can be observed frequently. This is not surprising since the adjacent pixels are coming from independent feature maps. This is the checkerboard artifact problem that all deconvolutional layers suffer, no matter calculated in 2D or 3D space.
Gao et al. [7] solved the checkerboard artifact of deconvolutional layers in 2D space by adding relations to the intermediate feature maps. Inspired by [7], we propose the voxel deconvolutional layer to solve the same issue in 3D space. As we mentioned in Section 3.2, the computational cost and complexity of deconvolutional operations in 3D space are much higher than those in 2D space, thereby making this task challenging.
Back to the example in Section 3.2, we use X ∈ ℝl×m×n to denote the input and Y ∈ ℝ2l×2m×2n to denote the output. The eight intermediate feature maps are Y1,Y2,…,Y8, each of size l × m n .
In voxel deconvolutional layers, Y1,Y2,…,Y8 are formed sequentially to build direct relations in-between.·Suppose X, Y1,Y2,…,Yi 1 are already generated, Yi will be built on X together with Y1,Y2,…Yi-1 instead of simple X as in traditional deconvolutional layers. The generation of Y1 remains the same as it is the first intermediate feature map. There are mainly two ways to combine X, Y1, Y2, Yi-1 together; namely addition or concatenation.
We first introduce the naming conventions of the proposed voxel deconvolutional layers and corresponding networks in below:
Suffix c: We use concatenation when combining multiple inputs to generate a new intermediate feature map.
Suffix a: We use addition when combining multiple inputs to generate a new intermediate feature map.
Prefix iVoxel: Both the original input and existing intermediate feature maps are included to generate a new feature map.
Prefix Voxel: Only existing intermediate feature maps are included to generate a new feature map.
We first introduce iVoxelDCLc. In iVoxelDCLc, the input X and intermediate feature maps Y1,Y2,…,Yi-1 are concatenated together to form the input to generate Yi as
| (6) |
where ⊗ denotes a convolutional operation, [∙,∙] represents the concatenation ki denotes the corresponding convolutional·kernel. By using concatenation, X, Y1, …, Yi 1 are stacked channels of a single input to generate Yi. There will be weights assigned to each of X, Y1, …, Yi−1, indicating their importance to Yi . However, concatenation will cause memory and computational issues due to the large amount of parameters needed. This problem can be reduced by using addition when combining multiple related feature maps as input, which will be denoted as iVoxelDCLa.
In iVoxelDCLa, the input X and intermediate feature maps Y1,Y2,…,Yi−1 are added together to form the input to generate Yi as
| (7) |
In iVoxelDCLc and iVoxelDCLa, the input X is included in the generation of every intermediate feature map. This might be redundant since the information carried in X will be carried over in Y1 to Y8 through this sequential process. In the next two versions of VoxelDCL, we take out the input X when generating Y2,…,Y8. Only the first intermediate feature map Y 1 is generated using·X.· Similarly, we first use concatenation to combine multiple inputs, which will be denoted as VoxelDCLc.
In VoxelDCLc, the intermediate feature maps Y1,Y2,…,Yi-1 are concatenated together to form the input to generate·Yi while Y1 is generated from the input X :
| (8) |
To further reduce memory usage and computational complexity, we use addition instead of concatenation the same way as we described in iVoxelDCLa layer. This layer is known as VoxelDCLa.
In VoxelDCLa, intermediate feature maps Y1,Y2,…,Yi 1 are added together to form the input to generate Yiwhile Y1 is generated from the input X :
| (9) |
Once all the eight intermediate feature maps are generated, we can obtain the final output using Eq. (5). In Figure 2, we provide an example to illustrate how the VoxelDCLa and VoxelDCLc work.
3.4. Efficient Implementation
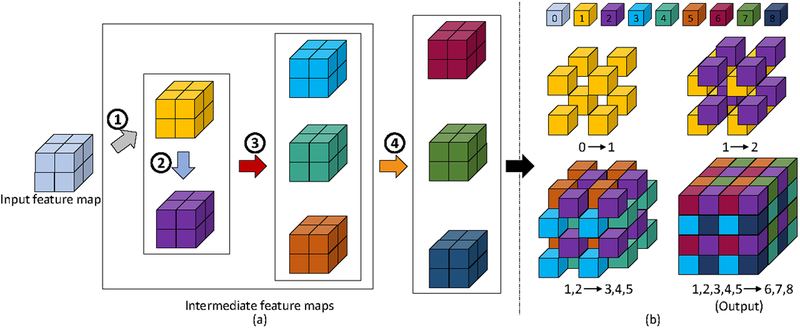
We propose an efficient way to implement all of the above voxel deconvolutional layers in order to scale down the computational cost. The goal is to reduce unnecessary dependencies among the intermediate feature maps. The basic principle is that, for voxels that are not adjacent to each other but linked to the same pivot voxel in the output, we generate their corresponding feature maps in parallel. In this way, we remove the dependency of unrelated inputs when generating new feature maps, hence simplifying the process and expediting the computation. In this new design, the intermediate feature maps are generated in 4 steps. Specifically, Y1, which denotes the 1st intermediate feature map, is generated from the input X . Then Y2 is generated from Y1. Since voxels from Y3, Y4, Y5 are not adjacent to each other but are all linked to voxels from Y1, we generate them in parallel using previously generated Y1 and Y2. The same strategy is used for generating Y6, Y7, Y8. They are generated in parallel from all the previously generated Y1,…,Y5. In iVoxelDCLa and iVoxelDCLc, the input X is also included in each step. By using parallel generation in steps 3 and 4, the computational time for VoxelDCL is reduced. In this way, we build a reasonable relationship among these intermediate feature maps. Figure 3 illustrates how VoxelDCLa and VoxelDCLc work.
Figure 3:
Illustration of the proposed efficient implementation of the VoxelDCLa and VoxelDCLc layers. The notation remains the same as introduced in Figure 2. In addition, each step in the efficient implementation is denoted as numbers with circles in (a). (a) shows the efficient generation process of intermediate feature maps step by step. Step 1 is to generate the 1st feature map directly from the input. Step 2 is to generate the 2nd feature map from the 1st one. The 3rd to 5th feature maps are generated from the 1st and 2nd feature maps in step 3. Finally, the last three feature maps are generated from all previous five feature maps in step 4. (b) shows how these eight intermediate feature maps are shuffled and combined to form the final 4×4×4 output. In VoxelDCLa layers, multiple feature maps are added together to form the input for the next feature map while in VoxelDCLc layers they are concatenated.
3.5. Overview of Network Architectures
U-Net [23] is a convolutional neural network architecture commonly used for dense prediction. It has an encoder path which extracts high-level feature maps from raw images and a decoder path which recovers feature maps to the original spatial size. In the classic U-Net architecture, there is repeated application of three convolutional layers, followed by a max pooling layer for down-sampling in each encoder block. Batch normalization [10] is used after each convolutional layer. The number of channels is doubled after each down-sampling operation. In each decoder block, there is a deconvolutional layer followed by two convolutional layers. The output of the deconvolutional layers are concatenated with corresponding feature maps from encoder blocks before going to the next block. The proposed architecture in this work, which is denoted as voxel deconvolutional network (VoxelDCN), is based on this U-Net framework. But we replace the deconvolutional layers in the decoder path with voxel deconvolutional layers. So there are five architectures implemented for comparison:
U-Net: We use U-Net as our baseline method. It is a classic neural network architecture with encoder and decoder parts. It uses deconvolutional layers for up-sampling in decoder path.
iVoxelDCNc: In this method, we replace all deconvolutional layers in U-Net with iVoxelDCLc layers.
iVoxelDCNa: In this method, we replace all deconvolutional layers in U-Net with iVoxelDCLa layers.
VoxelDCNc: In this method, we replace all deconvolutional layers in U-Net with VoxelDCLc layers.
VoxelDCNa: In this method, we replace all deconvolutional layers in U-Net with VoxelDCLa layers.
Figure 4 shows the architecture we implemented on the ADNI dataset. On the LONI LPBA40 dataset, we use a similar architecture with more blocks in both encoder and decoder paths to avoid under-fitting problem.
Figure 4:
Network architecture implemented on the ADNI dataset. The encoder has two max pooling layers with sizes of 2×2×2. We replace the regular deconvolutional layers in U-Net with variations of the proposed voxel deconvolutional layers in the decoder path.
4. EXPERIMENTAL STUDIES
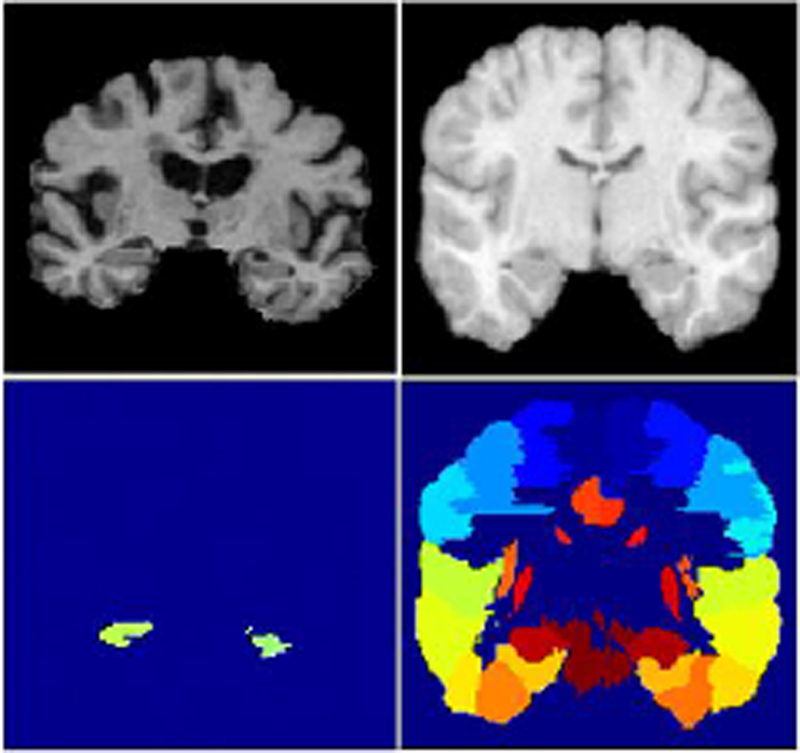
In this section, we demonstrate the performance of our proposed methods on two public datasets that have been widely used for brain images labeling, namely the Alzheimer’s disease neuroimaging initiative (ADNI) dataset [20] and the LONI LPBA40 dataset [25]. We select these two datasets since they represent different types of brain image labeling. The ADNI dataset has rich brain MR images for labeling hippocampal regions. It can be treated as a segmentation task with binary classes. On the contrary, the LONI LPBA40 dataset has various regions of interest, mostly inside the cortex of the brain. It can be treated as a multi-class segmentation task. Examples from these datasets are provided in Figure 5. Our code is publicly available1.
Figure 5:
Examples of MR images from the ADNI dataset (left) and the LONI LPBA40 dataset (right). The top row displays the intensity images, and the bottom row displays the manually segmented labels.
We use classic U-Net as the baseline method to evaluate the performance of our proposed methods . Dice ratio is used to measure the labeling accuracy. It calculates the degree of overlap between the predicted area and its corresponding ground truth for each target class. It is defined by
| (10) |
where A is the predicted result and B is the corresponding true label. For k different regions of interest (ROI), an averaged dice ratio is calculated, given by
| (11) |
where Ai represents the prediction for the i th ROI and Bi represents the corresponding ground truth label.
4.1. ADNI Dataset
The ADNI dataset is mostly used to label hippocampus in brains. The task is to determine whether a certain part of the brain is hippocampus or not. We consider it as a segmentation task with binary classes.
Data Preparation:
There are 64 samples in the ADNI dataset with sizes of 96 × 124 × 96. We randomly split the dataset into training data with 59 samples and testing data with 5 samples. We repeat this process for five times and build five segmentation models respectively. The averaged dice ratio is the reported performance of this experiment.
Experimental Setup:
We build the baseline model using U-Net architecture as shown in Figure 4. The number of output channels in the first encoder block is 16. The convolutional kernel size is 3×3×3 and the stride size used in the max pooling layers is 2×2×2. The last convolutional operation in the final decoder block has 2 output channels, which corresponds to the total number of classes. We apply batch normalization after each convolutional layer, except for the output layer. The training batch size is 4. We implement our methods on Tensorflow and use AdamOptimizer to update the network with moment estimates β1 = 0.9 and β2 = 0.999.
Analysis of Results:
Table 1 shows the overall dice ratios of the baseline method and the proposed methods. We can see that all the proposed methods have higher dice ratios than the baseline method. Model iVoxelDCNa achieves 83.34% in dice ratio, which improves the baseline method by 1.39%. The result demonstrates that the proposed methods, which intend to build relationships among intermediate feature maps, can help networks better capture local information of images than the baseline method.
Table 1:
Experimental results on the ADNI and LONI LPBA40 datasets.
| Dataset | Model | Dice Ratio (%) |
|---|---|---|
| ADNI | U-Net | 82.1985 |
| iVoxelDCNc | 82.8784 | |
| iVoxelDCNa | 83.3403 | |
| VoxelDCNc | 82.2777 | |
| VoxelDCNa | 82.9553 | |
| LONI LPBA40 | U-Net | 77.4209 |
| iVoxelDCNc | 78.3524 | |
| iVoxelDCNa | 79.1294 | |
| VoxelDCNc | 78.7590 | |
| VoxelDCNa | 77.7654 |
4.2. LONI LPBA40 Dataset
The LONI LPBA40 dataset is designed as a multi-class labeling task. It requires 54 regions of interest to be labeled in brain images automatically.
Data Preparation
There are 40 brain image samples with sizes of 220 × 220 × 220 in the dataset. Each image has 54 manually labeled ROIs along with cerebrum, brainstem, and background. When calculating result, only dice ratios of the 54 ROIs are included. Since we are not interested in predicting background, we first crop the image to drop the excessive background area around boundaries. The cropped image size is 180 × 145 × 137. Then we split the dataset into training set with 16 samples, validation set with 4 samples and testing set with the remaining 20 samples. We flip the images across all three directions on training and validation datasets. This increases the number of training samples to 128 and the number of validation samples to 32. The size of testing data remains 20 as we do not apply data augmentation on testing data.
Experimental Setup:
The architecture of U-Net implemented on this dataset consists of five blocks in both the encoder path and decoder path. The number of output channels in the first encoder block is 32. The convolutional kernel size is 3×3×3 and stride size used in the max pooling layers is 1×2×2. The last convolutional operation in the final decoder block×has 57 output channels, which corresponds to the total number of classes (54 ROIs, cerebrum, brainstem and background). The training batch size is 1. Since each data sample provided is too large to be stored in memory, we use training patch with size of 128 × 128 × 32 as input in the training process. Each training patch are randomly cropped from training data. At the testing time, we pick one patch at a time from a single testing data sample with the same size in turn. The predicted patches are concatenated together with a linear weighted summation on overlapped part to get the final prediction results. We implement our models on Tensorflow and use AdamOptimizer to update the network with moment estimates β1 = 0.9 and β2 = 0.999.
Analysis of Results:
The dice ratio of ROIs in the left and the right hemispheres are provided in Figure 6. Compared with the baseline method, iVoxelDCNa shows improvement in 44 out of 54 ROIs; VoxelDCNc shows improvement in 35 out of 54 ROIs; iVoxelDCNc shows improvement in 30 out of 54 ROIs; VoxelDCNa shows improvement in 29 of 54 ROIs. Table 1 shows the experimental results in terms of average dice ratio. All the proposed methods have better performance than the baseline model. Network iVoxelDCNa has the best performance and achieves 2.21% improvement compared with baseline. The result demonstrates that the proposed methods can help networks better capture the local information of images than the baseline method by eliminating the checkerboard artifact, yielding a better labeling result.
Figure 6:
Experimental results on the LONI LPBA40 datasets. Each set of bars represents the dice ratios of 3D U-Net, VoxelDCLa, VoxelDCLc, iVoxelDCLa, iVoxelDCLc on testing data for each ROI.
4.3. Timing Comparison
Table 2 shows the comparison of the training and testing time between baseline and proposed methods. We can see that iVoxelDCLa and iVoxelDCLc take more time to train than VoxelDCLa and VoxelDCLc in that they take original input when generating each intermediate feature map. In VoxelDCL, the use of concatenation slightly increases the training and testing time. All the proposed methods take more time to train and test than the baseline model, but the increase is not dramatic. Overall, we do not expect this to be a major bottleneck of the proposed methods.
Table 2:
Training and testing time on the two datasets using Tesla K80 GPU. We compare the training time of 10,000 (ADNI) and 100,000 iterations (LONI LPBA40), and testing time of 5 (ADNI) and 20 testing subjects for the baseline UNet and the proposed methods.
| Dataset | Model | Training time | Testing time |
|---|---|---|---|
| ADNI | U-Net | 45 h 43 min | 19.45 sec |
| VoxelDCNa | 54 h 57 min | 20.80 sec | |
| VoxelDCNc | 57 h 12 min | 19.18 sec | |
| iVoxelDCNa | 59 h 31 min | 19.87 sec | |
| iVoxelDCNc | 59 h 54 min | 19.65 sec | |
| LONI LPBA40 | U-Net | 52 h 05 min | 12 min 12 sec |
| VoxelDCNa | 60 h 37 min | 20 min 35 sec | |
| VoxelDCNc | 63 h 24 min | 19 min 85 sec | |
| iVoxelDCNa | 71 h 12 min | 20 min 32 sec | |
| iVoxelDCNc | 75 h 40 min | 20 min 05 sec |
5. CONCLUSION AND DISCUSSION
In this work, we propose the VoxelDCL to address the checkerboard artifact problem of 3D deconvolutional layers. VoxelDCL generates the intermediate feature maps of 3D deconvolutional layers sequentially, thereby building relationships among the adjacent voxels on the output feature maps. We then build four variations of the voxel deconvolutional networks (VoxelDCN) and apply them to the ADNI and LONI PBA40 datasets for volumetric brain image labeling tasks. Experimental results demonstrate the effectiveness of our methods. All of the proposed methods outperform U-Net with regular 3D deconvolutional layers. This indicates that developing dependencies among the intermediate feature maps in deconvolutional layers indeed alleviates the checkerboard artifact issue, thereby improving the prediction results. In out current study, we apply the VoxelDCL to U-Net for voxel-wise prediction tasks. Generally, this layer can be applied to various 3D deep network architectures with up-sampling operations. We plan to apply the proposed methods to models like 3D generative adversarial networks for image generation task in the future.
CCS CONCEPTS.
• Theory of computation → Structured prediction; • Computer systems organization → Neural networks; • Computing methodologies → Artificial intelligence;
ACKNOWLEDGMENTS
This work was supported in part by National Science Foundation grants DBI-1641223, DBI-1661289, IIS-1615035, and National Institutes of Health grants EB008374 and AG041721.
Footnotes
Contributor Information
Yongjun Chen, Washington State University, Pullman, WA, USA, yongjun.chen@wsu.edu.
Min Shi, Washington State University, Pullman, WA, USA, min.shi@wsu.edu.
Hongyang Gao, Washington State University, Pullman, WA, USA, hongyang.gao@wsu.edu.
Dinggang Shen, University of North Carolina, Chapel Hill, NC, USA, dgshen@med.unc.edu.
Lei Cai, Washington State University, Pullman, WA, USA, lei.cai@wsu.edu.
Shuiwang Ji, Washington State University, Pullman, WA, USA, sji@eecs.wsu.edu.
REFERENCES
- [1].Aitken Andrew, Ledig Christian, Theis Lucas, Caballero Jose, Wang Zehan, and Shi Wenzhe. 2017. Checkerboard artifact free sub-pixel convolution: A note on sub-pixel convolution, resize convolution and convolution resize. arXiv preprint arXiv:1707.02937 (2017).
- [2].Chen Liang-Chieh, Papandreou George, Kokkinos Iasonas, Murphy Kevin, and Yuille Alan L. 2016. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. arXiv preprint arXiv:1606.00915 (2016). [DOI] [PubMed]
- [3].Ciresan Dan, Giusti Alessandro, Gambardella Luca M, and Schmidhuber Jürgen. 2012. Deep neural networks segment neuronal membranes in electron microscopy images. In Advances in neural information processing systems. 2843–2851. [Google Scholar]
- [4].Dai Angela, Ritchie Daniel, Bokeloh Martin, Reed Scott, Sturm Jürgen, and Nießner Matthias. 2017. ScanComplete: Large-Scale Scene Completion and Semantic Segmentation for 3D Scans. arXiv preprint arXiv:1712.10215 (2017).
- [5].Dosovitskiy Alexey, Fischer Philipp, Ilg Eddy, Hausser Philip, Hazirbas Caner, Golkov Vladimir, van der Smagt Patrick, Cremers Daniel, and Brox Thomas. 2015. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision. 2758–2766. [Google Scholar]
- [6].Fennema-Notestine Christine, Hagler Donald J, McEvoy Linda K, Fleisher Adam S, Wu Elaine H, Karow David S, and Dale Anders M. 2009. Structural MRI biomarkers for preclinical and mild Alzheimer’s disease. Human brain mapping 30, 10 (2009), 3238–3253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Gao Hongyang, Yuan Hao, Wang Zhengyang, and Ji Shuiwang. 2017. Pixel Deconvolutional Networks. arXiv preprint arXiv:1705.06820 (2017).
- [8].Gao Yaozong, Liao Shu, and Shen Dinggang. 2012. Prostate segmentation by sparse representation based classification. Medical physics 39, 10 (2012), 6372–6387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Goodfellow Ian, Pouget-Abadie Jean, Mirza Mehdi, Xu Bing, Warde-Farley David, Ozair Sherjil, Courville Aaron, and Bengio Yoshua. 2014. Generative adversarial nets. In Advances in neural information processing systems. 2672–2680. [Google Scholar]
- [10].Ioffe Sergey and Szegedy Christian. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In International Conference on Machine Learning 448–456. [Google Scholar]
- [11].Md Amirul Islam Neil Bruce, and Wang Yang. 2016. Dense Image Labeling Using Deep Convolutional Neural Networks. In Computer and Robot Vision (CRV), 2016 13th Conference on IEEE, 16–23. [Google Scholar]
- [12].Ji Shuiwang, Xu Wei, Yang Ming, and Yu Kai. 2013. 3D Convolutional Neural Networks for Human Action Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence 35, 1 (2013), 221–231. [DOI] [PubMed] [Google Scholar]
- [13].Johnson Justin, Alahi Alexandre, and Fei-Fe Li. 2016. Perceptual losses for real-time style transfer and super-resolution. In European Conference on Computer Vision. Springer, 694–711. [Google Scholar]
- [14].Krizhevsky Alex, Sutskever Ilya, and Hinton Geoffrey E. 2012. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems. 1097–1105. [Google Scholar]
- [15].Yann LeCun Léon Bottou, Bengio Yoshua, and Haffner Patrick. 1998. Gradient-based learning applied to document recognition. Proc. IEEE 86, 11 (1998), 2278–2324. [Google Scholar]
- [16].Lee Kisuk, Zung Jonathan, Li Peter, Jain Viren, and Seung H Sebastian. 2017. Superhuman Accuracy on the SNEMI3D Connectomics Challenge. arXiv preprint arXiv:1706.00120 (2017).
- [17].Li Rongjian, Zhang Wenlu, Suk Heung-Il, Wang Li, Li Jiang, Shen Dinggang, and Ji Shuiwang. 2014. Deep Learning Based Imaging Data Completion for Improved Brain Disease Diagnosis. In Proceedings of the 17th International Conference on Medical Image Computing and Computer Assisted Intervention 305–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Ma Guangkai, Gao Yaozong, Wu Guorong, Wu Ligang, and Shen Dinggang. 2016. Nonlocal atlas-guided multi-channel forest learning for human brain labeling. Medical physics 43, 2 (2016), 1003–1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Magnotta Vincent A, Heckel Dan, Andreasen Nancy C, Cizadlo Ted, Corson Patricia Westmoreland, Ehrhardt James C, and Yuh William TC. 1999. Measurement of brain structures with artificial neural networks: two-and three-dimensional applications. Radiology 211, 3 (1999), 781–790. [DOI] [PubMed] [Google Scholar]
- [20].Mueller Susanne G, Weiner Michael W, Thal Leon J, Petersen Ronald C, Jack Clifford, Jagust William, Trojanowski John Q, Toga Arthur W, and Beckett Laurel. 2005. The Alzheimer’s disease neuroimaging initiative. Neuroimaging Clinics of North America 15, 4 (2005), 869–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Noh Hyeonwoo, Hong Seunghoon, and Han Bohyung. 2015. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision 1520–1528. [Google Scholar]
- [22].Odena Augustus, Dumoulin Vincent, and Olah Chris. 2016. Deconvolution and Checkerboard Artifacts. Distill (2016). 10.23915/distill.00003 [DOI]
- [23].Ronneberger Olaf, Fischer Philipp, and Brox Thomas. 2015. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention Springer, 234–241. [Google Scholar]
- [24].Sanroma Gerard, Wu Guorong, Gao Yaozong, and Shen Dinggang. 2014. Learning to rank atlases for multiple-atlas segmentation. IEEE transactions on medical imaging 33, 10 (2014), 1939–1953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Shattuck David W, Mirza Mubeena, Adisetiyo Vitria, Hojatkashani Cornelius, Salamon Georges, Narr Katherine L, Poldrack Russell A, Bilder Robert M, and Toga Arthur W. 2008. Construction of a 3D probabilistic atlas of human cortical structures. Neuroimage 39, 3 (2008), 1064–1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Shelhamer Evan, Long Jonathan, and Darrell Trevor. 2017. Fully convolutional networks for semantic segmentation. IEEE transactions on pattern analysis and machine intelligence 39, 4 (2017), 640–651. [DOI] [PubMed] [Google Scholar]
- [27].Shi Wenzhe, Caballero Jose, Ferenc Huszár Johannes Totz, Andrew P Aitken Rob Bishop, Rueckert Daniel, and Wang Zehan. 2016. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition1874–1883. [Google Scholar]
- [28].Shi Wenzhe, Caballero Jose, Theis Lucas, Huszar Ferenc, Aitken Andrew, Ledig Christian, and Wang Zehan. 2016. Is the deconvolution layer the same as a convolutional layer? arXiv preprint arXiv:1609.07009 (2016).
- [29].Tong Tong, Wolz Robin, Hajnal Joseph V, and Rueckert Daniel. 2012. Segmentation of brain MR images via sparse patch representation. In MICCAI Workshop on Sparsity Techniques in Medical Imaging (STMI). [Google Scholar]
- [30].Wang Hongzhi, Jung W Suh, Sandhitsu R Das, John B Pluta, Caryne Craige, and Paul A Yushkevich. 2013. Multi-atlas segmentation with joint label fusion. IEEE transactions on pattern analysis and machine intelligence 35, 3 (2013), 611–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Wang Li, Gao Yaozong, Shi Feng, Li Gang, John H Gilmore Weili Lin, and Shen Ding-gang. 2015. LINKS: Learning-based multi-source IntegratioN frameworK for Segmentation of infant brain images. NeuroImage 108 (2015), 160–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Wu Guorong, Kim Minjeong, Sanroma Gerard, Wang Qian, Brent C Munsell Dinggang Shen, Alzheimer’s Disease Neuroimaging Initiative, et al. 2015. Hierarchical multi-atlas label fusion with multi-scale feature representation and label-specific patch partition. NeuroImage 106 (2015), 34–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Wu Guorong, Wang Qian, Zhang Daoqiang, Nie Feiping, Huang Heng, and Shen Dinggang. 2014. A generative probability model of joint label fusion for multi-atlas based brain segmentation. Medical image analysis 18, 6 (2014), 881–890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Zeiler Matthew D, Taylor Graham W, and Fergus Rob. 2011. Adaptive deconvolutional networks for mid and high level feature learning. In Computer Vision (ICCV), 2011 IEEE International Conference on IEEE, 2018–2025. [Google Scholar]
- [35].Zeng Tao, Wu Bian, and Ji Shuiwang. 2017. DeepEM3D: Approaching human-level performance on 3D anisotropic EM image segmentation. Bioinformatics 33, 16 (2017), 2555–2562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Zhang Lichi, Wang Qian, Gao Yaozong, Wu Guorong, and Shen Dinggang. 2016. Automatic labeling of MR brain images by hierarchical learning of atlas forests. Medical physics 43, 3 (2016), 1175–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Zhang Shaoting, Zhan Yiqiang, Dewan Maneesh, Huang Junzhou, Metaxas Dimitris N, and Zhou Xiang Sean. 2012. Towards robust and effective shape modeling: Sparse shape composition. Medical image analysis 16, 1 (2012), 265–277. [DOI] [PubMed] [Google Scholar]
- [38].Zhang Wenlu, Li Rongjian, Deng Houtao, Wang Li, Lin Weili, Ji Shuiwang, and Shen Dinggang. 2015. Deep convolutional neural networks for multi-modality isointense infant brain image segmentation. NeuroImage 108 (2015), 214–224. [DOI] [PMC free article] [PubMed] [Google Scholar]