Identifying implausible gestational ages in preterm babies with Bayesian mixture models

Abstract

Infant birth weight and gestational age are two important variables in obstetric research. The primary measure of gestational age used in US birth data is based on a mother’s recall of her last menstrual period, which has been shown to introduce random or systematic errors. To mitigate some of those errors, Oja et al., Platt et al., and Tentoni et al. estimated the probabilities of gestational ages being misreported under the assumption that the distribution of infant birth weights for a true gestational age is approximately Gaussian. From this assumption, Oja et al. fitted a three-component mixture model, and Tentoni et al. and Platt et al. fitted two-component mixture models. We build on their methods and develop a Bayesian mixture model. We then extend our methods using reversible jump Markov chain Monte Carlo to incorporate the uncertainty in the number of components in the model. We conduct simulation studies and apply our methods to singleton births with reported gestational ages of 23–32 weeks using 2001–2008 US birth data. Results show that a three-component mixture model fits the birth data better for gestational ages reported as 25 weeks or less; and a two-component mixture model fits better for the higher gestational ages. Under the assumption that our Bayesian mixture models are appropriate for US birth data, our research provides useful statistical tools to identify records with implausible gestational ages, and the techniques can be used in part of a multiple-imputation procedure for missing and implausible gestational ages.

1. Introduction

Gestational age and infant birth weight are two important variables in obstetric and perinatal research and clinical practice [1–6]; consequently, this information is routinely collected and reported for births in the USA [7, 8]. Infant birth weight can be measured accurately; however, the accuracy of reported gestational ages has been questioned. In national reports and research using US birth certificate data, gestational ages are primarily calculated on the basis of a mother’s recall of her last menstrual period (LMP) [9]. The use of LMP can introduce random or systematic errors because of, for example, early or delayed ovulation, bleeding in early pregnancy, and inaccurate recall of the first day of the LMP [10–14]. Although obstetric (year 2003 and onward) or clinical estimates (year 1989 to year 2002) are provided for most births, the sources of these estimates are not consistent [15, 16].

Inaccurate reported gestational ages can have serious impacts on obstetric and perinatal research, especially for the very early preterm deliveries (infants delivered at less than 28 weeks of gestation). Preterm delivery rates can be overestimated and preterm infant mortality rates underestimated when inaccurate gestational ages exist [17]. Many researchers have attempted to address the problem of incorrect gestational ages [18–27]. Combined information on gestational age and birth weight can be used to identify birth records with implausible gestational age values. Under the assumption that infant birth weights are normally distributed, conditional on their true gestational ages, records for infants with birth weights inconsistent with the primary gestation-specific birth weight distribution can be identified as having implausible gestational ages.

A simple method to deal with implausible gestational ages is based on cut-off values [10, 22]. All birth records with birth weights beyond the cut-off values, that is, birth weights too big or too small for a reported gestational age, would be considered as having misreported gestational ages. Using cut-points is simple to implement and explain to data users and clinicians. However, deleting birth records with birth weights beyond the reported gestational age-specific cut-off values leads to truncated birth weight distributions, and information beyond the cut-off values is lost.

Mixture models are an alternative approach to address issues of inaccurate reported gestational ages [20, 24–26]. Under the assumption of normality, one indication that a mixture model may be appropriate is that at early reported gestational ages, instead of a symmetric, bell-shaped curve, the birth weight distribution is often skewed to the right (unimodal, with a long tail) or even bimodal, appearing as a combination of two normal curves. Oja et al. [20] used a three-component mixture model to model the distribution of infant birth weight within each observed gestational age category. They assumed all the errors are one menstrual cycle, that is, the only possible errors are −4 weeks (underestimation) or +4 weeks (overestimation). Platt et al. [24] also used a mixture model to study the birth records with misreported gestational ages. They assumed that the records with accurate gestational ages could be separated from those with inaccurate gestational ages by fitting a mixture of two normal distributions, and the true gestational age for all births with misreported gestational ages was 40 weeks, or full term. Consequently, Platt et al. assumed that only true full term births were wrongly specified as preterm births. Tentoni et al. [25] proposed to use a mixture model to identify two groups, with one group containing records with birth weights for the correctly reported gestational ages and the other group containing records with birth weights corresponding to the misreported gestational ages. In the work by Tentoni et al., no assumptions were made about the true gestational age(s) to which the second group belonged. Parker et al. [28] further extended the method of Tentoni et al. by including covariates in the mean function of each mixture component. All of the methods just described based on mixture models used the expectation–maximization (EM) algorithm to fit the models via maximum likelihood estimation.

We extend the mixture model approach using Bayesian methods. Similar to Tentoni et al. [25], we do not specify the true gestational ages to which the misreported records belong. In addition, we develop both two-component and three-component mixture models as well as mixture models with varying dimensions. Bayesian mixture models can be used to estimate probabilities of misreporting gestational ages. They can also be used to create posterior predictive draws of the status—correct or incorrect—for each reported gestational age in a data set. The latter use can serve as part of a multiple-imputation approach to dealing with misreporting of gestational ages, as we now describe briefly.

Multiple imputation is a technique that fills in the missing values with multiple reasonable replacements based on statistical methods. Parker and Schenker [26] discussed the application of multiple imputation for missing or implausible gestational ages in US birth data using basically a two-step process. The first step would be to use a Bayesian mixture model to impute a status of correct or incorrect for each reported gestational age. The second step would be to impute gestational ages, using a prediction model, for the cases that were imputed as incorrect in the first step as well as cases with no reported gestational ages. Multiple imputation would be created by independently repeating the two steps. Different analysts can use the resulting imputed data sets for different research purposes, without dealing with the issues of missing and misreported gestational ages. The use of the two-step multiple-imputation procedure of Parker and Schenker would reflect both the uncertainty about whether each reported gestational age is correct (first step) as well as the uncertainty in predicting gestational ages for cases with misreported or missing gestational ages (second step). The work in this paper applies to the first step, whereas future research will develop prediction models for gestational age to be used in the second step.

We organize the paper as follows. We describe the methods of Oja et al. [20], Platt et al. [24], and Tentoni et al. [25] in detail in Section 2. In Section 3, we develop both two-component and three-component Bayesian mixture models; then we relax the model assumptions by including the uncertainty in the number of components in the model using reversible jump Markov chain Monte Carlo method (RJMCMC) [29–31]. We conduct simulations in Section 4 and apply our methods to US birth data from the years 2001 to 2008 in Section 5. Section 6 contains concluding remarks.

2. Mixture models proposed by Oja et al., Platt et al., and Tentoni et al.

2.1. The method of Oja et al.

Oja et al. [20] assumed two types of errors for the misreported gestational ages, corresponding to a menstrual cycle: −4 weeks or +4 weeks. Let X be the reported gestational age, Y be the birth weight, and X * be the true gestational age (an unobserved, latent variable). At X = x, where x is a specific gestational age (e.g., 25 weeks), let Z₁ be an indicator variable such that Z₁ = 1 if X * = x+4 (the true gestational age is 4 weeks greater than the reported gestational age) and Z₁ = 0 otherwise. Similarly, let Z₂ be an indicator variable such that Z₂ = 1 if X * = x − 4 (the true gestational age is 4 weeks less than the reported gestational age) and Z₂ = 0 otherwise. The true gestational age is equal to the reported gestational age when both Z₁ and Z₂ are equal to 0. Let p₁ and p₂ be the probabilities of making errors of −4 weeks and +4 weeks at observed gestational age X = x; p₁ and p₂ are assumed to be independent of birth weight and the true gestational age X *. Let $q_x^{*}=\mathrm{Prob}\left(X^{*}=x\right)$ be the unknown proportion at a true gestational age. Then the joint density function of X and Y is given by the following:

$$\begin{gathered} f(x,y)=p_1{q}_{x+4}^{*}f(y|X^{*}=x+4;{\mu }_{x+4},{\sigma }_{x+4}^2)+p_2{q}_{x-4}^{*}f(y|X^{*}=x-4;{\mu }_{x-4},{\sigma }_{x-4}^2) \\ +\left(1-p_1-p_2\right)q_x^{*}f(y|X^{*}=x;{\mu }_x,{\sigma }_x^2), \end{gathered}$$

where $f(y|X^{*}=x;{\mu }_x,{\sigma }_x^2)$ is the pdf of birth weight Y at the true gestational age X * = x with mean μ_x and variance ${\sigma }_x^2$. The posterior probabilities of error variables Z₁ and Z₂ are $\text{P}(Z_1=1|X=x,Y=y)=p_1{q}_{x+4}^{*}f(y|X^{*}=x+4)/f(x,y)$ and $\text{P}\left(Z_2=1|X=x,Y=y\right)=p_2{q}_{x-4}^{*}f(y|X^{*}=x-4)/f(x,y)$. The maximum likelihood estimates of the parameters were derived using the EM algorithm.

2.2. The method of Platt et al.

Platt et al. [24] considered one type of misreporting: the true gestational age is either the observed gestational age or is 40 weeks. Let X, Y, X *, and $q_x^{*}$ have the same definitions as in Section 2.1, and let Z be an indicator variable such that Z = 1 if X * = 40 and Z = 0 otherwise. Let p be the probability that a term birth is misclassified as a specific observed gestational age x (p = Prob (X = x|X * = 40)). Platt et al. assumed that p is the same for all the observed gestational ages. On the basis of the assumptions that only term births are misspecified as preterm births, the joint density function of X and Y is given by

$$f(x,y)=p{q}_{40}^{*}f(y|X^{*}=40;{\mu }_{40},{\sigma }_{40}^2)+q_x^{*}f(y|X^{*}=x;{\mu }_x,{\sigma }_x^2).$$

The first term corresponds to misreported records and the second term to correctly reported records. The proportion of misreported records within the observed gestational age. x is $p{q}_{40}^{*}/\left(p{q}_{40}^{*}+q_x^{*}\right)$, and the proportion of correctly reported records is $q_x^{*}/\left(p{q}_{40}^{*}+q_x^{*}\right)$. The posterior probability of error is $\text{P}(\text{Z}=1|X=x,Y=y)=p{q}_{40}^{*}f(y|X^{*}=40;{\mu }_{40},{\sigma }_{40}^2)/f(x,y)$. Platt et al.combined data from different observed gestational ages to have a better estimate of p. The maximum likelihood estimates of the parameters were derived using the EM algorithm.

2.3. The method of Tentoni et al.

Tentoni et al. [25] assumed that within each reported gestational age stratum, the observed birth weights arise from a mixture of two normal distributions. Continuing with the notation of Sections 2.1 and 2.2, let $f_1=f(y|X^{*}=x;{\mu }_x,{\sigma }_x^2)$ be the density of the primary distribution of birth weights, where the true gestational age is equal to the observed gestational age, with mean birth weight of μ_x and variance of ${\sigma }_x^2$; and let $f_0=f(y|X^{*}\ne x;{\mu }_{x0},{\sigma }_{x0}^2)$ be the density of the secondary distribution consisting of births with birth weights corresponding to misreported gestational ages, with mean birth weight of μ_x0 and variance of ${\sigma }_{x0}^2$. Let θ_x (0< θ_x <1) be the stochastic weight or the proportion of births in the primary distribution and 1 – θ_x be the stochastic weight for the secondary distribution. Then the mixture model is defined as

$$f(y|X=x)={\theta }_x{f}_1+\left(1-{\theta }_x\right)f_0.$$

The model was applied to each observed gestational age, and the maximum likelihood estimates of the parameters θ_x, μ_x, ${\sigma }_x^2$, μ_x0, and ${\sigma }_{x0}^2$ were derived using the EM algorithm.

2.4. Comparison of the aforementioned three methods and their relation with our methods

All three methods described previously assumed that within each observed gestational age, birth weight follows a mixture of normal distributions. Oja et al. assumed all the errors are a menstrual cycle and ignored other types of errors. The method of Tentoni et al. does not specify to which gestational ages the second group belongs; thus, the second group could consist of records from multiple gestational ages (although the assumption of normality would then be questionable). The work of Platt et al. assumed that all the misreported cases are from term births.

The assumptions underlying these three approaches may raise some questions. For example, for the 2008 US birth data, at reported gestational age of 26 weeks, the largest birth weight is 2999 g, which is much lower than the mean birth weight of the term births (around 3400 g at 39 weeks and around 3500 g at 40 weeks). Thus, it is not realistic to assume that all the misreported records correspond to term births. On the other hand, putting all the misreported cases from a wide range of gestational ages into one group, as in the work of Tentoni et al., may oversimplify the problem. Although Oja et al. specified a mixture of three components, they restricted one group to be 4 weeks lower and the other group to be 4 weeks higher than the observed gestational age. This limits flexibility for other types of errors.

In our Bayesian approach, we do not specify the gestational ages to which the misreported records belong. Furthermore, we test whether a three-component mixture model can yield a better fit than a two-component model, without any restrictions on the different groups of the three-component model. We use the Bayesian information criterion (BIC) [32] to select the better fitting model. As an additional generalization, to incorporate the uncertainty in the number of components in the mixture model, we include that number as an unknown parameter and let it vary by using RJMCMC [29–31]. Results of RJMCMC can be directly incorporated into our future research project on multiple imputation of misreported gestational ages, thus allowing the multiple imputations to reflect uncertainty in the number of components in the mixture model.

3. Bayesian mixture model and reversible jump Markov chain Monte Carlo

We fit both two-component and three-component mixture models in this paper. For the lower reported gestational ages (e.g., 25 weeks or less), the implausible gestational ages could arise from a wide range of true gestational ages. The two-component model groups all the implausible gestational ages in one component, and the normality assumption for this component may be questionable. The three-component model, on the other hand, groups the implausible gestational ages in different components, which could yield a better fit than the two-component mixture model. In Section 3.1, we discuss the Bayesian mixture model with three components. The treatments for two components or more than three components are straightforward analogs and are not discussed here. In Section 3.2, we discuss the use of RJMCMC to allow the number of components to vary within the model.

3.1. Bayesian mixture model with three components

Let X be the observed gestational age and Y be the birth weight. Let Z, Z = 1, …, 3, be an unobserved indicator variable for group membership and θ = (θ₁, θ₂, θ₃), with θ₁ + θ₂ + θ₃ = 1, be the stochastic weight for each group. Within each value x of the observed gestational age, the probability density function of a mixture model with three components is written as

$$f(y)={\sum }_{j=1}^3{\theta }_{j}f(y|{\mu }_j,{\sigma }_j^2),$$

where f (y|μ, σ²) denotes the normal density function of Y with mean μ and variance σ². We can rewrite the mixture model by including the latent variable Z as follows:

$$f(y,z)=f(z)f(y|z)={\prod }_{j=1}^3{\left[{\theta }_{j}f(y|{\mu }_j,{\sigma }_j^2)\right]}^{I(z=j)},$$

where I(Z = j) is an indicator function such that I(Z = j) = 1 if Z = j and I(Z = j) = 0 otherwise. Z follows a multinomial distribution with P(Z = j) = θ_j. Let f(θ) and f(η) be the prior densities specified for θ and η, respectively, where $\eta =\left\{{\mu }_1,{\sigma }_1^2,{\mu }_2,{\sigma }_2^2,{\mu }_3,{\sigma }_3^2\right\}$. For a sample of size n, with i = 1, …, n indexing the sample units, the full conditional distributions of η, θ, and Z for MCMC sampling are as follows:

1. $f(\theta |\eta ,y_i,z_i:i=1,\dots ,n)\propto f(\theta ){\prod }_{i=1}^n{\theta }_1^{I\left(z_i=1\right)}{\theta }_2^{I\left(z_i=2\right)}{\left[1-{\theta }_1-{\theta }_2\right]}^{I\left(z_i=3\right)};$

2. $f(\eta |\theta ,y_i,z_i:i=1,\dots ,n)\propto f(\eta ){\prod }_{i=1}^n{\prod }_{j=1}^3{\left[f\left(y_i|{\mu }_j,{\sigma }_j^2\right)\right]}^{I\left(z_i=j\right)};$

3. $\mathrm{Pr}\left(Z_i=j|\theta ,\eta ,y_i:i=1,\dots ,n\right)\propto {\theta }_{\text{j}}f\left({\text{y}}_{\text{i}}|{\mu }_{\text{j}},{\sigma }_{\text{j}}^2\right),i=1,\dots ,n.$

Fitting of Bayesian mixture models can be implemented using the Gibbs sampler. With conjugate priors

$$\begin{gathered} {{\sigma }_{\text{j}}}^2~\text{inverse}\text{gamma}\text{IG}\left({\alpha }_j,{\beta }_j\right), \\ {\mu }_j|{{\sigma }_j}^2~\text{N}\left({\lambda }_j,{\sigma }_j^2/{\tau }_{\text{j}}\right), \\ f(\theta )~\text{Dirichlet}\left({\gamma }_1,{\gamma }_2,{\gamma }_3\right), \end{gathered}$$

and initial values θ⁰ and ${\mu }_j^0$, ${({\sigma }_j^2)}^0$, the Gibbs sampling is as follows

• Generate Z_i with $\text{P}\left(Z_i=j\right)\propto {\theta }_j\exp \left(-\frac{{\left(y_i-{\mu }_j\right)}^2}{2{\sigma }_j^2}\right)/{\sigma }_j$

• Generate θ from Dirichlet (γ₁ + n₁, γ₂ + n_2, γ₃ + n₃), where $n_j={\sum }_{i=1}^{n}I\left(Z_i=j\right)$

• Generate μ_j from $\text{N}(\left({\lambda }_j{\tau }_j+y_{\text{sum},j}\right)/\left({\tau }_j+n_j\right),{\sigma }_j^2/\left({\tau }_j+n_j\right))$, where $y_{\text{sum},j}={\sum }_{i=1}^{n}I\left(Z_i=j\right)y_i$

• Generate ${\sigma }_j^2$ from $\text{IG}\left({\alpha }_j+\left(n_j+1\right)/2,{\beta }_{\text{j}}+0.5{\tau }_{\text{j}}{\left({\mu }_j-{\lambda }_{\text{j}}\right)}^2+0.5{\sum }_{i=1}^{n}I\left(Z_i=j\right){\left(y_i-{\mu }_j\right)}^2\right)$

To let the data dominate the posterior estimates, we can use non-informative priors for μ_j and ${\sigma }_j^2$, $f({\mu }_j,{\sigma }_j^2)\propto 1/{\sigma }_j^2$, which is the equivalent to using the conjugate priors with α_j, β_j, λ_j, and τ_j all set to 0; we can use a Dirichlet(1;1;1) prior for θ. Then, the Gibbs sampling steps for μ_j and ${\sigma }_j^2$ are simplified as follows:

• Generate μ_j from $\text{N}\left(y_{\text{sum},j}/n_j,{\sigma }_j^2/n_j\right),$

• Generate ${\sigma }_j^2$ from $\text{IG}\left(n_j/2,{\sum }_{i=1}^{n}I\left(Z_i=j\right){\left(y_i-{\mu }_j\right)}^2/2\right)$

To select the number of components for a Bayesian mixture model, we can calculate Akaike’s information criterion (AIC) [33] and BIC [32]. Both criteria are based on information theory, with penalty terms to discourage overfitting. Mixture models with different numbers of components can be fitted, and the model with the smallest AIC or BIC suggests the best fit to the data. Compared with AIC, BIC has a larger penalty term for a more complicated model. In this paper, we calculate BIC to compare Bayesian mixture models with two components to those with three components.

In the approach to develop a Bayesian mixture model described previously, the number of components in the model is assumed to be fixed, and statistical criteria are used to select the number most parsimonious with the data. To accommodate the uncertainty in the model structure and to avoid the uncertainty of statistical testing in model selection, we can include the number of components as an extra, unknown parameter using RJMCMC [29–31]. The RJMCMC method allows simulation of the posterior distribution on varying dimensions. As mentioned earlier, results of RJMCMC can be incorporated into the multiple-imputation procedure for missing and misreported gestational ages directly.

3.2. Reversible jump Markov chain Monte Carlo

RJMCMC [29–31] is a method for ‘trans-dimensional’ problems, where the dimension of the model is not fixed and is treated as an unknown parameter. It is an extension to standard MCMC methodology. The posterior distribution of the unknown dimension is generated from a Markov chain, which allows the dimension to change from one step to the next, and the probability of each dimension can be estimated on the basis of the posterior draws.

Let K be the dimension parameter, the number of unknown components of a mixture model. Let Z be a categorical variable indicating to which group the observation belongs under K and assume Z follows a multinomial distribution with P(Z = j) = θ_j, j = 1;2, …,K. Let η and θ be the vector of unknown parameters under K, with $\eta =\left\{{\mu }_1,{\sigma }_1^2,\dots ,{\mu }_K,{\sigma }_K^2\right\}$ and θ = {θ₁, …, θ_K}. For different values of K, η and θ have different dimensions and different component values. Let X be the observed gestational age and Y be the birth weight; then, the joint probability density function of K, Z, and Y within each value x of the observed gestational age is

$$f(k,z,y)=f\left(k\right)f(z|k\left)f\right(y|z,k),$$

where f(k) is the density function of the number of unknown components and follows a multinomial distribution; the latter two components are the same as the mixture model in Section 3.1 under a fixed value for K. We used initial values k⁰;θ⁰, and η⁰ and a uniform prior for K, a Dirichlet.(1, …, 1) prior for θ, and non-informative priors for μ_j and ${\sigma }_j^2$, j = 1, …, K, with the latter two priors being analogous to those used in our mixture model with a fixed number of components (Section 3.1). These priors will allow the data to dominate the parameter estimates.

The basic procedure for RJMCMC is as follows:

1. Update the variable Z with $\text{P}\left(Z_i=j|k,y,\eta ,\theta \right)\propto {\theta }_{j}f\left(y_i|{\mu }_j,{\sigma }_j^2\right).$

2. Update θ from the posterior distribution Dirichlet (1 + n₁, …, 1 + n_K), where $n_j={\sum }_{i=1}^{n}I\left(Z_i=j\right),j=1,\dots ,\text{K}$.

3. Update μ_j from $\text{N}\left(y_{\text{sum},j}/n_j,{\sigma }_j^2/n_j\right)$ and ${\sigma }_j^2$ from $\text{IG}\left(n_j/2,{\sum }_{i=1}^{n}I\left(Z_i=j\right){\left(y_i-{\mu }_j\right)}^2/2\right)$, j = 1, …, K. Steps 1–3 are analogous to those carried out for a model with a fixed number of components, as described in Section 3.1. The next step contains the reversible jump procedure.

4. Split one mixture component into two or combine two components into one. We describe the splitting move in detail; the combining move is a reverse process of the splitting move. Let ω = (k, η, θ, z) denote a generic symbol that represents the values of all unknown parameters at state ω, and let ωˊ = (kˊ, ηˊ, θˊ, zˊ) represent the values of all unknown parameters at a higher state ωˊ. To move from state ω to state ωˊ, draw a vector a of continuous random variables and set ωˊ using an invertible deterministic function g, such that ωˊ = g(ω, a). In this paper, we draw a a = (a₁, a₂, a₃) from beta(2,2), beta(2,2), and beta(1,1) independently. To split a group, for example, the j th group with parameters θ_j*, μ_j*, and σ_j*, into two groups j₁ and j₂, we derive the parameters θ_j1, θ_j2, μ_j1, μ_j2, σ_j1, and σ_j2 for the new groups as follows

$$\begin{gathered} {\theta }_{j1}={\theta }_{j*}\times a_1 \\ {\theta }_{j2}={\theta }_{j*}\times \left(1-a_1\right), \\ {\mu }_{j1}={\mu }_{j*}-a_2\times {\sigma }_{j*}\times \mathrm{sqrt}\left({\theta }_{j2}/{\theta }_{j1}\right), \\ {\mu }_{j2}={\mu }_{j*}+a_2\times {\sigma }_{j*}\times \mathrm{sqrt}\left({\theta }_{j1}/{\theta }_{j2}\right), \\ {\sigma }_{j1}^2=a_3\times \left(1-a_2\times a_2\right)\times {\sigma }_{j*}^2\times {\theta }_{j*}/{\theta }_{j1}, \\ {\sigma }_{j2}^2=\left(1-a_3\right)\times \left(1-a_2\times a_2\right)\times {\sigma }_{j*}^2\times {\theta }_{j*}/{\theta }_{j2}. \end{gathered}$$

Re-assign subjects from the j th group to these two new groups with $\text{P}\left(Z_i={\text{j}}_1\right)\propto {\theta }_{j1}f\left(y_i|{\mu }_{j1},{\sigma }_{j1}^2\right)$ and $\text{P}\left(Z_i={\text{j}}_2\right)\propto {\theta }_{j2}f\left(y_i|{\mu }_{j2},{\sigma }_{j2}^2\right)$. The acceptance probability of the splitting move is $A=\min \left\{1,\frac{f\left({\omega }^{\prime }|y\right)\rho \left({\omega }^{\prime }\right)}{f(\omega |y)\rho (\omega )q(a)}\left|\frac{d\left({\omega }^{\prime }\right)}{d(\omega ,a)}\right|\right\}$, where f (ω|y) is the posterior density of ω; ρ(ω) is the probability of choosing the current move type at state ω—in this paper, ρ (ω) = 1 because we have only one type of move (splitting move when K = 2 and combining move when K = 3); q(a) is the density function of a; and $\left|\frac{d\left({\omega }^{\prime }\right)}{d(\omega ,a)}\right|$ is the Jacobian derived from changing variables (ω, a) to ωˊ. For the corresponding combining move, the acceptance probability is min(1, A⁻¹). More details on the splitting and combining moves are available in [30].

4. Simulation studies

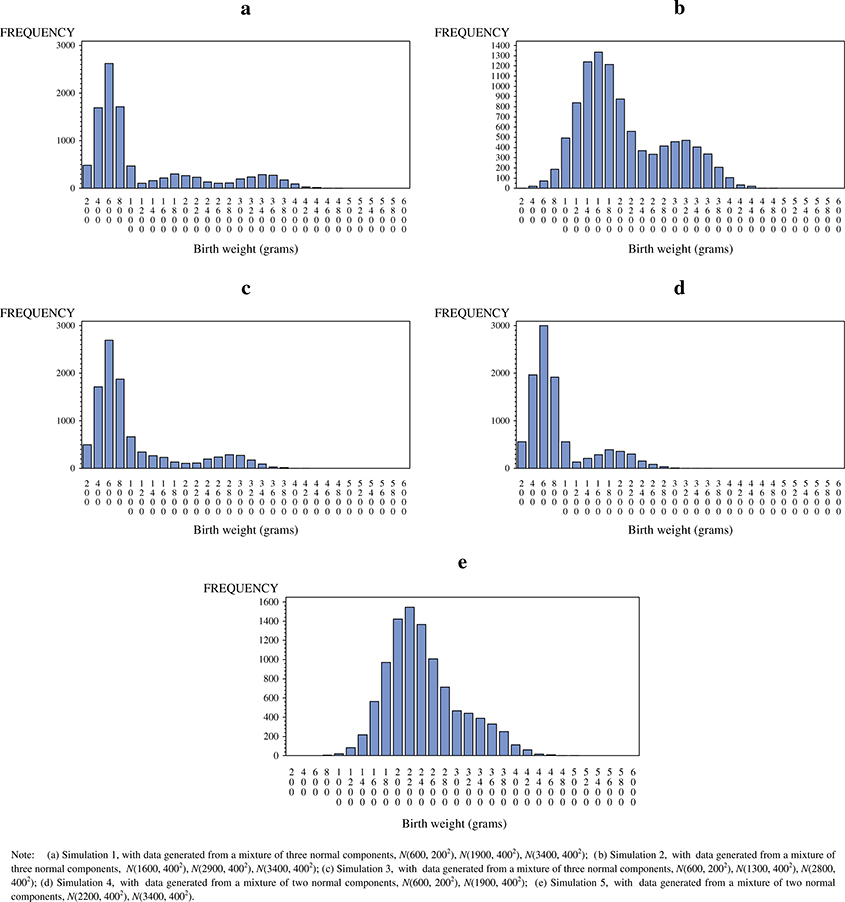
We conducted five simulation studies. Simulated birth weight data for simulations 1–3 were generated using a three-component normal mixture distribution, whereas data for simulations 4 and 5 were generated using a mixture of two normal components. For all the simulations, we assumed that the first component includes simulated birth weight values from birth records with correctly reported gestational ages and the rest of the groups contain values from birth records with misreported gestational ages.

Table I summarizes the means (μ), standard deviations (SDs; σ), and proportions (θ) of the simulated birth weight distributions in the components. The mean values of the first group range from 600 to 2200 g to mimic the means of actual birth weight at different true gestational ages. The means of the second group and the third group (if it exists) are higher than those for the first group, consistent with the assumption that only higher gestational ages are misreported as lower gestational ages; and the mean values of these groups range from 1300 to 3400 g, with the latter corresponding to the mean birth weight of term births. The three groups in simulation 1 are well separated, whereas for simulation 2, the last two components are close to each other; and simulation 3 is in between, with the last two groups more separated than in simulation 2, but less separated than in simulation 1. For simulations 4 and 5, all of the misreported gestational ages are grouped into one component, a condition commonly assumed in the previous studies [24–26]. For each simulation, we have two sample sizes (10,000 and 50,000) and 50 replicates. Figure 1(a–e) shows the histograms for the simulated birth weight data for the sample size of 10,000 based on one replicate.

Table I.

Simulated mean birth weight (grams), standard deviation (SD), and mixing proportion (θ) within each component, by simulation number.

Component	Simulation 1			Simulation 2			Simulation 3			Simulation 4			Simulation 5
	Mean	SD	θ	Mean	SD	θ	Mean	SD	θ	Mean	SD	θ	Mean	SD	θ
1	600	200	0.70	1600	400	0.70	600	200	0.70	600	200	0.80	2200	400	0.80
2	1900	400	0.15	2900	400	0.15	1300	400	0.15	1900	400	0.20	3400	400	0.20
3	3400	400	0.15	3400	400	0.15	2800	400	0.15

Figure 1.

Histograms of the simulated birth weight (grams) at a sample size of 10,000.

We fitted Bayesian mixture models with two components and three components separately, and we also applied the RJMCMC procedure to the simulated data sets. We implemented the models using SAS (SAS Institute Inc., Cary, NC, USA) interactive matrix language (iml) and derived trace plots of the parameters over the iteration index to assess convergence. We used non-informative priors in the Bayesian procedures. Specifically, we chose a uniform prior for K and Dirichlet(1, …, 1) for θ and non-informative priors $f({\mu }_j,{\sigma }_j^2)\propto 1/{\sigma }_j^2$ for μ_j and ${\sigma }_j^2$. For fitting Bayesian mixture models with two or three components separately, we used 1000 iterations to burn in the MCMC procedure and then calculated the means of the subsequent 1000 iterations. We calculated BIC values for each simulated data set and then averaged these values over the 50 simulated data sets. For RJMCMC, we used 8000 iterations for the burn-in and then calculated the means based on the subsequent 2000 iterations. We calculated means and SDs of parameter estimates over the 50 simulated data sets. Table II shows the results.

Table II.

Average estimated means of birth weight (grams), standard deviations (SD), and mixing proportions (θ) from the Bayesian mixture models and RJMCMC for the simulation studies; also shown are the average percentages of iterations for which RJMCMC chose the given values of K.

Simulation	Sample size	component	Fit separately								RJMCMC
			Two components				Three components				Two components				Three components
			Mean	SD	θ	BIC	Mean	SD	θ	BIC	Mean	SD	θ	K = 2	Mean	SD	θ	K = 3
1	10,000	1	597	195	0.68	154,672	600	199	0.70	153,967	590	180	0.62	10%	600	199	0.70	90%
			(2.38)1	(1.62)	(0.001)	(110.97)	(2.36)	(1.67)	(0.001)	(114.11)	(3.95)	(2.44)	(0.001)		(2.20)	(1.56)	(0.001)
		2	2557	926	0.32		1898	402	0.15		2250	1098	0.38		1897	401	0.15
			(10.38)	(9.19)	(0.001)		(14.05)	(16.13)	(0.003)		(8.19)	(6.82)	(0.001)		(13.94)	(16.01)	(0.003)
		3					3399	399	0.15						3401	398	0.15
							(16.02)	(11.45)	(0.002)						(15.17)	(11.93)	(0.002)
	50,000	1	597	195	0.68	773,118	600	199	0.70	769,531	–2	–	–	<0.01%	600	199	0.70	>99.99%
			(1.18)	(0.80)	(0.001)	(292.15)	(1.22)	(0.81)	(0.001)	(303.97)					(1.24)	(0.82)	(0.001)
		2	2558	926	0.32		1900	402	0.15		–	–	–		1900	402	0.15
			(4.83)	(3.60)	(0.001)		(6.35)	(6.86)	(0.001)						(6.31)	(6.90)	(0.001)
		3					3401	399	0.15		–	–	–		3400	399	0.15
							(7.20)	(5.03)	(0.001)						(7.01)	(4.96)	(0.001)
2	10,000	1	1601	402	0.70	159,764		Did not converge3			1601	402	0.70	>99.99%	–	–	–	<0.01%
			(6.07)	(4.94)	(0.004)	(114.56)					(5.18)	(4.12)	(0.002)
		2	3149	474	0.30						3149	473	0.30		–	–	–
		3	(12.94)	(9.64)	(0.004)						(9.77)	(7.95)	(0.002)
	50,000	1	1601	401	0.70	798,607	1599	400	0.70	798,627	1601	401	0.70	>99.99%	–	–	–	<0.01%
			(2.69)	(1.96)	(0.001)	(279.03)	(5.12)	(2.81)	(0.01)	(277.20)	(2.36)	(1.82)	(0.001)
		2	3150	474	0.30		2815	396	0.10		3149	474	0.30		–	–	–
			(5.30)	(4.06)	(0.001)		(99.16)	(65.46)	(0.04)		(4.01)	(3.15)	(0.001)
		3					3299	425	0.20						–	–	–
							(59.91)	(16.87)	(0.04)
3	10,000	1	617	212	0.73	152,126	601	199	0.70	151,453	625	224	0.76	0.86%	601	199	0.70	99.15%
			(3.14)	(2.77)	(0.004)	(107.40)	(3.22)	(2.10)	(0.006)	(108.64)	–4	–	–		(3.29)	(2.21)	(0.006)
		2	2165	815	0.27		1310	381	0.15		2292	736	0.24		1310	381	0.15
			(17.88)	(7.39)	(0.004)		(22.76)	(16.66)	(0.007)		–	–	–		(23.88)	(17.03)	(0.007)
		3					2794	402	0.15						2793	402	0.15
							(17.17)	(12.34)	(0.002)						(16.99)	(12.49)	(0.002)
	50,000	1	617	211	0.73	760,424	601	199	0.70	757004	–	–	–	<0.01%	601	199	0.70	>99.99%
			(1.38)	(1.28)	(0.002)	(286.71)	(1.42)	(0.93)	(0.003)	(290.75)					(1.35)	(0.91)	(0.003)
		2	2165	816	0.27		1312	384	0.15		–	–	–		1312	384	0.15
			(8.05)	(3.20)	(0.002)		(12.02)	(8.11)	(0.003)						(11.65)	(7.97)	(0.003)
		3					2794	404	0.15		–	–	–		2796	402	0.15
							(7.24)	(5.18)	(0.001)						(7.21)	(5.20)	(0.001)
4	10,000	1	600	199	0.80	146,555		Did not converge			600	199	0.80	>99.99%	–	–	–	<0.01%
			(2.34)	(1.41)	(0.001)	(124.66)					(2.33)	(1.38)	(0.001)
		2	1898	402	0.20						1898	402	0.20		–	–	–
			(11.20)	(9.55)	(0.001)						(10.91)	(9.31)	(0.001)
		3													–	–	–
	50,000	1	600	199	0.80	732,514		Did not converge			600	199	0.80	>99.99%	–	–	–	<0.01%
			(1.13)	(0.77)	(0.001)	(323.19)					(1.11)	(0.76)	(0.001)
		2	1899	401	0.20						1900	401	0.20		–	–	–
			(4.40)	(4.57)	(0.001)						(4.29)	(4.42)	(0.001)
		3													–	–	–
5	10,000	1	2199	400	0.80	155,733		Did not converge			2200	401	0.80	>99.99%	–	–	–	<0.01%
			(8.25)	(5.02)	(0.01)	(110.12)					(4.79)	(3.37)	(0.002)
		2	3396	402	0.20						3400	401	0.20		–	–	–
			(25.85)	(15.87)	(0.01)						(11.72)	(9.50)	(0.002)
		3													–	–	–
	50,000	1	2200	400	0.80	778,442		Did not converge			2200	400	0.80	>99.99%	–	–	–	<0.01%
			(3.64)	(2.02)	(0.003)	(296.97)					(2.21)	(1.60)	(0.001)
		2	3399	401	0.20						3400	400	0.20		–	–	–
			(9.95)	(6.86)	(0.003)						(4.06)	(4.57)	(0.001)
		3													–	–	–

¹The standard deviation of the parameter estimate over the 50 replicates is shown in the parentheses.

²No results are reported when RJMCMC remained at a model for fewer than 0.01% of the iterations.

³Gibbs sampling stopped before convergence, and no results are reported.

⁴The two-component model was from a single replicate, so the standard deviation across replicates was not available.

When the simulated birth weight data contain three well-separated components (simulation 1), a mixture model with three components yields means, SDs, and proportions very close to the true values for both sample sizes. The mixture model with two components can still identify the first component, with the average estimate of θ₁ a little lower than the truth (68% vs. 70%), while the second and third components are combined into one group. The average BICs for the three-component model are smaller than those of the two-component model, suggesting that the three-component model fits the data better. RJMCMC jumps between the two models when the sample size is small, with the three-component model chosen in 90% of the iterations and the two-component model chosen in 10% of the iterations on average. When sample size increases to 50,000, RJMCMC remains at the three-component model in more than 99.99% of the iterations and yields average estimates close to the truth. (Results of RJMCMC are not shown for a value of K when RJMCMC chooses that value in less than 0.01% of the iterations.)

In the second simulation, we defined three groups, but we set up the last two groups to be very close to each other (Figure 1(b)). At the smaller sample size, the three-component mixture model cannot separate the last two groups. The Gibbs sampling does not converge when the probability of a third group is too small, and no observations can be assigned to that group. At the large sample size, a mixture model with three components can identify three groups; however, the estimates for groups 2 and 3 are not close to the truth on average. A significant number of observations from the second group are assigned to the third group, so that the average estimated proportion is higher than the truth for the third group and is lower than the truth for the second group. The average mean for the second group is greater than the true value, and the average mean for the third group is smaller than the true value, because of this misassignment. On the other hand, the two-component model identifies the first group well, with means, SDs, and proportions close to the truth on average at both sample sizes. The average BIC for the two-component model is smaller than that for the three-component model at sample size of 50,000, suggesting the two-component model fits the data better. RJMCMC stays at the two-component model in more than 99.99% of the iterations, with the second and third groups combined and the average estimates for the first group very close to the truth. Increasing the sample size to 50,000 does not change the results. This simulation suggests that if the misreported gestational ages are from groups too close to each other, then the mixture model will treat them as one group. The result is acceptable, particularly for our future multiple-imputation project, as long as the combined group can be separated from the group consisting of correctly reported gestational ages.

In the third simulation, we defined the three groups to be better separated than in simulation 2, although the histogram does not show these groups clearly (Figure 1(c)). At both sample sizes, the three-component mixture model identifies the three groups with average estimated means, SDs, and proportions close to the truth. The two-component model assigns some misreported cases into the first component; thus, the average estimated mean for the first group is higher than the truth, and the average estimate of θ₁ is higher than the true proportion (73% vs. 70%). The average BICs for the three-component model are smaller than those for the two-component model, suggesting the three-component model fits better. RJMCMC stays at the two-mode model for less than 1% of the iterations at the sample size of 10,000. When the sample size increases to 50,000, RJMCMC stays at the three-component model for more than 99.99% of the iterations, with average parameter estimates close to the truth.

We set up the last two simulations to contain data from mixtures of two normal distributions. Use of a mixture model with two components yields results very close to the truth on average. With non-informative priors, a mixture model with three components cannot identify three groups, as expected. RJMCMC stays at the two-component model more than 99.99% of the time, with average estimates close to the true values.

Variability of the parameter estimates over the 50 replicates was relatively small, except in the case the three-component mixture model of simulation 2. The last two components in simulation 2 were close to each other, and the three-component mixture model could not separate those two groups properly, which leads to much larger SDs of the parameter estimates compared with the other simulation studies. The results of the simulation studies suggest that the Bayesian mixture model can identify different components well if they are well separated. However, for data generated from a three-component model with the last two groups close to each other (simulation 2), the mixture model cannot distinguish the last two groups and will treat them as one group. Our goal for the multiple-imputation project is to identity the first component, which contains the correctly reported gestational ages. The implausible cases, whether classified into one group or separate groups, will not change the results as long as the first group is identified well. On the other hand, correctly modeling different groups still affects identification of the first group. As shown in simulations 1 and 3, when a two-component model is fitted to a mixture of three components, the proportion and the mean for the primary group tend to be slightly further away from the truth, compared with the estimates from the three-component mixture model.

The RJMCMC procedure yields similar results as does fitting two-component and three-component mixture models separately and then using BIC as a model selection tool. When the sample size is small, the RJMCMC procedure jumps between different components, the majority of times selecting models consistent with BIC. When the sample size is large, RJMCMC selects the same models as the BIC procedure. The advantage of RJMCMC is that it reflects uncertainty in the selection of the model; this uncertainty can be integrated into the multiple imputation of the misreported gestational ages in our future research project.

In our simulation studies, we generated data to mimic the real world; however, because of the complexity of the problem, we could not cover all possible scenarios. The next section contains results of applying our procedures to actual US birth data.

5. Analysis of US birth data

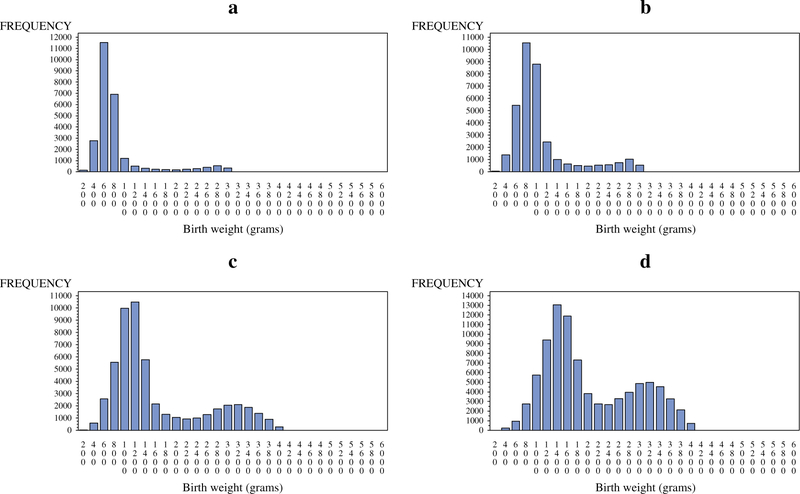
We use US singleton birth data from 2001 through 2008, available from the National Center for Health Statistics [34, 35]. These data contain parental and infant information collected on birth certificates. Table III contains the mean, SD, minimum and maximum values, and the number of observations within each reported gestational age from 23 to 32 weeks. The minima and maxima reflect crude edits during processing of the data before dissemination. Figure 2(a–d) shows the histograms of birth weight by reported gestational age for four selected gestational ages. Table IV contains results of fitting Bayesian mixture models with two or three components separately as well as results of the RJMCMC procedure. As in the simulation studies, we used non-informative priors for these analyses.

Table III.

Summary statistics of birth weight (grams) by reported gestational age (weeks) (US birth data 2001–2008).

Statistics	Week 23	Week 24	Week 25	Week 26	Week 27	Week 28	Week 29	Week 30	Week 31	Week 32
N	18,295	25,903	29,913	34,820	38,616	53,183	64,443	88,517	113,902	160,440
Min	227	227	227	227	227	227	227	227	227	507
Max	1995	2999	2999	2999	2999	3998	3999	3999	3999	8165
Mean	636	840	950	1070	1188	1624	1817	2022	2164	2348
SD	246	556	577	592	589	918	908	882	815	765

Figure 2.

Histograms of birth weight (grams) by reported gestational age for US birth data from the years 2001 to 2008: (a) 24, (b) 26, (c) 28, and (d) 30 weeks.

Table IV.

Estimated means of birth weight (grams), standard deviations (SD), and mixing proportions (θ) from the Bayesian mixture models and RJMCMC for US birth data (2001–2008); also shown are the percentages of iterations for which RJMCMC chose the given values of K.

Week	component	Fit separately								RJMCMC
		Two components				Three components				Two components				Three components
		Mean	SD	θ	BIC	Mean	SD	θ	BIC	Mean	SD	θ	K = 2	Mean	SD	θ	K = 3
23	1	569	110	0.86	239,354	564	105	0.82	238,936	–	–	–	<0.01%	564	104	0.81	>99.99%
	2	1053	405	0.14		834	265	0.16		–	–	–		828	266	0.16
	3					1691	178	0.03		–	–	–		1691	178	0.03
24	1	650	140	0.85	359,727	646	135	0.83	358,196	–	–	–	<0.01%	646	135	0.83	>99.99%
	2	1958	746	0.15		1260	465	0.10		–	–	–		1254	460	0.10
	3					2666	242	0.07		–	–	–		2663	244	0.07
25	1	740	169	0.85	426,162	737	165	0.83	424,576	733	155	0.78	21%	736	164	0.83	79%
	2	2107	654	0.15		1645	562	0.11		1726	814	0.22		1560	540	0.11
	3					2766	157	0.06						2737	183	0.06
26	1	842	207	0.83	506,764	836	201	0.82	506,955	842	206	0.83	99%	841	205	0.83	1%
	2	2224	563	0.17		1797	520	0.12		2213	571	0.17		1895	452	0.11
	3					2777	147	0.06						2801	127	0.06
27	1	963	244	0.84	570,331	954	236	0.82	571,167	964	244	0.84	>99.99%	–	–	–	<0.01%
	2	2354	463	0.16		1959	434	0.11		2357	461	0.16		–	–	–
	3					2775	144	0.07						–	–	–
28	1	1096	284	0.71	832,521	1078	269	0.68	848,637	1094	282	0.71	> 99.999%	–	–	–	<0.01%
	2	2937	568	0.29		2170	539	0.13		2929	576	0.29		–	–	–
	3					3231	369	0.19						–	–	–
29	1	1251	322	0.68	1,021,410	1234	307	0.66	1,026,773	1256	326	0.68	>99.99%	–	–	–	<0.01%
	2	3001	512	0.32		2526	494	0.17		3015	500	0.32		–	–	–
	3					3309	336	0.18						–	–	–
30	1	1436	364	0.64	1,414,529	1425	355	0.63	1,413,529	1437	366	0.64	>99.99%	–	–	–	<0.01%
	2	3077	459	0.36		2840	421	0.24		3081	456	0.36		–	–	–
	3					3460	274	0.13						–	–	–
31	1	1639	395	0.64	1,819,585	1637	393	0.64	1,818,515	1639	395	0.64	>99.99%	–	–	–	<0.01%
	2	3112	430	0.36		2987	373	0.29		3112	430	0.36		–	–	–
	3					3610	210	0.07						–	–	–
32	1	1836	381	0.59	2,560,568	1834	378	0.59	2,560,229	1836	381	0.59	>99.99%	–	–	–	<0.01%
	2	3104	522	0.41		3066	904	0.03		3104	522	0.41		–	–	–
	3					3097	496	0.38						–	–	–

No results are reported when the RJMCMC remained at a model for fewer than 0.01% of the iterations.

For reported gestational age of 23 weeks, the fitted two-component mixture model estimates 86% of gestational ages as correctly reported. The mixture model with three components identifies three well-separated groups. The first group contains newborns with correct gestational ages, which constitute an estimated 82% of cases; the second and third groups are cases with misreported gestational ages. The third group has an estimated mean value of 1691 g, which is far from that for term births, suggesting the third group does not come from term births. The BIC value for the three-component model is smaller than that for the two-component model, suggesting the three-component model is a better fit. RJMCMC stays at the three-component model more than 99.99% of the time with results close to the separately fitted three-component model.

The data for 24 weeks are similar to those for 23 weeks, with three well-separated groups. The fitted two-component and three-component mixture models estimate, respectively, 85% and 83% of the observations as having correctly reported gestational ages. RJMCMC stays at the three-component model for more than 99.99% of the iterations with results close to the three-component mixture model.

Behavior of estimates for 25 weeks shows some differences from that for the lower gestational ages. The fitted two-component model estimates 85% observations as correctly reported cases, and the fitted three-component model estimates 83% as correctly reported. The BIC value for the three-component model is smaller than that for the two-component model. The behavior of RJMCMC is more like that in simulation 1 at the small sample size: RJMCMC stays at the three-component model 79% of the time and at the two-component model 21% of the time. The results of the three-component model within RJMCMC are close to those of the three-component model fitted separately, whereas the results of the two-component model within RJMCMC are not close to the two-component model fitted separately.

At 26 weeks, RJMCMC jumps between the two-component and three-component models as well. Unlike at 25 weeks, however, it stays at the two-component model most of the time (99% of iterations). RJMCMC yields estimated means, SDs, and proportions for the first component that are close to those for the Bayesian mixture models when fitting separately. Starting from 26 weeks, the two-component mixture model is more likely to be selected than the three-component model.

Data for 27–31 weeks are more like simulation 2, with the implausible gestational ages close to each other and not easily separated into different groups. When fitting the two-component and three-component models separately, the first groups have similar estimated means, SDs, and proportions. The estimated percentages of the misreported records increase dramatically at the higher gestational ages, with more than 35% of records estimated to be misreported starting at 30 weeks. BIC selects the two-component model for 27–29 weeks and selects the three-component model for 30 and 31 weeks. RJMCMC, on the other hand, stays at the two-component model more than 99.99% of the time for all these reported gestational ages. One possible reason for this discrepancy is that the data structure for the higher reported gestational ages (30 and 31 weeks) is complicated, with large sample sizes and birth weights from different groups close to each other. As a result, the variations of different groups at the splitting move have a larger impact over the likelihood function, and RJMCMC does not select the same model as BIC. This discrepancy deserves further research and is not within the scope of this paper.

When we apply our methods to gestational ages of 32 weeks and above, a mixture model, especially the three-component model, is no longer appropriate. The birth weight distributions for the components are too close, so the models cannot separate different groups properly. As an example, Table IV shows the results for 32 weeks. The mixture model with three modes identifies the last two groups as being very close to each other. Even though the BIC for the three-component model is smaller, the model does not fit the data well. Parker et al. [28] observed similar issues when applying mixture models to gestational ages of week 32 and above. Hence, we do not include results for the higher gestational ages in this paper.

To show the variability of the posterior distribution, we derived quantiles of the parameter estimates (see Web-based Supporting Information). In general, the range of the posterior distribution (maximal value ‒ minimal value) for the primary component, which consists of the correctly reported gestational ages, is smaller compared with the other components for both two-component and three-component mixture models. Week 25, where the transition of the better fitting models from three components to two components starts, shows the largest variability for the parameter estimates. However, once the transition stabilizes (week 27 and above), the variability of the posterior draws remains stable and small.

In summary, the results for the US birth data suggest that the three-component model is appropriate for lower gestational ages and the two-component model fits better for the higher gestational ages. The transition from the three-component model to the two-component model is around 25 to 26 weeks. Using our models, we found that the estimated percentages of misreported gestational ages vary, with values less than 20% for the lower gestational ages (23–27 weeks) and values around 30% to 35% for the higher gestational ages (28–31 weeks).

6. Discussion

We develop Bayesian mixture models inspired by the previous work of Oja et al., Tentoni et al., and Platt et al. Unlike the mixture models with a fixed number of distributions, we allow the number of components to change. We also allow different proportions of misreporting within each reported gestational age. With non-informative prior information, our methods yield average estimated means, SDs, and proportions close to the true values based on the simulation studies. We have tested the impact of using conjugate priors and found that the prior information on the mean and proportion has more effect on the parameter estimates for the Bayesian mixture models than does prior information on the variance (results not shown). However, because we do not have prior information available for this study, we combined the data from year 2001 to year 2008 so that we have relatively large sample sizes to allow the data to dominate the model fit with non-informative priors. Our method only includes birth weight and gestational age in the model. The US birth data have rich information on maternal demographic characteristics, maternal medical characteristics, medical care utilization, and infants’ characteristics. The clinical estimate of gestational ages based on ultrasound also contains important information on gestation [36]. Parker et al. [28] included covariates to model the mean function of each mixture component but did not find that covariates significantly improved the model fitting for a mixture model with two components, except for stratifying on gender. Whether covariates will improve model fitting in Bayesian mixture models and RJMCMC deserves further investigation, especially if they are used to model the proportions in the components rather than just the mean functions.

The ultimate goal of this research is to use multiple imputation to address the problem of missing and implausible gestational age data in US Natality public use data sets. Parker and Schenker [26] discussed general approaches to dealing with this problem. By using a Bayesian mixture model with a prespecified number of components (K) as one step in our multiple-imputation procedure, we will have the advantage of retaining the approximate normality of the birth weights, in contrast to truncating at specific birth weight—gestational age combinations; our multiple imputations will reflect both the uncertainty in identifying the misreported gestational ages under the given value for K and the uncertainty in prediction for the implausible and missing gestational ages. Moreover, if we allow K to vary by using the RJMCMC procedure, we will incorporate the uncertainty about K into the multiple imputations as well. On the basis of our research, the results of RJMCMC are consistent with the results when fitting two-component and three-component models separately and then using an information criterion to choose one of the models. For the next step of our research, we will develop a prediction model to impute the implausible and missing gestational ages. As is true for any procedure to adjust for misreporting and/or missing data, multiple imputation depends on the accuracy of the models used, and misspecification of the models will lead to biased results. Therefore, the use of model diagnostics and sensitivity analyses will be important steps in the model building process.

Although we use a mixture of two or three components to identify the implausible gestational ages, a model with more than three modes could be formulated similarly. We assume that birth weight within each reported gestational age follows a mixture of normal distributions. However, the misreported cases are from a wide range of gestational ages, and the normality assumption for the misreported cases may be questionable, especially for the lower gestational ages. An alternative to the normal mixture model approach is to use semiparametric models, which allow a more flexible distribution for the misreported group(s). Wilcox and Russell [37] proposed a two-component mixture distribution for birth weight. One component consists of a ‘predominant distribution’ that has a normal density function and represents normal births. The second component is a ‘residual distribution’ with an unspecified form, representing low weight births. Similar approaches could be applied within each reported gestational age to identify the plausible and implausible reported gestational ages.