Applying a Novel Population-Based Model Approach to Estimating Breath Alcohol Concentration (BrAC) from Transdermal Alcohol Concentration (TAC) Biosensor Data

Abstract

Alcohol biosensor devices have been developed to unobtrusively measure transdermal alcohol concentration (TAC), the amount of ethanol diffusing through the skin, in nearly continuous fashion in naturalistic settings. Because TAC data are affected by physiological and environmental factors that vary across individuals and drinking episodes, there is not an elementary formula to convert TAC into easily-interpretable metrics like blood and breath alcohol concentrations (BAC/BrAC). In our prior work, we addressed this conversion problem in a deterministic way by developing physics/physiological-based models to convert TAC to estimated BrAC (eBRAC), in which the model parameter values were individually determined for each person wearing a specific transdermal sensor using simultaneously collected TAC (via a biosensor) and BrAC (via a breath analyzer) during a calibration episode. We found these individualized parameter values produced relatively good eBrAC curves for subsequent drinking episodes, but our results also indicated the models were not fully capturing the dynamics of the system and variations across drinking episodes. Here, we report on a novel mathematical framework to improve our ability to model eBrAC from TAC data that uses aggregate population data instead of individualized calibration data to determine model parameter values via a random diffusion equation. We first provide the theoretical mathematical basis for our approach, and then test the efficacy of this method using datasets of contemporaneous BrAC/TAC measurements obtained by a) a single subject during multiple drinking episodes and b) multiple subjects during single drinking episodes. For each dataset, we used a set of drinking episodes to construct the population model, and then ran the model with another set of randomly-selected test episodes. We compared raw TAC data to model-simulated TAC curve, breath analyzer BrAC data to model eBrAC curves with 75% credible bands, episode summary scores of peak BrAC, times of peak BrAC, and area under the drinking curve also with 75% credible intervals, and report the percent of the raw BrAC captured within the eBrAC curve credible bands. We also display results when stratifying the data based on the relationship between the raw BrAC and TAC data. Results indicate the population-based model is promising, with better fit within a single participant when stratifying episodes. This study provides initial proof-of-concept for constructing, fitting, and using a population-based model to obtain estimates and error bands for BrAC from TAC. The advancements in this study, including new applications of math, the development of a population-based model with error bars, and the production of corresponding Matlab codes, represent a major step forward in our ability to produce quantitatively- and temporally-accurate estimates of BrAC from TAC biosensor data.

Graphical Abstract

Background

Alcohol research and treatment communities have long recognized the potential value of being able to measure alcohol levels in ecologically-valid settings (see Leffingwell et al., 2013; Swift, 2003). Traditional methods for studying naturalistic drinking patterns and consumption levels have primarily included self-report diaries in the field or observer-rated monitoring of ad libitum drinking in the laboratory. These methods, however, have a number of drawbacks. Self-report of alcohol consumption is often unreliable (e.g., due to not knowing alcohol contents of drinks or total quantity consumed, not recording information reliability or accurately) and self-monitoring may interfere with naturalistic drinking and behavior. Drinking in the laboratory also does not necesssarily generalize to real-world conditions, and there are limits to the levels of intoxication permitted in these settings by human subjects review boards that are often below typical levels of heavy drinkers. Thus, researchers and clinicians would benefit greatly from a source of more accurate data on naturalistic alcohol consumption to study alcohol-related health outcomes, disease progression, treatment efficacy, and recovery (NIAAA, 2016; 2017). In addition, providing lay individuals with personal information on their alcohol levels during drinking episodes may help people improve decision-making while drinking and make better health choices.

Small, wearable, unobtrusive alcohol biosensor devices are being developed to make continuous, passive monitoring of alcohol consumption feasible. Currently, the alcohol biosensors that are closest to meeting these specifications are those measuring transdermal alcohol concentration (TAC), the amount of alcohol diffusing through the skin. Devices have been available for decades to accurately measure TAC via electrochemical sensors (see Swift & Swette, 1992), but despite this, TAC has yet to be developed into an interpretable, quantitative output to fully maximize its usefulness. This is due, in part, to the fact that the raw TAC data these devices record do not consistently correlate with breath and blood alcohol concentrations (BrAC/BAC) across individuals, devices, and environmental conditions (Hill-Kapturczak et al., 2015; Swift, 2000; 2003; Webster & Gabler, 2007a, 2007b). There are relatively simple and robust models for converting BrAC into BAC (e.g., Dominick, 1990; Labianca, 1990), but the transport and filtering of alcohol by the skin is affected by variations in factors such as skin layer thickness and hydration, ambient temperature and humidity, and biosensor device features (Dumett et al., 2008; Leffingwell et al., 2013; see Swift, 2003). All of these variations need to be taken into account when developing models that convert TAC into quantitatively- and temporally-accurate measurements of alcohol levels in the body.

Prior Deterministic Mathematical Approach

Our research team previously developed models that convert TAC data into eBrAC using a two-step deterministic approach. The first step, the calibration phase, fit first principles physics-based models (Banks & Ito, 1997; Banks & Kunish, 1989; Gibson & Rosen, 1988) using individual-level data to capture the propagation of alcohol from the blood, through the skin, and its measurement by the sensor (i.e., the forward model). The second step, the inversion phase, then used the individualized parameters determined in the calibration phase to invert the model to produce eBrAC based on the TAC for all subsequent drinking episodes for that individual wearing that device (Dumett et al., 2008; Rosen, Luczak, Hu, & Hankin, 2013; Rosen, Luczak, & Weiss, 2014). These models were compiled in our BrAC Estimator software program (Luczak & Rosen, 2014), which uses the individualized calibration data to choose optimal values for the model parameters for each person-device pair and then inverts TAC into eBrAC for all drinking episodes. The software produces parameter values, drinking summary scores (e.g., peak eBrAC, time of peak eBrAC, area under the drinking curve, AUC), and plots of both TAC and eBrAC data for all drinking episodes. Our results were generally good using this approach, but also indicated that un-modeled dynamics were contributing to reduced fit across drinking episodes. In addition, the participant and researcher burden for obtaining the simultaneously-collected TAC and breath analyzer BrAC data in the laboratory reduced the feasibility for non-researchers to use this approach.

In several subsequent publications, we sought to reduce the burden of laboratory data collection by replacing the breath analyzer BrAC data used to determine the individualized model parameters with drinking diary data converted into calculated BAC using various equations (Dai, Rosen, Wang, Barnett, & Luczak, 2016) and an iPhone application (Luczak et al., in press). We showed using a calculated BAC produced similar results to using breath analyzer data in both the calibration and inversion phases of our model when examining 10 drinking episodes obtained by a single subject. Summary scores of the two methods were within 0.000–0.003% for peak BrAC, within 17–18 minutes for time of the peak BrAC, and within 0.01–0.03% alcohol–hours for AUC.

We also examined ways to remove the individualized calibration step in the modeling via the development of population-based parameters. Our first attempt at doing this was when modifying our BrAC Estimator codes for inclusion in the TASMAC Excel macro (Barnett et al., 2015), which was designed to detect drinking episodes and did not allow for the calibration of the models using individualized data. For the TASMAC, we constructed a simple population model by replacing the parameters in our individual model with the mean of the parameters obtained by fitting a set of 11 drinking episode from participants wearing the SCRAM sensor (Alcohol Monitoring Services, Inc., Boulder, CO) in laboratory clamping experiments (data provided by S. J. O’Connor from P50 AA007611; e.g., O’Connor, Morzorati, Christian, & Li 1998). Results obtained using the TASMAC population model look promising (see, e.g., Fairbairn, Rosen, Luczak, & Venerable, submitted to this special issue), but this relatively crude approach does not provide any statistically-derived error bars to accompany the eBrAC curve and summary statistics. We also investigated the use of model parameters obtained by fitting our model simultaneously using population estimates derived from multiple drinking episodes from a single subject and then testing the fit on other drinking episodes from this same subject, again with relatively good results (Dai et al., 2016). These results indicated there was potential for using population-based parameters to convert TAC to eBRAC, but new models that were appropriate for this type of data would need to be developed. Such a model would retain the physics/physiological structure of the model, but now attribute all un-modeled effects (which necessitate the calibration of the individual model) to random effects, and then would estimate the distribution of the parameters across the population. Using this approach, it would also become possible to estimate credible bands for the BrAC curves and credible intervals for the associated summary statistics, providing a more comprehensive understanding of the fit of the eBrAC outcomes.

Novel Population-Based Mathematical Approach

The current study describes our efforts to model the TAC-eBrAC system by applying a population-based approach to better account for uncertainty in the blood-skin-TAC sensor system. Such an approach, while attractive, poses a number of mathematical challenges that require the development and analysis of new theoretical and computational techniques before a population model of this form can be used in a practical manner to provide eBrAC and credible bands. We start with a mathematical system of equations to model the diffusion of ethanol through 1) the epidermal layer of the skin, which does not contain blood vessels, together with boundary conditions that capture ethanol’s transportation 2) between the epidermal layer and the dermal layer of the skin, which does have blood vessels, and 3) ethanol’s evaporation on the skin surface. This basic model consists of a diffusion equation with input and output on the boundary of the domain with two unknown parameters. We assume that the dynamics of the process that is described by this model is common to every individual in the population. On the other hand, due to environmental and physiological conditions and hardware being used, there is a significant amount of variation across each person, environment, and device combination, which is explained by variation in the parameters. The data we use in these models include BrAC and TAC measurements collected from various subjects during various drinking episodes, which we refer to as the population data. To account for any uncertainty/un-modeled dynamics in the system and to base the estimation on the population data, we assume that the parameters are random variables and hence obtain a random transport model rather than a deterministic one. Then in this case, estimation of the distribution of the random parameters based on population data replaces the calibration phase of the deterministic approach. To obtain the desired estimation, we formulate our estimation problem using a least squares or maximal likelihood approach, which yields a mathematical optimization problem. We aim to minimize the difference between the observed TAC data and the expectation of the output of the model. By solving this minimization problem, we obtain the desired estimate of the distribution of the random parameters. We use aggregate population BrAC/TAC data to estimate the mean, covariance matrix, and support of the underlying joint distribution function of the two parameters in the form of a truncated bivariate normal. This set of steps corresponds to the calibration phase in the prior deterministic approach (see Sirlanci, Luczak, & Rosen, 2017; Sirlanci & Rosen, submitted; Sirlanci et al., submitted b, for mathematical details).

The next step is estimating BrAC based on the estimated distribution of parameters and given TAC data. This step corresponds to the inversion phase of the deterministic approach. Before formulating the estimation problem, we first construct our population model using the estimated distribution. Because we developed the population model to describe the mean behavior of the population, the model does not include any of the parameters that vary across person-device pairs. Then, again using a least squares approach, we formulate the estimation problem for BrAC estimation. This time, we aim to minimize the difference between the TAC data and the output obtained via the population model, which is written as a function of the input by using the formulation of the population model. In addition to this difference term, we also include a regularization term, which prevents the solution from having excessive magnitude and oscillations. Then, again using a least squares approach, we obtain the solution of this optimization problem, which is the desired eBrAC curve. In addition to the estimate and because of the uncertainty in the system, we also obtain a credible band around the estimate to provide information on its accuracy (see Sirlanci et al., submitted a, for mathematical details).

In this way, we have developed an abstract convergence and approximation framework for 1) the estimation of the distribution of the random parameters in our model based on population data, and 2) the use of this population model to estimate BrAC (i.e., input) given the TAC (i.e., output).

Study Purpose

The purpose of this study is to test how this novel population-based mathematical framework works in practice and to establish initial proof-of-concept of this approach. To test our models, we wrote MATLAB code for the models and then ran the code with simulated data. After observing that we obtained satisfactory results for our distribution estimation problem with simulated data, we then used actual BrAC-TAC data to obtain the mean, covariance matrix, and the support of the joint probability density function of the random parameters, which were presumed to have bivariate normal distribution. We used two datasets—one dataset of multiple drinking episodes collected by a single subject, and one dataset of multiple subjects each drinking once. For each dataset, we first formed our population model from a subset of the data, and formulated the deconvolution problem to obtain eBrAC given TAC data. Then we obtained the simulated TAC (sTAC) output via the population model, and compared this output with the actual TAC data to see the effectiveness of our population model and the inversion process. Finally, we examined the fit of our resulting population models using a subset of drinking episodes from each dataset that was not used to create the population model to estimate the eBrAC curve, summary statistics, and 75% credible bands and intervals.

Methods

Datasets

We used two sets of data to test our models. In both datasets, participants wore a WrisTAS™ 7 alcohol biosensor (Giner, Inc., Waltham, MA) that was set to measure the local alcohol vapor concentration over the skin surface at 5-minute intervals. Contemporaneously breath measurements were obtained by an Alco-sensor IV breath analyzer (Intoximeters, Inc., St. Louis, MO), which obtains readings considered valid up to ±0.005.

Single Subject.

One of the co-authors (SEL) collected data on 11 drinking episodes over the course of 18 days (see Figure 1). The first drinking episode was conducted in the laboratory and was designed to reach a peak BrAC of approximately 0.05%. The alcoholic beverage was administered evenly over the course of 15 minutes, and BrAC measurements were taken every 15 minutes from the start of the drinking session until BrAC returned to 0.000. The subsequent 10 drinking episodes were collected in the field while consuming alcohol ad libitum. For each of the field drinking episodes, BrAC readings were taken every 30 minutes until BrAC returned to 0.000. To avoid mouth alcohol affecting BrAC readings, the participant rinsed her mouth twice and refrained from consuming alcohol for at least 5 minutes before taking each BrAC reading. This data collection was not considered human subjects research by the University of Southern California Institutional Review Board (see Luczak & Rosen, 2014 for additional details).

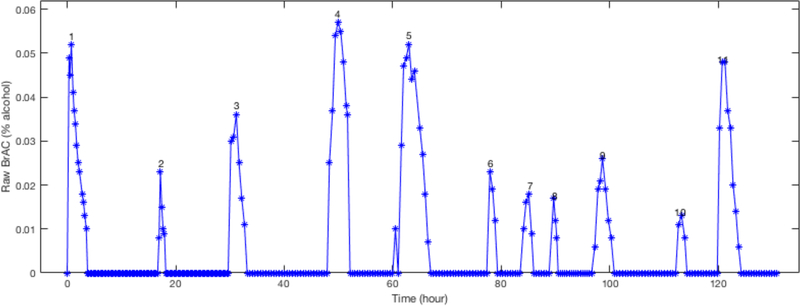
Figure 1.

Dataset 1 contained 11 drinking episodes obtained over 18 days, with the first episode conducted in the laboratory and the 10 subsequent naturalistic drinking episodes obtained in the field. The raw BrAC are shown here over the entire 18 days.

Multiple Subjects.

Using the same protocol as in the first episode in Dataset 1, 32 participants (47% female; age 23.1 +/− 2.69 years; 100% Asian American college students) were administered a moderate, gender- and weight-adjusted dose of alcohol designed to reach a peak BrAC of approximately 0.05% (see Figure 2). All participants were monitored in the laboratory with breathalyzer readings taken by study staff at 15-minute intervals until BrAC returned to 0.000. The study was approved by the University of California, San Diego Human Research Protection Program and written informed consent for participation was obtained (see Luczak, Rosen, & Wall, 2015 for additional sample details).

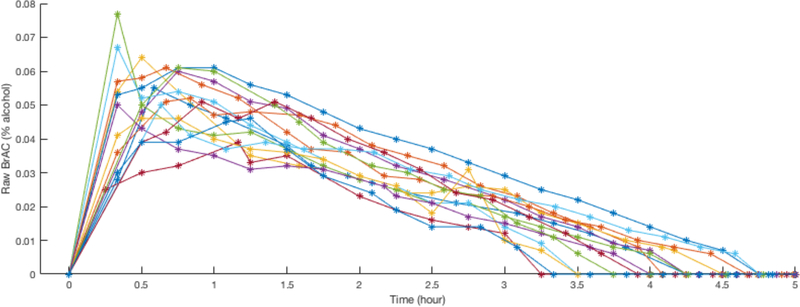
Figure 2.

Dataset 2 contained 15 drinking laboratory drinking episodes by 15 Asian American college students (47% female). The raw BrAC are shown here overlaying all 15 episodes.

Data Selection for Population and Test Samples

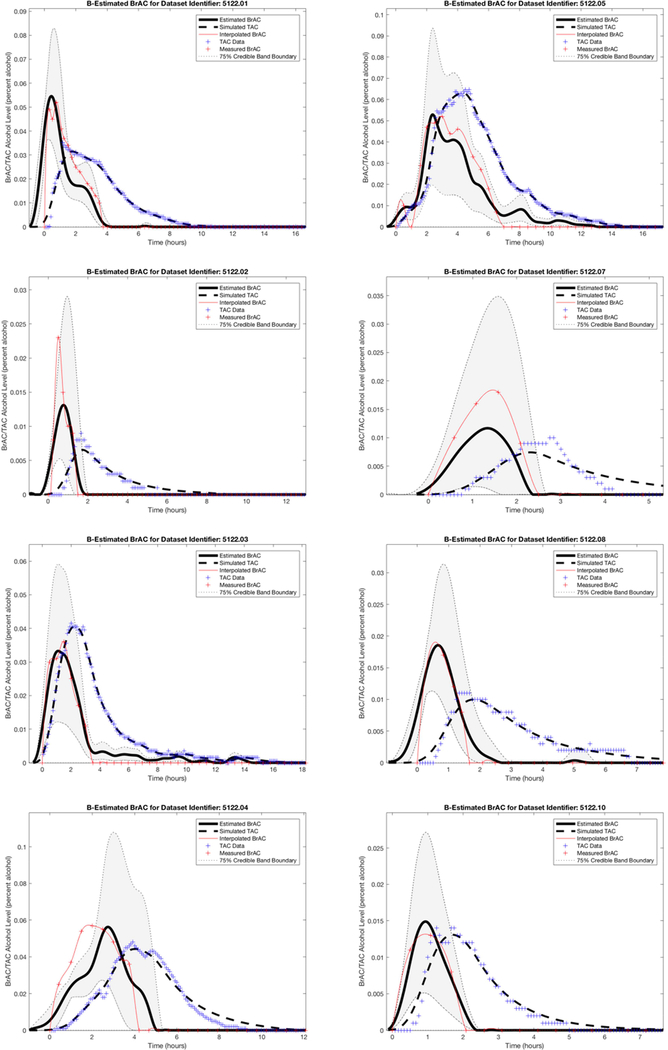
For Dataset 1, we first plotted the TAC and BrAC data to observe their relationship. We found peak BrAC was higher than peak TAC in seven episodes (e.g., see episodes 1, 2, 4, 7, and 8 in Figure 3), and peak TAC was higher than peak BrAC in four episodes (e.g., see episodes 3, 5, and 10 in Figure 3). We then randomly selected two of the seven episodes with higher BrAC (episodes 6 and 11) and one of the four episodes with higher TAC (episode 9) to use as the three (~25% of the data) test episodes, which were held out of the data used for the population model estimates. The remaining eight episodes were used as the training data for establishing the parameters that characterize the population model.

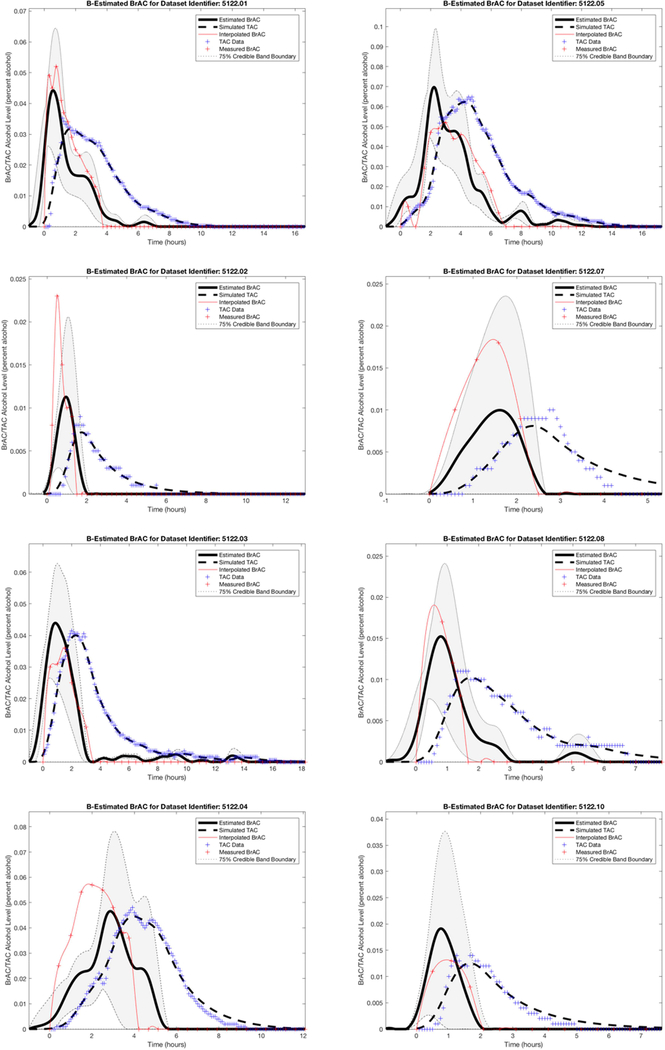
Figure 3.

Dataset 1 training phase estimation results, including the estimated BrAC (eBrAC) curve and 75% credible bands along with raw BrAC, raw TAC, and simulated TAC (sTAC), when all eight episodes are used as one sample in the training phase.

For Dataset 2, we first used the raw BrAC and TAC from each drinking episode to estimate the two model parameters deterministically for the 32 subjects separately, which provided start values for the model and improved the computational efficiency of the model, as would be done for any data screened to be included as part of the population sample. Seven of the episodes produced parameter values that were outliers (i.e., exponentially out-of-range). To avoid overfitting of the models or increasing computational burden and to be consistent with standard procedure in optimization problems, these episodes were excluded from being considered for the population sample. In addition, due to sensor failures (i.e., peak TAC < .02, which is the threshold typically required to indicate a drinking episode, n = 4) and glitches/artifacts in the TAC recordings (i.e., spikes that could be attributed to exposure of the device to external alcohol sources, n = 3, and dips due to lack of direct contact with the skin, n = 4), we removed an additional 11 episodes from these analyses (see Luczak et al., 2015 for additional details on sensor failure rates). This resulted in a final sample of 15 subjects (47% female; age 22.5 +/− 1.55 years; 100% Asian American college students). (Note that additional regularization or smoothing techniques could have been used to retain more data, but this was not needed for the testing of the models where 8–12 sets of TAC-BrAC data were considered sufficient, nor was this seen as beneficial given the population sample should prioritize selecting data that maximizes computational efficiency and the ease of convergence and minimizes the likelihood of overfitting noise.)

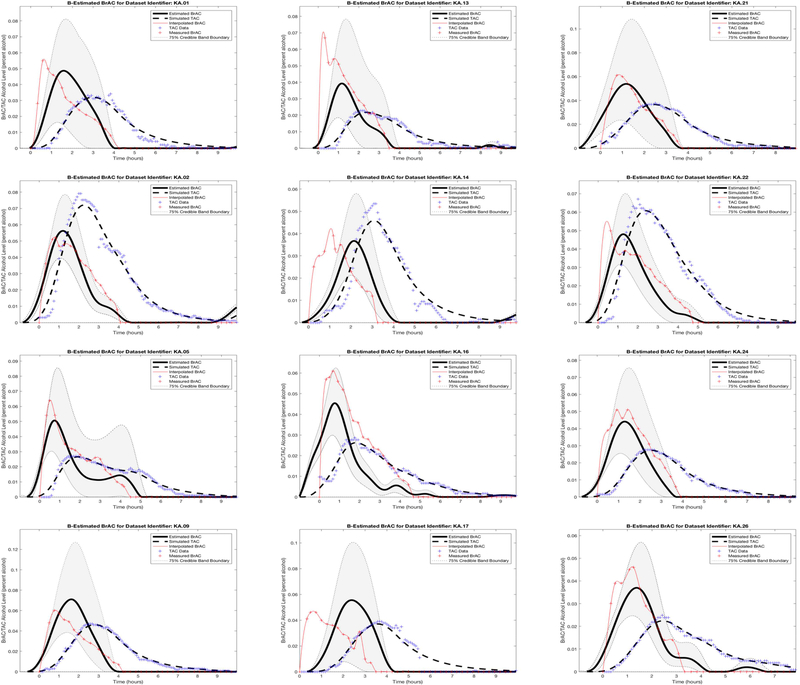
We then plotted the TAC and BrAC data of the 15 episodes. Similar to Dataset 1, we saw that in 11 episodes peak BrAC was higher than peak TAC (e.g., see KA episodes 1, 5, 9, 13, 16, 17, 21, 24, and 26 in Figure 4), and in 4 episodes peak TAC was higher than peak BrAC (e.g., see KA episodes 2, 14, and 22 in Figure 4). We randomly selected two of the 11 episodes with higher BrAC (episodes 12 and 20) and one of the four episodes with higher TAC (episode 15) to use as the three test episodes, which were held out of the data used for the population model estimates. The remaining 12 episodes were used as the training data for establishing the parameters that characterize the population model.

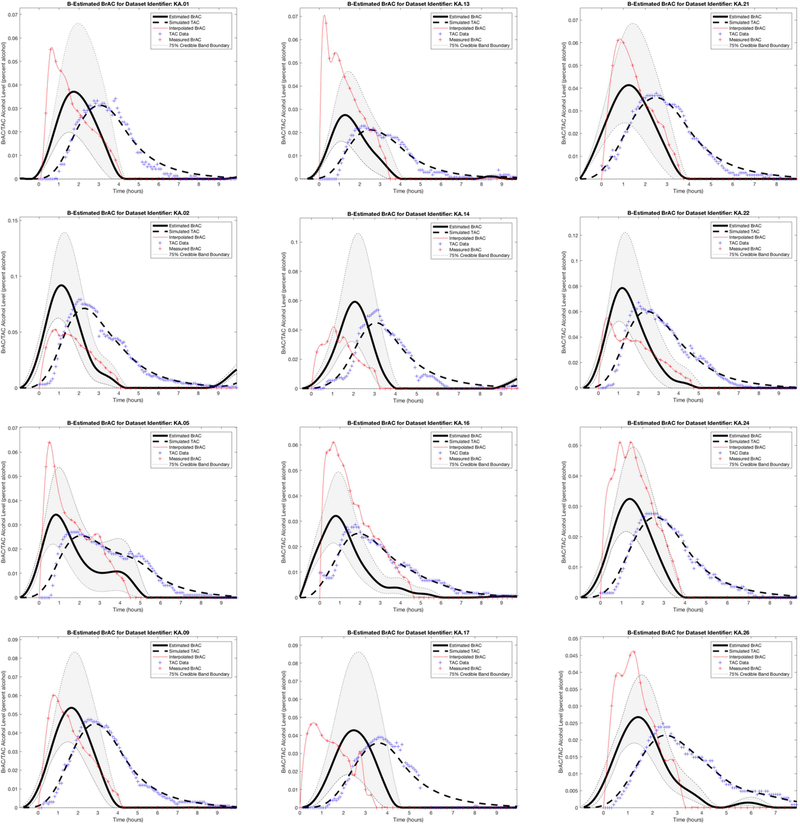
Figure 4.

Dataset 2 training phase estimation results, including the estimated BrAC (eBrAC) curve and 75% credible bands along with raw BrAC, raw TAC, and simulated TAC (sTAC), when all 12 episodes are used as one sample in the training phase.

Computational Data Analysis

We took the following three computational steps using MATLAB:

1. Estimate the distribution of parameters using the training dataset: We developed code that used the adjoint method for derivative calculation. We then compared the derivatives obtained by this adjoint method with the same derivatives obtained by the finite differences method, which is the method used by the FMINCON routine when the derivatives are not provided by the user.

2. Determine the optimal parameters for the regularization term: We used the FMINSEARCH routine to solve the optimization problem, yielding the optimal regularization parameters.

3. Estimate BrAC: Based on the results of steps 1 and 2 and incorporating the TAC data, we used LSQNONNEG routine to obtain eBrAC. Note that this procedure is repeated for each available drinking episode data, including both the episodes used as training data and the ones used for testing model fit.

The system of equations we used to model the alcohol biosensor problem contained two parameters, which in this novel approach we assume to be random. With our mathematical assumptions, these two parameters can be described by a joint probability density function, which contains all the information about the behavior of these random parameters.

After running our codes, we examined plots of our results for all drinking episodes. We included BrAC, TAC, sTAC, eBrAC, and the eBrAC 75% credible band on the same figure to allow for visual comparison of our estimates against the raw data. We report credible bands (or intervals) consistent with Bayesian estimation (Casella & Berger, 2002; Lee, 2004) and not confidence bands (or intervals). The 75α% credible interval is a region that, based on the TAC measurements we have been given, has a 75α% chance or probability that the true value of the quantity estimated lies in this region. We also calculated the percent of the raw BrAC curve captured within the eBrAC curve 75% credible bands. We then obtained estimates and credible intervals for the three summary statistics, including Peak, Time of Peak, and AUC. Lastly, we reran the models stratifying by whether peak raw BrAC was higher or peak raw TAC was higher to determine whether clustering of the data could improve the fit for the test episodes. This final stratification step clustered both the training and test episodes by the BrAC-TAC relationship and held out the same test episodes as in the analyses of the total sample to allow for direct comparison of the results across these two protocols in both datasets.

Results

Dataset 1

Figure 3 shows the Dataset 1 estimation results, including the eBrAC curve and credible band along with raw BrAC, raw TAC, and sTAC, for all eight episodes used in the training phase. The plots show the sTAC consistently mapped onto the raw TAC in all episodes. Since sTAC is obtained using eBrAC as the input to the population model, this demonstrates the effectiveness of the accuracy of the inversion process. Among the eBrAC curves, however, we found a wider range of estimation results and greater variability in mapping onto the raw BrAC curve, which is indicative of the accuracy of the forward (population) model. For example, the eBrAC curve in episode 1 is relatively close to the raw BrAC both in terms of Peak and Time of Peak, whereas in episode 7 the Time of Peak raw BrAC and eBrAC are similar, but the Peak eBrAC itself is lower than the Peak raw BrAC, and in episode 4 both the Peak and Time of Peak eBrAC deviated from raw BrAC, even though the shape of the curve mapped relatively well. The 75% credible bands also captured much of the raw BrAC data (see Table 1).

Table 1.

Percentage of raw BrAC captured within the 75% eBrAC credible bands for each episode used in the training and testing samples for Datasets 1 and 2.

	Dataset 1			Dataset 2
Episode	Total Population	Stratified Population	Episode	Total Population	Stratified Population
Training Episodes
1	75%	86%	1	75%	80%
2	54%	69%	2	49%	75%
3	71%	98%	5	71%	93%
4	45%	54%	9	73%	78%
5	60%	91%	13	65%	77%
7	58%	100%	14	33%	37%
8	73%	92%	16	5%	19%
10	98%	87%	17	46%	63%
			21	83%	97%
			22	76%	86%
			24	41%	76%
			26	55%	75%
Mean	67%	85%		56%	71%
Range	(45–98%)	(54–100%)		(5–83%)	(19–97%)
Testing Episodes
6	54%	70%	12	63%	62%
9	71%	77%	15	59%	90%
11	52%	51%	20	70%	51%
Mean	59%	66%		64%	68%
Range	(52–71%)	(51–77%)		(59–70%)	(51–90%)

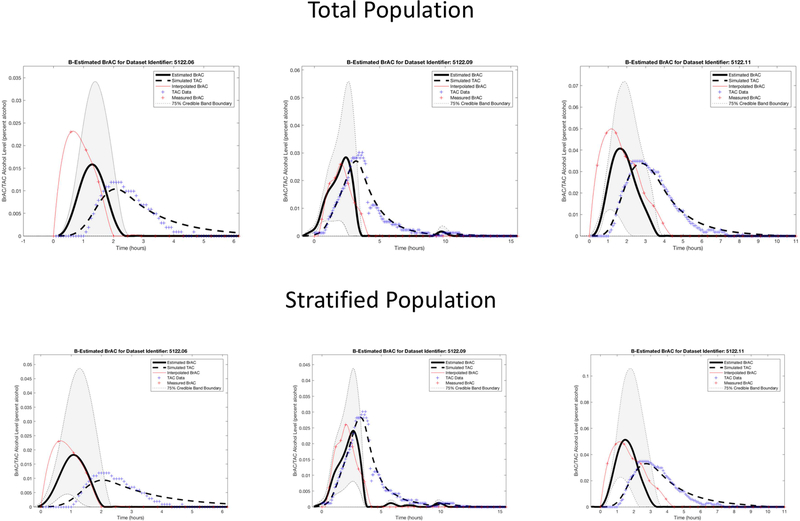
The testing phase results for the three episodes held out of the training data are shown in the top row of Figure 5 and the left column for each episode in Table 2. Again, we found that sTAC mapped onto the raw TAC data, indicating the inversion process worked well when episodes outside of the population data were run in the model. The eBrAC curve results were more variable, with good fit in terms of both Peak and Time of Peak for episode 9, and poorer fit for episodes 6 and 11. Differences between the eBrAC and raw BrAC summary scores, however, were reasonable, with differences in Peak ranging from .002-.007% (similar to the .005 error range for the breath analyzer), Time of Peak from 25–43 minutes, and AUC from .005-.045% alcohol-hours. The 75% credible bands captured 52–71% of the actual BrAC curve, with omissions largely due to the eBrAC curve being slightly delayed (shifted forward) from the raw BrAC, despite being similar shapes (see Table 1).

Figure 5.

Dataset 1 testing phase estimation results, including the estimated BrAC (eBrAC) curve and 75% credible bands along with raw BrAC, raw TAC, and simulated TAC (sTAC), when using all eight episodes as one sample (top row) or when stratified in the training phase into two groups based on whether raw BrAC or raw TAC is higher (bottom row).

Table 2.

Dataset 1 test episode results for Peak, Time of Peak, and Area Under the Curve when using the training sample in total or when stratified by raw BrAC-raw TAC relationship to establish the population parameters.

	Episode 6		Episode 9		Episode 11
Population model	Total	Stratified	Total	Stratified	Total	Stratified
Peak BrAC
BrAC	0.023	0.023	0.026	0.026	0.048	0.048
eBrAC	0.016	0.018	0.028	0.024	0.041	0.051
75% credible interval	[0, 0.034]	[0.005, 0.049]	[0.006, 0.056]	[0.008, 0.044]	[0.012, 0.072]	[0.023, 0.106]
|BrAC-eBrAC|	0.007	0.005	0.002	0.002	0.007	0.003
Time of Peak BrAC
BrAC	0.58	0.58	2.00	2.00	0.92	0.92
eBrAC	1.28	1.08	2.42	2.63	1.63	1.48
75% credible interval	[0, 1.38]	[0.88,1.28]	[1.83, 2.60]	[2.60, 2.67]	[1.10, 1.87]	[1.20,1.78]
|BrAC-eBrAC|	0.70	0.50	0.42	0.63	0.72	0.57
Area Under the Curve
BrAC	0.027	0.027	0.055	0.055	0.118	0.118
eBrAC	0.017	0.020	0.061	0.052	0.073	0.085
75% credible interval	[0, 0.039]	[0.003, 0.060]	[0.012, 0.111]	[0.017, 0.095]	[0.015, 0.134]	[0.029, 0.192]
|BrAC-eBrAC|	0.009	0.006	0.005	0.004	0.045	0.033

Note. Peak BrAC in % alcohol, Time of Peak in hours, Area Under the Curve in % alcohol-hours

We then stratified the episodes based on whether raw TAC or raw BrAC was higher, and reran the models using these two groups separately as the population data. The results of these analyses are shown in Figure 6 for the training data. The sTAC continued to fit well, and now the eBrAC curves mapped more closely to the BrAC curves. The test episode results are shown in the bottom row of Figure 5 and the right column for each episode in Table 2. Episode 11 is the most improved from this stratification, now with the eBrAC curve mapping more closely to the BrAC for Peak (from within .007 to within .003), Time of Peak (from within 43 to 34 minutes), and AUC (from within .045 to .033% alcohol-hours), and the 75% credible band similarly captured 51% instead of 52% of the BrAC measurements (see Table 1). Episode 6 also improved for mapping onto the curve and for all summary scores, with Peak improving from within .007 to .005, Time of Peak improving from within 42 to 35 minutes, AUC improving from within .009 to .006% alcohol-hours), and the 75% credible band capturing 70% instead of 54% of the BrAC measurements. Episode 9 remained a good fit, with Peak staying within .002, Time of Peak increasing from within 25 to 38 minutes, AUC improving slightly from within .005 to .003% alcohol-hours, and the 75% credible band capturing 77% instead of 71% of the BrAC measurements.

Figure 6.

Dataset 1 training phase estimation results, including the estimated BrAC (eBrAC) curve and 75% credible bands along with raw BrAC, raw TAC, and simulated TAC (sTAC), when the eight episodes are stratified in the training phase into two groups based on whether raw BrAC or raw TAC is higher.

Dataset 2

Figure 4 shows the Dataset 2 estimation results, including the eBrAC curve and credible bands along with raw BrAC, raw TAC, and sTAC, for all 12 episodes used in the training phase. As in Dataset 1, the sTAC curves consistently mapped onto TAC, and there was greater variability in the eBrAC curves, with some of the eBrAC curves close to the BrAC curves (e.g., episode 9) and others not so close (e.g., episode 13). Overall, though, the respective 75% credible bands captured a good portion of raw BrAC (see Table 1), and even in episodes where eBrAC was not so close to the BrAC, the general shape of the eBrAC curve was similar to the BrAC curve.

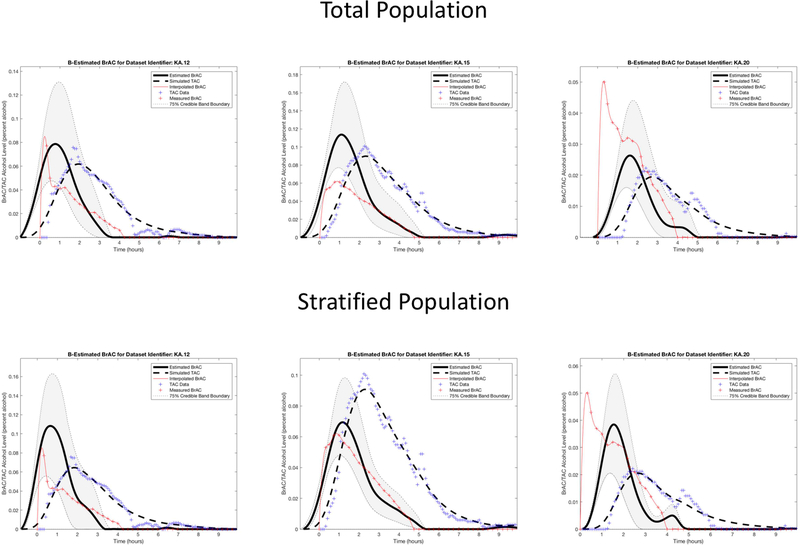
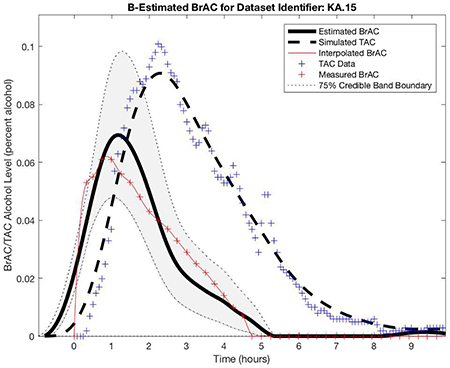
The results for the three test episodes held out of the training data are shown in the top row of Figure 7 and the left column for each episode in Table 3. Again, we observed that sTAC mapped onto the raw TAC data well when episodes outside of the population data were run in the model. The eBrAC curve results were more variable, with relatively good fit for episode 12, but relatively poor fit for episodes 15 and 20. Differences between the eBrAC and raw BrAC summary scores showed similar results, with differences in Peak ranging from .002-.053%, Time of Peak from 21–77 minutes, and AUC from .04-.12% alcohol-hours. The 75% credible bands captured 59–70% of the actual BrAC measurements (see Table 1).

Figure 7.

Dataset 2 testing phase estimation results, including the estimated BrAC (eBrAC) curve and 75% credible bands along with raw BrAC, raw TAC, and simulated TAC (sTAC), when using all 12 episodes as one sample (top row) or when stratified in the training phase into two groups based on whether raw BrAC or raw TAC is higher (bottom row).

Table 3.

Dataset 2 test episode results for Peak, Time of Peak, and Area Under the Curve when using the training sample in total or when stratified by raw BrAC-raw TAC relationship to establish the population parameters.

Population model	Episode 12		Episode 15		Episode 20
	Total	Stratified	Total	Stratified	Total	Stratified
Peak BrAC
BrAC	0.077	0.077	0.061	0.061	0.050	0.050
eBrAC	0.079	0.108	0.114	0.069	0.026	0.036
75% credible interval	[0.048, 0.131]	[0.056, 0.207]	[0.077, 0.172]	[0.048, 0.098]	[0.016, 0.044]	[0.021, 0.074]
|BrAC-eBrAC|	0.002	0.031	0.053	0.008	0.024	0.012
Time of Peak BrAC
BrAC	0.33	0.33	0.75	0.75	0.33	0.33
eBrAC	0.77	0.65	1.10	1.17	1.67	1.55
75% credible interval	[0.58, 0.95]	[0.43, 0.93]	[0.93, 1.23]	[1.03, 1.28]	[1.45, 1.78]	[1.37, 1.73]
|BrAC-eBrAC|	0.43	0.32	0.35	0.42	1.28	1.22
Area Under the Curve
BrAC	0.116	0.116	0.164	0.164	0.096	0.096
eBrAC	0.173	0.209	0.279	0.175	0.054	0.066
75% credible interval	[0.092, 0.309]	[0.083, 0.468]	[0.173, 0.447]	[0.112, 0.259]	[0.028, 0.103]	[0.028, 0.167]
|BrAC-eBrAC|	0.056	0.093	0.115	0.011	0.042	0.030

Note. Peak BrAC in % alcohol, Time of Peak in hours, Area Under the Curve in % alcohol-hours.

When we stratified the training episodes based on whether raw TAC or raw BrAC was higher, sTAC continued to fit TAC well, and now the eBrAC curves mapped more closely to the BrAC curves in the training episodes (see Figure 8). Compared with results using the total population, when using the stratified population Peak BrAC improved for episodes 15 (from within .053 to within .008) and 20 (from within .024 to within .012), but was worse for episode 12 (from within .002 to within .031); Time of Peak improved slightly for episodes 12 and 20 (4–7 minutes) and worsened slightly for episode 15 (4 minutes); and AUC improved the most for episode 15 (from within .12 to .01% alcohol-hours), showed slight improvement for episode 20 (from within .04 to .03% alcohol-hours), and slight worsening for episode 12 (from within .06 to .09% alcohol-hours; see Table 3). Finally, the changes in the 75% credible bands were varied, capturing 31% more BrAC data points for episode 15, 1% less for episode 12, and 19% less for episode 20 (see Table 1). Thus, the stratification produced mixed results for the test episodes, despite consistently improving the eBrAC curve credible bands overlap with raw BrAC for the population sample episodes.

Figure 8.

Dataset 2 training phase estimation results, including the estimated BrAC (eBrAC) curve and 75% credible bands along with raw BrAC, raw TAC, and simulated TAC (sTAC), when the 12 episodes are stratified in the training phase into two groups based on whether raw BrAC or raw TAC is higher.

Discussion

This study represents our efforts to use a population-based model to model the TAC-BrAC relationship and produce eBrAC curves that include credible bands and summary scores that include credible intervals. The advancements in this study, including new applications of math, the development of a population-based model with error bars, and the production of corresponding Matlab codes, represent a major step forward in our ability to produce quantitatively- and temporally-accurate estimates of BrAC from TAC biosensor data. The fit of sTAC in all episodes provides strong evidence of the accuracy of the inversion process. These results further indicate that our model with random parameters having a bivariate normal distribution is an appropriate physics-based model for capturing these data.

The fit of the eBrAC curves produced a wider range of estimation results across episodes, which is an indication of the fit of the forward (population) model. This increased variability in the fit from the sTAC through to the eBrAC is expected in this type of two-step modeling approach, with uncertainties in each step of the model sequentially building upon each other up through the final step of producing the eBrAC. Furthermore, because this approach performs the estimation process based on population data, it is mathematically inevitable to have some uncertainty/error in the estimations, which we can quantify via credible bands and intervals to provide valuable information on the accuracy of our estimations. In fact, examining the amount of raw BrAC data captured by the eBrAC curve credible bands is probably the most reasonable way to evaluate the efficiency of this approach (i.e., as opposed to comparing only raw BrAC and eBrAC point estimates). Our eBrAC curve credible bands show that this method captured a relatively high proportion of the raw BrAC measurements, even in this initial proof-of-concept work when the population estimates were constructed from only 8 and 12 drinking episodes in the two datasets, respectively. The propogation of error in this model results in larger uncertainty around the peak BrAC than at the tail ends of the drinking curve, even if the credible bands do a good job of containing the raw peak BrAC. This widening of the error around the peak is not something we predicted apriori, and is an area for future investigation using techniques from math analysis including the implicit function theorem. Examining model fit of drinking episodes with more varied shapes (e.g., longer plateaus including data from clamping studies, a greater range slopes on the ascending limb) will also be informative for understanding the propogation of error over the eBrAC curve. By building the population sample in future work and including a large enough sample to capture individual-level differences that are found to affect the BrAC-TAC relationship, the credible bands should narrow and the accuracy of the eBrAC curve fit will improve. The results of this study, however, indicate that relatively few sets of data are required to begin this process.

Our results estimating eBrAC of test episodes that were outside of the population sample indicated our approach provides reasonable estimations. We observed greater variation in the fit when using the multiple subjects dataset (where participants wore different devices but episodes were conducted in the laboratory in a hospital setting with controlled ambient temperature and humidity) than when using the single subject dataset (where one participant wore a single device in the field under varied environmental conditions). This greater variation in fit for the multiple subjects dataset makes sense given we are solving the estimation problem based on the population data and forming a single model for everyone in the population, and indicates a single model likely will not capture all model dynamics for all people under all conditions. We will continue to investigate how uncertainty propogates through the models within and across individuals, settings, environmental conditions, and devices.

Our findings also provide evidence that stratifying the data is a potentially valuable method for improving estimates. In this study, we stratified the population data by observing relative differences in peak BrAC and peak TAC values. This improved the test episode results more consistently in the single-subject dataset than in the multi-subject dataset, indicating that the variability captured by this stratification variable may be related more to within-subject factors such as skin hydration. Future studies that manipulate environmental conditions (e.g., ambient temperature, humidity) as well as skin hydration (e.g., via exercise, hydration) will help to better understand factors that affect the raw BrAC-raw TAC relationship within and across individuals. Furthermore, although it might seem that stratification according to peak BrAC vs. peak TAC is not viable with data collected outside of the laboratory or in non-research settings due to BrAC not being available for a drinking episode, obtaining this information may be possible even for lay individuals for some episodes in naturalistic drinking environments. For example, we recently reported upon a hybrid data collection system in which participants would record their naturalistic alcohol consumption on a smartphone app, which would convert the drinking diary data into eBAC and then be downloaded to the BrAC Estimator software along with the TAC data to provide improved estimates for that episode and that individual (Luczak et al., 2018). By leveraging such technology and relying on lay users’ motivation to improve their own eBrAC estimates, we will learn how much the models can be improved by individuals obtaining some BrAC estimates on their own.

The stratification variable selected in this study provides an example of how an episode-level variable can be used to fine-tune the population data to better map onto a test episode. It also is reasonable to examine person-level stratification variables, such as age, sex, ethnicity, and body fat percentage, which may affect skin layer thicknesses, alcohol absorption, and metabolism/diffusion of alcohol through the skin. If person-level factors were found to consistently affect parameters, these variables easily could be obtained and then included in the models to further refine estimates for each individual (i.e., by customizing the population used to create the parameter estimates for that particular individual by matching it to the person’s relevant individual-level characteristics). In addition, if episode-level variations like skin hydration or ambient temperature affect parameter estimates, then it is possible to incorporate weather or location data into models to include these types of environmental variation. Finally, it also is possible to include within-subject variation across episodes, such as skin temperature or hydration (e.g., the WrisTAS device has temperature and skin conductance sensors in addition to the TAC sensor). This type of a multilevel stratification process should enhance our estimation results and narrow the credible bands and intervals, with subgroups of the population who share similar person-level and/or episode-level characteristics providing more efficient estimates than those using a single population model for all people in the population.

We recognize that validity and reliability issues with the WrisTAS 7 affected our ability to use some of the data in our analyses and that this is an issue for both currently-available TAC biosensors (e.g., Clapp, Madden, Mooney, & Dahlquist, 2017; Luczak et al., 2015, Sakai, Mikulich-Gilberston, Long, & Crawley, 2006). Some of these hardware issues will be addressed by improvements made to the biosensors and wiring in newer versions of existing devices and in brand new devices that come to the market. In addition, wearing the TAC device on the ankle rather than the wrist also may reduce the likelihood of exposing the sensor to external sources of alcohol (e.g., from holding a drink, using hand sanitizer; see Croff et al., submitted to this special issue) and thus increase the validity of the raw TAC. However, many of the new devices submitted in the NIAAA Challenges that are being developed for commercial use are designed to be worn on the wrist and are less sturdy than, for example, the SCRAM CAM device that is designed to withstand tampering. Thus, it remains to be seen if TAC devices that have improved size, comfort, and visual appeal will be able to maintain a secure connection with the skin, withstand daily wear, and produce reliable and valid data over the long run.

In their current form, it seems inevitable that TAC devices will have some level of noise in the raw TAC data, including spikes from ambient alcohol, drops from loss of direct contact with the skin, and other glitches in the recording due to unknown factors. Thus, adjusting for glitches in the datafile will remain important to address (see Barnett, 2014). One mathematical way to handle this is to smooth datasets to eliminate obvious noise in the data (e.g., Clapp et al., 2017). This could be done in the laboratory when a subject’s alcohol consumption is known. It could also be done in the field by lay users who monitor their own raw TAC data—similar to using personal tracking devices that monitor exercise and allow individuals to provide information on whether they were driving vs. running vs. biking to adjust their number of steps or calories burned, individuals wearing a TAC device who wish to improve personal feedback on their drinking and eBrAC could view their raw TAC and clean their data based on knowing whether or not they consumed alcohol, exposed the device to alcohol (e.g., decided to wear perfume or use hand sanitizer), or noticed the device was not securely fit to their skin (e.g., similar to the monitoring provided by AMS for SCRAM devices). In future research, we will examine mathematical options for smoothing data and fine-tuning the raw TAC data prior to fitting it in the software program.

In summary, this study provides proof-of-concept for the use of a population-based model in place of, or in conjunction with, our earlier deterministic approach to estimating BrAC from TAC and marks a major advancement in this research program. Our previous approach required an individualized calibration process with simultaneously-collected BrAC and TAC measurements to estimate the parameters of the model for each subject in order to produce eBrAC. Although the individualized parameters may work perfectly in estimating BrAC based on TAC for a particular drinking episode, variations in the environmental and physiological conditions across drinking episodes mean these parameters may not work adequately for other drinking episodes by the same subject wearing the same device. Our novel population model approach provides many improvements for the problem of estimating BrAC/BAC based on TAC by not requiring a calibration process, being able to provide estimations for every subject in the population, and providing credible bands and intervals around these estimates. By adapting our approach, we can obtain an estimate for any drinking episode given only TAC data using a population model based on previously collected data. In future work, we aim to address remaining limitations to this method by adapting a machine learning approach for data stratification and processing based on the demographics, environmental conditions, and episode-level factors and by integrating all data obtained on each individual into fine-tuned parameters with narrow enough credible bands to provide clinically-valid and easily interpretable results. We will continue to test these models and software with a more diverse range of participants including heavier drinking samples (e.g., Fairbairn et al., submitted to this special issue), in more naturalistic drinking situations, and under more varied environmental conditions. These improvements will be packaged into an advanced version of the BrAC Estimator software that researchers and clinicians can use (without requiring knowledge of the underlying math) to produce eBrAC estimates that are scientifically and clinically useful across diverse sets of people and conditions.

• Presents a population-based model for estimating BrAC from biosensor data

• Model fit was better within a single participant than across multiple participants

• Model fit improved when stratifying episodes by BrAC-TAC relationship

• Provides initial proof-of-concept for constructing, fitting, and using this approach

• Population-based model is a promising replacement for individual calibration