Abstract
Microbially driven nitrate-dependent iron (Fe) oxidation (NDFO) in subsurface environments has been intensively studied. However, the extent to which Fe(II) oxidation is biologically catalyzed remains unclear because no neutrophilic iron-oxidizing and nitrate reducing autotroph has been isolated to confirm the existence of an enzymatic pathway. While mixotrophic NDFO bacteria have been isolated, understanding the process is complicated by simultaneous abiotic oxidation due to nitrite produced during denitrification. In this study, the relative contributions of biotic and abiotic processes during NDFO were quantified through the compilation and model-based interpretation of previously published experimental data. The kinetics of chemical denitrification by Fe(II) (chemodenitrification) were assessed, and compelling evidence was found for the importance of organic ligands, specifically exopolymeric substances secreted by bacteria, in enhancing abiotic oxidation of Fe(II). However, nitrite alone could not explain the observed magnitude of Fe(II) oxidation, with 60–75% of overall Fe(II) oxidation attributed to an enzymatic pathway for investigated strains: Acidovorax (A.) strain BoFeN1, 2AN, A. ebreus strain TPSY, Paracoccus denitrificans Pd 1222, and Pseudogulbenkiania sp. strain 2002. By rigorously quantifying the intermediate processes, this study eliminated the potential for abiotic Fe(II) oxidation to be exclusively responsible for NDFO and verified the key contribution from an additional, biological Fe(II) oxidation process catalyzed by NDFO bacteria.
Graphical Abstract
INTRODUCTION
Iron (Fe) minerals play an important role in the attenuation of contaminants within aquifer environments. The significant influence microorganisms have on Fe cycling has led to a burgeoning of research into bioremediation technologies that stimulate the formation and/or transformation of Fe minerals to remove metal(loid)s and radionuclides from groundwater.1–8 One of the most promising approaches for bioremediation relies on enhancing the activity of nitrate-dependent Fe oxidizing (NDFO) bacteria that couple Fe(ll) oxidation to nitrate reduction (Reaction 1):9,10
| 1 |
These NDFO bacteria play an important role in the generation of Fe(III) and mixed valence minerals in subsurface environments, particularly in systems low in other oxidants such as manganese and nitrite.11 Understanding how NDFO bacteria oxidize Fe(II) and how widespread this metabolic capability is among bacteria has been a focus of research since it was first observed in enrichment cultures.9,12 All neutrophilic NDFO bacterial strains isolated are mixotrophic, requiring an organic cosubstrate for growth.13–15 This complicates our understanding of NDFO as conflicting results in the literature have failed to resolve whether NDFO bacteria utilize an unknown enzymatic process to directly oxidize dissolved Fe(II) or if reactive intermediate compounds, such as nitrite or nitric oxide, abiotically oxidize Fe(II) during mixotrophic growth.16–18 While lithoautotrophic growth by neutrophilic NDFO pure-culture isolates have been described, their capacity for autotrophy has subsequently been questioned.19,20 Deciphering the NDFO mechanism using model enrichment cultures such as KS9, which is unambiguously capable of enzymatic NDFO, may also not necessarily resolve these outstanding questions as the interspecies interactions and metabolic interdependencies21 are equally challenging to untangle. Without a model NDFO autotroph and the scarcity of genetic information explaining electron transfers pathways,18 quantitatively determining the contributions from interconnected abiotic and potential biotic reactions during mixotrophic NDFO is a substantial challenge.
Although the abiotic oxidation of dissolved Fe(II) by nitrate is slow in the absence of a catalyst,22 there are pathways involving nitrite that can facilitate abiotic Fe(II) oxidation. Bacteria capable of NDFO have been found to produce appreciable quantities of nitrite only when dissolved Fe(II) is supplemented in the basal growth medium.13,14,17,23,24 This nitrite can chemically oxidize dissolved Fe(II) at a relatively fast rate, which produces ferric (oxyhydr)oxides along with nitric (NO) and nitrous oxide (N2O) gases, a process known as chemodenitrification (Reaction 2): 25–28
| 2 |
Chemodenitrification experiments performed in anoxic sterile homogeneous media, using initial nitrite concentrations that fall within the range (1–4 mM nitrite) of what many NDFO incubation experiments accumulate,13,14,23,29 showed extensive Fe(II) oxidation over 24 h.25 The potential of these abiotic reactions to oxidize Fe(II) has raised questions of whether enzymatic NDFO exists and to what extent biotic Fe(II) oxidation contributes to their overall metabolism. Measuring the rate of oxidation can be a means of determining the effect of (fast) abiotic Fe(II) oxidation. However, such measurements are often complicated by the presence of the mixed valence solid substrates, which make it difficult to determine the exact extent of oxidation and their catalytic activity.16,26,30,31 Nitrous oxide is also seldom analyzed in the headspace of NDFO cultures, which could otherwise be used to infer the extent of chemodenitrification or combined with stable isotope systematic measurements to discriminate between abiotic and biotic processes.25,32 Furthermore, it is difficult to critically review and interpret previous studies due to the fact that experimental conditions, such as the basal growth media, often differ between studies, which can influence Fe (trans)formations.17,33,34
While it is challenging to quantify NDFO-related processes experimentally due to the sensitivity of these geomicrobiological systems, developing biogeochemical models of NDFO experiments provides an effective means of quantifying the contribution of individual reaction pathways and evaluating the potential for strictly biological Fe(II) oxidation. So far, while a substantial number of experimental NDFO studies have generated comprehensive data sets, no attempts have been made to interrogate those data sets through process-based biogeochemical modeling, specifically quantifying the extent to which reactive intermediates contribute to overall dissolved Fe(II) oxidation.
The main objective of this study was therefore to derive a rigorous, data-constrained quantification of the relative contributions of biotic and abiotic processes during NDFO by integrating measured Fe(II) oxidation kinetics with suitable numerical modeling approaches based on previously generated data and conceptual models. While there is no clear evidence for the existence of an enzymatic pathway, assumptions were made on its theoretical mechanism to specifically test whether it is required to explain the overall Fe oxidation observed or if chemodenitrification alone could be exclusively responsible. Extensive data sets generated from incubations with different NDFO bacteria were sourced from the literature and used to constrain the development of the numerical implementations of different conceptual models.
METHODS
Conceptual Models of Biogeochemical Processes and Reaction Network Implementation.
To quantify the rates of chemical and biological Fe(II) oxidation, a biogeochemical model was developed using the knowledge of the physiology and respiratory processes of NDFO bacteria and translating different conceptual models into process-based numerical models. The reactive processes that were considered in the modeling framework were limited to heterotrophic nitrate reduction to nitrite (Reaction 3) and nitrite reduction to nitrogen gas (Reaction 4),
| 3 |
| 4 |
In the case of enzymatic NDFO, microbial respiration couples dissolved Fe(II) oxidation and nitrate reduction, where nitrate is assumed to be exclusively reduced to nitrite:
| 5 |
With a single exception,35 NDFO bacteria have not yet demonstrated the capability of utilizing solid-phase Fe(II), and consequently, this source of Fe(II) was ignored. The nitrite produced from Reactions 3 and 5 can react with dissolved Fe(II) as per Reaction 2.
Two plausible conceptual models were used to explore NDFO: the first (S1) assumes that dissolved Fe(II) is oxidized through both an abiotic and a biotic pathway. S1 simulations were performed as three separate simulations (S1a, S1b, and S1c) using the three separate chemodenitrification rates determined from abiotic experiments reported under differing geochemical conditions. S1a represented conditions under which Fe(II) was complexed to the greatest extent by both inorganic and organic chelators; S1b represented conditions where Fe(II) was complexed only by inorganic chelators, and S1c was where no Fe(II) complexation occurred. The second conceptual model (S2) assumed that dissolved Fe(ll) oxidation is exclusively controlled by biogenic nitrite (i.e., chemodenitrification only). Conceptual models S1a,b,c and S2 were then translated into numerical models consisting of a mix of equilibrium and kinetically controlled reactions (Table 1).
Table 1.
Overview of the Conceptual Models Employed in the Biogeochemical Model
| conceptual model |
enzymatic NDFO |
chemodenitrification conditions |
|---|---|---|
| S1a | yes | organic Fe chelators + ferrous carbonate species |
| S1b | yes | ferrous carbonate species |
| S1c | yes | aqueous ferrous iron (no complexation) |
| S2 | no | organic Fe chelators + ferrous carbonate species |
Literature Data for Developing the Biogeochemical Model.
To develop the numerical model, important biogeochemical reactions affecting dissolved Fe(II) oxidation within NDFO growth cultures were identified and relevant data was collated from three comprehensive studies by Klueglein et al.,17 Carlson et al.,24 and Chakraborty et al.14 Separately, the kinetic quantification of abiotic dissolved Fe(II) oxidation by biogenic nitrite was explored from chemodenitrification experiments performed by Kopf et al.,36 Klueglein and Kappler,16 and Jones et al.25
Model results were compared against the measured data reported in the NDFO growth culture studies. The study by Klueglein et al.17 investigated four bacterial strains including the Acidovorax strain BoFeNl, Paracoccus denitrificans, and Pseudogulbenkiania sp. strain 2002, all grown simultaneously under balanced electron donor—acceptor conditions. The data sets from studies by Carlson et al. and Chakraborty et al. explored NDFO using the strains A delafieldii strain 2AN14 and A. ebreus strain TPSY24 from the genus Acidovorax and were included here for a more robust model validation.
General Rate Law for Microbial Respiration.
Microbial respiration was modeled using the chemiosmotic model37 and irreversible thermodynamics.38 In this model, the overall microbial respiration rate, v (mol L−1 s−1), is described by eq 6:
| 6 |
where k is a rate constant (mol s−1 mol biomass−1), FD and FA are unitless kinetic factors, FT is a unitless thermodynamic factor, and X is the biomass concentration (mol L−1), in accordance with the formulation proposed by Jin and Bethke. 38 Factors FD and FA (eqs 7 and 8) control the kinetics of the electron donating ([D]/[D+]) and accepting half reactions ([A]/[A-]) as reactant and product concentrations change over time with constants KD and KA reflecting the standard free energy changes for each of the half reactions. Exponents βD and βA were assumed to equal 1 for all investigated microbial respiratory pathways.
| 7 |
| 8 |
Thermodynamic calculations (eq 9) used for evaluating the term FT in the rate expression were based on commonly used thermodynamic data39 and studies on aqueous Fe2+aq-Fe3+aq oxide redox couples.40
| 9 |
where ΔG is the Gibbs free energy of the reaction, R is the gas constant, T is absolute temperature, ᵡ is the average stoichiometric number, m is the number of ATP molecules synthesized per electron transferred (assuming 3 protons are consumed per ATP synthesized), and ΔGp is the phosphorylation potential and assumed to be 50 kJ mol−1, as in Jin and Bethke.41 The two key parameters that need to be defined for FT are ᵡ and m. However, as the mechanism for enzymatic NDFO is currently unknown, plausible values of ᵡ and m were derived on the basis of the functioning of the anaerobic respiratory cycle.42 Values for both ᵡ and m are proportional to the number of electrons transferred and in this instance were equal to 1 and 1/3, respectively, for the enzymatic NDFO reaction (Table S1).
Model Assumptions for Denitrification Processes.
The primary objective of the biogeochemical model development was to elucidate the contribution of biotic and abiotic processes on dissolved Fe(II) oxidation, not to provide a versatile, general tool to predict denitrification. Therefore, several reasonable assumptions allowed for simplification of the quantitative description of chemical and biological denitrification. (a) Microbial denitrification was modeled as a two-step process where nitrate is reduced to nitrite (Reaction 3) and nitrite, to dinitrogen gas (Reaction 4). Alternatively, nitrite could undergo chemical reduction via facile chemodenitrification.28,36,43 (b) Due to the overwhelmingly favorable thermodynamics of nitrate reduction, with acetate as the electron donor, the FT term could safely be assumed to be unity in this study. Consequently, the generalized rate law (eq 6) was simplified to Reactions 10 and 11:
| 10 |
| 11 |
where v1 and v2 are the microbial respiration rates for each step of denitrification, k1 and k2 represent the rate constants (mol s−1 mol biomass−1) for either nitrite or dinitrogen, KD and KA are unitless kinetic factors in v1 but mol L−1 for KA in v2 (i.e. half saturation constant) for electron donating and accepting reactions, X is the biomass concentration (mol L−1), and [NO2-] represents the nitrite concentration (mol L−1).
An electron balance calculation for experimental studies with BoFeN1 and Paracoccus denitrificans demonstrated that there is not enough reducing equivalents supplied from the growth medium to achieve both the observed extent of nitrate reduction and expected increases in cell density using dissolved Fe(II) oxidation alone (Table S2).13,17 It was therefore concluded that an endogenous carbon source must have been utilized and was therefore included in the conceptual/numerical modeling framework. It was assumed that, (i) once exogenous carbon (i.e., acetate) is exhausted, bacteria are capable of switching to their stored endogenous carbon source and (ii) that this stored carbon source consists of polyhydroxybutyrate (PHB), a common product for bacteria synthesizing polyhydroxyalkanoates.44 The amount of stored PHB was calculated for each strain on the basis of the amount of nitrate reduced in a nongrowth medium, where no exogenous carbon was supplied (Figure S1; PHB quantities for BoFeN1 were based off Acidovorax sp. strain 2AN, as no literature data was available). The rate of PHB driven denitrification was similarly determined from eqs 10 and 11, using calibrated parameters (Table 2). For growth experiments, where it was apparent that the bacteria did not utilize any potentially stored endogenous carbon (e.g., where nitrate is not completely consumed but all acetate is exhausted), this process was deactivated. For results presented in Figure 2, only the simulations for BoFeN1 and Pd 1222 included this process.
Table 2.
Calibrated Model Parameters for All Model Simulations of Model Variant S1a
| parameters | definition | value | unit |
|---|---|---|---|
| Parameters for Microbial Respiration of Nitrate Reduction to Nitrite | |||
| k1 | rate constant | 7.99 × 10−5 | mol s−1 mol biomass−1 |
| kA | electron acceptor kinetic factor | 2.38 × 10−5 | dimensionless |
| kD | electron donator kinetic factor | 2.18 × 10−3 | dimensionless |
| Parameters for Microbial Respiration of Nitrite Reduction to Dinitrogen | |||
| k2 | rate constant | 1.10 × 10−4 | mol s−1 mol biomass−1 |
| kA | electron acceptor kinetic factor | 3.50 × 10−6 | mol L−1 |
| kD | electron donator kinetic factor | 2.25 × 10−5 | dimensionless |
| Parameters for Microbial Enzymatic NDFO | |||
| k3 | rate constant | 5.0–12.5 × 10−5 a | mol s−1 mol biomass−1 |
| kA | electron acceptor kinetic factor | 1.00–5.00 × 10−4 a | dimensionless |
| kD | electron donator kinetic factor | 1.00–2.50 × 10−3a | mol L−1 |
| kd | encrustation inhibition | 7.59 × 10−3 | mol L−1 |
| Solution Geochemistry | |||
| k4 | chemodenitrification | rate 9.84 × 10−4 b | mol−1 L sec−1 |
| k5 | GR-CO3 oxidation rate | 4.12 × 10−5 c | sec−1 |
Figure 2.
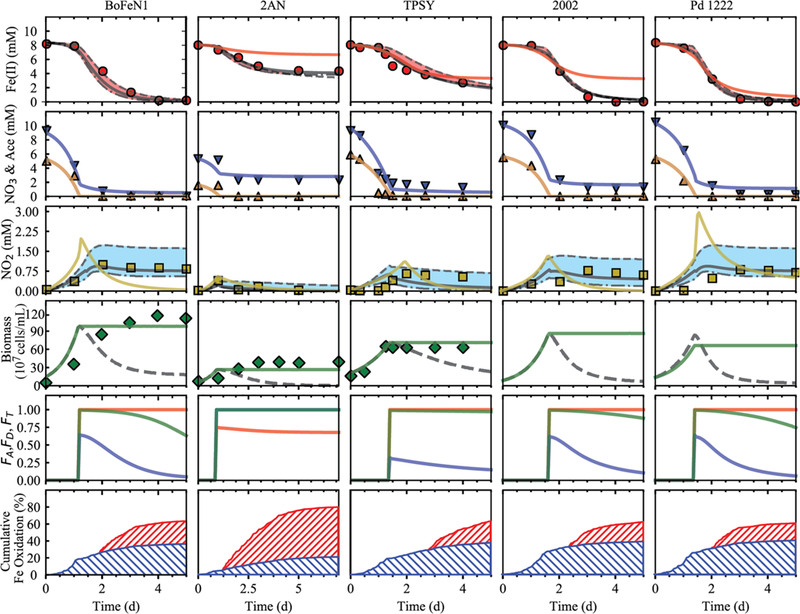
Simulation and experimental results for three Acidovorax strains BoFeNl, 2AN, and TPSY as well as Paracoccus denitrificans strain Pd 1222 and Pseudogulbenkiania strain 2002. Symbols represent observed concentrations for total Fe(II) (red circle), nitrate (blue down triangle), acetate (yellow up triangle), nitrite (yellow square), and biomass (filled green diamonds) from Klueglein and Kappler,16 Chakraborty et al.,14 and Carlson et al.24 Simulations Sla (solid black line), Slb (dashed black line), and Slc (dash dot black line) were compared against S2 (solid red/gold line). All model results are similar for parameters presented in rows 2 and 4 to 6 and are therefore excluded to improve figure clarity. The fifth row presents the kinetic factors FA and FD (red and blue, respectively) and the thermodynamic potential factor FT (green). The sixth row presents the contribution of chemodenitrification (red hatches) and enzymatic NDFO (blue hatches) to overall Fe(II) oxidation. Biomass subject to encrustation is provided (solid black line) as well as uninhibited biomass for reference (solid green line).
The stoichiometric reactions for all denitrification reactions and associated biomass growth were derived using thermodynamic and bioenergetic literature data14,23,45,46 while applying the principles described in Rittmann and McCarty (Table S2). Where the specific growth yield coefficient was unknown, it was determined from the measured net growth in biomass per mole of acetate supplied. Biomass was represented using the generic formula, C5H7O2N,47 and only assumed to increase while acetate, which was the electron donor and organic carbon source in all cases, was oxidized to carbon dioxide and bicarbonate during nitrate reduction. None of the bacteria investigated are capable of lithoautotrophic growth. Therefore, changes to biomass due to enzymatic NDFO was excluded. Biomass growth was described by eq 12:
| 12 |
where t is time (s), Y is a biomass yield coefficient (mol cells per mole of acetate), v is the microbial respiration rate (mol L−1 s−1), and DE is an encrustation term (mol L−1 s−1). A factor of 10−13 g cell−1 was used to convert from cells mL−1 to mol L−1 using the formula for biomass given above. Due to the short duration of the investigated incubation experiments,14,16,24 biomass decay was considered to be insignificant. However, cells in batch incubations capable of NDFO quickly became heavily encrusted by Fe(III) or mixed valence mineral precipitates,13,17 especially within the periplasm, inhibiting cellular activity.48 Consequently, an encrustation inhibition term was employed to account for this process (eq 13):
| 13 |
where microbial inhibition is expressed using a Monod equation49 where v2 is the microbial respiration rate for enzymatic NDFO (conceptually, the cause of Fe mineral aggregation within the periplasm), Kd is the half saturation constant, and [GR-CO3] and [FeOOH] are the concentrations (mol L−1) of green rust carbonate and goethite, respectively.
Chemodenitrification.
Chemodenitrification has been detailed in many literature reports, where Fe2+aq reduces nitrite to nitrous oxide with a 2:1 stoichiometry (Reaction 2), and ferric oxyhydroxides25,28 or mixed valence Fe minerals are produced.28,30,32 The kinetics of chemodenitrification was described using a second order rate law (eq 14):25,31
| 14 |
where k3 is the pH-dependent rate constant (L mol−1 s−1), [Fe(II)] is the dissolved Fe(II) concentration (mol L −1), t is time (s), and [NO2-] is the nitrite concentration (mol L−1). In this modeling study, chemodenitrification was defined as an extracellular abiotic oxidation process. The rate constants applied for S1a, S1b, and S1c were based on recent studies investigating chemodenitrification as a single process at pH 7.0. S1a represented conditions where dissolved Fe(II) was complexed by organic chelators and/or bicarbonate species by using rate constants reported in chemodenitrification experiments amended with 0.5 mM citrate in a bicarbonate basal medium (BBM);36 S1b represented conditions without organic chelators where chemodenitrification experiments were performed in sterile BBM solution,16 and S1c was used to explore the chemodenitrification rates for cases where no complexation of Fe(II) occurred and where experiments were not performed in BBM but instead buffered with PIPES.25 Rate constants for S1b and S1c were derived from data sets using nonlinear regression based on the decay equations suggested by Kopf et al.,36 where S1a used the rate reported in the same study for 0.5 mM citrate. Model fits using the reported and derived rate constants are given in Figure 1 and range from 2.43 × 10−4 to 1.86 × 10−3 mol L−1 s−1. For conceptual model S2, the chemodenitrification rate used in the simulations was the same as for S1a. These chemodenitrification experiments were all performed in anoxic, sterile environments at pH 7.0, similar to the NDFO growth experiments.16,17,25,36
Figure 1.
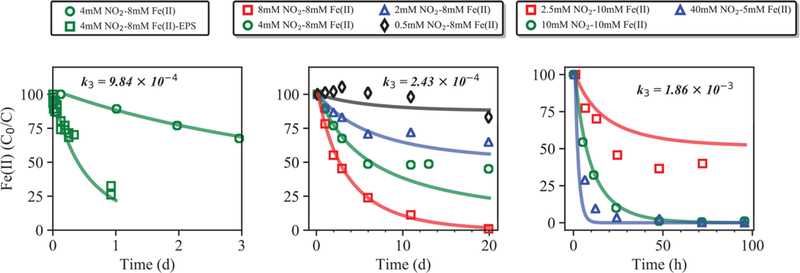
Chemodenitrification rates for experiments by Klueglein et al.17 (left); Klueglein and Kappler16 (middle); Jones et al.25 (right) (used in simulations S1a, S1b, and S1c, respectively). Experiment 4 mM NO2—8 mM Fe(II) is replotted on the left panel with 4 mM NO2—8 mM Fe(II)-EPS for reference. Chemodenitrification kinetics were described using eq 14. Observed Fe(II) concentrations are presented as a percentage of initial concentration (C/C0).
Enzymatic NDFO.
Alongside chemodenitrification, enzymatic NDFO provided an alternative biological pathway for dissolved Fe(II) oxidation. Because the existence of a dedicated Fe(II) oxidoreductase for NDFO has not been demonstrated, the enzymatic NDFO pathway in this modeling study was broadly defined as any Fe(II) oxidation pathway dependent on cells. The mechanisms outlined by Carlson et al.24 were primarily used to inform the numerical implementation of this separate respiratory process, where dissolved Fe(II) oxidation is potentially catalyzed by respiratory complexes (e.g., nitrate reductase, Nar, nitrite reductase, Nir).
Enzymatic NDFO was assumed to be suppressed until most of the acetate was consumed (<0.5 mM). This represented the point at which electrons donated by acetate to the quinone pool were thought to no longer be able to keep respiratory complexes reduced and continue dissolved Fe(II) efflux pumping from the periplasm.24 Consequently, dissolved Fe(II) accumulated and was oxidized via one or more of the potential mechanisms mentioned previously. Nitrate was assumed to be exclusively reduced to nitrite, supported by NDFO causing encrustation of the nitrite reductase enzyme within the periplasm, diminishing its activity and leading to the accumulation of nitrite.14,24,50 Direct oxidation of Fe2+aq to Fe3+aq by nitrate was not considered as it is not thermodynamically favorable (i.e., ΔG0f > 0). Instead, for thermodynamic calculations within the FT term, green rust carbonate (GR-CO3) was included as the Fe end product for enzymatic NDFO (see further explanation below, Table S3).
As the biochemical mechanism for NDFO is unknown, the parameters suggested by Jin and Bethke38 for anaerobic respiration were used. The average stoichiometric number, ᵡ, was taken to equal the number of times the rate-determining step occurs in the overall reaction, which is typically the proton translocation step during each instance of the quinone cycle.38,42 Each instance of the quinone cycle consumes a pair of electrons and translocates two protons.42 Therefore, in the case of NDFO, where dissolved Fe(II) donates a single electron, ᵡ and m are equal to 1 and 1/3, respectively (eq 15). Conceptually, this mechanism is the equivalent of assuming extracellular electron transport through a series of enzymes capable of direct dissolved Fe(II) oxidation to drive electron flow along the cell respiratory chain to reduce the quinone pool and ultimately generate proton motive force.18,21 The microbial respiration rate of NDFO was described by
| 15 |
where v3 is the microbial respiration rate for enzymatic NDFO and all parameters and units are consistent with eqs 10 and 11. The rate constants for enzymatic Fe(II) oxidation were calibrated using data from chemolithotrophic growth experiments of Acidovorax spp. strains BoFeN1, 2AN, and TPSY, where dissolved Fe(II) and stored PHB were the only available electron donors (Figure S3). Quantities of stored PHB were estimated on the basis of the amount of nitrate consumed (Table S2).
Iron Mineral Formations and Transformations.
Due to its extremely low solubility at circumneutral pH, any Fe3+aq produced from Fe(II) oxidation would immediately precipitate in the solution medium. Green rust is known to be the initial precipitate in NDFO cultures.51 Green rust carbonate (GR-CO3) was therefore included in the model and assumed to be an equilibrium phase. Furthermore, previous studies have found GR-CO3 to be an intermediate product during microbial Fe(II) oxidation,30,51 which actively transforms to more stable Fe mineral products (e.g., goethite). In our study, structural Fe(II) in GR-CO3 was modeled to abiotically reduce nitrite to ammonium while transforming to goethite.30,51 The reduction of nitrite by GR-CO3 was modeled using an overall first order kinetic rate law:
| 16 |
where k5 is the rate constant (s−1) and [Fe(II)GR] is the moles of Fe(II) within green rust. Nitrate reduction by [Fe(II)]GR was not included as it only competes with microbial respiration at higher pH.52 The rate constant k5 was calibrated using literature data from studies that investigated the rate of nitrite reduction by green rust sulfate,53 but it should be noted that rates between different green rusts are not necessarily comparable.54
Modeling Tools and Calibration.
Aqueous and solid phase biogeochemistry for all model variants were simulated with PHREEQC-3.55 Conceptual models S1a, S1b, S1c, and S2 contained 12 adjustable parameters and were initially calibrated using the heuristic particle swarm optimization56,57 method due to the severe nonlinearity common to similar geochemical models.58,59 The resulting parameter estimates were subsequently used as initial values for the Gauss-Levenberg-Marquardt method contained in PEST++60 for final calibration refinement and sensitivity analysis; this two-step procedure is consistent with Rathi et al.58 The sum of squared residuals between l65 measurements and their associated model-simulated results was used as the objective function and minimized during both steps of the calibration procedure. The observation data used to constrain the models consisted of measurements of Fe(II), acetate, nitrate, nitrite, and biomass concentrations taken from studies by Klueglein et al.,17 Klueglein and Kappler,l6 and Carlson et al.24 Table 2 provides calibrated parameters used for S1a simulations for all bacteria with further pertinent statistical information provided in Table S1.
RESULTS AND DISCUSSION
Quantification of Chemodenitrification Rate.
To determine the contributions of both abiotic and biotic Fe oxidation that occur simultaneously, it is critical to properly estimate the chemodenitrification rate. The rate constant reported by Kopf et al.36 for a chemodenitrification experiment amended with 0.5 mM citrate (36 mg C L−1, broadly equivalent to previously reported concentrations of exopolymeric substances (EPS) of ~100 mg C L−1, based on representative carbohydrate production61) provided a good model fit for the data set obtained from abiotic experiments that were sourced from an active growth experiment17 (Figure 1). Consequently, chemodenitrification was constrained using the rate constant derived for this experiment (9.84 × 10−4 mol L−1 s−1) in model S1a and provided the best overall fit for all NDFO experiments (Figure 2). Simulations of S1b, where the slower sterile BBM rate was employed (k3 = 2.43 × 10−4 mol L−1 s−1), caused nitrite concentrations to be consistently elevated above the observed concentrations in order to compensate for the lower rate constant. Alternatively, simulated nitrite concentrations for S1c that used the faster rate constant derived from a PIPES buffered solution (k3 = 1.86 × 10−4 mol L−1 s−1) were consistently below the observed nitrite concentrations.
The rate constant reported by Kopf et al.36 and used in the S1a provided the best overall fit for a number of reasons. Chemodenitrification rates from experiments reported in Jones et al. and used here in S1c were performed in a Good’s buffered medium (GBM), which differs from most NDFO growth cultures that commonly used a BBM. The different geochemical conditions between experiments, such as differences in potential mineral catalysts, are significant and likely altered the overall kinetics. The experiments performed by Klueglein and Kappler16 used a typical BBM medium, from which a chemodenitrification rate constant of 2.43 × 10−4 mol L s−1 was derived. The problem with constraining chemodenitrification based on experiments utilizing sterilized BBM is that they fail to account for biologically produced Fe(II)-chelating organic ligands,17,62,63 that are known to exist within active NDFO cultures and to enhance dissolved Fe(II) oxidation by nitrite.36 Consequently, applying the chemodenitrification rate constant from Kopf et al.36 to the experiment performed by Klueglein et al.,17 utilizing spent BBM, provides valuable insight into the potential significance of dissolved organic ligands on overall Fe(II) oxidation rates in NDFO cultures (Figure 1). EPS are secreted by many bacteria, including NDFO species, and have previously been found to strongly complex with Fe(II) and enhance its oxidation rate (Figure 1).62
Chemodenitrification produces nitrous oxide (Reaction 2); however, measured data were only available for Acidovorax spp. strain TPSY cultures.24 The nitrous oxide concentrations measured in Carlson et al.,24 while not included as observations during model calibration, were used as additional verification of the biogeochemical model. Simulation results of nitrous oxide concentrations in model variant S1a for strain TPSY broadly matched the observations, whereas S2 model results were significantly above the measured data (Figure S4). Further experimental work is required to investigate the yields of nitrous oxide in NDFO cultures for different bacteria to better constrain nitrous oxide production rates from chemodenitrification. Characterizing stable isotope systematics in NDFO cultures to determine the fraction of nitrous oxide produced via biological or chemical pathways25,32 would further elucidate the impact chemodenitrification has on nitrous oxide production in Fe rich environments.
Quantification of Iron(II) Oxidation Processes.
Model variant S2 underpredicted the rate of total Fe(II) oxidation and overpredicted nitrite concentrations by as much as 300% (Figure 2), indicating biological oxidation was contributing to Fe(II) oxidation (all model variants of S1). The maximum rate and onset of Fe(II) oxidation was better matched using variants of S1 compared to S2, lending further support to the presence of a biological Fe(II) oxidation pathway (observed max oxidation rates of 3.60, 1.22, 3.20, 4.50, and 3.60 mM d−1 versus S1a simulated max oxidation rates of 4.74, 1.94, 2.37, 4.48, and 2.96 mM d−1 for BoFeN1, 2AN, TPSY, Pd1222, and 2002, respectively). The contribution of chemodenitrification was consistent across all bacteria (Figure 2). In growth media where acetate was supplied, chemodenitrification was responsible for 35%, 39%, 25%, 37%, and 40% of the overall dissolved Fe(II) oxidized for Acidovorax spp. strains BoFeN1, TPSY, 2AN, Pseudogulbenkiania strain 2002, and Paracoccus denitrificans, respectively, with enzymatic NDFO responsible for the remaining proportion. The extent of chemodenitrification was similar across all bacteria strains, potentially indicative of biological process(es) common to most denitrifers, as has been postulated previously.24 The extent of abiotic and biotic Fe(II) oxidation processes for the lithoautotrophic Pseudogulbenkiania strain 2002 yielded similar results to those found by Kopf et al.36 In their experiments, abiotic oxidation accounted for 30–35% of the total dissolved Fe(II) oxidized using the Pseudogulbenkiania sp. strain MAI-1, which is closely related to Pseudogulbenkiania strain 2002. Acidovorax spp. Strain BoFeN1 cultures oxidized ~35% of Fe(II) via chemo-denitrification, consistent with previous studies that used Fe(II)-EDTA to discern biotic and abiotic dissolved Fe(II) oxidation contributions and found chemodenitrification played a major role.64
In all of the simulations for model variant S2, the thermodynamic drive of enzymatic Fe(II) oxidation never reached zero as long as the dissolved Fe(II) and nitrate concentrations remained above zero (Figure 2). Similarly, the concentrations of nitrate, the electron acceptor, had little impact on the overall rate, with the kinetic factor FA being consistently at or close to 1 for much of the experiment, while falling rapidly when concentrations approached zero. Consequently, enzymatic Fe(II) oxidation was controlled predominantly by mineral encrustation, particularly for strains TPSY and 2AN, as well as the kinetic factor FD. Given NDFO was never thermodynamically constrained, in the natural environment where substrate concentrations are significantly lower, enzymatic NDFO could still be an active metabolic pathway for nitrate reducing species.
Green Rust Carbonate (GR-CO3) as a Reactive Intermediate.
GR-CO3 was assumed to precipitate as the initial Fe mineral product and was an equilibrium phase in the model simulations for all bacteria.30,51 Structural Fe(II) within green rust (Fe(II)GR) was oxidized by nitrite and transformed GR-CO3 into goethite30,51,65 at a rate calibrated using experimental data collected by Hansen et al.53 The calibrated rate constant for Fe(II)GR oxidation by nitrite (4.12 × 10−5 s−1) was faster than the rate determined by Weber et al.35 for Fe(II) in magnetite and biologically reduced goethite (3.38 × 10−5 and 3.18 × 10−6 s−1, respectively) and almost 1 order of magnitude faster than Fe(II)GR oxidation by nitrate (0.4–6.6 × 10−6 s−1).54 GR was responsible for reducing between ~15% and 39% of all the nitrite formed in simulation S1a, demonstrating that it can strongly control nitrite accumulation in the growth culture.
In all model simulations, the reduction of nitrite to ammonium by GR-CO3 provided the best fit to the observed nitrite data. However, a number of different nitrogen species can be produced from the oxidation of Fe(II)GR by nitrite, including nitrous oxide, dinitrogen gas, or ammonium and is a function of the solution pH, redox potential, and concentration of phosphorus.30,54,66 While previous studies investigating the reduction of nitrite by green rust have found significant quantities of nitrous oxide,26,28 inclusion of this reaction within the S2 simulation causes excessive nitrous oxide production, significantly above the limited number of observed nitrous oxide concentrations. Etique et al.30 found total Fe(II) oxidation by biogenic nitrite produced stoichiometric amounts of ammonium in a heterotrophic nitrate reducing growth culture, geochemically similar to the cultures investigated in this study. Moreover, ammonium production during the partial reduction of nitrate by GR-CO3 has previously been found to be greater than 70% at circumneutral pH, where Fe2+aq was supplied in excess.54 Understanding the products of secondary Fe mineral reactions with biogenic nitrogen species would be improved if a full nitrogen mass balance could be calculated, but few NDFO studies have been published that include such comprehensive data.
lmplications of the Model-Derived Findings.
Although several studies had already investigated the role of biotic and abiotic Fe(II) oxidation,16,24,36,64 experimentally determining their relative contributions is challenging as both are intrinsic-cally coupled during NDFO.16,33 By translating different conceptual models into process-based numerical models, this study was able to isolate and quantify the rates of abiotic and biotic dissolved Fe(II) oxidation. Furthermore, through the model development and application, several processes were identified that require further investigation through additional targeted experiments to reduce model conceptual and parameter uncertainty. Figure 3 summarizes the conceptual model of NDFO processes that were considered in the biogeochemical model in this study. It also summarizes alternative pathways that are currently omitted from the model which could, however, potentially warrant inclusion if future experiments would demonstrate their existence and relevance.
Figure 3.
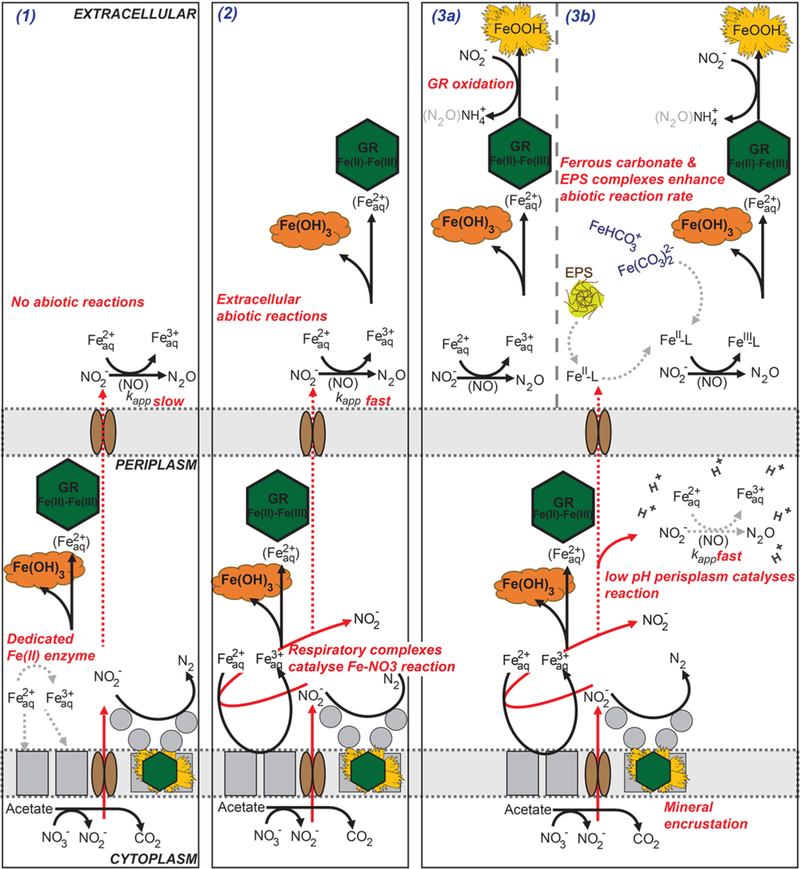
Conceptual models of NDFO with varying levels of complexity. Model (3a) represents the processes included in the biogeochemical model developed for this study. Dashed gray arrows represent processes that are either unknown or potential processes active in NDFO cultures that require ongoing investigation. (1) A dedicated Fe(II) oxidoreductase exclusively responsible for NDFO. (2) Respiratory complexes catalyze NDFO (enzymatic NDFO) with additional Fe(II) oxidation occurring extracellularly via chemodenitrification. (3a) Identical to (2) but with the inclusion of green rust oxidation by nitrite, producing goethite and ammonium. (3b) Identical to (3a) but including species-specific rates for Fe(II) carbonate/organic complexes; enhanced abiotic Fe(II) oxidation within the periplasm due to low pH.
The most pressing issue identified through our biogeochemical modeling study that demands attention is the characterization of EPS secreted by NDFO bacteria in pure cultures.17 This is a crucial knowledge gap given that EPS is commonly a combination of macromolecules that includes polysaccharides62 which are known to complex with Fe(II) and enhance chemodenitrification.36 Undertaking experiments similar to those performed by Norman et al.,62 where the role of EPS on the oxidation rate and solubility of Fe were assessed, will be beneficial to understand the extent to which components within EPS complex with Fe(II) and affect its biogeochemical cycling within NDFO cultures. These experiments could also examine whether changing the initial Fe concentrations or varying the electron-donor balance affects the composition of EPS and hence the chemodenitrification rate. Furthermore, quantifying the species specific oxidation rate of Fe carbonate species by nitrite or nitric oxide is yet to be investigated in the same vein as its oxidation rate by molecular oxygen.67 The development of a more comprehensive chemodenitrification model would improve the utility of any future biogeochemical modeling of NDFO and would allow the identification of key reactive species to assess their prevalence in natural sediments likely to inhabit NDFO bacteria. These contributions would improve the understanding of NDFO and its significance on the cycling of Fe in natural environments.
Determining the rate of enzymatic NDFO could be improved by performing NDFO growth cultures using prestarved cells. This will mitigate the potential interference of internally stored carbon within NDFO cells driving significant nitrate reduction to nitrite and causing the interfering chemodenitrification reaction even in the absence of an exogenous carbon source. The same set of prestarved batch experiments could also clarify whether nitrite is formed as a result of biological Fe(II) oxidation. Reaction kinetics may potentially be slower in prestarved culture experiments which would be beneficial for identifying the presence of reactive intermediate Fe mineral phases and their influence on Fe(II) oxidation rates.
Finally, few studies report gaseous nitrogen products nitric oxide,24 nitrous oxide,15,24 or dinitrogen gas9,29 within NDFO cultures prohibiting the calculation of the nitrogen mass balance, which would also assist in determining the potential major biotic and abiotic Fe(II) oxidation processes. Combined with stable isotope experiments, the fate of the nitrogen could be well traced to refine the conceptual model.68 Extending this model framework to a controlled well-characterized field trial, such as the one reported by Smith et al.,68 would be valuable to further understand the interplay between chemical and biological NDFO processes and the production on various nitrogen products.
Supplementary Material
ACKNOWLEDGMENTS
This study was financially supported by an Australian Postgraduate Award to J.J., CSIRO Land and Water (Australia), and the U.S. National Institute of Environmental Health Sciences (Superfund Basic Research Program grant ES010349). We thank Grant Douglas, Geoffrey Puzon, Mike Donn, and five anonymous reviewers for their constructive comments on earlier versions of this manuscript.
Footnotes
ASSOCIATED CONTENT
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.est.8b01122.
Tables including the stoichiometry of reactions used in the model, parameter uncertainty, potential enzymatic NDFO reactions, and calculated electron balances of select studies as well as additional figures including enzymatic Fe(II) oxidation rate for all strains investigated, solid green rust-Fe(II) oxidation rate calibration, simulation of Fe(II) concentrations during NDFO in Acidovorax sp. incubations, and model simulation results for nitrous oxide for Acidovorax sp. strain TPSY (PDF)
The authors declare no competing financial interest.
REFERENCES
- (1).Sun J; Chillrud SN; Mailloux BJ; Stute M; Singh R; Dong H; Lepre CJ; Bostick BC Enhanced and stabilized arsenic retention in microcosms through the microbial oxidation of ferrous iron by nitrate. Chemosphere 2016, 144, 1106–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Cutting RS; Coker VS; Telling ND; Kimber RL; Pearce CI; Ellis BL; Lawson RS; van der Laan G; Pattrick RA; Vaughan DJ; Arenholz E; Lloyd JR Optimizing Cr(Vl) and Tc(VII) remediation through nanoscale biomineral engineering. Environ. Sci. Technol. 2010, 44 (7), 2577–84. [DOI] [PubMed] [Google Scholar]
- (3).Lack JG; Chaudhuri SK; Kelly SD; Kemner KM; O’Connor SM; Coates JD Immobilization of Radionuclides and Heavy Metals through Anaerobic Bio-Oxidation of Fe(II). Appl. Environ. Microbiol. 2002, 68 (6), 2704–2710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Xiu W; Guo H; Shen J; Liu S; Ding S; Hou W; Ma J; Dong H Stimulation of Fe(II) Oxidation, Biogenic Lepidocrocite Formation, and Arsenic Immobilization by Pseudogulbenkiania Sp. Strain 2002. Environ. Sci. Technol. 2016, 50 (12), 6449–6458. [DOI] [PubMed] [Google Scholar]
- (5).Hohmann C; Winkler E; Morin G; Kappler A Anaerobic Fe(II)-Oxidizing Bacteria Show As Resistance and Immobilize As during Fe(lIl) Mineral Precipitation. Environ. Sci. Technol. 2010, 44 (1), 94–101. [DOI] [PubMed] [Google Scholar]
- (6).Katsoyiannis IA; Hug SJ; Ammann A; Zikoudi A; Hatziliontos C Arsenic speciation and uranium concentrations in drinking water supply wells in Northern Greece: Correlations with redox indicative parameters and implications for groundwater treatment. Sci. Total Environ. 2007, 383 (1), 128–140. [DOI] [PubMed] [Google Scholar]
- (7).Omoregie EO; Couture R-M; Van Cappellen P; Corkhill CL; Charnock JM; Polya DA; Vaughan D; Vanbroekhoven K; Lloyd JR Arsenic Bioremediation by Biogenic Iron Oxides and Sulfides. Appl. Environ. Microbiol. 2013, 79 (14), 4325–4335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Sun J; Chillrud SN; Mailloux BJ; Bostick BC Situ Magnetite Formation and Long-Term Arsenic Immobilization under Advective Flow Conditions. Environ. Sci. Technol. 2016, 50 (18), 10162–10171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Straub KL; Benz M; Schink B; Widdel F Anaerobic, nitrate-dependent microbial oxidation of ferrous iron. Appl. Environ. Microbiol. 1996, 62 (4), 1458–1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Hafenbradl D; Keller M; Dirmeier R; Rachel R; Roßnagel P; Burggraf S; Huber H; Stetter KO Ferroglobus placidus gen. nov., sp. nov., a novel hyperthermophilic archaeum that oxidizes Fe2+ at neutral pH under anoxic conditions. Arch. Microbiol. 1996, 166 (5), 308–314. [DOI] [PubMed] [Google Scholar]
- (11).Kappler A; Straub KL Geomicrobiological Cycling of Iron. Rev. Mineral. Geochem. 2005, 59 (1), 85–108. [Google Scholar]
- (12).Straub KL; Schönhuber WA; Buchholz-Cleven BEE; Schink B Diversity of Ferrous Iron-Oxidizing, Nitrate-Reducing Bacteria and their Involvement in Oxygen-Independent Iron Cycling. Geomicrobiol. J. 2004, 21 (6), 371–378. [Google Scholar]
- (13).Kappler A; Schink B; Newman DK Fe(III) mineral formation and cell encrustation by the nitrate-dependent Fe(II)- oxidizer strain BoFeN1. Geobiology 2005, 3 (4), 235–245. [Google Scholar]
- (14).Chakraborty A; Roden EE; Schieber J; Picardal F Enhanced Growth of Acidovorax sp. Strain 2AN during Nitrate- Dependent Fe(II) Oxidation in Batch and Continuous-Flow Systems. Appl. Environ. Microbiol. 2011, 77 (24), 8548–8556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Benz M; Brune A; Schink B Anaerobic and aerobic oxidation of ferrous iron at neutral pH by chemoheterotrophic nitrate-reducing bacteria. Arch. Microbiol. 1998, 169 (2), 159–165. [DOI] [PubMed] [Google Scholar]
- (16).Klueglein N; Kappler A Abiotic oxidation of Fe(II) by reactive nitrogen species in cultures of the nitrate-reducing Fe(II) oxidizer Acidovorax sp. BoFeN1 - questioning the existence of enzymatic Fe(II) oxidation. Geobiology 2013, 11 (2), 180–190. [DOI] [PubMed] [Google Scholar]
- (17).Klueglein N; Zeitvogel F; Stierhof Y-D; Floetenmeyer M; abiotic Fe(II) oxidation and cell encrustation during nitrate reduction by denitrifying bacteria. Appl. Environ. Microbiol. 2014, 80, 1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Carlson HK; Clark IC; Melnyk RA; Coates JD Towards a Mechanistic Understanding of Anaerobic Nitrate Dependent Iron Oxidation: Balancing Electron Uptake and Detoxification. Front. Microbiol. 2012, 3, 57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Ishii S; Joikai K; Otsuka S; Senoo K; Okabe S Denitrification and Nitrate-Dependent Fe(II) Oxidation in Various Pseudogulbenkiania Strains. Microbes and Environments 2016, 31 (3), 293–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Byrne-Bailey KG; Weber KA; Coates JD Draft Genome Sequence of the Anaerobic, Nitrate-Dependent, Fe(II)-Oxidizing Bacterium Pseudogulbenkiania ferrooxidans Strain 2002. J. Bacterioi 2012, 194 (9), 2400–2401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).He S; Tominski C; Kappler A; Behrens S; Roden EE Metagenomic Analyses of the Autotrophic Fe(II)-Oxidizing, Nitrate- Reducing Enrichment Culture KS. Appl Environ. Microbiol. 2016, 82 (9), 2656–2668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Ottley CJ; Davison W; Edmunds WM Chemical catalysis of nitrate reduction by iron (II). Geochim. Cosmochim. Acta 1997, 61, (9) 1819–1828. [Google Scholar]
- (23).Weber KA; Pollock J; Cole KA; O’Connor SM; Achenbach LA; Coates JD Anaerobic Nitrate-Dependent Iron(II) Bio-Oxidation by a Novel Lithoautotrophic Betaproteobacterium, Strain 2002. Appl. Environ. Microbiol. 2006, 72 (1), 686–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Carlson HK; Clark IC; Blazewicz SJ; Iavarone AT; Coates JD Fe(II) Oxidation Is an Innate Capability of Nitrate- Reducing Bacteria That Involves Abiotic and Biotic Reactions. J. Bacteriol. 2013, 195 (14), 3260–3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Jones LC; Peters B; Lezama Pacheco JS; Casciotti KL; Fendorf S Stable Isotopes and Iron Oxide Mineral Products as Markers of Chemodenitrification. Environ. Sci. Technol. 2015, 49 (6), 3444–3452. [DOI] [PubMed] [Google Scholar]
- (26).Grabb KC; Buchwald C; Hansel CM; Wankel SD A dual nitrite isotopic investigation of chemodenitrification by mineral-associated Fe(II) and its production of nitrous oxide. Geochim. Cosmochim. Acta 2017, 196, 388–402. [Google Scholar]
- (27).Sørensen J; Thorling L Stimulation by lepidocrocite (7- FeOOH) of Fe(II)-dependent nitrite reduction. Geochim. Cosmochim. Acta 1991, 55 (5), 1289–1294. [Google Scholar]
- (28).Kampschreur MJ; Kleerebezem R; de Vet WWJM; van Loosdrecht MCM Reduced iron induced nitric oxide and nitrous oxide emission. Water Res. 2011, 45 (18), 5945–5952. [DOI] [PubMed] [Google Scholar]
- (29).Zhao L; Dong H; Kukkadapu R; Agrawal A; Liu D; Zhang J; Edelmann RE Biological oxidation of Fe(II) in reduced nontronite coupled with nitrate reduction by Pseudogulbenkiania sp. Strain 2002. Geochim. Cosmochim. Acta 2013, 119, 231–247. [Google Scholar]
- (30).Etique M; Jorand FPA; Zegeye A; Gregoire B; Despas C; Ruby C Abiotic Process for Fe(II) Oxidation and Green Rust Mineralization Driven by a Heterotrophic Nitrate Reducing Bacteria (Klebsiella mobilis). Environ. Sci. Technol. 2014, 48 (7), 3742–3751. [DOI] [PubMed] [Google Scholar]
- (31).Tai Y-L; Dempsey BA Nitrite reduction with hydrous ferric oxide and Fe(II): Stoichiometry, rate, and mechanism. Water Res. 2009, 43 (2), 546–552. [DOI] [PubMed] [Google Scholar]
- (32).Buchwald C; Grabb K; Hansel CM; Wankel SD Constraining the role of iron in environmental nitrogen transformations: Dual stable isotope systematics of abiotic NO2- reduction by Fe(II) and its production of N2O. Geochim. Cosmochim. Acta 2016, 186, 1–12. [Google Scholar]
- (33).Picardal F Abiotic and microbial interactions during anaerobic transformations of Fe(II) and NOx. Front. Microbiol. 2012, 3, 112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Larese-Casanova P; Haderlein SB; Kappler A Biomineralization of lepidocrocite and goethite by nitrate-reducing Fe(II)- oxidizing bacteria: Effect of pH, bicarbonate, phosphate, and humic acids. Geochim. Cosmochim. Acta 2010, 74 (13), 3721–3734. [Google Scholar]
- (35).Weber KA; Picardal FW; Roden EE Microbially Catalyzed Nitrate-Dependent Oxidation of Biogenic Solid-Phase Fe(II) Compounds. Environ. Sci. Technol. 2001, 35 (8), 1644–1650. [DOI] [PubMed] [Google Scholar]
- (36).Kopf SH; Henny C; Newman DK Ligand-Enhanced Abiotic Iron Oxidation and the Effects of Chemical versus Biological Iron Cycling in Anoxic Environments. Environ. Sci. Technol. 2013, 47 (6), 2602–2611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Mitchell P Coupling of Phosphorylation to Electron and Hydrogen Transfer by a Chemi-Osmotic type of Mechanism. Nature 1961, 191, 144. [DOI] [PubMed] [Google Scholar]
- (38).Jin Q; Bethke CM A New Rate Law Describing Microbial Respiration. Appl. Environ. Microbiol. 2003, 69 (4), 2340–2348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Stumm W; Morgan JJ Aquatic Chemistry, 3rd ed; John Wiley & Sons: New York, 1995. [Google Scholar]
- (40).Gorski CA; Edwards R; Sander M; Hofstetter TB; Stewart SM Thermodynamic Characterization of Iron Oxide- Aqueous Fe2+ Redox Couples. Environ. Sci. Technol. 2016, 50 (16), 8538–8547. [DOI] [PubMed] [Google Scholar]
- (41).Jin Q; Bethke CM Kinetics of Electron Transfer through the Respiratory Chain. Biophys. J. 2002, 83 (4), 1797–1808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Jin Q; Bethke CM Predicting the rate of microbial respiration in geochemical environments. Geochim. Cosmochim. Acta 2005, 69 (5), 1133–1143. [Google Scholar]
- (43).Moraghan JT; Buresh R J. Chemical reduction of nitrite and nitrous oxide by ferrous iron. Soil Sci. Soc. Am. J. 1977, 41 (1), 47–50. [Google Scholar]
- (44).Barak Y; van Rijn J Atypical Polyphosphate Accumulation by the Denitrifying Bacterium Paracoccus denitrificans. Appl. Environ. Microbiol. 2000, 66 (3), 1209–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (45).Muehe EM; Gerhardt S; Schink B; Kappler A Ecophysiology and the energetic benefit of mixotrophic Fe(II) oxidation by various strains of nitratereducing bacteria. FEMS Microbiol. Ecol. 2009, 70 (3), 335–343. [DOI] [PubMed] [Google Scholar]
- (46).Strohm TO; Griffin B; Zumft WG; Schink B Growth Yields in Bacterial Denitrification and Nitrate Ammonification. Appl. Environ. Microbiol. 2007, 73 (5), 1420–1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Rittmann BE; McCarty PL Environmental Biotechnology: Principles and Applications; McGraw-Hill: Boston, 2001. [Google Scholar]
- (48).Miot J; Remusat L; Duprat E; Gonzalez A; Pont S; Poinsot M Fe biomineralization mirrors individual metabolic activity in a nitrate-dependent Fe(II)-oxidizer. Front. Microbiol. 2015, 6, 879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Monod J The Growth of Bacterial Cultures. Annu. Rev. Microbiol. 1949, 3 (1), 371–394. [Google Scholar]
- (50).Miot J; Benzerara K; Morin G; Kappler A; Bernard S; Obst M; Ferard C; Skouri-Panet F; Guigner J-M; Posth N; Galvez M; Brown GE Jr; Guyot F Iron biomineralization by anaerobic neutrophilic iron-oxidizing bacteria. Geochim. Cosmochim. Acta 2009, 73 (3), 696–711. [Google Scholar]
- (51).Pantke C; Obst M; Benzerara K; Morin G; Ona-Nguema G; Dippon U; Kappler A Green Rust Formation during Fe(II) Oxidation by the Nitrate-Reducing Acidovorax sp. Strain BoFeN1. Environ. Sci. Technol. 2012, 46 (3), 1439–1446. [DOI] [PubMed] [Google Scholar]
- (52).Hansen HCB; Koch CB; Nancke-Krogh H; Borggaard OK; Sørensen J Abiotic Nitrate Reduction to Ammonium: Key Role of Green Rust. Environ. Sci. Technol. 1996, 30 (6), 2053–2056. [Google Scholar]
- (53).Hansen HCB; Borggaard OK; S0rensen J Evaluation of the free energy of formation of Fe(II)-Fe(III) hydroxide-sulphate (green rust) and its reduction of nitrite. Geochim. Cosmochim. Acta 1994, 58 (12), 2599–2608. [Google Scholar]
- (54).Etique M; Zegeye A; Gregoire B; Carteret C; Ruby C Nitrate reduction by mixed iron(II-III) hydroxycarbonate green rust in the presence of phosphate anions: The key parameters influencing the ammonium selectivity. Water Res. 2014, 62, 29–39. [DOI] [PubMed] [Google Scholar]
- (55).Parkhurst DL; Appelo CAJ Description of input and examples for PHREEQC version 3—A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations: U.S. Geological Survey Techniques and Methods; USGS: Reston, VA, 2013; book 6, chap. A43, 497 p.; available only at https://pubs.usgs.gov/tm/06/a43/. [Google Scholar]
- (56).Eberhart R; Kennedy J A new optimizer using particle swarm theory. In Sixth International Symposium on Micro Machine and Human Science; IEEE Publishing: Piscataway, NJ, 1995; pp 39–43. [Google Scholar]
- (57).Kennedy JF Swarm intelligence; Morgan Kaufmann Publishers: San Francisco, 2001. [Google Scholar]
- (58).Rathi B; Neidhardt H; Berg M; Siade A; Prommer H Processes governing arsenic retardation on Pleistocene sediments: Adsorption experiments and model-based analysis. Water Resour. Res. 2017, 53 (5), 4344–4360. [Google Scholar]
- (59).Rawson J; Prommer H; Siade A; Carr J; Berg M; Davis JA; Fendorf S Numerical Modeling of Arsenic Mobility during Reductive Iron-Mineral Transformations. Environ. Sci. Technol 2016, 50 (5), 2459–2467. [DOI] [PubMed] [Google Scholar]
- (60).Welter DE; White JT; Hunt RJ; Doherty JE Approaches in highly parameterized inversion: PEST++ Version 3, a Parameter ESTimation and uncertainty analysis software suite optimized for large environmental models: U.S. Geological Survey Techniques and Methods; USGS: Reston, VA, 2015; book 7, section C12, 54 p. [Google Scholar]
- (61).Aquino SF; Stuckey DC Soluble microbial products formation in anaerobic chemostats in the presence of toxic compounds. Water Res. 2004, 38 (2), 255–266. [DOI] [PubMed] [Google Scholar]
- (62).Norman L; Worms IAM; Angles E; Bowie AR; Nichols CM; Ninh Pham A; Slaveykova VI; Townsend AT; David Waite T; Hassler CS The role of bacterial and algal exopolymeric substances in iron chemistry. Mar. Chem. 2015, 173, 148–161. [Google Scholar]
- (63).Schmid G; Zeitvogel F; Hao L; Ingino P; Floetenmeyer M; Stierhof YD; Schroeppel B; Burkhardt CJ; Kappler A; Obst M 3-D analysis of bacterial cell-(iron)mineral aggregates formed during Fe(II) oxidation by the nitrate-reducing Acidovorax sp. strain BoFeN1 using complementary microscopy tomography approaches. Geobiology 2014, 12 (4), 340–361. [DOI] [PubMed] [Google Scholar]
- (64).Klueglein N; Picardal F; Zedda M; Zwiener C; Kappler A Oxidation of Fe(II)-EDTA by nitrite and by two nitrate-reducing Fe(II)-oxidizing Acidovorax strains. Geobiology 2015, 13 (2), 198–207. [DOI] [PubMed] [Google Scholar]
- (65).Feng X; Wang X; Zhu M; Koopal LK; Xu H; Wang Y; Liu F Effects of phosphate and silicate on the transformation of hydroxycarbonate green rust to ferric oxyhydroxides. Geochim. Cosmochim. Acta 2015, 171, 1–14. [Google Scholar]
- (66).Lu Y; Yang X; Wu Z; Xu L; Xu Y; Qian G A novel control strategy for N2O formation by adjusting Eh in nitrite/Fe(II-III) carbonate green rust system. Chem. Eng. J. 2016, 304, 579–586. [Google Scholar]
- (67).King DW Role of Carbonate Speciation on the Oxidation Rate of Fe(II) in Aquatic Systems. Environ. Sci. Technol. 1998, 32 (19), 2997–3003. [Google Scholar]
- (68).Smith RL; Kent DB; Repert DA; Bӧhlke JK Anoxic nitrate reduction coupled with iron oxidation and attenuation of dissolved arsenic and phosphate in a sand and gravel aquifer. Geochim. Cosmochim. Acta 2017, 196, 102–120. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


